Tumor Margin Classification of Head and Neck Cancer Using Hyperspectral Imaging and Convolutional Neural Networks

Abstract

One of the largest factors affecting disease recurrence after surgical cancer resection is negative surgical margins. Hyperspectral imaging (HSI) is an optical imaging technique with potential to serve as a computer aided diagnostic tool for identifying cancer in gross ex-vivo specimens. We developed a tissue classifier using three distinct convolutional neural network (CNN) architectures on HSI data to investigate the ability to classify the cancer margins from ex-vivo human surgical specimens, collected from 20 patients undergoing surgical cancer resection as a preliminary validation group. A new approach for generating the HSI ground truth using a registered histological cancer margin is applied in order to create a validation dataset. The CNN-based method classifies the tumor-normal margin of squamous cell carcinoma (SCCa) versus normal oral tissue with an area under the curve (AUC) of 0.86 for inter-patient validation, performing with 81% accuracy, 84% sensitivity, and 77% specificity. Thyroid carcinoma cancer-normal margins are classified with an AUC of 0.94 for inter-patient validation, performing with 90% accuracy, 91% sensitivity, and 88% specificity. Our preliminary results on a limited patient dataset demonstrate the predictive ability of HSI-based cancer margin detection, which warrants further investigation with more patient data and additional processing techniques to optimize the proposed deep learning method.

1. INTRODUCTION

Each year about 16 per 100,000 males and 6 per 100,000 females are diagnosed with cancer of the oral cavity, of which approximately 90% are squamous cell carcinoma (SCCa) at sites including the surfaces of the lips, gums, mouth, plate, and anterior two-thirds of the tongue.¹ The safest margin for surgical resection of oral cancer is typically considered 5 mm from the permanent edge of the tumor.² Recently, the definition of a negative margin was proposed to 2.2 mm, decreasing from the previous standard of 5 mm for the oral tongue.³ Another study found cuts within 1 mm of oral cavity SCCa tumor margins are associated with significantly increased recurrence rates.⁴ Additionally, the incidence rate for differentiated thyroid carcinomas in the United States is approximately 20 per 100,000 females and 6 per 100,000 males, predominantly papillary and follicular carcinoma.⁵ Similarly, negative resection margins are the primary prevention of disease recurrence for thyroid cancer.⁶ This study aims to investigate the ability of HSI using convolutional neural networks to classify tissue at the cancer margin. If proven reliable, this method could help surgeons achieve negative margins during intraoperative cancer resection for successful patient remission.

2. METHODS

2.1. Experimental Design

In collaboration with the Otolaryngology Department and the Department of Pathology and Laboratory Medicine at Emory University Hospital Midtown, freshly excised, ex-vivo tissue samples were obtained from previously consented patients undergoing surgical cancer resection.^7,8 Three tissue samples were collected from each patient: a sample of the tumor, a normal tissue sample, and a sample at the tumor-normal interface. Tissues were kept cold and imaged fresh. Twenty head and neck cancer patients were included in this study and divided into two groups, comprising thyroid gland tissue and oral cavity tissue. Tissue samples that are entirely tumor and entirely normal will be used for the training dataset, and the sample that contains the tumor-normal margin will be used for the validation dataset.

The average patient age was 51, 60% were men and 40% were women, and 25% had smoking history. Nine patients with SCCa of the oral cavity or aerodigestive tract comprised the SCCa group. For this group, tissues were obtained from the maxillary sinus, mandibular mucosa, hard palate, buccal mucosa, and oropharynx. Eleven patients with differentiated thyroid carcinoma made up with thyroid group, which was comprised of 8 cases of papillary thyroid carcinoma and 3 cases of medullary thyroid carcinoma.

2.2. Hyperspectral Imaging and Preprocessing

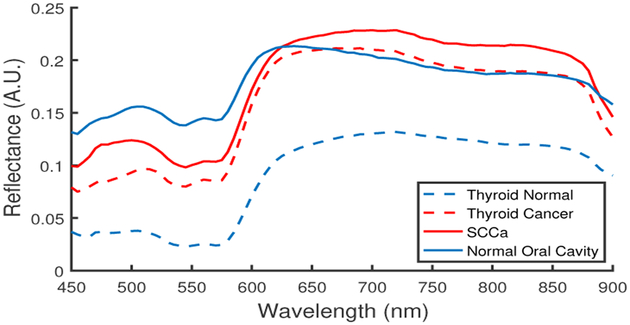
The 3D HSI cubes (hypercubes) were acquired from 450 to 900 nm at 5 nm spectral frequency using a previously described CRI Maestro imaging system (Perkin Elmer Inc., Waltham, Massachusetts).^9–11 In summary, the HSI system is comprised of a light source, tunable filter, and camera that captures 1040 by 1,392 pixel resolution and 25 μm per pixel spatial resolution.¹² The HS data were normalized at each wavelength, λ, over all pixels, i and j, by subtracting the inherent dark current (captured by imaging with a closed camera shutter) and dividing by a white reference disk according to (1). Figure 1 shows the normalized reflectance spectra for cancer and normal tissues from both groups, tissue obtained from the aerodigestive tract and thyroid tissue.

Figure 1:

Normalized reflectance spectra of thyroid and SCCa tissue samples

$$I_{norm}(\lambda ,i,j)=\frac{I_{raw}(\lambda ,i,j)-I{}_{darkcurrent}(\lambda ,i,j)}{I_{whiteref}(\lambda ,i,j)-I_{darkcurrent}(\lambda ,i,j)}$$ (1)

Specular glare is created on the tissue surfaces due to wet surfaces completely reflecting incident light. Glare pixels do not contain useful spectral information for tissue classification and are hence removed from each HSI by converting the RGB composite image of the hypercube to gray scale and experimentally setting an intensity threshold that sufficiently removes the glare pixels, assessed by visual inspection.

2.3. Histology and Gold Standard

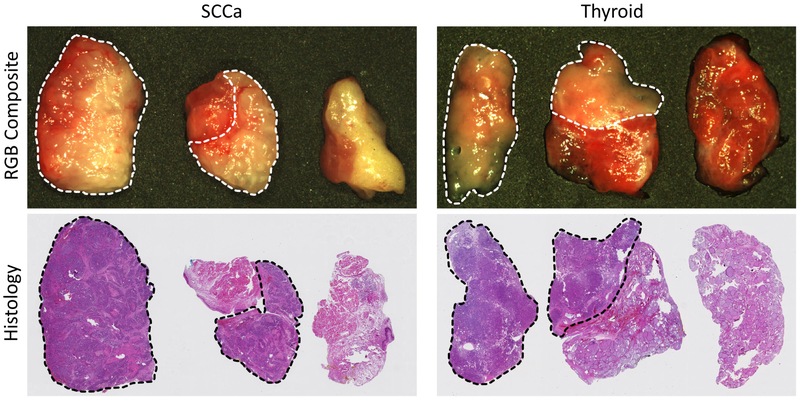
After HSI are acquired from the patient ex-vivo tissue samples, tissues are fixed in formalin, stained with haemotoxylin and eosin, and scanned. A head and neck specialized, certified pathologist (J.V.L) outlined the cancer margin on the digital slides using Aperio ImageScope (Leica Biosystems Inc, Buffalo Grove, IL, USA). The histological images serve as the ground truth for the experiment, as shown in Figure 2, but registration is necessary to create gold-standard masks for HSI.^13–15

Figure 2:

Representative HSI-RGB composite and histological images from oral cavity with SCCa (left) and thyroid tissue with papillary thyroid carcinoma (right) patients. Three tissue samples are collected from each patient: tumor, tumor-normal cancer-margin, and normal. The dotted line indicates cancer margin on RGB and histology images.

The histological cancer margin is registered to the respective gross HSI using a pipeline (Figure 3) involving affine followed by deformable demons registration to produce a binary mask of three specimens (tumor, tumor-normal, and normal). Registration is performed separately using MATLAB (MathWorks Inc, Natick, MA, USA). The demons registration is performed using five pyramid levels with one thousand iterations per pyramid level and an accumulated field smoothing value of 0.5.^16,17 This binary mask is used to create a gold-standard for training and a validation group for testing the CNN.

Figure 3:

Flowchart of registration pipeline for obtaining the cancer-margin of HSI samples, using digitized histopathology slides as the gold-standard.

A patch-based method is implemented to train the CNN in batches. Patches are produced from each HSI after pre-processing using a stride of 20 pixels to create overlapping patches. Patches are constructed to exclude any glare pixels to produce patches that are 25 × 25 × 91 pixels and are labeled corresponding to the center pixel. Patches from the tumor and normal tissue samples are used for the training group, and the validation group is comprised of patches from the tumor-normal margin sample.

2.4. Convolutional Neural Network

Patient HS data were used to train and test a convolutional neural network (CNN) classifier, implemented in TensorFlow.¹⁸ Three distinct network architectures of CNN were used: 2D-CNN, 3D-CNN, and Inception CNN, which was inspired by the inception module that concatenates simultaneous convolutions of different kernel sizes.¹⁹ For all architectures, convolutional layers were calculated using the valid specification, and the crossentropy loss was reduced using AdaDelta, adaptive learning.²⁰ Training was performed using a batch method, feeding 5 patches into the network every step, and then optimizing loss. Due to a limited training sample size, validation performance was evaluated every one-thousand steps, and additionally the training data were randomly shuffled for improved training. Each iteration of training was run for twenty-thousand steps, and the best validation performance was used. Group parameters between validation methods were optimized for each group and varied slightly due to small sample sizes, see Table 1.

Table 1:

Description and parameters used for each CNN architecture and validation group (intra- or inter-patient)

	Inter-pt. thyroid	Intra-pt. thyroid	Inter-pt. SCCa	Intra-pt. SCCa
CNN Architecture	3D-CNN	2D-CNN	3D-Inception CNN	2D-CNN
Kernel Size	3 × 3 × 11	5 × 5	Multiple	5 × 5
Learning Rate	0.005	0.005	0.005	0.005
AdaDelta ρ	0.90	0.90	0.85	0.875
AdaDelta ε	1 × 108	1 × 10−8	1 × 108	1 × 104
No. Conv. Layers	4	4	15	4
Total Conv. Filters.	100	328	350	328
Batch Size	5	5	5	5
Dropout	0.7	0.6	0.7	0.7
Initial Neuron Bias	0.05	0.05	0.07	0.05

The 2D-CNN architecture was inspired by the AlexNet architecture.²¹ It consisted of four convolutional layers, which were performed by a 5 × 5 kernel with convolutional filters sizes of 100, 88, 76, and 64, respectively. The convolutional layers were followed by two fully connected layers comprised of 500 and 250 neurons each. A drop-out rate of 0.6 was applied after each layer. The final, soft-max layer converted the connections down to two classes. Training was performed with a learning rate of 0.005 using the AdaDelta optimizer for loss.

The 3D-CNN architecture was implemented similarly to the 2D-CNN architecture. It consisted of four convolutional layers, with a 2 × 2 max-pool after the second and fourth convolutional layers. Convolutions were performed by a 3 × 3 × 11 kernel with convolutional filters sizes of 40, 30, 20, and 10, respectively. The convolutional layers were followed by two fully connected layers comprised of 200 and 100 neurons each. A drop-out rate of 0.7 was applied after each layer. The final, soft-max layer converted the connections down to two classes. Training was performed with a learning rate of 0.005 using the AdaDelta optimizer for loss.

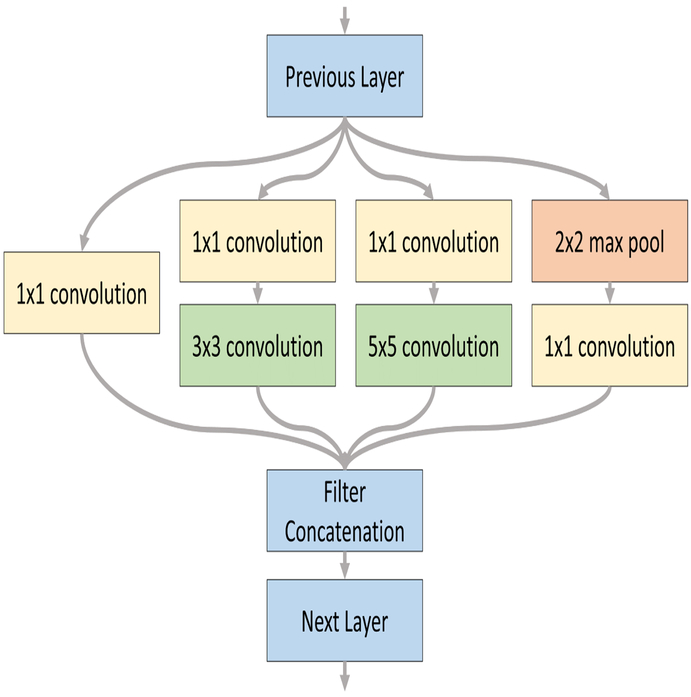
The 2D inception-based CNN architecture was constructed by expanding the AlexNet architecture with the inception module.¹⁹ As shown in Figure 4, the inception module simultaneously performs a convolution with a 1 × 1 kernel, convolutions with 3 × 3 and 5 × 5 kernels following the 1 × 1 convolution, and lastly a 2 × 2 max pool followed by a 1 × 1 convolution. After performing the individual operations, the outputs filters of each are concatenated in the features dimension and used as input for the next convolutional layer. The overall 2D inception CNN architecture used consisted of two inception modules followed by a convolutional layer with 9-by-9 kernel. Convolutional filters sizes were 100, 88, 76, and 64, respectively. The convolutional layers were followed by two fully connected layers comprised of 500 and 250 neurons each. A drop-out rate of 0.6 was applied after each layer. The final, soft-max layer converted the connections down to two classes. Training was performed with a learning rate of 0.005 using the AdaDelta optimizer for loss.

Figure 4:

Inception module in two-dimensional form.

The 3D-CNN inception architecture consisted of two 3D convolutional layers followed by two inception modules followed by a final 3D convolutional layer. To adjust the inception module to 3D form, the kernel size used for convolutions or max pool was simply extended in the z-direction by the same length as the 2D kernel. Convolutional filters sizes were 40, 30, 20, and 10, respectively. The convolutional layers were followed by two fully connected layers comprised of 500 and 250 neurons each. A drop-out rate of 0.6 was applied after each layer. The final, soft-max layer converted the connections down to two classes. Training was performed with a learning rate of 0.005 using the AdaDelta optimizer for loss.

2.5. Validation

A separate validation dataset was used to evaluate performance of the CNN, after training on the training dataset. Intra-patient classification was performed by training on patches obtained from tumor and normal samples of all patients and testing on the tumor-normal margin of an in-group patient tumor-normal sample. Inter-patient classification was performed by training on patches obtained from tumor and normal samples of all patients except the held-out testing patient, and testing on that corresponding patients tumor-normal margin. The CNN classification performance was evaluated using leave-one-out validation to obtain average performances. Therefore, nine iterations of leave-one-out validation were performed for the thyroid group, and seven iterations were performed for the SCCa group. To assess classifier performance, accuracy, sensitivity, and specificity were calculated according to equations (2)-(4).

$$\text{Accuracy=}\frac{\text{True Positives + True Negatives}}{\text{Total Number of Samples}}$$ (2)

$$\text{Sensitivity=}\frac{\text{True Positives}}{\text{True Positives + False Negatives}}$$ (3)

$$\text{Specificity=}\frac{\text{True Negatives}}{\text{True Negatives + False Positives}}$$ (4)

The final output of the CNN assigns a probability of each patch belonging to either class, which adds to 100%. Using the best performing trained model, the validation group is classified to obtain probabilities, which are used to construct a receiver operating characteristic (ROC) curve. Therefore, nine ROC curves were obtained for the thyroid group and eight were obtained for the SCCa group; one for each patient. From each ROC curve, the area under the curve (AUC) is calculated, and accuracy, sensitivity, and specificity are calculated from the threshold at the optimal operating point.

To compare the performance of the CNN to other machine learning algorithms, the same training and testing data were used to evaluate the performance of three classifiers: support vector machines, ensemble linear discriminant analysis, and random forest. In MATLAB, the pixel reflectance values of each patch were averaged per wavelength to create a 91 element one dimensional spectra vector for each patch. Training data were used to optimize model parameters using internal cross-validation, and testing data were withheld until after training. Support vector machines (SVM) was performed with both a linear and radial basis function (RBF) kernel.^22–24 Ensemble linear discriminant analysis (LDA) was performed with up to 500 learners, using the optimal number of learners determined by cross-validation.¹⁰ Random forest algorithm was implemented using bootstrap-aggregated (bagged) decision trees with a random subset of predictors at each decision split.^25,26

3. RESULTS

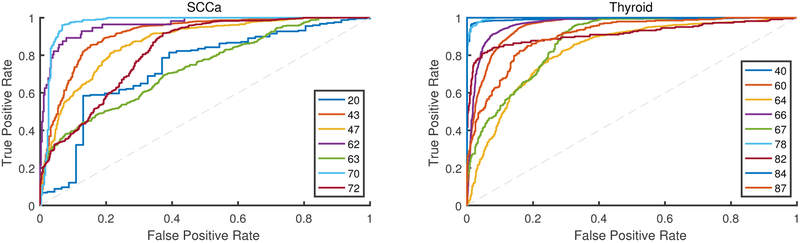
Eleven thyroid patients were used to train the CNN, which was tested on the thyroid validation group, comprised of 9 thyroid patients. Two thyroid patients were not used for testing because they did not have a complete tumor, normal, and tumor-normal sample, so they were used only to expand the training dataset. A representative patient classification is shown in Figure 5. Thyroid carcinoma cancer margins are classified with an AUC of 0.94 and accuracy of 89% for intra-patient validation using the 2D-CNN architecture. Thyroid carcinoma interpatient cancer margins are classified with an AUC of 0.94 and accuracy of 90% using the 3D-CNN architecture, see Table 2 for detailed results shown with standard deviations and Figure 6 for ROC curves.

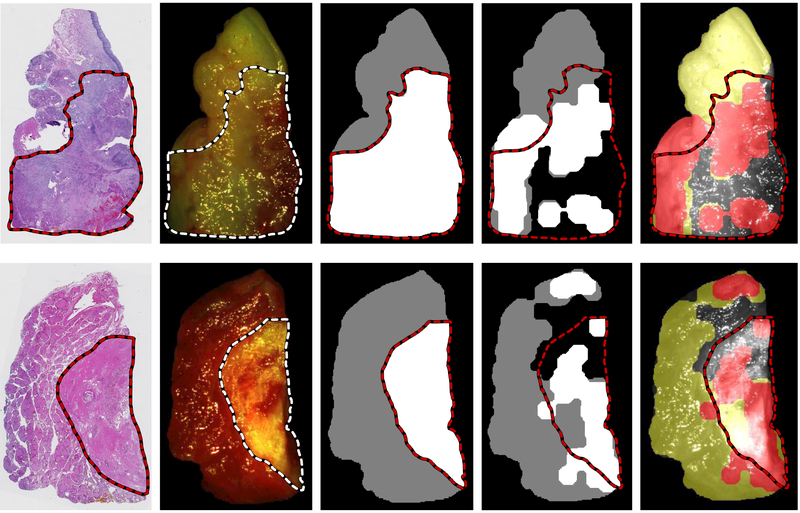
Figure 5:

Representative CNN classification results of non-glare regions of of oral cavity SCCa sample (top) and medullary thyroid carcinoma (bottom). From left to right: digitized histology slide, gross RGB composite of HSI with registered histological cancer-margin, binary ground truth image of tissue sample using registered histological cancer-margin (cancer is white, normal is grey), CNN classification result of tumor-normal tissue sample excluding regions with high glare pixel density (cancer is shown as white, normal is shown as grey), and artificial color visualization of CNN classification result overlaid on gray-scale HSI composite image (cancerous regions are shown in red and normal as yellow).

Table 2:

Results of CNN classification with inter- and intra-patient validation, values are shown as averages with standard deviation.

		Training Patches	Testing Patches	AUC	Accuracy	Sensitivity	Specificity
Thyroid	Intra-patient	44,517 (n=11)	16,464 (n=9)	0.94 ± 0.06	89 ± 7%	89 ± 8%	89 ± 7%
	Intra-patient	44,517 (n=11)	16,464 (n=9)	0.94 ± 0.06	90 ± 8%	91 ± 7%	88 ± 10%
SCCa	Intra-patient	30,286 (n=9)	8,668 (n=7)	0.84 ± 0.16	80 ± 14%	82 ± 14%	79 ± 16%
	Intra-patient	30,286 (n=9)	8,668 (n=7)	0.86 ± 0.10	81 ± 10%	84 ± 8%	77 ± 13%

Figure 6:

Receiver operator characteristic (ROC) curves of testing group patients for oral cavity SCCa (left) and thyroid carcinoma (right) patients. An ROC curve is produced from each patient, with patient numbers shown in legend. Accuracy, sensitivity, and specificity are calculated using the threshold of the optimal operating point on each patient’s respective ROC curve.

Classical machine learning techniques classify with lower performance than the proposed CNN method, as shown in Table 3. Linear SVM and RBF SVM perform with an AUC of 0.85 and 0.80; ensemble LDA performs at an AUC of 0.85; and random forest performs with an AUC of 0.87, the best of the traditional machine learning methods.

Table 3:

Results of classical machine learning techniques compared to the proposed CNN method, values are shown as averages with standard deviation.

	Classifier	AUC	Accuracy	Sensitivity	Specificity
Thyroid	3D-CNN	0.94 ± 0.06	90 ± 8%	91 ± 7%	88 ± 10%
Inter-Patient	Random Forest	0.87 ± 0.13	84 ± 13%	87 ± 11%	82 ± 17%
(n=9)	Ensemble LDA	0.85 ± 0.21	83 ± 15%	81 ± 23%	84 ± 10%
	Linear SVM	0.85 ± 0.23	76 ± 24%	81 ± 27%	87 ± 11%
	RBF SVM	0.80 ± 0.02	80 ± 11%	87 ± 11%	74 ± 14%
SCCa	3D-Inception CNN	0.86 ± 0.10	81 ± 10%	84 ± 8%	77 ± 13%
Inter-patient	Ensemble LDA	0.81 ± 0.14	75 ± 13%	78 ± 11%	76 ± 17%
(n=7)	Linear SVM	0.72 ± 0.17	73 ± 14%	84 ± 16%	59 ± 30%
	Random Forest	0.65 ± 0.06	65 ± 8%	62 ± 10%	71 ± 17%
	RBF SVM	0.58 ± 0.22	62 ± 12%	64 ± 18%	61 ± 23%

After training on 9 oral SCCa patients, the CNN was tested on the SCCa validation group, comprised of 7 SCCa patients. Two oral SCCa patients were removed from the testing group after conducting the experiment, so were only used to expand the training dataset. One patient sample was removed because histopathological analysis showed it was a different type of carcinoma. The other patient sample was removed because it was the only sample of tongue tissue, which differs substantially histologically from the oral and aerodigestive mucosa patients; therefore, it was removed to avoid testing on a patient that contains features significantly unlike the training data.

Squamous cell carcinoma tumor-normal margins are classified with an AUC of 0.84 and accuracy of 80% for intra-patient validation using the rudimentary 2D-CNN architecture. Inter-patient SCCa cancer margins are classified with an AUC of 0.86 and accuracy of 81% using the more sophisticated 3D-inception CNN architecture, see Table 2 for detailed results shown with standard deviations and Figure 6 for ROC curves. Additionally, the inter-patient SCCa group performance was evaluated with two previous architectures. The 2D inception CNN architecture classified the margins with an AUC of 0.85 ± 0.13 and 78 ± 13% accuracy, and the 3D-CNN architecture classified the cancer margins with an AUC of 0.81 ± 0.09 and 77 ± 9% accuracy.

Compared to the proposed deep learning technique, traditional machine learning techniques classify with lower performance than the proposed CNN method, evaluated by inter-patient validation. As shown in Table 3, ensemble LDA is the best performing traditional classifier with an AUC of 0.81 and accuracy of 75%, representing a 5% lower performance compared to the proposed CNN method.

4. CONCLUSION

The proposed deep learning method using CNNs out-performs traditional machine learning algorithms by a few percentage points with regards to AUC, accuracy, sensitivity, and specificity, between both SCCa and thyroid groups. The classical machine learning algorithms can only make predictors using one-dimensional vectors as features for data classification, which inherently requires dimensionality reduction for HSI, limiting features only to the spectral domain. Therefore, classical methods do not incorporate the textural and spatial information of the data rich HSI system. Convolutional neural networks can incorporate both spectral and spatial features simultaneously to take advance of the full HSI dataset. For this reason, our results indicate that the proposed algorithm is promising for a reliable cancer margin classification.

The use of spectral-spatial features for CNN classification can also introduce some error. As demonstrated in Figure 5, the edge regions of the tissue are typically where error occurs due to greater curvature of the tissue. Another source of classification error is glare pixels. In our method, they are automatically removed and not included in classification results. However, not all glare can be removed and still remains problematic due to obfuscation of useful spectral information. These two problems can potentially be overcome when translating into clinical practice. For example, glare pixels could be reduced using a polarized filter on the imaging device, but this could potentially alter the spectral signatures. The curvature can be accounted for in two ways: there is potential to mathematically factor for tissue curvature by the edges; or in a clinical environment, one can potentially reposition the imaging device to capture from multiple angles to ensure accurate classification results.

The cancer margin from the digitized histology slide is registered to the gross-level HSI using deformable registration. In tissue which is less deformable, such as oral cavity tissue which tends to be more rigid, there is less deformation, so the cancer-margin is usually well represented on the HS. On the other hand, in tissues with large potential for deformation, such as thyroid tissue due to its glandular composition, the cancer-margin can be visibly incorrect after our registration pipeline. For thyroid samples, the cancerous areas are usually visibly discernible from normal tissue, so the margin can be adjusted if necessary after performing deformable registration. Despite the fact that our methodology requires using histopathology as the gold-standard for HSI, there will always be some inherent error because it involves reducing a 3D tissue sample to a 2D histology image and reconstructing the margin to 3D again.

Intra-patient classification, using a known sample of tumor and normal for training data supplementation, simulates a potential method to improve performance. However, intra-patient classification does not have the potential clinical and translational viability of inter-patient validation. The results of our experiment with different CNN architectures indicate that a more sophisticated and intricate CNN architecture can improve performance of inter-patient classification to comparable levels of performance as that of intra-patient classification.

Selecting an architecture to pursue with deep learning is challenging and often depends on the classification task, but our results suggest that for a more complicated problem requires a more advanced architecture that can extract higher-order features and predictors necessary for classification. For example, oral SCCa tumor-normal margin classification is generally more challenging than thyroid carcinoma tumor-normal margins because the tissue is more difficult to visually discriminate between. This phenomenon is demonstrated in the reported results because a more sophisticated and deeper architecture is needed for SCCa classification compared to thyroid carcinoma. Thyroid inter-patient classification with a 3D-CNN is comparable to intra-patient classification with only a 2D-CNN. However, SCCa inter-patient classification requires a 3D-inception-based CNN to achieve results comparable to 2D-CNN intra-patient classification.

In summary, CNNs are able to classify the tumor-normal boundary with an acceptable accuracy. Deep learning requires a large patient dataset, and more sophisticated architectures and longer computing time are needed for solving more challenging and complex problems. Therefore, our promising results suggest the potential of HSI for cancer-margin delineation and encourage further investigation.