Automatic Segmentation of Hippocampus for Longitudinal Infant Brain MR Image Sequence by Spatial-Temporal Hypergraph Learning

Abstract

Accurate segmentation of infant hippocampus from Magnetic Resonance (MR) images is one of the key steps for the investigation of early brain development and neurological disorders. Since the manual delineation of anatomical structures is time-consuming and irreproducible, a number of automatic segmentation methods have been proposed, such as multi-atlas patch-based label fusion methods. However, the hippocampus during the first year of life undergoes dynamic appearance, tissue contrast and structural changes, which pose substantial challenges to the existing label fusion methods. In addition, most of the existing label fusion methods generally segment target images at each time-point independently, which is likely to result in inconsistent hippocampus segmentation results along different time-points. In this paper, we treat a longitudinal image sequence as a whole, and propose a spatial-temporal hypergraph based model to jointly segment infant hippocampi from all time-points. Specifically, in building the spatial-temporal hypergraph, (1) the atlas-to-target relationship and (2) the spatial/temporal neighborhood information within the target image sequence are encoded as two categories of hyperedges. Then, the infant hippocampus segmentation from the whole image sequence is formulated as a semi-supervised label propagation model using the proposed hypergraph. We evaluate our method in segmenting infant hippocampi from T1-weighted brain MR images acquired at the age of 2 weeks, 3 months, 6 months, 9 months, and 12 months. Experimental results demonstrate that, by leveraging spatial-temporal information, our method achieves better performance in both segmentation accuracy and consistency over the state-of-the-art multi-atlas label fusion methods.

1 Introduction

Since hippocampus plays an important role in learning and memory functions of human brain, many early brain development studies are devoted to finding the imaging biomarkers specific to hippocampus from birth to 12-month-old [1]. During this period, the hippocampus undergoes rapid physical growth and functional development [2]. In this context, accurate hippocampus segmentation from Magnetic Resonance (MR) images is important to imaging-based brain development studies, as it paves way to quantitative analysis on dynamic changes. As manual delineating of hippocampus is time-consuming and irreproducible, automatic and accurate segmentation method for infant hippocampus is highly needed.

Recently, multi-atlas patch-based label fusion segmentation methods [3–7] have achieved the state-of-the-art performance in segmenting adult brain structures, since the information propagated from multiple atlases can potentially alleviate the issues of both large inter-subject variations and inaccurate image registration. However, for the infant brain MR images acquired from the first year of life, a hippocampus typically undergoes a dynamic growing process in terms of both appearance and shape patterns, as well as the changing image contrast [8]. These challenges limit the performance of the multi-atlas methods in the task of infant hippocampus segmentation. Moreover, most current label fusion methods estimate the label for each subject image voxel separately, ignoring the underlying common information in the spatial-temporal domain across all the atlas and target image sequences. Therefore, these methods provide less regularization on the smoothness and consistency of longitudinal segmentation results.

To address these limitations, we resort to using hypergraph, which naturally caters to modeling the spatial and temporal consistency of a longitudinal sequence in our segmentation task. Specifically, we treat all atlas image sequences and target image sequence as whole, and build a novel spatial-temporal hypergraph model, for jointly encoding useful information from all the sequences. To build the spatial-temporal hypergraph, two categories of hyperedges are introduced to encode information with the following anatomical meanings: (1) the atlas-to-target relationship, which covers common appearance patterns between the target and all the atlas sequences; (2) the spatial/temporal neighborhood within the target image sequence, which covers common spatially- and longitudinally-consistent patterns of the target hippocampus. Based on this built spatial-temporal hypergraph, we then formulate a semi-supervised label propagation model to jointly segment hippocampi for an entire longitudinal infant brain image sequence in the first year of life. The contribution of our method is two-fold:

First, we enrich the types of hyperedges in the proposed hypergraph model, by leveraging both spatial and temporal information from all the atlas and target image sequences. Therefore, the proposed spatial-temporal hypergraph is potentially more adapted to the challenges, such as rapid longitudinal growth and dynamically changing image contrast in the infant brain MR images.

Second, based on the built spatial-temporal hypergraph, we formulate the task of longitudinal infant hippocampus segmentation as a semi-supervised label propagation model, which can unanimously propagate labels from atlas image sequences to the target image sequence. Of note, in our label propagation model, we also use a hierarchical strategy by gradually recruiting the labels of high-confident target voxels to help guide the segmentation of less-confident target voxels.

We evaluate the proposed method in segmenting hippocampi from longitudinal T1-weighted MR image sequences acquired in the first year of life. More accurate and consistent hippocampus segmentation results are obtained across all the time-points, compared to the state-of-the-art multi-atlas label fusion methods [6, 7].

2 Method

For labeling the longitudinal target images with T time-points {I_O,t|t = 1, …, T, the first step is to linearly align S longitudinal atlas image sequences {I_s,t|s = 1, …, S; t = 1,…,T} into the target image space. Then, the spatial-temporal hypergraph is constructed as detailed in Sect. 2.1. Finally, hippocampus is longitudinally segmented through the label propagation based on the semi-supervised hypergraph learning, as introduced in Sect. 2.2.

2.1 Spatial-Temporal Hypergraph

Denote a hypergraph as 𝒢 = (𝒱, ℰ, w), composed of the vertex set 𝒱 = {v_i|i = 1, …, |𝒱|}, the hyperedge set ℰ = {e_i|i = 1, …, |ℰ|} and edge weight vector w ∈ ℛ^|ℰ|. Since each hyperedge e_i allows linking more than two vertexes included in 𝒱, 𝒢 naturally characterizes groupwise relationship, which reveals high-order correlations among a subset of voxels [9]. By encoding both spatial and temporal information from all the target and atlas image sequences into the hypergraph, a spatial-temporal hypergraph is built to characterize various relationships in the spatial-temporal domain. Generally, our hypergraph includes two categories of hyperedges: (1) the atlas-to-target hyperedge, which measures the patch similarities between the atlas and target images; (2) the local spatial/temporal neighborhood hyperedge, which measures the coherence among the vertexes located in a certain spatial and temporal neighborhood of atlas and target images.

Atlas-to-Target Hyperedge

The conventional label fusion methods only measure the pairwise similarity between atlas and target voxels. In contrast, in our model, each atlas-to-target hyperedge encodes groupwise relationship among multiple vertexes of atlas and target images. For example, in the left panel of Fig. 1, a central vertex v_c (yellow triangle) from the target image and its local spatial correspondences v₇ ∼ v₁₂ (blue square) located in the atlases images form an atlas-to-target hyperedge e₁ (blue round dot curves in the right panel of Fig. 1). In this way, rich information contained in the atlas-to-target hyperedges can be leveraged to jointly determine the target label. Thus, the chance of mislabeling an individual voxel can be reduced by jointly propagating the labels of all neighboring voxels.

Fig. 1.

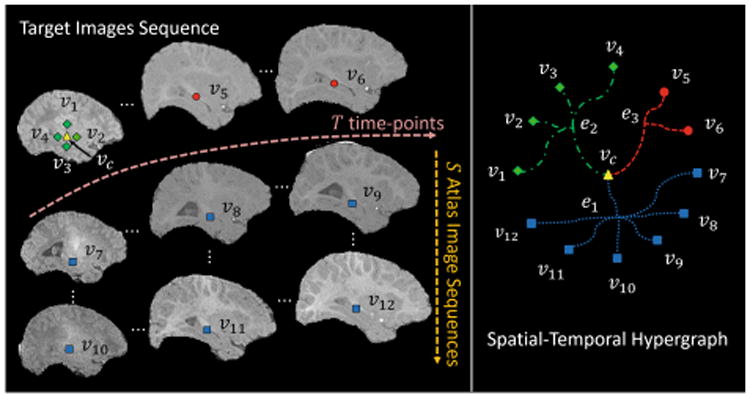
The construction of spatial-temporal hypergraph.

Local Spatial/Temporal Neighborhood Hyperedge

Without enforcing spatial and temporal constraints, the existing label fusion methods are limited in labeling each target voxel at each time-point independently. We address this problem by measuring the coherence between the vertexes located at both spatial and temporal neighborhood in the target images. In this way, local spatial/temporal neighborhood hyperedges can be built to further incorporate both spatial and temporal consistency into the hypergraph model. For example, spatially, the hyperedge e₂ (green dash dot curves in the right panel of Fig. 1) connects a central vertex v_c (yellow triangle) and the vertexes located in its local spatial neighborhood v₁ ∼ v₄ (green diamond) in the target images. We note that v₁ ∼ v₄ are actually very close to v_c in our implementation. But, for better visualization, they are shown with larger distance to v_c in Fig. 1. Temporally, the hyperedge e₃ (red square dot curves in the right panel of Fig. 1) connects v_c and the vertexes located in its local temporal neighborhood v₅ ∼ v₆ (red circle), i.e., the corresponding positions of the target images at different time-points.

Hypergraph Model

After determining the vertex set 𝒱 and the hyperedge set ℰ, a |𝒱| × |ℰ| incidence matrix H is obtained to encode all the information within the hypergraph 𝒢. In H, rows represent |𝒱| vertexes, and columns represent |ℰ| hyperedges. Each entry H(v, e) in H measures the affinity between the central vertex v_c of the hyperedge e ∈ ℰ and each vertex v ∈ e as below:

$$\mathit{H}(v,e)=\{\begin{array}{cc}\mathit{exp}(-\frac{\mathit{p}(v)-\mathit{p}{(v_c)}_2^2}{{\sigma }^2})& \mathit{\text{if}}v\in e\\ 0& \mathit{\text{if}}v\notin e\end{array}$$ (1)

where ‖.‖₂ is the L₂ norm distance computed between vectorized intensity image patch p(v) for vertex v and p(v_c) for central vertex v_c. σ is the averaged patchwise distance between v_c and all vertexes connected by the hyperedge e.

Based on Eq. (1), the degree of a vertex v ∈ 𝒱 is defined as d(v) = Σ_e∈εw(e)H(v, e), and the degree of hyperedge e ∈ ℰ is defined as δ(e) = Σ_v∈vH(v, e). Diagonal matrices D_v, D_e and W are then formed, in which each entry along the diagonal is the vertex degree d(v), hyperedge degree δ(e) and hyperedge weights w(e), respectively. Without any prior information on the hyperedge weight, w(e) is uniformly set to 1 for each hyperedge.

2.2 Label Propagation Based on Hypergraph Learning

Based on the proposed spatial-temporal hypergraph, we then propagate the known labels of the atlas voxels to the voxels of the target image sequence, by assuming that the vertexes strongly linked by the same hyperedge are likely to have the same label. Specifically, this label propagation problem can be solved by a semi-supervised learning model as described below.

Label Initialization

Assume Y = [y₁, y₂] ∈ ℛ^|𝒱|×2 as the initialized labels for all the |𝒱| vertexes, with y₁ ∈ ℛ^|𝒱| and y₂ ∈ ℛ^|𝒱| as label vectors for two classes, i.e., hippocampus and non-hippocampus, respectively. For the vertex v from the atlas images, its corresponding labels are assigned as y₁(v) = 1 and y₂(v) = 0 if v belongs to hippocampus regions, and vice versa. For the vertex v from the target images, its corresponding labels are initialized as y₁(v) = y₂(v) = 0.5, which indicates the undetermined label status for this vertex.

Hypergraph Based Semi-Supervised Learning

Given the constructed hypergraph model and the label initialization, the goal of label propagation is to find the optimized relevance label scores F = [f₁,f₂] ∈ ℛ^|𝒱|×2 for vertex set 𝒱, in which f₁ and f₂ represent the preference for choosing hippocampus and non-hippocampus, respectively. A hypergraph based semi-supervised learning model [9] can be formed as:

$${arg\; min}_{\mathit{F}}\{\lambda \cdot {\sum }_{i=1}^2{\mathit{f}}_i-{\mathit{y}}_i^2+\mathrm{\Omega }(\mathit{F},\mathit{H},\mathit{W})\}$$ (2)

There are two terms, weighted by a positive parameter λ, in the above objective function. The first term is a loss function term penalizing the fidelity between estimation F and initialization Y. Hence, the optimal label prorogation results are able to avoid large discrepancy before and after hypergraph learning. The second term is a regularization term defined as:

$$\mathrm{\Omega }(\mathit{F},\mathit{H},\mathit{W})=\frac{1}{2}{\sum }_{i=1}^2{\sum }_{e\in \mathcal{E}}^2{\sum }_{v_c,v\in \mathcal{V}}\frac{\mathit{w}(e)\mathit{H}(v_c,e)\mathit{H}(v,e)}{\delta (e)}\times {(\frac{{\mathit{f}}_i(v_c)}{\sqrt{d(v_c)}}-\frac{{\mathit{f}}_i(v)}{\sqrt{d(v)}})}^2$$ (3)

Here, for the vertexes v_c and v connected by the same hyperedge e, the regularization term tries to enforce their relevance scores being similar, when both H(v_c, e) and H(v, e) are large. For convenience, the regularization term can be reformulated into a matrix form, i.e., ${\sum }_{i=1}^2{\mathit{f}}_i^T\mathbf{\Delta }{\mathit{f}}_i$, where the normalized hypergraph Laplacian matrix Δ = I − Θ is a positive semi-definite matrix, $\mathit{\Theta }={\mathit{D}}_v^{-\frac{1}{2}}{\mathit{\text{HWD}}}_e^{-1}{\mathit{H}}^T{\mathit{D}}_v^{-\frac{1}{2}}$ and I is an identity matrix.

By differentiating the objective function (2) with respect to F, the optimal F can be analytically solved as $\mathit{F}=\frac{\lambda }{\lambda +1}{(\mathit{I}-\frac{1}{\lambda +1}\cdot \mathit{\Theta })}^{-1}\mathit{Y}$. The anatomical label on each target vertex v ∈ 𝒱 can be finally determined as the one with larger score: $arg\underset{i}{max}{\mathit{f}}_i(v)$.

Hierarchical Labeling Strategy

Some target voxels with ambiguous appearance (e.g., those located at the hippocampal boundary region) are more difficult to label than the voxels with uniform appearance (e.g., those located at the hippocampus center region). Besides, the accuracy of aligning atlas images to target image also impacts the label confidence for each voxel. In this context, we divide all the voxels into two groups, such as the high-confidence group and the less-confidence group, based on the predicted labels and their confidence values in terms of voting predominance from majority voting. With the help of the labeling results from high-confident region, the labeling for the less-confident region can be propagated from both atlas and the newly-added reliable target voxels, which makes the label fusion procedure more target-specific. Then, based on the refined label fusion results from hypergraph learning, more target voxels are labeled as high-confidence. By iteratively recruiting more and more high-confident target vertexes in the semi-supervised hypergraph learning framework, a hierarchical labeling strategy is formed, which gradually labels the target voxels from high-confident ones to less-confident ones. Therefore, the label fusion results for target image can be improved step by step.

3 Experimental Results

We evaluate the proposed method on a dataset containing MR images of ten healthy infant subjects acquired from a Siemens head-only 3T scanner. For each subject, T1-weighted MR images were scanned at five time-points, i.e., 2 weeks, 3 months, 6 months, 9 months and 12 months of age. Each image is with the volume size of 192 × 156 × 144 voxels at the resolution of 1 × 1 × 1 mm³. Standard preprocessing was performed, including skull stripping, and intensity inhomogeneity correction. The manual delineations of hippocampi for all subjects are used as ground-truth.

The parameters in the proposed method are set as follows. The patch size for computing patch similarity is 5 × 5 × 5 voxels. Parameter λ in Eq. (2) is empirically set to 0.01. The spatial/temporal neighborhood is set to 3 × 3 × 3 voxels. The strategy of leave-one-subject-out is used to evaluate the segmentation methods. Specifically, one subject is chosen as the target for segmentation, and the image sequences of the remaining nine subjects are used as the atlas images. The proposed method is compared with two state-of-the-art multi-atlas label fusion methods, e.g., local-weighted majority voting [6] and sparse patch labeling [7], as well as a method based on a degraded spatial-temporal hypergraph, i.e., our model for segmenting each time-point independently with only spatial constraint.

Table 1 gives the average Dice ratio (DICE) and average surface distance (ASD) of the segmentation results by four comparison methods at 2-week-old, 3-month-old, 6-month-old, 9-month-old and 12-month-old data, respectively. There are two observations from Table 1. First, the degraded hypergraph with only the spatial constraint still obtains mild improvement over other two methods. Second, after incorporating the temporal consistency, our method gains significant improvement, especially for the time-points after 3-month-old. Figure 2 provides a typical visual comparison of segmenting accuracy among four methods. The upper panel of Fig. 2 visualizes the surface distance between the segmentation results from each of four methods and the ground truth. As can be observed, our method shows more blue regions (indicating smaller surface distance) than red regions (indicating larger surface distance), hence obtaining results more similar to the ground truth. The lower panel of Fig. 2 illustrates the segmentation contours for four methods, in which our method shows the highest overlap with the ground truth. Figure 3 further compares the temporal consistency from 2-week-old to 12-month-old data between the degraded and full spatial-temporal hypergraph. From the left panel in Fig. 3, it is observed that our full method achieves better visual temporal consistency than the degraded version, e.g., the right hippocampus at 2-week-old. We also use a quantitative measurement to evaluate the temporal consistency, i.e. the ratio between the volume of the segmentation result based on the degraded/full method and the volume of its corresponding ground truth. From the right panel in Fig. 3, we can see that all the ratios of full spatial-temporal hypergraph (yellow bars) are closer to “1” than the ratios of the degraded version (blue bars) over five time-points, showing the better consistency globally.

Table 1.

The DICE (average ± standard deviation, in %) and ASD (average ± standard deviation, in mm) of segmentation results by four comparison methods for 2-week-old, 3-month-old, 6-month-old, 9-month-old and 12-month-old data.

Time-point	Metric	Majority voting [6]	Sparse labeling [7]	Spatial-temporal hypergraph labeling
				Degraded	Full
2-week-old	DICE	50.18 ± 18.15 (8e−3)*	63.93 ± 8.20 (6e−2)	64.09 ± 8.15 (9e−2)	64.84 ± 9.33
	ASD	1.02 ± 0.41 (8e−3)*	0.78 ± 0.23 (1e−2)*	0.78 ± 0.23 (1e−2)*	0.74 ± 0.26
3-month-old	DICE	61.59 ± 9.19 (3e−3)*	71.49 ± 4.66 (7e−2)	71.75 ± 4.98 (1e−1)	74.04 ± 3.39
	ASD	0.86 ± 0.25 (6e−3)*	0.66 ± 0.14 (5e−2)*	0.66 ± 0.15 (9e−2)	0.60 ± 0.09
6-month-old	DICE	64.85 ± 7.28 (2e−4)*	72.15 ± 6.15 (5e−3)*	72.78 ± 5.68 (4e−2)*	73.84 ± 6.46
	ASD	0.85 ± 0.23 (1e−4)*	0.71 ± 0.19 (3e−3)*	0.70 ± 0.17 (4e−2)*	0.67 ± 0.20
9-month-old	DICE	71.82 ± 4.57 (6e−4)*	75.18 ± 2.50 (2e−3)*	75.78 ± 2.89 (9e−3)*	77.22 ± 2.77
	ASD	0.73 ± 0.16 (9e−4)*	0.65 ± 0.07 (1e−3)*	0.64 ± 0.09 (9e−3)*	0.60 ± 0.09
12-month-old	DICE	71.96 ± 6.64 (8e−3)*	75.39 ± 2.87 (7e−4)*	75.96 ± 2.85 (1e−2)*	77.45 ± 2.10
	ASD	0.67 ± 0.10 (6e−3)*	0.64 ± 0.08 (2e−3)*	0.64 ± 0.07 (1e−2)*	0.59 ± 0.07

^*Indicates significant improvement of spatial-temporal hypergraph method over other compared methods with p-value < 0.05

Fig. 2.

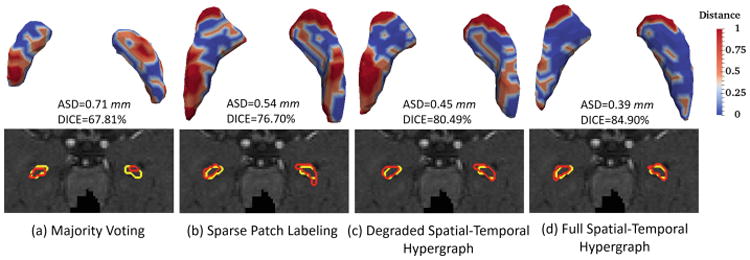
Visual comparison between segmentations from each of four comparison methods and the ground truth on one subject at 6-month-old. Red contours indicate the results of automatic segmentation methods, and yellow contours indicate their ground truth. (Color figure online)

Fig. 3.

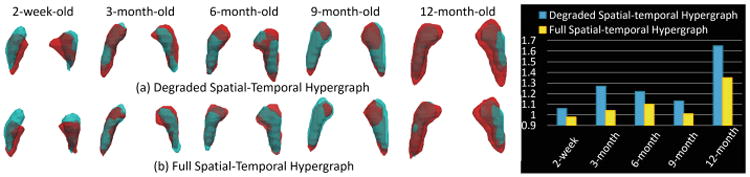
Visual and quantitative comparison of temporal consistency between the degraded and full spatial-temporal hypergraph. Red shapes indicate the results of degraded/full spatial-temporal hypergraph methods, and cyan shapes indicate their ground truth. (Color figure online)

4 Conclusion

In this paper, we propose a spatial-temporal hypergraph learning method for automatic segmentation of hippocampus from longitudinal infant brain MR images. For building the hypergraph, we consider not only the atlas-to-subject relationship but also the spatial/temporal neighborhood information. Thus, our proposed method opts for unanimous labeling of infant hippocampus with temporal consistency across different development stages. Experiments on segmenting hippocampus from T1-weighted MR images at 2-week-old, 3-month-old, 6-month-old, 9-month-old, and 12-month-old demonstrate improvement in terms of segmenting accuracy and consistency, compared to the state-of-the-art methods.