Abstract

Density functional theory within the Kohn–Sham density functional theory (KS-DFT) ansatz has been implemented into our bubbles and cube real-space molecular electronic structure framework, where functions containing steep cusps in the vicinity of the nuclei are expanded in atom-centered one-dimensional (1D) numerical grids multiplied with spherical harmonics (bubbles). The remainder, i.e., the cube, which is the cusp-free and smooth difference between the atomic one-center contributions and the exact molecular function, is represented on a three-dimensional (3D) equidistant grid by using a tractable number of grid points. The implementation of the methods is demonstrated by performing 3D numerical KS-DFT calculations on light atoms and small molecules. The accuracy is assessed by comparing the obtained energies with the best available reference energies.
1. Introduction
Kohn–Sham density functional theory (KS-DFT) is nowadays among the most popular quantum mechanical methods employed in molecular and material science simulations.1 The exchange-correlation functional is the key component of the DFT theory and searching for approximate and more accurate functional forms has been going on since the invention of KS-DFT.2
There are several aspects that need to be considered when implementing exchange-correlation (XC) functionals for efficient and accurate calculations. Many different basis-set options are employed, while Gaussian-type3 basis functions dominate the quantum chemistry field. These global analytic atomic-centered basis functions capture the main features of the orbitals near the nuclei. However, high accuracy is hard to achieve by systematically increasing the basis set size without running into linear dependence problems.4−7 Despite using global basis sets, the XC energy contribution cannot be obtained analytically but has to be computed numerically,8−15 implying that the quadrature must be fast and accurate.
The bubbles and cube numerical framework is a finite-element approach developed in our group.16,17 The functions containing the steep nuclear cusps are expanded using local functions on atom-centered one-dimensional (1D) numerical grids multiplied with spherical harmonics (bubbles). The remainder, which is the cusp-free and smooth difference between the main atomic contributions and the exact molecular function, is represented by a tractable amount of equidistant grid points (cube).
Grid-based fast multiple methods (GBFMM) can be used for speeding up the computations, and they allow an efficient and even distribution of the memory and computational load between the computational nodes.18,19 General-purpose graphics processing unit (GPGPU), message-passing interface (MPI) and open multiprocessing (OpenMP) parallelizations are utilized in our software in order to effectively use the available computational resources.20 Tensor decomposition approaches are used for reducing memory requirements.21,22
The aim of this work is to implement the KS-DFT method into the above framework. The implementation of the XC functional in the double basis (bubbles and cube) involves novel challenges because of the nonlinear nature of the XC term. As most of the needed components have already been implemented, we concentrate here on the missing part, namely the algorithms and the detailed implementation employed in the calculation of the exchange-correlation potential and the corresponding energy.
In the following section, we briefly present the basic KS-DFT theory. After that, we give the mathematical details of representing functions using the double bubbles and cube basis. We discuss the SCF-algorithm at the KS-DFT level in this framework and calculation of the exchange-correlation terms. We apply the methods on a few molecules and present energies obtained in KS-DFT calculations using the LDA and GGA functionals. Finally, we compare our results with accurate energies obtained using multiwavelet calculations.5,23
2. Kohn–Sham Density Functional Theory
The electronic energy in Kohn–Sham density functional theory (KS-DFT) can be expressed as
| 1 |
where the T[ρ], Vext[ρ], J[ρ], and EXC[ρ] are the kinetic energy, external potential energy, the energy of the Coulomb repulsion between electrons, and the exchange-correlation energy, respectively. The energy contributions are functions of the total electron density ρ, which is computed using the occupied molecular orbitals, ψi, as
| 2 |
where Nocc is the number of occupied molecular orbitals.
EXC has an integral form:
| 3 |
where ε(r⃗) is the exchange-correlation energy per particle.
The orbital energies, ϵi, can be obtained from the Kohn–Sham eigenvalue equation
| 4 |
where the Kohn–Sham potential consists of the external potential, vext, the Coulomb potential, vJ, and the exchange-correlation potential, vXC:
| 5 |
At the local density approximation (LDA), the exchange-correlation functional and the corresponding potential depend only on the electron density
| 6 |
Density functionals at the generalized gradient approximation (GGA) also depend on the gradient of the electron density ∇ρ. At the restricted GGA level, the vXC can be written as
| 7 |
which can also
be expressed using the second
derivative 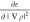 instead of
instead of 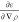 as
as
| 8 |
3. Bubbles and Cube
In the numerical bubbles and cube framework, the three-dimensional (3D) functions, f(r⃗), are represented as a linear combination of the cube, fΔ(r⃗), expanded on a 3D equidistant grid and the bubbles, which are radial functions fAlm(rA) expanded on a one-dimensional (1D) radial grid multiplied with real spherical harmonic functions, Ylm(θA,ϕA) centered on nucleus A. The radial grids of the bubbles are denser closer to the atom centers. The 1D radial grids of the bubbles and the grid of the cube overlap and all the grid points of the cube are independent of the grid points of the bubbles and vice versa.16,17 A general scalar function f(r⃗) is expressed in the double basis of bubbles and cube as
| 9 |
The bubbles functions take care of the cusp behavior of functions near the nuclei implying that also core electrons can be considered in the calculations. Thus, there is no need to use soft pseudo potentials or to refined the grid for representing the core electrons.4,24−40 The 1D radial functions represent each function accurately in the vicinity of the nuclei with only a small fraction of the total computational costs. The remaining cube part is smooth and a good accuracy is obtained with a relatively coarse 3D grid.
We divide the range of each Cartesian direction of the cube and the radial range of the bubbles into a number of cells with 7 grid points. The first and the last grid point of each cell are shared with the neighboring cell. Each grid point in a cell corresponds to a Lagrange interpolation polynomial (LIP) and all the LIPs of a given cell are used when interpolating or calculating derivatives at any point of interest between grid points. Having 7 grid points in a cell implies that when differentiating the functions, the maximum error is in the order of O(h6), where h is the spacing between two grid points. In our framework and in this article, the entities consisting of the cube and the bubbles are called Function3D below.
4. KS-DFT SCF Using Bubbles and Cube
The simplest possible self-consistent field (SCF) orbital optimization scheme in the numerical framework is an iterative process with only a few steps namely: calculation of the orbital energies ϵi and the total energy, E; calculation of the Kohn–Sham potential, vKS; updating and orthonormalizing the orbitals. The main advantage of the optimization process of numerical KS-DFT SCF is that the algorithm scales linearly as only one bracket element per orbital is needed in order to calculate the orbital energies.
In the present approach, the orbitals are updated by integrating the Helmholtz kernel for each orbital
| 10 |
Integration of the six-dimensional Helmholtz kernel has been discussed in detail in our previous publications.19,41 At the end of each Helmholtz integration step the orbitals are reorthogonalized using the Gram–Schmidt method. Calculation of electron–electron interaction potentials
| 11 |
and the corresponding energies have been discussed in our earlier work.18−20 Calculation of the kinetic energy of the orbitals has also been discussed before,17
| 12 |
We have previously developed computational algorithms needed for computing all terms that are needed for Hartree–Fock calculations. For KS-DFT calculations, we need accurate and efficient algorithms for calculating the exchange-correlation potential, vXC, and the corresponding energy, EXC, respectively. Our approach to calculate these entities will be discussed in the next section.
5. Exchange-Correlation Terms with Bubbles and Cube
Calculating the exchange-correlation energy and the exchange-correlation potential for a known electron density is straightforward and can be done with existing libraries such as LibXC.42 However, in our framework the density is divided into several parts and the exchange-correlation terms are not linearly dependent on the density, implying that they cannot be calculated separately. Thus, some additional steps are required before and after the library call, as we want to partition the resulting function and some intermediate ones into bubbles and cubes. The calculation of the input density and the gradient also requires some special attention.
We discuss the reconstruction of the output bubbles in section 5.1 and the calculation of density and its gradient in section 5.2. In section 5.3, we conclude this part by presenting the algorithms we use to compute the exchange-correlation energy and the exchange-correlation potentials for the functionals of the local density approximation (LDA) and the generalized gradient approximation (GGA).
5.1. Reconstruction of Bubbles
When a function f(r⃗) can be calculated in any point in space, a straightforward method to construct the bubbles is by direct projection. Following Becke’s fuzzy cells concept,8 a function can be partitioned into atomic cell contributions
The radial part of the bubbles, fA(r⃗), is obtained by projecting the angular part of f(r⃗) using spherical harmonics
| 13 |
where ω is the solid angle, wA is a Becke partition function, and w′i is the integration weight of the ith point. The numerical integration on a sphere uses Lebedev grids. fΔ(r⃗) is obtained by subtracting the bubbles from f(r⃗). In the projection, the 3D information is compressed into 1D radial grid functions multiplied with the corresponding spherical harmonics. The efficiency of the compression can be evaluated by calculating the norm of the cube, ∫(fΔ(r⃗))2dr⃗.
5.2. Calculation of Electron Density and Its Gradient
In our DFT implementation, we use two different ways to calculate the electron density at the points of interest, p. The advantages and disadvantages of the two approaches are discussed in this section.
In the first approach, the electron density is calculated by adding the squared occupied orbitals in the Function3Ds and storing it in another Function3D object. The electron density at the points of interest can be obtained by computing the resulting Function3D electron density using eq 9. The three gradient components of the electron density of the cube are evaluated and stored as the cubes of three independent Function3D objects, whereafter the gradient of the bubbles contribution to the electron density is calculated and stored as bubbles to the Function3D objects using the relations derived in appendix A. After the gradient Function3Ds are formed, the exact values of gradient at points of interest are calculated using the same procedure as used for the density. This algorithm is described as a pseudocode in Figure 1.
Figure 1.
Simple algorithm for calculating the electron density and its gradient at points of interest, p.
The second way to get the electron density and its gradient is to perform the steps of the first algorithm in reversed order. The orbital values are calculated in the desired points, p, which are squared and added with the contributions from the other orbitals to form the electron density. The gradient is obtained via the differentiation product rule using orbital gradient values and the orbital values in the points of interest as described in Figure 2.
Figure 2.
More involved algorithm for calculating the electron density and its gradient at points of interest.
The differences between the two algorithms are in speed and accuracy. The first algorithm is faster, as there are fewer point-wise calculations of Function3Ds. However, the latter algorithm increases the precision of the electron density and especially of the gradient, because it has fewer multiplications between Function3D objects prior to the calculation of the gradient. The smaller part of the differentiated functions in Function3Ds are stored in cubes prior to the calculation of the gradient.
In both algorithms, the gradients of the functions are calculated by first determining the gradients as Function3D objects instead of calculating the gradients directly from the electron density or the orbitals, rendering the resulting gradients slightly less accurate. However, the values near the nuclei are more stable, resulting in a higher precision for the optimized electron density.
5.3. The Exchange-Correlation Algorithm
We have now all algorithms needed for calculation of the exchange-correlation potential (vXC) and energy (EXC) within the bubbles and cube framework. The main algorithm for obtaining vXC and EXC at the restricted LDA and GGA level is given as pseudocode in Figure 3. We discuss the GGA algorithm, whereas the LDA algorithm can be obtained by omitting the steps involving the gradient of the electron density in the GGA algorithm.
Figure 3.
Calculation of the exchange-correlation potential (vXC) and the corresponding energy (EXC) in the bubbles and cube scheme.
In order to calculate vXC and EXC at the GGA level, the occupied orbitals,
{ψi...ψNocc}, are used as input when computing ερ, 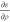 ,
,  using the best bubble and cube representation
for each term. The individual steps are described as pseudo code in
the Figures 4 and 5.
using the best bubble and cube representation
for each term. The individual steps are described as pseudo code in
the Figures 4 and 5.
Figure 4.
Calculation of the exchange-correlation terms ερ, 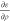 , and
, and  as
bubbles.
as
bubbles.
Figure 5.
Calculation of the exchange-correlation terms ερ, 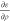 , and
, and  as
cubes.
as
cubes.
Calculations of the three exchange-correlation
terms begin by computing
the electron density, ρp, and its
gradient, ∇ρp, at the points
of interest. In the bubbles case, ρp and ∇ρp are calculated
in the Lebedev integration points for distances from the nuclei corresponding
to 1D-grid points. For the cube, ρp and ∇ρp are calculated
for all grid points of the cube. The second common step is the call
to the LibXC library,42 which provides
the values for the derivatives of the energy,  ,
, 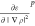 , and
the energy per particle, εp, for
the chosen points. εp is then multiplied
with the electron density, ρp, and
, and
the energy per particle, εp, for
the chosen points. εp is then multiplied
with the electron density, ρp, and 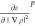 is multiplied with ∇ρp followed by an reordering of the data to
cube or bubbles format. For the cube, the data are reshaped into a
3D grid of the correct dimension size, whereas for the bubbles one
has to employ the procedure described in section 5.1.
is multiplied with ∇ρp followed by an reordering of the data to
cube or bubbles format. For the cube, the data are reshaped into a
3D grid of the correct dimension size, whereas for the bubbles one
has to employ the procedure described in section 5.1.
The bubbles contributions of the
three terms are extracted from
the cubes, leaving only those parts in the cube that cannot be accurately
expanded in bubbles. The exchange-correlation potential, vXC, is obtained by calculating the divergence of the Function3D
containing 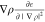 . The
obtained contribution to the potential
is multiplied with −2 and added to
. The
obtained contribution to the potential
is multiplied with −2 and added to  . The exchange-correlation energy (EXC) is obtained by integrating ερ.
. The exchange-correlation energy (EXC) is obtained by integrating ερ.
6. Results
The accuracy of our approach is demonstrated by calculating total energies for a few atoms and molecules at the LDA level43,44 using the VWN5 correlation functional45 as well as at the GGA level using the PBE exchange-correlation functional.46,47 The total energies and the relative errors are compared in Tables 1, 2, and 3 with values calculated using the multiwavelet approach.5,23 For atoms, a cube grid step, h, of 0.05 was used. For molecules, h values of 0.05, 0.07, and 0.10 were used. The maximum angular momentum quantum number of the bubbles, lMAX, was 3, 4, or 5 depending on the size of the molecule and the employed exchange-correlation functional. The 1D radial grid of the bubbles had 9000–14000 grid points within a radius of 14 bohr from the atom centers. The number of grid points of the bubbles depends on the charge of the corresponding nucleus. In the PBE calculations, the dimension of the cube grid was chosen such that the distance between the outermost nucleus and the edge of the cube was at least 9–10 bohr in each direction. In the LDA calculations, the distance between the outermost nucleus and the cube edge was 7 bohr.
Table 1. Total Energies and Energy Deviations from Reference Data in Atomic Units (au) Calculated at the LDA Level for Atoms Using h = 0.05a.
| ELDA | |ΔE| | reference | EPBE | |ΔE| | Reference | |
|---|---|---|---|---|---|---|
| He | –2.83483557 | 7 × 10–8 | –2.83483564 | –2.89293478 | 8 × 10–8 | –2.89293486 |
| Be | –14.44720932 | 2 × 10–7 | –14.44720953 | –14.62994712 | 8 × 10–7 | –14.62994787 |
| Ne | –128.23347426 | 7 × 10–6 | –128.23348141 | –128.86642698 | 9 × 10–7 | –128.86642789 |
The reference energies are taken from ref (5).
Table 2. Total Energies and Absolute Energy Deviations from Reference Data (in au) Calculated for Molecules at the LDA Level Using Three Different h Values and an lMAX Value of 3a.
| h | E | |ΔE| | reference | |
|---|---|---|---|---|
| H2 | 0.10 | –1.13737932 | 1.0 × 10–4 | |
| 0.07 | –1.13746630 | 1.5 × 10–5 | ||
| 0.05 | –1.13748154 | 5.4 × 10–7 | –1.1374810 | |
| N2 | 0.10 | –108.699920957 | 4.5 × 10–5 | |
| 0.07 | –108.69994408 | 4.5 × 10–5 | ||
| 0.05 | –108.69989293 | 1.7 × 10–5 | –108.699876 | |
| C2H4 | 0.10 | –77.86313942 | 4.1 × 10–5 | |
| 0.07 | –77.86310547 | 7.5 × 10–6 | ||
| 0.05 | –77.86310014 | 2.1 × 10–6 | –77.863098 |
The reference energies are taken from ref (23).
Table 3. Total Energies and Absolute Energy Deviations from Reference Data (in au) Calculated for Molecules at the PBE Level Using Three Different h Valuesa.
| lMAX | h | E | |ΔE| | Reference | |
|---|---|---|---|---|---|
| H2 | 4 | 0.10 | –1.16666517 | 3.5 × 10–5 | |
| 0.07 | –1.16668483 | 1.5 × 10–5 | |||
| 0.05 | –1.16670022 | 6.0 × 10–8 | –1.16670016 | ||
| LiH | 4 | 0.10 | –8.04731512 | 3.6 × 10–5 | |
| 0.07 | –8.04740301 | 5.1 × 10–5 | |||
| 0.05 | –8.04734292 | 9.0 × 10–6 | –8.04735195 | ||
| BH | 4 | 0.10 | –25.24162080 | 9.8 × 10–5 | |
| 0.07 | –25.24150547 | 2.8 × 10–5 | |||
| 0.05 | –25.24149493 | 2.8 × 10–5 | –25.24152300 | ||
| H2O | 4 | 0.10 | –76.38848643 | 3.5 × 10–5 | |
| 0.07 | –76.38862009 | 9.9 × 10–5 | |||
| 0.05 | –76.38856690 | 4.5 × 10–5 | –76.38852144 | ||
| CH4 | 5 | 0.10 | –40.46792421 | 1.9 × 10–4 | |
| 0.07 | –40.46819020 | 8.1 × 10–5 | |||
| 0.05 | –40.46819293 | 8.4 × 10–5 | –40.46810927 |
The reference energies are taken from ref (5).
In the LDA calculations, we used the simple method described in Figure 1 to evaluate the electron density at the points of interest, whereas in the PBE calculations, we utilized the more complex method described in Figure 2. The straightforward approach can without doubt be used in the LDA-calculations, because the two approaches yield practically the same accuracy. However, the accuracy of the electron-density gradient depends on the employed approach. The accuracy is increased by an order of magnitude when using the more complex approach in PBE calculations.
The complex approach is computationally more expensive, because it involves an additional computational step that scales linearly with respect to the number of occupied molecular orbitals. However, the complex approach is a more effective way to increase the accuracy of the calculation than the alternative of decreasing the grid step of the cube. The complex approach can be turned on at a later stage of a GGA calculation when aiming at a higher accuracy.
The results of the atomic calculations are summarized in Table 1. The calculations demonstrate that a high accuracy can be obtained using the two exchange-correlation functionals. The obtained LDA energies for the studied molecules given in Table 2 are also accurate. The total energies are within the reported error bars of 3 × 10–6 and 3 × 10–5 au of the reference values for C2H4 and N2, respectively.23 For the coarser grids, our calculations have errors in the total energy that are still smaller than threshold for chemical accuracy of 10–4 au.
The PBE results for molecules are given in Table 3 where one sees that accuracy of our calculations does not reach the level of the reference values with any of the used grid steps. However, the errors are much smaller than the chemical accuracy of 10–4 au when using the smaller grid steps of 0.05 and 0.07. When the sparse grid with spacings of 0.10 au is employed, the error is smaller than 10–4 au for all studied molecules except CH4, whose energy has an error of 1.9 × 10–4 au.
Some of the energies in Tables 1, 2, and 3 lie below the reference value showing that the numerical calculations are not completely variational. The nonvariational behavior is caused by accumulations of numerical errors without any predefined sign. In this regard, numerical methods differ from analytical approaches, where the deviations from the exact values are most likely due to limitations in the employed basis set, whereas in that case numerical rounding errors are much smaller.
The reason for the somewhat larger inaccuracy of the GGA approach is the uncertainties introduced when calculating the gradient. Especially, the gradient of cube is very prone to errors as even the densest grid is still relatively sparse from the point of view of numerical differentiation. The effect of the numerical differentiation error can be reduced by increasing the lMAX, i.e., the length of the spherical harmonics expansion of the bubbles. However, the computational cost of the algorithm also increases when larger lMAX values are used.
Reducing h even further would increase the accuracy. However, the use of denser grids is not feasible for the single node implementation of the software used here due to memory limitations of the available hardware. Thus, testing the accuracy limits of our DFT implementation has to be left to the future, when we have implemented a multinode version of the approach.
7. Conclusions
We have developed and implemented a fully numerical method for molecular electronic structure calculations at the density functional theory (DFT) level using exchange-correlation functionals at the local density approximation (LDA) and the generalized gradient approximation (GGA). The numerical methods can be extended to hybrid functionals that mix DFT and Hartree–Fock (HF) exchange potentials, because methods for GGA and HF calculations have been developed, whereas implementation of range-separated functionals requires development of new algorithms.
The numerical algorithms used for calculating the exchange-correlation potential and energy contributions are presented in detail. In our bubbles and cube approach, we expand the steep part of the functions in one-center atom-like contributions and the remainder is expanded on an equidistant grid. We also discussed a simple way to calculate gradient for the bubbles part and real spherical harmonics expansions in general. The accuracy of our approach was demonstrated by performing calculations on atoms and small molecules at the LDA level and at the GGA level using the PBE functional. The obtained energies were compared with values calculated using multiwavelet codes. The accuracy can be improved by using larger grid sizes, which require more memory and increase the computational effort. The computational time and memory requirement increase linearly with the number of grid points.
The LDA and PBE calculations demonstrate that chemical accuracy can be achieved using our approach. Excellent accuracy is easily obtained at the LDA level even when relatively sparse grids are employed. The calculations showed that it is hard to reach a very high accuracy at the GGA level due to the uncertainies introduced by numerical differentiation of the electron density. A few extra computational steps had to be introduced in order to improve the accuracy of gradient of the electron density for obtaining sufficiently precise energies.
Presently, we use a single-node implementation without utilizing the parallelization of the recently developed grid-based fast multipole method (GBFMM),19,41 which limits the size of the grids that are currently feasible. Consequently, the accuracy of the PBE calculations leaves room for improvement. Although, multinode parallelization of the calculation of the DFT contributions to energy and the exchange-correlation potential should be a relatively simple to implement, an efficient implementation needs some considerations. The GPGPU parallelization of the DFT part will therefore be implemented later.
Acknowledgments
This research has been supported by the Academy of Finland through Project 275845 and by the Magnus Ehrnrooth foundation. CSC IT Center for Science, Finland and the Finnish Grid and Cloud Infrastructure (FGCI) are acknowledged for computer time.
Appendix A: Gradient of Real Spherical Harmonics Expansions
The gradient of the real spherical harmonics expansion
| 14 |
can be calculated using the product rule
| 15 |
where
 |
16 |
The real spherical harmonics, Yl,m, can be represented as a product of the solid harmonics, Sl,m, divided by the corresponding power of the distance from the center of the expansion, r as
| 17 |
The corresponding gradient can analogously be expressed as
| 18 |
Simple recursion relations can be derived for eq 18 by using Cartesian coordinates. The first four values of the solid harmonics in Cartesian coordinates are
| 19 |
The solid harmonics of higher order can be obtained using the well-known recursion relations
 |
20 |
where 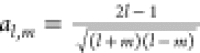 ,
, 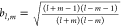 , and
, and 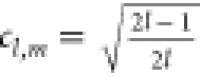 . From eq 20 one sees that differentiation
of solid harmonics with
respect to the z direction can be expressed as
. From eq 20 one sees that differentiation
of solid harmonics with
respect to the z direction can be expressed as
| 21 |
where
 |
In x and y directions, the corresponding expressions become
| 22 |
| 23 |
where
 |
and
 |
The auxiliary functions nl,m, ol,m, and pl,m are defined as
 |
 |
 |
Combining the above equations shows that the gradient of a solid harmonics expansion is another solid harmonics expansion, implying that gradients of the bubbles expansions can be accurately represented by using bubbles objects.
The authors declare no competing financial interest.
References
- Becke A. D. Perspective: Fifty Years of Density-Functional Theory in Chemical Physics. J. Chem. Phys. 2014, 140, 18A301. 10.1063/1.4869598. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Schmidt K. Jacob’s Ladder of Density Functional Approximations for the Exchange-Correlation Energy. AIP Conf. Proc. 2000, 577, 1–20. 10.1063/1.1390175. [DOI] [Google Scholar]
- Boys S. F. Electronic Wave Functions I. A General Method of Calculation for the Stationary States of Any Molecular System. Proc. R. Soc. London, Ser. A 1950, 200, 542–554. 10.1098/rspa.1950.0036. [DOI] [Google Scholar]
- Jensen S. R.; Flå T.; Jonsson D.; Monstad R. S.; Ruud K.; Frediani L. Magnetic Properties with Multiwavelets and DFT: The Complete Basis Set Limit Achieved. Phys. Chem. Chem. Phys. 2016, 18, 21145–21161. 10.1039/C6CP01294A. [DOI] [PubMed] [Google Scholar]
- Jensen S. R.; Saha S.; Flores-Livas J. A.; Huhn W.; Blum V.; Goedecker S.; Frediani L. The Elephant in the Room of Density Functional Theory Calculations. J. Phys. Chem. Lett. 2017, 8, 1449–1457. 10.1021/acs.jpclett.7b00255. [DOI] [PubMed] [Google Scholar]
- Jensen F. How Large is the Elephant in the Density Functional Theory Room?. J. Phys. Chem. A 2017, 121, 6104–6107. 10.1021/acs.jpca.7b04760. [DOI] [PubMed] [Google Scholar]
- Feller D.; Dixon D. A. Density Functional Theory and the Basis Set Truncation Problem with Correlation Consistent Basis Sets: Elephant in the Room or Mouse in the Closet?. J. Phys. Chem. A 2018, 122, 2598–2603. 10.1021/acs.jpca.8b00392. [DOI] [PubMed] [Google Scholar]
- Becke A. D. A. Multicenter Numerical Integration Scheme for Polyatomic Molecules. J. Chem. Phys. 1988, 88, 2547–2553. 10.1063/1.454033. [DOI] [Google Scholar]
- te Velde G.; Baerends E. Numerical Integration for Polyatomic Systems. J. Comput. Phys. 1992, 99, 84–98. 10.1016/0021-9991(92)90277-6. [DOI] [Google Scholar]
- Franchini M.; Philipsen P. H. T.; Visscher L. The Becke Fuzzy Cells Integration Scheme in the Amsterdam Density Functional Program Suite. J. Comput. Chem. 2013, 34, 1819–1827. 10.1002/jcc.23323. [DOI] [PubMed] [Google Scholar]
- Treutler O.; Ahlrichs R. Efficient Molecular Numerical Integration Schemes. J. Chem. Phys. 1995, 102, 346–354. 10.1063/1.469408. [DOI] [Google Scholar]
- Köster A. M.; Flores-Moreno R.; Reveles J. U. Efficient and Reliable Numerical Integration of Exchange-Correlation Energies and Potentials. J. Chem. Phys. 2004, 121, 681–690. 10.1063/1.1759323. [DOI] [PubMed] [Google Scholar]
- Kong J.; Brown S. T.; Fusti-Molnar L. Efficient Computation of the Exchange-Correlation Contribution in the Density Functional Theory Through Multiresolution. J. Chem. Phys. 2006, 124, 094109. 10.1063/1.2173244. [DOI] [PubMed] [Google Scholar]
- Rodríguez J. I.; Thompson D. C.; Ayers P. W.; Köster A. M. Numerical Integration of Exchange-Correlation Energies and Potentials Using Transformed Sparse Grids. J. Chem. Phys. 2008, 128, 224103. 10.1063/1.2931563. [DOI] [PubMed] [Google Scholar]
- Chang C.-M.; Russ N. J.; Kong J. Efficient and Accurate Numerical Integration of Exchange-Correlation Density Functionals. Phys. Rev. A: At., Mol., Opt. Phys. 2011, 84, 022504. 10.1103/PhysRevA.84.022504. [DOI] [Google Scholar]
- Sundholm D. Universal Method for Computation of Electrostatic Potentials. J. Chem. Phys. 2005, 122, 194107. 10.1063/1.1898206. [DOI] [PubMed] [Google Scholar]
- Losilla S. A.; Sundholm D. A. Divide and Conquer Real-Space Approach for All-Electron Molecular Electrostatic Potentials and Interaction Energies. J. Chem. Phys. 2012, 136, 214104. 10.1063/1.4721386. [DOI] [PubMed] [Google Scholar]
- Toivanen E. A.; Losilla S. A.; Sundholm D. The Grid-Based Fast Multipole Method - a Massively Parallel Numerical Scheme for Calculating Two-Electron Interaction Energies. Phys. Chem. Chem. Phys. 2015, 17, 31480–31490. 10.1039/C5CP01173F. [DOI] [PubMed] [Google Scholar]
- Parkkinen P.; Losilla S. A.; Solala E.; Toivanen E. A.; Xu W.-H.; Sundholm D. A Generalized Grid-Based Fast Multipole Method for Integrating Helmholtz Kernels. J. Chem. Theory Comput. 2017, 13, 654–665. 10.1021/acs.jctc.6b01207. [DOI] [PubMed] [Google Scholar]
- Losilla S. A.; Watson M. A.; Aspuru-Guzik A.; Sundholm D. Construction of the Fock Matrix on a Grid-Based Molecular Orbital Basis Using GPGPUs. J. Chem. Theory Comput. 2015, 11, 2053–2062. 10.1021/ct501128u. [DOI] [PubMed] [Google Scholar]
- Solala E.; Parkkinen P.; Sundholm D. Tensor Decompositions for the Bubbles and Cube Numerical Framework. Comput. Phys. Commun. 2018, 10.1016/j.cpc.2018.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolda T. G.; Bader B. W. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. 10.1137/07070111X. [DOI] [Google Scholar]
- Yanai T.; Harrison R. J.; Handy N. C. Multiresolution Quantum Chemistry in Multiwavelet Bases: Time-Dependent Density Functional Theory with Asymptotically Corrected Potentials in Local Density and Generalized Gradient Approximations. Mol. Phys. 2005, 103, 413–424. 10.1080/00268970412331319236. [DOI] [Google Scholar]
- Kobus J.; Laaksonen L.; Sundholm D. A Numerical Hartree-Fock Program for Diatomic Molecules. Comput. Phys. Commun. 1996, 98, 346–358. 10.1016/0010-4655(96)00098-7. [DOI] [Google Scholar]
- Kobus J. A Finite Difference Hartree-Fock Program for Atoms and Diatomic Molecules. Comput. Phys. Commun. 2013, 184, 799–811. 10.1016/j.cpc.2012.09.033. [DOI] [Google Scholar]
- Cohen O.; Kronik L.; Brandt A. Locally Refined Multigrid Solution of the All-Electron Kohn-Sham Equation. J. Chem. Theory Comput. 2013, 9, 4744–4760. 10.1021/ct400479u. [DOI] [PubMed] [Google Scholar]
- Fattebert J.-L.; Hornung R.; Wissink A. Finite Element Approach for Density Functional Theory Calculations on Locally-Refined Meshes. J. Comput. Phys. 2007, 223, 759–773. 10.1016/j.jcp.2006.10.013. [DOI] [Google Scholar]
- Lehtovaara L.; Havu V.; Puska M. All-Electron Density Functional Theory and Time-Dependent Density Functional Theory with High-Order Finite Elements. J. Chem. Phys. 2009, 131, 054103. 10.1063/1.3176508. [DOI] [PubMed] [Google Scholar]
- Bylaska E. J.; Holst M.; Weare J. H. Adaptive Finite Element Method for Solving the Exact Kohn-Sham Equation of Density Functional Theory. J. Chem. Theory Comput. 2009, 5, 937–948. 10.1021/ct800350j. [DOI] [PubMed] [Google Scholar]
- Bao G.; Hu G.; Liu D. An h-Adaptive Finite Element Solver for the Calculations of the Electronic Structures. J. Comput. Phys. 2012, 231, 4967–4979. 10.1016/j.jcp.2012.04.002. [DOI] [Google Scholar]
- Motamarri P.; Nowak M.; Leiter K.; Knap J.; Gavini V. Higher-Order Adaptive Finite-Element Methods for Kohn-Sham Density Functional Theory. J. Comput. Phys. 2013, 253, 308–343. 10.1016/j.jcp.2013.06.042. [DOI] [Google Scholar]
- Andrade X.; et al. Real-Space Grids and the Octopus Code as Tools for the Development of New Simulation Approaches for Electronic Systems. Phys. Chem. Chem. Phys. 2015, 17, 31371–31396. 10.1039/C5CP00351B. [DOI] [PubMed] [Google Scholar]
- Schauer V.; Linder C. The Reduced Basis Method in All-Electron Calculations with Finite Elements. Adv. Comput. Math. 2015, 41, 1035–1047. 10.1007/s10444-014-9374-z. [DOI] [Google Scholar]
- Engeness T. D.; Arias T. A. Multiresolution Analysis for Efficient, High Precision All-Electron Density-Functional Calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2002, 65, 165106. 10.1103/PhysRevB.65.165106. [DOI] [Google Scholar]
- Harrison R. J.; Fann G. I.; Yanai T.; Gan Z.; Beylkin G. Multiresolution Quantum Chemistry: Basic Theory and Initial Applications. J. Chem. Phys. 2004, 121, 11587–11598. 10.1063/1.1791051. [DOI] [PubMed] [Google Scholar]
- Yanai T.; Fann G. I.; Gan Z.; Harrison R. J.; Beylkin G. Multiresolution Quantum Chemistry in Multiwavelet Bases: Analytic Derivatives for Hartree–Fock and Density Functional Theory. J. Chem. Phys. 2004, 121, 2866–2876. 10.1063/1.1768161. [DOI] [PubMed] [Google Scholar]
- Mohr S.; Ratcliff L. E.; Genovese L.; Caliste D.; Boulanger P.; Goedecker S.; Deutsch T. Accurate and Efficient Linear Scaling DFT Calculations with Universal Applicability. Phys. Chem. Chem. Phys. 2015, 17, 31360–31370. 10.1039/C5CP00437C. [DOI] [PubMed] [Google Scholar]
- Kottmann J. S.; Höfener S.; Bischoff F. A. Numerically Accurate Linear Response-Properties in the Configuration-Interaction Singles (CIS) Approximation. Phys. Chem. Chem. Phys. 2015, 17, 31453–31462. 10.1039/C5CP00345H. [DOI] [PubMed] [Google Scholar]
- Frediani L.; Fossgaard E.; Flå T.; Ruud K. Fully Adaptive Algorithms for Multivariate Integral Equations Using the Non-Standard Form and Multiwavelets with Applications to the Poisson and Bound-State Helmholtz Kernels in Three Dimensions. Mol. Phys. 2013, 111, 1143–1160. 10.1080/00268976.2013.810793. [DOI] [Google Scholar]
- Durdek A.; Jensen S. R.; Juselius J.; Wind P.; Flå T.; Frediani L. Adaptive Order Polynomial Algorithm in a Multiwavelet Representation Scheme. Appl. Num. Math. 2015, 92, 40–53. 10.1016/j.apnum.2014.12.006. [DOI] [Google Scholar]
- Solala E.; Losilla S.; Sundholm D.; Xu W.-H.; Parkkinen P. Optimization of Numerical Orbitals Using the Helmholtz Kernel. J. Chem. Phys. 2017, 146, 084102. 10.1063/1.4976557. [DOI] [PubMed] [Google Scholar]
- Marques M. A.; Oliveira M. J.; Burnus T. Libxc: A Library of Exchange and Correlation Functionals for Density Functional Theory. Comput. Phys. Commun. 2012, 183, 2272–2281. 10.1016/j.cpc.2012.05.007. [DOI] [Google Scholar]
- Bloch F. Bemerkung zur Elektronentheorie des Ferromagnetismus und der Elektrischen Leitfähigkeit. Eur. Phys. J. A 1929, 57, 545–555. 10.1007/BF01340281. [DOI] [Google Scholar]
- Dirac P. A. M. Note on Exchange Phenomena in the Thomas Atom. Math. Proc. Cambridge Philos. Soc. 1930, 26, 376–385. 10.1017/S0305004100016108. [DOI] [Google Scholar]
- Vosko S. H.; Wilk L.; Nusair M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin-Density Calculations - a Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple (vol. 77, pg 3865, 1996). Phys. Rev. Lett. 1997, 78, 1396–1396. 10.1103/PhysRevLett.78.1396. [DOI] [PubMed] [Google Scholar]







