Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 May 2;34(20):5759–5771. doi: 10.1021/acs.langmuir.8b00650

Particulate Coatings via Evaporation-Induced Self-Assembly of Polydisperse Colloidal Lignin on Solid Interfaces

Oriol Cusola †,∥,*, Samu Kivistö ‡, Sampsa Vierros ‡, Piotr Batys †,‡,⊥, Mariko Ago †, Blaise L Tardy †, Luiz G Greca †, M Blanca Roncero ∥, Maria Sammalkorpi ‡, Orlando J Rojas †,§,*
PMCID: PMC6150720  PMID: 29718673

Abstract

graphic file with name la-2018-00650y_0007.jpg

Polydisperse smooth and spherical biocolloidal particles were suspended in aqueous media and allowed to consolidate via evaporation-induced self-assembly. The stratification of the particles at the solid–air interface was markedly influenced, but not monotonically, by the drying rate. Cross-sectional imaging via electron microscopy indicated a structured coating morphology that was distinctive from that obtained by using particles with a mono- or bimodal distribution. Segregation patterns were found to derive from the interplay of particle diffusion, interparticle forces, and settling dynamics. Supporting our experimental findings, computer simulations showed an optimal drying rate for achieving maximum segregation. Overall, stratified coatings comprising nano- and microparticles derived from lignin are expected to open opportunities for multifunctional structures that can be designed and predicted on the basis of experimental Péclet numbers and computational order.

Introduction

The structure of dried, consolidated film containing particles depends on several parameters such as those inherent to the particles (morphology, electrostatic charge, concentration, and glass transition temperature, Tg), the medium (rheology of the continuous system), and the drying conditions. Particle stratification can be useful in multifunctional coatings whose surface properties may differ from those of the layers located underneath, neighboring the solid support. Film formation effects are of paramount importance in applications such as layered coatings for adhesives, inks, paints, cosmetics, flexible electronics, and advanced materials. However, gaining control on the detailed structure of the dried films is the only way to facilitate the development of property spaces, for example, to adjust porosity and tortuosity, roughness and friction, plasmonic and optical performance, and permeability as well as conductivity (fluid, sound, or thermal).

The fundamentals of latex film formation have been thoroughly addressed by Keddie and Routh,1 who identified the main steps involved in the transformation of a dispersion into a continuous film. In brief, such process starts from a stable dispersion that consolidates under drying into a structure of given packing, depending on the deformation, interdiffusion, and coalescence. The deformation of the particles is driven by a combination of capillary, osmotic, and surface forces that may overcome the elastic modulus of the polymeric particles.2 For hard particles that are not subjected to deformation, the resulting films are expected to crack if the temperature at which they form is below the particle’s Tg.

The drying mechanisms of colloidal dispersions have been discussed in recent reports.1,3−7 Typically, particulate films tend to dry nonhomogeneously, leading to horizontal and vertical drying profiles, which are often investigated independent of each other. Experimentally, it has been observed that upon drying, the in-plane (horizontal) front may cause movement and flow of the particles in the same direction. However, their movement can be neglected in films formed with large lateral dimensions.8 Significant to our work is the observation that in such cases, out-of-plane or vertical stratification determines the microstructure of the resulting film.

The vertical distribution of particles involves a balance of the time scales for evaporation, diffusion, and sedimentation. The sedimentation can be neglected if the size of the particles is in the colloidal range. In this case, evaporation and Brownian diffusion become the two main competing processes. As the surface of the drying film recedes, the Brownian diffusion tends to distribute the particles evenly in the film, along the height, whereas the descending fluid front, i.e., via evaporation, places the system out of equilibrium. The time scales for diffusion and evaporation are H2/Do and H/Ė, respectively, where H is the film height (m), Do is the diffusion coefficient (m2/s), and Ė is the evaporation rate (m/s), related to the receding rate of the fluid front. The two time scales can be grouped in the dimensionless Péclet number (Pe)

graphic file with name la-2018-00650y_m001.jpg 1

where η is the viscosity of the solvent, R is the particle radius, k is the Boltzman’s constant, and T is the temperature.6 For Pe ≫ 1, particle diffusion is weak compared to evaporation, and a nonuniform particle distribution is expected, tending to form a close-packed structure on top of the film. For Pe ≪ 1, diffusion is faster than evaporation, and the particles tend to remain uniformly dispersed; thus, a homogeneous film will be formed.

Various experimental methods have been used to tune particle stratification, for example, by adjusting the values of the variables in the Péclet number, most simply, by changing the particle size and the drying rate. Trueman et al.8 used bimodal dispersions of latex particles to study the stratification and the structure of the formed films. Stratification of colloidal blends of large and small latex particles leading to Pe ≫ 1 were studied by Fortini et al.4 The experiments were combined with computational modeling to identify a gradient of osmotic pressure as the driving force that caused stratification. In other reports, stratified coatings were developed using pH-responsive polymethacrylic acid-modified colloids, which could be switched to homogeneous structures upon pH change.9 Besides experimental analyses, particulate stratification has also been thoroughly studied using mathematical modeling and simulation of evaporation-, diffusion-, and sedimentation-driven systems.5,7,10−13 The evaporation-induced self-assembly (EISA) of hybrid systems containing mixtures of organic/inorganic particles is a field of interest in the scientific community. In the work by Luo et al.,14 some few processing variables were relevant to the formation of coatings comprising bimodal silica/latex dispersions. Cryo-scanning electron microscopy (SEM) images of the cross sections of drying films revealed the formation sequence in the coating microstructure. Finally, radiation-assisted evaporation of blends of gold and polymer nanoparticles was used to obtain two-dimensional nanogrids with photonic and plasmonic effects.15

Lateral effects that emerge upon drying can also be relevant in the arrangement of particles. For example, uneven drying conditions, along a given area in a coating layer, may generate a lateral flow that is effective in assembling nanoparticles into directed architectures. Such effects can be attained by using a heat-generating element (for example, an infrared lamp) and a mask, known as infrared-assisted evaporative lithography. This method has been used by several authors do develop topographically patterned coatings.16,17

The study of the out-of-plane or vertical particle distribution in the films, especially when using soft latex particles, requires “freezing” the structure at the desired stages of drying. This enables the imaging of particle distribution before film deformation and consolidation. Atomic force microscopy is commonly used to access the final, dried films. However, this technique only provides surface information and, in the case of films consolidated from latex, the particles may not be visible. Thus, GARField NMR is an attractive option because it provides indirect information on the film structure by quantification of the unbound water remaining throughout the height of the film.18 This technique allows identifying “skin” effects in the drying film, but it cannot provide the morphological information, such as particle size distribution and film porosity.

Although bimodal and trimodal particle systems have been used in some of the few efforts cited previously, the case of polydisperse systems has remained unexplored. This is surprising because most of the industrial powders and particles in common use, for example, inks, paints, and coatings, are inherently polydisperse, i.e., exhibit a broad distribution of sizes. Therefore, it is essential to investigate, by means of experimental, computational, and analytical methods, the stratification involved in such polydisperse systems. Of further interest is the fact that work reported during the last several decades has considered stratification effects only for latexes, acrylic copolymers, metal (gold and silica), and other inorganic materials. However, self-assembly and stratification of particles comprising biopolymers have been neglected even though they provide enticing possibilities in the production processes and in products, especially if they are renewable and biodegradable. In this regard, lignin particles (LPs), which have emerged recently as interesting biocolloids, can bring truly unique opportunities. Indeed, lignin is present in plant cell walls as a complex, amorphous polymer of phenylpropane units linked by a large number of bond types. Lignin has several functions in plants, including structural functions. Over the years, the traditional industrial processes that convert lignocellulosic materials into goods have treated lignin as a byproduct for energy recovery. However, the advent of biorefineries for cellulosic biomass conversion into value-added streams has triggered the development of new sugar and polymer constructs as well as bioproducts. This has raised the prospects of lignin given its expected availability. Nowadays, lignin is used as a dispersant, adhesive, and binder, which are still niche applications. However, lignin represents an interesting source for the development of advanced materials. This is achieved by taking advantage of its antioxidant, UV-blocking, antimicrobial, and other properties. For example, when incorporated in composites, it can provide increased mechanical, thermal, and barrier effects.19

Recently, an increased interest has been observed in structuring lignin in the form of spherical micro- and nanoparticles.20,21 Spherical lignin particles can bring several advantages compared to the amorphous counterparts, for example, in coatings, emulsions, and composite materials. Among the advantages of using nanosized, spherical particles, one can cite (a) achieving large surface area-to-volume ratio, which improves the solubility and boost given properties, such as antioxidant activity; (b) making materials stronger while often being lighter; (c) increasing light absorption; and (d) enabling faster reactions, useful in catalysis.22 These interesting properties have stimulated the demonstration of lignin particles for Pickering emulsions20,23 and as fillers to improve the mechanical properties of polymer blends.24,25 However, to our knowledge, the synthesis of films and coatings from lignin particles have not been attempted so far.

Here, we used experimental and computational approaches to investigate the polydisperse lignin particles (LPs) undergoing evaporation-induced self-assembly. The results offer, for the first time, a discussion about effects relevant to LP stratification and consolidation, upon drying, on solid supports. The results demonstrate particulate lignin systems with tunable structure and porosity. We show that the drying rate is a controlling factor that defines the coating structure. Our findings are expected to open new applications for LP in coatings, paintings, and advanced catalysts.

Experimental and Computational Methods

Synthesis of the Lignin Particles (LPs)

The lignin particles were produced with an aerosol-flow reactor according to our recently reported method.20 Briefly, kraft lignin was dissolved in dimethylformamide and used as precursor solution. The lignin particles were synthesized using a collison-type jet atomizer with nitrogen gas as carrier. The generated droplets were suspended at a nitrogen gas flow rate of 3 L/min and carried to a heated laminar flow stainless steel tube with an inner diameter and length of 30 and 80 mm, respectively, and kept at 153 °C. During flow-through, the droplets were dried into solid particles, which were subsequently cooled and diluted at the reactor downstream with a turbulent air flow volume of 30 L/min before collection.

EISA of the Lignin Particles

The obtained particles were used to produce coatings on solid supports. The LPs were casted with a micropipette on silica substrates. The initial volume fraction of the LP suspension was 4%. To prepare the suspensions, the given amount of LP and double distilled water were mixed in plastic vials under a vortex agitator for a minute. Thereafter, the mixture was submitted to ultrasound treatment in a bath for a minute. Before casting, the silica wafers used as solid supports were thoroughly rinsed with acetone and Milli-Q water, dried with nitrogen, and final UV–O3 exposure for 20 min to eliminate any contamination.

To ensure reproducibility and identical coverage, the films were casted over a circular area of 177 mm2. A well was built onto the silica surface using a plastic laminate, using a wade punch to cut a hole in the adhesive laminate, which was subsequently applied onto the cleaned silica. The coatings were dried under different temperature conditions (20, 50, 80, and 110 °C) using a Full-Sight Glass Door Memmert oven equipped with a glass window to monitor the evaporation process. The fast evaporation at 110 °C produced no bubbles. The coatings were removed from the oven just after complete evaporation. To measure the drying rate, separate coatings were casted and placed into a moisture analyzer equipped with an infrared lamp, whose intensity was adjusted automatically to heat the sample at different temperatures. The weight loss upon film evaporation was monitored continuously until constant weight. The weight was translated into height values using the area of the films (1.77 cm2) and the density of the casting suspension (ρS), which was calculated from

graphic file with name la-2018-00650y_m002.jpg 2

where ρP and ρL are the densities of the particles and that of the dispersing liquid, respectively, and c is the particle concentration % (w/w).

SEM Analyses

Scanning electron microscopy (SEM) images of the cross section and the surface of the coatings were obtained using a Zeiss Sigma VP, Germany, with an acceleration voltage of 2 kV. Before imaging, the samples were sputtered with a 3 nm platinum layer. To study the cross section, the coatings were fractured and the images were taken in the central third of the fracture to avoid edge artifacts.

Image Analysis of the Cross Sections

The cross sections of the coatings were analyzed using ImageJ software by using three areas, namely, bottom, middle, and top. The size of the particles present in each layer was measured. For the void area determination, the images of the cross sections were thresholded to obtain binary images in which the pixels accounted for the RGB values corresponding to 0, 0, 0 (black) and 255, 255, 255 (white), which could be identified and quantified over a given area of A × B pixels (where A and B are arbitrary values) to obtain the void area in %.

Computational Methods

For additional insights into the EISA response, we modeled the effect of drying rate on a ternary mixture of colloidal, spherical particles with diameters dL = 230 nm, dM = 130 nm, and dS = 70 nm, where the subscript refers to large (L), medium (M), or small (S) sizes. Although in the experimental system, the particle diameters were between 50 and 2000 nm, we used a ternary set of particle sizes to simplify the computational effort. The sizes were assumed to correspond to the purely colloidal fraction of the systems (particles with diameter < 300 nm).

The modeling system consisted of initially randomly distributed particles that were confined to a simulation box with dimensions LxLyLz. The coordinates were set so that the colloidal coating formed along the xy-plane and the z-axis was perpendicular to it. As the model described a large area, periodic boundary conditions were applied in the x- and y-directions. In the z-direction, the volume available to the particles was capped by a model substrate at one end and by the air–water interface at the other end. The model substrate plane was at z = 0 throughout the simulation, and the air–water interface moved from an initial position (at z = 61.4 μm) to z = 4.0 μm at a constant rate. The moving of the interface was taken to model the drying of the EISA coating layer. The range covered by the air–water interface motion (film thickness change upon drying) was set to match in proportion the change in the drying water droplet height in the experiments. The system size in the xy-direction was Lx = Ly = 2.0 μm throughout the simulation. The system was set up so that particles were of equal density ρ = 1.39 g/cm3, matching bulk lignin. The initial volume fraction of the simulation box filled by the particles was 0.04, and each of the three particle populations made 1/3 of the total particle volume in the system. This corresponds to 514 large, 2848 medium, and 18 241 small particles. The consistency of the response and the effect of finite size effects were assessed using a system twice as large. Whereas the sediment thicknesses and sedimentation strength varied, qualitatively, the response persisted for the larger system.

The interaction between particles was modeled by a short-range repulsive Yukawa interaction, i.e., the particles were modeled as screened charged particles that interacted pairwise via

graphic file with name la-2018-00650y_m003.jpg 3

when rij < rc and 0 otherwise. Here, rij is the center-of-mass distance between particles i and j, di and dj are the particle diameters, and 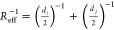Inline graphic is their effective radius following the Derjaguin approximation. The relative permittivity of the medium εr = 80, the colloidal particle surface potential ϕ = 25 mV, the inverse screening parameter κ–1 = 5 nm, and ε0 is the permittivity of the vacuum. The colloidal particle surface potential and the screening parameter were thus chosen to ensure a stable, nonsettling colloidal system with physically reasonable characteristics. The Yukawa potential was cutoff at a distance corresponding to 1% of the contact energy.

The air–water interface was modeled as a harmonic wall Uw(rw) = k(rw – di)2, when rw < di and 0 otherwise. Here, rw is the distance of the center of mass of the particle to the wall and k = 40ϵdi2 a harmonic force constant. The interaction with the substrate followed numerically the purely repulsive Lennard-Jones potential

graphic file with name la-2018-00650y_m005.jpg 4

where rs is the distance of the center of mass of the particle to the substrate, the parameter σ = 100 nm, and the energy scale ϵ converted to SI units ϵ = 1.39 × 10–19 J.

A note of caution is that our approach did not consider evaporation-induced particle segregation at the air–water interface. The effects associated with surface tension and liquid evaporation from the interior of the film were also neglected. In fact, owing to the simplicity of our model, the contributions of van der Waals, capillary forces, and structure formation at the air–water-particle interfaces were omitted. However, they are most relevant to the latter stages of drying and, therefore, critical for any description of adhesive interactions between particles or cracking stresses in coatings. Obviously, a model to accurately capture such factors would be extremely complex. Despite these issues, we believe that the validity of our model in describing the experimental observations is justified because the simulations ended before the effects mentioned above became dominant. Moreover, their influence on the large-scale, bulk segregation of particles is limited relative to those represented by our evaporation model.

We assumed that colloidal particles followed Langevin dynamics26

graphic file with name la-2018-00650y_m006.jpg 5
graphic file with name la-2018-00650y_m007.jpg 6

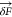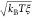where m is particle mass, a⃗ is the acceleration, and U is the internal energy of the colloidal particles comprising of the pairwise Yukawa potential Up and possible interactions with the air–water interface Uw or the substrate Us. r⃗i is the position of particle i, v⃗ is the velocity, and Inline graphic is a random force that follows a Gaussian distribution of width Inline graphic. Here, kB is the Boltzmann constant and T = 0.03ϵ/kb is the temperature. The reduced unit temperature was set to correspond to approximately room temperature (the experimental measurement temperature). The friction coefficient ξ = 3πηdi was set by the solution viscosity η. Here, a value of η = 0.89 mPa s, corresponding to water at room temperature, was employed. Langevin dynamics captures the Brownian diffusion of the particles but neglects the dynamic contributions that originate from the hydrodynamic flow.26

The ordering of the particles was measured in the simulations by an order parameter Q6(27)

graphic file with name la-2018-00650y_m010.jpg 7

Here, ⟨Ylm⟩ = ⟨Ylm(θ(r⃗ij), φ(r⃗ij))⟩ is the mean of the spherical harmonic functions of degree l = 6 and order m is calculated over the standard spherical coordinate angles θ and φ, corresponding to the position vectors to the neighboring same-sized particles r⃗ij for each particle i. Here, the asterisk denotes complex conjugation. A neighboring particle was defined as a particle of the same size and residing within a cutoff rcut = 1.3d, where d is the particle diameter. The cutoff was chosen so to capture effectively the nearest neighbors but to exclude the second nearest neighbors in a close-packed structure. The reported order parameter value was an average over all the particles of that size ⟨Q6⟩.

Results and Discussion

LP Coatings and Morphology

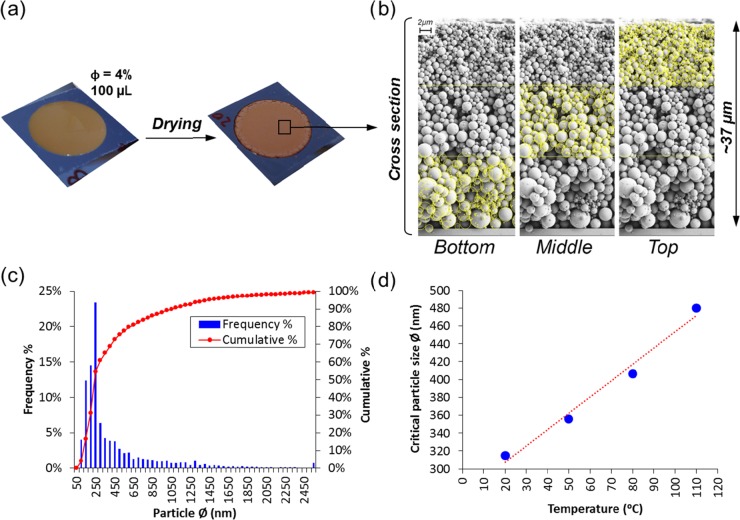
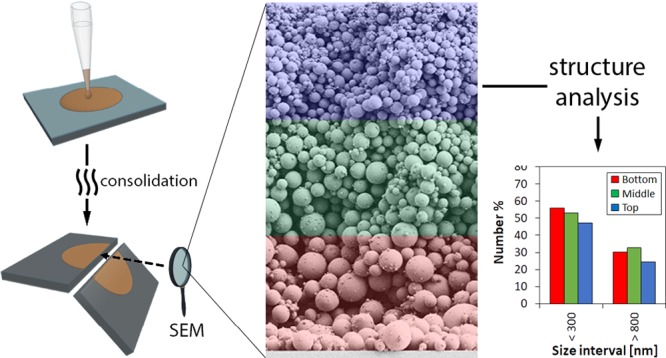
Lignin particles (LPs) were casted and dried under controlled conditions. Once dried, smooth and homogeneous coatings were observed macroscopically (Figure 1a). The coating layers were fractured and imaged (SEM) to study particulate stratification along the out-of-plane direction of the coating, which were divided into three equidistant layers for analysis: bottom (B), middle (M), and top (T), Figure 1b. The particle size profile was identified in each layer via image analysis and a polydispersity index of 1.2 was determined from the Sauter diameter d32 (volume-to-surface area) distribution from 23 kiloparticles (kps) counted. As the histogram in Figure 1c shows, the particles in the 150–300 nm size range were the most abundant; the cumulative analysis indicated that the median particle size was 250 nm, which was used as the threshold value to classify the “small” and “large” size fractions.

Figure 1.

Figure 1

Open in a new tab

Coatings comprising lignin particles assembled on silica wafers before and after drying from a dispersion with 4% volume fraction (a). A representative cross section of the coating is shown in (b) and divided for image analysis in three sections in the out-of-plane direction (bottom, middle, and top). The histogram showing the particle size distribution, by number %, is shown in (c) for a particulate population of 23 000 units (23 kps) (c). The critical particle size setting the boundaries of colloidal stability is shown as a function of drying temperature, indicating a linear relationship (R2 = 0.982) (d).

The stratification by the size of the particles is evident in Figure 1b, but the polydispersity of the sample adds a high degree of complexity, and the limit between particles of true “colloidal” size and those that settle under gravity is not obvious; this is especially relevant in the case of particles of low density, such as LP, where the size threshold for colloidal behavior may be larger compared to that for metal or inorganic particles. Therefore, before studying the stratification effects, we identified the size threshold for LP colloidal stability.

The particle motion characteristic of colloidal dispersions (constant and erratic Brownian motion) can hold small particles fully suspended for an indefinite time. As the particle size is increased, the effects of Brownian motion become more limited and large particles tend to settle under gravity if their density (ρP) and that of the dispersing liquid (ρL) are different enough (ρP > ρL). Transport processes fix the lower limits of colloidal stability in a gravitational field. Therefore, the critical (or lowest) particle size for which Brownian motion remains dominant can be obtained by equating the shift produced by Brownian motion to that produced by the gravity-induced sedimentation. In a polydisperse system, such limiting particle size allows identifying threshold value for particles behaving as “colloids” or as settling units.28−30 Einstein derived the translational motion of particles undergoing Brownian diffusion as

graphic file with name la-2018-00650y_m011.jpg 8

where x̅ is the shift due to Brownian motion at a certain time t and D is the Einstein’s diffusion coefficient. In the case of spheres, and under laminar flow, particles diffuse according to the Stokes–Einstein equation

graphic file with name la-2018-00650y_m012.jpg 9

where kB is the Boltzman’s constant (1.38 × 10–16 g cm2/s2 K), T is the temperature in K, η is the viscosity of the medium, and R is the radius of the particles. On the other hand, the Stokes’ law of sedimentation gives the distance traveled by spherical particles upon sedimentation in the period of constant velocity fall

graphic file with name la-2018-00650y_m013.jpg 10

where h is the distance traveled by the spherical particles in time t and g is the acceleration of the gravity. Combining eqs 8–10, we obtain

graphic file with name la-2018-00650y_m014.jpg 11

which gives the critical particle size for which the shift produced by Brownian motion equals the distance traveled due to sedimentation. In the present work, we considered four drying conditions and, as can be seen from eq 9, the critical size depends on T, the viscosity η, and density of the medium (water) ρL. The critical particle size was calculated for the different drying temperatures assuming a density of 1.4 g/cm3 for the lignin particles,31 and as Figure 1d shows, a linear correlation was apparent between the critical size and the drying temperature.

Particle Stratification

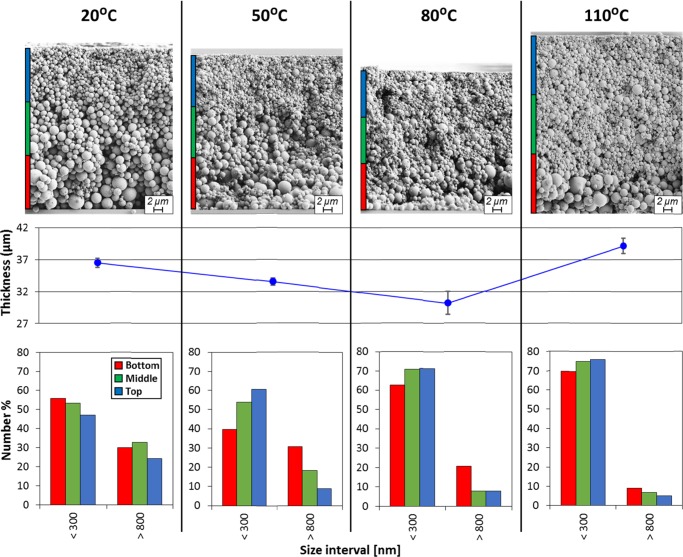
The cross sections of the coatings dried under different conditions are shown in Figure 2, and to ensure proper discrimination of the colloidal fractions, we used the calculated ∼315 nm as the lower limit for the critical size for particles dried at 20 °C (Figure 1d). The limit size for colloidal behavior was set at 300 nm, i.e., particles with sizes <300 nm were assumed to behave as colloids. Noting that there is a distribution of colloidal particles in the range below 300 nm, different Péclet numbers (eq 1) can be calculated, corresponding to different behaviors upon drying. Theoretically, all the particles with sizes larger than the critical value would experience settling. However, in polydisperse systems, convective effects and hindered settling phenomena, make it difficult for any effort to set the boundaries for colloidal behavior. For instance, it is not certain if the particles with sizes slightly higher than 300 nm behave either as colloids or not; to simplify, we removed the particles in the 300–800 nm size range from the analysis. Thus, the stratification effects were identified by grouping the particles into two bins or fractions, namely, those between 0 and 300 nm (colloids) and >800 nm (settling particles), and we investigated how drying affects the particles contained in these fractions, as a whole.

Figure 2.

Figure 2

Open in a new tab

From top to bottom: SEM cross sections, coating layer thickness, and number distribution by particle size for the bottom, middle, and top layers of the particulate assemblies formed under different drying conditions (temperatures). In all cases, the initial volume fraction of LPs was the same (same number of particles). For simplicity and comparison purposes, the particles were divided into 2 bins or fractions, namely, colloidal (<300 nm) and “settling” particles (>800 nm). The layer thickness (out-of-plane direction) was divided into three equidistant zones, bottom, middle, and top, identified with different colors as a guide to the eyes.

The diffusion effects upon drying can be identified in Figure 2. First, taking into account the colloidal fraction in the upper layer of the assembled particles (identified with a blue bar on the side, as a guide), there is a clear tendency for this layer to increase the number of the small particles with the drying rate. This is caused by the increasing rate of the descending liquid–air interface upon drying, so that the colloids do not have enough time to diffuse to lower regions in the structure.4,8,15 Considering the number of colloids in the middle and bottom layers (shown with the green and red bars drawn on the side), one would expect a continuous decrease upon drying. However, the experimental results showed an initial decrease for the coatings dried at 20 and 50 °C, followed by an increase for those dried above 50 °C (cases at 80 and 110 °C are shown). This observation may be explained by the contribution of lateral interactions, which affect specially the colloidal size fraction. When the particles consolidate into a close-packed solid near the particulate edge (air–liquid interface), upon evaporation, a flux of material from the fluid center toward the consolidated edge makes the particles move in the same direction, propagating the front of close-packed particles across the system.1 For slow drying (drying at 20 °C), there was enough time for the colloids to flow toward the drying edge. On the contrary, for particle dispersions subjected to fast drying, the consolidation of the systems is so fast that a large number of colloids remained “locked” in the middle section of the coating layer. Thus, even if the initial volume fraction was the same in all the systems, the number density of small particles in the coatings dried at high temperature (80 and 110 °C) was larger in all the layers of the cross sections. This effect can be observed clearly in the cross sections shown in Figure 2. The accumulation of larger quantities of material in the middle part of the coating area produced an increased layer thickness, Figure 2. This is further evidence that lateral effects cannot be neglected in this system.

The LP colloidal diffusion and distribution along the different layers in each individual cross section was also strongly dependent on the drying rate. Thus, when the drying rate was very slow, as for the system dried at 20 °C, the colloids had enough time to diffuse away from the moving interface. Indeed, one can even find a larger number density of colloids in the bottom layer of the cross section (Figure 2). Besides diffusion, the assembly of the bottom layer was also favored by the downward dragging effect that the settling particles may cause on the diffusing colloidal fraction. For simplicity, we considered a regime in which particles were allowed to diffuse and settle freely, cognizant that the diffusion and settling may be both hindered by the surrounding particles as the particle number density increases upon drying. The phenomenon discussed above is not evident in the images because the very small colloids cannot be identified at the magnification used for the cross sections shown in Figure 2. As the drying rate increased, the segregation of the colloids along the cross section reversed, and larger number of colloidal particles assembled in the top layer of the cross sections of coatings after drying at 50, 80, and 110 °C. The segregation reached a maximum in the coating dried at 50 °C and tended to decrease at higher temperatures (drying rates). This can be explained by the very fast drying tending to “lock” the colloids in its initial position along the layer. Therefore, fast drying promoted the accumulation of colloids on the receding liquid–air interface, but when the drying was very fast, the layers tended to form maintaining their initial particle distribution along the thickness. The lower segregation at higher temperatures can also be explained by the increased concentration of colloids in the whole cross section caused by the reduced lateral flow, as discussed previously.

The effects of drying rate on the settling particles, i.e., those having a diameter >800 nm, were identified from the histograms from the cross sections (Figure 2). A clear depletion on the large, settling particles occurred in the bottom layer with increasing drying rate. This was expected because the fast evaporation rates did not allow enough time for the settling particles to reach the bottom of the coating, and they were locked in the upper layers. Then, one would have expected, with the increased drying rate, to find a higher number of the large particles (>800 nm) in the middle and top layers; this was not the case in the histograms in Figure 2. This is explained because of the increased concentration of small particles in the whole cross section at high temperatures (due to lateral effects, as explained previously) that prevented the observation (by SEM) of the large particles due to a “masking” artifact. Nevertheless, some particles of about 2 μm in diameter were seen in the top layer of the cross sections images of the coatings dried at high temperatures; in contrast, this did not hold for the top layer of the coating dried under 20 °C.

The distribution of particles in coatings was studied by modeling and also experimentally by Cardinal et al.3 The behavior of the systems accounting Brownian diffusion, sedimentation, and evaporation were assessed using drying regime maps that predicted the development of the coating microstructure. They observed similar structure formation as in our case, but with a bimodal silica dispersion containing particles sizes of 1 μm and 200 nm, with a top layer entirely composed of smaller particles and a bottom one with the small particles dispersed between large particles. Wu and co-workers32 also observed the particle size gradients through the thickness of coatings of polydisperse calcium carbonate, where the smaller particles accumulated on the surface, whereas larger particles settled.

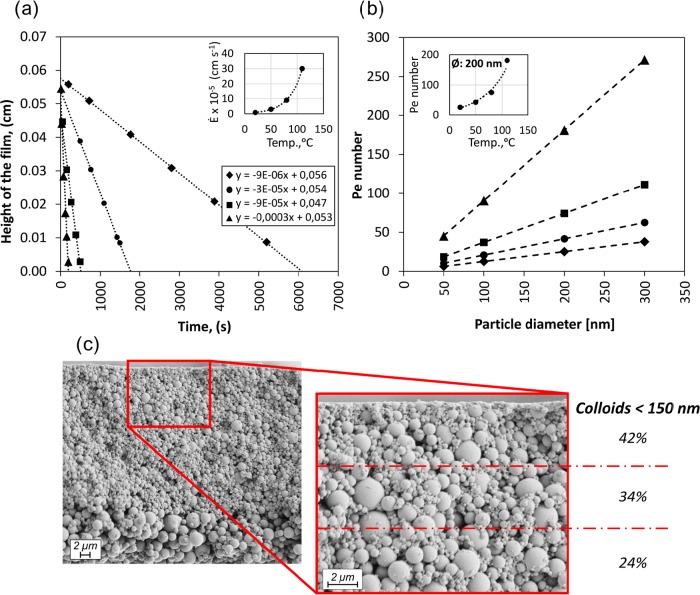
To inquire further into these interesting observations, Figure 3a shows the profiles corresponding to the displacement of the coating top interface upon drying at given different temperatures. The profiles fitted linear equations, whose slope allowed identification of the drying rates. The obtained drying rates showed an exponential relationship with temperature, inset in Figure 3a. With the drying rates, the Péclet numbers were calculated for the colloidal fraction of the coating formed at the given temperature, Figure 3b. All the Péclet numbers were higher than unity, which means that the diffusion of all the colloidal particles was slow compared to the evaporation rates. Accordingly, for these Péclet numbers, all the colloids would accumulate near the descending interface, producing a homogeneous layer of colloidal material on top of the settled material in the dried coating. However, given the polydisperse nature of our system, we observed also stratification within the colloids in the upper layer of the cross sections, with a tendency for the smaller particles to locate atop the larger ones (Figure 3c).

Figure 3.

Figure 3

Open in a new tab

Changes in the receding air–dispersion interface over time as a function of drying temperature (a). The inset corresponds to the evaporation rate as a function of temperature. The relationship between Péclet number and particle size is illustrated with the profiles in (b). The inset corresponds to a plot of the Péclet number as a function of drying temperature for 200 nm LP. The SEM cross section of a coating or particle assembly after drying at 110 °C is shown in (c) with a detailed view of the distribution of colloids of size <150 nm, within the top layer. Symbol nomenclature: ◆: 20 °C; ●: 50 °C; ■: 80 °C; ▲: 110 °C.

Modeling of LP Particulate Coatings

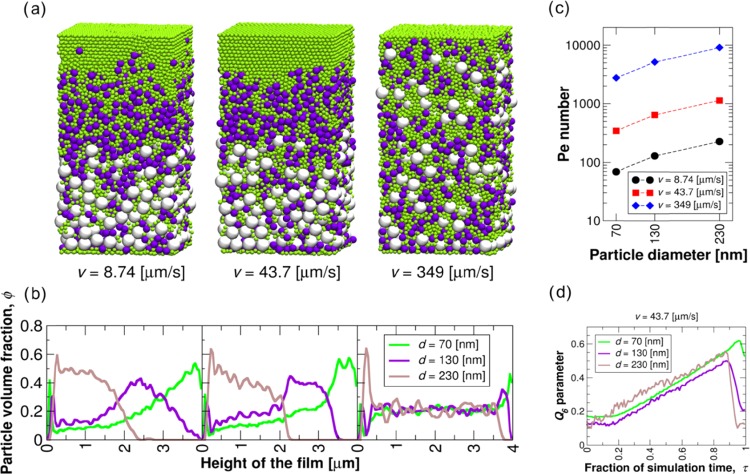
To resolve the origins of the observed behavior of the LP colloidal fraction and to gain additional insights into the observed stratification in the upper layer, we modeled the behavior of the colloidal fraction of the particles by assuming a ternary mixture of spherical particles under varying drying rates. Figure 4 includes a summary of the sedimentation response obtained in the simulations via graphical visualization, analysis of the particle distribution in terms of occupied volume, the Péclet numbers, and the time evolution of the Q6 order parameter for the three particle populations. The simulations indicated that for the colloidal particle population described here, the strength of stratification was strongly dependent on the drying rate, as seen in Figure 4a,b, which show both visually and via the calculated particle volume fraction the dependency for three different drying rates. As expected, slower drying favored a dominant Brownian motion effect and a mixing of the particles occurred. However, the data show that the least degree of mixing of particles sizes in the out-of-plane (z) direction was obtained with the intermediate drying rate. Also, a faster rate deteriorated the ordering.

Figure 4.

Figure 4

Open in a new tab

Results from computational modeling assuming a LP population that included three different sizes, as shown in different colors (green, magenta, and white for small, medium, and large colloidal sizes), respectively. The graphical visualizations of simulated coatings are shown in (a), whereas the corresponding particle volume fraction distributions are included in (b). The Péclet numbers for the investigated drying rates and particle sizes are determined in (c). Q6 order parameter calculated for the coating dried at a rate 43.7 μm/s (d). The fraction of simulation time τ is the simulation time normalized by the entire duration of the drying process.

The simulations were conducted for drying under three different rates as measured by the velocity of the receding air–dispersion interface (8.74, 43.7, or 349 μm/s). These considered drying rates clearly exceeded those measured in the experiments, with the exception of the slowest one, which was of the same order. The higher rates used in the computation, compared to those in the experiments, were selected for the model system to equilibrate via Brownian motion at a significantly faster speed to that in the experiments. This is because (1) the system size was smaller and the formed coating was thinner and (2) the Péclet number ratio calculated between the large and small particles in the ternary mixture of the model system was smaller than measured experimentally, see Figure 4c for the Péclet numbers in the simulations. This is due to the smaller relative difference in the particle size. As a consequence, the modeled rates need to be significantly higher to capture similar response as in the experimental system.

The response was systematic for drying rates beyond the presented one and over small variations of particle sizes in the ternary mixture; however, quite intuitively, similar particle mixing deteriorated the ordering. Due to the better mixing of similar-size particles, the polydisperse experimental system showed, as expected, a gradual change in the colloid particle concentration as a function of distance from the interface, as Figure 3c. An optimal drying rate for a higher degree of stratification occurred from the combination of diffusion-led mixing of the particles and glassy particle jamming in the sediment due to a solvent evaporation that was faster than particle diffusion; at slow drying rates, the diffusion mixing dominated and at faster rates, particles locked in the bottom layer. An optimal stratification was obtained somewhere in the middle, where the particles could diffuse sufficiently to differ in the degree of settling ordering.

Fortini et al.4 reported similar behavior for blends of colloids with very different Péclet numbers (PeB = 100 and PeS = 14 for big and small colloids, respectively, PeB/PeS ≈ 7) joined by other very recent reports.5,7 Comparing experiments and simulations, they identified a gradient of osmotic pressure driven by the descending interface that pushed the larger particles away from the moving interface faster than it did the smaller ones. Figures 3b and 4c include the experiments with large difference in Péclet numbers for the big and small colloids and for the given drying ratios. PeB/PeS was always ∼6 in the experiments for the coatings dried at the various temperatures. For the simulations, the ratio varied between 2 and 3, but more rapid drying rates were consequently employed. Actually, the interplay of the Péclet number ratio and the drying rate drove the segregation of coatings of different particle compositions.

To assess the stratification process in the model system, the time evolution in Figure 4d of the Q6 order parameter was calculated for the particles in the coating dried at 43.7 μm/s. Here, τ = 0 corresponds to the beginning and τ = 1.0 to the end of drying. The data show that in the range 0.2–0.8τ, the largest particles underwent systematically the highest Q6 values, whereas the lowest order parameter value corresponded to the medium-sized particles. The higher value of Q6 for the large and small particles, in comparison to the medium-sized ones, is related to the presence of the substrate and the air/water interface. These limited the mixing of the small and the large particles. Interestingly, for each particle type, the profiles exhibited a maximum just before reaching the final thickness and then dropped significantly. We propose that this decrease in Q6 order parameter at the very last stages of drying is related to the increased compaction of the coating due to the moving interface pushing the smaller particles between the larger ones.

Although the Péclet ratio PeB/PeS was constant for all the drying conditions, significant differences were observed on the microstructure of the top surface or layer (Figure 5). As shown in the inset of Figure 3b, for a given particle size, the Péclet number increased exponentially with drying rate (temperature). Moreover, the segregation of the particles was more sensitive for low Péclet numbers, Figure 5. Thus, a lower number density of colloidal material was found on the top layer of the coating dried at the slower rates (Figure 5a). For faster drying conditions (Figure 5b–d), similar amount of colloidal material was observed on the top layer.

Figure 5.

Figure 5

Open in a new tab

SEM images of the top surface of coatings dried at different temperatures: 20 °C (a), 50 °C (b), 80 °C (c), and 110 °C (d). The red arrow in (d) indicates the unusual presence of particles of the largest size (>2 μm, normally, settling particles) on the top layer of the coating formed at the fastest drying rate (110 °C). The schematic illustration in (e) highlights the differences in the observed (⌀o) and actual (⌀a) diameters of the large particles that assemble atop the coating.

Note that large particles (∼1 μm) were observed on the surfaces, even if not clearly displayed because of the “burying” effect in the dried structure that somewhat hid them (see particles pointed with the red arrow in Figure 5d). This effect was driven by the colloidally enriched falling interface, resulting in an embedding of large particles into the colloidal fraction. As shown in Figure 5e, when two large particles of given sizes were embedded in a bed of small particles, the latter ones obscured the determination of the actual size of the former. The difference between the exposed and real size of the particles was higher for the large ones; therefore, for those particles, the sizing error was larger. Keeping this in mind, large particles, of about 1 μm, were identified on the surface of coatings obtained at a fast drying rate. Even larger particles (>2 μm, normally, settling particles) were observed on the top layer of the coating dried at the fastest drying conditions (110 °C), which were not seen in the other cases (red arrows in Figure 5d). This is explained by the very fast evaporation rate in these conditions, and in line with our hypothesis to explain the presence of large particles on the top layer.

Particle Packing Analysis

The dense packing of equal-size spheres into the so-called cubic close packing or hexagonal close packing cannot produce a higher packing density than that predicted by the well-known Kepler conjecture. This states that no packing of congruent balls in Euclidean three space has a density greater than that of the face-centered cubic packing with a density of π/√18 ≈ 0.74.33 Then, if smaller particles are blended with larger ones in the right proportion, the density of packing can be substantially increased, giving rise to the so-called second- and third-generational packing.

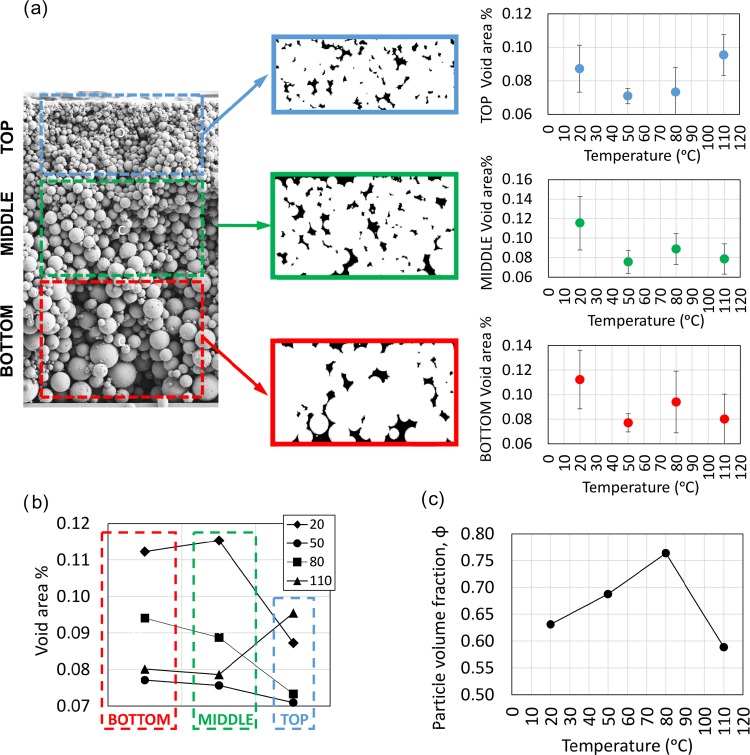
When considering real polydisperse systems, the particle size distributions, and therefore the ratio between large and small particles, may not be optimal for the highest packing density. Santiso et al.34 studied the packing of polydisperse systems and found that the packing fraction may be larger than the highest packing assumed for monodisperse systems, >0.74. In the present work, the areas of the coating layer devoid of particles were identified in the three layers of the cross sections by means of image analysis, Figure 6a. As shown in Figure 6b, the void area % in all the layers of the films dried at low rates (20 °C) was higher than those in the films dried at higher rates. This is indicative that the drying rate promoted a denser and tightly packed structure. These observations explain the obtained coating thickness displayed for the same condition in Figure 2. Considering the effect of drying rates within the layers (Figure 6a), the void area % remained constant except for the top layer of the coating dried at the fastest rate (110 °C). It appears that a higher drying rate promoted an increased porosity, especially for the top layer of the coatings, and this effect may be related to the higher number of large particles on the top (Figure 5). Due to the fast drying, very large particles assembled on the top, promoting a less-packed structure.

Figure 6.

Figure 6

Open in a new tab

Void area distribution for the different LP coating layers obtained after drying at given rates (or temperatures) (a). The coating sections, bottom, middle, and top, were analyzed via imaging to obtain the profiles shown on the right. The plot in (b) summarizes the change in void area for the three layer sections assembled at the given temperature. The total particle volume fraction in the coating layer as a function of the drying temperature is shown in (c).

The particle volume fraction in the coatings was extrapolated taking into account the volume of the coating (surface and thickness) and the LP density (1.4 g/cm3). As depicted in Figure 6c, the particle volume fraction ranged between 0.6 and 0.8, which agrees with the postulation of Santiso et al. for polydisperse systems.34 The particle volume fraction tended to increase with increasing drying rate (temperatures between 20 and 80 °C), but then decreased drastically at the highest drying rate (110 °C). This is in accordance with the increased void area % and our image analyses.

Lignin Particle Coatings and Prospects

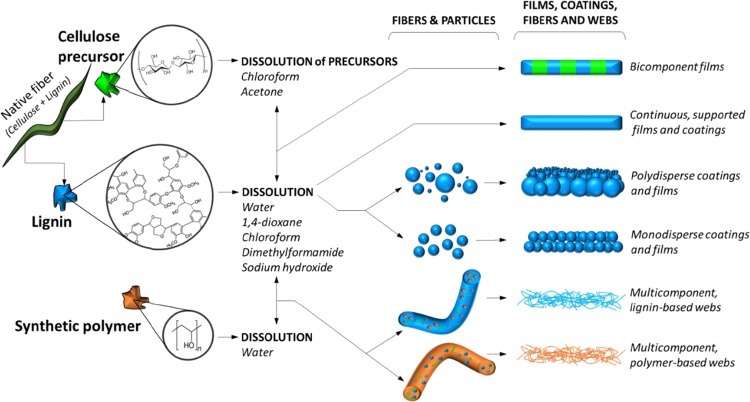
Lignin has been used to produce supported, continuous films to study enzyme and polymer adsorption35,36 and also in bicomponent films of cellulose–lignin to model the action of cellulases and adsorption of proteins (Figure 7).37,38 Lignin has also been used to produce fibers in electrospun mats. For example, Ago et al.39,40 obtained electrospun fibers with lignin as the main component in aqueous dispersions. They related the bulk composition of the fibers with the surface distribution of the polymer for tailoring webs for different applications. In all such efforts, lignin has been dissolved before the formation of films or fibers. However, lignin utilization in coatings, in the form of particulate coatings, has remained unexplored (Figure 7). There are many reasons to use micro- and nanoparticles, and in the case of lignin, their nanoparticles help preserving its structure, composition, and colloidal features.22 The closely related cellulose, in its native, regenerated, and nanostructured forms have been used to produce films, alone or in combination with synthetic polymers. In contrast to monodispersed particle systems, the use of polydisperse particles is highly relevant and attractive. For example, to enable high mechanical resistance, as in concrete and hard ceramics, extremely dense granular packing is needed, which is possible only if polydisperse systems are used.41 The polydispersity also has an influence on the permeation of fluids through the porous media. For instance, the permeability greatly depends on the stratification degree and the spatial and size distribution of the particles.42 Therefore, the adoption of polydisperse particulate systems allows tailoring the stratification and thus fluid transport. Moreover, low viscosities can be achieved with these systems when dispersed in a liquid medium,43 increasing the resistance to cracking, enhancing processability, making synthesis easier, among others. Thus, the results of the present study provides new insights into the use of lignin particles. While keeping the advantages of lignin as a macromolecule that forms renewable, organic particles, the possibility of synthesizing structured films and coatings self-assembled during drying44 brings a huge opportunity for the design or modification of novel material structures.

Figure 7.

Figure 7

Open in a new tab

Different approaches in which lignin can been used to produce films, coatings, fibers, and fiber webs. Cellulose, lignin, and synthetic polymers are represented in green, blue, and orange, respectively. Given the processing routes to achieve films35−38 and fibers and webs.39,40 The case of mono- and polydispersed films and coatings with particulate lignin systems brings a new dimension in the utilization of such renewable, widely available and inexpensive bioresource.20,22

Conclusions

We used, for the first time, lignin particles (LPs) to synthesize structured layers via evaporation-induced self-assembly into coatings and films. The structure of the LP assemblies correlated with drying rate, as determined both by experimental and simulation efforts. A colloidal threshold of 300 nm in size was calculated for the polydisperse particulate system by using the shift produced by Brownian motion and that of settling. The particle size measurements along cross-sectional analyses (SEM) allowed the identification of the diffusion effects upon drying, and the results revealed a clear increase in the number density of the particles of small sizes on the top layer formed at increased drying rates owing to the effects of the receding air–liquid interface. On the contrary, slow drying and dragging effects led to a more homogeneous distribution of the colloids in the out-of-plane direction of the coating. The colloidal segregation within the different coating layers reached a maximum at intermediate drying rates and tended to decrease at higher drying rates. A “locking” effect of the particles in the film dried at fast drying rates was found to be responsible for (i) lower colloidal segregation; (ii) accumulation of large particles on the top coating layer; (iii) increased thickness, and (iv) larger number of colloidal particles in the middle section of the film. The Péclet number for the colloidal fraction revealed that the formation of the coating layer was driven by evaporation rather than diffusion. However, stratification was observed within the colloids in the upper layers, with the smaller particles on top. We explored the origins of this observation by simulations and propose that the colloidal, polydisperse fraction has an optimal drying rate for maximal particular size segregation. This effect largely depends on the differences between the particulate Péclet numbers. The particle packing analysis revealed that by increasing the drying rates, it is possible to form dense and highly packed structures. However, extreme rates reverse this effect and promote an increased porosity, especially in the top layer of the coatings.

In sum, we demonstrated that it is possible to produce LPs coatings and films whose structure can be tuned by adjusting the drying conditions. This provides a first insight into the possibilities of using polydisperse LP-based systems for applications that could include coatings, catalysis, barrier materials, flexible electronics, drug-release, among others.

Acknowledgments

We acknowledge funding support by NordForsk Project “High-Value Products from Lignin”. O.J.R. is thankful for his ERC-2017-Advanced Grant-H2020, BioELCell (788489). O.C. acknowledges FILMBIOCEL (CTQ2016-77936-R) and funding from the “FEDER” and MICROBIOCEL projects (CTQ2017-84966-C2-1-R) within the framework of the Spanish’s MINECO as well as AGAUR 2017 SGR 30 at Universitat de Barcelona. The authors are grateful for the support by the Academy of Finland through Centres of Excellence Programme (2014–2019) under Project 264677 “Molecular Engineering of Biosynthetic Hybrid Materials Research” (HYBER). S.V. acknowledges funding by Aalto University School of Chemical Engineering doctoral programme. M.S. acknowledges funding by Academy of Finland. Computational resources by CSC IT Centre for Science, Finland, are also gratefully acknowledged.

Author Contributions

O.J.R. and O.C. conceived the idea and planned the research effort. M.A. provided the lignin particles and discussed their morphology. S.K., S.V., and P.B. developed the computational work under the direction of M.S., B.L.T., and L.G.G. shared their ideas and helped with the experimental work. All the authors contributed in the writing of the manuscript.

The authors declare no competing financial interest.

References

  1. Keddie J.; Routh A. F.. Fundamentals of Latex Film Formation, 1st ed.; Springer: Netherlands: Dordrecht, 2010. [Google Scholar]
  2. Ribeiro T.; Baleizão C.; Farinha J. P. S. Functional Films from Silica/polymer Nanoparticles. Materials 2014, 7, 3881–3900. 10.3390/ma7053881. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Cardinal C. M.; Jung Y. D.; Ahn K. H.; Francis L. F. Drying Regime Maps for Particulate Coatings. AIChE J. 2010, 56, 2769–2780. 10.1002/aic.12190. [DOI] [Google Scholar]
  4. Fortini A.; Martín-Fabiani I.; De La Haye J. L.; Dugas P.-Y.; Lansalot M.; D’Agosto F.; Bourgeat-Lami E.; Keddie J. L.; Sear R. P. Dynamic Stratification in Drying Films of Colloidal Mixtures. Phys. Rev. Lett. 2016, 116, 118301 10.1103/PhysRevLett.116.118301. [DOI] [PubMed] [Google Scholar]
  5. Fortini A.; Sear R. P. Stratification and Size Segregation of Ternary and Polydisperse Colloidal Suspensions during Drying. Langmuir 2017, 33, 4796–4805. 10.1021/acs.langmuir.7b00946. [DOI] [PubMed] [Google Scholar]
  6. Routh A. F.; Zimmerman W. B. Distribution of Particles during Solvent Evaporation from Films. Chem. Eng. Sci. 2004, 59, 2961–2968. 10.1016/j.ces.2004.04.027. [DOI] [Google Scholar]
  7. Makepeace D. K.; Fortini A.; Markov A.; Locatelli P.; Lindsay C.; Moorhouse S.; Lind R.; Sear R. P.; Keddie J. L. Stratification in Binary Colloidal Polymer Films: Experiment and Simulations. Soft Matter 2017, 13, 6969–6980. 10.1039/C7SM01267E. [DOI] [PubMed] [Google Scholar]
  8. Trueman R. E.; Lago Domingues E.; Emmett S. N.; Murray M. W.; Keddie J. L.; Routh A. F. Autostratification in Drying Colloidal Dispersions: Experimental Investigations. Langmuir 2012, 28, 3420–3428. 10.1021/la203975b. [DOI] [PubMed] [Google Scholar]
  9. Martín-Fabiani I.; Fortini A.; Lesage De La Haye J.; Koh M. L.; Taylor S. E.; Bourgeat-Lami E.; Lansalot M.; D’Agosto F.; Sear R. P.; Keddie J. L. PH-Switchable Stratification of Colloidal Coatings: Surfaces “on Demand.”. ACS Appl. Mater. Interfaces 2016, 8, 34755–34761. 10.1021/acsami.6b12015. [DOI] [PubMed] [Google Scholar]
  10. Dance S. L.; Maxey M. R. Particle Density Stratification in Transient Sedimentation. Phys. Rev. E 2003, 68, 031403 10.1103/PhysRevE.68.031403. [DOI] [PubMed] [Google Scholar]
  11. Zhou J.; Jiang Y.; Doi M. Cross Interaction Drives Stratification in Drying Film of Binary Colloidal Mixtures. Phys. Rev. Lett. 2017, 118, 108002 10.1103/PhysRevLett.118.108002. [DOI] [PubMed] [Google Scholar]
  12. Howard M. P.; Nikoubashman A.; Panagiotopoulos A. Z. Stratification Dynamics in Drying Colloidal Mixtures. Langmuir 2017, 33, 3685–3693. 10.1021/acs.langmuir.7b00543. [DOI] [PubMed] [Google Scholar]
  13. Wang M.; Brady J. F. Microstructures and Mechanics in the Colloidal Film Drying Process. Soft Matter 2017, 13, 8156–8170. 10.1039/C7SM01585B. [DOI] [PubMed] [Google Scholar]
  14. Luo H.; Cardinal C. M.; Scriven L. E.; Francis L. F. Ceramic Nanoparticle/monodisperse Latex Coatings. Langmuir 2008, 24, 5552–5561. 10.1021/la800050u. [DOI] [PubMed] [Google Scholar]
  15. Utgenannt A.; Maspero R.; Fortini A.; Turner R.; Florescu M.; Jeynes C.; Kanaras A. G.; Muskens O. L.; Sear R. P.; Keddie J. L. Fast Assembly of Gold Nanoparticles in Large-Area 2D Nanogrids Using a One-Step, Near-Infrared Radiation-Assisted Evaporation Process. ACS Nano 2016, 10, 2232–2242. 10.1021/acsnano.5b06886. [DOI] [PubMed] [Google Scholar]
  16. Georgiadis A.; Routh A. F.; Murray M. W.; Keddie J. L. Bespoke Periodic Topography in Hard Polymer Films by Infrared Radiation-Assisted Evaporative Lithography. Soft Matter 2011, 7, 11098–11102. 10.1039/c1sm06527k. [DOI] [Google Scholar]
  17. Utgenannt A.; Keddie J. L.; Muskens O. L.; Kanaras A. G. Directed Organization of Gold Nanoparticles in Polymer Coatings through Infrared-Assisted Evaporative Lithography. Chem. Commun. 2013, 49, 4253–4255. 10.1039/C2CC37844B. [DOI] [PubMed] [Google Scholar]
  18. Carter F. T.; Kowalczyk R. M.; Millichamp I.; Chainey M.; Keddie J. L. Correlating Particle Deformation with Water Concentration Profiles during Latex Film Formation: Reasons That Softer Latex Films Take Longer to Dry. Langmuir 2014, 30, 9672–9681. 10.1021/la5023505. [DOI] [PubMed] [Google Scholar]
  19. Espinoza-Acosta J. L.; Torres-Chávez P. I.; Ramírez-Wong B.; López-Saiz C. M.; Montaño-Leyva B. Antioxidant, Antimicrobial, and Antimutagenic Properties of Technical Lignins and Their Applications. BioResources 2016, 11, 5452–5481. 10.15376/biores.11.2.. [DOI] [Google Scholar]
  20. Ago M.; Huan S.; Borghei M.; Raula J.; Kauppinen E. I.; Rojas O. J. High-Throughput Synthesis of Lignin Particles (∼30 nm to ∼2 μm) via Aerosol Flow Reactor: Size Fractionation and Utilization in Pickering Emulsions. ACS Appl. Mater. Interfaces 2016, 8, 23302–23310. 10.1021/acsami.6b07900. [DOI] [PubMed] [Google Scholar]
  21. Zhao W.; Simmons B.; Singh S.; Ragauskas A.; Cheng G. From Lignin Association to Nano-/micro-Particle Preparation: Extracting Higher Value of Lignin. Green Chem. 2016, 18, 5693–5700. 10.1039/C6GC01813K. [DOI] [Google Scholar]
  22. Ago M.; Tardy B. L.; Wang L.; Guo J.; Khakalo A.; Rojas O. J. Supramolecular Assemblies of Lignin into Nano- and Microparticles. MRS Bull. 2017, 42, 371–378. 10.1557/mrs.2017.88. [DOI] [Google Scholar]
  23. Yang Y.; Wei Z.; Wang C.; Tong Z. Lignin-Based Pickering HIPEs for Macroporous Foams and Their Enhanced Adsorption of Copper(ii) Ions. Chem. Commun. 2013, 49, 7144–7146. 10.1039/c3cc42270d. [DOI] [PubMed] [Google Scholar]
  24. Miao C.; Hamad W. Y. Controlling Lignin Particle Size for Polymer Blend Applications. J. Appl. Polym. Sci. 2017, 134, 44669 10.1002/app.44669. [DOI] [Google Scholar]
  25. Yeo J.-S.; Seong D.-W.; Hwang S.-H. Chemical Surface Modification of Lignin Particle and Its Application as Filler in the Polypropylene Composites. J. Ind. Eng. Chem. 2015, 31, 80–85. 10.1016/j.jiec.2015.06.010. [DOI] [Google Scholar]
  26. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  27. Steinhardt P. J.; Nelson D. R.; Ronchetti M. Bond-Orientational Order in Liquids and Glasses. Phys. Rev. B 1983, 28, 784–805. 10.1103/PhysRevB.28.784. [DOI] [Google Scholar]
  28. Bernhardt I. C.Particle Size Analysis: Classification and Sedimentation Methods, 1st ed.; Springer: Netherlands, 1994. [Google Scholar]
  29. Troy D. B.Remington: The Science and Practice of Pharmacy; Lippincott, Williams & Wilkins: Philadelphia, PA, 2005. [Google Scholar]
  30. Wu C.; Li S.; Sassa K.; Chino Y.; Hattori K.; Asai S. Theoretical Analysis on Crystal Alignment of Feeble Magnetic Materials under High Magnetic Field. Mater. Trans. 2005, 46, 1311–1317. 10.2320/matertrans.46.1311. [DOI] [Google Scholar]
  31. Vainio U.; Maximova N.; Hortling B.; Laine J.; Stenius P.; Simola L. K.; Gravitis J.; Serimaa R. Morphology of Dry Lignins and Size and Shape of Dissolved Kraft Lignin Particles by X-Ray Scattering. Langmuir 2004, 20, 9736–9744. 10.1021/la048407v. [DOI] [PubMed] [Google Scholar]
  32. Wu Y.; Francis L. F. Effect of Particle Size Distribution on Stress Development and Microstructure of Particulate Coatings. J. Coat. Technol. Res. 2017, 14, 455–465. 10.1007/s11998-016-9866-5. [DOI] [Google Scholar]
  33. Hales T. C. A Proof of the Kepler Conjecture. Ann. Math. 2005, 162, 1065–1185. 10.4007/annals.2005.162.1065. [DOI] [Google Scholar]
  34. Santiso E.; Müller E. A. Dense Packing of Binary and Polydisperse Hard Spheres. Mol. Phys. 2002, 100, 2461–2469. 10.1080/00268970210125313. [DOI] [Google Scholar]
  35. Salas C.; Rojas O. J.; Lucia L. A.; Hubbe M. A.; Genzer J. On the Surface Interactions of Proteins with Lignin. ACS Appl. Mater. Interfaces 2013, 5, 199–206. 10.1021/am3024788. [DOI] [PubMed] [Google Scholar]
  36. Pereira A.; Hoeger I. C.; Ferrer A.; Rencoret J.; Del Rio J. C.; Kruus K.; Rahikainen J.; Kellock M.; Gutiérrez A.; Rojas O. J. Lignin Films from Spruce, Eucalyptus, and Wheat Straw Studied with Electroacoustic and Optical Sensors: Effect of Composition and Electrostatic Screening on Enzyme Binding. Biomacromolecules 2017, 18, 1322–1332. 10.1021/acs.biomac.7b00071. [DOI] [PubMed] [Google Scholar]
  37. Strasser S.; Niegelhell K.; Kaschowitz M.; Markus S.; Kargl R.; Stana-Kleinschek K.; Slugovc C.; Mohan T.; Spirk S. Exploring Nonspecific Protein Adsorption on Lignocellulosic Amphiphilic Bicomponent Films. Biomacromolecules 2016, 17, 1083–1092. 10.1021/acs.biomac.5b01700. [DOI] [PubMed] [Google Scholar]
  38. Martín-Sampedro R.; Rahikainen J. L.; Johansson L.-S.; Marjamaa K.; Laine J.; Kruus K.; Rojas O. J. Preferential Adsorption and Activity of Monocomponent Cellulases on Lignocellulose Thin Films with Varying Lignin Content. Biomacromolecules 2013, 14, 1231–1239. 10.1021/bm400230s. [DOI] [PubMed] [Google Scholar]
  39. Ago M.; Jakes J. E.; Rojas O. J. Thermomechanical Properties of Lignin-Based Electrospun Nanofibers and Films Reinforced with Cellulose Nanocrystals: A Dynamic Mechanical and Nanoindentation Study. ACS Appl. Mater. Interfaces 2013, 5, 11768–11776. 10.1021/am403451w. [DOI] [PubMed] [Google Scholar]
  40. Ago M.; Jakes J. E.; Johansson L.-S.; Park S.; Rojas O. J. Interfacial Properties of Lignin-Based Electrospun Nanofibers and Films Reinforced with Cellulose Nanocrystals. ACS Appl. Mater. Interfaces 2012, 4, 6849–6856. 10.1021/am302008p. [DOI] [PubMed] [Google Scholar]
  41. Herrmann H. J.; Baram R. M.; Wackenhut M. Polydisperse Packings. Braz. J. Phys. 2003, 33, 591–593. 10.1590/S0103-97332003000300020. [DOI] [Google Scholar]
  42. Otomo R.; Harada S. Fluid Permeability in Stratified Unconsolidated Particulate Bed. Transp. Porous Media 2013, 96, 439–456. 10.1007/s11242-012-0098-6. [DOI] [Google Scholar]
  43. Farris R. J. Prediction of the Viscosity of Multimodal Suspensions from Unimodal Viscosity Data. Trans. Soc. Rheol. 1968, 12, 281–301. 10.1122/1.549109. [DOI] [Google Scholar]
  44. Fröberg J. C.; Rojas O. J.; Claesson P. M. Surface Forces and Measuring Techniques. Int. J. Miner. Process. 1999, 56, 1–30. 10.1016/S0301-7516(98)00040-4. [DOI] [Google Scholar]

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES