The Nucleation Rate of Single O₂ Nanobubbles at Pt Nanoelectrodes

Abstract

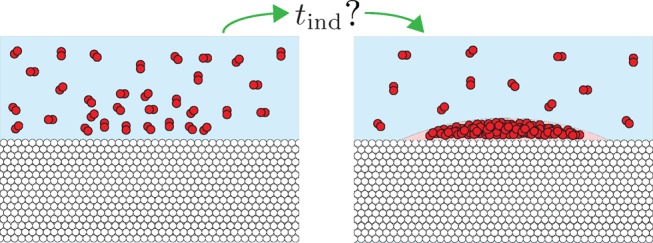
Nanobubble nucleation is a problem that affects efficiency in electrocatalytic reactions since those bubbles can block the surface of the catalytic sites. In this article, we focus on the nucleation rate of O₂ nanobubbles resulting from the electrooxidation of H₂O₂ at Pt disk nanoelectrodes. Bubbles form almost instantaneously when a critical peak current, i_nb^p, is applied, but for lower currents, bubble nucleation is a stochastic process in which the nucleation (induction) time, t_ind, dramatically decreases as the applied current approaches i_nb, a consequence of the local supersaturation level, ζ, increasing at high currents. Here, by applying different currents below i_nb^p, nanobubbles take some time to nucleate and block the surface of the Pt electrode at which the reaction occurs, providing a means to measure the stochastic t_ind. We study in detail the different conditions in which nanobubbles appear, concluding that the electrode surface needs to be preconditioned to achieve reproducible results. We also measure the activation energy for bubble nucleation, E_a, which varies in the range from (6 to 30)kT, and assuming a spherically cap-shaped nanobubble nucleus, we determine the footprint diameter L = 8–15 nm, the contact angle to the electrode surface θ = 135–155°, and the number of O₂ molecules contained in the nucleus (50 to 900 molecules).

Introduction

The generation of bubbles in chemical reactions is a process that has been well known by scientists throughout history. When these bubbles are extremely small (on the order of nanometers), the problem becomes much more challenging to analyze.¹⁻³ However, the technology used to visualize such surface nanobubbles has been very recently developed.^2,4−6 The biggest concern that surface nanobubbles cause is their generation in chemical reactions, such as electrolysis⁷ and catalysis.⁸ Nanobubbles nucleating on top of reacting surfaces or electrodes influence the efficiency of chemical reactions since they partially block the reactive surface and consequently impede the reaction of interest.⁹ A similar situation occurs in the case of nanodroplet and nanocrystal nucleation.¹⁰ In other scenarios, such as redox reactions in cells, the nanobubbles can form within the nanoprobes and induce current amplification.¹¹ The high internal pressures of nanobubbles make their behavior rather different from that of micro- or macrobubbles.^2,12 Nanobubbles often adhere to the surface at which they originate, forming a spherical cap that strongly attaches to the active surface.^2,13 Without pinning, i.e., when the nanobubbles are not attached to a specific location on the surface, due to the high pressure inside them,^14,15 nanobubbles would dissolve extremely rapidly once the reaction stops. However, if there are pinning sites and constant gas supersaturation is provided at the surface, then nanobubbles on reacting surfaces are very stable^16,17 and do not dissolve.² Molecular dynamics simulations¹⁸ support this view.

In this article, we measure the nucleation rate of single O₂ nanobubbles generated at Pt nanodisk electrodes by the electro-oxidation of H₂O₂. When the local dissolved O₂ concentration at the nanoelectrode is sufficiently high,¹⁹ a nanobubble nucleates and blocks the reacting surface, as depicted in Figure 1. We study the factors affecting the nucleation rate of O₂ nanobubbles under different applied currents.

Figure 1.

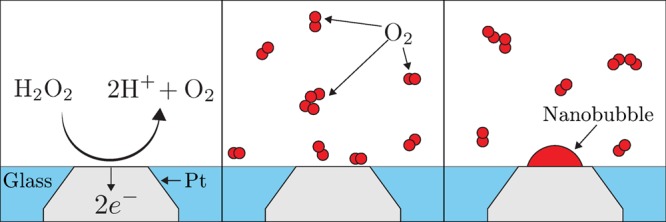
O₂ nanobubble generation by electro-oxidation of H₂O₂. When the O₂ concentration at the nanoelectrode is sufficiently high, a nanobubble nucleates after some time and partially blocks the electrode surface.

Experimental Methods

The fabrication and measurement of the size of Pt nanoelectrodes are described in detail in the Supporting Information (section 1). All experiments were performed in an aqueous solution of 1 M H₂O₂ and 1 M HClO₄, prepared using purified deionized water (18.2 MΩ·cm).

A HEKA EPC10 patch clamp amplifier was used to collect current, i, voltage, E, and time, t, data, which were filtered with a 4-pole Bessel low-pass filter at 10 kHz and sampled at 50 kHz. A LabVIEW program employing a FPGA card (National Instruments, PCIe-7852) was used to monitor the voltage and to control current steps for galvanostatic experiments. The program was capable of lowering the current to 0 nA within 80 μs after the detection of nanobubble nucleation. A mercury sulfate electrode (BASi) was employed (E = +0.64 V relative to a normal hydrogen electrode, NHE) as a reference/counter electrode in a two-electrode configuration. For convenience, all potentials are presented vs NHE.

Results and Discussion

Cyclic Voltammogram in a Solution of 1 M H₂O₂ and 1 M HClO₄

The generation of a single nanobubble at a Pt nanoelectrode can be observed in cyclic voltammetric measurements, as reported in previous work.^20,21Figure 2 shows the cyclic voltammogram of a 6-nm-radius electrode in an aqueous solution of 1 M H₂O₂ and 1 M HClO₄.

Figure 2.

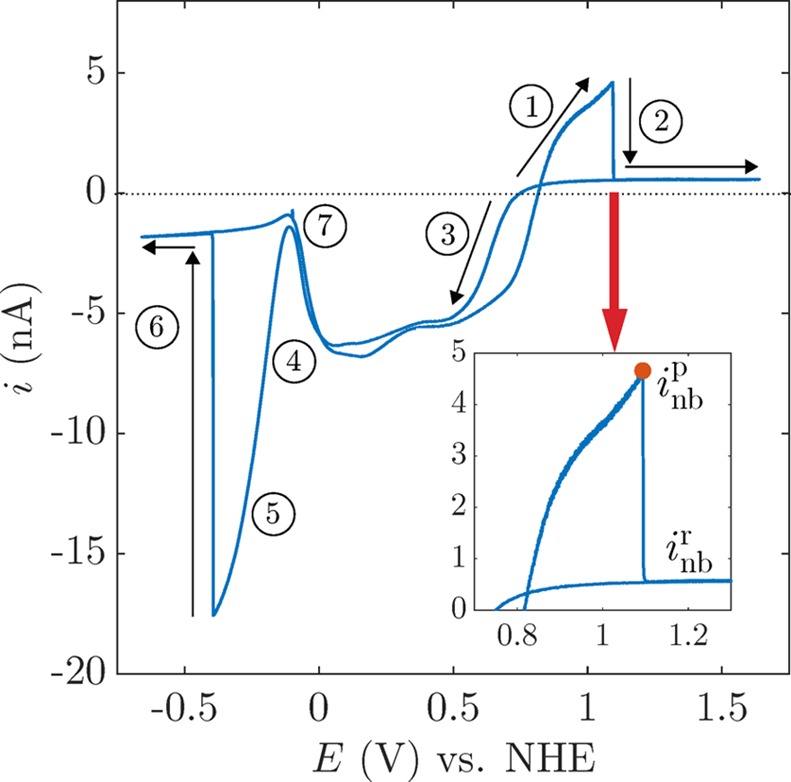
Cyclic voltammogram of a 6-nm-radius Pt nanoelectrode in a solution of 1 M H₂O₂ and 1 M HClO₄. The red dot on the close-up area corresponds to the peak current i_nb^p at which a nanobubble nucleates and then grows to block the electrode surface. The scan rate is 200 mV/s.

The i–E response reflects several potential-dependent electrochemical reactions,²¹ as labeled in Figure 2:

• 1.H₂O₂ → 2H⁺ + 2e^– + O₂: above 0.8 V, H₂O₂ is electrochemically oxidized to produce dissolved O₂. The higher the current, the faster the rate of O₂ production and the higher the local supersaturation.¹⁹
• 2.O₂ nanobubble formation: when the current reaches the peak value, i_nb^p, the concentration of O₂ is sufficiently high that a nanobubble nucleates at the nanoelectrode, grows, and blocks it, as depicted in Figure 1. Consequently, the current rapidly drops to a residual current, i_nb, which corresponds to the balance of the steady-state O₂ dissolution from the bubble to the bulk with the O₂ production at the circumference of the nanoelectrode (which is not fully covered by the nanobubble).^20,22 Increasing the voltage from that point on causes no change in the current, which remains constant at i_nb^r.²⁰ This current also stays constant when we subsequently reduce the voltage until O₂ electrogeneration ceases and the nanobubble dissolves.
• 3.H₂O₂ + 2e^– + 2H⁺ → 2H₂O: from 0.8 to 0 V, H₂O₂ is reduced to form H₂O, resulting in a cathodic current.
• 4.H⁺ + e^– → Pt–H: a monolayer of H· is reductively adsorbed at the Pt surface,²³ reducing the rate of H₂O₂ reduction, resulting in a decrease in the cathodic current.
• 5.2H⁺ + 2e^– → H₂: from −0.1 to −0.4 V, protons are reduced to produce H₂.
• 6.H₂ nanobubble formation: when enough H₂ molecules cluster together, a H₂ nanobubble nucleates at the nanoelectrode, as indicated by a sudden decrease in current to a potential-independent residual current.
• 7.As the electrode potential is scanned toward positive voltages (from 0 to 0.8 V), H desorbs from the Pt and the rate of H₂O₂ reduction increases.

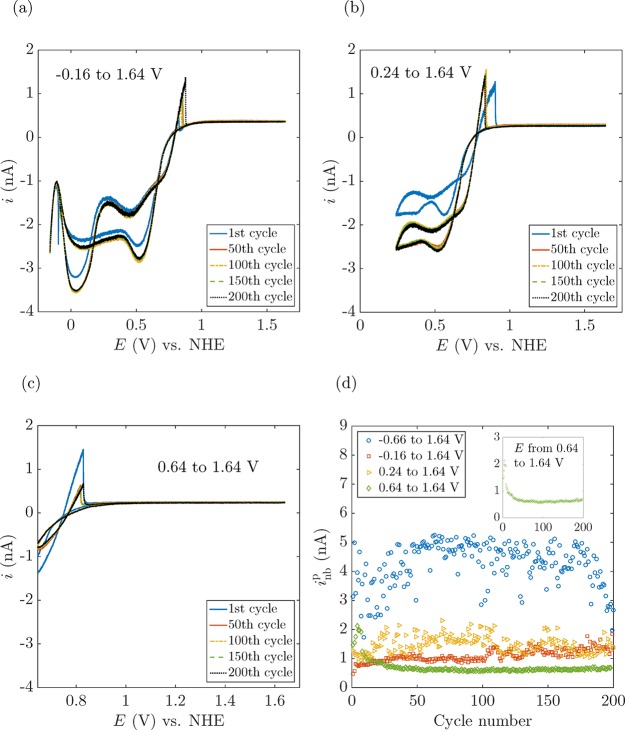
This cyclic voltammogram may be scanned hundreds of times, with repeated formation and dissolution of the O₂ and H₂ nanobubbles on each scan.²⁴ However, large variability in i_nb^p is observed after an extensive repetition of voltammetric cycles. This is likely due to the restructuring of the surface in the repetitive scans, as the voltammetric responses involve H· absorption and desorption (from 0 to 0.8 V, steps 3 and 7 in Figure 2) and the oxidation and reduction of H₂O₂ involve the generation of PtO_x as well as the reduction of PtO_x to Pt.²³ However, the self-decomposition of H₂O₂ to O₂ caused by the Pt surface^25,26 does not play a significant role in the case of eventual bubble nucleation since the O₂ generation rate is negligible compared to the gas production rate once a certain current is applied.²¹ The electrode apparent radius a is also affected during the application of the conditioning cycles (section 1 in the Supporting Information); consequently, i_nb may be affected.^21,22,27Figure 3 shows several cyclic voltammograms recorded at the same electrode, displaying a different i_nb^p in every cycle. However, by reducing the scan range or applying a “conditioning cycle”, a reproducible electrode surface and a constant apparent radius, and therefore a consistent i_nb, can be achieved. We can thus influence the surface chemistry of the Pt electrode, achieving a more reproducible i_nb^p.²⁸Figure 4 presents several voltammograms of the same electrode covering different scan ranges, with the resulting variability of i_nb shown in Figure 4d. It is important to notice the different mean values of i_nb^p for different scan ranges, which emphasizes the importance of the surface chemistry on bubble nucleation.

Figure 3.

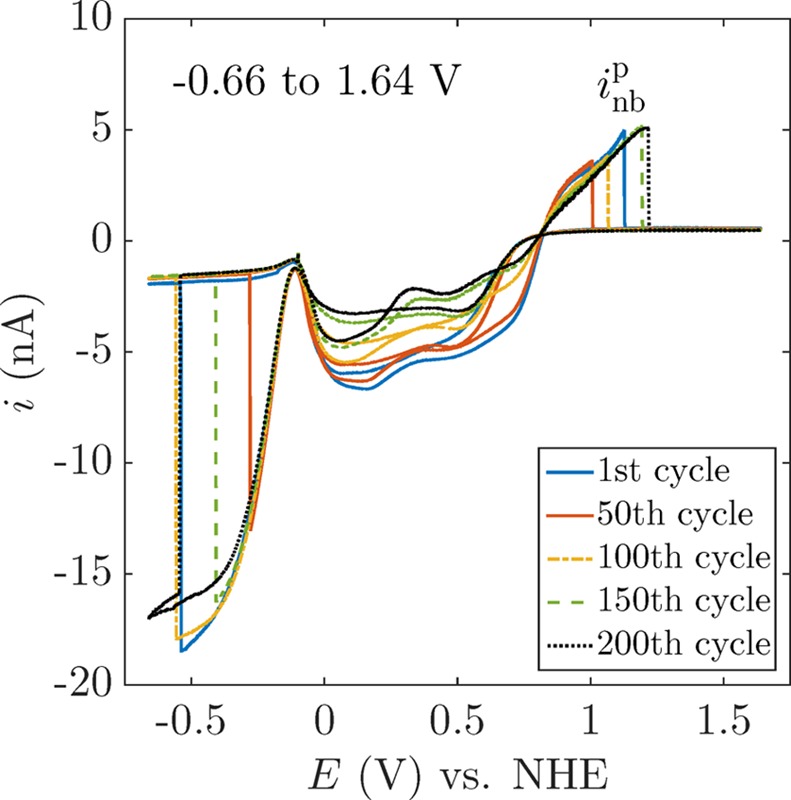
Multiple voltammetric cycles demonstrating the generation of O₂ and H₂ nanobubbles. Note that the curves show a large variation. More specifically, the current i_nb^p at which an O₂ nanobubble forms varies significantly from cycle to cycle. The voltammograms were recorded at a 6-nm-radius electrode at a scan rate of 200 mV/s.

Figure 4.

(a–c) Multiple cycles of voltammograms performed over different potential scan ranges for the determination of experimental conditions giving rise to reproducible i_nb^p for O₂ nanobubble formation on a 6-nm-radius electrode. (d) i_nb vs cycle number for O₂ nanobubble formation for different scan ranges corresponding to voltammograms in panels a–c and Figure 3. The voltammetric cycle shown in panel (c) is the one that involves the least surface chemistry and thus, results in the most reproducible results (green diamonds in panel (d)). Note that the mean value of i_nb^p changes for different scan ranges, again highlighting the importance of the surface chemistry.

Once we have secured a reproducible i_nb^p, we can turn to the objective of our story: the measurement of the different rates at which nanobubbles nucleate if a certain current below i_nb is applied.

Measurement of the Nucleation Rate

Our experiments aim at measuring the time to nucleate a nanobubble as a function of the applied current i_app. In the experiments described above, the nanobubbles nucleate “instantaneously” on the voltammetric time scale when the current reaches i_nb^p (which is approximately linearly related to the electrode apparent measurable radius a(21,22)). However, if i_app is lower than i_nb, then a measurable stochastic induction time is required for nucleation.²¹

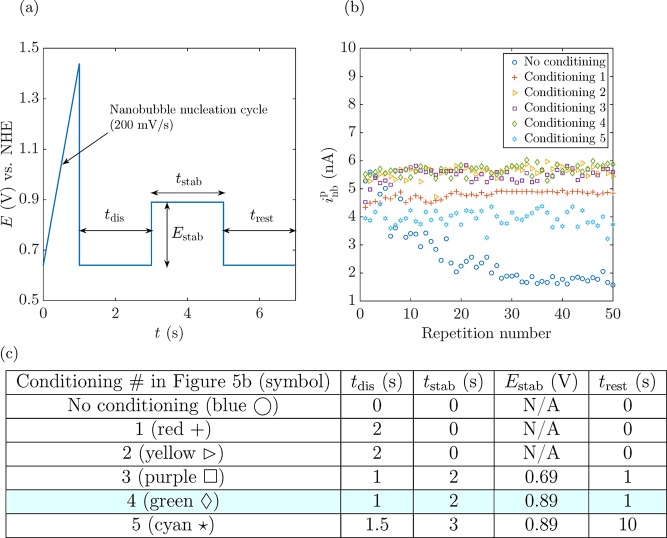
As shown in Figure 4d, at least 40 cycles need to be performed before a good i_nb^p reproducibility is reached. Therefore, we designed the conditioning cycle shown in Figure 5a to obtain reproducible results during the nucleation rate experiments. First, the voltage is swept positively until an O₂ nanobubble nucleates and blocks the electrode. The voltage is then stepped to E = 0.64 V for a defined time, t_dis, to allow the nanobubble to dissolve; this dissolution is followed by a stabilization process in which the electrode surface is conditioned by holding it at a voltage, E_stab, for a time, t_stab. Finally, we let the electrode rest at E = 0.64 V for a time t_rest before repeating the cycle. Conditioning waveforms using different combinations of t_dis, t_stab, E_stab, and t_rest have been experimentally tried and are presented in the table in Figure 5c. The optimized conditions correspond to t_dis = 1 s, t_stab = 2 s, E_stab = 0.89 V, and t_rest = 1 s, corresponding to conditioning protocol #4 (green diamonds) in Figure 5b, where we represent i_nb vs the cycle number corresponding to the most representative data among 20 different conditioning configurations. The different i–E vs t plots of these conditioning cycles have been included in the Supporting Information (Figure S4).

Figure 5.

(a) Voltammetric electrode conditioning cycle used to rapidly achieve a state where the O₂ nanobubble forms at a consistent current. (b) i_nb^p for the most representative combinations of t_dis, t_stab, E_stab, and t_rest as indicated in the table in panel (c). The configuration with the smallest standard deviation used throughout this article corresponds to configuration 4, with t_dis = 1 s, t_stab = 2 s, E_stab = 0.89 V, and t_rest = 1 s. (c) Table with the different configurations for conditioning the electrode to obtain reproducible results. The configuration which achieves the lowest standard deviation is highlighted in blue (diamond symbol) and is used in the remainder of the article and is referred to as “the electrode conditioning cycle”.

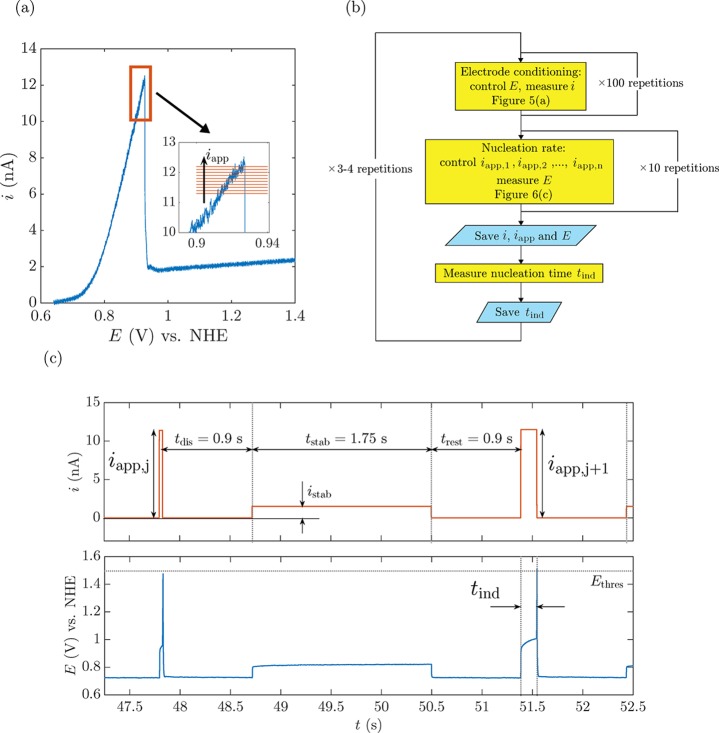
Now we can measure the nucleation rate at different supersaturation levels, which are directly controlled by the applied current.²⁹ We chose to control current rather than voltage because the experiment is very sensitive to any drift in the voltage. For example, in the region very close to i_nb^p, a change of 20 mV generated a change of 8% in current, as can be seen in Figure 6a, in which we plot a voltammogram for O₂ nanobubble nucleation. Such an apparent “small variation” in current causes a significant variation in the nucleation rate of nanobubbles. Control of the voltage is difficult to achieve with the desired precision. Therefore, we decided to control the current, which can be precisely adjusted to the level of pA.

Figure 6.

(a) Forward scan of a voltammogram for bubble formation at a 41-nm-radius Pt electrode. Inset: the range of i_app where bubble nucleation times are measured. (b) Experimental sequence used to determine bubble nucleation time as a function of i_app. (c) Applied current cycle (top) and measured potential (bottom) for determining the bubble nucleation time at the same electrode as in panel (a). The different times are defined similarly to the intervals in Figure 5a, whereas i_stab is the measured value of the current obtained during the application of E_stab in the same figure.

A LabVIEW script was used to control the current i_app applied to the electrode. By subsequent step increases from ∼0.7i_nb^p to ∼1.0i_nb, we can measure different nucleation times, which become smaller the closer i_app is to i_nb^p. The applied current loop is represented in Figure 6c, in which i_stab corresponds to the current response obtained during the application of E_stab in the course of electrode conditioning (Figure 5a). Once a nanobubble forms, according to the voltammogram presented in Figure 6a, if i_app is maintained fixed at a certain value, then the voltage will dramatically increase to values that correspond to water oxidation, damaging the nanoelectrode. Therefore, a threshold voltage E_thres = 1.5 V is established, so when a nanobubble nucleates and the voltage spikes, i_app will automatically return to zero.

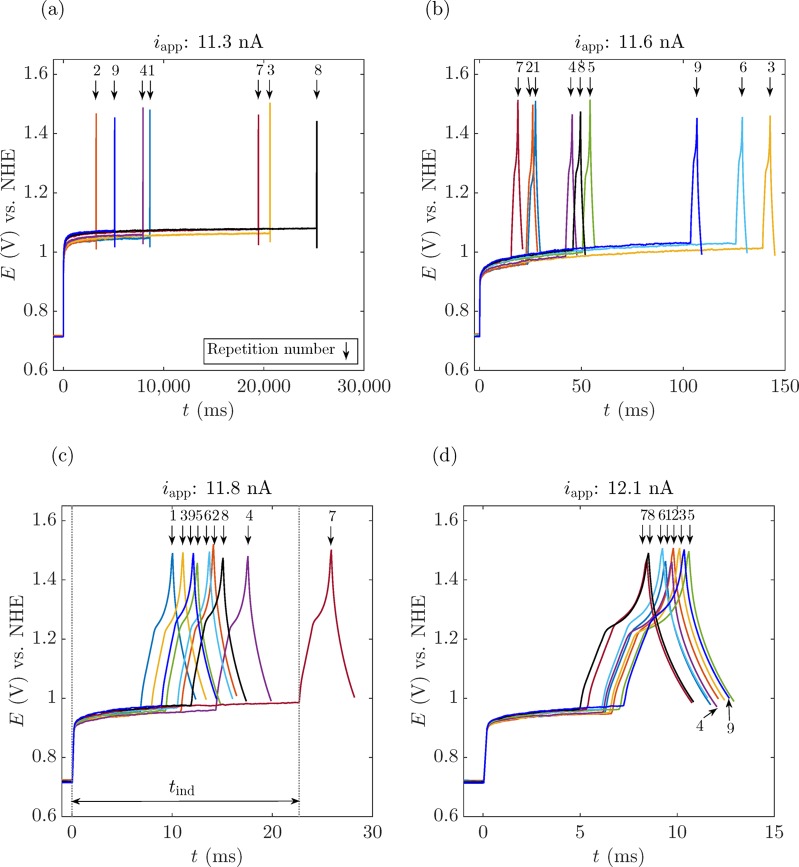
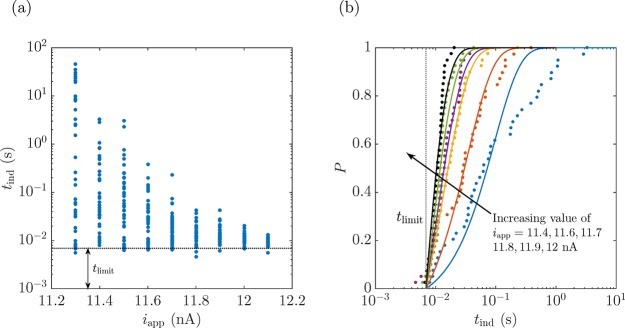
We design a full experiment as shown in the flowchart of Figure 6b. First, the electrode surface is conditioned by applying the cycle in Figure 5a over a hundred times with voltage control. Afterward, we switched to current control, applying a fixed i_app until a nanobubble nucleates and blocks the electrode, while measuring the corresponding nucleation time t_ind. For the purpose of avoiding electrode surface reconditioning, if no bubble nucleated after 30 s, the current was manually set to zero and the process continued as designed. We repeated this loop for different currents 10 times before conditioning the electrode surface again. Several voltage responses are shown for a 41-nm-radius electrode corresponding to different i_app values in Figure 7 (see more results for different currents and different electrodes in the Supporting Information, Figures S5–S7). It can be perfectly appreciated that the closer i_app is to i_nb^p, the shorter t_ind becomes, e.g., t_ind ≈ 15 s at i_app = 11.3 nA (Figure 7a), whereas when i_app is increased by 0.8 nA, t_ind drastically decreases to ∼7 ms (Figure 7d). An increase of 7% in i_app causes a decrease in the nucleation time of 3 orders of magnitude. We report the different nucleation times t_ind for different i_app values on an a = 41 nm electrode in Figure 8a (refer to the Supporting Information, Figures S8 and S9, for the results corresponding to the different electrodes used in Figures S6 and S7). The stochasticity of the process can be appreciated in the different nucleation times measured at the same i_app. Notably, the closer i_app is to i_nb (i_nb^p = 12.2 nA for this case), the lower the variability of t_ind, i.e., the curves for different repetitions lie closer together. This effect originates from the shorter exposure time to a certain i_app, thus avoiding any reconditioning of the electrode surface. The shorter the exposure, the less the surface chemistry and consequently the more reproducible the results. For values of i_nb of approximately 0.9i_nb^p, the stochastic variability in t_ind ranges over 2 to 3 orders of magnitude,²⁹ moving toward values with variability within 1 order of magnitude for 0.99i_nb.

Figure 7.

Potential–time measurements to determine the time needed to nucleate an O₂ nanobubble. Each panel shows a different i_app < i_nb^p = 12.2 nA and is presented on a different time scale. The electrode was 41 nm in radius. In some repetitions, for the lowest i_app, bubble nucleation did not occur within 30 s; therefore, the process was manually stopped. Panel (c) illustrates the interval in which the nucleation time, t_ind, is measured, from the moment in which the current is applied until the moment in which the nanobubble nucleates (indicated by a sudden increase in the voltage as the bubble blocks the surface of the nanoelectrode). The arrows indicate the cycle number.

Figure 8.

(a) Experimentally measured t_ind for different i_app values on a 41-nm-radius Pt electrode. (b) Corresponding cumulative probability P of a nanobubble nucleation event for i_app = 11.4, 11.6, 11.7, 11.8, 11.9, and 12 nA (other currents have similar results but are not shown, aiming for clarity in the figure). The theoretical curves correspond to the best fit of eq 1 to the data. The curves become increasingly vertical with increasing i_app: the higher the current, the higher the nucleation rate J.

The cumulative probability of a nanobubble nucleating at a nanoelectrode can be expressed as P = N(t)/N_T, where N(t) represents the number of nanobubbles whose nucleation occurs before a specific time t and N_T is the total number of nucleation events recorded at a certain i_app.³⁰ This cumulative probability can be theoretically expressed by an exponential relationship:^30,31

1

where J refers to the nucleation rate at a specific current and t_limit is the shortest accessible experimental time, which can be physically associated with the response time of the electronic circuit coupled to the capacitance of the electrochemical cell²⁹ and determines the minimum experimentally achievable t_ind. By fitting eq 1 to the data in Figure 8a, the nucleation rate, J, for each value of i_app can be measured as a best-fitting parameter. An estimate can be calculated as J ≈ 1/(t̅_ind – t_limit), where t̅_ind is the mean value of the nucleation time at a certain i_app. A single value of t_limit was fit to all measurements with each electrode. The probability distribution for the different i_app values in Figure 8a is represented in Figure 8b. The best match between the fits and experiments occurs for intermediate levels of i_app since for the lower values, nanobubbles take a longer time to nucleate and therefore the nanoelectrode surface can be reconditioned to a different state, whereas for i_app very close to i_nb^p the process is so fast that any uncertainty in t_limit may result in a very significant uncertainty in J.

The nucleation rate, J, depends on i_app, increasing its value as i_app increases, as can be depicted from the more vertical sigmoidal curves in Figure 8b for higher values of i_app. From Classical Nucleation Theory (CNT), the nucleation rate of a nanobubble at the surface of the electrode can be expressed as^{9,12,16,32,33}

2

where J₀ is the pre-exponential factor which describes the statistical molecule-by-molecule process of nucleus growth (which can be considered to be constant with respect to i), γ is the surface tension of the gas–liquid interface (variations in the surface tension at molecular length scale, which have been shown to be minimal down to 10 nm,²⁰ are not considered), ϕ(θ) = (1 + cos(θ))²(2 – cos(θ))/4 is a geometric function which depends on the nanobubble contact angle θ to the electrode surface^24,34,35 (which implicitly accounts for the minute effect of the surface tension between the electrode and the bubble³⁶), kT = 4.11 × 10^–21 J is the product of Boltzmann constant k and thermodynamics temperature T = 298 K, and P_s and P₀ refer to the pressure in the bubble and the ambient pressure in the bulk liquid, respectively. Note again that in the derivation of eq 2 a spherical cap shape of the bubble nucleus has been assumed. Once van der Waals forces and thus the disjoining pressure play a role, this is no longer the case and the nanobubble shape may differ from that of a perfect spherical cap.³⁷ Given the nanometric size of the bubbles, these considerations may apply. These deviations from a perfect spherical-cap shape are nevertheless known to be very small,³⁷ so our assumption may still be valid.

Assuming Fickian diffusion on a planar disk electrode, we can relate the steady-state current i to the local concentration of O₂ being produced at the electrode surface, C_O2^surface:^21,22,35

3

In eq 3, n = 2 is the number of exchanged electrons per molecule of O₂ generated, F = 96 485 C/mol is Faraday’s constant, D_O2 = 1.67 × 10^–9 m²/s is the diffusivity of O₂,³⁸ and C_O2^surface and C_O2 are the O₂ concentrations locally at the surface of the electrode and in the bulk, respectively. C_O2^bulk is approximately zero compared to C_O2 in our experiments. Applying Henry’s law, we can relate this supersaturated concentration at the electrode surface to P_s and therefore³⁵

4

where K_H = 1.283 × 10^–5 mol/m³Pa is Henry’s constant for O₂.³⁹Equation 4 can be rewritten as

5

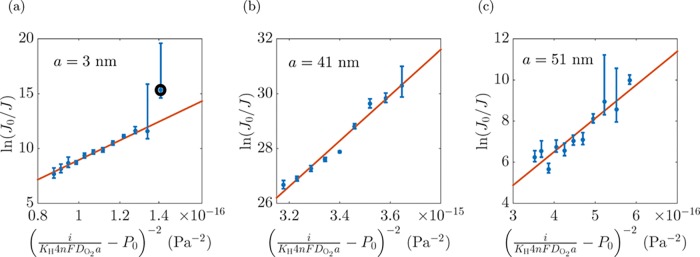
where B = 16πγ³ϕ(θ)/3kT and J₀ are calculated as best-fit parameters. Figure 9 shows experimentally measured nucleation rates vs the bracketed expression in eq 5 for three different electrodes, indeed displaying the linear behavior suggested by this equation. From the slope B, we can extract the contact angle θ. See below.

Figure 9.

Logarithmic linear relation between nucleation rate J and the inverse of the squared supersaturated pressure difference for (a) a = 3 nm, (b) a = 41 nm, and (c) a = 51 nm. An outlier in (a) has been indicated by a black circle.

The nucleation rate is related to the activation energy E_a of a nanobubble nucleation by Arrhenius’ law.³² Therefore, we can achieve a one-to-one relation between both physical magnitudes:²⁹

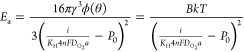6

E_a thus decreases with increasing current; i.e., E_a decreases with increasing supersaturation ζ = (c_s – c₀)/c₀, where c_s and c₀ refer to the O₂ concentration at supersaturation and under ambient conditions. These concentrations are related to pressure by Henry’s law at constant temperature, thus ζ can be rewritten as the pressure difference, ζ = (P_s – P₀)/P₀. Associating this definition with eqs 2 and 4, we obtain an expression for the supersaturation level at the nucleation time for a bubble:

7

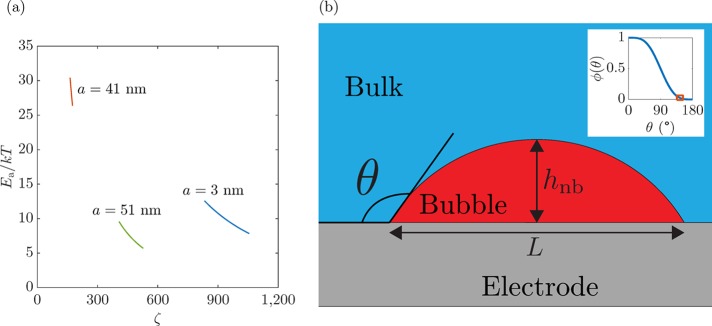
The different E_a values for different electrodes are represented in Figure 10a vs the corresponding levels of ζ achieved at different i_app values and tabulated in Table 1. As expected, the increase in supersaturation causes a decrease in the activation energy for every case.

Figure 10.

(a) Activation energy, E_a, as a function of the supersaturation, ζ, at different electrodes. E_a decreases with increasing i, i.e., increasing ζ. (b) Sketch of a surface nanobubble nucleus under the assumption of a spherical cap shape. The contact angle, θ, is defined on the water side, where h_nb corresponds to the nucleus height and L determines the nucleus footprint. Inset: geometric relation ϕ(θ) = (1 + cos(θ))²(2 – cos(θ))/4 needed for the calculation of the nucleus volume assuming a spherical cap shape. The framed region indicates the domain in which all of the nanobubbles studied in this article are situated.

Table 1. Fitting Parameters B and J₀ in Equation 5, Activation Energy E_a from Equation 6, and Supersaturation ζ at Bubble Nucleation from Equation 7 for Different Electrodes^a.

a(nm)	B(Pa2)	ln(J0s)	Ea/kT	ζ
3	9.0 ± 1.0 × 1016	14.3 ± 1.1	12.5 – 7.9 ± 1.2	835–1050
41	8.3 ± 1.3 × 1015	32.2 ± 4.2	30.3 – 26.4 ± 4.2	160–175
51	1.6 ± 0.5 × 1016	12.1 ± 2.1	9.5 – 5.7 ± 2.1	410–525

^aThe tolerances in B, J₀s, and E_a/kT indicate the error measurement when fitting Equations 5 and 6. The intervals shown in ζ represent the calculated supersaturation level at the different applied currents for each electrode.

From Figure 10a, there is no apparent relation between the different values of the activation energy E_a and the apparent radius of the electrode a nor is there a clear relation between a and fitting parameters B and J₀, as indicated in Table 1.

As mentioned above, the contact angle θ can be calculated from the slope B, namely, by the implicit equation:

8

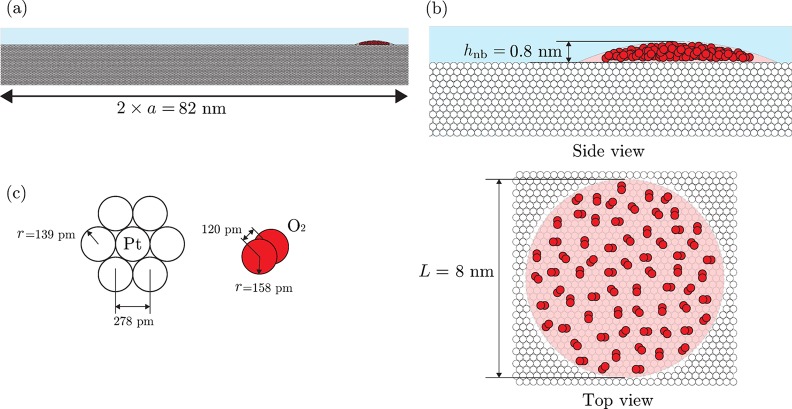
For all the different electrodes, θ ranges from 135 to 155° (inset in Figure 10b), similar to the case of H₂ nanobubbles.²⁹ The radius of curvature of the nucleus for an O₂ nanobubble has been reported to be r_nb = 10 nm,^21,22,40 which implies a Laplace pressure of P_nb = 2γ/r_nb = 14.2 MPa. The extremely high pressure within the nanobubble justifies the surprisingly high supersaturation levels achieved locally around it at nucleation. Knowing r_nb and θ, the nanobubble nucleus geometry is fully determined, assuming a spherical cap shape^22,33,40 (Figure 11 and Table 2).

Figure 11.

(a) Scale drawing⁴¹ of a nanobubble nucleus at an a = 41 nm electrode. The white circles (best seen in panel (b)) represent Pt atoms, whereas the red ones represent O atoms. The molecular structure is defined in detail in panel (c). The close-up view of the area covered by the nanobubble nucleus is depicted from the top and the side in panel (b). The nucleus (as shown) initially covers a very small portion of the electrode surface before growing and blocking the majority of the electrode. The volume occupied by the O₂ molecules contained in the nucleus is small compared to the total nucleus volume, which may suggest that the nucleus shape may be deformed by the disjoining pressure.³⁷

Table 2. Geometrical Dimensions of Different Nanobubble Nuclei^a.

a(nm)	inbp(nA)	θ(deg)	L(nm)	hmb(nm)	nnb
3	5.3	144 ± 12	11.4 ± 3.2	2.0 ± 1.2	550–900
41	12.1	156 ± 1	4.1 ± 1	0.9 ± 0.0.1	50–85
51	45	151 ± 2	4.8 ± 0.3	1.2 ± 0.0.1	100–170

^aApparent electrode radius, a; peak current, i_nb^p; contact angle, θ; nucleus footprint, L; nucleus height, h_nb; and number of O₂ molecules in the nucleus, n_nb. The tolerances are the standard deviations which are derived from the calculation of the contact angle, θ, from fitting parameter B.

From the small size of the bubble nucleus footprint, L, when compared to the elctrode radius, a (Table 2), we conclude that the nanobubble nucleus covers a very small portion of the electrode. There is one exception to this case: a = 3 nm. In this particular case, the nucleus of the nanobubble is larger than the electrode. This result has several possible origins: either the nucleus is attached to some irregularities on the nanoelectrode surface, i.e., the electrode has a very nonflat surface, or the Pt disk is recessed within the glass seal,⁴² providing an apparent radius determined volumetrically to be much smaller than the actual electrode size, or the disjoining pressure within the nanobubble deforms its shape in a high manner such that the assumption of a spherical cap is no longer applicable. On the other hand, the total volume occupied by the number of molecules contained in the nuclei (∼50–900) is small compared to the presumed initial bubble volume. From the drawing to scale in Figure 11, we can appreciate this fact: within the nanobubble nucleus volume, there is empty space which cannot be occupied by the number of molecules present. This may result in a deformed shape of the nanobubble nucleus due to the disjoining pressure.³⁷ From our results in Tables 1 and 2, we can conclude that there is a direct relationship between the supersaturation level ζ and the number of molecules in the nucleus n_nb. However, there is no apparent relation between n_nb and i_nb^p nor a. This issue can be due to the electrode surface properties and especially the surface chemistry that applies to the electrode during its conditioning to achieve reproducible results.

Conclusions

The nucleation of single O₂ nanobubbles at a Pt nanoelectrode has been studied in detail. The importance of surface chemistry has been exposed throughout all of this research. The necessary treatment of the Pt surface to generate a reproducible peak current i_nb^p at which nanobubbles are formed is of extreme importance if good stochastic results are to be obtained concerning the nucleation rate of nanobubbles (the corresponding analysis for a non-preconditioned electrode can be found in section 4 in the Supporting Information). In a region very close to i_nb, the nucleation time t_ind rapidly changes with a small variation on the order of tenths of a nA in the applied current i_app. The nucleation rate J(i_app) can be calculated from the different induction times for bubbles to nucleate when i_app is fixed at a certain level below i_nb^p. The Classical Nucleation Theory (eq 2) provides an accurate mathematical expression for J. Because of stochasticity, the nucleation time can vary for the same i_app within 2 orders of magnitude. The higher the i_app, the higher the supersaturation ζ and consequently the higher the nucleation rate. ζ values are large in an area local to where the nanobubble nucleates, which results from the high Laplace pressure of the nanobubble nucleus due to its small radius. From the different measured J at different ζ, the activation energies E_a have been derived along with the contact angle θ between the bubble and the electrode surface if the geometry of the nucleus of the nanobubble is approximated as a spherical cap. We can estimate the number of O₂ molecules contained in the critical bubble nucleus, which is higher for higher ζ; i.e., the more molecules are locally produced, the more molecules will form the nanobubble nucleus. Though disjoining pressure may affect the nanobubble final shape,³⁷ for the scope of this research the assumption of a spherical cap is more than justified since the disjoining pressure barely cause the bubble shape to deviate from a spherical cap.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.8b01372.

• Fabrication of nanoelectrodes. Nanoelectrode conditioning. Nucleation rate measurements for additional values of i_app and electrodes. Bubble nucleation measurements without electrode surface conditioning. (PDF)

The authors declare no competing financial interest.