Automated analysis of breathing waveforms using BreathMetrics: a respiratory signal processing toolbox

Abstract

Nasal inhalation is the basis of olfactory perception and drives neural activity in olfactory and limbic brain regions. Therefore, our ability to investigate the neural underpinnings of olfaction and respiration can only be as good as our ability to characterize features of respiratory behavior. However, recordings of natural breathing are inherently nonstationary, nonsinusoidal, and idiosyncratic making feature extraction difficult to automate. The absence of a freely available computational tool for characterizing respiratory behavior is a hindrance to many facets of olfactory and respiratory neuroscience. To solve this problem, we developed BreathMetrics, an open-source tool that automatically extracts the full set of features embedded in human nasal airflow recordings. Here, we rigorously validate BreathMetrics’ feature estimation accuracy on multiple nasal airflow datasets, intracranial electrophysiological recordings of human olfactory cortex, and computational simulations of breathing signals. We hope this tool will allow researchers to ask new questions about how respiration relates to body, brain, and behavior.

Introduction

Nasal breathing is inextricably linked to olfactory sampling behaviors, which involve complex interactions between olfactory and limbic brain regions. A growing body of data collected from humans and rodents suggest that nasal inhalation, with or without the presence of an odor (Grosmaitre et al. 2007; Wu et al. 2017), drives neural activity in olfactory, limbic, and prefrontal brain regions. This is reflected by changes in local field potential (LFP) oscillations (Fontanini and Bower 2006; Ito et al. 2014; Rojas-Líbano et al. 2014; Nguyen Chi et al. 2016; Zelano et al. 2016; Heck et al. 2017; Herrero et al. 2018) and single-unit firing patterns (Roux and Uhlhaas 2014; Tsanov et al. 2014; Nguyen Chi et al. 2016; Sauer et al. 2017). Even though humans breathe up to 10 times slower than rodents, both rodent and human LFPs in the respiratory frequency range align to breathing (Nguyen Chi et al. 2016; Zelano et al. 2016; Heck et al. 2017; Herrero et al. 2018) and modulate functional network connectivity as well (Segers et al. 2008; Yu et al. 2016; Herrero et al. 2018). Notably, higher-frequency oscillations in the theta and gamma ranges also align to respiration (Zhong et al. 2017).

Investigating the neural basis of olfaction necessarily requires information about nasal airflow. Because olfactory sampling can only naturally occur at nasal inhales, any study seeking to link neural activity to sniff onsets must first identify when sniff onsets occur in nasal airflow recordings. Accurately labeling the time points when sniffs occur is crucial to understanding olfactory processing because olfactory signals are encoded not only spatially but also temporally on the order of single milliseconds (Luo and Katz 2001; Spors and Grinvald 2002; Gupta et al. 2015). Therefore, inaccurate labeling of sniff onsets blurs our ability to detect the dynamics of this temporal encoding. In most olfactory neuroscience studies, sniff onsets are identified visually by researchers. Although this methodology has its advantages, it may be unintentionally biased because different researchers may use different criteria for determining the instant a sniff has occurred. This, paired with the unknown accuracy of manual labeling across labs, reduces the comparability of findings across studies. Finally, this method is limited to studies analyzing breathing recordings of a limited duration—as it is not feasible for researchers to hand-label extensive numbers of individual respiratory features, precluding analysis of datasets with large numbers of subjects or hundreds of respiratory and olfactory events.

In addition to the challenges of manually labeling sniff onsets, many features of nasal airflow during a sniff influence olfactory processing. Odorants with different volatility, sorptiveness, and water solubility elicit responses of different amplitudes in the olfactory nerve when flowed across the nasal mucosa at different rates (Mozell et al. 1991). For this reason, the direction and rate of airflow during nasal breathing are important parameters in studies investigating olfactory processing. Furthermore, humans naturally modulate inspiratory volumes when olfactory stimuli with different concentrations and hedonics are sniffed (Johnson et al. 2003). Differences in olfactory processing have also been observed between odorants sniffed with a single nasal inhale compared with those that were sniffed in series (Laing 1983). Finally, it is possible that other characteristics of nasal inhales modulate olfactory processing such as durations of respiratory pauses, durations of sniffs, and the shape of individual sniff waveforms, but the breadth of features embedded in nasal airflow recordings are not well defined. For these reasons, accurately characterizing the full set of features contained in nasal airflow recordings is critical for interpreting the neural bases of olfaction.

Relating characteristics of airflow recordings to neural activity have widespread implications for other neuroscientific research beyond olfaction. In line with the established links between respiratory rhythms and neural oscillations, perturbations in human respiration have been linked to emotional states (Nielsen and Roth 1929; Bloch et al. 1991; Boiten 1998; Yackle et al. 2017), memory performance (Wientjes et al. 1998; Zelano et al. 2016), fear learning (Castegnetti et al. 2017), and social interaction (Butler et al. 2006). It is well known that opioid-mediated circuitry plays a key role in governing respiratory patterns (Bouillon et al. 2003; Lalley 2003), but an eclectic collection of neurological and psychiatric conditions is associated with changes in respiration as well. Respiratory disturbances are associated with epileptic seizures (Dlouhy et al. 2015; Lacuey et al. 2017), Parkinson’s disease (Hardie et al. 1986; Sobel et al. 2001; Rice et al. 2002; Sadagopan and Huber 2007), Alzheimer’s disease (Smallwood et al. 1983; Cooke et al. 2006; Osorio et al. 2014), Rett syndrome (Julu et al. 2008), and schizophrenia (Peupelmann et al. 2009). Dyspnea and hyperventilation are common physical symptoms of anxiety, often occurring in patients with panic disorders (Wilhelm et al. 2001; American Psychiatric Association 2013). Characteristic changes in respiration have also been found in autism spectrum disorder (Rozenkrantz et al. 2015; Ming et al. 2016), and mood disorders (Ohayon 2003; Leander et al. 2014). In line with the prevalence of respiratory correlates of these disorders, respiratory training has been an effective component for treatments of anxiety and mood disorders (Han et al. 1996; Brown and Gerbarg 2009), attention-deficit/hyperactivity disorder (Sonne and Jensen 2016), and can help reduce stress in otherwise healthy individuals (Perciavalle et al. 2017). Extracting components of respiratory waveforms could also support analyses relating features of respiration to cardiovascular activity (Helfenbein et al. 2014).

In the preceding studies, quantifying respiratory data is generally limited to analyzing the pronounced features of the signal such as inhales, exhales, and breathing rate—discarding the many other features present in these waveforms. Relative to the electrocardiogram (EKG), where research has precisely defined each component of the waveform (Ponikowski et al. 2016), established standard methods to detect them (Addison 2005), and used this information to predict cardiovascular disease (Václavík et al. 2014; Chen et al. 2016), the tools and methodology available for interpreting respiratory signals have been relatively limited. Several manuscripts mention a need for more sophisticated respiratory signal processing methods to advance our understanding of respiration and its clinical applications (Boiten et al. 1994; Folke et al. 2003; Van Duinen et al. 2010; Vlemincx et al. 2011; Meredith et al. 2012; Grassmann et al. 2016). The unique difficulty of analyzing human respiratory recordings has also been hypothesized to drive the sometimes-contradictory findings reported in respiratory research (Boiten et al. 1994). Similarly, inaccurate respiratory feature estimation may confound certain functional magnetic resonance imaging (MRI) results (Giardino et al. 2007; Hutton et al. 2011). Therefore, a tool for automatically characterizing the many features embedded in respiratory waveforms would be a boon to several fields of research.

Previous algorithmic approaches to analyzing respiratory data have proven to be successful at describing certain aspects of these data including: estimating inhale onset times in rodents (Roux et al. 2006), psychometrically modeling event-related respiratory modulations from human breathing belt recordings (Bach et al. 2016), and classifying human respiratory data into states such as apnea (Nepal et al. 2002; Varady et al. 2002). By algorithmically deriving the full set of components from respiratory signals, we may reveal novel understandings of neural control of breathing that cannot be addressed with the current methodology. However, automatically characterizing the full set of respiratory waveforms has remained an unsolved and unique technical barrier to our understanding of olfactory and respiratory neuroscience.

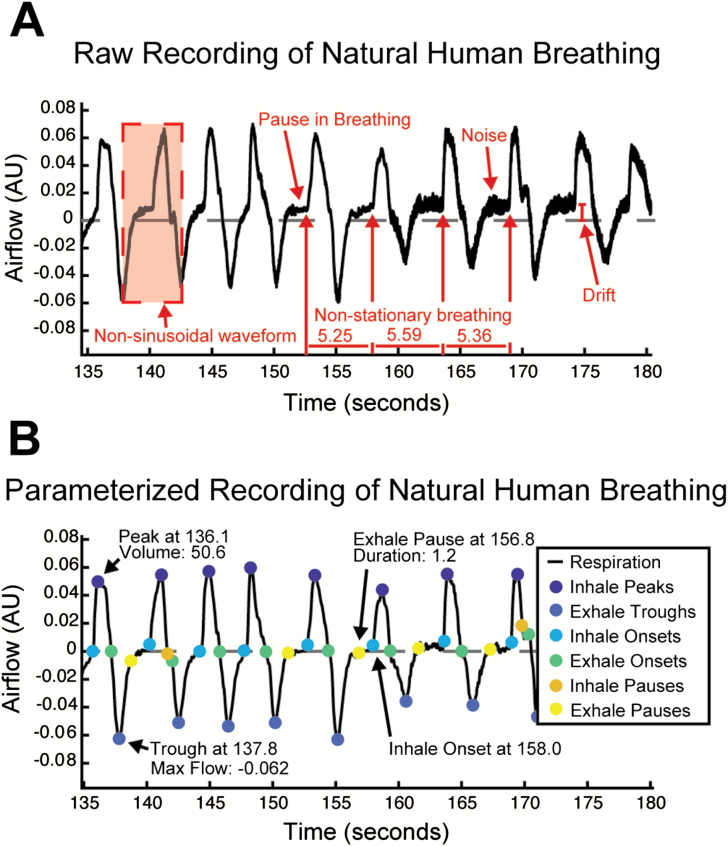
Automatically characterizing the full set of features in respiratory waveforms is challenging for many reasons. Like other oscillatory biological signals, human airflow recordings are nonsinusoidal and have nonstationary statistics (Figure 1A). But unlike other oscillatory biological signals such as EKG that have highly stereotyped sequences of activity, breathing patterns are surprisingly complex (Del Negro et al. 2018) as individuals regularly breathe at varying rates, with different individual breath volumes, and may choose to pause their breathing for up to minutes at a time. Human respiratory signals present a unique set of challenges to decompose compared with respiratory recordings from rodents. These signals tend to have a high degree of noise due to the inherent difficulties of working with humans as experimental subjects, whose comfort during experimental tasks is of utmost importance. Humans breathe up to 10× slower than rodents and express complex waveforms with a high degree of variability between individuals. These innate aspects of human respiratory signals do not meet the assumptions made by most traditional automated digital signal processing analyses, meaning that other methods must also be used for accurate feature decomposition of respiratory signals. For this reason, a reliable algorithmic approach to extracting these features must be validated on a broad, heterogeneous set of data to demonstrate that it is flexible enough to accommodate the wide range of idiosyncratic characteristics that individual respiratory waveforms may contain.

Figure 1.

(A) Representative segment of a human respiratory flow recording where some important signal properties are annotated. (B) The same recording after removing drift and noise, and estimating features with BreathMetrics.

Here, we present BreathMetrics, a respiratory signal processing toolbox. BreathMetrics is an algorithm (implemented here in Matlab) that automatically extracts the full set of features embedded in raw human respiratory flow recordings and contains additional methods for calculating event-related respiratory waveforms, statistical summaries of breathing, several visualizations for features of breathing, and a GUI for manual inspection of respiratory feature estimations. We validated our algorithm in 4 ways. First, we compared the magnitude and variability of trial-averaged inhale peaks computed with inhale onsets defined by different methods on a data set of human nasal airflow recordings (N = 23). Second, we compared the magnitude of hallmark odor-evoked theta increases computed using nasal inhale onsets defined by different methods. Third, we directly compared automated BreathMetrics inhale onsets with those that were marked by hand in 2 recordings. Finally, we show that BreathMetrics’ feature estimations had 95% confidence intervals on the order of single milliseconds by evaluating thousands of simulated respiratory recordings. With a raw recording of respiratory airflow and a single-input parameter (the sampling rate), BreathMetrics can estimate the following features and metrics of the data:

• Denoised and drift-corrected respiratory signal

• Inhale and exhale onsets and offsets

• inhale and exhale pause (breath holding) onsets and offsets

• Durations of inhales, exhales, and respiratory pauses

• Peak respiratory flow of inhales and exhales

• Volumes of individual inhales and exhales

• Instantaneous phase

• Breathing rate and average interbreath interval

• Tidal volume

• Minute ventilation

• Duty cycle of each breath

• Breathing-rate-normalized breath waveforms for comparison between subjects

• Summary statistics of respiratory recordings, such as variation in breathing rate and duty cycles, percent of breaths with pauses, and average peak flow rates and volumes

• Several visualizations of these features

By providing a data processing pipeline that automatically and precisely computes the full set of respiratory features embedded in respiratory flow recordings, BreathMetrics simplifies respiratory waveform decomposition and enables analysis of high-throughput respiratory datasets. This will simplify investigation into how respiration relates to body, brain and behavior.

Materials and methods

Accessibility, implementation, and organization of BreathMetrics algorithm

The implementation of BreathMetrics used in this manuscript is publicly available online as a Matlab package with source code (including simulations), documentation, and a tutorial at https://github.com/zelanolab/breathmetrics. This package is organized as a custom Matlab class object with functions for calculating, storing, and visualizing features of human respiratory flow data. All code was designed to conform to the standard Matlab style guide. Some functions described later have modular parameters for custom processing but were designed to work reliably on human recordings without any parameter tuning. Our methods have preprocessing steps that can flexibly handle data with sampling rates between 20 and 5000 Hz and include at least 2 full breaths. The analysis pipeline assumes that raw data comes in the form of a vector where the amplitude of inhalation is represented as having more positive values than exhalation. All functions are designed to be part of the class object and their output saved as parameters, but each function can also be called independently for researchers to customize their analyses. This toolbox is dependent on Matlab 2017. All functions described here do not require the Matlab Signal Processing package except for instantaneous phase estimation, and the GUI tool is dependent on the GUI layout toolbox (MATLAB and Signal Processing Toolbox, Sampson and Tordoff 2014).

Human subjects

BreathMetrics was designed using data collected from 23 participants (78% female) whose nasal respiration was recorded while they performed an emotion recognition task for approximately 15 min. This task was chosen so that participants would elicit a wide range of natural respiratory behaviors that would not be present in sleeping or resting conditions. The task included 180 trials, each beginning with the presentation of a face expressing either fear or surprise. Participants were instructed to indicate, via button press, as quickly and accurately as possible, which emotion the face was expressing. Faces were presented for 100 ms at jittered time intervals ranging between 3.5 and 6.5 s apart (average 5 s).

Participants were instructed to breathe naturally through their nose for the duration of the experiment. No participant reported any psychological disorders or major health problems or was currently taking any medication known to affect breathing. All subjects were recruited from flyers posted around Northwestern University Chicago campus and gave written informed consent prior to the beginning of the experiment. The Institutional Review Board of Northwestern University approved all experimental procedures, and this study complies with the Declaration of Helsinki for Medical Research involving Human Subjects.

Human electrophysiology recordings

To validate our toolbox using an objective, independent neural correlate of respiration in humans, we analyzed intracranial electroencephalography (iEEG) data from a patient with surgically implanted depth electrodes in piriform cortex (primary olfactory cortex) as part of a clinical evaluation for medication-resistant epilepsy. The data analyzed here were collected while the patient was performing a cued odor-identification task. iEEG data were recorded using the clinical Nihon Kohden EEG acquisition system in place at Northwestern Memorial Hospital. The patient provided informed consent to take part in the study, and the Institutional Review Board of Northwestern University approved this experiment.

iEEG data were collected with a sampling rate of 2000 Hz, with an online high-pass filter of 0.08 Hz. The reference and ground consisted of a surgically implanted electrode strip facing toward the scalp, though data were re-referenced to a common average following exportation into Matlab. Odor stimulus presentation was synchronized with the ongoing iEEG data trace using a data acquisition board (Measurement Computing, USB-1208FS) connected to a laptop computer on one end and Nihon Kohden’s DC input port on the other end. The USB-1208FS was controlled by Matlab using PsychToolBox’s PsychHID scripts (Brainard 1997). Trials began with an auditory cue consisting of either the word “rose” or “mint,” followed by presentation of odor. The patient’s task was to indicate whether the odor matched the cue.

Electrode locations were determined using preoperative structural MRI scans and postoperative computed tomography (CT) scans using FSL’s registration tool flirt. Individual CT images were registered to MRI images using 6 degrees of freedom (df) with a cost function of mutual information, which was followed by an affine registration with 12 df.

Respiratory flow recordings

In the behavioral data set, respiration was recorded using a pneumotachometer (high-sensitivity flowmeter model #4719, Hans Rudolph, Inc., Kansas City, MO) attached to a nasal mask worn by the participants. The pressure differential measured by the pneumotachometer was converted to a voltage signal using a spirometer (ADInstruments). Amplified pneumotachometer traces were then recorded using Powerlab and Chart software (ADInstruments).

In the electrophysiological data set, respiration was recorded using a nasal cannula attached to a piezoelectric pressure sensor (Salter Labs), providing a measure of airflow through the nose. The signal from the sensor was directly recorded into the Nihon Kohden software, allowing perfect synchronization between respiratory and iEEG data. Respiratory and iEEG data were exported from the Nihon Kohden NeuroWorkBench software text files and then imported into Matlab for all further processing and analysis.

Simulation of respiratory flow recordings

We simulated respiratory flow recordings to evaluate the accuracy of BreathMetrics’ feature estimations on a large collection of data expressing respiratory characteristics varying from those observed in our other datasets. Respiratory flow recordings were simulated by seeding a custom algorithm with the following input parameters: number of breaths to simulate, sampling rate, breathing rate, average peak flow amplitude, variance in peak flow amplitude, variance in interbreath interval, percent of breaths with inhale pauses, average duration of inhale pause, variance in the duration of inhale pauses, percent of breaths with exhale pauses, average duration of exhale pauses, variance in the duration of exhale pauses, noise range of pause amplitudes, variance in pause amplitude noise, and signal noise. The values chosen for these parameters were randomly selected from within the range observed in the human datasets. With these parameters, our simulation algorithm composes individual breaths with characteristics that fall within the input constraints and saves their values (inhale onsets, exhale max flow, etc.). By independently manipulating the specific components of each simulated breath, we could recover the estimation accuracy of BreathMetrics on an extensive array of respiratory recordings that it might encounter. Furthermore, we could determine the resilience of BreathMetrics’ feature estimations with regard to signal noise by manipulating the noise saturation in the simulated recording. Code for simulating human respiratory data is available at https://github.com/zelanolab/breathmetrics.

Data normalization and smoothing

Before decomposing raw respiratory flow recordings into their basic components, measurement noise and signal drift must be removed. First, the signal is left-right padded and mean-smoothed by a 25-ms window. The window size of 25 ms was chosen because it is large enough to reduce signal noise but not so large that it would influence the shape of natural breathing waveforms, which oscillate at approximately 0.2 Hz in humans. Like other hard-coded parameters used in this toolbox, this value can easily be adjusted by the user. Mean smoothing is used rather than other filtering techniques to avoid introducing an artificial time shift and minimize any distortions of signal waveforms across an unlimited range of respiratory wavelengths. Next, global linear drift is removed by subtracting the slope of the linear regression model of the data. Local signal drifts are corrected to continuous, minute-long sliding mean baseline windows, and padding is removed. These methods are parameterized such that researchers can customize noise removal and drift correction, or z-score respiratory amplitudes if they choose, although custom options are not validated here.

Inhale and exhale extrema detection

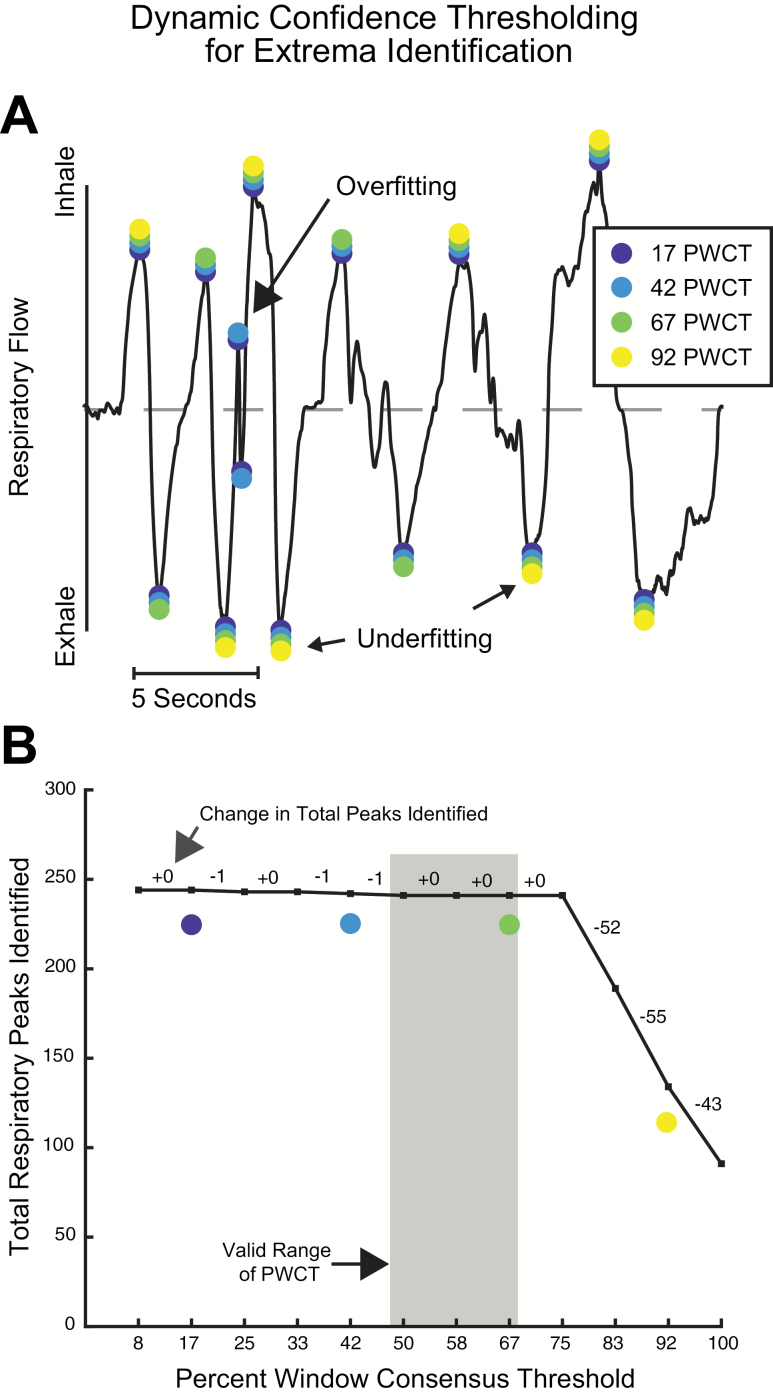
The amplitudes of inhale and exhale extrema vary in human respiratory recordings, which renders simple threshold-based approaches to respiratory peak finding infeasible. We achieved algorithmic labeling of inhale peaks and exhale troughs using a custom multiple sliding-window peak-finding method. This involved 2 steps: first, we scored peaks by their likelihood of being a true peak, and second, we determined the best recording-specific confidence threshold to use. To programmatically score respiratory extrema, the respiratory vector was sectioned into a range of window sizes (300, 500, 700, 1000, and 5000 ms), each with 3 shifts in their starting index (0%, 33%, and 66% of the window size). Multiple windows were used because small windows tend to falsely identify local maxima as peaks (false positives), and large windows tend to falsely reject true peaks (false negatives). This technique produces a score for each time point that represents how many windows identify it is a peak or trough (Figure 2A).

Figure 2.

Identification of respiratory flow extrema using dynamic confidence thresholding. (A) Scoring putative extrema using multiple sliding windows. (B) The most stable PWCT is identified by finding the largest inclusion criterion where the marginal requirement of window agreement produces the smallest difference in total extrema identified. PWCT values that are too low result in overfitting noise as extrema, and PWCT values that are too high underfit the signal by falsely rejecting true extrema.

With scored peaks, we could then determine the most appropriate threshold for how many windows must agree for a point to be considered a putative peak or trough, minimizing both false positives and false negatives. Because breathing rates and breath sizes vary across individuals, the appropriate Percent Window Consensus Threshold (PWCT) for accurate extrema labeling—or how many distinct windows must independently agree that each extremum is valid—must be calculated dynamically for each recording session. By calculating the PWCT score for each peak and then finding the largest PWCT value that excluded the fewest peaks compared with the number of peaks found in the previous iteration, we could find the most stable threshold for peak identification (Figure 2B). Although this is a custom technique, it is similar to the elbow method, which is a technique that can be used to determine the optimal number of clusters in k-means clustering (Thorndike 1953).

Detecting onsets and offsets of inhales, exhales, and respiratory pauses

Using the peaks and troughs of respiratory flow determined by the preceding method, we could now estimate the onset of inhales and exhales. In human respiratory flow recordings, both inhale and exhale onsets are often preceded by a phase pause, or plateau, in the respiratory cycle (Figure 1, Wientjes et al. 1998) and breath onsets do not always occur at every instant that the trace crosses the zero threshold, even if the data have been noise corrected. These factors make inhale onset identification challenging. To overcome this, we created a custom algorithm that identifies whether a pause occurs in a breath, the point where the pause initiates, and the point where the pause ends and the next breath begins.

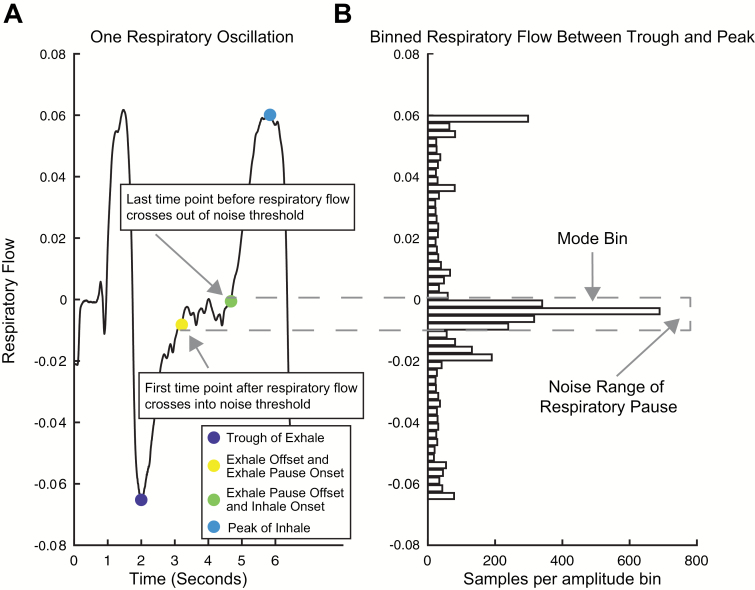
We first made the assumption that exactly one inhale begins between each trough of exhalation airflow and subsequent peak of inhalation air flow and that exactly one exhale begins between each peak of inhalation air flow and subsequent trough of exhalation air flow. To check for the existence of a respiratory pause in the window between a peak and trough, we tested whether respiratory amplitudes were evenly distributed within this window or rather if they clustered around a certain value. To this end, we first binned all of the time points between the extrema. Then, a pause was presumed to exist if the mode bin (the bin with the most data points) did not coincide with a peak or trough and had 5 times more samples than the average bin (Figure 3B).

Figure 3.

Method for detecting breath pauses and onsets. (A) A single respiratory oscillation where a pause occurs after exhalation. The point of maximum exhale flow (dark blue marker) and maximum inhale flow (cyan marker) are defined by the extrema identification method described in Figure 2. Offset of preceding exhale/onset of exhale pause (yellow marker) and offset of exhale pause/onset of subsequent inhale (green marker) are determined using the respiratory flow binning method. (B) Time points between extrema are binned by amplitude of respiratory flow. If there is an uneven amplitude distribution, a respiratory pause is identified and the threshold of its noise range is fit. The first samples to cross this threshold in either direction, respectively, indicate 1) the offset of the preceding breath and onset of the pause and 2) the offset of the pause and onset of the subsequent breath.

In the absence of a respiratory pause, the first point where the trace crosses zero is used as both the breath offset and the subsequent breath onset. However, when a respiratory pause is found, the onset and offset of the pause must be determined. To do this, the offset of the pause must be distinguished from noise because natural amplitude variation in respiratory flow recordings can mimic real respiratory events. To distinguish between the two, we first find the noise range of the potential pause by iteratively checking the number of time points collected in 5 amplitude bins adjacent to the mode bin in either direction. If the number of time points in an adjacent bin exceeds 25% of the mode bin, this suggests amplitude noise in the respiratory pause extends to this range. The choices to iterate over 5 bins and appending a bin to the noise range if it exceeds 25% were made after testing multiple values and examining the results. Using looser values resulted in falsely identifying pauses where there were none and tighter values resulted in falsely missing pauses when they were present. Like other hard-coded parameters used in this toolbox, these values can easily be adjusted by the user. Using this technique, we can dynamically fit the noise range of each breath. The first point that crosses into the noise range now defines the offset of the preceding breath and the onset of the pause, and the first point before respiratory flow passes out of the noise range defines the offset of the pause and the onset of the next breath (Figure 3A).

Calculation of breath volumes and additional features

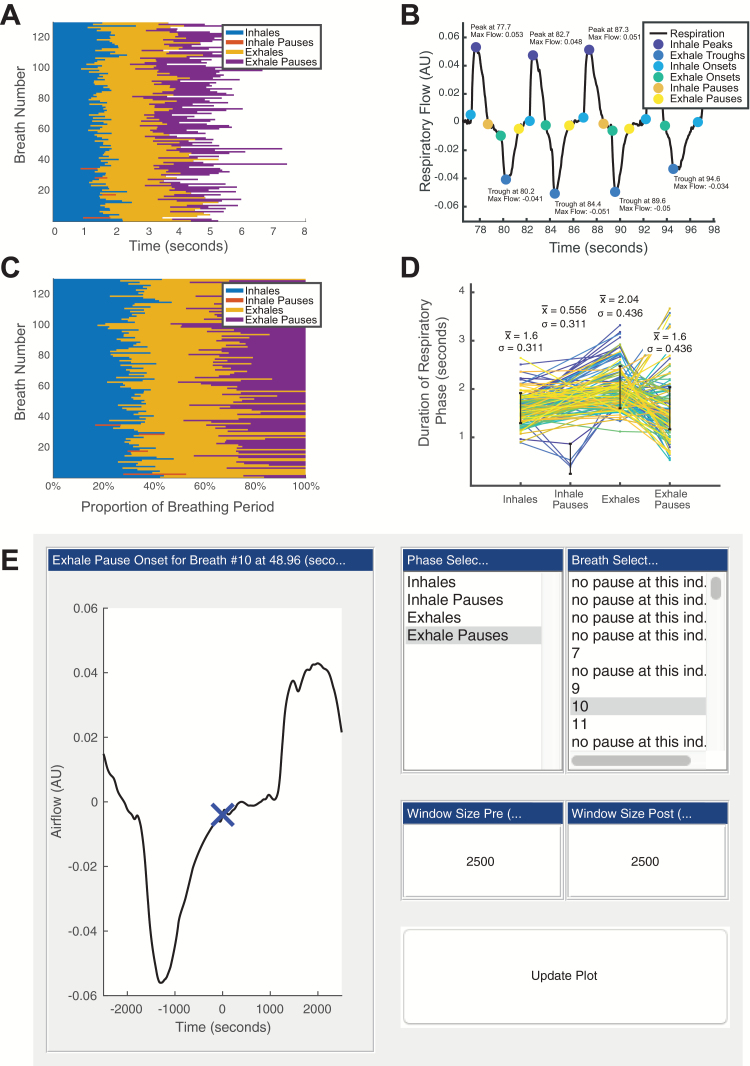
Because BreathMetrics is designed to analyze respiratory airflow, which is a measure of instantaneous airflow over time, we can mathematically derive the volume of each breath by calculating the integral of the airflow amplitudes within each breath’s onset and offset. Although a ground-truth calculation of volume requires temperature and barometric information (Jacky 1980), we provide code to estimate normalized breath volumes by assuming these measures are constant. In addition to breath volumes, we can compute many other respiratory characteristics using the features calculated earlier. Table 1 summarizes the respiratory features that BreathMetrics can compute, along with their corresponding equations. BreathMetrics also includes code to generate several visualizations of respiratory characteristics as well as a GUI for inspecting individual respiratory events (Figure 4).

Table 1.

List of respiratory metrics implemented in BreathMetrics and their respective calculations

Metric	Calculation
Breathing rate	1/average time between inhale onsets
Inter-breath interval	Average time between inhale onsets
Inhale and exhale volumes	Sum of airflow between breath onset and offset
Tidal volume (average volume of air displaced per breath)	Average inhale volume + average exhale volume
Minute ventilation (volume of air displaced each minute)	(Breathing rate × average tidal volume)/1 min
Duty cycle (proportion of breath that is inhaled)	Average inhale duration/average interbreath interval
Coefficient of variation of duty cycle	SD of inhale duration/average inhale duration
Coefficient of variation of breathing rate	SD of difference between inhale onsets/average difference between inhale onsets
Coefficient of variation of breath volumes	SD of breath volumes/average breath volume

Figure 4.

BreathMetrics tools for visualizing breathing recordings. (A) Duration of each component of every breath. (B) Baseline-corrected breathing with labeled features and annotated extrema. (C) Proportion each respiratory phase contributes to each breathing cycle. (D) Each breath is plot as a line where its x-value represents its progression through each respiratory phase and y-value represents the time spent in each phase. Lines representing individual breaths are colored by order (the first breath is dark blue, and the last breath is yellow). (E) GUI for inspecting individual respiratory features.

Time–frequency analysis of human electrophysiology

Natural respiratory rhythms and odor stimulation induce characteristic theta-band power increases in human piriform cortex (Adrian 1942; Zelano et al. 2016; Jiang et al. 2017). To validate our method, we took advantage of this hallmark feature of piriform LFPs and compared the strength of odor-evoked theta power using sniff onsets defined by our method and the other methods. To examine odor-evoked amplitude changes, we computed spectrograms of LFP amplitude recorded from human piriform cortex. Raw LFP data were bandpass filtered in 100 logarithmic-spaced frequencies from 1 to 200 Hz with the bandwidth increasing from 2 to 50 Hz (logarithmic spaced). The envelope at each frequency was obtained using the Hilbert transform (Matlab’s hilbert.m) and segmented into epochs of [−0.5, 5] s relative to inhalation onsets. The epochs were averaged across trials, and the baseline ([−0.5, 0] s) was subtracted, producing a spectrogram for each condition. To test the statistical significance of the spectrogram, the real events were shifted a random amount, and the mean amplitude of those permuted events was calculated. By repeating the above procedure 10000 times, a null distribution was obtained at each time–frequency point. A z-score map was calculated by dividing the spectrogram with the standard deviation (SD) of the distribution. These z-score maps were reported as the spectrogram in this article. The z-scores were converted to P values by assuming a normal distribution. Multiple comparisons were corrected using false discovery rate (FDR) method.

To compare spectrograms aligned to sniff onsets determined by BreathMetrics compared with other methods, we subtracted the condition-specific spectrograms from each other. The significance of these differences was tested using a permutation method. In each permutation, the trial labels of the 2 conditions were shuffled, and the permuted spectrogram difference was calculated as described earlier. Then, a null distribution of permuted spectrogram difference was obtained by repeating the above procedure 1000 times. The z-score map of the real difference was corrected for multiple comparisons using the FDR method.

Results

Rationale for validation methods

The features estimated by our toolbox are visually accurate (Figure 1B). However, numerical validation of respiratory feature estimation is nontrivial because there is no established set of respiratory features to which we can compare our estimations. To address this limitation, we propose that a respiratory feature extraction pipeline is accurate and reliable if it meets the following criteria:

• 1) Features estimated using our method must outperform other feature estimation methods across multiple subjects.

• 2) Feature estimations must be reliable across multiple data sets and recording devices.

• 3) Feature estimations must resemble those that were hand labeled by an expert.

• 4) Feature estimations must be correlated with independent and objective measures of respiration.

Because inhale onset estimations are dependent on other measures computed by BreathMetrics, including respiratory extrema and pause characterizations, we chose to validate the accuracy of inhale onsets as an indicator of the validity of the rest of our estimations. In the following subsections, we evaluate the performance of BreathMetrics’ respiratory onset estimations on 2 human datasets that together satisfy all of the criteria described earlier. Furthermore, we evaluate BreathMetrics’ performance on a comprehensive body of simulated respiratory recordings to ascertain its estimation accuracy and resilience to signal noise.

Validating inhale onset accuracy with inter-inhale similarity

To demonstrate that BreathMetrics-derived inhale onsets outperform other onset-detection methods, we compared the performance of BreathMetrics to 2 other methods on a dataset of nasal breathing collected from 23 participants. The first was a zero-crossing referenced method (ZC). In this method, 2 criteria were used to define an inhale onset: 1) a baseline crossing of the preprocessed respiratory trace and 2) an average amplitude of one-tenth of an SD above average for the next 3 s of data following the baseline crossing. The second method was motivated by previous work by Roux et al. (2006) who could accurately estimate inhale onsets from respiratory flow in rodents with instantaneous respiratory phase referencing. In this method, the breathing rate was calculated by finding the peak of the power spectrum of the preprocessed trace. The instantaneous phase of the respiratory signal was then calculated by bandpass filtering it around this peak using a 2-way low-pass Butterworth filter and taking the angle of its Hilbert transform (Matlab’s hilbert.m). Each point where the instantaneous phase passed π/2 (where the respiratory trace crosses baseline toward a peak) was considered an inhale onset.

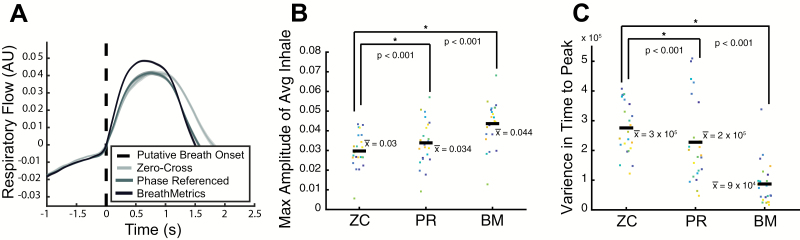
The reliability of the 3 methods was scored in 2 ways. First, we compared the magnitude of peaks of each subject’s average inhale as defined by each method. Decreases in accuracy of inhale onset estimation will introduce temporal shifts in each inhale trace, which will wash out the true maxima of inhales when averaged. Therefore, we hypothesized that trial-averaged inhale maxima calculated with BreathMetrics would be larger than those calculated with the other 2 methods. Second, we compared the variability in onset-to-peak latency as defined by each method. Although individual breath waveforms naturally vary, inaccurate labeling of breath onsets will introduce additional variance in the time each breath takes to reach its point of max inspiratory flow. Therefore, we hypothesized that the variance in time-to-peak would decrease as the onset estimation accuracy increases. Thus, we hypothesized that BreathMetrics would have smaller variance in time-to-peak than the other methods.

We found an overall effect of method on both inhale maxima (F_2,66 = 10.37, P = 0.0001) and time-to-peak variance (F_2,66 = 23.12, P < 1 × 10⁻⁷). Follow-up paired t tests confirmed that BreathMetrics produced inhales with larger maxima than both ZC (T₂₂ = 7.55, P < 1 × 10⁻⁶) and PR (T₂₂ = 6.98, P < 1 × 10⁻⁶) (Figure 5B). Similarly, follow-up paired t tests confirmed that BreathMetrics had smaller variance in time-to-peak flow than ZC (T₂₂ = −11.10, P < 1 × 10⁻⁹) and PR (T₂₂ = −6.60, P < 1 × 10⁻⁵) (Figure 5C).

Figure 5.

Scoring reliability of 3 inhale estimation methods by calculating average within-subject peak of inhale and variance in time-to-peak. (A) Single-subject example of average inhales calculated using different methods. Hue of shade represents the method used and shaded areas indicate SEM. BreathMetrics has smaller variance throughout the course of the average inhale and a higher peak than the other methods. (B) Inhales identified using BreathMetrics have larger within-subject average maxima than other methods. (C) Inhales identified using BreathMetrics have smaller variance in time-to-peak than other methods. (B, C) Color represents individual subjects and horizontal bars indicate the mean. P values are derived from paired t tests.

Validation using LFP recordings from human piriform cortex

The preceding validation indicates that our method finds more consistent onset estimations than the other methods across subjects, satisfying the first criterion described earlier. To show that these estimations are linked to ground-truth respiratory features, and not just internally consistent, we took advantage of the well-established fact that inhalation and sniffing induce increases in LFP theta-band power in human piriform cortex (Zelano et al. 2016; Jiang et al. 2017). In this way, we could use human piriform theta power as an independent and objective indicator of respiratory onset accuracy. To do so, we analyzed concurrent recordings of nasal respiration and human piriform cortical LFPs collected from an epilepsy patient with intracranial depth wires implanted in piriform cortex. Respiratory recordings were obtained using a nasal cannula attached to a piezoelectric sensor, a different recording device than the pneumotachometer and spirometer used in the first dataset. Thus, evaluating our method’s performance on this dataset also confirmed that BreathMetrics parameters can generalize to unseen data collected using different instrumentation in a hospital setting, satisfying validation criterion 2.

To perform the validation test, one author calculated the inhale onsets using each method. Time points of inhale onsets using each of these methods were then submitted, unlabeled, to another author for use into calculating the piriform LFP response following each set of estimations. Because this data set had not been evaluated as part of designing the toolbox and because both experimenters were blind to the conditions being tested, this validation method was as unbiased as possible.

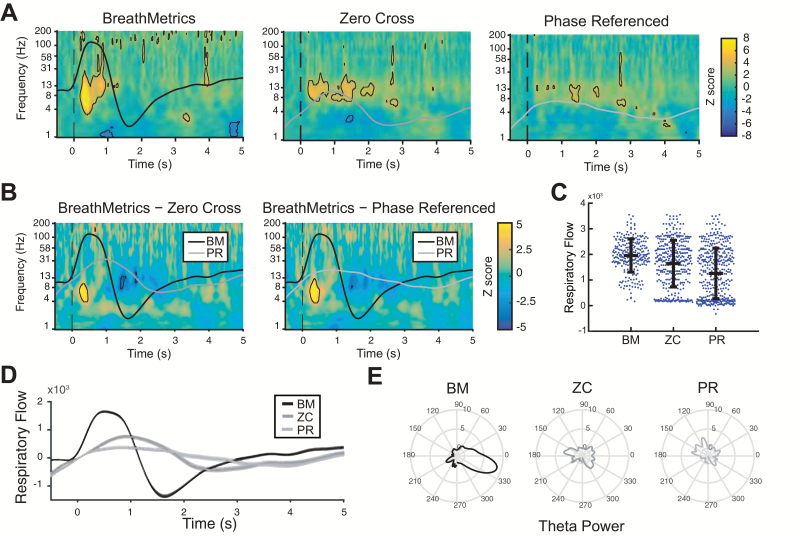
To compare the differences in sniff-evoked piriform theta amplitude across methods, spectrograms (time–frequency plots) were computed by aligning trials to onsets determined by each method (Figure 6). Statistically significant sniff-evoked amplitude increases (FDR corrected P < 0.05) were observed for all 3 methods (Figure 6A). However, we found that spectrograms computed using BreathMetrics onsets had significantly larger theta responses in human piriform cortex compared with the other 2 methods (Figure 6B, black outlined areas indicate a significant difference, P < 0.05, FDR corrected for multiple comparisons). Corresponding with this theta power increase, respiratory peaks following inhales identified using BreathMetrics were larger than both ZC (T₆₁₃ = 4.73, P < 1 × 10⁻⁵) and PR (T₆₆₄ = 9.99, P < 1 × 10⁻²¹) (Figure 6C, D).

Figure 6.

Piriform theta responses and respiratory features computed using different inhale onset-detection methods. (A) Spectrograms of piriform LFP power following the patient’s inhales computed using each method. Black outlines indicate statistically significant clusters (FDR corrected P < 0.05). (B) Difference in spectrograms computed using each method. Black outlines in indicate statistically significant clusters (FDR corrected P < 0.05) for between-method differences. (C) Maximum respiratory flow in the 2-s window following each inhale onset. Each dot indicates 1 peak, and the horizontal lines indicate mean ± SEM. (D) Average inhale defined using each method. Shaded area indicates SEM. (E) Mean theta (4–8 Hz) power across phase of respiratory cycle.

Comparison between sniff onsets identified using hand labeling and BreathMetrics

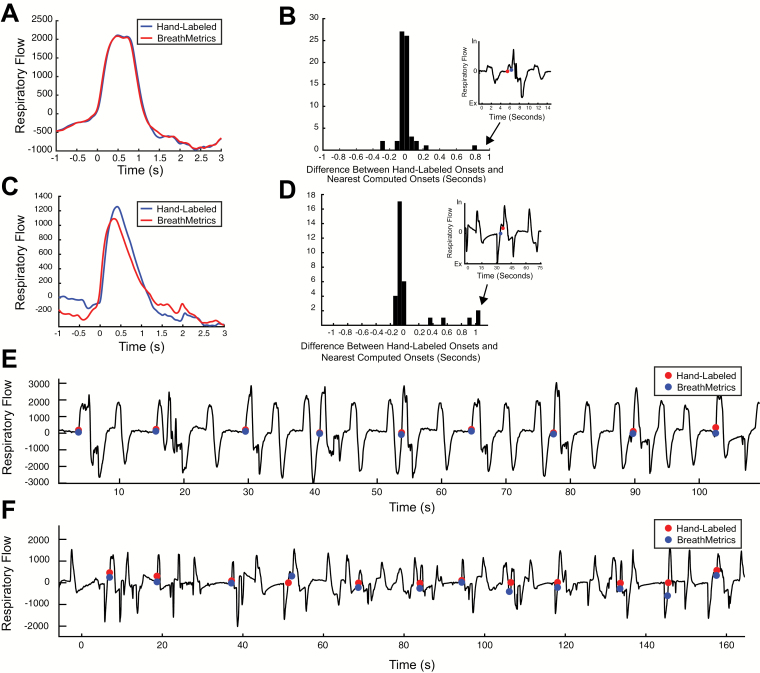
We have shown that BreathMetrics outperforms other methods across subjects, in 2 datasets, and that its estimations accurately match an independent neurological correlate of respiration. In human olfactory studies that rely on accurate sniff onset-detection methods, experimenters frequently resort to manual checking of each sniff onset. Here, we analyzed 2 recordings of subjects performing different sniffing tasks to test whether sniff onsets calculated with BreathMetrics are similar to those that were hand labeled. The first recording we analyzed was the same one analyzed earlier in Figure 6. Because this was collected while a subject was performing an odor-identification task, a subset of inhalations in this data set coincided with sniffs during odor presentations. The second recording was collected from a different subject who moved a lot during the task, resulting in a noisy respiratory recording. By testing the similarity of BreathMetrics’ sniff onsets to hand-labeled sniff onsets in both clean and noisy datasets we were able to evaluate whether BreathMetrics’ feature estimations remain stable as a function of data quality. The similarity of BreathMetrics’ sniff onsets to hand-labeled sniff onsets was compared by first hand labeling each sniff onset in both recordings (64 sniffs in recording 1 and 32 sniffs in recording 2). These time points were then compared with the closest corresponding inhale onset automatically computed by BreathMetrics.

BreathMetrics produced sniff onset estimations that closely resemble hand-labeled ones in both recordings (Figure 7). The average sniff waveform computed using onsets identified by BreathMetrics was nearly identical to that computed using hand-labeled onsets in both recordings (Figure 7A, D). Although sniff onsets defined with BreathMetrics appear less accurate in recording 2, paired t tests revealed no significant statistical difference between the sniff onsets identified using hand labeling and BreathMetrics in either recording (recording 1: P = 0.52, recording 2: P = 0.29). Ninety-four percent of BreathMetrics estimations were within 100 ms of hand-labeled onsets in the first recording, and 72% were within 100 ms of hand-labeled onsets in the second recording (Figure 7B, E).

Figure 7.

Comparison between sniff onsets determined using hand labeling and BreathMetrics in 2 recordings of individuals performing sniffing tasks. (A–C) Data from the first recording. (D–F) Data from the second recording. (A, D) Average sniff computed using hand labeling and BreathMetrics. (B, E) Temporal differences in sniff onsets calculated using BreathMetrics and hand labeling. (C, F) Representative data showing similarity between sniff onsets identified using hand labeling and BreathMetrics.

Evaluation of BreathMetrics’ feature estimations on simulated data

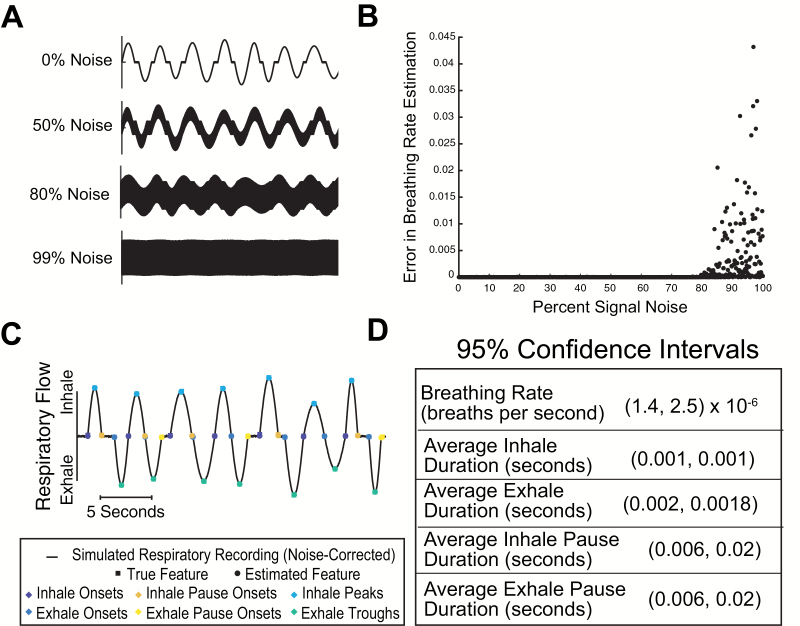
In the preceding section, we showed that BreathMetrics’ sniff estimations were accurate on both a clean and a noisy human respiratory recording. Because signal noise can take many forms and may corrupt certain characteristics of breathing waveforms differently, the fidelity of feature estimations made with BreathMetrics can be better evaluated by comparing its feature estimations to ground-truth values on a large dataset of breathing recordings that span a broad range of parameter values. Because ground-truth respiratory parameters are not obtainable in raw recordings, simulations of breathing recordings were used. One thousand simulations of respiratory flow recordings were generated, each with a random combination of characteristics (i.e., average breathing rate, variance in max flow rate, probability of pausing after inhales, etc.) and with known, ground-truth values for each characteristic. Each simulated respiratory recording was convolved with a vector of random numbers spanning the simulation’s amplitude range and multiplied by increasing weights ranging from 0% noise to 100% noise in the resultant signal (Figure 8A). Each simulated recording was evaluated using BreathMetrics, and then the error between the ground-truth breathing rate and the estimated breathing rate was compared (Figure 8B). This analysis revealed that BreathMetrics could robustly estimate breathing rates in a diverse collection of simulated recordings that were up to approximately 80% noise.

Figure 8.

Evaluating accuracy of feature estimations using simulations. (A) Segments of representative simulations with different noise saturations. (B) Breathing rate estimation error calculated on 1000 simulated respiratory flow recordings that vary in both respiratory characteristics and noise saturation. (C) Ground-truth feature values and estimated feature values for a segment of a representative simulated respiratory recording. (D) 95% confidence intervals for features calculated for 1000 simulations of respiratory recordings with 10% noise saturation and varying respiratory characteristics.

To determine the measurement error for the features that BreathMetrics extracts, we produced 1000 new simulations of respiratory flow recordings, each with a random combination of characteristics but a constant signal noise of 10%. The feature estimations for this dataset are visually matched with their ground-truth values (Figure 8C). For each simulation, we calculated the estimation error for breathing rate, average inhale duration, average inhale pause duration, average exhale duration, and average exhale pause duration. Using the errors calculated in each simulation, we could deduce 95% confidence intervals for each of these measures, which fell on the order of single milliseconds (Figure 8D).

Ongoing work to extend BreathMetrics functionality to rodent and belt data

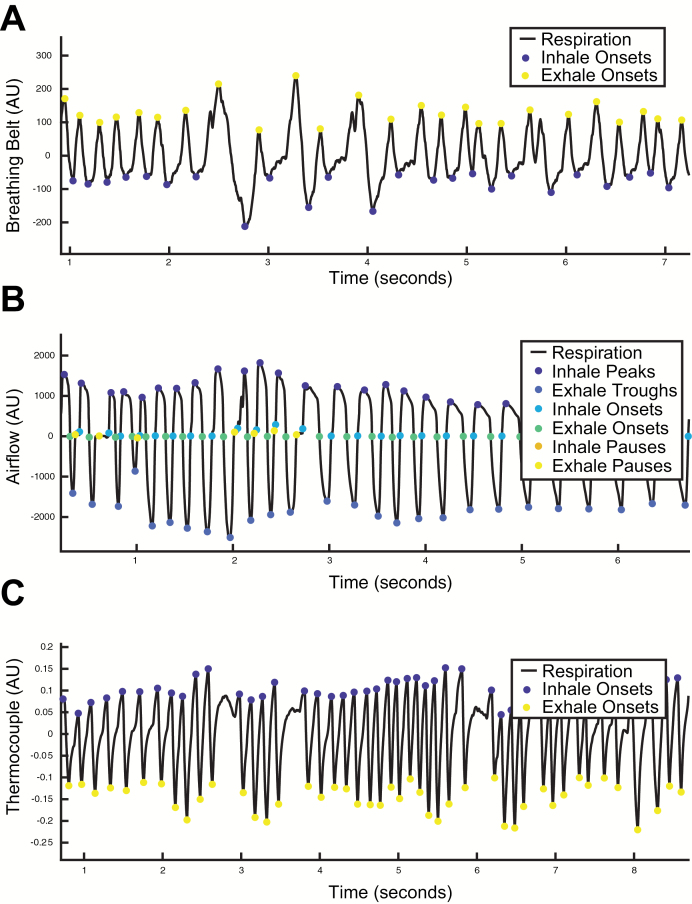
In the preceding sections, we have demonstrated that BreathMetrics can accurately recover features of nasal airflow recordings collected from humans using 2 devices that both directly measure airflow. These devices were chosen in favor of breathing belts, which measure chest and abdomen expansions, because respiratory flow provides a more sensitive measure of respiratory features (Johnson et al. 2006). However, many researchers use other tools to measure breathing in humans and animal models. Expanding the functionality of BreathMetrics to accommodate these other signals could benefit a broader community of researchers. Accomplishing this is nontrivial. Signals that measure respiration using different measures (temperature or chest wall expansions for example) require very different respective analysis strategies. Here, we show preliminary data indicating that the functions for extracting features from respiratory waveforms introduced here can be adjusted to extract information from other respiratory recording methods, enabling their analysis with BreathMetrics. Though not yet rigorously validated, we are currently expanding BreathMetrics to support other methods, including human breathing belts, rodent thermocouple, and rodent flow sensors.

Breathing belts measure respiration by quantifying chest/abdominal expansions. This results in a signal that represents an estimate of the instantaneous volume of air in the lungs. Because volume is a different property of breathing than airflow, the interpretation of a signal representing instantaneous volume is different than the instantaneous change in flow rate. Specifically, positive derivatives of the breathing signals indicate inhalation and negative derivatives represent exhalation, contrary to recordings of airflow where positive signals represent inhales and negative signals represent exhales. This means that breath onsets occur at the inflection points of extrema in breathing belt recordings, unlike recordings of airflow where breath onsets are (roughly) demarcated by sign changes in flow rate. Furthermore, breathing belt signals increase as lung volumes expand, meaning the inflection points of peaks represent exhale onsets, and troughs represent inhale onsets in these signals. By considering these aspects of breathing belt recordings, we can apply the same extrema detection method described for airflow data. However, in a breathing belt signal, we have to redefine the extrema such that peaks represent exhale onsets and troughs represent inhale onsets (Figure 9A). Although there are respiratory features embedded in breathing belt recordings in addition to breath onsets, estimating them remains a challenge.

Figure 9.

Preliminary data demonstrating accurate estimations of features in respiratory signals other than human nasal airflow. (A) Human breathing belt recording. (B) Mouse pressure sensor recording. (C) Mouse thermocouple recording.

Extracting respiratory features from rodents presents a different challenge because they can breathe up to 10 times faster than humans, well outside the range of parameters tested in our simulations of human breathing above. By using a bank of shorter sliding windows for extrema detection (5, 10, 20, and 50 ms), BreathMetrics was able to accurately extract respiratory features from a recording of airflow collected from an awake, behaving mouse (Figure 9B).

Finally, a large body of research in rodent olfaction and respiration uses thermocouples to infer respiration by measuring changes in temperature of air around the nose. During inhales, ambient air drawn into the nose decreases the temperature of the air in the nasal cavity. This means that in thermocouple recordings, inhales are demarcated by inflection points at peaks where temperature begins decreasing, and exhales are demarcated by inflection points at troughs where temperature begins increasing. We could reliably recover breath onsets from a thermocouple recording of an awake, behaving mouse by using the preceding extrema detection method for rodent airflow recordings. However, the inflection points have to be reinterpreted to represent breath onsets (Figure 9C).

Discussion

Our ability to understand the neural bases of olfaction and respiration can only be as good as our ability to relate them to features of respiratory waveforms. This end is limited by the lack of standardized, automated, and reliable estimation of respiratory features from recordings. To address this, we have developed BreathMetrics, a toolbox that estimates and calculates a host of meaningful respiratory features from nasal respiratory flow recordings. BreathMetrics expands upon the advantages to several previous algorithmic approaches to respiratory data analysis (Nepal et al. 2002; Varady et al. 2002; Roux et al. 2006; Bach et al. 2016). BreathMetrics differs from these methods in that it can identify the complete set of respiratory features including those typically imbedded in noise such as respiratory pauses at any phase of respiration, individual breath volumes, apneas, inhale onsets, exhale onsets, and many more. By allowing researchers to investigate the precise features of respiration that are perturbed under experimental conditions, biology and cognition can be more tightly linked to respiratory behaviors.

In this study, we satisfied rigorous validation criteria to ensure that BreathMetrics achieves accurate respiratory feature estimation across multiple datasets. We showed that BreathMetrics outperformed 2 other algorithmic approaches in 2 ways. First, BreathMetrics-defined inhale onsets resulted in larger and less-variable trial-average inhale peaks. Second, odor-evoked responses in human piriform cortex were significantly stronger when computed using sniff onsets defined by BreathMetrics. We demonstrated these estimations match land-labeled inhale onsets by showing that inhale onsets estimated using BreathMetrics were statistically indistinguishable from those that were hand labeled in 2 recordings. By using 1000 simulations of breathing, differing in many respiratory features, we showed that BreathMetrics’ estimations have high resilience to noise saturation and feature estimation accuracy on the order of single milliseconds. Finally, by adjusting BreathMetrics functions to account for differences in other respiratory signals, we were able to recover respiratory features from a human breathing belt recording, a mouse airflow recording, and a mouse thermocouple recording. Thus, BreathMetrics is a stable algorithm for fast, standardized, and objective analysis of respiratory data. In this way, our tool removes a large technical barrier to respiratory data analysis, enabling researchers to thoroughly analyze high-throughput respiratory datasets and address new questions about the nature of respiration.

Funding

This work was supported by National Institutes of Health (R00-DC-012803 and R01-DC-016364 to C.Z. and T32-NS047987 to T.N.).

Conflict of Interest

We have no conflicting financial or nonfinancial interests to declare.