Abstract
Microsurgical procedures, such as petroclival meningioma resection, require careful surgical actions in order to remove tumor tissue, while avoiding brain and vessel damaging. Such procedures are currently performed under microscope magnification. Robotic tools are emerging in order to filter surgeons’ unintended movements and prevent tools from entering forbidden regions such as vascular structures.
The present work investigates the use of a handheld robotic tool (Micron) to automate vessel avoidance in microsurgery. In particular, we focused on vessel segmentation, implementing a deep–learning–based segmentation strategy in microscopy images, and its integration with a feature-based passive 3D reconstruction algorithm to obtain accurate and robust vessel position. We then implemented a virtual–fixture–based strategy to control the handheld robotic tool and perform vessel avoidance. Clay vascular phantoms, lying on a background obtained from microscopy images recorded during petroclival meningioma surgery, were used for testing the segmentation and control algorithms.
When testing the segmentation algorithm on 100 different phantom images, a median Dice similarity coefficient equal to 0.96 was achieved. A set of 25 Micron trials of 80s in duration, each involving the interaction of Micron with a different vascular phantom, were recorded, with a safety distance equal to 2mm, which was comparable to the median vessel diameter. Micron’s tip entered the forbidden region 24% of the time when the control algorithm was active. However, the median penetration depth was 16.9 μm, which was two orders of magnitude lower than median vessel diameter.
Results suggest the system can assist surgeons in performing safe vessel avoidance during neurosurgical procedures.
Keywords: Robot-assisted surgery, Vessel segmentation, Virtual fixture control, Neurosurgery
1 Introduction
During neurosurgery procedures, surgeons perform accurate and minute operations with limited visibility [46]. Such procedures are currently performed under microscope magnification. Bleeding requiring transfusion is recognized as one of the most common complications in cranial surgeries (5.4%) [42]. Detaching the tumor from tiny or large arterial and venous vessels is a daunting challenge; damaging (and then blocking) the physiological blood flow in such structures usually causes brain infarction and a consequent grim neurological performance and prognosis, being the worst neurosurgical scenario to be faced [31,57].
In particular, petroclival meningioma resection is known to be among the most technically challenging neurosurgical procedures, due to the meningioma proximity to major blood vessels that serve key and vital nervous structures [12].
As preserving large vessels is of primary importance for lowering postoperative morbidity, an assistive robotic device could be used to filter surgeons’ unintended movements of the human hand and prevent entering forbidden regions such as vascular structures [47].
Examples of assistive devices developed for forbidden-region robotic control include neuroArm [61,60], a magnetic resonance-compatible robot for image-guided, ambidextrous microneurosurgery. Cooperative control for precision targeting in neurosurgery was explored in [5,6]. In [62,59] and in [22], cooperatively controlled robots were proposed with applications in retinal surgery.
Recently, handheld robotic systems have been proposed [24]. Compared to teleoperated and cooperative systems, the biggest advantages of handheld systems are (i) intuitive operation, (ii) safety, and (iii) economy [4]. Moreover, handheld tools have the strong advantage of offering the same intuitive feel as conventional unaided tools. This results in improving the likelihood of acceptance by the surgeon [24].
Among handheld tools, the Navio PFS [37] is a sculpting tool designed for knee arthroplasty. The system combines image-free intraoperative registration, planning, and navigation for bone positioning. KYMERAX has been designed for laparoscopic applications [25]. The system is made of a console, two handles, and interchangeable surgical instruments that can be attached to the handles.
Micron [38] has emerged as a powerful actively stabilized handheld tool for applications in retinal vessel microsurgery. Micron is equipped with an optical tracking system and a microscopy stereocamera vision system. Despite Micron control for tremor compensation being widely investigated (e.g. [38]), forbidden-region virtual-fixture control has been investigated only for retinal microsurgery applications [7]. In [7], vessel segmentation and tracking are performed using simultaneous localization and mapping [13].
However, more advanced solutions to the problem of vessel segmentation have been proposed in the last years, with a growing interest in deep-learning strategies [18]. Deep learning allows fast and accurate segmentation also in the presence of challenging vascular architectures, such as bifurcations, and of high noise level and intensity inhomogeneities, typical of microscopy images recorded during surgery [44].
In this context, the goal of this work is to investigate the use of deep learning to perform fast and accurate vessel segmentation from microscopy images as to implement reliable forbidden-region virtual-fixture Micron control. In this paper, we specifically focus on providing accurate vascular segmentation and, to control Micron, we exploit the control strategies presented in [38].
The paper is organized as follows: Sec. 2 surveys vessel segmentation strategies, with a focus on deep learning. Sec. 3 explains the proposed approach to vessel-collision avoidance. Sec. 4 deals with the experimental protocol used to test the proposed methodology. Results are presented in Sec. 5 and discussed in Sec. 6. Finally, strength, limitations and future work of the proposed approach are reported in Sec. 7.
2 State of the art
Despite the most popular vessel segmentation approaches in the past being focused on deformable models (e.g. [8,10]) or enhanced approaches (e.g. [17,56,69,9]), in the last years researchers are focusing more and more on machine learning. A comprehensive and up-to-date review of blood vessel segmentation algorithms can be found in [44].
There are two main classes of machine learning approaches: unsupervised and supervised. The former finds models able to describe hidden arrangements of image-derived input features, while the latter learns data models from a set of already labeled features.
Among supervised segmentation models, convolutional neural networks (CNNs) have emerged as a powerful tool in many visual recognition tasks [27,55,23]. A CNN is a feed-forward artificial neural network inspired by the organization of the human visual cortex.
The typical use of a CNN for vessel segmentation is based on pixel–wise classification: each pixel in the image is assigned to the class vessel or background. The CNN is either used to extract image features then classified with other supervised model approaches [65,64,21], or trained to directly obtain the pixel classification by encoding one or more fully-connected layers [53,58,35].
More complex architectures have been recently proposed to directly deal with the segmentation task [34,40,20]. A quite innovative solution is exploited in [43,11,41], where fully convolutional networks (FCNNs) are used for vessel segmentation. With respect to classification CNNs, FCNNs allow faster training time, lower computational cost during the testing phase and higher segmentation performance.
3 Methods
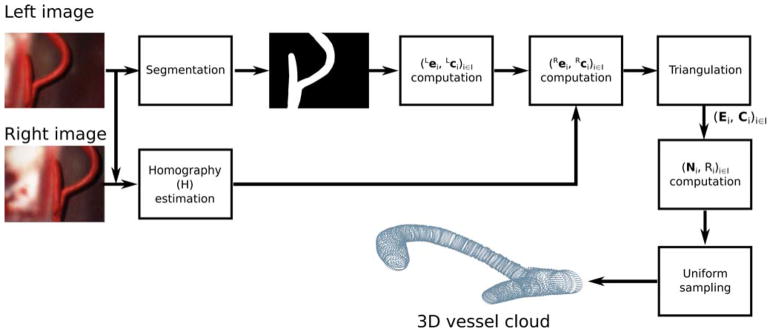
In this section, we describe the proposed approach to safety improvement in neurosurgery through vessel collision avoidance. We designed a forbidden-region virtual fixture strategy to control Micron and prevent its tip from colliding with vascular structures. To retrieve vessel segmentation, we used the deep-learning approach presented in Sec. 3.2. The vessel 3D reconstruction and registration to the Micron reference system are explained in Sec. 3.3. Finally, the control strategy is reported in Sec. 3.4.
3.1 Micron architecture
As introduced in Sec. 1, Micron is an actively stabilized handheld surgical robot [68,67,4,66]. The Micron handpiece contains a Gough-Stewart manipulator that uses piezoelectric micromotors to move the tool relative to the handpiece in 6-degrees-of-freedom (DOF), commanding tip motion covering a 4 × 4mm cylindrical workspace. Micron has two sets of infrared LEDs, of which three are mounted on the moving platform and three are fixed to the handle. The moving and fixed platforms are showed in Fig. 1(a). The LEDs are optically tracked by a custom-built tracking system called Apparatus to Sense Accuracy of Position (ASAP) [39]. The ASAP provides Micron position and orientation with a resolution of 4μm in a 27cm3 workspace [67]. The Micron real-time control loop runs at 1000 samples/s, and has a closed-loop bandwidth of 50 Hz. Micron implements tool stabilization by commanding the tool tip to track a low-pass filtered version of the hand 38]. The Micron microscopy stereocamera vision system is equipped with two Flea2 1024×768 cameras (Point Grey Research, Inc., Richmond, B.C.). The complete Micron setup, comprising Micron, ASAP and the stereomicroscope used for image acquisition, is shown in Fig. 1(b).
Fig. 1.
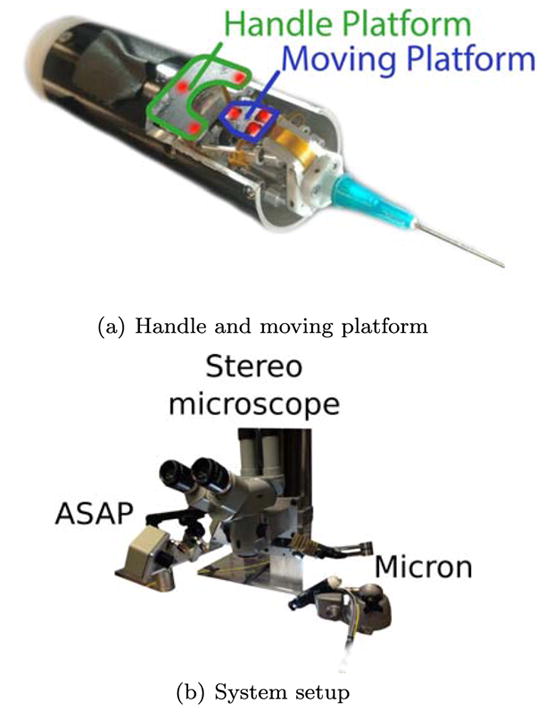
(a) Micron handle and moving platform on which infrared LEDs (highlighted in red) are mounted for Micron tip tracking. (b) Micron tip tracking system (ASAP), stereocameras for microscopy image acquisition and 3D reconstruction and Micron are shown.
3.2 Vessel segmentation algorithm
As introduced in Sec. 2, FCNNs have been successfully used for vessel segmentation [43,11,41].
In particular, we investigated the U-shaped FCNN (Fig. 2) architecture proposed n [55]. The architecture in [55] outperformed other FCNNs in the literature for the task of neuron segmentation in microscopy images. Despite the FCNN being proposed for neuron segmentation, our hypothesis is that the FCNN can be successfully exploited also for our vessel segmentation task, as both axons and vessels have similar tubular architectures.
Fig. 2.
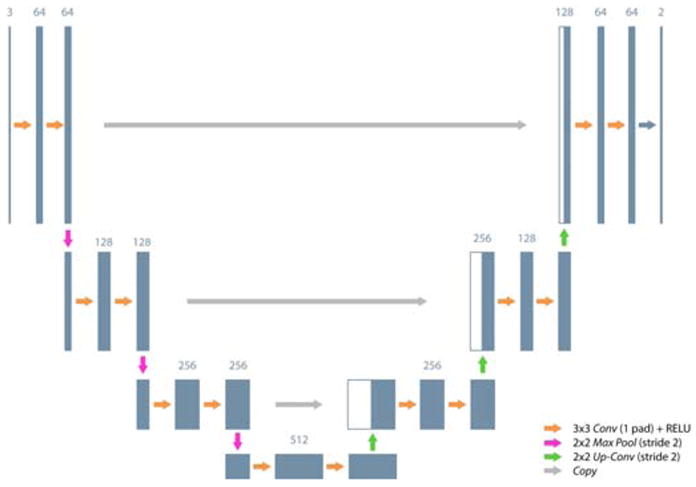
Fully convolutional neural network architecture exploited for vessel segmentation. Conv: Convolution; Pad: Padding; ReLU: Rectified linear unit; MaxPool: Max pooling; Up–Conv: Up-convolution; Copy: Copy layer. The number of feature maps are shown on top of the boxes.
The FCNN consisted of a contractive (descending) path and an expansive (ascending) one. The contractive path consisted of the repeated application of two 3×3 convolutions (Conv), each followed by a rectified linear unit (ReLU) and a 2×2 max-pooling (MaxPool) operation with stride 2 for downsampling. At each downsampling step, the number of feature channels was doubled. Every step in the expansive path consisted of an upsampling of the feature map with a 2×2 up-convolution (Up–Conv) that doubled the size of the feature map and halved the number of feature channels, followed by two 3×3 convolutions and a ReLU each. The copy layers (Copy), peculiar of the exploited architecture, were introduced in the expansive path to retrieve the information lost in the contractive path due to the MaxPool operations. In the original work [55], the introduction of Copy proved to be particularly useful for improving segmentation accuracy.
Our FCNN topology had only four out of the five original layers described in [55], as our hypothesis was that reducing the number of layers shortens the time consumption. To investigate this hypothesis, during our experimental protocol we investigated three FCNN topologies, i.e. with four, five and six layers, as described in Sec. 4. At the final layer, a 1 × 1 Conv was used to map each feature vector to our two classes (0: background, 1: vessel).
For training purposes, ADAM [26] was used. ADAM is an algorithm for first-order gradient-based optimization of stochastic objective functions and is based on the adaptive estimates of lower-order moments. The method is computationally efficient, has little memory requirements and is invariant to gradient diagonal rescaling.
Image segmentation was performed on the left microscopy image.
3.3 3D reconstruction algorithm
To compute the 3D vessel position in the Micron reference frame, we acquired vessel images from the surgical microscope (Fig. 1(b)). Following [67], the camera calibration was performed by matching the points corresponding to the Micron tip projections on the image planes of the two cameras and the real Micron tip coordinates acquired with the ASAP positioning system.
First, we computed the homographic transformation (H) between the left (L) and right (R) images using speeded up robust features (SURF) [3] and the fast library for approximate nearest neighbors (FLANN) [48].
Once H was computed, our assumption was that the 3D shape of vessels can be approximated by a bent tubular structure with variable radius, as is commonly done in the literature [18]. Thus, the vessel surface in 3D can be discretized as a set of points lying on I circumferences with different radius. The ith(i ∈ [0, I − 1]) circumference (Ci) was characterized by its center 3D position (Ci), orientation (N̂i) and radius (Ri), as shown in Fig. 3.
Fig. 3.
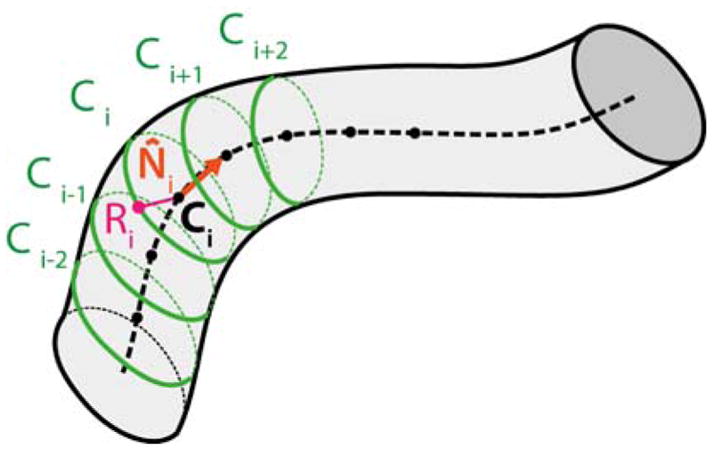
The vessel surface can be discretized as a set of point laying on I circumferences. The ith (i ∈ [0, I−1]) circumference (Ci) was characterized by its center 3D position (Ci), orientation (N̂i) and radius (Ri).
To compute Ci, N̂i and Ri, the vessel segmentation mask was thinned with the Zhang Suen algorithm [29] to obtain the vessel centerline. Each ith pixel of the centerline (Lci) represented the 2D projection of Ci in the left image plane. The 2D radius (Lri) of the projection of Ci in the left image plane was determined using the Euclidean distance transform [16]. The versor of each radius was computed as the normal to the tangent of the centerline computed in Lci. Once the versor and Lri were obtained, we retrieved the 2D coordinates of the rightmost point (Lei) on the vessel edge associated to Lci. We applied the H transformation to Lci and Lei ∀i to obtain the corresponding approximated centerline Rci and edge Rei points ∀i on the right image.
Using the direct linear transform [14], we triangulated Lci and Rci ∀i, obtaining Ci, ∀i. We did the same for Lei and Rei, obtaining the 3D edge point Ei, ∀i. We then estimated Ri as the 3D distance between each Ci and Ei. To obtain N̂i, we computed the tangent to the 3D vessel centerline in each Ci. We used the finite differences approach to approximate the tangent. Moving average of order 3 was then applied to the Ni, ∀i for smoothing purposes. Once N̂i, Ci and Ri were calculated ∀i, the Ci i ∈ [0, I − 1] was obtained with uniform circumference sampling with 36 points (ipj), j ∈ [0, 35].
The workflow of the 3D reconstruction algorithm is shown in Fig. 4. The nomenclature list that describes the 3D reconstruction algorithm is reported in Table 1.
Fig. 4.
3D reconstruction algorithm workflow. First, the homography transformation (H) between the left and right image planes is computed. After homography computation, our assumption is that the 3D shape of vessels can be approximated by a bent tubular structure with variable radius. Thus, the vessel surface in 3D can be discretized as a set of points lying on I different juxtaposed circumferences (Ci, i ∈ [0, I−1]). From the (left) segmented image, the 2D position of the center (Lci) and the 2D corresponding rightmost vessel edge point (Lei) of Ci are computed ∀i. From Lei and Lci, the homography is used to estimate the 2D position of the center (Rci) and edge point (Rei) of Ci (i ∈ [0, I−1]) in the right image plane. Direct linear transformation is used to triangulate and obtain Ci and Ei. From Ci ad Ei, the 3D vessel radius Ri and direction N̂i are computed, ∀i. Once Ci, N̂i and Ri are known, Ci is automatically identified. Uniform sampling is used to sample 36 equally spaced points on Ci. The set of 36 points on Ci, ∀i, represents the 3D vessel surface point cloud.
Table 1.
Nomenclature relative to the 3D reconstruction.
| Symbol | Meaning |
|---|---|
|
| |
| Ci | ith circumference that approximates the 3D vessel surface section |
| Ci | 3D center position of Ci |
| N̂i | 3D orientation versor of Ci |
| Ri | radius of Ci in space |
| Lci | 2D center position of Ci in the left image plane |
| Lri | radius of Ci in the left image plane |
| Lei | 2D rightmost vessel edge position on Ci associated to Lci the left image plane |
| Rci | 2D center position of Ci in the right image plane |
| Rri | radius of Ci in the right image plane |
| Rei | 2D rightmost vessel edge position on Ci associated to Rci in the right image plane |
| Ei | 3D point on Ci obtained triangulating Lei and Rei |
3.4 Forbidden-region virtual fixture
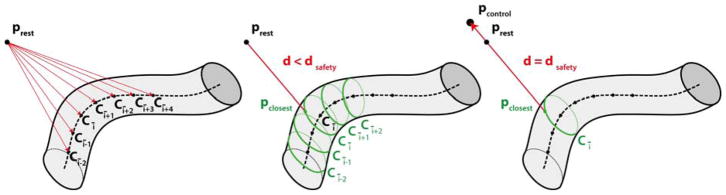
As shown in the schematic in Fig. 5, the Micron control command for the forbidden-region virtual fixture was triggered when the distance (d) between the tool tip resting position (prest) (i.e the position of the tip, when control was not triggered) and the 3D vessel position (pclosest) closest to the tool tip resting position was lower than a predefined threshold (dsafety):
| (1) |
Fig. 5.
The forbidden-region virtual-fixture control algorithm requires computation of the distance d between the tool tip resting position (prest) and the 3D vessel point (pclosest) closest to prest. prest is the position Micron takes when no control is triggered. To understand if the control command has to be triggered, first, (left image) the closest point Cī on the 3D vessel centerline Ci, i ∈ [0, I − 1], with I equal to the number of centerline points) is found. Then, (central image) pclosest is found among the points on the circumferences [Cī−2, Cī+2]. Finally (right image) if d is lower than a predefined threshold (dsafety), the Micron control is activated and the new Micron tip position (pcontrol) is defined, which lays on the line passing through pclosest and the current prest and is at a safety distance (dsafety) from pclosest.
To speed up the estimation of pclosest, we first searched among the Ci, i ∈ [0, I − 1], the point Cī = C̄ closest to the Micron tip resting position. Then, the point on the circumferences [Cī−2, Cī+2] were considered. The smallest distance was then found among the points of these five circumferences. Once pclosest was found, if the control law in Eq. 1 was not satisfied, a new Micron goal position of the tip (pcontrol) was defined. The new goal position laid on the line passing through pclosest and the current resting tip position and was at a distance dsafety from pclosest. Using prest instead of the current Micron tip position (ptip) to control Micron allowed a smoother trajectory of the tip, as suggested in [54]. In our control strategy, we also included tremor compensation as introduced in Sec. 3.1 and explained in [38].
It is worth noting that, as introduced in Sec. 3.1, the Micron control loop runs at 1000 samples/s, and has a closed-loop bandwidth of 50 Hz. The pcontrol updating (i.e. virtual-fixture control) was asynchronous with respect to the real-time control loop, and could be at a lower rate without greatly compromising the smoothness of voluntary motion that was passed through to the tool.
4 Experimental protocol
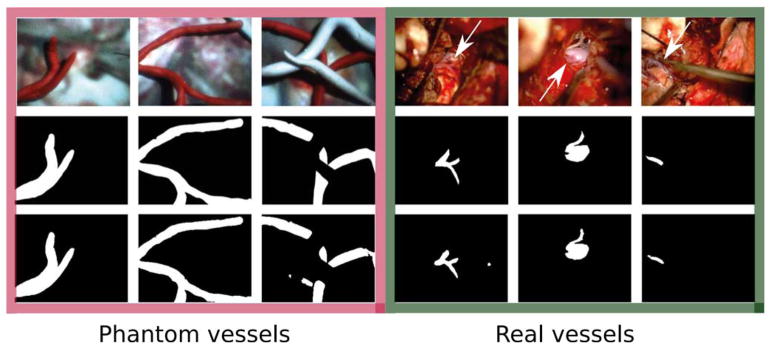
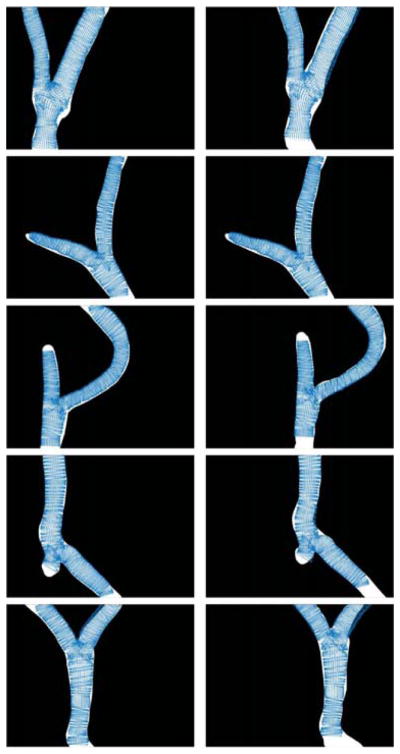
An experimental set-up was developed in order to simulate Micron–vessel interaction in a surgical environment. 230 phantoms were created, which contained modeling clay vessels lying on a background obtained from microscopy images recorded during real petroclival meningioma surgery. Vessels were different in shape and size, varying from straight cylinders to structures with variable radius and multiple branches. The diameter of these structures was created between 2 mm and 4 mm (median diameter = 2.58 mm). Phantom design was inspired by vascular structures recorded during real petroclival meningioma surgery images, as shown in Fig. 6.
Fig. 6.
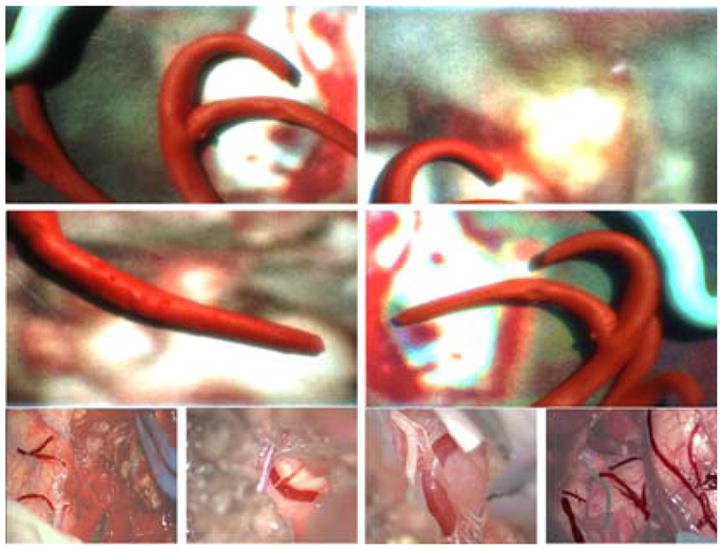
Phantom vascular samples used to test the proposed approach to vessel collision avoidance using Micron. Phantoms are reported in the first two rows. The last row shows images recorded during real petroclival meningioma surgery. Vessels are highlighted with respect to the background.
Each phantom was recorded with the microscope, obtaining 230 images of size 600 × 800 × 3 pixels. Challenges in the dataset included inhomogeneous background, instrumentation in the camera field of view, varying vessel orientation, width and distance from the camera.
To train the FCNN, the dataset was split in 220 training and 10 testing images. Data augmentation was performed. In particular, to each image in the original dataset 9 transformations were applied: 45°, 120° and 180° rotations, vertical and horizontal mirroring, barrel distortion, sinusoidal distortion, shearing and a combination of sinusoidal distortion, rotation and mirroring, as suggested in [27].
After data augmentation, the augmented dataset was composed of 2200 training and 100 testing images. Among the training images, 1800 were used for FCNN training and 400 for FCNN parameter tuning.
4.1 Parameter settings and implementation
The training images and the corresponding segmentation masks were used to train the FCNN using Caffe [1]. The training parameters are reported in Table 2. The maximum number of iterations and the batch size were determined with a trial-and-error procedure. The learning rate and the exponential decay rates were set as in [26].
Table 2.
Training parameters for vessel segmentation.
| Parameter | Value |
|---|---|
|
| |
| Maximum number of iterations | 18000 |
| Batch size | 10 |
| Learning rate | 0.001 |
| Exponential decay rate for the first moment estimates | 0.9 |
| Exponential decay rate for the second moment estimates | 0.999 |
The FCNN was trained on an Amazon Web Server (AWS) bitfusion Amazon Machine Image (AMI) controlled via SSH. The instance used was a p2.xlarge, which has 12 EC2 Compute Units (4 virtual cores), 61GB of memory, plus a GPU NVIDIA K80 (GK210).
The FCNN-based segmentation, 3D reconstruction and virtual fixture control were implemented in C++ using OpenCV1. An Intel Xeon CPU E5-1607 (3.10GHz with 4 Core), 16 Gb of memory and a GPU NVIDIA Quadro K420 was used.
4.2 Evaluation dataset and metrics
The segmentation algorithm was tested on the whole set of 100 testing images. Performance metrics were:
| (2) |
| (3) |
| (4) |
| (5) |
where TP are the true positive, TN the true negative, FN the false negative, and FP the false positive pixels. We also measured the segmentation computational time.
To investigate segmentation performance when varying the number of FCNN layers, we computed the segmentation DSC and measured the relative segmentation time also for FCNN with five and six layers. We used the Wilcoxon signed-rank test (significance level (α) = 0.05) to assess whether significant differences existed in DSC and segmentation time among the three configurations (i.e. proposed, with five, and with six layers). We also analyzed the performance of the exploited FCNN with four layers when varying the training-set size. Specifically, we repeated the training using only the 50% and 70% of the training set, keeping the same testing set. We then computed the DSC achieved by the FCNN when using the different training set.
We compared the performance of the exploited FCNN with three conventional methods in the literature of vessel segmentation, i.e. [69, 17, 9], which are among the most widely used when considering conventional vessel-segmentation methods [18, 44]. All these conventional methods require parameter tuning: vessel-scale range for [17], vessel width and orientation for [69, 9]. Here, we tuned these parameters with a trial-and-error procedure, privileging parameter combinations that gave the highest DSC. The set parameters were: vessel-scale range = [5:5:15], vessel width = [5:5:15], vessel orientation = [0 °:35°:170°). After segmentation, erosion was applied to remove isolated spots. We computed the DSC for the conventional-method segmentation and compared the obtained DSC values with the DSC obtained with the exploited FCNN using the Wilcoxon signed-rank test (α = 0.05).
We decided to investigate the performance of the FCNN in classifying real petroclival-meningioma surgery images. To this goal, we segmented brain vessels from a portion (~ 6 minutes long) of a microscopy video of meningioma surgery. Video frequency was 25 fps and frame size was 224 × 288. Besides focusing on superficial brain vessels (like the phantom ones), we also considered two other vascular structures: the petrosal vein and the basilar artery, which are among the most critical structures to preserve during meningioma surgery, too. In particular, we extracted and manually segmented: (i) 38 frames of the superficial vessels, (ii) 65 frames of the petrosal vein, (iii) 56 frames of the basilar artery. These numbers refer to the total number of frames in which the vessels were clearly visible and in focus. We decided to train the same FCNN architecture with three separate datasets, one per vascular structure, as the three considered vascular structures are quite different both in appearance and in location inside the brain. Thus, we obtained three FCNN models, each associated to one vascular architecture. In our preliminary analysis, this allowed more accurate segmentation than training a single FCNN model for segmenting the three structures simultaneously. It is worth noting that the three vascular structures appear in different phases of the surgery [2]. Thus, once the surgical phase is retrieved, e.g. exploiting the strategy proposed in [63], only the vascular structure in that phase should be segmented, using the (trained) FCNN model corresponding to that structure. In each of the three cases, we split the dataset into 90% raining images and 10% testing images. Data augmentation was performed as with phantoms, i.e. applying 9 different transformations to each image in the original dataset. We then computed the DSC for evaluating the segmentation of the three vascular structures.
To evaluate the performance of the 3D reconstruction, the 10 testing phantoms were recorded using the stereo microscope. For each stereoImage, once the vessel segmentation and 3D reconstruction were obtained as explained in Sec. 3.2 and Sec. 3.3, respectively, the number of points (Npoints) of the 3D point cloud (pcloud = {pcloudi} with i ∈ [0; Npoints]) was computed. The time required to reconstruct pcloud was measured, too. Further, the pcloud was reprojected on the left image plane, obtaining a set of reprojected points (Lproj = {Lproji} with i ∈ [0; Npoints]). lproj was made of several reconstructed circumferences (LĈj with j ∈ [0 : I − 1]) with center Lĉj, as shown in Fig. 7. For each LĈj, only the two extremes (Lextremesj) were retained. The Euclidean distances between Lextremesj and the points of LĈj closest to the vessel mask (∀j) were computed. Once the distances were computed ∀j, we split the set of distances in two subsets, depending on whether the extreme lay inside (Ldin) or outside (Ldout) the vessel mask, to understand whether we underestimated or overestimated the true vessel edges.
Fig. 7.
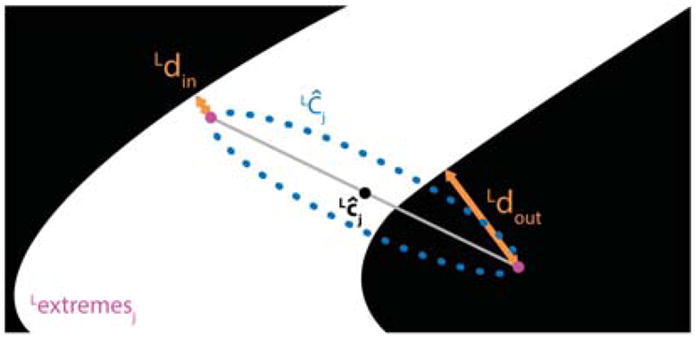
Evaluation of the 3D reconstruction algorithm. The 3D cloud was reprojected on the left image plane, obtaining a set of reprojected points (Lproj). Lproj was made of several reconstructed circumferences (LĈj with j ∈ [0 : I − 1] and I the number of reconstructed circumferences) with center Lĉj. For each LĈj, the 2 extremes were retained, obtaining a new set of points (lextremesj). The Euclidean distances between Lextremes and the points of LĈj closest to the vessel mask (∀j) were computed. Two distances were considered (Ldin and Ldout), depending on whether the extreme lay inside or outside the vessel mask, respectively.
For the forbidden-region virtual-fixture algorithm performance assessment, we used Micron to interact at random with 25 different vascular phantoms for ~ 80s per trial. Specifically, in each trial the user randomly moved the device toward the vascular phantom trying to touch it. The tunable dsafety was set equal to 2 mm after discussing with the clinical partners, as this was the median vessel diameter. We first evaluated, for each trajectory, the number of times the tool tip entered the forbidden zone. Specifically, we computed the percentage penetration error (err%), which is defined as:
| (6) |
where Ninforbidden is the number of pinforbidden, Ncontrol is the number of pcontrol, and pinforbidden is defined as:
| (7) |
We decided to express err% as a percentage with respect to the total number of points in which the Micron control was triggered to exclude Micron position far away from the safety zone (i.e. for which no control is required).
Then, for each trajectory, we computed the absolute error distance (err):
| (8) |
The err allowed understanding of how much the Micron tip entered the forbidden region.
5 Results
Visual samples of vessel-segmentation outcome are shown in Fig. 8. Table 3 reports median, first and third quartile of DSC, Se, Sp and Acc computed for the phantom-vessel segmentation performed on the 100 testing images as well as the computational time required for the segmentation. Segmentation performances were: 0.96 (DSC), 0.91 (Se), 0.99 (Sp) and 0.99 (Acc). The computational time required for segmenting one image was 0.77 s on the deployed GPU. When varying the number of FCNN layers, no significant differences were found in DSC, while significant differences were found when comparing segmentation time. Median segmentation-time increment was 27% (5 layers) and 67% (6 layers). When exploiting a reduced training set, the FCNN segmentation DSC deteriorated from 0.96 to (median) 0.90 (%70 of original training set) and 0.89 (%50 of original training set).
Fig. 8.
Visual samples of vessel segmentation outcomes. The images in the three leftmost columns show phantom vessels, those in the last three ones show a superficial brain vessel, the petrosal vein and the basilar artery, respectively. Real vessels are shown by the white arrows. Original RGB images are shown in the first row. The second and third row refer to the ground-truth manual segmentation and the segmentation outcome, respectively.
Table 3.
Vessel segmentation performance and computational cost for the 100 testing images. Median, first and third quartiles are reported for each metric. DSC: Dice similarity coefficient; Se: Sensitivity; Sp: Specificity; Acc: Accuracy; Time: Computational time [s].
| DSC | Se | Sp | Acc | Time | |
|---|---|---|---|---|---|
| First quartile | 0.94 | 0.95 | 0.99 | 0.98 | 0.77 |
| Median | 0.96 | 0.91 | 0.99 | 0.99 | 0.77 |
| Third quartile | 0.97 | 0.96 | 1.00 | 0.99 | 0.78 |
When analyzing segmentation performance of conventional segmentation methods, we obtained a median DSC of 0.45 [69], 0.54 [17] and 0.55 [9]. Significant differences were found when comparing the proposed FCNN with the three analyzed conventional methods. Relative boxplots are shown in Fig. 10.
Fig. 10.
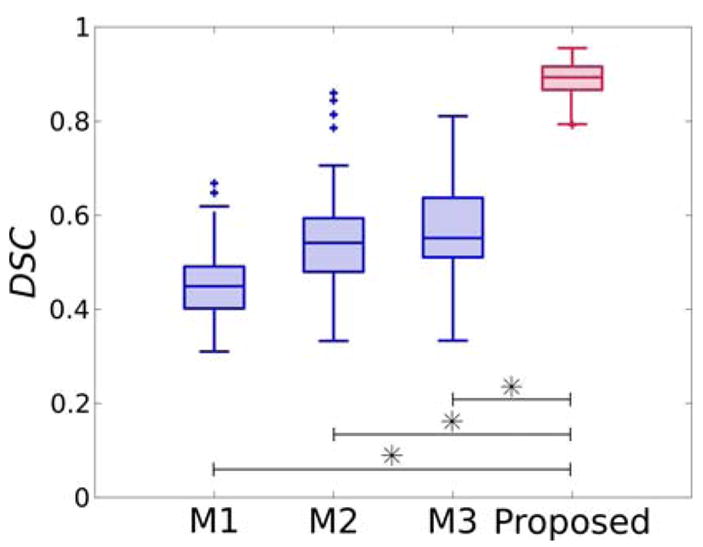
Dice similarity coefficient (DSC) for segmentation obtained using M1: [69], M2: [17], M3: [9] and the proposed FCNN-based approach.
When considering real-surgery images, we obtained a median DSC of: 0.76 (inter-quartile range (IQR)=0.03) for the superficial vessels, 0.71 (IQR = 0.10) for the petrosal vein, and 0.86 (IQR = 0.06) for the basilar artery. Relative boxplots are shown in Fig. 11.
Fig. 11.
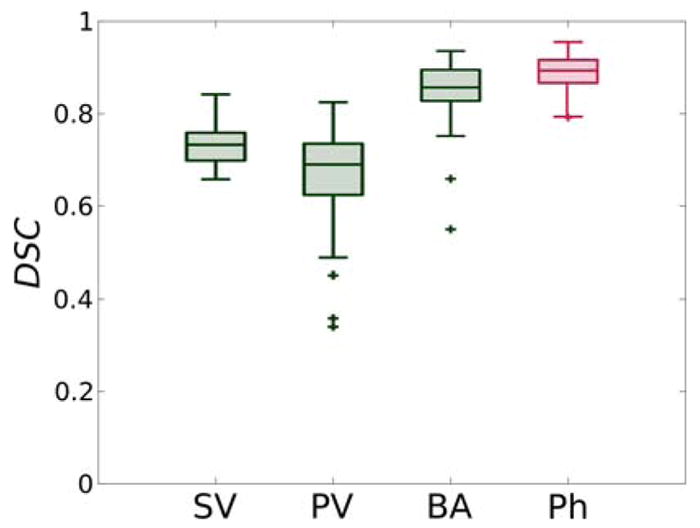
Dice similarity coefficient (DSC) for FCNN-based segmentation relative to SV: superficial vessels, PV: petrosal vein, BA: basilar artery and Ph: phantom vessels.
The number of reconstructed points for each cloud and the computational cost required to obtained the clouds are reported in Table 4. A median Npoints of 17170 was obtained, with a median computational cost of 0.48s. When compared to SURF- and FLANN-based 3D reconstruction, the computational cost was higher than the one required by SURF and FLANN (0.11s). However, the Npoints was significantly higher (Wilcoxon signed-rank test, significance level = 0.05) than the Npoints obtained using SURF and FLANN, equal to 12. The median values of Ldin and Ldout, computed among all the 10 point clouds, were 139.6 μm and 70.4 μm, respectively. The 71% of Lextremes lied inside and the 28% of Lextremes lied outside the vessel mask.
Table 4.
Number of points (Npoints) and computational cost (Time [s]) for each of the 10 reconstructed 3D vessel clouds considered for evaluating the 3D reconstruction algorithm. Median values are reported, too. The values are reported for the proposed algorithm and for the 3D reconstruction performed with speeded up robust features (SURF) [3] and the fast library for approximate nearest neighbors (FLANN) [48]. Significant differences were found when comparing Npoints computed with the proposed approach and with SURF and FLANN (Wilcoxon signed-rank test (significance level = 0.05)).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Median | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Npoints (SURF + FLANN) | 4 | 9 | 23 | 31 | 15 | 11 | 16 | 14 | 1 | 10 | 12.5 |
| Time [s] (SURF + FLANN) | 0.10 | 0.10 | 0.11 | 0.13 | 0.10 | 0.11 | 0.13 | 0.11 | 0.11 | 0.12 | 0.11 |
|
| |||||||||||
| Npoints (Proposed) | 10906 | 15190 | 12058 | 19654 | 17710 | 19186 | 14362 | 16630 | 17746 | 21778 | 17170 |
| Time [s] (Proposed) | 0.53 | 0.47 | 0.47 | 0.66 | 0.45 | 0.49 | 0.44 | 0.54 | 0.64 | 0.38 | 0.48 |
A median value of 114.16 μm, computed considering both Ldin and Ldout for all the 10 point clouds, was obtained. Visual samples of the point clouds reprojected on the left and right ground-truth image are shown in Fig. 9.
Fig. 9.
Point cloud reprojected on left and right image plane plotted over the left (left column) and right (right column) ground-truth vessel segmentation images.
A median err% among the 25 tested Micron trarjectories of 24% (IQR = 10%) was obtained. Median err was 16.9 μm (IQR = 5.86 μm). The d for a sample trajectory is reported in Fig. 12. Corresponding err% and err were 21% and 6.7 μm. Sample Micron trajectories with and without the virtual-fixture are shown in Fig. 13.
Fig. 12.
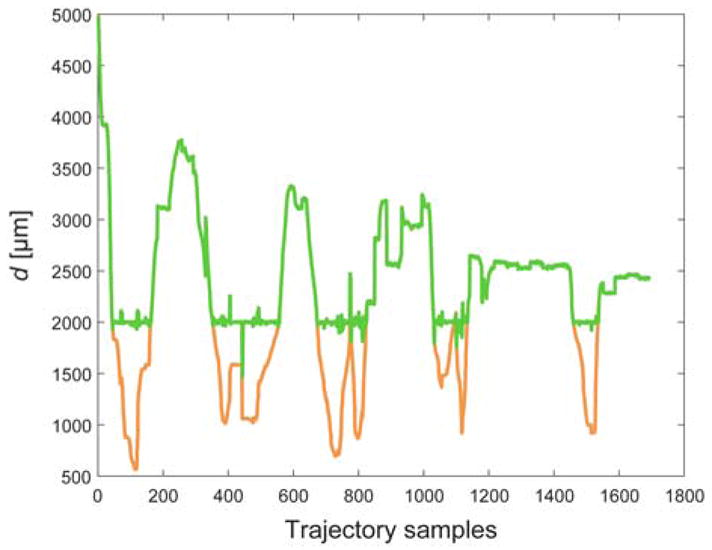
Distance (d) between Micron tip and 3D vessel point closest to the Micron tip. d with and without the virtual-fixture control is reported in green and orange, respectively.
Fig. 13.

Sample trajectory for virtual fixture evaluation. The reconstructed vessel point cloud is represented in blue; the trajectories with and without the virtual fixtures control are depicted in green and orange, respectively.
6 Discussion
The segmentation performance (median DSC = 0.96) proved that the neural network was able to encode the variability in the simulated surgical environment. Using a FCNN with only four layers helped reduce the segmentation computational cost without affecting segmentation performance. The major source of error, as shown in Fig. 8, was the presence of specular reflections (ie. bright and saturated areas) within the vessels. It is worth noting that complex vascular structures (i.e. bifurcation), which are usually challenging to segment [18], were correctly segmented.
As might be expected, the FCNN segmentation performance deteriorated when reducing the training size. This can be particularly critical when considering real surgical images. Indeed, the exploited experimental setup mainly dealt with vascular phantoms, which presented lower variability with respect to real images. Thus, with a view on translating the proposed work to actual clinical practice, large training dataset of real images should be exploited to train the FCNN, as so to encode the intra- and inter-patient vessel variability. With reference to recently published work in the literature of deep learning for medical-image analysis (e.g. [15,52]), training-size order of magnitude should be ~ 106, and we are currently working to build a labeled dataset of such a size. This was also confirmed by our exploratory analysis on real images, where DSC values were lower than the ones obtained for phantoms. This can be attributed both to the complexity of real images and to the (lower) amount of training data. However, segmentation outcomes were encouraging, as shown in Fig. 8, suggesting that the proposed segmentation strategy can be successfully pursued also for real-surgery images once a larger labeled dataset will be collected. In fact, the network was able to provide accurate segmentation also in challenging environments, e.g. where specular reflections were present and overlaid with the vessel surface. As a sample case, the image in column 5 of Fig. 8 (which corresponds to a surgical frame with the petrosal vein) shows specular reflections overlaid with the vessel surface. Nonetheless, the network was able to provide accurate segmentation, as can be seen by visually comparing the segmentation mask with the ground-truth segmentation. In fact, neural networks are known to be accurate for the segmentation task also in challenging environments, e.g. where specular reflections, blur and occlusions are present [36]. It is worth noting that the exploited FCNN outperformed conventional methods in the literature. This is probably due to the fact that vessel phantoms presented different width, orientation and complex architecture, such as bifurcation and vessel-kissing. These characteristics are known to strongly affect segmentation results when exploiting conventional segmentation methodologies [18].
The median time required by the FCNN to segment each image (0.77 s on the deployed GPU) was still not negligible for real-time control purposes. This problem may be overcome using a more powerful GPU. Indeed, during our experiments, the segmentation time was reduced by ~ 1/25 with the Amazon web server (Sec. 4.1) that we used to perform FCNN training.
The 3D reconstruction algorithm produced dense point clouds, with a median Npoints of 17170 points, which was crucial to enable reliable Micron control. This can be also seen from the visual samples of Fig. 9, where the reprojected points covered the vessel area homogeneously. The analysis of Ldin and Ldout showed that the median value of all the distances (114.16 μm) was two orders of magnitude lower than the median vessel diameter (2.58 mm). Vessel approximation as a tubular structure with varying radius is probably among the main sources of these (even small) reprojection errors. However, modeling vessels as tubular structures allowed a fast 3D reconstruction (median reconstruction time: 0.48 s), as only vessel centerline had to be reconstructed. A possible solution to further lower the computational time could be assuming even simpler vascular architectures (e.g. constant vessel radius) and having a parametric expression of the vessel. Considering that we have already achieved real-time segmentation performance on a more powerful GPU, we expect that further reducing the computational cost of the 3D reconstruction algorithm will enable the system to be fast enough to be used with a human in the loop.
When including tremor compensation and forbidden-region virtual-fixture control, the error on the tip position when it entered the forbidden zone was small (the median err was 16.9 μm). In fact, the median diameter and wall thickness of real brain vessels are ~ 3mm and 0.5mm, the wall thickness of arteries being slightly larger than that of veins [30,50]. Nonetheless, err outliers were present due to limits in the range of motion of Micron. When trying to reach points outside Micron’s range of motion, the forbidden-region virtual-fixture control algorithm brought the Micron motors to saturation. When this was the case, the tip entered the forbidden zone to a greater depth. It is worth noting that err was computed considering the reconstructed vessel 3D point cloud (and not the real 3D vessel position, which was not available). Thus, errors in performing 3D reconstruction potentially affected the estimate of the penetration error. This should be taken into account when tuning dsafety, which in our experiments was one order of magnitude higher than the error in projecting the point cloud back over the segmentation images.
Improving the control strategy and the virtual fixture algorithm could be the first natural evolution of the project. For example, once retrieved, the velocity of Micron could be used to influence the possible control choice to adopt. Faster movements of the handle are more likely to be unwanted and the last tip position before the abrupt movement might be maintained. Moreover, using the center of the range of motion might help to prevent the saturation of the motors. For example, instead of rejecting the tip along the direction between the closest point of the cloud and the resting position of the tip, other directions away from both cloud and saturation zone might be used. As future work, we will investigate further strategies that take into account collision detection and deviation of the robot motion from predefined anatomical virtual fixtures (e.g. [33,28,51]). Finally, ergonomics tests with surgeons actually performing tumor resection while avoiding vessels in a moving phantom will be performed.
One limitation of the proposed experimental protocol can be seen in the fact that phantom images were used to interact with Micron. When dealing with images actually recorded during surgery, some more aspects have to be taken into account. While illumination variation does not represent an issue for FCNN-based segmentation [32], issues arise when dealing with blurred frames. As deep-learning models work (at least if considering the layers at the top of the network architectures) as edge detectors, vessel segmentation may not be accurate in case of image blurring. Therefore, to avoid the processing of blurred frames, frame-selection strategies, such as the one proposed in [45], should be integrated. This way, the processing of uninformative frames, in which vessels are not clearly visible, would be avoided. Moreover, deblurring techniques (e.g., [49]) could be applied on blurred frames as to retrieve the image informative content and provide accurate segmentation. A further issue is related to vessel occlusion. In this case, more complex FCNN architecture should be taken into account, such as [19].
7 Conclusion
The work presented provided a new approach to vessel avoidance for safe robotic assisted neurosurgery, which exploits a handheld tool to reliably constrain surgeon movements outside predefined forbidden zones.
We proved the feasibility of the approach in a simulated scenario with phantom vessels, obtaining a median segmentation accuracy of 99% and avoiding the tool tip penetrating the forbidden region 76% of the time the control algorithm was active (median penetration depth 2 orders of magnitude lower than vessel median diameter).
Acknowledgments
Partial funding provided by U.S. National Institutes of Health (grant no. R01EB000526).
Footnotes
Contributor Information
Sara Moccia, Department of Advanced Robotics, Istituto Italiano di Tencologia, Italy. Department of Electronics, Information and Bioengineering, Politencnico di Milano, Italy.
Simone Foti, Department of Electronics, Information and Bioengineering, Politencnico di Milano, Italy.
Arpita Routray, Robotics Institute, Carnegie Mellon University, Pittsburgh, USA.
Francesca Prudente, Department of Electronics, Information and Bioengineering, Politencnico di Milano, Italy.
Alessandro Perin, Besta NeuroSim Center, IRCCS Istituto Neurologico C. Besta, Milan, Italy.
Raymond F. Sekula, Department of Neurological Surgery, University of Pittsburgh, Pittsburgh, USA
Leonardo S. Mattos, Department of Advanced Robotics, Istituto Italiano di Tencologia, Italy
Jeffrey R. Balzer, Department of Neurological Surgery, University of Pittsburgh, Pittsburgh, USA
Wendy Fellows-Mayle, Department of Neurological Surgery, University of Pittsburgh, Pittsburgh, USA.
Elena De Momi, Department of Electronics, Information and Bioengineering, Politencnico di Milano, Italy.
Cameron N. Riviere, Robotics Institute, Carnegie Mellon University, Pittsburgh, USA
References
- 1.Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. 2016 arXiv preprint arXiv: 1603.04467. [Google Scholar]
- 2.Al-Mefty O, Fox JL, Sr, Smith RR. Petrosal approach for petroclival meningiomas. Neurosurgery. 1988;22(3):510–517. doi: 10.1227/00006123-198803000-00010. [DOI] [PubMed] [Google Scholar]
- 3.Bay H, Tuytelaars T, Van Gool L. Surf: Speeded up robust features. European Conference on Computer Vision. 2006:404–417. [Google Scholar]
- 4.Becker BC, MacLachlan RA, Lobes LA, Hager GD, Riviere CN. Vision-based control of a handheld surgical micromanipulator with virtual fixtures. IEEE Transactions on Robotics. 29(3):674–683. doi: 10.1109/TRO.2013.2239552. (203) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Beretta E, De Momi E, Rodriguez y Baena F, Ferrigno G. Adaptive hands-on control for reaching and targeting tasks in surgery. International Journal of Advanced Robotic Systems. 2015;12(5):50. [Google Scholar]
- 6.Beretta E, Ferrigno G, De Momi E. Nonlinear force feedback enhancement for cooperative robotic neurosurgery enforces virtual boundaries on cortex surface. Journal of Medical Robotics Research. 2016;1(02):1650,001. [Google Scholar]
- 7.Braun D, Yang S, Martel JN, Riviere CN, Becker BC. EyeSLAM: Real-time simultaneous localization and mapping of retinal vessels during intraocular microsurgery. The International Journal Medical Robotics and Computer Assisted Surgery. 2017;14(1):e1848. doi: 10.1002/rcs.1848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chan TF, Vese LA. Active contours without edge. Transaction on Image processing. 2001;10(2):266–277. doi: 10.1109/83.902291. [DOI] [PubMed] [Google Scholar]
- 9.Chaudhuri S, Chatterjee S, Katz N, Nelson M, Goldbaum M. Detection of blood vessels in retinal images using two-dimensional matched filters. IEEE Transactions on Medical Imaging. 1989;8(3):263–269. doi: 10.1109/42.34715. [DOI] [PubMed] [Google Scholar]
- 10.Cheng Y, Hu X, Wang J, Wang Y, Tamura S. Accurate vessel segmentation with constrained B-snake. IEEE Transactions on Image Processing. 2015;24(8):2440–2455. doi: 10.1109/TIP.2015.2417683. [DOI] [PubMed] [Google Scholar]
- 11.Dasgupta A, Singh S. International Symposium on Biomedical Imaging. IEEE; 2017. A fully convolutional neural network based structured prediction approach towards the retinal vessel segmentation; pp. 248–251. [Google Scholar]
- 12.DiLuna ML, Bulsara KR. Surgery for petroclival meningiomas: a comprehensive review of outcomes in the skull base surgery era. Skull Base. 2010;20(05):337–342. doi: 10.1055/s-0030-1253581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Durrant-Whyte H, Bailey T. Simultaneous localization and mapping: part I. IEEE Robotics & Automation Magazine. 2006;13(2):99–110. [Google Scholar]
- 14.El-Manadili Y, Novak K. Precision rectification of SPOT imagery using the direct linear transformation model. Photogrammetric Engineering and Remote Sensing. 1996;62(1):67–72. [Google Scholar]
- 15.Esteva A, Kuprel B, Novoa RA, Ko J, Swetter SM, Blau HM, Thrun S. Dermatologist-level classification of skin cancer with deep neural networks. Nature. 2017;542(7639):115–118. doi: 10.1038/nature21056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Felzenszwalb P, Huttenlocher D. Tech rep. Cornell University; 2004. Distance transforms of sampled functions. [Google Scholar]
- 17.Frangi AF, Niessen WJ, Vincken KL, Viergever MA. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 1998. Multiscale vessel enhancement filtering; pp. 130–137. [Google Scholar]
- 18.Fraz MM, Remagnino P, Hoppe A, Uyyanonvara B, Rudnicka AR, Owen CG, Barman SA. Blood vessel segmentation methodologies in retinal images–a survey. Computer Methods and Programs in Biomedicine. 2012;108(1):407–433. doi: 10.1016/j.cmpb.2012.03.009. [DOI] [PubMed] [Google Scholar]
- 19.Fu H, Wang C, Tao D, Black MJ. Occlusion boundary detection via deep exploration of context. IEEE Conference on Computer Vision and Pattern Recognition. 2016:241–250. [Google Scholar]
- 20.Fu H, Xu Y, Lin S, Wong DWK, Liu J. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2016. Deep-Vessel: Retinal vessel segmentation via deep learning and conditional random field; pp. 132–139. [Google Scholar]
- 21.Ganin Y, Lempitsky V. Asian Conference on Computer Vision. Springer; 2014. N̂ 4-Fields: Neural Network Nearest Neighbor Fields for Image Transforms; pp. 536–551. [Google Scholar]
- 22.Gijbels A, Vander Poorten EB, Stalmans P, Reynaerts D. IEEE International Conference on Robotics and Automation. IEEE; 2015. Development and experimental validation of a force sensing needle for robotically assisted retinal vein cannulations; pp. 2270–2276. [Google Scholar]
- 23.Girshick R, Donahue J, Darrell T, Malik J. Rich feature hierarchies for accurate object detection and semantic segmentation. Conference on Computer Vision and Pattern Recognition. 2014:580–587. [Google Scholar]
- 24.Gonenc B, Balicki MA, Handa J, Gehlbach P, Riviere CN, Taylor RH, Iordachita I. International Conference on Intelligent Robots and Systems. IEEE; 2012. Preliminary evaluation of a micro-force sensing handheld robot for vitreoretinal surgery; pp. 4125–4130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hackethal A, Koppan M, Eskef K, Tinneberg HR. Handheld articulating laparoscopic instruments driven by robotic technology. First clinical experience in gynecological surgery. Gynecological Surgery. 2011;9(2):203. [Google Scholar]
- 26.Kingma D, Ba J. Adam: A method for stochastic optimization. 2014 arXiv preprint arXiv:1412.6980. [Google Scholar]
- 27.Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems. 2012:1097–1105. [Google Scholar]
- 28.Kwok KW, Tsoi KH, Vitiello V, Clark J, Chow GC, Luk W, Yang GZ. Dimensionality reduction in controlling articulated snake robot for endoscopy under dynamic active constraints. IEEE Transactions on Robotics. 2013;29(1):15–31. doi: 10.1109/TRO.2012.2226382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lam L, Lee SW, Suen CY. Thinning methodologies-a comprehensive survey. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1992;14(9):869–885. [Google Scholar]
- 30.Lang J. Clinical Anatomy of the Head: Neurocranium · Orbit · Craniocervical Regions. Springer Science & Business Media; 2012. [Google Scholar]
- 31.Lawrence JD, Frederickson AM, Chang YF, Weiss PM, Gerszten PC, Sekula RF., Jr An investigation into quality of life improvement in patients undergoing microvascular decompression for hemifacial spasm. Journal of Neurosurgery. 2017;128(1):193–201. doi: 10.3171/2016.9.JNS161022. [DOI] [PubMed] [Google Scholar]
- 32.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 33.Lee KH, Guo Z, Chow GC, Chen Y, Luk W, Kwok KW. IEEE International Conference on Robotics and Automation. IEEE; 2015. GPU-based proximity query processing on unstructured triangular mesh model; pp. 4405–4411. [Google Scholar]
- 34.Li Q, Feng B, Xie L, Liang P, Zhang H, Wang T. A cross-modality learning approach for vessel segmentation in retinal images. IEEE Transactions on Medical Imaging. 2016;35(1):109–118. doi: 10.1109/TMI.2015.2457891. [DOI] [PubMed] [Google Scholar]
- 35.Liskowski P, Krawiec K. Segmenting retinal blood vessels with deep neural networks. IEEE Transactions on Medical Imaging. 2016;35(11):2369–2380. doi: 10.1109/TMI.2016.2546227. [DOI] [PubMed] [Google Scholar]
- 36.Liu N, Li H, Zhang M, Liu J, Sun Z, Tan T. International Conference on Biometrics. IEEE; 2016. Accurate iris segmentation in non-cooperative environments using fully convolutional networks; pp. 1–8. [Google Scholar]
- 37.Lonner JH. Robotically assisted unicompartmental knee arthroplasty with a handheld image-free sculpting tool. Orthopedic Clinics of North America. 2016;47(1):29–40. doi: 10.1016/j.ocl.2015.08.024. [DOI] [PubMed] [Google Scholar]
- 38.MacLachlan RA, Becker BC, Tabarés JC, Podnar GW, Lobes LA, Jr, Riviere CN. Micron: an actively stabilized handheld tool for microsurgery. IEEE Transactions on Robotics. 2012;28(1):195–212. doi: 10.1109/TRO.2011.2169634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.MacLachlan RA, Riviere CN. High-speed microscale optical tracking using digital frequency-domain multiplexing. IEEE Transactions on Instrumentation and Measurement. 2009;58(6):1991–2001. doi: 10.1109/TIM.2008.2006132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Maninis KK, Pont-Tuset J, Arbeláez P, Van Gool L. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2016. Deep retinal image understanding; pp. 140–148. [Google Scholar]
- 41.Merkow J, Marsden A, Kriegman D, Tu Z. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2016. Dense volume-to-volume vascular boundary detection; pp. 371–379. [Google Scholar]
- 42.Michalak SM, Rolston JD, Lawton MT. Incidence and predictors of complications and mortality in cerebrovascular surgery: National trends from 2007 to 2012. Neurosurgery. 2016;79(2):182–193. doi: 10.1227/NEU.0000000000001251. [DOI] [PubMed] [Google Scholar]
- 43.Mo J, Zhang L. Multi-level deep supervised networks for retinal vessel segmentation. International Journal of Computer Assisted Radiology and Surgery. 2017;12(12):2181–2193. doi: 10.1007/s11548-017-1619-0. [DOI] [PubMed] [Google Scholar]
- 44.Moccia S, De Momi E, El Hadji S, Mattos LS. Blood vessel segmentation algorithms – Review of methods, datasets and evaluation metrics. Computer Methods and Programs in Biomedicine. 2018;158:71–91. doi: 10.1016/j.cmpb.2018.02.001. [DOI] [PubMed] [Google Scholar]
- 45.Moccia S, Vanone GO, De Momi E, Laborai A, Guastini L, Peretti G, Mattos LS. Learning-based classification of informative laryngoscopic frames. Computer Methods and Programs in Biomedicine. 2018;158:21–30. doi: 10.1016/j.cmpb.2018.01.030. [DOI] [PubMed] [Google Scholar]
- 46.Morita A, Sora S, Mitsuishi M, Warisawa S, Suruman K, Asai D, Arata J, Baba S, Takahashi H, Mochizuki R, et al. Microsurgical robotic system for the deep surgical field: development of a prototype and feasibility studies in animal and cadaveric models. Journal of Neurosurgery. 2005;103(2):320–327. doi: 10.3171/jns.2005.103.2.0320. [DOI] [PubMed] [Google Scholar]
- 47.Motkoski JW, Sutherland GR. Why robots entered neurosurgery. Experimental Neurosurgery in Animal Models. 2016:85–105. [Google Scholar]
- 48.Muja M, Lowe DG. Fast approximate nearest neighbors with automatic algorithm configuration. International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications. 2009;2(331–340):2. [Google Scholar]
- 49.Nah S, Kim TH, Lee KM. Conference on Computer Vision and Pattern Recognition. IEEE; 2017. Deep multi-scale convolutional neural network for dynamic scene deblurring. [Google Scholar]
- 50.Niu PP, Yu Y, Zhou HW, Liu Y, Luo Y, Guo ZN, Jin H, Yang Y. Vessel wall differences between middle cerebral artery and basilar artery plaques on magnetic resonance imaging. Scientific Reports 6. 2016;38:534. doi: 10.1038/srep38534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Pan J, Zhang L, Manocha D. Collision-free and smooth trajectory computation in cluttered environments. The International Journal of Robotics Research. 2012;31(10):1155–1175. [Google Scholar]
- 52.Poplin R, Varadarajan AV, Blumer K, Liu Y, McConnell MV, Corrado GS, Peng L, Webster DR. Prediction of cardiovascular risk factors from retinal fundus photographs via deep learning. Nature Biomedical Engineering. 2018;2:158–164. doi: 10.1038/s41551-018-0195-0. [DOI] [PubMed] [Google Scholar]
- 53.Prentašić P, Heisler M, Mammo Z, Lee S, Merkur A, Navajas E, Beg MF, Šarunić M, Lončarić S. Segmentation of the foveal microvasculature using deep learning networks. Journal of Biomedical Optics. 2016;21(7):075,008–075,008. doi: 10.1117/1.JBO.21.7.075008. [DOI] [PubMed] [Google Scholar]
- 54.Prudente F, Moccia S, Perin A, Sekula R, Mattos L, Balzer J, Fellows-Mayle W, De Momi E, Riviere C. Toward safety enhancement in neurosurgery using a handheld robotic instrument. The Hamlyn Symposium on Medical Robotics. 2017:15–16. [Google Scholar]
- 55.Ronneberger O, Fischer P, Brox T. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2015. U-net: Convolutional networks for biomedical image segmentation; pp. 234–241. [Google Scholar]
- 56.Salem N, Salem S, Nandi A. Segmentation of retinal blood vessels based on analysis of the Hessian matrix and clustering algorithm. European Signal Processing Conference. 2007:428–432. [Google Scholar]
- 57.Sekula RF, Frederickson AM, Arnone GD, Quigley MR, Hallett M. Microvascular decompression for hemifacial spasm in patients¿ 65 years of age: an analysis of outcomes and complications. Muscle & Nerve. 2013;48(5):770–776. doi: 10.1002/mus.23800. [DOI] [PubMed] [Google Scholar]
- 58.Smistad E, Løvstakken L. International Workshop on Large-Scale Annotation of Biomedical Data and Expert Label Synthesis. Springer; 2016. Vessel detection in ultrasound images using deep convolutional neural networks; pp. 30–38. [Google Scholar]
- 59.Song J, Gonenc B, Guo J, Iordachita I. IEEE International Conference on Robotics and Automation. IEEE; 2017. Intraocular snake integrated with the steady-hand eye robot for assisted retinal microsurgery; pp. 6724–6729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sutherland GR, McBeth PB, Louw DF. International Congress Series. Vol. 1256. Elsevier; 2003. Neuroarm: an MR compatible robot for microsurgery; pp. 504–508. [Google Scholar]
- 61.Sutherland GR, Wolfsberger S, Lama S, Zareinia K. The evolution of neuroArm. Neurosurgery. 2013;72(suppl_1):A27–A32. doi: 10.1227/NEU.0b013e318270da19. [DOI] [PubMed] [Google Scholar]
- 62.Taylor RH, Menciassi A, Fichtinger G, Fiorini P, Dario P. Springer Handbook of Robotics. Springer; 2016. Medical robotics and computer-integrated surgery; pp. 1657–1684. [Google Scholar]
- 63.Twinanda AP, Shehata S, Mutter D, Marescaux J, de Mathelin M, Padoy N. Endonet: A deep architecture for recognition tasks on laparoscopic videos. IEEE Transactions on Medical Imaging. 2017;36(1):86–97. doi: 10.1109/TMI.2016.2593957. [DOI] [PubMed] [Google Scholar]
- 64.Wang S, Yin Y, Cao G, Wei B, Zheng Y, Yang G. Hierarchical retinal blood vessel segmentation based on feature and ensemble learning. Neurocomputing. 2015;149:708–717. [Google Scholar]
- 65.Xue DX, Zhang R, Feng H, Wang YL. Cnn-SVM for microvascular morphological type recognition with data augmentation. Journal of Medical and Biological Engineering. 2016;36(6):755–764. doi: 10.1007/s40846-016-0182-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Yang S, MacLachlan RA, Riviere CN. IEEE International Conference on Robotics and Automation. IEEE; 2012. Design and analysis of 6 dof handheld micromanipulator; pp. 1946–1951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Yang S, MacLachlan RA, Riviere CN. International Conference on Intelligent Robots and Systems. IEEE; 2014. Toward automated intraocular laser surgery using a handheld micromanipulator; pp. 1302–1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Yang S, MacLachlan RA, Riviere CN. Manipulator design and operation of a six-degree-of-freedom handheld tremor-canceling microsurgical instrument. IEEE/ASME Transactions on Mechatronics. 2015;20(2):761–772. doi: 10.1109/TMECH.2014.2320858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Zhang B, Zhang L, Zhang L, Karray F. Retinal vessel extraction by matched filter with first-order derivative of Gaussian. Computers in Biology and Medicine. 2010;40(4):438–445. doi: 10.1016/j.compbiomed.2010.02.008. [DOI] [PubMed] [Google Scholar]