Surface Area to Volume Ratio: A Natural Variable for Bacterial Morphogenesis

Abstract

An immediately observable feature of bacteria is that cell size and shape are remarkably constant and characteristic for a given species in a particular condition, but vary quantitatively with physiological parameters such as growth rate, indicating both genetic and environmental regulation. However, despite decades of research, the molecular mechanisms underlying bacterial morphogenesis have remained incompletely characterized. We recently demonstrated that a wide range of bacterial species exhibit a robust surface area to volume ratio (SA/V) homeostasis. Because cell size, shape, and SA/V are mathematically interconnected, if SA/V is indeed the natural variable that cells actively monitor, this finding has critical implications for our understanding of bacterial morphogenesis, placing fundamental constraints on the sizes and shapes that cells can adopt. In this Opinion article we discuss the broad implications that this novel perspective has for the field of bacterial growth and morphogenesis.

Quantitative Bacterial Physiology

For quantitative laboratory experiments, bacteria are extraordinarily reliable partners for scientists interested in uncovering fundamental laws governing cell growth and form. Not only do they grow quickly, but their behavior from day to day and from culture to culture is so reproducible that all the complexities associated with their biological function can often be accurately summarized in simple mathematical equations [1,2]. In recent years there have been a number of technical advances that have made it possible to extend this quantitative analysis to dynamic observations of individual cells. These advances include improved methods for culturing bacteria under steady-state conditions for many generations on a microscope [3,4], improvements in the extraction of data from videomicroscopy experiments that enable precise, dynamic measurements on individual cells [5,6], and improvements in data analysis and storage that have enabled even subtle variations across large populations to be compared in statistically robust ways [7,8].

Using this kind of approach, we investigated the growth of aberrantly shaped Caulobacter crescentus mutants, and noticed that, although their overall sizes and shapes could vary wildly, cells moved toward and maintained a specific, condition-dependent SA/V [9]. This apparent SA/V homeostasis could not be explained using models of size and shape determination current in the field, which primarily focused on width and length of rod-shaped bacteria as separately controlled parameters [10–12]. We therefore hypothesized that SA/V might instead be the most illuminating property to consider – the ‘natural variable’ for this problem. By thus reframing the question of size control in terms of SA/V homeostasis, we were able to develop a unified model of bacterial growth and form with broad explanatory powers [13], the implications of which the bacterial research community has only just begun to explore [14–16]. In this Opinion article, we discuss the ‘relative rates’ mechanism by which cells appear to achieve SA/V homeostasis, we use this model to reconsider reports in the literature of changes in growth rate and/or cell wall biosynthesis altering SA/V, we re-examine Schaechter’s classic growth law relationship between cell size and growth rate from an SA/V-centric perspective, we speculate about what molecular cues might provide the signal to increase or decrease SA/V in different conditions, and finally we propose specific molecular mechanisms that rod-shaped bacteria could employ to alter their width and length in order to achieve SA/V homeostasis.

Cell Size, Shape, and SA/V Are Interconnected Variables

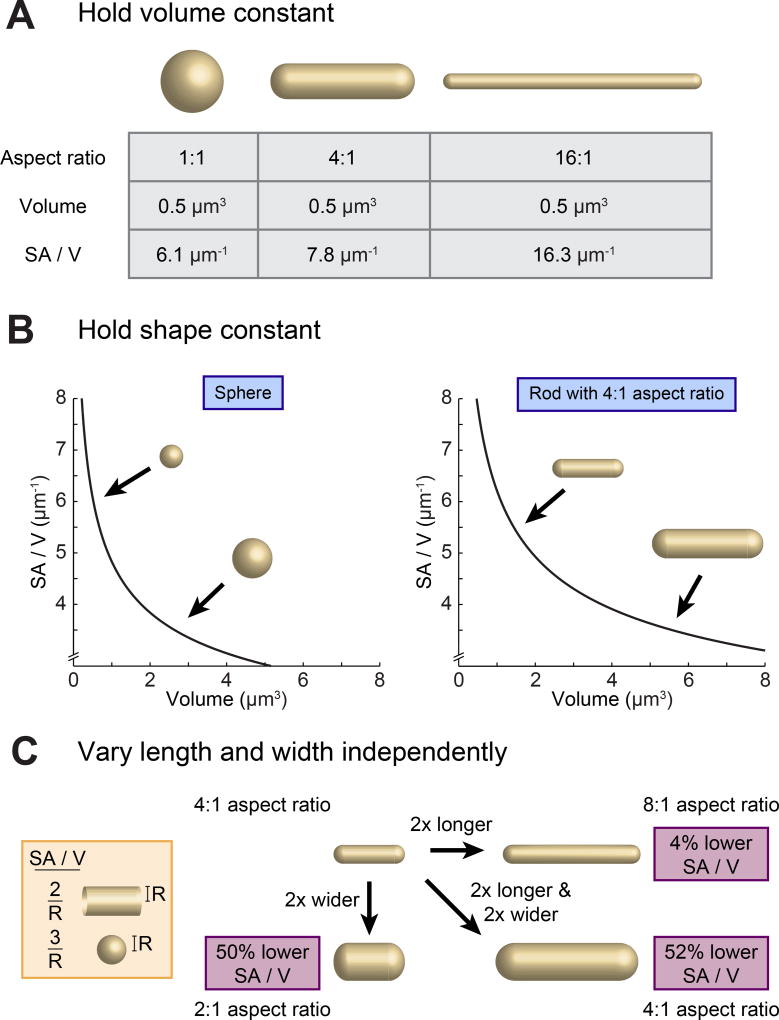
In considering the origins of bacterial morphogenesis it is essential to make explicit the necessary geometric connections between size (meaning volume), shape, and SA/V. If volume is held constant, cells of different shapes will typically adopt different SA/V values (Figure 1A). However, in many species, it is shape and not volume that is constant. In Escherichia coli, for instance, cell volume can vary over nearly an order of magnitude for cells grown at different growth rates, but cells typically maintain roughly the same shape – a rod with aspect ratio 4:1 [17]. So, if we now consider the scenario where shape is held constant, we find that increases in volume necessarily correspond to reductions in SA/V (Figure 1B). Thus, once shape is constrained, specification of a given volume is sufficient to determine SA/V, and vice versa. While many studies have treated volume as the actively controlled parameter in this scenario, our recent work suggests that it is likely the other way around, and that SA/V is the actively regulated variable, with size following along as necessary [13].

Figure 1.

Size, Shape, and Surface Area to Volume Ratio (SA/V) Are Interconnected Properties. (A) When volume is held constant, changing the shape of an object can significantly alter the overall SA/V. (B) When shape is held constant, changes in volume directly correspond to changes in SA/V, with larger objects having lower SA/V. (C) In the case of a rod-shaped cell with hemispherical end caps, increases in width and length both correspond to reductions in SA/V.

Focusing specifically on rod-shaped bacteria, many studies have described the impact of various genetic, nutritional, and pharmacological perturbations on cell width and/or length [10–12]. However, changes in either of these dimensions will also lead to changes in SA/V. On their own, increases in width reduce SA/V, as do increases in length, albeit to a lesser degree (Figure 1C). This impact of cell lengthening can be understood by considering the relative contributions of the cylindrical cell body and hemispherical end caps: as cells get longer, the contribution of the high-SA/V end caps is diminished and the overall SA/V goes down (see Figure 1C, inset). For these reasons, changes in width and length in different growth conditions must always be considered in the context of their combined impact on the overall SA/V of cells.

A ‘Relative Rates’ Model Quantitatively Explains SA/V Homeostasis

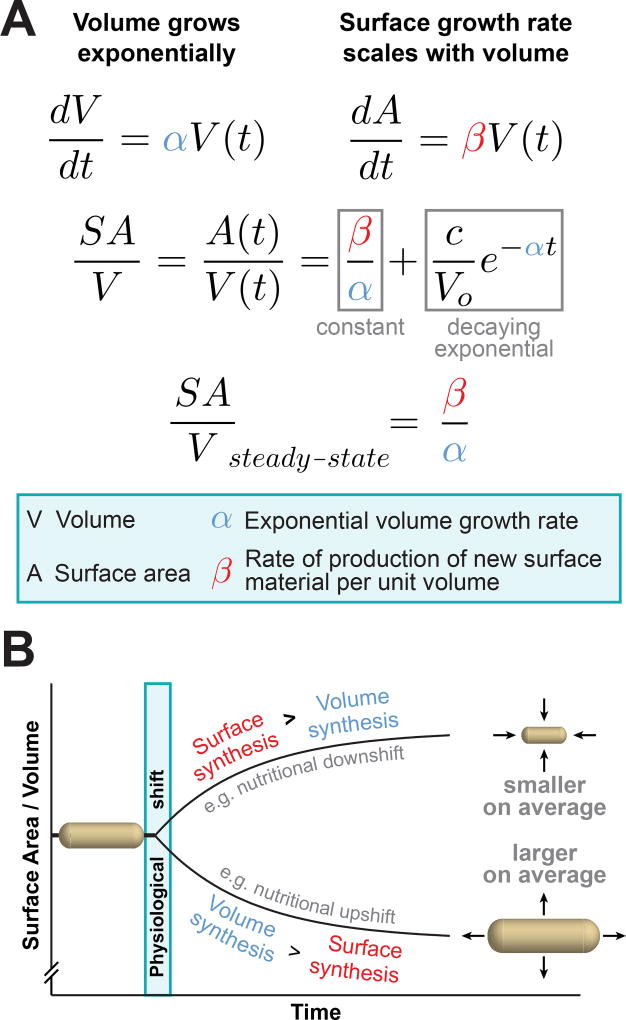
With the understanding that cell size, shape, and SA/V are intimately linked, and having observed individual cells alter both their size and shape in order to move toward a steady-state SA/V [9], we chose to focus strictly on how cells might achieve such SA/V homeostasis. First, we knew that bacteria increase both their mass and volume exponentially – that is, the rate of volume growth scales with cell volume [1,18,19]. We then realized that if we make the simple assumption that the rate of surface growth also scales with cell volume, this model predicts that cells will move toward a steady-state SA/V over time, that is, exhibit SA/V homeostasis. At the molecular level, we hypothesized that the scaling between volume and surface growth is due to the fact that the biosynthesis of new surface material begins in the 3D cell cytoplasm, where cytosolic enzymes synthesize precursors of various envelope components, including the peptidoglycan (PG) cell wall [11]. In this way, the biosynthetic flux through one or more envelope synthesis pathways in the cell cytoplasm might limit surface growth, causing the rate of surface growth to scale with volume.

This phenomenological ‘relative rates’ model can be formulated mathematically, and makes several experimentally testable, nontrivial predictions (Figure 2A). Specifically, SA/V at steady state is expected to be equal to the ratio β/α, where α is the exponential volume growth rate of cells and β is the rate of surface material synthesis per unit volume. Essentially, this means that, at steady state, SA/V will be determined by the ratio of surface growth to volume growth. Because we expect both α and β to vary in different physiological conditions, we can plot what we predict will happen when cells are shifted between conditions (Figure 2B). After the shift, cells are initially not at the ‘correct’ SA/V for their final condition (β_final/α_final), and the model predicts that cells will move toward that value in a trajectory that is described by a decaying exponential function with decay constant equal to α_final. Dynamic, single-cell imaging of distantly related bacterial species undergoing different types of physiological perturbations revealed that cells indeed move toward a new steady-state SA/V in this manner, providing strong, quantitative support for this mechanism of SA/V homeostasis [13]. Given the predictive power of this model, we propose that SA/V is the critical natural variable to consider when looking at bacterial morphogenesis. Importantly, achieving a particular SA/V does not dictate one specific size or shape, but rather the range of sizes and shapes that cells can adopt (Figure 1). Thus, any questions of bacterial size and shape determination must be considered within the context of their combined impact on SA/V.

Figure 2.

The Relative Rates of Surface and Volume Growth Dictate the Surface Area to Volume Ratio (SA/V) of Bacterial Cells. (A) A ‘relative rates’ model for SA/V homeostasis assumes that both volume and surface area grow at rates proportional to the current cell volume, with scaling factors α and β respectively. This model makes the quantitative prediction that cells will move toward a final steady-state SA/V in a trajectory described by a decaying exponential with decay constant α, and that the final SA/V will be equal to the ratio of the scaling factors β/α. These quantitative predictions were borne out by dynamic, single-cell imaging [13]. (B) This diagram depicts the predictions of the model, that cells will change SA/V depending on the relative rates of surface and volume synthesis. For instance, during a nutritional upshift, the rate of volume synthesis increases relatively more than the rate of surface synthesis, leading to an overall drop in SA/V and larger cells on average.

PG Synthesis Connects Surface Growth to Cell Volume

The central hypothesis underlying the ‘relative rates’ model is that surface growth rate scales with cell volume. It is critical, therefore, to identify the molecular mechanisms that give rise to this scaling. Given the hypothesis that the flux through one or more surface biosynthesis pathways in the cytoplasm sets the rate of surface growth, we wondered whether cell wall biosynthesis might be the primary pathway mediating this connection. The cell wall is a stiff, covalently linked network composed of PG that surrounds the cell, counteracts turgor pressure, and is a major structural component of the cell envelope. Additionally, PG precursor synthesis begins in the cytoplasm, after which precursors are attached to a lipid anchor (undecaprenyl phosphate, Und-P), flipped across the cytoplasmic membrane into the periplasm, and incorporated into the surrounding network [11,12]. For these reasons, PG biosynthesis was an attractive candidate for linking volume to the rate of surface growth.

Recently, a variety of pharmacological and genetic experiments from our laboratory and others support the proposal that PG biosynthesis does indeed serve as a significant connection between volume and surface growth rate. When diverse bacterial species were treated with very low doses of the antibiotic fosfomycin, which inhibits the first committed step of PG biosynthesis, cells continued growing their volume essentially uninterrupted (i.e., α did not change), but slowed down the rate of surface growth per unit volume (i.e., β was reduced) [13]. This implies that the scaling between volume and surface growth, at least in this regime, is determined by the flux through the PG biosynthesis pathway. Furthermore, cells treated with fosfomycin became larger and reduced their SA/V as predicted by the ‘relative rates’ model, where SA/V_steady-state = β/α. While it may seem counterintuitive that cells treated with a cell wall biosynthesis inhibitor should get bigger, this makes sense from an SA/V-centric point of view: because volume continued growing at the same rate while surface growth was slightly reduced, SA/V had to go down because cells simply had less surface material available to encapsulate the same amount of volume. Remarkably, three extremely divergent species – the Gram-negatives C. crescentus and Escherichia coli and the Gram-positive Listeria monocytogenes – all responded to fosfomycin in the same way, reducing their SA/V by increasing both their width and length in a dose-dependent manner, implying that the ability to flexibly change dimensions in response to PG precursor availability is a widely conserved trait.

Other groups have also observed that changes in the flux through the PG biosynthesis pathway can lead to alterations in cellular SA/V. Our fosfomycin results have been replicated by others [17], and it has also been shown in Bacillus subtilis that depletion of MurB, the second enzyme in the PG biosynthesis pathway, leads to wide, elongated cells [20]. Recently, a comprehensive, CRISPRi-based analysis of essential genes in B. subtilis revealed that knockdowns of several different enzymes in the PG biosynthesis pathway also led to wider cells, and that, of all essential genes, only cell wall biosynthesis and patterning genes were significantly enriched in this metric [21]. Additionally, a two-component system in Vibrio cholerae was identified, WigKR, that allows cells to tune the expression of the entire PG biosynthesis pathway. Activation of the system increased cell wall content and led to a 20% reduction in cell width, while blocking the system led to a comparable increase in cell width [22]. These results are exactly what the ‘relative rates’ model would predict: increased PG production led to thin cells with high SA/V, while reduced PG production led to wide cells with low SA/V.

The above examples all support the notion that PG biosynthesis serves as a significant link between cell volume and surface growth, and that PG availability somehow mediates changes in SA/V. Interestingly, disruption of late steps in the biosynthesis of two other envelope constituents – O-antigen and enterobacterial common antigen (ECA) – have also been shown to increase cell size [23,24]. However, in both cases it was shown that these effects are also ultimately due to a reduction in PG biosynthesis. O-antigen, ECA, PG, and many other surface constituents are synthesized in a similar manner, where precursors are attached to the same lipid anchor, Und-P, before being incorporated into their final structures. Disruption of late steps in the O-antigen and ECA biosynthesis pathways leads to a buildup of Und-P-linked dead end intermediates, which sequester Und-P away from PG biosynthesis [23,24]. The authors of these studies demonstrated that the observed increases in cell size are due specifically to reduced production of PG, not the other envelope constituents, further supporting the proposal that PG biosynthesis provides the main molecular link between cell volume and surface growth in the ‘relative rates’ model. Additional details of envelope biosynthesis pathways that go through Und-P-linked intermediates, and interesting possible implications of competition between these pathways and PG biosynthesis, have recently been reviewed [15].

Growth Rate Plays a Critical Role in Size Determination

So far we have focused on the role of surface material biosynthesis in determining SA/V and cell size. However, it is the ratio of surface growth (β) to volume growth (α) that sets the steady-state SA/V of cells. Therefore, changes in volume growth rate can also have profound impacts on SA/V and thus cell size. Because of this, it is important to always consider the possibility that changes in cell size in response to a genetic or pharmacological perturbation could be due primarily to changes in growth rate. For example, it has been proposed that fatty acid (FA) biosynthesis, a necessary precursor to synthesis of membrane lipids, is involved in setting cell size because disruption of this pathway leads to a reduction in cell size and an increase in SA/V [25,26]. However, this perturbation also leads to a severe growth rate defect – a 50% reduction in α. Because SA/V ~ β/α, this drop in α could cause an increase in SA/V, and hence the observed reduction in cell size.

In support of this idea, there is evidence that the reduction in cell size in response to FA inhibition is mediated by the small-molecule alarmones (p)ppGpp. These molecules are part of the stringent response in bacteria, and slow growth by dramatically altering the transcriptional profile of cells and facilitating a transition to a slow-growing state [27]. Similar to E. coli, C. crescentus typically slows down growth and reduces cell size in response to FA inhibition. However, in a (p)ppGpp null strain, cells no longer grew slowly or became small during FA inhibition [28]. This implies that the decrease in growth is mediated through (p)ppGpp, and that the reduction in size is indeed due to the impact on growth rate, not some other effect of FA inhibition. Interestingly, when a similar experiment was performed in E. coli, (p)ppGpp null cells exposed to a FA biosynthesis inhibitor lost membrane integrity and were killed at higher rates than wild-type cells [25]. This suggests that, for this species and inhibitor concentration, cells must slow down their volume growth using (p)ppGpp, lest volume growth outpace membrane capacity. More broadly, this example highlights the potential of (p)ppGpp signaling to coordinate volume growth with the physiological state of the cell, potentially tuning cytoplasmic expansion to keep it in balance with other biosynthetic rates [27].

A Re-examination of Schaechter’s Growth Law

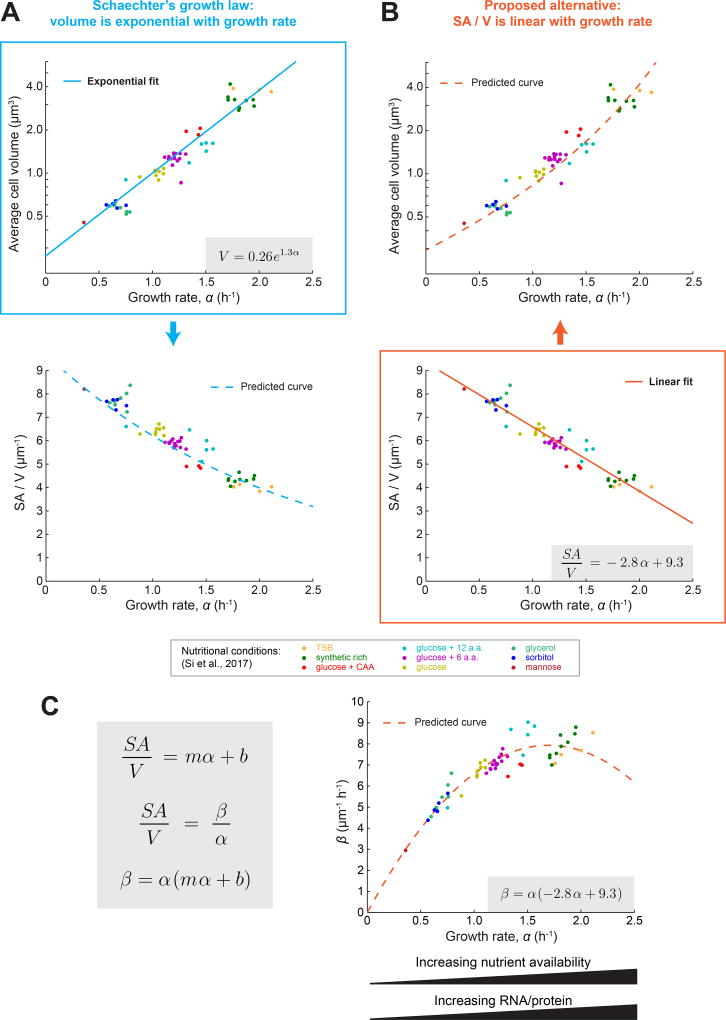
The observation that growth rate has a profound impact on cell size is not new. Indeed, it was first reported 60 years ago that E. coli cells grown quickly in nutrient-rich medium are larger than those grown slowly in nutrient-poor medium [29]. Specifically, it was observed that, for E. coli and closely related species, the average volume of cells appears to increase exponentially with growth rate when the nutritional content of the growth medium is varied. This relationship, termed Schaechter’s growth law, has held up beautifully over the years, and recent work from Si et al. – using multiplexed turbidostats to measure the size and shape of E. coli cells growing at steady state in different media conditions – confirmed that the average cell volume appears to increase exponentially with growth rate (reproduced in Figure 3A) [17]. However, it is not just volume that varies monotonically with growth rate in these conditions. In addition to being large, fast-growing cells also have lower SA/V values (reproduced in Figure 3B) [17]. Biochemically, this drop in SA/V corresponds to less envelope material per unit dry cell mass. In fact, the amount of surface material per unit dry weight was measured to be inversely proportional to growth rate [30]. This supports the idea that large, fast-growing cells are simply producing less surface material (PG) compared to volume (mass) – that is, β/α is lower. Interestingly, these experimental results were invoked in several theoretical papers in the 1970s in order to explain the changes in cell size observed when growth rates are shifted [31,32], similar to the recently proposed ‘relative rates’ model.

Figure 3.

A Linear Dependence of the Surface Area to Volume Ratio (SA/V) on Growth Rate Could Underlie Classically Observed Trends between Cell Size and Growth Rate. (A) Average cell volume versus growth rate and SA/V versus growth rate for E. coli cells growing at steady state in different media conditions [17]. Each point represents the average value for many cells from an experiment conducted in the indicated growth medium. The solid blue line represents an exponential fit to the data, and the extracted relationship is indicated in the gray box. The blue dashed line indicates the predicted dependence of SA/V on growth rate given the exponential fit between volume and growth rate, and assuming a rod shaped cell with 4:1 aspect ratio. (B) The same data as in (A), but here SA/V versus growth rate was fit with a linear function (solid orange line). The extracted relationship is indicated in the gray box. The orange dashed line indicates the predicted dependence of volume on growth rate given the linear relationship between SA/V and growth rate, and assuming a rod shaped cell with 4:1 aspect ratio. (C) Predicted dependence of surface synthesis (β) on growth rate (α) when growth rate is varied by changing media conditions. Assuming a linear relationship between SA/V and α where m and b are constants, and combining this with the conclusion from the ‘relative rates’ model that at steady state SA/V is equal to the ratio β/α, we predict that β has a parabolic dependence on α. We can then use the values of m and b extracted from (B) and plot the predicted dependence of β on α for the data from Si et al. [17]. Known competing trends between substrate availability and biosynthesis enzyme concentrations could contribute to the shape of this dependence.

Given our evidence that SA/V homeostasis underlies size determination, we wondered whether Schaechter’s observation that size varies with growth rate might actually be due to SA/V varying with growth rate. To investigate this, we examined the correlation between SA/V and growth rate using measurements from Si et al., and observed a remarkably simple relationship: SA/V appears to decrease linearly with growth rate (Figure 3B). This linear trend fits the data just as well as an exponential fit to volume (Figure 3A), meaning that even this very high quality dataset does not have the resolution to distinguish between these two models. Although it is not immediately clear why SA/V should vary linearly with growth rate, we can interpret this observation within the context of the ‘relative rates’ model as follows. If SA/V is linear with respect to growth rate (α), and given that SA/V is equal to β/α, we can conclude that β has a parabolic dependence on α in these conditions (Figure 3C). In other words, the amount of surface material synthesized per unit cytoplasm (β) increases with α at slow growth rates, but tapers off at rates close to the maximal growth rate for E. coli. Specifically, using the data from Si et al. we find that β = α (−2.8 α + 9.38). Essentially, β is comprised of one component that increases with growth rate (α), convolved with a component that decreases with growth rate (−2.8 α + 9.3). There are several intriguing hints from the literature about why this might be the case, which we highlight below.

First, we recall that increases in α correspond to increases in nutritional content of the medium. We therefore propose that the increasing component of β could be due to the increased availability of raw material available for PG biosynthesis – that is, the substrates for this reaction. For the decreasing component, we hypothesize that the concentration of surface biosynthesis enzymes decreases linearly with growth rate. It is well documented that the relative concentrations of many enzymes decrease with increasing growth rate [33,34]. This is because the global RNA/protein ratio increases linearly with growth rate as an increasing fraction of the cell mass is composed of ribosomes, allowing cells to achieve faster growth rates. Additionally, more of the proteome itself is dedicated to ribosome-associated proteins at fast growth rates, further reducing the relative concentration of other enzymes [34]. These changes in cell composition are both quantitative and reproducible, and if the relative concentrations of PG biosynthesis enzymes indeed decrease linearly with growth rate, then this enzyme activity decrease, combined with the increasing availability of substrates, could readily explain the parabolic dependence of β on α. Future work must directly measure both enzyme and substrate concentrations at different growth rates, and determine whether these trends can in fact explain the observed dependence of SA/V – and thus size – on growth rate.

What is the Molecular Cue to Modulate SA/V?

In choosing to focus on SA/V when formulating the ‘relative rates’ model, we remained agnostic about what morphological changes cells employ to achieve a specific SA/V. In reality, rod-shaped bacteria have two major dimensions that they can alter in order to change their SA/V – length and width (Figure 1). Much work has already been done to identify genes that are involved in width and length control, and many mutations only seem to alter one or the other dimension, implying that width and length control are somewhat independent processes [12]. However, we consistently observed cells changing both length and width in order to achieve whatever SA/V was necessary [13]. What molecular mechanisms might underlie these changes in dimension, and how do they conform quantitatively to the predictions of the ‘relative rates’ model? In the rest of this Opinion article, we propose ways that cells could achieve SA/V homeostasis, with an emphasis on reconciling what is already known about the molecular mechanisms of width and length control in rod-shaped bacteria with the phenomenological observation of SA/V homeostasis.

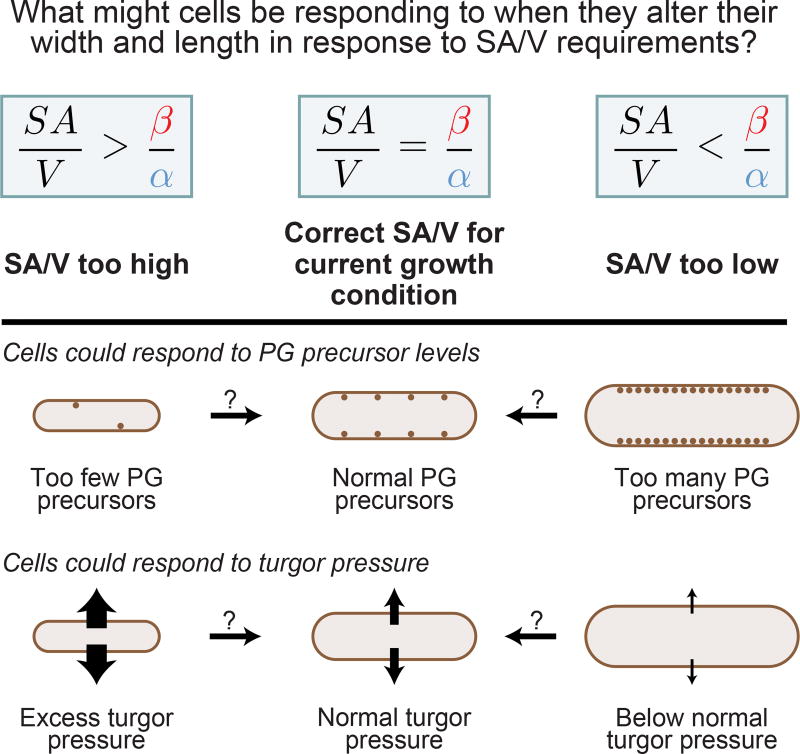
We can think of at least two general classes of mechanism, which are not mutually exclusive, that could allow cells to detect whether their SA/V is consonant with the current rates of surface and volume synthesis: mechanisms that are sensitive to turgor pressure, and those that are sensitive to PG precursor availability. In both cases, an imbalance in the rates of surface synthesis and volume growth would lead to changes in a cell-scale property that could signal to cells to alter their pattern of growth in an appropriate way to change their SA/V (Figure 4). We will focus exclusively on mechanisms involving PG precursor availability because more experiments have been performed on this topic, providing molecular clues about how precursors might influence cell width and length control. In contrast, little is known about the impact of turgor pressure on bacteria, though it has been shown to alter cell growth [35,36]. In the future, it will be important to identify the molecular ramifications of changes in turgor pressure, and determine if such changes play a role in SA/V homeostasis.

Figure 4.

Changes in Peptidoglycan (PG) Precursor Levels and/or Turgor Pressure Could Serve as a Signal to Cells to Alter Their Surface Area to Volume Ratio (SA/V). If SA/V is too high, that is, SA/V >β/α, surface synthesis is too slow and volume synthesis is too fast to be compatible with the current SA/V. Thus, in this case, there will potentially be a lack of available peptidoglycan (PG) precursors and/or excess turgor pressure. Conversely, if SA/V is too low, that is, SA/V <β/α, surface synthesis is too fast and volume synthesis is too slow. In this scenario, there could be an accumulation of excess PG precursors and/or a drop in turgor pressure. In this way, cells could use changes in either of these properties to decide whether they should alter their length and width to achieve the correct SA/V.

Length and width control mechanisms that respond to the relative availability of PG precursors are appealing for several reasons. First, the evidence presented above suggests that the flux through the PG biosynthetic pathway provides the molecular link between cell volume and surface growth, making this pathway an ideal candidate for orchestrating SA/V homeostasis. Second, the level of precursors in a cell would be expected to change depending on whether the cell is at the correct SA/V (Figure 4). Third, the same pool of PG precursors is used by the lateral and septal PG insertion machineries, which catalyze the elongation and division of cells respectively. Because of this, width and length could be modulated separately, but in a concerted fashion, by these two different machineries both responding to changes in the shared pool of PG precursors. This idea is similar to the ‘two competing sites’ model, which states that competition between the elongation and septation machineries dictates the balance between elongation and division [37]. Building on this model, we propose that, as PG precursors become more or less available, these machineries would both respond, tuning length and width as necessary to reach the proper SA/V. We believe that this type of coordinated response to changes in the shared pool of PG precursors could underlie the remarkable ability of some bacterial species to maintain a constant aspect ratio across a wide range of sizes and growth rates [17]. Interestingly, when C. crescentus cells were genetically prevented from dividing, cells became very long, a morphological change that would lead to a drop in SA/V if cells remained the same width (Figure 1C). However, as cells became longer, they also became thinner and maintained the same SA/V [13]. Thus, changes in width and length can be decoupled, but cells still retain the ability to achieve SA/V homeostasis – if not with one dimension, then with the other. This result supports a fluid sharing of PG precursors between the lateral and septal insertion machineries that robustly facilitates SA/V homeostasis. In the next sections we therefore consider mechanisms of width and length control separately, though in the future it will be critical to determine how and to what extent these systems interact in both time and space.

How Might Width Be Modulated in Response to SA/V Requirements?

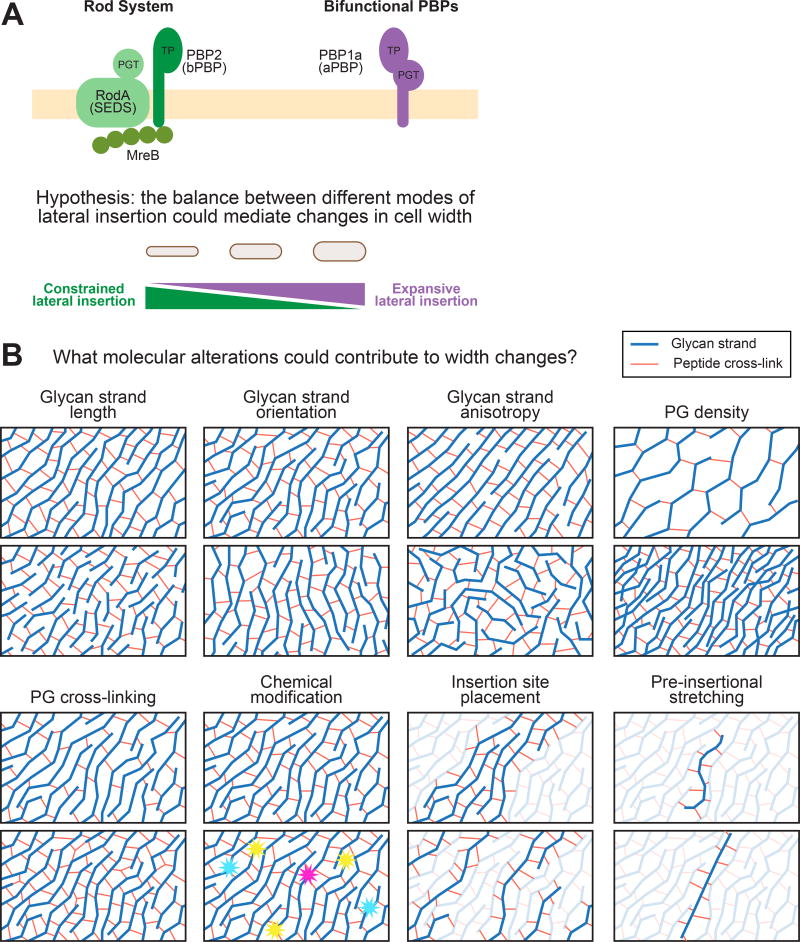
Most rod-shaped bacteria under normal, constant conditions elongate by incorporating new PG into their sidewall such that they elongate at a specific width. The lateral PG insertion machinery is therefore an obvious candidate effector of width control. During lateral wall synthesis, lipid-anchored PG precursors are polymerized into a growing glycan strand by a processive enzyme with PG transglycosylase (PGT) activity. This nascent strand is then cross-linked into the surrounding network through its peptide side chains by an enzyme with transpeptidase (TP) activity. The bacterial actin homolog MreB polymerizes into short filaments or patches that bind to the cytoplasmic face of the membrane and coordinate the circumferential movement of the Rod complex, a group of proteins that is known to help maintain width control and rod shape by promoting constrained lateral insertion, perhaps by ensuring that stiff glycan strands are inserted in their characteristic circumferential orientation [10,11,38] (Figure 5A).

Figure 5.

The Balance between Activity of Two Different Peptidoglycan (PG) Insertion Machineries and Alterations in the Molecular Properties of PG Could Contribute to Changes in Cell Width. (A) The Rod system inserts lateral wall material and is known to promote rod-like growth at a fixed width. Recently, it was shown that bifunctional penicillin-binding proteins (PBPs) insert material independent of the Rod system. It is thus possible that, while the Rod system promotes constrained lateral insertion, the bifunctional PBPs promote unconstrained, or expansive insertion. In this way, simply by tuning the relative activities of these different systems based on the surface area to volume ratio (SA/V) requirements, cells could flexibly alter their width. (B) A variety of different molecular alterations to the PG network could lead to changes in the overall cell width over time.

An interesting detailed hypothesis for how cells could change width in response to PG precursor levels is suggested by a series of recent experiments showing that, while the Rod complex contains both PGT and TP enzymes, another class of enzymes is bifunctional and contains both of these activities in a single protein [39,40]. Furthermore, these bifunctional penicillin-binding proteins (PBPs) do not appear to be governed by MreB. Thus, while the Rod complex promotes constrained lateral insertion, it is possible that bifunctional PBPs act as free agents, polymerizing and cross-linking PG in a way that does not seem to be width-constrained, leading to expansive lateral insertion. In principle then, cells could change their width by tuning the balance between these two different modes of lateral wall incorporation (Figure 5A). Critically, recent work showed that lipid-anchored PG precursors appear to recruit MreB to the membrane in B. subtilis [41]. This could create a homeostatic mechanism where low levels of PG precursors recruit less MreB to the cell surface, causing the bifunctional PBPs to take over and leading to cell widening. Conversely, high levels of PG precursors would recruit additional MreB and tilt the balance of synthesis toward the Rod complex, thereby causing the cells to narrow. More experiments are needed to test whether a homeostatic mechanism like the one described here does indeed facilitate width modulation in response to SA/V requirements.

Regardless of whether width homeostasis is achieved using the mechanism proposed above or some other scheme, it will be critical to identify the molecular alterations in the PG itself that are responsible for these width changes. The PG network has many physical properties that could, in principle, be modulated enzymatically at the local level to produce global changes in cell width. These are summarized in Figure 5B, and include changes in glycan strand length, orientation, or anisotropy, which would alter the mechanical properties of the network, as well as more general chemical properties such as the density of PG strands, their degree of cross-linking, or chemical modification. The spatiotemporal regulation of insertion site placement and the stretching of PG strands as they are being laid down could also have profound impacts on the shape and mechanical properties of the network and consequently cell width [42]. Piecing apart how these properties respond to changes in PG precursor availability – and also turgor pressure – will be critical to understand how the phenomenon of SA/V homeostasis is achieved at the molecular level.

How Might Length Be Modulated in Response to SA/V Requirements?

In addition to modulating their width, a diverse array of bacterial species also alter their length in response to SA/V requirements [13,17,23,24,43]. Indeed, C. crescentus, E. coli, and L. monocytogenes all increase their length in a dose-dependent manner when grown in the presence of a PG biosynthesis inhibitor [13]. Because rod-shaped bacteria grow through alternating phases of elongation and septation, this dose-dependent increase in length implies that cells delay division when PG precursors are scarce, suggesting that the availability of PG precursors can play a role in division timing. Because such a role for PG precursors in division would, in principle, allow cells to fluidly modulate their length in response to SA/V requirements, we sought to define a mechanism that might facilitate such coupling.

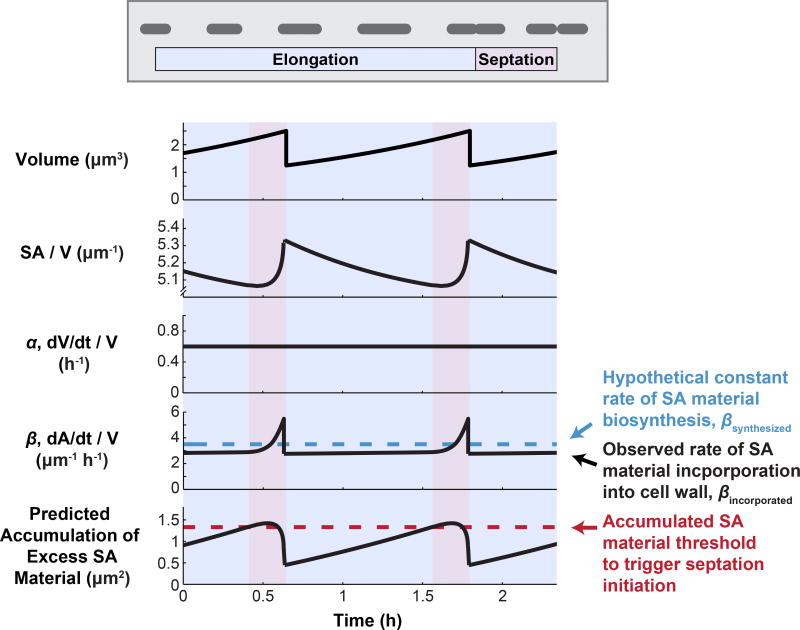
While the ‘relative rates’ model predicts what will happen to SA/V when averaged over multiple cells and cell cycles, on an individual cell basis, SA/V is expected to oscillate over the cell cycle. During elongation, SA/V will necessarily go down because more of the cell is composed of low-SA/V cylindrical cell body (Figure 1C), and then septation and the synthesis of two new daughter cell poles will raise the ratio again (Figure 6). Experimental evidence suggests that while volume growth, α, seems to be constant throughout the cell cycle, the observed rate of surface incorporation into the wall, β_incorporated, appears to fluctuate, speeding up particularly during constriction, when the high-SA/V end caps are being built [13,18,44–46]. However, we have no reason to assume that the underlying rate of PG biosynthesis is cell-cycle regulated. We therefore hypothesize that there is some constant rate of surface material synthesis, β_synthesized, which is unchanged across the cell cycle (blue dashed line in Figure 6). If this is the case, we predict that cells would produce excess surface material during elongation, leading to a build-up of surface material in the cytoplasm during this phase of the cell cycle. During septation, this excess would be used up during the surface-intensive process of end-cap construction, returning the level of accumulated material back to baseline (Figure 6).

Figure 6.

A Surface Material Accumulation Threshold Underlying Division Timing Could Couple Cell Length to the Surface Area to Volume Ratio (SA/V) Requirements of the Cell. During the cell cycle, natural variations in SA/V could lead to the accumulation of excess surface material if the underlying rate of surface material biosynthesis is constant. Cells could then use this accumulated material to trigger division once a threshold is reached, thus tying division timing to surface material availability. The traces shown here correspond to an ideal rod with hemispherical end caps growing exponentially.

If this is true, and cells indeed accumulate excess surface material in their cytoplasm during elongation, we realized that accumulation of a threshold amount of excess material could serve as a checkpoint for constriction initiation, allowing cells to couple division timing to the availability of PG precursors and thus the SA/V requirements of the cell. For example, in the case of PG biosynthesis inhibition, if cells were treated with increasing concentrations of drug, they would have to grow for longer times before reaching the same threshold. This would lead to a dose-dependent increase in cell length, as we have observed. Additionally, there is some evidence that length control is imposed at the point of constriction initiation [13,47,48], supporting the idea that there is a checkpoint prior to constriction initiation. Finally, several recent reports have found that bacteria appear to grow according to an adder pattern, where cells add, on average, the same amount of volume during each cell cycle before dividing [7,8,49,50]. If cells trigger division after accumulating a threshold amount of excess surface material, this scheme mathematically produces an adder pattern between cell birth and constriction initiation [13]. Thus, division according to this type of mechanism could potentially explain both the adder behavior that has been seen for a variety of bacterial species growing at steady state, as well as the dynamic changes in length that we have observed for diverse species in shifting physiological conditions.

Although the mechanism described above is an attractive model that could explain a wide range of observations, it has yet to be experimentally tested. In the future, it will be critical to directly measure the levels of different PG precursors across the cell cycle to determine if any of these species accumulate during elongation. Additionally, it will be important to determine if there is a PG precursor ‘sensor’ that measures the accumulated precursors and is responsible for triggering division. Bacterial division is orchestrated by the FtsZ ring, which forms at midcell, recruits a number of accessory proteins to form the divisome, and eventually begins to constrict [51]. We therefore favor the hypothesis that some late-arriving component of the divisome might sense accumulated PG precursors and trigger the FtsZ ring to begin constriction. Furthermore, our proposed model is predicted to produce an adder pattern only when the threshold is a certain amount of excess surface material, not a certain concentration [13]. Because the FtsZ ring remains relatively constant in size as cells grow, a sensor that is part of the FtsZ ring could thus enable cells to sense a specific amount, not concentration, of material. Finally, high-throughput, high-resolution single-cell imaging will be required to determine if division timing does indeed appear to be imposed at the point of constriction initiation, and if so, how this gives rise to the observed adder pattern.

What Role Does Chromosome Replication Play in Division Timing?

This proposal – that bacteria divide in response to surface material accumulation and SA/V requirements – is very different from traditional models of the bacterial cell cycle where division timing is intimately linked to chromosome replication. Particularly in E. coli, the Cooper–Helmstetter model of division timing has predominated, which states that after E. coli cells initiate another round of chromosome replication, it takes a set amount of time (the C period), to replicate their chromosomes, and that cells then divide a fixed amount of time later (the D period) [52]. From this perspective, the initiation of chromosome replication is the central event of the E. coli cell cycle, and with every initiation event a corresponding division event is ‘scheduled’ to happen C+D minutes later. After this model was proposed in 1968, Donachie pointed out that a constant C+D period, combined with the apparent exponential dependence of volume on growth rate known as Schaechter’s growth law (Figure 3), implies that cells initiate another round of chromosome replication at a fixed volume per origin of replication [53]. Experimental studies have since confirmed that E. coli cells do indeed initiate chromosome replication once they reach a critical volume per origin of replication [17,54,55], and for wild-type E. coli growing at moderate to fast growth rates the C+D period is remarkably constant [55,56]. However, the general constancy of the C+D period has been called into question. Although the C period does appear to remain the same in most conditions, various physiological and morphological perturbations have been identified that alter the D period in complex and unpredictable ways [13,17,57–59]. These data suggest that, although the D period originally appeared to be a fundamental constant of bacterial division, it is quite variable in different contexts.

We propose that these changes in the apparent D period can be understood if we let go of the chromosome-centric view of cell division, and instead adopt a chromosome-agnostic perspective. This type of model has been put forward by other groups [60–63], and generally states that, for E. coli cells growing at steady state, the division and chromosome replication cycles operate in parallel, with minimal feedback between the two. We build on these models, and propose that cells grow and divide according to their SA/V requirements, with chromosome replication separately keeping pace with volume growth. Because additional rounds of chromosome replication are triggered when cells reach a critical volume per origin of replication, this system allows chromosome number to automatically scale with volume, regardless of cell division. In support of this view, recent studies have found that perturbations which alter E. coli cell size have remarkably little effect on the DNA-to-cytoplasm ratio, indicating that chromosome replication is unaffected by such morphological perturbations [13,17,57,59]. While some groups have suggested that these changes in cell size arise because the perturbations are altering the D period, we argue the opposite – that the perturbations directly alter cell size, and therefore lead to changes in the apparent D period. From our perspective, the D period is not a key biological parameter that cells actively modulate, and is instead simply the time that happens to elapse from the completion of chromosome replication until division. Although this distinction can sound subtle, understanding whether division timing sets the D period or the D period sets division timing will be critical to identify the molecular players underlying length control in bacteria.

We can also apply this chromosome-agnostic view of division timing to Schaechter’s growth law. Historically, it has been thought that increases in cell size with growth rate are due to chromosome replication initiating at a constant volume per origin of replication followed by a constant C+D period. In Figure 3, we put forward an alternate hypothesis for Schaechter’s observations – one that does not invoke chromosome replication and instead relies on trends in SA/V. From this perspective, cell size is set independently of chromosome replication, and this dependence of cell size on growth rate, combined with replication initiating at a constant volume per origin of replication, result in the apparent C+D period appearing relatively constant over these nutritional conditions. Along these lines, in 1991 Cooper himself wrote: ‘Since 1968, when the temporal constancy of the period between termination of DNA replication and cell division was noted, it has been thought that termination of replication may trigger invagination. This observation is consistent with the alternate proposal that there is only a coincidental relationship between termination and division. It may be that the constant D period is a result of the cell evolving to have DNA replication terminate prior to division and that there is no causal relationship between division and termination.’ [64] We agree with this alternate proposal, and argue that there is no genuine ‘timer’ mechanism underlying the D period. Rather, E. coli seems to have evolved to scale its size (via trends in SA/V? via trends in β with α?) such that enough time is always left between termination of replication and the subsequent cell division.

Another argument against a chromosome-centric model of division timing is that there is little molecular evidence for a mechanism that causes E. coli to divide a set amount of time after chromosome replication. Generally, chromosome-centric models invoke the idea that once replication is terminated, it takes a set amount of time for the chromosomes to segregate, for the divisome to form, and for the cell to constrict. Consistent with this, nucleoid occlusion systems have been identified which prevent the cell from cutting across unsegregated chromosomes during cell division [65,66]. In these systems, the presence of DNA near the FtsZ ring directly inhibits ring constriction. However, nucleoid occlusion appears to be more of a fail-safe mechanism that kicks in when something has gone awry during the cell cycle, rather than a core feature that always dictates division timing. The evidence for this is that when nucleoid occlusion is genetically removed from cells, cells are not only viable, but the average cell size does not change [65,66], implying that this system is not at play during normal cell cycles. Furthermore, when nucleoid occlusion is removed and chromosomes are prevented from replicating altogether, cells go ahead and divide across unreplicated chromosomes, ‘guillotining’ them [65,66]. This means that neither chromosome replication nor segregation is required for cell division to occur, strongly arguing against a genuine molecular timer underlying the D period dictating when the cell will divide.

Finally, it is important to keep in mind that the Cooper–Helmstetter model of the cell cycle only applies to E. coli. Other species have very different chromosome replication control programs, such as C. crescentus, where compartmentalization of daughter cells is necessary to license another round of chromosome replication [67]. However, diverse species all delayed division in response to PG biosynthesis inhibition [13], implying that the availability of PG precursors is intimately tied to division timing in all of these species. Additionally, the ‘adder’ growth pattern has been observed not just for E. coli, but also for many other kinds of bacteria [7,8,50]. Thus, it seems unlikely that the origin of the ‘adder’ pattern would be rooted in a chromosome replication program unique to E. coli, as some have suggested [55,59]. In contrast, accumulation of excess surface material across the cell cycle could be a universal feature of rod-shaped bacteria (Figure 6), making this an attractive model that could explain why extremely divergent species all exhibit similar ‘adder’ behaviors and responses to PG biosynthesis inhibition. Excitingly, other bacterial shapes, such as growing spheres, also decrease their SA/V during an individual cell cycle (because SA/V = 3/R for a sphere, as the cell radius increases SA/V goes down). This raises the possibility that other shapes could also accumulate excess material during the cell cycle, making our proposed model of division timing perhaps even more broadly applicable.

Concluding Remarks

We recently reported that a strikingly simple ‘relative rates’ model is able to quantitatively explain SA/V homeostasis in a wide range of bacterial species. This model is phenomenological and makes intuitive sense: if the current SA/V is not equal to the ratio of the surface and volume growth rates, cells alter their dimensions until the proper ratio is achieved. Many observations in the literature, where changes in PG biosynthesis or volume growth rate led to changes in cell size, can be understood in the context of this model. However, the model still lacks molecular detail. In the future, it will be essential to identify the molecular players that enable bacterial cells to change their dimensions and exquisitely conform to the predictions of the ‘relative rates’ model. We believe that the availability of PG precursors is the most likely way that cells could be able to sense whether they need to increase or decrease their SA/V. Future studies must identify whether precursor levels change in different physiological contexts and across the cell cycle, whether the mode of lateral insertion varies based on precursor availability, and whether accumulation of precursors plays a role in division timing (see Outstanding Questions). Although much is known about the players that help to set the width and length of cells, a unified theory of bacterial size and shape determination has been lacking; by treating SA/V as the key natural variable, we have uncovered a powerful new framework that might finally enable a comprehensive understanding of bacterial morphogenesis.

Outstanding Questions.

What are the molecular cues that tell cells to change SA/V when the current ratio does not match the relative rates of surface and volume growth? Does the availability of PG precursors play a role? Does turgor pressure play a role? To examine the role of PG precursors it will be important to directly measure precursor availability in different steady-state conditions and after physiological shifts.

Can the effects of genetic and pharmacological perturbations that modulate cell size or shape be predicted within the context of the ‘relative rates’ model?

In addition to changing SA/V, what feedback mechanisms exist to modulate the rates of volume and surface growth when these rates are not well matched? For instance, if more volume is being synthesized than surface, do cells have mechanisms to slow down volume growth, or speed up surface synthesis?

Does a linear trend in SA/V with growth rate explain the classic exponential growth law observation? If so, why does surface synthesis, or β, have a parabolic dependence on growth rate? Does the concentration of PG biosynthesis enzymes decrease linearly with growth rate? If so, does this trend, combined with substrate availability, give rise to the parabolic dependence?

Does PG precursor availability modulate cell width? If so, does the balance between MreB-directed growth and non-MreB-directed growth tune width, and how can PG precursors shift the balance between these two systems? What molecular changes in the PG network correspond to changes in cell width?

Does PG precursor availability modulate cell length? Do PG precursors accumulate over the course of the cell cycle? If so, which intermediates? Does one of these serve as a trigger of cell division? If so, what is the sensor? Is this division timing mechanism at play in typical steady-state conditions, and is it the source of the recently observed ‘adder’ phenomenon?

Highlights.

Many bacterial species exhibit SA/V homeostasis, changing their size and shape to achieve an SA/V that is set by the ratio of surface synthesis to volume synthesis in a given growth condition.

SA/V homeostasis arises because the rate of surface growth scales with cell volume, and evidence suggests that this scaling is likely due to the biosynthesis of new peptidoglycan (PG) in the cytoplasm setting the rate of surface growth.

Reports in the literature of changes in growth rate and/or PG biosynthesis rate leading to changes in size and shape can be explained in the context of this framework.

The classic exponential ‘growth law’ relationship between cell size and growth rate can be equally well explained as a linear relationship between SA/V and growth rate.

The concentration of PG precursors could be a molecular indicator of whether cells must increase or decrease cellular SA/V.