Computational Neuroanatomy of Baby Brains: A Review

Abstract

The first postnatal years are an exceptionally dynamic and critical period of structural, functional and connectivity development of the human brain. The increasing availability of non-invasive infant brain MR images provides unprecedented opportunities for accurate and reliable charting of dynamic early brain developmental trajectories in understanding normative and aberrant growth. However, infant brain MR images typically exhibit reduced tissue contrast (especially around 6 months of age), large within-tissue intensity variations, and regionally-heterogeneous, dynamic changes, in comparison with adult brain MR images. Consequently, the existing computational tools developed typically for adult brains are not suitable for infant brain MR image processing. To address these challenges, many infant-tailored computational methods have been proposed for computational neuroanatomy of infant brains. In this review paper, we provide a comprehensive review of the state-of-the-art computational methods for infant brain MRI processing and analysis, which have advanced our understanding of early postnatal brain development. We also summarize publically available infant-dedicated resources, including MRI datasets, computational tools, grand challenges, and brain atlases. Finally, we discuss the limitations in current research and suggest potential future research directions.

Graphical abstract

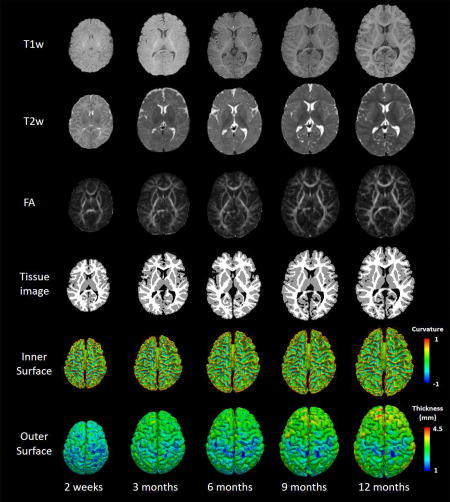
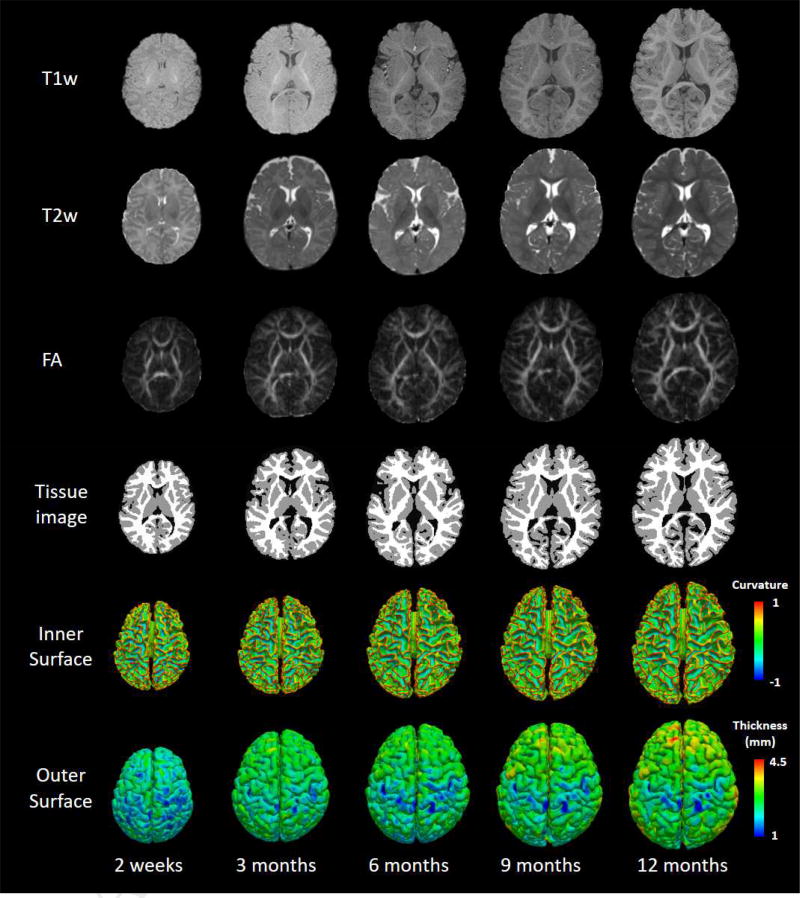
T1w, T2w, FA images, tissue segmentation results as well as the reconstructed inner and outer surfaces of a typically-developing infant, scanned longitudinally at 2 weeks, 3, 6, 9 and 12 months of age. Inner surfaces are color-coded with the maximum principal curvature, and outer surfaces are color-coded with cortical thickness.

1 Introduction

The first postnatal years are an exceptionally dynamic and critical period of structural, functional and connectivity development of the human brain. At term birth, although all primary and secondary cortical folds have been established, the average volume of the normal neonatal brain is only one third of that of the adult (Knickmeyer et al., 2008). During the first postnatal year, the brain volume doubles with regionally-heterogeneous growth patterns (Knickmeyer et al., 2008). Although the biological mechanisms of the early brain development remain unclear, complex underlying microstructural changes, e.g., myelination, increases in dendritic arborization, axonal elongation and thickening, synaptogenesis and glial proliferation, are typically considered as the main driving factors (Lyall et al., 2014). Increasing evidence suggests that many neurodevelopmental and psychiatric disorders are the consequence of abnormal brain development in this stage of rapid brain growth during infancy (Gilmore et al., 2010; Hazlett et al., 2005). For example, infants with autism, which affects >1.4% of children in the United States, demonstrate brain overgrowth associated with an increase in cortical surface area before 2 years of age (Hazlett et al., 2011). Identifying early biomarkers of neurodevelopmental and psychiatric disorders during infancy will allow designing targeted preemptive intervention strategies to improve prognosis or even prevent disorder onset.

The increasing availability of non-invasive infant brain multimodal MR images, e.g., T1-weighted (T1w), T2-weighted (T2w), diffusion-weighted (DW), and resting-state functional MR images, provides unprecedented opportunities for accurate and reliable charting of dynamic early brain developmental trajectories in understanding normative and aberrant growth. For example, the Baby Connectome Project (BCP) will acquire and release cross-sectional and longitudinal high-resolution multimodal MRI data from 500 typically-developing children from birth to 5 years of age (http://babyconnectomeproject.org). The Developing Human Connectome Project (dHCP) in the UK will release MRI data from 1500 subjects acquired from 20 to 44 weeks post-conceptional age (http://www.developingconnectome.org). These large-scale datasets will undoubtedly greatly increase our limited knowledge on normal early brain development, and provide important insights into the origins and abnormal developmental trajectories of neurodevelopmental disorders, such as autism, schizophrenia, bipolar disorder, and attention-deficit/hyperactivity disorder (ADHD).

However, infant brain MRI typically exhibits reduced tissue contrast (especially from 3 to 9 months of age), large within-tissue intensity variations, and regionally-heterogeneous dynamic image appearance and development, in comparison with adult brain MRI. In terms of white-gray matter contrast, infant brain T1w and T2w MR images exhibit three distinct phases, as shown in Fig. 1 (Paus et al., 2001): (1) the infantile phase (≤ 3 months), in which the gray matter shows a relatively higher signal intensity than the white matter in T1w images, and the tissue contrast in T2w images is better than in T1w images; (2) the isointense phase (5–9 months), in which the signal intensity of the white matter is increasing during the development due to the myelination and maturation process; in this phase, gray matter and white matter have the lowest signal differentiation in both T1w and T2w images; (3) the early adult-like phase (≥12 months), where the gray matter intensity is much lower than the white matter intensity in T1w images, largely similar to the tissue contrast pattern in adult T1w images. Hence, the existing computational tools typically developed for processing and analyzing adult brain MRI, e.g., SPM, FSL, BrainSuite, CIVET, FreeSurfer and HCP pipeline, often perform poorly on infant brain MRI.

Fig. 1.

T1w, T2w, FA images, tissue segmentation results (by LINKS, (Wang et al., 2015)) as well as the reconstructed inner and outer surfaces of a typically-developing infant, scanned longitudinally at 2 weeks, 3, 6, 9 and 12 months of age. Inner surfaces are color-coded with the maximum principal curvature, and outer surfaces are color-coded with cortical thickness.

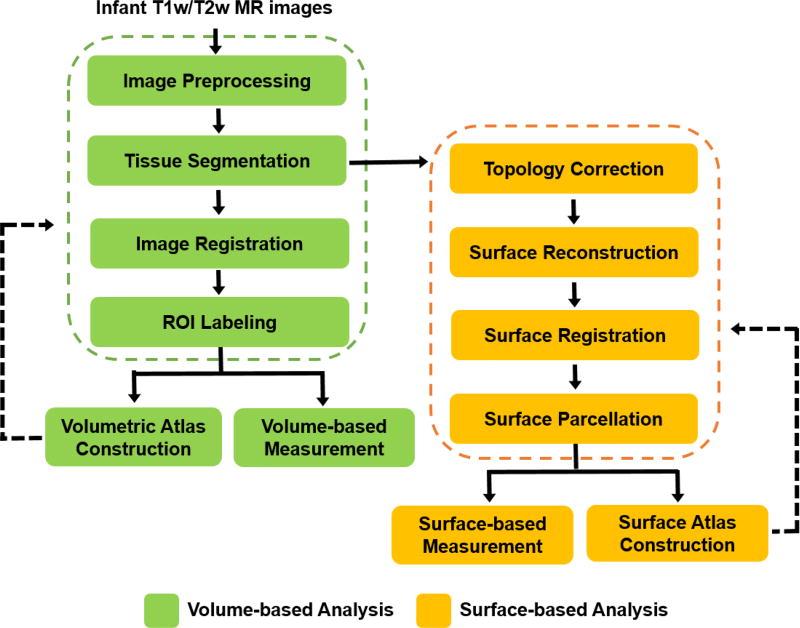
To address these challenging issues, many infant-tailored computational methods have been proposed for computational neuroanatomy of infant brains, and have led to many important discoveries on early postnatal brain development. This review article aims to provide a comprehensive review of the state-of-the-art computational methods dedicated for processing and analysis of infant brain structural T1w and T2w MR images. As illustrated in Fig. 2, for processing and analyzing structural T1w and T2w brain images, a computational pipeline typically consists of the following main steps: image preprocessing, tissue segmentation, image registration, regions of interest (ROIs) labeling, topology correction, surface reconstruction, surface registration, surface parcellation, volumetric/surface atlas construction, and measurement. In this review, we will discuss the challenges and the existing solutions for each of these major steps in infant brain studies, and also suggest future research directions. We will also list those publically available resources dedicated for advancing infant brain MRI studies, e.g., datasets, computational tools, grand challenges, and brain atlases. Note that the techniques for fetal brain MRI processing and analysis, which are different from processing infant brain MRI, is not the focus of this review and thus will not included in this review. But the respective techniques can be found in those fetus-dedicated review articles (Benkarim et al., 2017; Makropoulos et al., 2017a; Studholme, 2011).

Fig. 2.

Flowchart of a typical pipeline for analyzing T1w and T2w structural MR images. Note that, in infant studies, many steps need to be infant-specific.

2 Image Preprocessing

In brain MRI studies, image preprocessing is a fundamental step for subsequent image processing and analysis. This step usually includes motion correction, intensity inhomogeneity correction, and skull stripping, thus improving image quality and reducing undesired disturbance.

2.1 Motion Correction

Motion correction has been an active area of research within MRI community. Compared to adults, imaging infants is susceptible to motion, because it is difficult to expect infant subject to remain still during acquisition (Dean et al., 2014). Meanwhile, motion artifacts can manifest in the forms of ghosting, blurring, contrast changes or signal voids, which hampers accurate image processing, and thus often necessitate a rescan. To minimize motion-related artifacts, the most widely used strategy is to scan infants when they are asleep. However, infants are still prone to move or wake up. To date, advanced retrospective (Atkinson et al., 1999), prospective (Zaitsev et al., 2006), and hybrid (Aksoy et al., 2012) techniques have been developed for motion correction. Such techniques could be used in conjunction with the infant dedicated protocols to achieve high success rates with artifact-free images (Hughes et al., 2016). Recently, Cordero-Grande et al. (Cordero-Grande et al., 2018) proposed a method for reconstruction of multi-shot, multi-slice neonatal MRI to address the problem of rigid motion, leading to a remarkable improvement of image quality on 500+ neonates. Detailed reviews of motion correction techniques can be found in (Malamateniou et al., 2013; Zaitsev et al., 2015).

2.2 Intensity Inhomogeneity Correction

Intensity inhomogeneity refers to the smoothly varying signal intensities across an image, also referred to as radio-frequency coil non-uniformity, magnetic field inhomogeneity, etc. (Vovk et al., 2007). Intensity inhomogeneity could greatly decrease the performance of algorithms for infant MRI analysis, especially when algorithms assume intensity homogeneity within each tissue class. Therefore, correction of intensity inhomogeneity is important for accurate segmentation and registration of infant brain MRI. The widely used methods for intensity inhomogeneity correction for infant brain MRI are nonparametric nonuniform normalization (N3) algorithm (Sled et al., 1998) and its improved version, N4 (Tustison et al., 2010), despite they are not specifically designed for infants. Although most studies address intensity inhomogeneity at the pre-processing stage, some works incorporate intensity inhomogeneity correction into tissue segmentation techniques (Wang et al., 2011). Detailed reviews of intensity inhomogeneity correction techniques can be found in Belaroussi et al. (Belaroussi et al., 2006) and Vovk et al. (Vovk et al., 2007).

2.3 Skull Stripping

Background

Skull stripping, also known as brain extraction, aims to retain brain parenchyma and discard non-brain tissues, such as skull, scalp, and dura (Smith, 2002). Skull stripping has become a standard procedure to preprocess brain MR images and is important for subsequent image analysis. Accurate skull stripping is crucial, since incorrectly-removed brain tissues cannot be recovered in subsequent processing steps, and also unremoved non-brain tissues (especially the dura) could cause overestimation of the local brain volume or cortical thickness.

Challenges

Numerous skull stripping methods have been proposed over past years, while, most of them were validated only on adult brain MR images. In comparison, infant MR images are considerably more challenging for skull stripping, due to their low spatial resolution, dynamic changes of imaging intensity, brain size and shape. Hence, only a few methods have been developed for skull stripping of infant brain MR images.

Methods

Representative skull stripping methods developed for infant brain images can be categorized into deformable surface-based methods (Mahapatra, 2012) and learning-based methods (Serag et al., 2016; Shi et al., 2012a). In particular, Mahapatra et al. (Mahapatra, 2012) proposed a technique for skull stripping of the neonatal brain using the prior shape information within a graph cuts framework, with a validation on 20 neonates. Inclusion of the prior shape information obtained from a set of manually labeled training images facilitated accurate identification of brain and non-brain tissues. Thus, Shi et al. (Shi et al., 2012a) proposed a method named Learning Algorithm for Brain Extraction and Labeling (LABEL). The basic idea is to perform multiple complementary brain extractions for a given image by using a meta-algorithm including BET and BSE, where the parameters of each run of the meta-algorithm were effectively learned from the training data. Also, representative subjects were selected as exemplars and used to guide brain extraction of new subjects in different age groups. A level-set based fusion method was proposed to combine multiple brain extractions for obtaining the final extraction. This method has been extensively evaluated on 200+ infant subjects. Serag et al. (Serag et al., 2016) proposed a multi-atlas-based learning method for skull stripping. This method used a sparsity-based atlas selection strategy that required a very limited number of atlases ‘uniformly’ distributed in a low-dimensional data space, combined with a machine learning based label fusion technique, and has been validated on 50 newborns.

Future Directions

Due to the dynamic changes of imaging contrast in both T1w and T2w images, skull striping methods should adaptively choose the appropriate T1w or T2w image, or combine them together, to achieve the best performance. Recently, deep learning has achieved the state-of-the-art performance in many applications in neuroimaging. Using deep learning and its combination with existing methods could further improve the performance.

3 Image Segmentation and Registration

After image preprocessing in Section 2, brain tissue segmentation, registration, labeling and volumetric atlas construction can be performed. Tissue segmentation aims to segment the brain into different tissue types, such as white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF). Brain registration aims to establish inter-subject or intra-subject image correspondences. Brain ROI (region of interest) labeling is to partition the brain into anatomically or functionally meaningful regions, such as subcortical regions and cortical regions. Atlas construction aims to build an unbiased and population-based common space for brain analysis. Each of these 4 steps can help or guide each other to achieve more accurate results. For example, tissue segmentation results could be used for registration and atlas construction, and in turn the constructed atlas could be used to guide tissue segmentation and registration of new subjects. Each of these steps is reviewed in the following four sections.

3.1 Tissue Segmentation

Background

Accurate tissue segmentation of infant brain MR images into different regions, e.g., white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF), is a fundamental step for quantifying early brain development. A large amount of work has been dedicated to the segmentation of adult brain MRI, resulting in many successful software packages, e.g., FSL, SPM, FreeSurfer, BrainSuite, and CIVET.

Challenges

Segmentation tools developed for adult brains are not suitable for processing infant brains, due to the significant imaging appearance differences between infant and adult brain MRI as well as the dynamic contrast changes in infant brain MRI. To date, there is very limited publicly available software for infant brain MRI segmentation. In fact, segmentation of infant brain MRI is considerably more challenging than that of adult brain MRI due to the reduced tissue contrast (especially at around 6 months of age), severe partial volume effect, high image noise, strong motion effect, and dynamic white matter myelination. Actually, as shown in Fig. 1, there are three distinct phases in infant T1w and T2w MRI, i.e., the infantile phase (≤ 3 months), the isointense phase (5–9 months), and the early adult-like phase (≥12 months), with each phase having its distinct white-gray matter contrast pattern (Paus et al., 2001). As an illustration, the middle column of Fig. 1 shows examples of T1w and T2w images at around 6 months of age. It can be observed that the intensities of voxels in gray matter and white matter are in a similar range in both T1w and T2w images (especially around the cortical regions), resulting in the lowest image contrast and hence significant difficulty for tissue segmentation.

Methods

This section provides an overview of the representative infant brain MRI segmentation techniques in the literature, as also summarized in Table 1. According to the strategies used, we roughly divide the state-of-the-art segmentation methods into four categories: atlas-based, deformable-surface-based, learning-based, and hybrid approaches. The atlas-based approaches are further subdivided, based on the type of the atlases used, into population atlas based and subject-specific atlas based approaches. Similarly, learning-based approaches are subcategorized, based on the type of the features used, into hand-crafted features based approaches and deep learning based approaches. From Table 1, we can also see that the focus of infant brain segmentation has recently shifted from the infantile phase to the more challenging isointense phase. Algorithms have evolved from basic atlas-based label fusion methods to more advanced deep learning frameworks.

Table 1.

Representative infant brain segmentation algorithms in the literature.

Study	Dataset	Modality	Tissues segmented	Atlas/Features/ Architecture	Method
(a.1) Atlas based approaches – Population atlas based approaches
(Prastawa et al., 2005)	50 neonates	T1w, T2w	UWM, MWM, GM, CSF	Atlas built from 3 neonates	EM based framework for classification
(Xue et al., 2007a)	25 neonates	T2w	UWM, GM, CSF	Age-based templates from 27 to 45 gestational age	EM-MRF scheme
(Weisenfeld and Warfield, 2009)	13 training, 10 testing neonates	T1w, T2w	UWM, MWM, cGM, sGM, CSF	Atlas built from 15 newborn segmentations	Supervised classification, followed by iterative prototype editing
(a.2) Atlasbased approaches – Subject-specific atlas based approaches
(Shi et al., 2010a)	10 neonates	T2w	WM, GM, CSF	Atlas built from longitudinal scans	Probabilistic-atlas-based segmentation
(Shi et al., 2010b)	10 neonates	T2w	WM, GM, CSF	Atlas built by selection of similar exemplars	Multi-region-multi-reference framework
(Shi et al., 2011a)	10 neonates	T2w	WM, GM, CSF	Hybrid atlas built on subject-specific cortical structures, with population-based atlas	Use of phased array coil and creation of hybrid atlas
(Wang et al., 2014a)	32 infants at 6 months of age	T1w, T2w, FA	WM, GM, CSF	Subject-specific atlas built based on multi-modal sparse representation	Patch-based sparse representation of multi-modal images + anatomical/topological constraints
(b) Deformable surface based approaches
(Wang et al., 2011)	10 neonates	T2w	WM, GM, CSF	Population atlas from (Shi et al., 2011b)	Coupled level sets with incorporation of atlas, local intensity, and cortical thickness
(Wang et al., 2014b)	152 neonates	T2w	WM, GM, CSF	Subject-specific atlas built by sparse representation	Patch-driven level set method
(c.1) Learning based approaches – Hand-crafted features based approaches
(Anbeek et al., 2013)	7 training + 101 testing neonates	T1w, T2w	CB, MWM, UWM, BGT, BS, vCSF, eCSF, BGT	Intensity and spatial features	Supervised classification based on intensity and spatial values
(Wang et al., 2015)	10 training and 26, 22, 22, 23, and 26 testing subjects at 0-, 3-, 6-, 9-and 12-months, respectively	T1w, T2w, FA	WM, GM, CSF	3D Harr-like features extracted from T1w, T2w, FA, and also the intermediate WM, GM, and CSF probability maps	Learning-based multi-source integration framework (LINKS): Training a sequence of classifiers via random forest and auto-context model
(c.2) Learning based approaches – Deep learning based approaches
(Nie et al., 2016)	10 infants at 6 months of age	T1w, T2w, FA	WM, GM, CSF	3 convolutional layers + 2 deconvolutional layers	2D fully convolutional networks (FCN)
(Moeskops et al., 2016)	22 neonates	T2w	CB, MWM, UWM, BGT, BS, vCSF, eCSF, BGT	3 convolutional layers + 1 fully connected layer in a multi-scale fashion	2D Multi-scale CNN
(Nie et al., 2018)	11 infants at 6 months of age	T1w, T2w, FA	WM, GM, CSF	6 convolutional layers + 6 deconvolutional layers	3D multimodal FCN
(d) Hybrid approaches
(Gui et al., 2012)	30 neonates	T1w, T2w	CB, MWM, UWM, BGT, BS, CSF, eSF, BGT	Watershed + active contour model	Morphology-driven automatic segmentation
(Beare et al., 2016)	41 neonates	T2w	cGM, WM, sGM, CB, BS, CSF, amygdala, hippocampus	Unified segmentation with a population atlas, template adaptation and topological filtering	Morphological adaptation and unified segmentation

WM: white matter (WM=MWM+UWM); GM: gray matter (GM=cGM+sGM); CSF: cerebrospinal fluid (CSF=eCSF+vCSF); UWM: unmyelinated white matter; MWM: myelinated white matter, cGM: cortical gray matter; sGM: subcortical gray matter; eCSF: cerebrospinal fluid in the extracerebral space; vCSF: cerebrospinal fluid in the ventricles; BGT: basal ganglia and thalami; CB: cerebellum; BS: brainstem; BG: background.

3.1.1 Atlas based approaches

Most of the techniques for infant brain tissue segmentation rely on pre-segmented brain atlases (please refer to Section 3.4 for detailed introduction of atlases). The popularity of atlases stems from their widespread utility, as they can guide the segmentation process in areas of poor tissue contrast and help in distinguishing between tissues with similar intensities.

Population Atlas Based Approaches

An atlas can be generated from manual or automated segmentation of an individual image, or a population of images from different individuals. Population-based atlases provide a probabilistic estimate of each tissue at every voxel. This is essential for probabilistic segmentation approaches that require a prior probability model for each tissue label. For example, Prastawa et al. (Prastawa et al., 2005) generated an atlas by averaging three semi-automatically segmented images and then integrated it into the expectation-maximization (EM) scheme for tissue classification. Similarly, Xue et al. (Xue et al., 2007a) constructed multiple age-specific atlases and performed the EM algorithm for tissue segmentation, in conjunction with the Markov random field (MRF). Song et al. (Song et al., 2007) built a population-based atlas with diffeomorphic flow based registration. Weisenfeld et al. (Weisenfeld et al., 2006) built a population-based atlas from 20 preterm infants scanned at 42 GA weeks, which were manually segmented by an expert based on initially automatic segmentations produced by (Warfield et al., 2000). Later, Weisenfeld and Warfield (Weisenfeld and Warfield, 2009) also employed an atlas of spatial priors constructed from 15 newborns. Other methods directly employed those publicly available infant atlases, e.g., UNC Infant 0–1–2 atlas (Shi et al., 2011b), 4D neonatal atlas (Kuklisova-Murgasova et al., 2011), and Melbourne Children’s Regional Infant Brain (M-CRIB) atlas (Alexander et al., 2017). For example, Wang et al. (Wang et al., 2012b) proposed a neonatal segmentation algorithm based on the segmentation tool from SPM and the 4D neonatal atlas (Kuklisova-Murgasova et al., 2011).

Subject-specific Atlas Based Approaches

The performance of population atlas-based approaches highly depends on the quality of the atlas used and its spatial alignment with the to-be-segmented images. Moreover, a pre-defined atlas may not be able to account for the considerable anatomical variability among subjects. As proposed in (Aljabar et al., 2009; Shi et al., 2010a), a subject-specific atlas, which can be constructed from images that are similar to the to-be-segmented image, leads to more accurate segmentation results than the population-based atlases. Thus, Shi et al. (Shi et al., 2010a) proposed a novel approach for neonatal brain segmentation by utilizing an atlas built from the longitudinal follow-up image of the same subject (i.e., the image scanned at one or two years of age) to guide neonatal image segmentation. Since many neonatal subjects do not have longitudinal follow-up scans, Shi et al. later proposed a multi-region-multi-reference framework (Shi et al., 2010b) to generate a similar atlas for the to-be-segmented image. Wang et al. (Wang et al., 2014b) estimated a subject-specific atlas by using patch-based sparse representation. Nevertheless, these approaches still do not eliminate the use of atlases, although not population-based atlases.

3.1.2 Deformable surface based approaches

Most of the above-mentioned atlas are based on voxel-wise approaches. Consequently, prior geometric/anatomical information is not fully explored, e.g., cortical thickness, which can help constrain the relative locations of different tissue boundaries. To effectively explore this information, deformable surface based approaches provide an alternative way for infant brain segmentation. A representative work was proposed in (Wang et al., 2011), in which cortical thickness was easily incorporated into a coupled level sets framework. To provide a robust initialization of the zero level set, a population-based atlas or a subject-specific atlas was usually employed. For example, in (Wang et al., 2014b), a subject-specific atlas estimated by a patch-based sparse representation was used as an initialization for level set evolution.

3.1.3 Learning based approaches

It is worth noting that atlas-based approaches and deformable surface-based approaches mainly focus on the infantile phase (neonatal) brain. They typically donot work well on the isointense infant images, due to the extremely low image contrast in both T1w and T2w images, as shown in Fig. 1. To address this issue, learning-based approaches have been proposed and achieved better performance on the challenging isointense images. According to features used, we divided learning-based approaches into hand-crafted features based approaches and deep learning based approaches.

Hand-crafted Features Based Approaches

Anbeek et al. (Anbeek et al., 2013) proposed a neonatal brain segmentation method based on supervised classification. Each voxel was represented using its intensity and spatial features. Based on these features, each voxel was assigned to one of eight tissue classes using K-nearest neighbor classifier. Wang et al. (Wang et al., 2015) proposed a learning-based multi-source integration framework for segmentation of infant brain images (shorted as LINKS). They employed the random forest technique (Breiman, 2001) to train a classifier to effectively integrate 3D Haar-like features from multi-source images for tissue segmentation. Here, the multi-source images include initially only the multi-modal (T1w, T2w and FA) images and later also the iteratively estimated and refined tissue probability maps of WM, GM, and CSF. They evaluated their method on infant brain MR images at all three phases during the first year of age.

Deep Learning Based Approaches

In recent years, deep learning (LeCun et al., 2015) has achieved great success in many fields. Instead of designing hand-crafted features, deep learning can automatically learn effective feature hierarchies from the infant brain MR images. Zhang et al. (Zhang et al., 2015) proposed deep convolutional neural networks (CNNs) to segment isointense phase MR images, in which a hierarchy of increasingly complex features from MR images were learned. Moeskops et al. (Moeskops et al., 2016) proposed a CNN-based method for automatic segmentation of neonatal brain MR images. To well capture brain structural details and enforce spatial consistency, the proposed network used multiple patch sizes and multiple convolution kernel sizes to acquire multi-scale information of each voxel. Nie et al. (Nie et al., 2016) used fully convolutional networks (FCNs) for segmentation of isointense phase images, and later further proposed a 3D fully convolutional network (3D–FCN) trained in an end-to-end and voxel-to-voxel fashion for segmentation of isointense phase images (Nie et al., 2018).

3.1.4 Hybrid approaches

Many methods combined or integrated different strategies into a hybrid segmentation framework. For example, Beare et al. (Beare et al., 2016) utilized a combination of unified segmentation, a population-based neonatal atlas (Kuklisova-Murgasova et al., 2011), morphological segmentation tools and topological filtering, to segment neonatal images. Gui et al. (Gui et al., 2012) proposed an atlas-free neonatal segmentation method based on the high-level brain morphology knowledge, integrating relative tissue location, connectivity and structure. They employed some established segmentation methods, such as the marker-based watershed and region-based active contours, and then validated on neonatal images.

Future Directions

Although many algorithms have been proposed and achieved reasonable performances, there are still many open directions to explore. First, most infant brain images used in the previous studies are from normal subjects without visible pathology or severe imaging artifacts. However, in clinical routine, scans with artifacts, especially motion artifacts, as well as scans with pathology are very common. Second, myelinated white matter (MWM) was usually poorly segmented, compared to other tissues, due to the small volume of myelin in the infant brain and the extremely low contrast with the surrounding tissues in isointense phase. Third, most of previous methods ignore brain anatomical/topological information during segmentation, resulting in many geometric/topological errors, which will be discussed in Section 4. Fourth, ground-truth annotations, usually from manual segmentations, are critically important in developing algorithms, especially for the learning-based approaches. However, these resources are highly limited.

3.2 Image Registration

Background

Image registration aims to establish accurate inter-subject and intra-subject brain anatomical/functional correspondences. Image registration techniques are the cornerstone of many applications, such as segmentation (Section 3.1), ROI labeling (Section 3.3) and volumetric atlas constructions (Section 3.4). Herein, we mainly focus on the techniques for deformable/nonlinear image registration, necessary for both intra-subject and inter-subject comparisons in infants. For the affine or linear registration, tools developed for adults can be directly adopted.

Challenges

To date, a number of deformable registration methods have been developed (Klein et al., 2009; Sotiras et al., 2013), yet most of them are proposed for registering adult brain images and are not directly applicable to infant brain images. This is because the infant brain undergoes dramatic changes in imaging appearance, brain size, shape, and folding degree in region-specific manners as shown in Fig. 1. Therefore, it is very challenging to register two infant brain images with a large age gap, especially across different subjects.

Methods

To tackle the challenges in infant image registration, recent studies fully exploited the prior knowledge, such as the previously registered longitudinal infant images, to guide registration of new infant subject images. In general, the representative methods fall into three categories: intensity-based methods (Wang et al., 2014c; Wei et al., 2017; Wu et al., 2015), segmentation-based methods (Ha et al., 2011; Shi et al., 2010a; Wang et al., 2012a; Xue et al., 2007b), and hybrid methods (Dong et al., 2017; Xue et al., 2006), as listed in Table 2.

Table 2.

Representative registration methods for infant brain images.

Study	Dataset	Modality	Applied infant ages	Method
(a) Intensity-based approaches
(Wei et al., 2017)	24 infants (leave-two-out validation)	T1w or T2w	2 W to 12 M, 3 M to 12 M, 6 M to 12 M, 9 M to 12 M	Learning based method using random forest and auto-context
(Wang et al., 2014c)	9 infants (leave-one-out validation)	T1w or T2w	2 W to 6 M, 6 M to 12 M	Sparse learning based method
(Wu et al., 2015)	24 infants (leave-one-out validation)	T1w or T2w	2 W to 12 M, 3 M to 12 M, 6 M to 12 M, 9 M to 12 M	Longitudinal-image-guided correspondence detection
(b) Segmentation-based approaches
(Wang et al., 2012a)	28 infants	T1w, T2w, FA	2 W, 3 M, 6 M, 9 M, 12 M	Tissue maps based method
(Shi et al., 2010a)	10 infants (leave-one-out validation)	T1w and T2w	Neonate, 1 Y, 2 Y	Tissue maps based method
(Ha et al., 2011)	10 infants	T1w	Neonate to 2 Y	Tissue maps and geometric descriptors based method
(c) Hybrid approaches
(Dong et al., 2017)	10 infants (leave-two -out validation)	T1w and T2w	2 W to 12 M, 3 M to 12 M, 6 M to 12 M, 2 W to3 M, 2 W to 6 M, 3 M to 6 M	Joint segmentation and registration

(W: weeks; M: months; Y: years; GA: gestational age)

Intensity-based Methods

Intensity-based registration methods include learning-based methods and modeling-based methods. Learning-based methods can be further classified into two subcategories: supervised learning based methods, and sparse representation learning based methods. The supervised learning based methods aim to learn a complex mapping from an intensity image to its corresponding deformation field to a given reference image. In the training stage, machine learning techniques, such as random forest regression model and auto-context model (Wei et al., 2017), were applied to learn an appearance-to-displacement model and an appearance-to-appearance model in a patch-wise manner. The learned models were used to predict the deformation pathways as well as alleviate the appearance differences between infant MR images with a large age gap. In the testing stage, the learned models can be used to predict a deformation field and appearance change for the new infant subject image. Following the prediction, the conventional deformable registration methods, such as diffeomorphic demons (Vercauteren et al., 2009), can be further used to refine the image registration. On the contrary, sparse representation learning based methods can directly achieve good registration performance without using a registration refinement. For example, Wang et al. proposed a sparsity learning based method to detect spatio-temporal correspondences within the to-be-registered subjects with the help of a set of intermediate sequences with established longitudinal correspondences (Wang et al., 2014c). Wu et al. further improved the registration performance by using a hierarchical and symmetric registration strategy to iteratively increase the key points in the images and to symmetrically deform the two infant images towards their common space (Wu et al., 2015).

Segmentation-based Methods

Different from intensity-based methods, segmentation-based registration methods establish more accurate image correspondences using morphological features extracted from segmented images (Shi et al., 2010a; Wang et al., 2012a). These segmented images can be obtained by using the methods mentioned in Section 3.1. In addition to using the segmented images, Ha et al. proposed a method by incorporating both tissue probability maps and surface anatomical descriptors for longitudinal infant image registration (Ha et al., 2011).

Hybrid Methods

The last category above is the hybrid registration methods. On one hand, image registration can benefit from the segmentation, where geometric features can be extracted to help identify image correspondences. On the other hand, the refined image registration results can bring more useful information leading to better tissue maps for guiding the segmentation process. Inspired by this, Dong et al. proposed a novel joint segmentation and registration method for infant brain images by using spatiotemporal trajectories learned from a large number of training subjects with complete longitudinal data (Dong et al., 2017). By using a sparse learning multi-atlas based label fusion method, coupled with a level-set segmentation approach, the initial image correspondences can be established by registering segmented images. Then, with spatial correspondences, segmentation accuracy of the new infant image can be further improved by incorporating additional label fusion priors from the reference time domain. Thus, through iterative segmentation and registration steps, both segmentation and registration performances can be progressively improved.

Future Directions

Future research should still focus on improving both registration performance and computational efficiency. Considering the power of deep learning, one may employ deep learning techniques to learn a mapping model between infant brain image and its predicted deformation field as well as its predicted image appearance changes.

3.3 Brain ROI Labeling

Background

Brain ROI labeling aims to partition brain image into anatomically/functionally meaningful regions. These labeled regions provide the basis for many applications, such as quantitative measurement of regional development and serving as nodes for studying structural and functional networks. There are two major ways to label brain ROIs. One is to directly label volumetric images. The other one is to label the reconstructed cortical surfaces. In this section, we focus on the volumetric ROI labeling, while detailing cortical surface parcellation in Section 4.4.

Challenges

Existing methods for brain image labeling typically leverage multi-atlases with manul labels. For infant brain image labeling, there are three main challenges: 1) Infant-dedicated multi-atlases are scarce; 2) It is difficult to establish accurate image correspondences between the to-be-labeled image and multi-atlases; 3) ROI boundaries in the infant brain are typically not very clear.

Methods

Although many approaches have been proposed for labeling brain ROIs, very few works were dedicated to infant brains. Gousias et al. (Gousias et al., 2008) labeled 2-year-old brain images, by propagating the manually labeled ROIs from 30 normal adult brains, using the non-rigid registration and majority voting strategy. Gousias et al. further explored the term-born and preterm infant brain ROI labeling (Gousias et al., 2012). In particular, they defined a labeling protocol to manually label the preterm brain into 50 ROIs based on the macro-anatomical landmarks from both T1w and T2w images, and applied to 15 preterm subjects and 5 term subjects using label fusion. Later, they generated an atlas named ALBERT, consisting of the voxel-wise manual labeling template for each subject (Gousias et al., 2012). In their following works (Gousias et al., 2013), the ROI labels on the atlas were propagated onto individual subjects based on the multi-atlas registration and label fusion. In another work (Makropoulos et al., 2014), an Expectation-Maximization (EM) based labeling fusion strategy was adopted for propagating the ALBERT atlas labels onto the target image. Blesa et al. (Blesa et al., 2016) used the intermediate registration strategy to build the Edinburgh Neonatal Atlas (ENA33), which consists of 107 ROIs propagated from the adult brain. Alexander et al. (Alexander et al., 2017) built another neonatal cortical and subcortical atlas with 100 brain ROIs, which includes the popular FreeSurfer Desikan cortical parcellation scheme (Desikan et al., 2006) and subcortical regions.

Apart from labeling the whole brain, some studies just focused on the labeling of particular regions, for example, the hippocampus. Guo et al. used a multi-atlas registration based approach that integrated multimodal information of both T1w and T2w images (Guo et al., 2014). The hierarchical multi-set kernel canonical correlation analysis is used to obtain common feature representations for multi-modal data. These features are then used for sparse patch-based label fusion to propagate the hippocampus labels on atlases to the target images. Dong et al. (Dong et al., 2015) proposed a multi-atlas multi-modal label fusion method to label hippocampus at various ages from neonates to 1-year-old infants. A hypergraph was employed to leverage the label integration from both T1w and T2w multi-atlases. In a later sequential study, Guo et al. (Guo et al., 2016) further considered the longitudinal consistency by introducing cross-time point edges into the hypergraph. Table 3 summarizes the representative works on infant brain ROI labeling.

Table 3.

Representative works for infant brain ROI labeling.

Study	Dataset	Modality	ROIs from adult?	ROI NO.	Method
(a) Whole brain labeling
(Gousias et al., 2008)	33 infants at 2 Y	T1w	Yes	83	Multi-atlas + majority voting
(Gousias et al., 2010)	13 infants at 1 Y	T1w	Yes	83	Multi-atlas + majority voting
(Gousias et al., 2012)	15 preterm and 5 term infants	T1w, T2w	No	50	Manual delineation
(Gousias et al., 2013)		T1w, T2w	No	50	Multi-atlas + majority voting
(Makropoulos et al., 2014)		T1w, T2w	No	50	Multi-atlas + EM based labeling fusion
(Blesa et al., 2016)	33 neonates	T1w, T2w	Yes	107	Atlas + intermediate time points registration
(Alexander et al., 2017)	10 neonates	T1w, T2w	Yes	100	Manual delineation
(b) Specific ROI labeling
(Guo et al., 2014)	10 infants, each at 1, 3, 6, 9 M	T1w, T2w	No	hippoca mpus	Multi-atlas + multi-modal features based label fusion
(Dong et al., 2015)	10 infants, each at 1, 3, 6, 9, 12 M	T1w, T2w	No	hippoca mpus	Multi-atlas multi-modal + hypergraph based label fusion
(Guo et al., 2016)	10 infants, each at 1, 3, 6, 9, 12 M	T1w	No	hippoca mpus	Multi-atlas + spatial-temporal hypergraph based label fusion

(M: months; Y: years)

Future Directions

Future developments might include: 1) developing advanced learning-based methods for labeling; 2) creating more infant-specific labeling protocols and multi-atlases; 3) developing methods for temporally-consistent labeling of longitudinal infant images.

3.4 Volumetric Atlas Construction

Background

A brain atlas incorporates prior knowledge of voxel characteristics for neuroimaging studies. An atlas can be constructed by a single subject or a population of subjects. A typical population-based atlas usually includes an intensity model (also called template) that defines a spatial coordinate system, and additional features such as tissue probability maps and ROIs. Most atlases were developed using adult subjects, while infant-dedicated atlases are few. In fact, registration of infant images to adult atlases results in poor alignment, due to considerable differences between infant brains and adult brains.

Challenges

The main challenges in population-based atlas building are caused by inaccurate inter-subject registration due to complex cortical folds and poor image contrast, especially in the isointense phase. Hence, the constructed infant atlases are typically blur and fuzzy in image appearance, especially in the cortical regions with large inter-subject variability of cortical folding.

Methods

A population-based atlas can be generated from a population of subjects by registering individual images into a common space and then averaging them to get a mean template. Kazemi et al. proposed a neonatal atlas by a normalization process including an affine registration followed by a nonlinear registration with 7 individual images to represent their mean intensity and shape (Kazemi et al., 2007). Oishi et al. constructed a population-averaged atlas from 25 neonates through a multi-step alignment process with linear and nonlinear registrations (Oishi et al., 2011). Considering that infant images have low spatial resolution and insufficient tissue contrast, Shi et al. proposed to first segment the infant images with dedicated algorithms, and then register the segmented images (Shi et al., 2011b). In registration, as selecting one individual as a reference might hamper generalizability and induce bias, groupwise registration is considered as a better way, where no reference image is selected and all images are registered together to a hidden common space (Bhatia et al., 2007; Wu et al., 2011). As certain blurriness is always observed from the group averaged averaging, some works enhanced the sharpness of constructed atlas using sparse representation in intensity domain (Shi et al., 2014) and spatial-frequency domain (Zhang et al., 2016b).

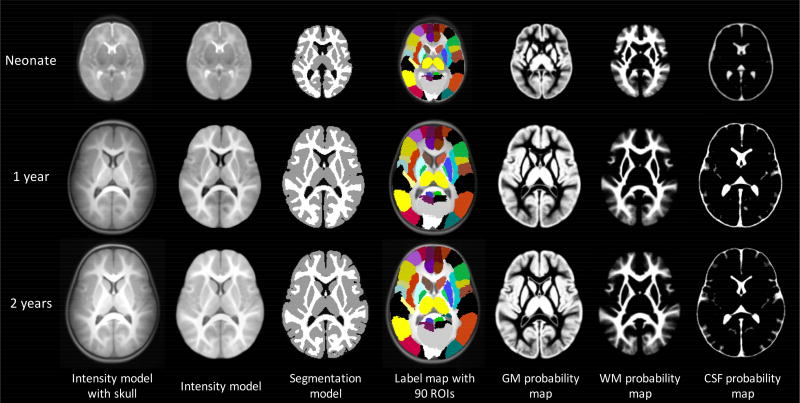
Due to the nature of the rapid development of infant brains, estimating age-specific infant brain atlases would be highly needed. For example, Kuklisova-Murgasova et al. proposed a 4D neonatal atlas covering the ages between 29 and 44 gestational weeks from 142 premature born neonates (Kuklisova-Murgasova et al., 2011). Through affine registration and a kernel-based regression method, age-specific templates and tissue probability maps were produced for a given age. Serag et al. further improved this 4D atlas by employing a more sophisticated nonlinear registration method (Serag et al., 2012a). Shi et al. proposed atlases for neonates, 1-year-olds and 2-year-olds, based on 95 subjects with longitudinal images (Shi et al., 2011b) (Fig. 3). Zhang et al. presented a 4D infant atlas covering 5 time-points from birth to 1 year of age with an interval of 3 months from 35 longitudinally scanned subjects, by using group-wise registration, patch-based atlas construction, and spatial-temporal consistency constraint (Zhang et al., 2016a).

Fig. 3.

An example of age-specific atlases for neonate, 1 year and 2 years with multiple components from (Shi et al., 201 1b).

The obtained average template, serving as a major component of the atlas, is widely used for spatial normalization of brain images. Furthermore, other maps with voxel-wise properties, such as tissue probabilities and ROI parcellation, can be transferred to the same coordinate system using the estimated deformation fields between individual intensity image and the average template. Beside ROIs defined by brain structures, functional connectivity based parcellation were also proposed (Shi et al., 2017).

Future Directions

Future developments might include improving the atlas sharpness with better registration approaches, using larger sample size, using longitudinal data densely covering a larger developmental period, and integrating multiple image modalities.

4 Cortical Surface Based Analysis

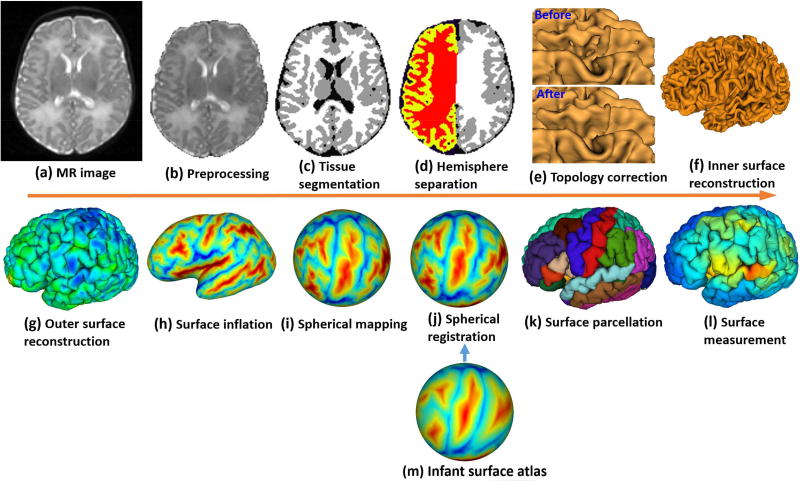
Based on the brain tissue segmentation results in Section 3, cortical surface-based analysis can be performed, which plays a central role in mapping brain structure, function and connectivity. Cortical surface-based analysis is advantageous over volume-based analysis by 1) respecting the topological properties of the cortex, 2) facilitating alignment, analysis, and visualization of the highly-folded cortical regions, and 3) precisely measuring multiple biologically-distinct cortical properties, e.g., cortical thickness, surface area, cortical folding, myelin content, and cortical diffusivity. Hence, cortical surface-based analysis is well suited to capture the dynamic and complex neurobiological changes of the cortex during early brain development. As shown in Fig. 2 and Fig. 4, typical pipelines for cortical surface-based analysis include topology correction, surface reconstruction, surface registration, surface parcellation, and surface measurement. This section provides a comprehensive review of representative computational methods for cortical surface-based analysis of the infant brain. Of note, compared to the abundant works on infant brain segmentation, infant-dedicated methods for cortical surface-based analysis are still very limited. As an alternative preliminary solution to the scarcity of such methods, many tools developed for examining the adult brain were adopted or modified to some extent to study the infant brain.

Fig. 4.

A typical computational pipeline for cortical surface-based analysis of infant brains.

4.1 Topology Correction

Background

Geometrically, the cortical surface of each hemisphere is topologically equivalent to a sphere, when closing the midline hemispheric connections. However, due to the highly-folded, thin cortex and low neuroimaging resolution, topological defects are inevitably present in tissue segmentation results. Even a subtle error in tissue segmentation could lead to a large topological defect, thus bringing large errors to the surface-based analysis. Therefore, topology correction is an important step for cortical surface-based analysis (Fig. 4(e)).

Challenges

Topological defects in infant brains are more prevalent and complicated, compared to adult brains, due to more segmentation errors in infant brains. Hence, directly applying topology correction methods developed for adult brains to infant brains typically leads to many anatomically-incorrect regions. Such errors are largely generated by confusing two different topologies, i.e., holes and handles (bridges across sulcal banks), which are typically hard to distinguish when solely relying on geometric information. Typically, holes incorrectly perforate the cortical surface, while handles erroneously bridge the geodesically nonadjacent regions. Cortical surface correction methods generally focus on two topological operations: either filling a “hole” or breaking a “handle”, thus fixing all topology defects and preserving the anatomical structures of the cortex.

Methods

Topology correction involves two sequential tasks, i.e., (1) localizing topologically defected regions, and (2) correcting these regions. Representative topology correction methods, which have been applied to infant studies, can be roughly classified into four categories (as summerized in Table 4): a) graph-based methods (Han et al., 2002; Shattuck and Leahy, 2001), b) surface mapping methods (Fischl et al., 2001; Segonne et al., 2007), c) topology-preserving deformation methods (Bazin and Pham, 2007; Han et al., 2003), and d) learning-based infant-specific method (Hao et al., 2016). Each category is briefly discussed in the following text.

Table 4.

Representative methods applied to infant cortical topology correction.

Study	Localizing defects	Correcting defects	Infant- dedicated	Method
(Shattuck and Leahy, 2001; Han et al., 2002)	Identifying circles in the graph of WM volume	Changing voxels in WM volume, based on rules	No	Graph-based
(Fischl et al., 2001; Segonne et al., 2007)	Detecting overlapping triangles of WM surface mapped on sphere	Re-tessellating of triangles	No	Surface mapping based
(Bazin and Pham, 2007; Han et al., 2003)	Detecting non-simple/critical points in topology	Preserving the topology of a deformable surface with a spherical topology	No	Topology-preserving deformation based
(Hao et al., 2016)	Difference of the WM volume before and after topology-preserving deformation	Multi-atlas based sparse representation	Yes	Learning-based

(WM: white matter)

Graph-based Methods

These methods typically convert a white matter (WM) volume into a graph, in which any circle indicates a topological defect. The circles can be removed by either changing the foreground voxels (WM voxels) into background (i.e., breaking a handle) or changing the background voxels into foreground (i.e., filling a hole), depending on the operation requiring minimal changes in the volume (Shattuck and Leahy, 2001) or constructing a maximum cycle-free sub-graph (Han et al., 2002). As many topological defects are complex in infant brains, this strategy may erroneously treat holes as handles, or vise versa, leading to anatomically less accurate results.

Surface Mapping Methods

These methods leverage spherical surface mapping to identify and remove topological defects (Fischl et al., 2001; Segonne et al., 2007). Specifically, first, the initially tessellated surface mesh of WM is mapped onto a spherical surface. The locations of topological defects on the mapped spherical surface have overlaps or self-intersections of triangular meshes. Topological defects can be corrected by re-tessellating their corresponding local meshes. For example, in (Fischl et al., 2001) a greedy-strategy is used to sort the intersected edges and meticulously add them back. In (Segonne et al., 2007), a set of non-separating loops are selected using a Bayesian framework for opening and sealing the surface. These methods are computationally expensive due to the spherical mapping, especially for large topological defects.

Topology-preserving Deformation Methods

These methods deform a surface with a spherical topology towards the WM surface, while preserving its initial topology by detecting cirtical points in topology (Bazin and Pham, 2007; Han et al., 2003). As the external forces typically rely on the image intensity, they may not work well for infant brain images, due to their dynamic, regionally-heterogeneous image intensity. However, as suggested in (Hao et al., 2016), if relying on the segmented image, such methods can properly fill all the holes when shrinking the initial surface to wrap the WM volume. However, all “handle” defects are erroneously treated as “hole” defects and thus are incorrectly filled.

Learning-based Method

To effectively distinguish handles from holes, a learning-based method, which does not rely on any ad hoc rules, was proposed to correct topological defects for infant cortical surfaces (Hao et al., 2016). To locate topologically defected regions, a topology-preserving level set method is leveraged. Specifically, a level set function with a spherical topology is first initialized by a large ellipsoid containing all WM voxels, and then gradually shrinks towards the WM surface, while preserving its initial topology. Next, a comparison between the converged WM volume and the original WM volume is performed to localize all topologically defected regions. To fix each topological defect, the correction scheme is learned from a number of well-defined segmentations that have been manually edited by experts. A region-specific dictionary is built for each defected region using the corresponding regions of these aligned reference images. Finally, the correct structure is inferred from the dictionary using a sparse representation method. For large topological defects that typically cannot be fully corrected using one-shot sparse representation, the above process can be iterated to gradually refine the results.

Future Directions

Although these methods can remove many topological errors, their performance is still less promising for the regions with large segmentation and topological errors, such as in the occipital cortex, frontal pole, and medial temporal cortex. More advanced methods, especially those based on machine learning, are highly desired.

4.2 Cortical Surface Reconstruction

Background

After tissue segmentation and topology correction, cortical surfaces can be reconstructed, which play a vital role in studying structure, function and connectivity of the human brain (Dale et al., 1999). Cortical surface reconstruction can usually be divided into two sub-problems: reconstruction of the inner surface (the interface between white matter and gray matter), and reconstruction of the outer/pial surface (the interface between gray matter and cerebrospinal fluid). The central/middle surface, which lies in the geometric middle layer of the cortex, is also often reconstructed for a more balanced representation of the cortical geometry.

Challenges

There are a few challenges that need to be paid attention to, when reconstructing infant cortical surfaces. First, due to the severe partial volume effects in infant MRI, accurate reconstruction of the outer cortical surface in deep narrow sulcal regions for infant brains is more challenging than for adult brains. This is because in deep sulci the opposing sulcal banks are often closer than the MRI resolution and the cerebrospinal fluid can hardly be seen. Second, because of the changing image contrast during the first year, low image resolution, severe partial volume effects, and the possible errors involved in the image processing, the reconstructed cortical surfaces of the same subject may be not longitudinally consistent, leading to inaccurate measurement of the longitudinal development of infant brains.

Methods

Existing approaches reconstruct cortical surfaces using a common framework, which is first to reconstruct the inner cortical surface (Fig. 4 (f)) and then to deform it into the central/outer cortical surface (Fig. 4 (g)). This common framework works for both adult and infant cortical surface reconstruction. In what follows, we briefly introduce this common framework, then several infant-specific methods will be discussed (as summarized in Table 5).

Table 5.

Representative methods for infant cortical surface reconstruction.

Study	Initialization	External forces	Internal forces	Self- intersection	Output Surfaces	Applied infant ages
(Leroy et al., 2011)	Coupled surfaces: brain bounding box and a surface in WM volume	Based on intensity image	Based on Ising model	N/A	Inner	1–4 M
(Li et al., 2014a)	Surface of topology-corrected WM volume	Based on tissue image	Based on Taubin smoothing filter	Explicitly detect intersecting triangles	Inner, middle, outer	1–24 M
(Kim et al., 2016b)	Genus-0 surface enclosing WM volume	Based on tissue image	Based on stretch and bending energy	Imposing self-proximity term	Inner, middle, outer	Neonates
(Makropoulos et al., 2017b)	Genus-0 surface enclosing WM volume	Based on tissue image and intensity image	Based on curvature	Explicitly detect intersecting triangles	Inner, middle, outer	Neonates

(WM: white matter; M: months)

• Common Framework

The most common framework for cortical surface reconstruction is to first reconstruct the inner surface based on the white matter segmentation, then to deform the inner surface outwardly to obtain the central or outer surface. Under this common framework, each method may use a different strategy to implement each step of cortical surface reconstruction. The methods can vary in the following important aspects: (a) surface initialization, (b) surface evolution, (c) deep sulci processing. Each aspect is briefly discussed as follows.

• Surface Initialization

There are mainly two surface initialization methods. The first one is to use the surface of the white matter volume following topology correction for initialization. The second one is to use the surface of a sphere/ellipsoid shape enclosing the white matter without topology correction for initialization. If the initial surface is an implicit surface (e.g., level set), then it is first deformed then tessellated. In contrast, if an explicit surface is used, it is first tessellated then deformed. Typical tessellation methods include Marching Cubes algorithm (Lorensen and Cline, 1987) and its variances, and the method in (Dale et al., 1999).

• Surface Evolution

The deformation of the initialized surface can either be driven by the explicitly defined forces or implicitly achieved by minimizing an energy function. Either ways, the deformable model should always include two important terms: a data fitting term and a smoothness (regularization) term. The data fitting term provides the external force to push the surface moving towards the desired location. It can be modeled either based on the intensity image (Dale et al., 1999) or the tissue segmented image (Han et al., 2004; Kim et al., 2005; Li et al., 2012), or both (Makropoulos et al., 2017b). The smoothness term provides the internal force to keep the surface tight and spatially smooth, while respecting the geometry of highly-convoluted cortical folding. The smoothness term can be based on local quadratic patch modeling (Dale et al., 1999), or curvature (Makropoulos et al., 2017b), or stretch and bending energy (Kim et al., 2005; MacDonald et al., 2000), or Taubin smoothing filter (Li et al., 2012). Another important component is the prevention of surface self-intersection. For implicit surface evolution, such intersections can be avoided by using topology-preserving level set algorithm (Han et al., 2004), while for explicit surface evolution, intersections can be avoided by introducing intersection prohibition terms in the energy function (MacDonald et al., 2000), or by explicitly detecting the potential intersecting triangles caused by evolution (Dale et al., 1999; Li et al., 2012).

• Deep Sulci Processing

Due to the severe partial volume effect, the CSF between the deep and narrow sulcal banks typically cannot be captured in MR imaging, giving no hint to correctly reconstruct the outer cortical surface. In (Dale et al., 1999; Makropoulos et al., 2017b), for the deep sulci, the opposing sulcal banks deformed towards each other until they are close enough but without self-intersection. In (Han et al., 2004; Li et al., 2014a; Li et al., 2012; Mangin et al., 1995), the deep sulci are recovered using an anatomically consistent enhancement method. Specifically, in the sulcal regions a central skeleton is built in the middle of two back-to-back sulcal banks based on the weighted geodesic distance measurement. The skeleton is thinned to be no more than one voxel and treated as CSF. A similar idea is also used in (Kim et al., 2005), where a partial volume classification algorithm is used to label and thin voxels containing CSF components.

Infant-specific methods

Some surface reconstruction tools developed for adult brains, e.g., FreeSurfer, Caret and CIVET, could be modified for reconstructing infant cortical surfaces, when providing infant tissue segmentation results (Hill et al., 2010; Kim et al., 2016b). Several infant-dedicated methods have also been proposed. Leroy et al. (Leroy et al., 2011) proposed an infant-specific method for inner cortical surface reconstruction. In this method, first, a feature field is constructed based on the contrast of the T2w image. Then, the inner cortical surface is reconstructed by simultaneously deforming two surfaces, which change at different speeds along different directions. Specifically, the first surface is initialized by setting a threshold of the feature field and deforms outwards; and the second surface is set as the brain bounding box and deforms inwards using a topology preserving method. When the two surfaces converge and meet, the second surface is used as the inner cortical surface. A neonate-specific method is proposed in (Makropoulos et al., 2017b). In this method, a triangular mesh is first initialized as a convex hull of the white matter volume, and further deformed to reconstruct the inner surface and outer surfaces. The internal forces are based on curvature information and repulsion forces. The external forces are based on tissue image and intensity image. Specially, the surface is first pushed towards the white matter volume, and then further refined based on the intensity information to obtain the inner surface. The outer surface is obtained by further deforming the inner surface.

Independent reconstruction of cortical surfaces at multiple time points of the same infant typically leads to temporally-inconsistent and inaccurate measurements, as surface reconstruction involves complex nonlinear optimization, which is typically sensitive to noise and initialization. Li et al. (Li et al., 2014a) proposed a method for reconstructing longitudinally-consistent cortical surfaces. Specifically, the inner cortical surfaces are first independently reconstructed then modeled by using a surface growth model. Next, the vertex-wise correspondence is established between each pair of successive inner surfaces. Then all cortical surfaces are jointly deformed with a spatio-temporal deformable surface method to reconstruct all longitudinal inner and outer cortical surfaces, with the same triangular mesh configuration, thus providing a more accurate measurement of the dynamic development of the infant cortex. When removing the temporal constraint, this method can also be used to reconstruct infant cortical surfaces at a single time point.

Future Directions

Regions with extremely low contrast and small folding structures, e.g., the medial occipital cortex, frontal pole, medical temporal cortex, and temporal pole, typically have less accurate segmentation results and thus the poor surface reconstruction. Leveraging the prior information of these regions may help improve the results. Moreover, for longitudinal infant studies, the longitudinal consistency of cortical surfaces is an important issue to consider.

4.3 Cortical Surface Registration and Atlas Construction

Background

Cortical surface registration aims to establish intra-subject and inter-subject cortical correspondences, so that longitudinal and cross-sectional analyses can be performed meaningfully. Cortical surface atlas construction aims to create population-based representative cortical properties based on surface registration. In turn, surface atlases can guide surface registration and play a fundamental role in analysis, visualization, and comparison of results across individuals and studies.

4.3.1 Cortical Surface Registration

Challenges

There are mainly two challenges in cortical surface registration. The first one is the remarkable inter-subject variability of the highly-convoluted cortical folding patterns. The second one is the dynamic changes of cortical properties during early brain development. Therefore, features used for driving surface registration need to be meaningful and reliable for capturing key characteristics of the infant cerebral cortex.

Methods

Many methods have been developed for cortical surface registration of adult brains, but infant-dedicated registration methods are still lacking. In this section, we mainly focus on those methods which have been successfully applied in infant studies.

The most popular and widely used methods for cortical surface registration are based on the spherical representation of the cortical surface (Fig. 4 (j)) (Fischl et al., 1999). These methods leverage the 2D nature of the cerebral cortex sheet, thus greatly facilitating the registration and analysis of the convoluted cortex. Typically, these methods first inflate and map the cortical surface onto the standard sphere with minimal distortion (Figs. 4 (h) and 4 (i)) (Fischl et al., 1999). Many cortical properties are computed either from the original surface (e.g., curvature, sulcal depth, myelin content, and sulcal-gyral curves) or the inflation procedure (e.g., average convexity). Then, the spherical surface registration can be performed based on slected cortical properties. A hallmark software for cortical surface registration is FreeSurfer (Dale et al., 1999; Fischl et al., 1999), which uses geometric features (e.g., curvature and average convexity) to drive the spherical registration. Later, Van Essen et al., proposed a surface registration method based on manually-delineated sulcal-gyral landmark curves (Van Essen, 2004; Van Essen et al., 2001). This method has been adopted for construction of the first neonatal cortical surface atlas (Hill et al., 2010). Robbins et al. (Robbins et al., 2004) proposed another strategy for the cortical surface registration based on spherical representation. Their method is based on the free-form deformation, with the control points’ similarities derived from the local geodesic distance from gyral crown vertices. Yeo et al. (Yeo et al., 2010) proposed a fast spherical demons algorithm using the same geometric features as FreeSurfer. This method has been leveraged to build the first 4D (spatial + temporal) infant cortical surface atlases (Li et al., 2015d). Robinson et al. (Robinson et al., 2014) modeled the spherical registration as a Markov random field labeling procedure. Besides cortical folding features, function related features (e.g., myelin content and functional connectivity) are also introduced into the registration framework for better functional alignment.

4.3.2 Cortical Surface Atlas Construction

Challenges

For adult MRI studies, many cortical surface atlases have been generated and widely adopted. However, they cannot be simply used in infant studies, due to the dynamic changes of brain size, shape and cortical folding. Given the dynamic development, the infant surface atlases should be constructed as spatiotemporal atlases with a dense sampling of age. However, very limited works (as summarized in Table 6) focused on building infant cortical surface atlases.

Table 6.

Representative works on infant cortical surface atlas construction.

Study	Ages of Atlases	Subject No (Scan No.)	Registration Method	ROI No. (per hemisphere)	Link
(Hill et al., 2010)	39 GW	12	Van Essen, 2004	N/A	http://brainvis.wustl.edu/wiki/index.php/Sums:About?id=7052056
(Li et al., 2013)	Neonate, 12, 24 M	73 (219)	Yeo et al., 2010	N/A	N/A
(Li et al., 2015d; Wu et al., 2017)	1, 3, 6, 9, 12, 18, 24, 36, 48, 60, 72 M	50 (339)	Yeo et al., 2010	35 & 180	https://www.nitrc.org/projects/infantsurfatlas/
(Kim et al., 2016a)	26 – 30, 31 – 33, 34 – 36, 37 – 40 GW	158 (231)	Robbins et al., 2004	39	N/A
(Bozek et al., 2016)	38, 39, 40, 41, 42 GW	44	Robinson et al., 2014	N/A	N/A
(Wu et al., 2018)	39, 40, 41, 42, 43, 44 GW	764	Yeo et al., 2010	35 & 180	https://www.nitrc.org/projects/infantsurfatlas/
(Wang et al., 2018)	0.5, 1, 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 24 M	32 (138) Rhesus Macaques	Yeo et al., 2010	8	N/A

(GW: gestational weeks; M: month)

Methods

Hill et al. (Hill et al., 2010) constructed the first neonatal cortical surface atlas, PALS-term12 atlas, by co-registration of spherical cortical surfaces of 12 term-born neonates based on constraints of manually-delineated sulcal-gyral curves, using the method in (Van Essen, 2004; Van Essen et al., 2001). Kim et al. (Kim et al., 2016a) built spatiotemporal cortical surface atlases for preterm-born neonates from 26 to 40 weeks postmenstrual age based on SURFTRACC framework (Lyttelton et al., 2007; Robbins et al., 2004) from the CIVET pipeline. Specifically, they used 231 scans from 158 preterm-born neonates and built atlases at four age ranges, i.e., 26–30, 31–33, 34–36, and 37–40 weeks of gestation. Bozek et al. (Bozek et al., 2016) created spatiotemporal neonatal cortical surface atlases at each week from 38 to 42 gestational weeks, based on 44 subjects, by co-registration of cortical surfaces in each age group using MSM registration method (Robinson et al., 2014). As atlases constructed from small datasets may not be representative to the neonatal population, Wu et al. (Wu et al., 2018) thus constructed spatiotemporal cortical surface atlases at each week from 37 to 44 gestational weeks, based on a large-scale dataset with 764 neonates.

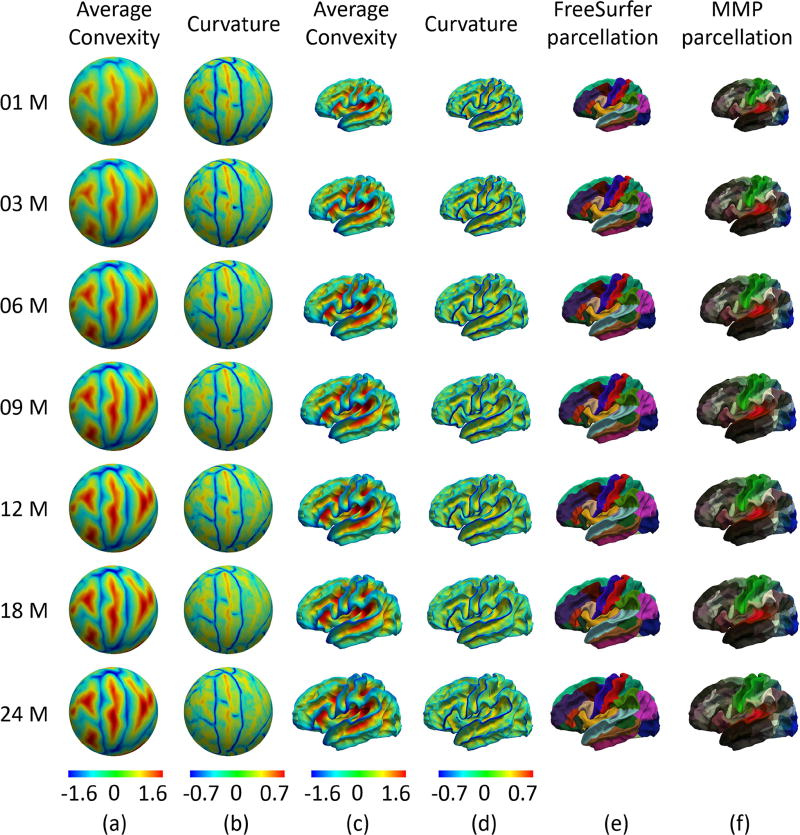
All these atlases only cover the neonatal stage, and thus are still not able to accurately characterize the dynamic, regionally-heterogeneous cortical development during infancy. To address this issue, Li et al. (Li et al., 2013) created the first longitudinal infant cortical surface atlases at 0, 1, and 2 years of age, based on 219 serial MRI scans from 73 healthy infants, by groupwise registration of spherical cortical surfaces of all subject at each age using spherical demons (Yeo et al., 2010). To more comprehensively capture the dynamic development during the first two years, Li et al. (Li et al., 2015d) further constructed the first 4D (spatiotemporal) infant cortical surface atlas at seven densely-sampled time points (as shown in Fig. 5), including 1, 3, 6, 9, 12, 18, and 24 months of age, based on 202 serial MRI scans from 35 healthy term-born infants, with each infant scanned longitudinally since birth. To ensure the longitudinal consistency and unbiasedness to any specific subject and age in this 4D surface atlas, they first computed the within-subject mean cortical folding by groupwise co-registration of all longitudinal cortical surfaces of each infant, by using spherical demons. Then, they further established longitudinally-consistent and unbiased inter-subject cortical correspondences by groupwise co-registration of within-subject mean cortical folding across all infants. Thus, this 4D surface atlas captured both longitudinally-consistent dynamic mean shape changes and the individual variability of cortical folding during early brain development. Recently, Wu et al. (Wu et al., 2017) extended the 4D surface atlas to densely cover the first 6 years with 11 time points (i.e., at 1, 3, 6, 9, 12, 18, 24, 36, 48, 60, and 72 months of age), based on 339 longitudinal MRI scans from 50 healthy infants. Moreover, to improve the clarity and sharpness of the atlas, instead of simply averaging of cortical folding features across the co-registered surfaces, a spherical patch-based sparse representation technique was also developed to eliminate the possible registration errors across subjects, thus preserving more details of cortical folding patterns.

Fig. 5.

UNC 4D infant cortical surface atlases and parcellations, created by the method in (Li et al., 2015d). (a) and (c) are the average convexity maps on the spherical space and mean cortical shape, respectively. (b) and (d) are the mean curvature maps on the spherical space and mean cortical shape, respectively. (e) and (f) are the FreeSurfer parcellation and HCP parcellation, respectively. The left-hand column indicates the age in months.

Future Directions

Cortical folding geometries are typically used for driving surface registration and for representing surface atlases. More cortical properties, e.g., myelin content, functional connectivity, and structural connectivity, could be potentially encoded in surface atlases and used for surface registration. However, as some cortical properties develop dynamically during infancy, they should not be simply used in surface registration involving subjects at very different ages. Meanwhile, as cortical development during the first months is extremely dynamic, surface atlases would be better to have denser time points during this stage.

4.4 Cortical Surface Parcellation

Background

Cortical surface parcellation aims to divide the cerebral cortex into small parcels that are distinguishable from each other according to their micro/macro structures, functional properties or connectivity patterns (Eickhoff et al., 2017). Parcellation can be performed on a population level or an individual level. A population-level parcellation captures the commonly distinct cortical regions in population of subjects and can be defined on surface atlases, while an individual-level parcellation more accurately reflects the individualized cortical regionalization. In this section, we mainly focus on infant cortical surface parcellation based on structural MRI information.

Challenges

There are two main challenges in infant cortical surface parcellation. First, due to dramatic differences in cortical properties between infants and adults, the available cortical parcellation protocols defined in adults may not be optimal for infant studies. Second, in longitudinal infant studies, the dynamic cortical development may cause longitudinally-inconsistent parcellations, especially for those ambiguous regions.

Methods

There are very limited works on infant cortical surface parcellation. Existing methods can be roughly categorized into two groups: 1) sulcal-gyral based parcellation, where the cortical sulcal-gyral macro-structures are used to define basic units of the cortical surface (Fig. 4 (k)), and 2) development based parcellation, which aims to define the basic cortical units that are distinct in developmental trajectories of cortical properties.

• Sulcal-gyral Based Parcellation

Some existing methods developed for adult cortical parcellation could be modified for infant cortical parcellation at a single time point. To address the issue of longitudinal consistency, Li et al. (Li et al., 2014b) proposed a multi-atlas labeling approach for simultaneous parcellation of multiple longitudinal infant cortical surfaces. In this method, an energy function was explicitly formulated to adaptively enforce the spatial smoothness and temporal consistency in the longitudinal surface parcellation. Of note, this method can also be applied to infant cortical parcellation at a single time point, when removing the temporal consistency term. Due to the lack of infant-specific multi-atlas surfaces, this study was based on adult multi-atlas surfaces with manual labels by experts. Using infant-specific multi-atlas surfaces may improve the parcellation results, given that adult brains are not representative of infant brains.

• Development Based Parcellation

Given that cortical microstructural and functional borders do not always match the sulcal-gyral structures, Li et al. (Li et al., 2015c) proposed a population-level parcellation of infant cortical surfaces based on the developmental trajectories of cortical properties, e.g., cortical thickness and surface area. The central idea is that the developmental trajectories indirectly reflect the underlying changes of microstructures and their connectivity, which jointly determines the functional principal of each region (Zilles and Amunts, 2010). Thus, compared to sulcal-gyral structures, the development based cortical parcellation may lead to a better definition of developmentally, micro-structurally, and functionally distinct regions. Given the development trajectory of a cortical property, they first built the affinity matrix for each subject between each pair of vertices in the cortical surface. Then, after fusion of the affinity matrices for all subjects, the output parcellation was produced by performing spectral clustering algorithm on the fused affinity matrix. To more precisely localize each individual’s distinct regions and better understand the inter-subject variability, Li et al. (Li et al., 2017) further proposed to derive an individualized parcellation with the prior guidance from the population-level parcellation. The developmental trajectory requires multiple longitudinal infant scans, this may potentially limit its immediate extension to other applications.

Future Directions

As existing infant cortical surface parcellations are based on a single cortical property, development of methods using multiple cortical properties are highly desired, as multiple properties provide complementary information on cortical architecture (Glasser et al., 2016). To this end, numerous questions remain open to future research, such as how different cortical properties contribute to the parcellation and which properties are more correlated with each other.

4.5 Surface-based Measurement

With the results of surface reconstruction, registration and parcellation, one can quantitatively measure multiple biologically distinct cortical properties, such as cortical thickness, surface area, myelin content, and cortical folding, at both vertex-wise level and region-level in the infant brain. To quantify the cortical folding, many methods have been proposed, e.g., gyrification index (GI), local GI, sulcal depth, and curvature derived measurements. These cortical properties are discussed below.

• Surface Area

At each vertex, the vertex-wise surface area can be computed as one-third the sum of the areas of all triangles associated with this vertex. The total surface area is the sum of vertex-wise surface areas of all vertices. Although surface area can be computed based on any surface, the central/middle surface is frequently used, as it is a more balanced representation of the sulci and gyri of the cerebral cortex. Of note, for vertex-wise comparison in both longitudinal and cross-sectional studies, the vertex-wise surface area should be computed based on the registered and resampled cortical surfaces for ensuring vertex-to-vertex cortical correspondences.

• Cortical Thickness

At each vertex, the cortical thickness can be computed based on the reconstructed inner and outer surfaces, e.g., the minimum distance between inner to outer surfaces. The mean cortical thickness is computed as the average thickness values of all cortical vertices.

• Cortical Volume

At each vertex, the cortical volume can be computed as the product of the surface area and cortical thickness. The total cortical volume is calculated as the sum of each vertex’s cortical volume, or the sum of the volume of each voxel. As can be seen, the cortical volume development is jointly determined by two distinct cortical measurements.

• Myelin Content

At each vertex on the central surface, the myelin content, which is related to brain functional areas, is defined as the ratio of the original T1w/T2w image intensities prior to intensity inhomogeneity correction (Glasser and Van Essen, 2011).

• GI and Local GI

The global cortical folding degree can be quantified by using GI (Zilles et al., 1988), i.e., the ratio of the surface area of the pial surface and that of the cerebral hull tightly wrapping the brain in 3D space. Given the regional variations of cortical folds, it is desired to measure the local gyrification. Li. et al. (Li et al., 2014c) proposed an infant-dedicated method to ensure a meaningful comparison and measurement of local GI for the dynamic developing brain (Fig. 4 (l)). Specifically, they first established intra-subject and inter-subject cortical correspondences and resampled all cortical surfaces using the same triangular mesh configuration. Then, they computed the local GI for each vertex as the area ratio of its N-ring neighborhood vertices on the outer surface and that of their corresponding regions on the cerebral hull surface.

• Sulcal Depth

Sulcal depth provides a continuously varying measurement of both coarse and fine shape information. For each vertex, it can be computed as the distance from the outer surface to the nearest point on the cerebral hull surface. Based on the sulcal depth map, sulcal pits, the locally deepest points in sulci, can be extracted based on the watershed method (Meng et al., 2014).

• Curvature-based Measurements

The curvature reflects fine-scale properties of the cortical folding. Many measurements based on curvature have been proposed, mainly based on the maximum principal curvature and the minimum principal curvature, e.g., mean curvature, Gaussian curvature, shape index, curvedness, to measure the complexity of the cortical folding (Awate et al., 2010; Kim et al., 2016b; Pienaar et al., 2008; Rodriguez-Carranza et al., 2008).

4.6 Multimodal Information Mapping

Multimodal information from functional MRI and diffusion MRI can be mapped and integrated onto the infant cortical surface to study the cerebral cortex in a more accurate and comprehensive way, as in HCP (Glasser et al., 2013). For functional MRI, functional signals can be resampled on the central/middle cortical surface for studying functional connectivity. For diffusion MRI, cortical diffusivity information can also be mapped onto the central cortical surface for studying cortical microstructure. For example, white matter fibers extracted from diffusion MRI can be mapped onto the inner cortical surface for studying cortical structural connectivity (Li et al., 2015b; Nie et al., 2014; Rekik et al., 2015b). Thus, all cortical information from structural, diffusion and functional MRI can be integrated and mapped onto the cortical surface for multimodal analysis.

4.7 Growth Modeling and Prediction

Background

Modeling and prediction of the dynamic brain development during infancy can help us better understand the normal brain development and provide insights into neurodevelopmental disorders. However, predictive models which can track the dramatic spatiotemporal changes in infant brains remain very scarce.

Challenges

Scarcity of such predictive models might be primarily due to: (1) the lack of longitudinal infant multimodal MRI data with dense acquisition timepoints from birth, and (2) the complex changes in both highly-folded cortical shape and MRI appearance during the first years.

Methods

Recently, a few pioneering models have been devised to predict the development of brain MRI, cortical surface shape, brain multishape (cortical surface and white matter fibers), and cortical property maps from neonatal data. Nie et al. pioneered the first mechanical cortical growth model (Nie et al., 2010; Nie et al., 2011) to simulate the dynamics of cortical folding from longitudinal MRI data in the first postnatal year, by modeling the cerebral cortex as a deformable elastoplasticity surface. Although promising, this method requires the use of cortical surfaces at later timepoints of the same infant to guide the growth model. Fishbaugh et al. (Fishbaugh et al., 2013) developed a geodesic shape regression in the framework of currents to estimate subcortical structures at 6 months of age based on shapes from 9 to 24 months. However, this model also requires more than one timepoint to predict the developmental trajectory from later to early acquisition timepoints. Rekik et al. proposed the first learning-based framework that predicts the dynamic cortical shape from a single baseline cortical surface at birth using a diffeomorphic surface regression model (Rekik et al., 2015a). This model used the current metric to first learn a population-based cortical shape atlas then individualize it to predict subject-specific cortical shape development. A more advanced version was proposed in (Rekik et al., 2016), where the varifold metric, a more robust and elegant mathematical representation of shapes, was used to predict cortical shape development. Since the human brain can be modeled as multiple interrelated shapes (multishape), such as the cortex and white matter pathways, Rekik et al. (Rekik et al., 2017) further proposed the first infant brain multishape development prediction model to jointly predict the development of cortical surface shape and underlying whiter matter fiber connectivity. Meng et al. (Meng et al., 2017) proposed a Dynamically-Assembled Regression Forest (DARF) learning framework to predict the development of the cortical property maps (e.g., cortical thickness) during the first postnatal year, based on neonatal MRI features. This provides complementary information to the cortical shape prediction model, as a few cortical properties, e.g., cortical thickness, cannot be directly derived from the cortical shape.

Future Directions

Building models that predict not only time-varying anatomy but also time-varying function and connectivity, as well as cognitive/behavioral scores and risk for brain disorders, is a compelling research direction that remains unexplored.

5 Resources

5.1 Datasets and Challenges

Table 7 lists publicly available large-scale datasets of baby brain images, including the Baby Connectome Project (BCP), Developing Human Connectome Project (dHCP) and National Database for Autism Research (NDAR). Especially, the BCP, a joint effort between the University of North Carolina at Chapel Hill and the University of Minnesota, aims to map detailed functional and structural connectome of the human brain during the first five years of life. The ongoing BCP will acquire and release cross-sectional and longitudinal high resolution multimodal brain MRI scans (including T1w, T2w, DTI and rs-fMRI) of 500 typically developing children from 0 to 5 years of age. The imaging quality and resolution from BCP will be comparable to that in the Human Connectome Project (HCP).

Table 7.

Publicly available datasets of infant brain T1w and T2w MR images.

Dataset	Imaging parameters	Subjects	Link
BCP	T1w: TR/TE = 2400/2.24 ms, voxel size = 0.8 × 0.8 × 0.8 mm3 T2w: TR/TE = 3200/564 ms, voxel size = 0.8 × 0.8 × 0.8 mm3	Normal children 0–5 Y	http://babyconnectomeproject.org
dHCP	T1w: TR/TE = 11/4.6 ms, voxel size = 0.8 × 0.8 × 0.8 mm3 T2w: TR/TE = 12,000/156 ms, voxel size = 0.8 × 0.8 × 1.6 mm3	Neonates and fetuses	http://www.developingconnectome.org
NDAR	T1w: TR/TE = 2400/3.16 ms, voxel size =1×1×1 mm3 T2w: TR/TE = 3200/499 ms, voxel size =1×1×1 mm3	Normal and autistic infants at 6, 12, 24 M	https://ndar.nih.gov

(Y: years; M: months)

Table 8 lists grand challenges for the infant brain MR images segmentation. For NeoBrainS12, 2 axial scans (acquired at 40 weeks corrected age) and 2 coronal scans (acquired at 30 weeks corrected age) are available for training and 15 neonatal subjects are available for testing. For iSeg-2017, 23 isointense infant subjects are randomly chosen from the pilot study of BCP, of which 10 subjects are provided for training and the remaining 13 subjects are provided for testing. These manual labels provided by the challenge organizers are highly valuable for methodological development from the community.

Table 8.

Segmentation challenges for infant brain MR images.

Challenge	Subjects	Link
NeoBrainS12	Neonates: 4 training subjects, 15 testing subjects	http://neobrains12.isi.uu.nl/
iSeg-2017	6-month-olds: 10 training subjects, 13 testing subjects	http://iseg2017.web.unc.edu/

5.2 Computational Tools and Atlases

Publicly available computational tools for infant brain MR image processing are listed in Table 9. It is worth-noting that iBEAT (Dai et al., 2013) successfully integrates many major steps of infant MR image processing, including preprocessing, skull stripping, tissue segmentation, image registration and ROI labeling. Also, it will be further extended to include tools for surface-based analysis. However, as can be seen, still limited software packages are available for processing the infant brain MR images, especially for the isointense and early-adult phases.

Table 9.

Publicly available computational tools for infant brain MR images.

Tool	Functionality	Applicable Stage	Link
iBEAT	Preprocessing, skull stripping, tissue segmentation, image registration, ROI labeling, surface-based analysis (available soon)	Infantile, isointense, early-adult	http://www.nitrc.org/projects/ibeat
ALFA	Skull stripping	Infantile	http://brainsquare.org
Neoseg	Tissue segmentation	Infantile	https://www.nitrc.org/projects/neoseg
DrawEM	Tissue segmentation	Infantile	https://github.com/MIRTK/DrawEM
MANTiS	Tissue segmentation	Infantile	https://github.com/DevelopmentalImagingMCRI/mantis
INSTAR	Joint tissue segmentation and registration	Infantile	https://www.nitrc.org/projects/instar
dHCP Structural Pipeline	Segmentation and surface-based analysis	Infantile	https://github.com/DevelopingHCP/structural-pipeline

The available infant brain volumetric atlases are listed in Table 10. Especially, Zhang et al. (Zhang et al., 2016) presented the first set of detail-preserved longitudinal volumetric atlases at 1, 3, 6, 9, and 12 months of age. For each time point, both T1w and T2w atlases, and the tissue probability maps are provided. The available cortical surface atlases are listed in Table 6. Especially, Li et al. (Li et al., 2015d) created the first 4D infant cortical surface atlases from neonates to 2 years of age, including 1, 3, 6, 9, 12, 18, and 24 months, based on 339 serial MRI scans from 50 healthy infants, with each being scanned longitudinally from birth. Meanwhile, they have also mapped both the FreeSurfer parcellation (Desikan et al., 2006) and the HCP multi-modal parcellation (MMP) (Glasser et al., 2016) onto the 4D infant cortical surface atlases, as shown in Fig. 5. These infant volumetric and cortical surface atlases with dense time points will greatly facilitate neuroimaging mapping of the dynamic early brain development in many pediatric studies.

Table 10.

Representative infant brain volumetric T1w and T2w atlases.

Studies	Subject No.	Age	Template	Tissue Probability Maps	Parcellation	Link
(Altaye et al., 2008)	76	1 Y	Yes	Yes	-	https://irc.cchmc.org/software/infant.php
(Gousias et al., 2008)	33	2 Y	-	-	83 ROIs	http://brain-development.org/brain-atlases/pediatric-brain-atlas/
(Fonov et al., 2009)	108	0 – 4.5 Y	Yes	-	-	http://www.bic.mni.mcgill.ca/ServicesAtlases/NIHPD-obj2
(Shi et al., 2011b)	95	Neonate, 1Y, and 2 Y*	Yes	Yes	90 ROIs	https://www.nitrc.org/projects/pediatricatlas
(Kuklisova-Murgasova et al., 2011)	153	Preterm (26 – 44 W GA)	Yes	-	-	http://brain-development.org/brain-atlases/neonatal-brain-atlas
(Oishi et al., 2011)	25	0 – 4 D	Yes	-	122 ROIs	http://lbam.med.jhmi.edu/
(Serag et al., 2012b)	204	Preterm (27–44 W PA)	Yes	-	-	http://brain-development.org/brain-atlases/consistent-high-definition-spatio-temporal-neonatal-brain-atlas/
(Gousias et al., 2012)	33	Preterm (37–43 W PA)	-	-	50 ROIs	http://brain-development.org/brain-atlases/neonatal-brain-atlas-albert/
(Broekman et al., 2014)	119, 32	0 M, 6 M	Yes	-	-	http://www.bioeng.nus.edu.sg/cfa/infant_atlas.html#atlas
(Blesa et al., 2016)	33	39 – 47 W PA	Yes	Yes	107 ROIs	http://brainsquare.org
(Makropoulos et al., 2016)	338	Preterm and term (23–42 W GA)	-	-	7/50/87 ROIs	http://brain-development.org/brain-atlases/multi-structural-neonatal-brain-atlas/
(Zhang et al., 2016a)	35 (150 scans)	0, 3, 6, 9, 12 M *	Yes	Yes	90 ROIs	https://www.nitrc.org/projects/infant_atlas_4d/

(Yes: the item is available; “-”: item is not available; GA: gestational age; PA: postmenstrual age; “*”: denotes longitudinal subjects were used; D: days; W: weeks; M: months; Y: years)

Besides T1w and T2w atlases, we also summarize in Table 11 for baby brain diffusion-weighted (DW) atlases that have been reported in the literature. A good summary of DW atlases can also be found in (Dickie et al., 2017). Most atlases are cross-sectional, except the UNC-CH atlases (Kim et al., 2017), which are constructed from a longitudinal dataset acquired every three months since birth. Except the UNC-CH and NUS atlases, all atlases provide group-averaged diffusion tensor (DT) images (Oishi et al., 2013; Oishi et al., 2011) or DTI-based contrasts, such as fractional anisotropy (FA) and mean diffusivity (Avants et al., 2015; Blesa et al., 2016). The UNC-CH and NUS atlases provide group DW images, allowing the flexibility of fitting any diffusion models (Bai et al., 2012; Broekman et al., 2014; Kim et al., 2017; Saghafi et al., 2017). The atlases constructed by (Oishi et al., 2013; Oishi et al., 2011) include a parcellation map of WM structures of the neonatal brain.

Table 11.

Representative diffusion-weighted atlases for the infant brain.

Study	Age	Modality/ Diffusion Model	Components	Atlas name	Link
(Akazawa et al., 2016; Oishi et al., 2013; Oishi et al., 2011)	0 – 4 D	T1w, T2w, DW / Diffusion tensor model	Templates, WM Parcellation Map, Fiber Probability Map	JHU Neonatal Atlas	http://cmrm.med.jhmi.edu/
(Oishi et al., 2013)	18 , 24 M	T1w, T2w, DW / Diffusion tensor model	Templates, WM Parcellation Map	JHU Pediatric Atlas	http://cmrm.med.jhmi.edu/
(Bai et al., 2012; Broekman et al., 2014)	5 – 17 D	T2w, DW / No specific model	Templates	NUS Neonatal Atlas	http://www.bioeng.nus.edu.sg/cfa/infant_atlas.html
-	6 M	T2w, DW / No specific model	Templates	NUS Pediatric Atlas	http://www.bioeng.nus.edu.sg/cfa/infant_atlas.html
(Blesa et al., 2016)	39 – 47 W PA	T1w, T2w, DW / Diffusion tensor model	Templates, AAL parcellation map, Tissue probability map	UE Neonatal Atlas	http://brain-development.org/brain-atlases/neonatal-brain-atlas-albert/
(Saghafi et al., 2017)	14 – 48 D	DW / No specific model	Templates	UNC-CH Neonatal Atlas
(Kim et al., 2017)	0, 3, 6, 9, 12 M	DW / No specific model	Templates, Fiber probability map	UNC-CH Longitudinal Infant Atlas*

(D: days; W: weeks; M: months; WM: white matter; PA: postmenstrual age)

^*Brain atlas based on longitudinal dataset

Abbreviations: JHU. Johns Hopkins University; NUS. National University of Singapore; UE. University of Edinburgh; UNC-CH. University of North Carolina at Chapel Hill; AAL. Automated Anatomical Labeling.

6 Discussion and Conclusion

Based on the above discussed infant-specific methods and tools, researchers can comprehensively quantify brain development in both typically-developing infants and infants with or at-risk of neurodevelopmental disorders, thus addressing a variety of questions on early postnatal brain development. For example, how the gray matter and white matter volumes grow in specific brain regions during infancy (Gilmore et al., 2011; Knickmeyer et al., 2008)? What are the spatiotemporal developmental patterns of multiple biologically-distinct brain properties, e.g., cortical thickness, surface area, cortical gyrification, sulcal depth, curvatures, and myelin content, in the first two postnatal years (Hill et al., 2010; Li et al., 2015a; Li et al., 2013; Li et al., 2014c; Lyall et al., 2014; Meng et al., 2014; Meng et al., 2017)? How the inter-subject variability and left-right hemispheric asymmetries of these brain properties emerge and evolve during infancy (Duan et al., 2017; Dubois et al., 2010; Glasel et al., 2011; Hill et al., 2010; Li et al., 2014c; Meng et al., 2016)? How these brain properties relate to gender, cognitive/behavioral functions, genetics and environments (Jha et al., 2018)? How these properties are differentially associated with risks for neurodevelopmental disorders (Hazlett et al., 2017; Kapellou et al., 2006; Li et al., 2016; Melbourne et al., 2014)? What are the structural and maturational covariance patterns of these properties (Fan et al., 2011; Geng et al., 2017; Shi et al., 2012b)? How these properties co-develop with structural and functional connectivity? More neuroscientific and clinical applications of infant-specific computational methods and tools can be found in (Dubois and Dehaene-Lambertz, 2015; Gilmore et al., 2018).

Although remarkable progress has been achieved on computational neuroanatomy of infant brains, there are still various limitations and open questions, which have been discussed in the previous sections and are also briefly summarized here:

• Methods

Due to the partial volume, dynamic, and regionally-varing apparances of infant MR images, conventional methods are often unable to achieve satisfactory accuracy, especially for isointense images around 6 months of age with insufficient tissue contrast. Recently, machine learning techniques have been shown to boost the accuracy in several challenging tasks, such as tissue segmentation and image registration. In particular, deep learning has recenly emerged as a powerful tool in medical image analysis. For example, in iSeg-2017 MICCAI Grand Challenge, the majority of the top performing methods were based on deep learning. Hence, development of advanced learning-based methods for infant MRI processing and analysis is an important avenue of research.

• Validation

Most existing methods are only validated on small-scale datasets acquired using a single imaging protocol. Therefore, their performance might be limited in the studies involving different imaging protocols, scanners, brain disorders/pathologies, and age groups. To make the developed methods truly useful, validation on multiple datasets capturing different scenarios as mentioned above is recommended.

• Resources

The accessibility to infant MRI datasets, computational tools, and brain atlases is critical for advancing research in pediatric neuroimaging studies. However, due to challenges in image acquisition and processing, freely accessible resources for computational neuroanatomy of infant brains are still very limited. Efforts should be directed to make those carefully validated resources publically available.

This article has been focused on T1w and T2w. Also important for understanding the early development of the human brain is diffusion MRI (DMRI), which is capable of revealing tissue microstructural properties due to its sensitivity to the diffusion of water molecules. Besides the infant-dedicated DMRI atlases summarized in Table 11, infant-specific computational tools also need to be developed for DMRI, so that DMRI can be used effectively for understanding early brain development. For example, the following issues need to be addressed: (1) Low SNR caused by signal attenuation due to water diffusion that is much less restricted in the developing brain (Hüppi and Dubois, 2006); (2) Insufficient spatial resolution due to smaller brain size; (3) Partial volume effects, requiring greater microstructural models to tease apart signal contributions from different tissue compartments (Assaf et al., 2004; Fieremans et al., 2011; Kaden et al., 2016; White et al., 2013; Zhang et al., 2012); (4) Tractography uncertainty resulting from the significantly lower diffusion anisotropy in the developing brain (Yap et al., 2011).

In summary, we have reviewed state-of-the-art computational methods dedicated to processing and analyzing infant brain MRI. We have also briefly discussed their representative applications to advancing our understanding of normal and abnormal brain development. We believe that future improvements and disseminations of computational tools for infant brain MRI processing and analysis will allow us to better chart and understand the dynamic brain developmental trajectories in typically-developing infants as well as the roots of abnormal neurodevelopmental trajectories in infants with disorders, thus informing early diagnosis and intervention.

Highlights.

1. A comprehensive review of infant-dedicated computational methods and tools

2. A discussion of contributions to the understanding of infant brain development

3. A discussion on current limitations and potential future directions