Non-rigid registration of 3D ultrasound for neurosurgery using automatic feature detection and matching

Abstract

Purpose

The brain undergoes significant structural change over the course of neurosurgery, including highly nonlinear deformation and resection. It can be informative to recover the spatial mapping between structures identified in preoperative surgical planning and the intraoperative state of the brain. We present a novel feature-based method for achieving robust, fully automatic deformable registration of intraoperative neurosurgical ultrasound images.

Methods

A sparse set of local image feature correspondences is first estimated between ultrasound image pairs, after which rigid, affine and thin-plate spline models are used to estimate dense mappings throughout the image. Correspondences are derived from 3D features, distinctive generic image patterns that are automatically extracted from 3D ultrasound images and characterized in terms of their geometry (i.e., location, scale, and orientation) and a descriptor of local image appearance. Feature correspondences between ultrasound images are achieved based on a nearest-neighbor descriptor matching and probabilistic voting model similar to the Hough transform.

Results

Experiments demonstrate our method on intraoperative ultrasound images acquired before and after opening of the dura mater, during resection and after resection in nine clinical cases. A total of 1620 automatically extracted 3D feature correspondences were manually validated by eleven experts and used to guide the registration. Then, using manually labeled corresponding landmarks in the pre- and post-resection ultrasound images, we show that our feature-based registration reduces the mean target registration error from an initial value of 3.3 to 1.5 mm.

Conclusions

This result demonstrates that the 3D features promise to offer a robust and accurate solution for 3D ultrasound registration and to correct for brain shift in image-guided neurosurgery.

Introduction

Neuronavigation systems can be used to determine the position of brain tumors during surgical procedures relative to preoperative imaging, typically magnetic resonance (MR) images [1]. Commercial systems employ an electromagnetic or optical device to track the surgical tools and model the patient’s head and its content as a rigid body. Paired-point registration based on anatomical features or surface-based registration methods are commonly used to determine the rigid body transformation from the coordinate system of the preoperative image to the coordinate system of the patient during surgery. During surgery, cerebrospinal fluid drainage, use of diuretics and tumor resection cause the brain to deform and therefore invalidate the estimated rigid transformation [2]. Brain deformation during surgery, known as brain shift, along with registration and tracking errors reduces the accuracy of image-guided neurosurgery based on neuronavigation systems [3–5].

Because maximum safe resection is the single greatest modifiable determinant of survival [6] and strongly correlated with prognosis in patients with both low-grade [7] and high-grade gliomas [8], the development of intraoperative imaging techniques is desirable because they guide the surgeon toward obtaining a more complete resection while helping to prevent damage to normal brain [9].

Intraoperative magnetic resonance (iMR) imaging has been used during surgery offering high contrast for visualization of tissues using multiple sequences [10–13]. However, MR devices are expensive and require a dedicated operating room and specialized non-magnetic tools making this technology unavailable in most centers worldwide. iMR is also time-consuming, adding an hour or more per scan to a surgical intervention.

On the other hand, intraoperative ultrasound (iUS) appears to be a promising technology to compensate for brain shift [14–17]. iUS is relatively inexpensive and does not require changes to the operating room. However, awareness of artifacts in ultrasound images that may occur during tumor resection is a necessity for successful and safe surgery when using iUS for resection control.

Registration of intraoperative imaging is challenging, especially of iUS images. Brain ultrasound images acquired prior to resection often have high image quality, providing the capability of localizing surgical targets, typically defined in the preoperative MR during surgical planning. During surgery, e.g., right after opening the dura membrane, this capability degrades as artifacts may occur. Moreover, brain deformation is a complex and spatiotemporal phenomenon [3], requiring non-rigid registration algorithms capable of mapping structures in one image that have no correspondences in a second image, such as the tumor and resection site [18].

A solution is to use biomechanical modeling to combine intraoperatively acquired data with computational models of brain deformation to update preoperative images during surgery [19–22]. Development of accurate biomechanical models is important to compensate for brain displacement and is an ongoing focus of a large portion of the research community. However, most of the research work that has been done in biomechanical modeling of the brain tissue for this purpose is not completely independent of the registration methods.

We investigate the use of intraoperative 3D ultrasound to compensate for brain shift during neurosurgical procedures.

A body of prior work has investigated iUS image registration in the context of neurosurgery [23–25]. For reducing computational complexity, deformable registration approaches typically adopt iterative algorithms that are only guaranteed to converge to locally optimal solution. They are thus prone to identifying erroneous, suboptimal solutions if not initialized correctly, particularly if there is no smooth geometric transformation that models the differences between the images, e.g., following brain tumor resection. These methods may require initialization within a “capture range” of the correct solution, where initialization is typically provided via external labels or segmentation of regions of interest within ultrasound images and the alignment is optimized primarily for the specific labels [26,27]. Alternatively, generic salient image features have been applied using a wide variety of methods [28–32], and distinctive local neighborhoods surrounding edges and texture features can be used to identify image-to-image correspondences prior to registration [33]. While correspondences between distinctive local features may be achieved, a challenge remains when computing registration throughout the image space, particularly in regions where one-to-one correspondence is ambiguous or nonexistent.

A major advance in image recognition was the development of invariant feature detectors, capable of reliably identifying the same distinctive image features in a manner independent of geometrical deformations. In particular, scale-invariant features (SIFT) are invariant to translation, rotation and scale changes and provide robust feature matching across a substantial range of addition of noise and changes in illumination [34]. SIFT features were extended to 3D imaging with the 3D SIFT-Rank algorithm [35]. 3D SIFT-Rank matching was previously used to stitch multiple hepatic ultrasound volumes into a single panoramic image of a health liver [36]. Ultrasound volumes were acquired from healthy subjects with a breath holding protocol; thus, soft tissue deformation is minimal and modeled as rigid. Additionally, keypoints are encoded using a 2048-element 3D SIFT descriptor, whereas the memory efficient 64-element SIFT-Rank descriptor was adopted. 3D SIFT-Rank was also used to align left and right ventricle volumes in 4D cardiac ultrasound sequences to enlarge the field of view [37]. Correspondences are identified between 3D volumes at similar points in the cardiac cycle, where deformation is minimal and approximately rigid.

In this paper, feature-based registration aims to identify a globally optimal spatial mapping between 3D iUS images, based on a sparse set of scale-invariant feature correspondences. We demonstrate the application of a fully automated feature extraction and matching [35] for iUS registration to compensate for brain shift. To the best of our knowledge, it is the first work to apply 3D SIFT-Rank features to iUS registration in image-guided neurosurgery.

Methods

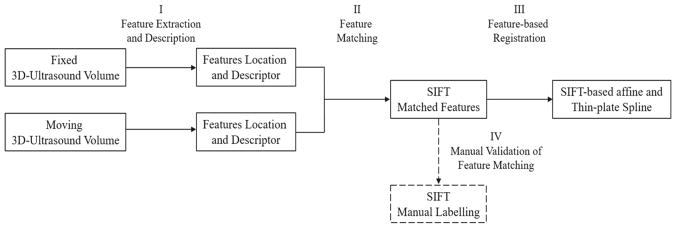
3D ultrasound images consist of image patterns that are challenging to localize or register across datasets. For efficient and robust registration, we adopt a local feature-based registration strategy, where the image is represented as a collection of scale-invariant features, generic salient image patches that can be identified and matched reliably between different images of the same underlying object. Feature-based registration operates by identifying a set of pairwise feature correspondences between a pair of images to be registered based on local appearance descriptor similarity, after which feature geometry is used to prune spurious, incorrect correspondences via the generalized Hough transform. Feature correspondences were manually validated by radiologist and non-radiologist physicians. Figure 1 presents a summary of the proposed feature-based registration for intraoperative 3D ultrasound.

Fig. 1.

Summary of feature-based registration for intraoperative 3D ultrasound images

Feature extraction

We use the 3D SIFT-Rank algorithm [35] to automatically extract and match features from 3D iUS. Feature extraction seeks to identify a set of salient image features from a single image. Each feature f = {g, ā} is characterized by geometry g = {x̄, σ, θ} and appearance descriptor ā. Feature geometry consists of a 3D location x̄ = (x, y, z), a scale σ, and a local orientation specified by a set of three orthonormal unit vectors θ = {θ̂₁, θ̂₂, θ̂₃}. Appearance descriptor ā is a vector that encodes the local image appearance. Feature extraction operates first by (1) detecting the location and scale of distinctive image regions and then (2) encoding the appearance of the image within the region. In general, feature detection involves identifying a set of distinctive regions {(x̄_i, σ_i)} that maximize a function of local image saliency, e.g., entropy [38] and Gaussian derivative magnitude [39]. Following the SIFT method, we identify regions as extrema of the difference-of-Gaussian (DoG) function, given by Eq. (1).

$$\{({\overline{x}}_i,{\sigma }_i)\}=\text{local}\underset{\overrightarrow{x},\sigma }{\text{argmax}}\mid f(\overline{x},k\sigma )-f(\overline{x},\sigma )\mid$$ (1)

where f (x̄, σ) = I (x̄) * G (x̄, σ) represents the convolution of image I (x̄) with a Gaussian kernel G (x̄, σ) of variance σ² and k is a multiplicative sampling rate in scale σ.

Once a set of features has been detected, the image content surrounding each region (x̄_i, σ_i) is encoded as a local appearance descriptor ā_i to compute feature correspondences between images. We adopt the 3D SIFT-Rank descriptor [35], where the image content about each region (x̄_i, σ_i) is first cropped and normalized to a 11 × 11 × 11 voxel patch, after which local image gradients are grouped into a 64-element descriptor ā_i based 8 = 2 × 2 × 2 spatial bins and 8 orientation bins. Each image gradient sample increments a bin defined by location and orientation, and the bin is incremented by the gradient magnitude. Finally, this vector is rank ordered, where each element of ā_i takes on its index in a sorted array rather than the original gradient histogram bin value. Rank ordering provides invariance to monotonic deformations of image gradients and results in more accurate nearest-neighbor-matched feature [40].

Feature matching

Let T : F → M be a spatial mapping between feature sets F = {f_i } and M = {f_j} in fixed and moving images, respectively. Feature-based registration seeks a maximum a posteriori (MAP) transform T^* = argmax_T { p (T|F, M)}, which can be achieved by a 2-step image-to-image feature matching process. First, a set of candidate feature correspondences (f_i, f_j) are identified between all features in the moving image and the fixed image based on minimum appearance descriptor difference. Descriptor difference is evaluated via the Euclidean distance d(ā_i, ā_j) = ||ā_i − ā_j||. Second, for each candidate matching feature pair (f_i, f_j), a hypothesis T_{i j} : g_i → g_j is estimated as to an approximate linear transform between images based on geometry descriptors (g_i, g_j). This can be viewed as maximizing the likelihood p(g_i |T_ij, g_j), and as each feature incorporates a position, orientation and scale, a single pair of features contains sufficient information for estimating a scaled rigid transform hypothesis (or linear similarity transform) between images. Transform hypotheses estimated from all features pairs are generated and then grouped to identify a dense cluster of geometrically consistent pairs/transforms that are “inliers” of a single global transform at a specified tolerance level, where clustering is achieved via the robust mean-shift algorithm [28]. Intuitively, the transform hypothesis supported by the highest number of inliers represents the MAP transform T^*, given a Gaussian mixture model over the appearance and geometry of individual features. The result of the matching process is the MAP transform T^*, along with a set of inlier feature pairs represent valid image-to-image correspondences.

Feature-based registration

Deformable registration algorithms must often be initialized near the correct solution where initialization may take the form of an approximate, initial rigid or affine registration [41]. A 12-parameter affine transformation was used to find a spatial transform that maps two ultrasound images. The most widely applied method for landmark-based non-rigid registration is based on thin-plate splines as they have regularization properties that are, at least loosely, inspired by mechanics [42,43]. Thin-plate splines were used to get the deformation field between two ultrasound images.

Experiments

Patients

Nine patients (3 females, 6 males; mean age 44 years) scheduled for resection of suspected/known primary or metastatic brain tumor in a multi-modality image-guided surgical suite [44] were included in this study. After histologic examination, it was determined that 4 patients had low-grade gliomas, 4 had high-grade gliomas, and 1 had metastatic brain tumor. Mean tumor volume was 19.5 cm³, ranging from 0.1 to 57.0 cm³. Two of the cases were first operations, and seven were reoperations. All patients provided informed consent. Clinical details, including the demographics, pathologic diagnosis, volume and location of tumor, are shown in Table 1.

Table 1.

Clinical details of the group of patients undergoing brain tumor resection

#	Age	Gender	Diagnosis	Location	Preoperative tumor volume (cm3)	Postoperative residual tumor volume (cm3)
1	21	M	Ganglioglioma	Right temporal	0.1	0
2	30	F	Anaplastic astrocytoma WHO grade 3	Right frontal	18.7	7.9
3	69	F	Metastasis (high-grade serous carcinoma) (recurrent)	Right frontal	3.1	1.1
4	36	M	Oligodendroglioma grade 2 (recurrent)	Left parietal	12.2	0
5	61	M	Glioblastoma multiforme grade 4	Left parietoccipital	39.2	4.6
6	45	M	Glioblastoma multiforme grade 4 (recurrent)	Right temporal	57.0	Not available
7	46	M	Oligodendroglioma grade 2 (recurrent)	Right frontal	11.3	5.0
8	27	M	Dysembryoplastic neuroepithelial tumor	Right frontal	10.1	Not available
9	57	F	Glioblastoma multiforme grade 4 (recurrent)	Left temporoparietal	24.0	4.1

MR data acquisition

For preoperative planning and integration into the neuronavigation system, images were acquired on a 3-Tesla MR scanner after the administration of 0.1–0.2 mmol/kg of Gadabutrol (Gadavist, Bayer Schering Pharma, Germany). Intraoperative MR was performed on a 3-Tesla MR scanner (Siemens Healthcare GmbH, Erlangen, Germany). Postoperative brain MR protocols were identical to the preoperative acquisitions. Two patients did not have postoperative MR. Tumor volume was calculated on the iPlan Cranial 3.0 software (Brainlab, Munich, Germany) using the contrast enhancing portion of the tumor.

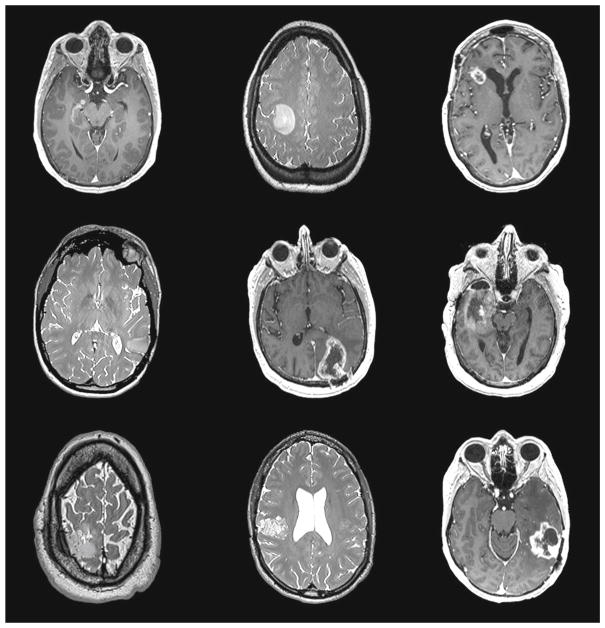
Figure 2 shows the representative axial slices (T2 or T1 post-contrast) from the preoperative MR of the nine subjects.

Fig. 2.

Axial slices of 9 preoperative MR subject images showing tumor locations

US data acquisition

During surgery, two freehand ultrasound sweeps were acquired, before and after the opening of the dura membrane but before inducing other structural changes. After the first two acquisitions, the surgeon resected the tumor until what he thought was the maximum possible resection. For some patients, it was also possible to acquire iUS images during resection and prior to intraoperative MR. The ultrasound images were acquired by two neurosurgeons (attending and clinical fellow) with significant expertise in the use of intra-operative tracked 3D ultrasound as it is a routine part of neurosurgical procedures in our institution.

The position of the ultrasound probe relative to the patient’s head was monitored via optical tracking using the VectorVision Sky neuronavigation system (target registration error equal to 1.13 ± 0.05 mm) (Brainlab, Munich, Germany) [45]. A touch-based pointer (Softouch, BrainLab) was used to collect a cloud of points from the surface of the head and facial region. A surface-based registration was used to determine the rigid body transformation from the coordinate system of the preoperative image to the coordinate system of the patient.

Intraoperative ultrasound was acquired on a BK Ultrasound 3000 system (BK Medical, Analogic Corporation, Peabody, USA) that is directly connected to the Brainlab neuronavigation system. The BK craniotomy probe 8861 was used in the scanning B-mode with frequency range of 10–3.8 MHz. The stylus calibration error of the probe is less than 0.5 mm.

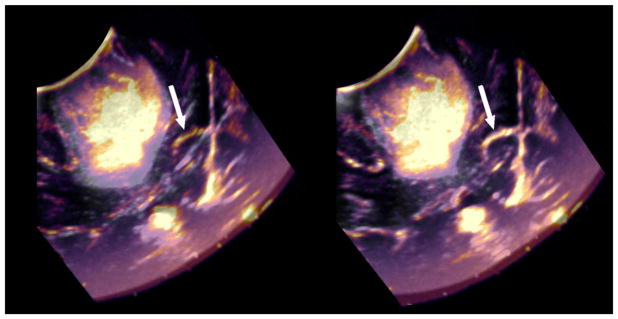
An Epiphan USB video grabber was used to capture iUS images from the BK monitor. Image data were imported into 3D Slicer using OpenIGTLink [46] and reconstructed as 3D volumes using the PLUS library [47]. The volume reconstruction method in PLUS is based on the work of [48,49]. The first step of the procedure is the insertion of 2D image slices into a 3D volume. This is implemented by iterating through each pixel of the rectangular or fan-shaped region of the slice and distributing the pixel value in the closest 8 volume voxels. The voxel value is determined as a weighted average of all coinciding pixels. Slice insertion is performed at the rate the images are acquired; therefore, individual image slices do not have to be stored and the reconstructed volume is readily available at the end of the acquisition. Typically, sweeps contained between 100 and 300 frames of 2D ultrasound data and were reconstructed at a voxel size of 0.5 × 0.5 × 0.5 mm³. A typical example of pre- and partial post-resection ultrasound images and their initial misalignments is shown in Fig. 3. As most brain tumors have higher mass density and sound velocity than the surrounding normal brain [50], the ultrasound images can result in sharp interfaces as shown in Fig. 3.

Fig. 3.

Pre-resection (gray shades) and post-partial resection (warm shades) ultrasound images. Arrows indicate the falx and show its misalignment in images taken at different time points (far right)

Feature extraction and matching

For each 3D ultrasound image, 3D SIFT-Rank features were extracted and matched as explained in the “Methods” section. Figure 4 shows a collection of 3D SIFT-Rank features extracted from iUS acquired before opening the dura membrane.

Fig. 4.

3D SIFT-Rank features of a 3D ultrasound image representing a right-frontal anaplastic astrocytoma. Axial, sagittal and coronal views are presented from the left to the right. Each white circle overlaying the image represents the location x̄ and scale σ of an automatically detected local feature

Figure 5 shows examples of feature correspondences between iUS images acquired before opening the dura membrane and prior to iMR (after partial resection).

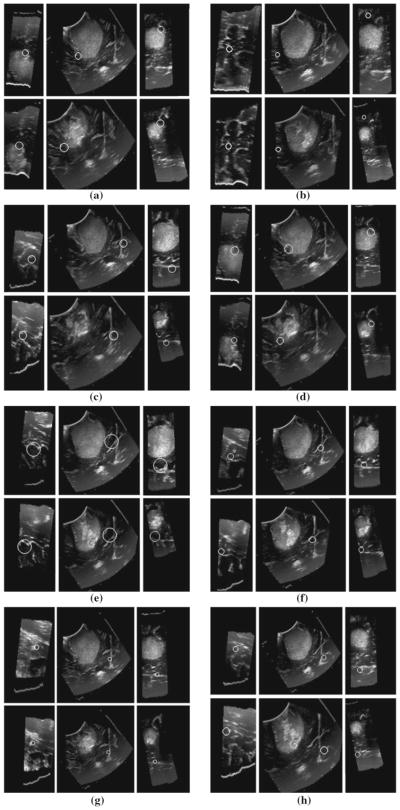
Fig. 5.

3D SIFT-Rank feature correspondences in a right-frontal anaplastic astrocytoma between 3D ultrasound images. In each of a–h white circles represent the local and scale of a single scale-invariant feature in three orthogonal image slices, automatically identified in two different ultrasound volumes (upper and lower triplets). Note the high degree of visual similarity in the upper and lower images, surrounding the feature of interest

Table 2 shows the number of 3D SIFT-Rank feature correspondences found in each pair of 3D ultrasound images. In this paper, pre-dura, post-dura, intraoperative and pre-iMR ultrasound images correspond to intraoperative ultrasound images acquired before opening the dura, after opening the dura, during tumor resection and prior to iMR, respectively.

Table 2.

Number of 3D SIFT-Rank feature correspondences on pairs of ultrasound volumes acquired at different time points during surgery

US data	Patient 1	Patient 2	Patient 7
Post-dura US/pre- iMR US	81	22	46
Pre-dura US/pre-iMR US	123	71	12
Pre-dura US/post-dura US	124	57	30
US Data	Patient 3	Patient 4	Patient 8
Pre-dura US/post-dura US	84	14	37
US Data	Patient 5		Patient 6
Pre-dura US/pre-iMR US	49		N/A
Post-dura US/pre-iMR US	N/A		98
US Data			Patient 9
Intraop US/pre-iMR US			250
Post-dura US/pre-iMR US			123
Post-dura US/intraop US			133
Pre-dura US/pre-iMR US			64
Pre-dura US/intraop US			50
Pre-dura US/post-dura US			151

Feature extraction and matching is a completely automated process that takes less than 30 s on average to extract and match features between two 3D ultrasound images using a 2.5 GHz Intel Core 2 processor. Virtually, all feature-based alignment running time is due to Gaussian convolution during feature extraction, and this represents a one-time preprocessing step that could be significantly reduced via GPU optimization. With features extracted, feature-based alignment requires less than 1 s using the same processor.

Feature-based registration

3D Slicer software was used for image visualization and registration [51]. Figure 6 shows the alignment between the pre-resection and post-resection (prior to intraoperative MR) ultrasound images before registration and after nonlinear correction.

Fig. 6.

Pre-resection (gray shades) and post-resection (warm shades) ultrasound images. A typical example of pre- and post-resection ultrasound images and their initial misalignments is shown on the left. Alignment after SIFT-Rank-based thin-plate spline (on the right) between two iUS images

Evaluation

Validation of SIFT-Rank correspondences via manual labeling

SIFT-Rank features were presented in the pre-resection volume. Each expert was then asked to manually locate the correspondence for pre-resection feature in a second volume that was acquired at a different stage of the surgery. The discrepancy between manually and automatically located correspondences in the second volume can thus be used to quantify the accuracy of automatic correspondence, where a low discrepancy would indicate high agreement between automatic and manual correspondence. A user interface for the manual validation was built using 3D Slicer [51]. The 3D Euclidean distance between manual labels in the second volume was used to determine the inter-rater variability. The 3D Euclidean distance between the SIFT-Rank feature and the manual labels in the second volume was determined to know the discrepancy between SIFT-Rank features and manual labels.

Registration validation using manual tags

The ultrasound–ultrasound alignment was defined by selecting corresponding anatomical landmarks in the ultrasound images. Registration accuracy was measured as a function of the distance between these landmarks before and after registration [52]. We use mean target registration error (mTRE) metric, which shows the average distance between corresponding landmarks. Let V₁ and V₂ represent two ultrasound volumes and x and x′ represent corresponding landmarks in the V₁ and V₂ respectively, then mTRE can be calculated by Eq. (2).

$$\mathit{mTRE}=\frac{1}{n}\sum _i^n\Vert T(x_i)-{x^{\prime }}_i\Vert$$ (2)

where T is the deformation and n is the number of landmarks.

Qualitative registration evaluation by neurosurgeons

The quality of the alignment of the pre- and post-resection ultrasound volumes was visually assessed by 2 physicians with 2 and 5 years of experience in medical imaging. Cross sections of the post-resection ultrasound volume were overlaid on (1) the original pre-resection ultrasound, (2) the pre-resection ultrasound after affine transform and (3) the pre-resection ultrasound after thin-plate spline. The experts accessed the registration accuracy at (1) anatomical landmarks such as the sulcal patterns, vessels, choroid plexus, falx and configuration of ventricles and (2) the tumor boundary to subjectively determine quality of registration with “bad” reflecting grossly visible misregistration, “good” reflecting minor visible misalignments, and “great” reflecting near undetectable misregistration.

Other publicly available datasets

Our registration framework was also validated using pre- and post-resection ultrasound images from the BITE [53] and RESECT [54] publicly available databases. Previous works have reported non-rigid registration results on intraoperative 3D ultrasound using BITE: RESOUND [23] presents a mTRE equal to 1.5 (0.5–3.0) mm, and, more recent, NSR (non-rigid symmetric registration) [15] reported a mTRE equal to 1.5 (0.4–3.1) mm.

Results

Validation of SIFT-Rank correspondences via manual labeling

A total of 1620 correspondences were manually validated by eleven experts, including medical imaging experts, radiologists and non-radiologist physicians. Figure 7 shows the manual validation of feature correspondences for pre- and post-resection ultrasound, where 71 feature correspondences were found. Given an automatically detected feature (circled in green), the experts were asked to locate the corresponding point in the second ultrasound volume (circled in orange).

Fig. 7.

3D SIFT-Rank features manual validation. The orange circles represent the locations of a feature as estimated manually by different human experts, and the green circles represent the location identified via automatic SIFT-Rank features matching. The upper row corresponds to three different views of the pre-dura volume, and the lower row corresponds to an ultrasound volume acquired prior to iMR

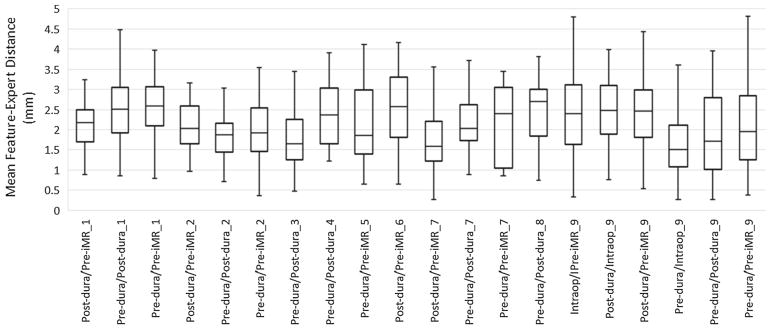
For each feature correspondence, the 3D Euclidean distance was calculated between automatic and manually located features in the second volume. This distance measures the discrepancy between manually determined locations and automatically identified feature locations. This experiment was performed by 11 experts; each expert was randomly assigned a set of features to validate, and every feature correspondence was validated by at least 2 experts. The median, maximum and minimum distances were calculated on a per-feature basis, and the mean distance was calculated across all features. Figure 8 shows the mean feature-expert distance, where each column represents feature-expert distances for all feature correspondences between a specific pair of ultrasound volumes. The average target localization distance across all patients was equal to 2.20 ± 0.43 mm. The inter-rater variability was found to be equal to 1.89 ± 0.37 mm.

Fig. 8.

Feature-to-expert distances (mm) between each pair of ultrasound volumes and across different patients

A second experiment was performed where we presented a set of experts with the automatic feature from the first volume and then both the automatic and manual matched features in the second volume. A total of 800 feature correspondences were used in this experiment. The experts were asked to choose which one was a better match. To avoid bias, the experts were blinded to which of the displayed correspondences were identified via SIFT-Rank and which were manually specified correspondences. We found that experts preferred the automatically detected features over the manually located features 88% of the time.

Registration validation using manual tags

For each patient, 10 unique landmarks were identified. Eligible landmarks include deep grooves and corners of sulci, convex points of gyri and vanishing points of sulci. Table 3 presents the number of landmarks and the mean, maximum and minimum initial 3D euclidean distance between landmark pairs. The mean, maximum and minimum distance after 3D SIFT-Rank-based affine and thin-plate spline are also presented.

Table 3.

mTREs and range, in mm, of initial alignment between landmarks (obtained by rigidly registering ultrasound images using tracking information) and after SIFT-Rank-based affine and SIFT-Rank-based thin-plate spline

Patient	Data	SIFT feature correspondences	Initial	After SIFT-based Affine	After SIFT-based TPS
1	Pre-dura/post-dura	124	3.38 (2.44–4.38)	1.16 (0.34–3.29)	1.12 (0.07–3.00)
	Pre-dura/pre-iMR	123	5.33 (4.08–7.35)	1.77 (0.36–3.40)	1.43 (0.18–3.22)
	Post-dura/pre-iMR	81	3.08 (1.04–4.79)	1.40 (0.51–3.10)	1.23 (0.29–2.81)
2	Pre-dura/post-dura	57	2.11 (1.37–3.41)	1.39 (0.42–2.63)	1.20 (0.30–2.21)
	Pre-dura/pre-iMR	71	3.88 (2.11–8.23)	2.36 (0.69–7.61)	1.95 (0.58–7.58)
	Post-dura/pre-iMR	22	3.71 (1.66–8.18)	2.87 (0.94–6.96)	2.48 (0.56–6.17)
3	Pre-dura/post-dura	84	2.62 (1.11–3.55)	1.49 (0.89–2.67)	1.43 (0.73–2.56)
4	Pre-dura/post-dura	14	2.50 (0.17–4.28)	2.40 (0.12–4.10)	2.12 (0.10–3.33)
5	Pre-dura/pre-iMR	49	2.36 (0.60–4.00)	2.20 (0.56–3.75)	2.19 (0.35–2.34)
6	Post-dura/pre-iMR	98	3.32 (1.28–4.74)	1.66 (0.41–3.39)	1.13 (0.33–3.16)
7	Pre-dura/post-dura	30	3.11 (1.82–4.85)	1.68 (0.62–2.95)	1.49 (0.31–2.04)
	Pre-dura/pre-iMR	12	3.70 (2.43–5.16)	1.71 (0.56–3.92)	1.69 (0.54–3.63)
	Post-dura/pre-iMR	46	2.00 (0.79–3.14)	1.25 (0.36–2.54)	1.19 (0.22–2.13)
8	Pre-dura/post-dura	37	4.31 (1.09–5.81)	1.67 (0.62–3.36)	1.06 (0.54–3.12)
9	Pre-dura/post-dura	151	3.01 (0.83–4.12)	1.54 (0.75–2.31)	1.32 (0.39–2.22)
	Pre-dura/pre-iMR	64	3.56 (1.80–5.84)	1.52 (0.56–2.77)	1.42 (0.48–2.51)
	Post-dura/pre-iMR	123	3.22 (1.55–6.22)	1.76 (0.76–3.21)	1.74 (0.62–3.19)
Grand mean			3.25 (1.54–5.18)	1.75 (0.56–3.54)	1.54 (0.39–3.25)

Each cell contains the mean Euclidean distance (mm) between the 10 tag sets and the range

The average initial mTRE for the 9 patients is 3.25 mm. This value was reduced to 1.75 mm using SIFT-Rank-based affine and to 1.54 mm using SIFT-Rank-based thin-plate spline. To determine whether the mean distances were statistically different, a variance analysis (ANOVA) was applied. This yielded F (1, 32) = 56.69, p < .001, indicating that the differences were significant. There was also a statistically significant improvement between the initial displacements and after the SIFT-based thin-plate spline (p < .001).

Qualitative registration evaluation by neurosurgeons

For the 9 clinical cases, the neurosurgeons agree that the affine transform achieved acceptable registration in regions such as the falx and sulci (where deformation is expected to be small compared to the resection area) and thin-plate spline gave a good first approximation of the tumor boundary deformation. From a total of 20 pairs of ultrasound images, the alignment of 8 cases was classified as “good” and 12 cases as “great” after affine transform. After thin-plate spline, 4 cases were classified as “good” and 16 cases were classified as “great.”

Other publicly available datasets

Our registration framework was also validated using pre- and post-resection ultrasound images from the BITE [53] and RESECT [54] publicly available databases. Tables 4 and 5 provide details on number of manually located anatomical landmarks of each dataset, and the mean, maximum and minimum initial 3D Euclidean distance between landmark pairs. The mean, maximum and minimum 3D Euclidean distance after SIFT-Rank-based affine and thin-plate spline are also presented. For each ultrasound image pair from BITE, 10 homologous landmarks were manually located. The number of 3D SIFT-Rank feature correspondences used to guide the registration per 3D ultrasound image pair is also presented in the second column of Table 4.

Table 4.

BITE database: mTREs and range, in mm, of initial alignment between landmarks and after SIFT-Rank-based affine and SIFT-Rank-based thin-plate spline

Patient	SIFT feature correspondences	Initial	After SIFT-based affine	After SIFT-based TPS
1	No post-resection US
2	54	2.30 (0.57–5.42)	1.80 (0.39–5.16)	1.66 (0.38–4.07)
3	55	3.78 (2.80–5.09)	1.31 (0.63–2.33)	1.30 (0.38–2.15)
4	26	4.60 (2.96–5.88)	1.26 (0.53–3.00)	1.13 (0.42–2.74)
5	27	4.11 (2.58–5.26)	1.24 (0.59–1.77)	1.24 (0.50–1.70)
6	183	2.26 (1.36–3.10)	1.33 (0.63–2.34)	1.18 (0.59–2.11)
7	58	3.87 (2.60–5.07)	1.39 (0.56–2.31)	0.86 (0.39–1.38)
8	29	2.51 (0.67–3.93)	2.15 (0.60–3.83)	1.12 (0.49–3.08)
9	19	2.21 (1.00–4.59)	2.03 (0.70–3.95)	1.38 (0.44–3.71)
10	45	3.86 (0.98–6.68)	2.68 (0.78–5.65)	2.59 (0.72–3.51)
11	82	2.88 (0.76–8.95)	2.87 (0.74–7.95)	2.52 (0.48–3.23)
12	67	10.53 (7.85–13.06)	3.68 (0.67–8.06)	2.37 (0.14–3.74)
13	93	1.62 (1.33–2.21)	1.04 (0.53–2.76)	1.01 (0.29–2.03)
14	188	2.19 (0.59–3.99)	1.32 (0.27–2.66)	1.04 (0.25–2.40)
Grand means		3.59 (2.00–5.63)	1.85 (0.59–3.98)	1.52 (0.42–2.76)

Table 5.

RESECT database: mTREs and range, in mm, of initial alignment between landmarks and after SIFT-Rank-based affine and SIFT-Rank-based thin-plate spline

Patient	Manual landmarks	SIFT feature correspondences	Initial	After SIFT-based affine	After SIFT-based TPS
1	13	34	5.80 (3.62–7.22)	1.64 (0.14–3.71)	1.48 (0.17–3.51)
2	10	16	3.65 (1.71–6.72)	2.63 (0.85–5.14)	2.62 (0.62–4.89)
3	11	30	2.91 (1.53–4.30)	1.19 (0.64–2.50)	1.04 (0.62–1.52)
4	12	43	2.22 (1.25–2.94)	0.92 (0.22–1.50)	0.83 (0.27–1.53)
6	11	24	2.12 (0.75–3.82)	1.97 (0.51–3.73)	1.55 (0.67–2.88)
7	18	46	3.62 (1.19–5.93)	2.59 (0.84–5.11)	2.38 (0.45–4.33)
12	11	39	3.97 (2.58–6.35)	1.21 (0.24–3.78)	1.20 (0.44–3.09)
14	17	204	0.63 (0.17–1.76)	0.53 (0.08–1.21)	0.53 (0.18–1.18)
15	15	146	1.63 (0.62–2.69)	0.79 (0.26–2.42)	0.74 (0.29–2.31)
16	17	24	3.13 (0.82–5.41)	1.97 (0.48–4.25)	1.94 (0.20–3.84)
17	11	26	5.71 (4.25–8.03)	1.97 (0.94–4.72)	1.99 (0.21–4.51)
18	13	81	5.29 (2.94–9.26)	1.71 (0.71–3.36)	1.69 (0.58–3.03)
19	13	28	2.05 (0.43–3.24)	2.46 (0.67–5.19)	2.78 (0.65–5.04)
21	9	120	3.35 (2.34–5.64)	1.23 (0.49–3.57)	1.07 (0.56–3.20)
24	14	32	2.61 (1.96–3.41)	1.32 (0.44–2.63)	1.35 (0.35–2.24)
25	12	73	7.61 (6.40–10.25)	1.51 (0.35–3.87)	1.24 (0.21–3.57)
27	12	47	3.98 (3.09–4.82)	0.48 (0.05–0.96)	0.83 (0.20–0.93)
Grand means			3.55 (2.10–5.40)	1.54 (0.47–3.39)	1.49 (0.39–3.04)

The average initial mTRE value over the 13 patients from BITE dataset is 3.59 mm, which is reduced to 1.85 mm after SIFT-Rank-based affine and 1.52 mm after SIFT-Rank-based thin-plate spline. To determine whether the mean distances were statistically different, a variance analysis (ANOVA) was applied. This yielded F (1, 24) = 9.86, p < .001, indicating a statistically significant improvement between the initial and the nonlinear transformation.

Our registration framework was also validated using pre-and post-resection ultrasound images from the RESECT [54] database.

The average initial mTRE value over the 17 patients from RESECT dataset was 3.54 mm. This was reduced to 1.54 mm after SIFT-based affine and 1.49 mm after SIFT-based thin-plate spline deformation. To determine whether the mean distances were statistically different, a variance analysis (ANOVA) was applied. This yielded F (1, 32) = 20.42, p < .001 indicating a statistically significant improvement between the initial and the nonlinear transformation.

Conclusions

We presented an efficient registration method for 3D iUS images achieved from a sparse set of automatically extracted feature correspondences. In this work, we focused mainly on intraoperative US registration in neurosurgery. The proposed methodology is particularly robust to missing or unrelated image structure and produces a set of feature correspondences that can be used to initialize more detailed and dense ultrasound registration. 3D SIFT-Rank features were shown to provide reasonable non-rigid registration of 3D iUS images while requiring low computational time for features extraction and matching. We found that our registration algorithm reduces the mTRE from an initial value of 3.3 to 1.5 mm (n = 9). Our long-term goal is to use non-rigid registration to map pre-surgical image data (e.g., pre-surgical MR) to intra-operative image data (e.g., iUS or MR) to correct for brain tissue deformations that arise from brain shift and surgical interventions.