Accuracy Loss Due to Selection Bias in Cohort Studies with Left Truncation

Abstract

Background:

Selection is a common problem in paediatric and perinatal epidemiology, and truncation can be thought of as missing person time that can result in selection bias. Left truncation, also known as late or staggered entry, may induce selection bias and/or adversely affect precision. There are two kinds of left truncation: fixed left truncation where the start of follow-up is initiated at a set time, and variable left truncation where follow-up begins at a stochastically varying time-point.

Methods:

Using data from a time-to-pregnancy study, augmented by a simulation study, we demonstrate the effects of fixed and variable truncation on estimates of the hazard ratio.

Results:

First, fixed or variable non-differential left truncation results in a loss of precision. Fixed or variable differential left truncation results in a bias either towards or away from the null as well as a loss of precision. The extent and direction of this bias is a function of the size and direction of the association between exposure and outcome, and occurs in common scenarios and under a wide range of conditions.

Conclusions:

As demonstrated in simulation studies, selection bias due to left truncation could have a serious impact on inferences, especially in the case of fixed or variable differential left truncation. When present in epidemiologic studies, proper accounting for left truncation is just as important as proper accounting for right censoring.

Confounding and measurement bias are fairly well described throughout the epidemiologic literature. However, selection bias is not characterised as well.^1–5 Selection bias is a form of missing person-time, often including the entire person. It has been shown that selection bias is a result of conditioning on a collider,⁶ and can be manifest as a result of censoring or truncation. It is generally accepted that a loss in sample size or person-time typically results in a loss of precision for estimates of exposure effects. Right-censoring, which occurs when the survival time exceeds the censoring time,² may induce selection bias, and can similarly be thought of as missing person-time.^1,5

Left truncation, also known as late or staggered entry, may also induce selection bias or adversely affect precision, resulting in a loss of accuracy. Accuracy is defined as the convolution of validity and precision, and is typically quantified by mean squared error. Formally, when the survival time is less than the left truncation time, no information about the subject is known. Hence, the person-time in the cohort is a sample from a conditional (or truncated) distribution.⁷ It is important to contrast left truncation, in which the occurrence of the event and the existence of the individual is unknown, to right or left censoring, in which a subject is known to exist but the survival time is only partially known (i.e. the timing of the outcome is unknown). A possible example of left censoring could be when girls are recruited into a study of age at menarche and some have already experienced menarche.

There is a rich history of statistical work in truncation^8–17; however, little attention has been given to left truncation in the epidemiologic literature. The few exceptions, to our knowledge, have dealt solely with the setting where the amount of left truncation differs for subjects (which we denote variable truncation), as opposed to the setting where the timing of the left truncation is fixed, i.e. the follow-up starts at a fixed time-point.^11,18,19 Here we describe the potential for lost accuracy due to left truncation, including the effect of truncation on the proportionality of hazards.

In the following two sections, we define left truncation and demonstrate its effects on bias and precision.

Definitions

Fixed left truncation

The start of follow-up is initiated at a set time-point s > 0, for all study participants, where s is predetermined by design and the origin, and 0 is the initiation of the time at risk. An example in perinatal epidemiology of fixed truncation occurs when assembling a cohort of pregnant women to study the effects of preconception smoking on early pregnancy losses (Figure 1a-b). Current technology has the capability to detect pregnancies after implantation using human chorionic gonadotropin pregnancy tests (approximately s = 6 days after conception). Thus, pregnancy losses that occur between fertilisation (day zero) and implantation (day six) are not detectable by any method and therefore induce fixed left truncation at day six. Consequently, in analysing risk of early pregnancy losses, there is a potential for paradoxical dose-response patterns.^20,21 If a small dose of a reproductive toxin causes pregnancy loss, then a larger dose may cause loss at an even earlier stage in gestation, such as before implantation. Thus, the higher dose may show no apparent effect on early loss, or may even show an apparent ‘protective’ effect. Another example of fixed truncation is when a cohort is assembled at a fixed recruitment age. If studying mortality only among subjects older than s = 40 years, any deaths that occurred before the fixed truncation time (s = 40) may remain unknown. These situations can also be depicted by Figure 1, which displays scenarios of fixed truncation where deaths may occur before the start of follow-up, and where the truncation is non-differential (1a) and differential (1b) by exposure status.

Figure 1.

Graphs of fixed and variable truncation where deaths may occur before the start of follow-up, both differential and non-differential by exposure status. Horizontal lines represent subjects (solid = exposed, dashed = unexposed). Dots represent events. (a) Fixed truncation − non-differential; (b) fixed truncation − differential; (c) variable truncation − non-differential; (d) variable truncation − differential; (e) fixed and variable truncation − non-differential; (f) fixed and variable truncation − differential.

Variable left truncation

Variable left truncation occurs when follow-up begins at stochastically varying time-points for each participant (Figure 1c-f). Enrollment of a cohort of pregnant women is likely to be subject to variable truncation, as it is common for women to begin study follow-up at the first doctor’s visit to confirm pregnancy. The timing of this visit is determined by multiple factors, some related to the exposure of interest (e.g. socioeconomic factors). Therefore, women enroll in the study at different gestational ages or times since conception. In this case, the pregnancies lost due to spontaneous abortions prior to the first confirmatory appointment are not observed or recruited into the study, thus leading to variable truncation. Formally, individuals, indexed by i, enter the cohort at different times s_i, where 0 < s_i. The factors affecting the probability distribution of times s_i can be conditionally independent of the exposure, i.e. f_s(s | X, T) = f_s(s | T), or not, where X and T denote exposure and outcome, respectively. Entry into the cohort is conditional on the outcome.

Example

In prospective cohort studies, such as time to pregnancy (TTP) studies, left truncation is commonly introduced because time at risk does not always coincide with the study time under observation. For example, Buck Louis et al.²² describe a prospective TTP study which included couples whose pregnancy attempts began at study enrollment as well as couples who had been attempting pregnancy for up to 3 months prior to enrollment. In many TTP studies, truncation is introduced through the design of the study and typically goes unrecognised. The source of the truncation can be understood by first describing the ideal source population. This population should be comprised of couples of reproductive age, at risk of pregnancy (i.e. having unprotected intercourse in the fertile window) and enrolled in the study from the first time they are at risk of pregnancy. If they are not enrolled from the first time they are at risk of pregnancy, left truncation will be induced through the design of the study. It is common that a fraction of the ideal study population experienced the outcome (pregnancy) before they are recruited to the study. The source population of Buck Louis’ study was all couples having unprotected intercourse in the fertile window within 3 months prior to the start of the study; those who became pregnant prior to the start of the study would not enter the study and their information would be truncated. The ideal TTP study is analogous to Ray’s²³ ‘new user’ design, and might be called a ‘new trier’ design. Given that the reproductive process involves complex human behaviour, this design is often infeasible and truncation is essentially guaranteed.

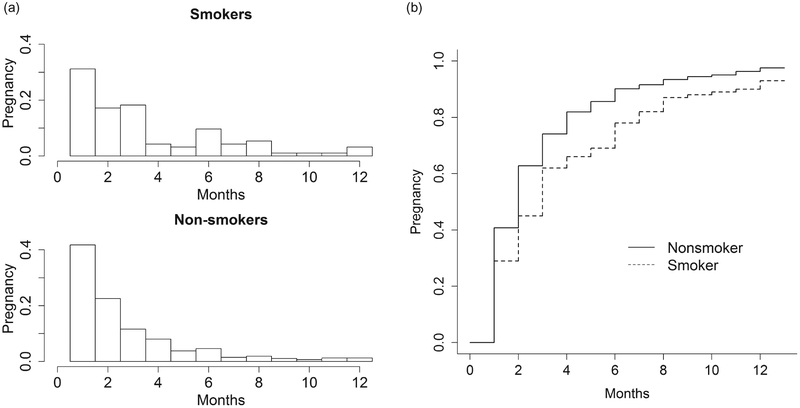
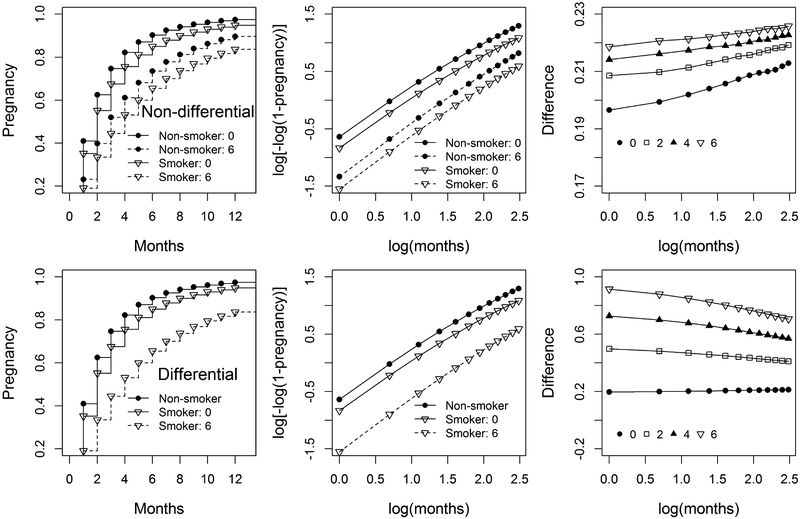
Baird and Wilcox²⁴ describe a study that measures the effect of smoking on reduced fecundity. Among 586 women attempting pregnancy, TTP was measured as the number of consecutive menstrual cycles from the study enrollment to pregnancy. Women were administratively censored at 13 cycles, the time-point at which medical interventions often begin. Smoking was defined as a fixed exposure measured during the first cycle/month of study, and dichotomised as current (reporting an average of one or more cigarettes per day) vs. former and never. For illustrative purposes only, we will make the strong assumption that the members of this cohort were a random sample from the source population (i.e. all the couples were at risk of pregnancy for the first time and there was no induced truncation). The histograms and the Kaplan-Meier (KM) curves for smoking and non-smoking women are shown in Figure 2. The pregnancy rate for non-smokers is higher than that for smokers. When the proportional hazards assumption (PHA) holds, the plot of log[-log(KM)] curves should result in a graph with parallel curves. Figure 3 gives plots for the cohort under different levels of imposed left truncation. In Figure 3, the distance between the two log[-log(KM)] curves does not change dramatically. It indicates that there is not serious violation of the PHA. The pregnancy number and the probabilities of pregnancy that would be expected to be observed under various levels of truncation for smokers and non-smokers in the original data are presented in Table A1 in the Appendix.

Figure 2.

(a and b) Number of pregnancies and Kaplan-Meier curves for time to pregnancy by smoking status for 586 women followed 12 months^a. ^aAdministratively censored in month 13.

Figure 3.

Pregnancy and l = log[−log(1 − pregnancy)] for fixed non-differential (top) and differential (bottom) truncation at months 0 (no truncation) and 6, the difference of l between non-smokers and smokers (δ = l_non-smoker − l_smoker) for truncation at months 0, 2, 4, and 6.

Simulation study

We performed a simulation study to demonstrate the possible consequences of left truncation on parameters of interest with respect to accuracy (bias and precision). The parameters for the simulation were chosen to mimic the Baird and Wilcox TTP data example (assumed not to have truncation).²⁴ We explored a scenario where the PHA held, and assessed the bias due to fixed and variable truncation when fitting a beta-geometric model²⁵ and (discrete-time) Cox model. We also considered two truncation strategies for non-smokers and smokers: non-differential truncation where both non-smokers and smokers have the same truncation time, and differential truncation where only smoking observations are truncated (in practice, smokers are more likely to be truncated than non-smokers).

We generated fixed truncation at month 2, 4, and 6, and variable truncation using the following algorithm: When the TTP for individual i t_i (t_i > 1) is truncated, we select a truncation time s_i randomly from {1, 2 , … , t_i − 1} with equal probability p = 1/(t_i − 1). Here, the equal probability assumption (which may not hold in practice) is made for simplicity. We consider three scenarios for variable truncation, with p = 0.1, 0.2, and 0.4 yielding 10%, 20%, and 40% variable truncation, respectively. In all cases, to ensure that differences observed in simulation were not due simply to reductions in sample size, we augmented the truncated samples to maintain a consistent sample size across simulation runs.

For each scenario, we generated studies of size 1000 with 500 exposed and 500 unexposed. We also explored a study size of 10 000, which showed the same patterns and an expected decrease in standard error (not presented). We generated 10 000 studies to obtain the mean, standard derivation, and 95% confidence limits. For each simulated study, we applied the beta-geometric model to estimate the relative risk (RR) using non-linear least squares (R function ‘nls’) and the discrete-time Cox model using maximum partial likelihood to estimate the hazard ratio (HR). We tested the PHA using the Schoenfeld residuals as described by Grambsch and Therneau.²⁶

The PHA is satisfied in the untruncated data for the simulations presented. We generated two beta-geometrically distributed populations with parameters c_ns = 2.438, d_ns = 0.313 for non-smokers, and c_s = 2.840, d_ns = 0.400 for smokers, where c is the mean TTP and d = 0 if the TTP is truly geometrically distributed. Further details are available in Appendix and Cole et al.²⁷ If (c_ns − 1)/d_ns = (cs − 1)/d_s, the PHA holds. Table 1 presents the means, standard errors, and 95% confidence intervals of the parameters, percentage of bias, and the percentage of simulated cases that satisfy the PHA among all simulations. The PHA percentage holding is 95% for a moderate sample size of 500 and 90% for large sample size of 10 000 when there is no truncation.

Table 1.

The estimated mean and standard error (SE) of non-smoker TTP_ns, smoker TTPS, difference TTP_s-TTP_ns, relative risk of non-smoker to smoker (RR) in beta-geometric model, hazard ratios (HR) in discrete Cox model, 95% confidence limits (CL), CL width, and percentage of relative bias for 500 non-smokers and 500 smokers when proportional hazards assumption strictly holds

Truncation (Month)	Beta-geometric					Discrete Cox
	TTPns (SE)	TTPs (SE)	TTPs-TTPns(SE)	Relative riska (95% CI)	CL widthb	Hazard ratio (95% CL)	CL widthc	Biasd (%)	Hold (%)	Hold (%)e
None	2.44 (0.12)	2.85 (0.16)	0.41 (0.20)	0.86 [0.74, 0.99]	1.34	0.82 [0.72, 0.92]	1.28	0	95	90
Fixed truncation:
Non-differential
2	3.06 (0.17)	3.66 (0.23)	0.60 (0.28)	0.84 [0.71, 0.98]	1.37	0.81 [0.71, 0.92]	1.29	−1	95	93
4	3.69 (0.23)	4.47 (0.30)	0.78 (0.36)	0.83 [0.70, 0.97]	1.40	0.80 [0.71, 0.91]	1.29	−2	95	94
6	4.30 (0.28)	5.27 (0.36)	0.97 (0.43)	0.82 [0.69, 0.97]	1.41	0.80 [0.70, 0.91]	1.30	−2	95	94
Differentialf
2	2.44 (0.12)	3.66 (0.23)	1.21 (0.26)	0.67 [0.57, 0.78]	1.37	0.64 [0.57, 0.73]	1.28	−18	91	19
4	2.44 (0.12)	4.47 (0.30)	2.03 (0.31)	0.55 [0.47, 0.64]	1.37	0.54 [0.48, 0.61]	1.27	−28	80	0
6	2.44 (0.12)	5.28 (0.36)	2.83 (0.38)	0.47 [0.40, 0.55]	1.38	0.47 [0.41, 0.53]	1.27	−35	69	0
Variable truncation:
Non-differential
10%g	2.27 (0.11)	2.62 (0.14)	0.35 (0.18)	0.87 [0.75, 1.00]	1.34	0.82 [0.72, 0.93]	1.29	0	95	86
20%	2.12 (0.10)	2.42 (0.13)	0.30 (0.16)	0.88 [0.76, 1.01]	1.32	0.82 [0.73, 0.93]	1.28	0	94	82
30%	1.86 (0.08)	2.11 (0.08)	0.25 (0.12)	0.88 [0.78, 0.98]	1.26	0.82 [0.73, 0.92]	1.26	0	96	76
Differential
10%	2.44 (0.12)	2.62 (0.15)	0.18 (0.19)	0.93 [0.81, 1.08]	1.34	0.86 [0.76, 0.97]	1.29	4	87	3
20%	2.45 (0.12)	2.42 (0.13)	−0.03 (0.18)	1.01 [0.88, 1.17]	1.33	0.91 [0.80, 1.03]	1.29	9	66	0
40%	2.45 (0.12)	2.10 (0.09)	−0.35 (0.15)	1.17 [1.02, 1.32]	1.29	1.01 [0.89, 1.13]	1.27	19	22	0

^aRelative risk = p_s/p_ns, where p_ns and p_s are the overall conception probability for non-smokers and smokers respectively, and p = 1 /TTP.

^bCL width = RR_upper/RR_lower.

^cCL width = OR_upper/OR_lower.

^dRelative Bias = (HR_truncated — HR_un-truncated)/HR_un-truncated.

^eFor 10 000 non-smokers and 10 000 smokers.

^fFor the differential scenarios, only the smokers were truncated.

^gPercentage of the truncated observations.

The results are based on 10 000 simulations.

Fixed non-differential left truncation

Figure 3 illustrates the TTP and l = log[−log(1 − pregnancy)] for truncation at months 0 (i.e. no truncation) and 6, as well as the difference of l between non-smokers and smokers (δ = l_non-smoker − l_smoker) for truncation at months 0, 2, 4, and 6. The TTP values are obtained by the mean of 10 000 simulations with sample size 1000. If the PHA is satisfied, the graph of l vs. log(months) should result in parallel lines, and the graph of δ vs. log(months) results in a horizontal line.

When the truncation time increases from 0 to 6, the upper plots in Figure 3 show that both the pregnancy rates and l for smokers and non-smokers decrease (dash lines), and the difference δ slightly increases from 0.2 to 0.22 at month 1. When the month increases from 1 to 12, difference δ hardly change (although δ slightly increase due to the finite sample size), which indicates that the PHA holds.

Table 1 shows that as the fixed truncation time increases, neither the RR from the beta-geometric model nor the HR from the (discrete-time) Cox model exhibits notable bias. Moreover, there is a slight decrease of efficiency for beta-geometry model as the fixed truncation time increases, as illustrated by the increase of the CL width (recall that the sample size is augmented such that truncation does not deplete the sample size). Note that the (discrete-time) Cox model appears slightly more efficient than the beta-geometric for all scenarios. However, even for large sample sizes of 10 000, the pattern of results were similar (data not shown). Finally, as expected, more than 90% of the simulated data sets satisfy the PHA

Fixed differential left truncation

For differential truncation, only the smoking observations were truncated. When the fixed truncation time increases from 0 to 6, the lower plots in Figure 3 show that both the pregnancies and l for smokers decrease (dash lines), the difference δ largely increases from 0.2 to 0.9 at month 1, while δ for fixed non-differential truncation slightly increases from 0.20 to 0.22. As the month increases, δ decreases. The δ curves are no longer horizontal, which indicates that the PHA is violated.

Table 1 shows that as the fixed differential truncation time increases, both the RR from the beta-geometric model and the HR from the (discrete-time) Cox model exhibit notable bias. Also, the efficiency for beta-geometry models increases as the fixed differential truncation time increases. However, similar to non-differential truncation, for large sample size of 10 000, the pattern of results do not change. No simulated data sets satisfy the PHA for truncation at months 4 and 6 for large sample sizes as shown in the last column in Table 1. However, for a moderate sample size of 500, 91% of the simulated data sets truncated at month 2 satisfy the PHA. Finally, 70% of the simulated data sets truncated at month 6 satisfy the PHA. Ideally, for infinite sample size, in the true underlying data the PHA holds, but in the truncated data it does not hold as shown in the last column in Table 1. However, when the sample size is moderate, e.g. 500, the PHA test does not reject the hypothesis that PHA violates. This can be explained intuitively by the plot of the difference δ between non-smokers and smokers in Figure 3. If PHA holds, the plot of δ shows a horizontal line. The points for small samples scatter more than those for large samples. It is more likely to fit them with a horizontal line for small samples than large samples. So the PHA was more likely to appear to hold for smaller samples. Even when PHA does not hold, the HR for large samples is the same as that for small samples, although the CL width for large sample is smaller than that for small sample.

When the PHA is violated, the Cox model is not appropriate, and we should use other alternative models, e.g. the beta-geometric model. However, in our simulation, even when the PHA does not hold based on the PHA test for large sample, the results from beta-geometry model are similar to those from discrete Cox model. Although fixed differential truncation can induce non-proportional hazards for a large sample size, in some cases with only modest non-proportional hazards (that does not have practical implications), the Cox model still can be applied.

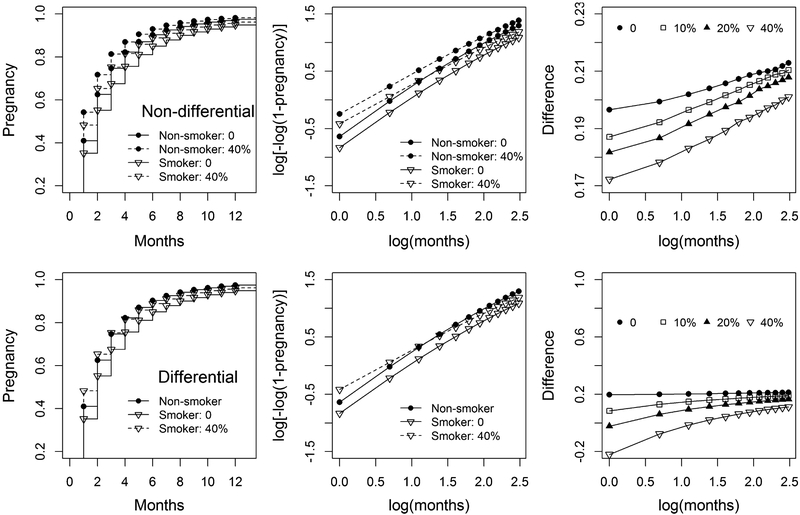
Variable non-differential left truncation

Figure 4 illustrates pregnancy and l for variable non-differential (top) with 0% (no truncation) and 40% truncation, the difference of l between non-smokers and smokers for 0%, 10%, 20%, and 40% truncation. When the truncation proportion increases, both the pregnancies and l (dash lines) for smokers and non-smokers increase, and the difference 8 slightly decreases from 0.20 to 0.17 at month 1. As month increases, 8 slightly increases, indicating that the PHA is slightly violated.

Figure 4.

Pregnancy and l = log[−log(1 − pregnancy)] for variable non-differential (top) and differential (bottom) truncation with 0% (no truncation) and 40% truncation, the difference of l between non-smokers and smokers (δ = l_non-smoker − l_smoker) for 0%, 10%, 20%, and 40% truncation.

Table 1 shows that as the variable non-differential truncation proportion increases, neither the RR from the beta-geometric model nor the HR from the (discrete-time) Cox model exhibits notable bias. The slight decrease of CL width for beta-geometry model indicates that the efficiency slightly increases. However, for large sample sizes of 10 000, the pattern of results does not change for either model as the variable truncation time increases. The proportion of observations in which the PH assumption holds decreases to 76% for truncation proportion 0.4 with a large sample size of 10 000; however, the PHA holding remains as large as 95% for a moderate sample size of 500 due to the robustness of Cox model.

Variable differential left truncation

When the variable truncation time increases, the lower plots in Figure 4 show that both the pregnancies and l for smokers increase, δ largely decreases from 0.20 to −0.20 at month 1, while δ for variable non-differential truncation slightly decreases from 0.20 to 0.17. When the time increases, δ increases, which indicates that the PHA is violated.

Table 1 shows that as the variable differential truncation proportion increases, both the RR from the beta-geometric model and the HR from the (discrete-time) Cox model exhibit notable biases. Moreover, there is a slight increase in the efficiency for beta-geometry models. However, for a sample size of 10 000, the pattern of results does not change for either model as the variable truncation time increases. The percentage of the PHA satisfaction for a sample size of 10 000 decreases, illustrating that variable differential truncation can also induce non-proportional hazards.

Comment

Left truncation can be classified as fixed or variable, with different implications for effect estimation. Fixed left truncation may result in bias of the total effect (i.e. total effects is defined as the HR for the entire risk period under truncation s > 0) towards or away from the null, depending on whether the truncation is differential (expected bias may be towards or away null) or non-differential (unbiased) with respect to the exposure. The fixed differential left truncation causes underestimation of the HR. With proper methods of estimation, total effects are identifiable under the non-differential variable left truncated study design as long as the minimum truncated time is zero. While non-differential variable left truncation is unbiased, differential variable left truncation will induce bias for the total effect. The variable differential left truncation overestimates the HR. However, as is always the case with experimental (simulation) work, the patterns observed in the limited simulations may or may not hold generally

With fixed left truncation, the survival function prior to the fixed left truncation time cannot be identified, and total effects are inestimable. However, under non-differential fixed left truncation, effects conditional on survival to the fixed time can be identified and may have important public health implications as long as they are carefully interpreted as conditional effects. However, conditional effects may not be informative in some scenarios (e.g. What is the effect of smoking on TTP for a couple that has been trying to become pregnant for 3 months or longer? If smoking affects TTP, those with TTP <3 months will be disproportionately non-smokers). Researchers have to be acutely aware of the hypotheses that can be tested in each setting.

It is important to note that there may be certain situations in which we can assume that the conditional or truncated effects are equivalent to the total or non-truncated effects. In particular, if one can be certain that no events occur between the initiation of risk and truncation time s, then the total and conditional effects would be equivalent (P(Y = 1 | X = x, S > s) = P(Y = 1 | X = x). For example, in the case of atherosclerotic cardiovascular events, few to no events occur before the age of 30, although individuals are at risk. However, exercise exertion could be an important trigger before age 30, possibly a more important cause of these events than it is protective. At older ages, protective effects of exercise may dominate triggering effects. Thus, the exposure contrast paired with an outcome determines the relevancy of left truncation, and only when disease paired with a cause is taken into consideration can one evaluate whether truncation is of importance. Therefore, starting a CVD cohort at age 30 is a form of fixed truncation where one can safely assume that the total and conditional effects are approximately equivalent because few to no events will occur before age 30. Another scenario where estimation of a fixed left truncated conditional effect may provide insight into a total relative effect of exposure is when events occur proportionally before left truncation in both exposed and unexposed groups, which may result in a loss of efficiency.

In some studies, both fixed and variable left truncation may be operating simultaneously. For example, pregnancy has a fixed left truncation time of 6 days (gestational age > 6 days) and studies of pregnancy outcomes are often subject to variable left truncation at the date when women enter prenatal care or the study of interest. In fact, whenever variable left truncation is present, and the minimum entry time is greater than zero, say s, then that minimum entry time acts as a fixed left truncation time point because there is no information regarding the survival function between zero and s.

To account for fixed or variable left truncation introduced through the design of the study, Flanders and Klein1 suggest beginning follow-up before exposure occurs, an approach analogous to Ray’s new user design.²³ In such approaches, one strives to design and conduct studies to preclude left truncation by enrolling subjects at a common origin of risk and exposure. This design solution of beginning follow-up at a common origin, while ideal, is unrealistic in many instances, such as in the case of unavoidable occupational exposures or when studying long-term exposure levels. This design solution is akin to forcing 100% study follow-up to preclude selection bias due to dropout. In the pregnancy example discussed previously, in designing a prospective study to ascertain the effect of smoking on pregnancy loss, we would have to start the study early enough after conception to ensure that no pregnancy losses occurred from the time of pregnancy/exposure. Given current pregnancy detection methods, this is not a feasible design.

Failing to discover a design solution, one must account for fixed or variable left truncation in the analysis. In the absence of left truncation, epidemiologists estimate the survival curve using KM methods. In the presence of fixed left truncation, under certain assumptions one can estimate a truncated survival curve beyond the truncation time using standard KM methods.¹⁰ Here, however, the survival curve prior to s is not identifiable given the observed data. In principle, missing data methods, which capitalise on information external to the observed data, may be used to provide a complete survival curve. In the presence of variable left truncation, one can estimate the survival curve using the extended KM method.^28–30 Analogous to the assumption of no informative censoring, the extended KM method provides an unbiased estimate of the survival curve if the variable left truncation is non-informative.¹⁰ Again, missing data methods that capitalise on external data can be used to estimate the survival curve in the presence of informative left truncation.²⁷ Regardless of what method is used, one cannot identify the survival curve for pregnancy loss before the minimum observed left truncation time.

Careful application of the proportional hazards model to cohort study analysis is needed to limit the detrimental effects of non-differential variable left truncation. The model assumes that the hazard in an exposed population is a constant multiple of the hazard in an unexposed population. Howards et al.¹⁸ applied these models in a setting of variable left truncation and reached similar conclusions as presented in Table 1. However, truncation can lead to nonproportionality of the proportional hazard models. Careful consideration should be given to the source of non-proportionality and appropriate estimation models should be applied.

A problem arises, however, when determining the initial time-point for the hazards model. A naive proportional hazards analysis that defines risk sets in the standard way (all individuals with event times greater than or equal to t_i and not previously censored) can yield biased estimates of the relative hazard. To account for variable truncation, a modified definition of the risk set based on event times greater than or equal to t_i and not left truncated needs to be utilised in order to properly account for variable left truncation.

Conclusion

We have demonstrated situations where selection bias is generated by left truncation. This bias occurs in common scenarios and across a wide range of conditions. When no events occur before the truncation time s, no bias is induced. However, as seen in the TTP example, null-bias can be induced when events do occur prior to s. When deaths occur before the truncation time s, it is important to identify whether these prior events are likely associated with exposure; if so, then selection bias is induced. As demonstrated in the simulation study, selection bias due to left truncation could have a serious impact on inferences, especially in the case of fixed or variable differential left truncation. It is important to take steps to account for left truncation in both the design and analysis of epidemiologic studies.

Appendix

Pregnancy numbers in Baird and Wilcox’s study²⁴

Table A1.

Pregnancy numbers (n) in the original clinical data²³ and probabilities of pregnancy $\left(w_{k-s}^{\pm }\right)$ that would be expected to be observed for cycle k − s (k > s) under truncation at cycle s for non-smoker (−) and smoker (+) $\left(w_{k-s}^{\pm }=n_k^{\pm }/{\displaystyle {\sum }_{j=s+1}^{13}{n}_j^{\pm }}\right)$

Cycle (k)	Non-smokers (−)					Smokers (+)
	n−	$w_{k-s}^{+}$				n+	$w_{k-s}^{-}$
Truncation time		0	2	4	6		0	2	4	6
1	198	0.407				29	0.290
2	107	0.220				16	0.160
3	55	0.113	0.304			17	0.170	0.309
4	38	0.078	0.210			4	0.040	0.073
5	18	0.037	0.099	0.205		3	0.030	0.055	0.088
6	22	0.045	0.122	0.250		9	0.090	0.164	0.265
7	7	0.014	0.039	0.080	0.146	4	0.040	0.073	0.118	0.182
8	9	0.019	0.050	0.102	0.188	5	0.050	0.091	0.147	0.227
9	5	0.010	0.028	0.057	0.104	1	0.010	0.018	0.029	0.045
10	3	0.006	0.017	0.034	0.063	1	0.010	0.018	0.029	0.045
11	6	0.012	0.033	0.068	0.125	1	0.010	0.018	0.029	0.045
12	6	0.012	0.033	0.068	0.125	3	0.030	0.055	0.088	0.136
≥13	12	0.025	0.066	0.136	0.250	7	0.070	0.127	0.206	0.318
Total	486	1.0	1.0	1.0	1.0	100	1.0	1.0	1.0	1.0

II. Beta-geometric model

Assume that the fecundability follows a beta distribution:

$$f(p)=p^{(\text{μ-θ)/θ}}{(1-p)}^{(1-\text{μ-θ)/θ}}B{\left[\frac{\text{μ}}{\text{θ}},\frac{\text{1-μ}}{\text{θ}}\right]}^{-1},$$

w here p is the per-cycle conception probability, μ is the mean of the conception probability p, and θ is a ‘shape’ parameter, B[.] is Beta function. Then the probability that conception occurs at cycle x for a randomly selected couple follows a beta-geometric distribution:

$$\mathrm{Pr}\left(X=x\right)=\frac{\text{μ}{\displaystyle {\prod }_{i=1}^{x-1}\left[\text{1-μ+(}i\text{-1)θ}\right]}}{{\displaystyle {\prod }_{i=1}^x\left[\text{1+(}i\text{-1)θ}\right]}}.$$

Following Weinberg et al.²⁵, define new parameters c and d by

$$c=1/\text{μ},d=\text{θ}/\text{μ,}$$

where c is the mean TTP and d = 0 if the TTP is truly geometrically distributed. The mean rate after j-1 unsuccessful cycles is

$${\text{μ}}_j=1/\left[c+d(j-1)\right].$$ (A1)

Note that the beta-geometric model does not assume proportional hazard. If (c-1)/day is the same for two beta-geometric distributions, the PHA is satisfied, and a (discrete-time) Cox model will provide an unbiased estimate of the hazard ratio. When two populations are to be compared, the above model can be extended as follows:

$$\text{μ}=1/\left(c+eI\right),d=\text{θ}/\text{μ}$$ (A2)

where I is an indicator variable for the second population, e is the mean difference of TTP between populations.

We applied the beta-geometric model to the Baird and Wilcox’s TTP data example²⁴ in Table A1 for non-smokers and smokers, respectively, and obtained c_ns = 2.44, d_ns = 0.31 for nonsmokers, and c_s = 3.50, d_ns = 0.36 for smokers. Because (c_ns − 1)/d_ns = 4.65 and (c_s − 1)/d_s = 6.94, (c_ns − 1)/d_ns ≠ (c_s − 1)/ds, the PHA is not satisfied in this example.