Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Sep 4;9(18):5539–5547. doi: 10.1021/acs.jpclett.8b01695

Pulsed Electron Decoupling and Strategies for Time Domain Dynamic Nuclear Polarization with Magic Angle Spinning

Edward P Saliba 1, Erika L Sesti 1, Nicholas Alaniva 1, Alexander B Barnes 1,*
PMCID: PMC6151657  PMID: 30180584

Abstract

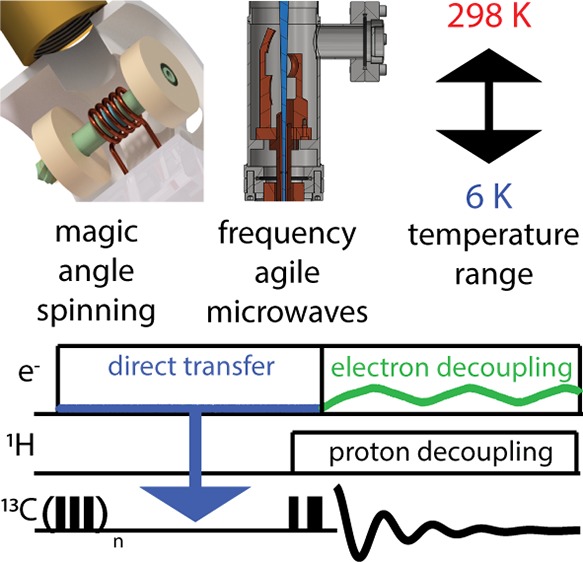
graphic file with name jz-2018-016955_0009.jpg

Magic angle spinning (MAS) dynamic nuclear polarization (DNP) is widely used to increase nuclear magnetic resonance (NMR) signal intensity. Frequency-chirped microwaves yield superior control of electron spins and are expected to play a central role in the development of DNP MAS experiments. Time domain electron control with MAS has considerable promise to improve DNP performance at higher fields and temperatures. We have recently demonstrated that pulsed electron decoupling using frequency-chirped microwaves improves MAS DNP experiments by partially attenuating detrimental hyperfine interactions. The continued development of pulsed electron decoupling will enable a new suite of MAS DNP experiments that transfer polarization directly to observed spins. Time domain DNP transfers to nuclear spins in conjunction with pulsed electron decoupling is described as a viable avenue toward DNP-enhanced, high-resolution NMR spectroscopy over a range of temperatures from <6 to 320 K.

Nuclear magnetic resonance (NMR) spectroscopy is a powerful tool that can provide details about the molecular structure and dynamics of myriad systems.1−5 NMR can routinely yield multiple distinguishable signals with site-specific resolution.6 Not only does the chemical shift provide information about the electronic environment, but spatial and through-bond magnetic interactions provide distance and connectivity information, which determine constraints on the molecular structure.7−12 Solid-state NMR (ssNMR) is often employed in conjunction with magic angle spinning (MAS) to extend coherence lifetimes and improve spectral resolution.13−16

While NMR has advantages over other forms of spectroscopy, it suffers from an inherent lack of sensitivity due to the small Boltzmann polarization of nuclear spins, given by eq 1

graphic file with name jz-2018-016955_m001.jpg 1

where h is Planck’s constant, kB is Boltzmann’s constant, ν0 is the Larmor frequency of the spin, and T is the temperature in Kelvin.17−19 The small spin polarization results in a weak electromotive force induced in the probe receive coil and a correspondingly poor signal-to-noise ratio (S/N) in the NMR spectrum.20−22 Common strategies to increase the NMR S/N involve performing experiments at high magnetic fields (7–25 T), using large samples, and averaging signals for as long as months.23

Dynamic nuclear polarization (DNP) can increase the NMR S/N by orders of magnitude, greatly shortening signal-averaging times and expanding the range of systems that can be studied with NMR.24 In MAS DNP, samples are typically doped with an exogenous stable radical (known as a polarizing agent), and upon continuous wave (CW) irradiation with an appropriate microwave frequency,50 the large electron spin polarization is transferred to nuclear spins through hyperfine interactions. Most applications of DNP also rely on proton dipolar couplings to spread the enhanced polarization throughout a proton network, resulting in bulk nuclear hyperpolarization.25

The gyromagnetic ratio of a bare electron (g = 2.0023) is 658 times larger than that of a proton, leading to higher spin polarization and also strong hyperfine couplings. Dipolar hyperfine couplings are typically leveraged in DNP for polarization transfer but can also lead to detrimental paramagnetic relaxation effects of nuclear spins in the vicinity of the polarizing agent. An example of the exceptional NMR sensitivity achievable with DNP is shown in Figure 1, which compares cross-polarization (CP) MAS 13C-NMR spectra recorded with and without microwave irradiation. DNP increases the NMR signal intensity by a factor of 328 using microwaves from a high-power, 198 GHz gyrotron. MAS DNP is commonly performed below 120 K, but improved technology and methodology will result in better DNP performance at room temperature (RT).

Figure 1.

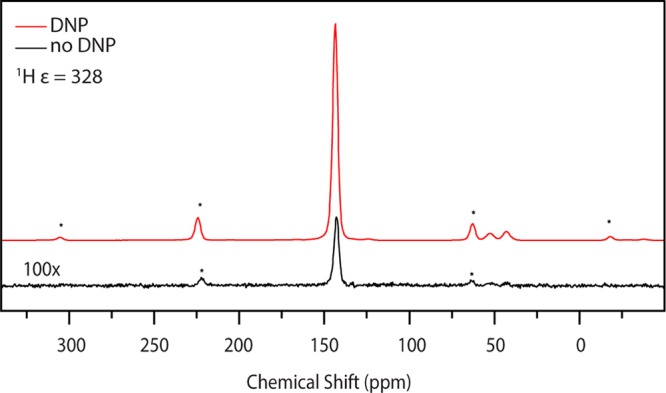
Figure 1

Open in a new tab

(a) CP MAS enhancement spectra of 1 M [U–13C,15N] urea with 20 mM AMUPol at 81 K at 6 kHz. The 1H enhancement was 328. The black curve is 100× the signal obtained with no microwaves. The red curve denotes measurements taken with microwaves present. Figure reproduced with modifications by permission of the Journal of Magnetic Resonance.32

Much of the success and popularity of MAS DNP is derived from the microwave and probe technology development at M.I.T. by Griffin, Temkin, and co-workers.6,26−31 CW gyrotron oscillators and cryogenic MAS probes provide access to sufficient microwave powers and sample temperatures to transform DNP into a widely applicable magnetic resonance technique. Improvements in microwave technology and cryogenics are also expected to play a primary role in future DNP development. Coherent, frequency-agile microwave sources will permit time domain DNP transfers, and access to sample temperatures below 6 K will be achieved by employing helium cryogens. Our laboratory has already shown the advantages of frequency-chirped microwave control in MAS experiments by demonstrating the first attenuation of detrimental hyperfine couplings using pulsed electron decoupling (eDEC). This perspective reviews recent developments in time domain microwave methods and cryogenics employed in MAS DNP. We also discuss progress toward time domain DNP with MAS for applications between 4.2 and 320 K.

The spectra shown in Figure 1 were recorded with a sample temperature of 81 K, which is typical in MAS DNP experiments. Cryogenic temperatures are required in MAS DNP experiments (with notable exceptions in model systems33−36) due to electronic spin relaxation at RT interfering with polarization transfer and nuclear relaxation preventing the buildup of bulk nuclear spin polarization via proton spin diffusion.

The major disadvantage of cryogenically freezing biological samples is that the cryogenically trapped molecular state is not necessarily the same conformation that exists at physiological temperature. This is because the freezing time ranges from hundreds of microseconds to hours. Molecules can change structure to occupy altered minima in the free energy landscape throughout the freezing process. For example, crystallography shows pronounced differences of protein structures determined at cryogenic and RT.37 Hydrogen bonding networks are particularly prone to rearrangement upon cryogenic freezing, and detailed structural measurements on molecular conformations that differ from the relevant ones are less meaningful. In addition, cryogenic DNP severely limits measurements of molecular dynamics.

Magnetic resonance is superbly suited to experimentally determine the molecular dynamics that play a fundamental role in molecular function. Nuclear and electronic interactions yield rich information on motion ranging from nanoseconds to seconds. However, low thermal energy at cryogenic temperatures results in a mostly static snapshot of molecules; therefore, current cryogenic DNP ssNMR methods cannot be used to study extensive molecular dynamics. DNP NMR experiments near RT will allow for the determination of molecular dynamics. Molecular motion near RT can also result in exquisite spectral resolution in ssNMR.

Although MAS NMR spectra of many solids exhibit excellent resolution near RT due to dynamic averaging of multiple conformations with different chemical shifts, they often smear into broad, indistinguishable line shapes at cryogenic temperatures.6 This is true even for cryoprotected samples. Notable exceptions include model systems with cryogenic MAS, in which more homogeneous conformational ensembles result in narrow resonances, even after freeze-trapping.6,22,38−40 Performing DNP near RT will result in well-resolved spectra of a much wider range of samples and also reduce the cost of DNP spectrometers. Refrigerators, liquid nitrogen dewars, cryostats, and associated equipment are expensive and require valuable laboratory space. Noncryogenic DNP spectrometers will result in broader dissemination of high-sensitivity ssNMR technology.

Time domain DNP performed directly to nuclei of interest with subsequent pulsed eDEC is a promising route toward broadly applicable RT MAS DNP. For instance, the relatively slow proton spin diffusion that partially prevents RT DNP is not required. The polarization rate is instead dominated by the hyperfine interaction, radio frequency (RF), and microwave (MW) fields. Repetition rates in such “direct-transfer” DNP experiments are only limited by the longitudinal electronic relaxation (T1S) rather than much longer nuclear T1I,DNP. Such experiments have already been applied in static NMR, resulting in DNP enhancements above 200 at RT.41−43 Additionally, the resulting short polarization times allow for a very low duty cycle of the microwave source, preventing excessive heating.

Although delays between transients are reduced by eliminating the requirement for spin diffusion, electrons must be in direct dipolar contact with the nuclear spin of interest. This can lead to dramatic paramagnetic effects such as large hyperfine shifts and hyperfine broadening of the nuclear resonances.44 We have recently successfully attenuated these detrimental effects by employing pulsed eDEC with frequency-chirped microwave irradiation.45 Although pulsed eDEC has been demonstrated in conjunction with MAS, this has yet to be accomplished with time domain DNP. Challenges include generating sufficiently intense microwave fields within MAS rotors and shaping microwave pulses in the time domain.

Several pulse sequences could potentially be employed for time domain DNP with MAS. We use the term “time domain DNP” to describe coherent electron nuclear polarization transfers that do not rely on electron nuclear cross relaxation. However, we reserve the term “pulsed DNP” to describe experiments in which the Fourier transform of the microwave irradiation results in a bandwidth sufficient to dominate all internal electron spin interactions. In other words, pulsed DNP requires pulses that cover the EPR line shape.

Here, we consider the integrated solid effect (ISE),42,46 off-resonance nuclear orientation via electron spin locking (NOVEL),41 and electron–nuclear CP (eNCP).47,48 Importantly, all three of these time domain DNP transfers can be implemented with chirped frequency microwave irradiation, rather than square, hard pulses. Such frequency-swept strategies are not only robust to microwave field inhomogeneity but also can be readily implemented with existing frequency-agile gyrotrons. We previously discussed the advantages of frequency-swept microwaves for time domain DNP and characterized the substantial microwave field inhomogeneity of MAS DNP.49 We note that pulsed DNP strategies, which require very homogeneous microwave fields, will be restricted to small sample volumes and perhaps negate increases in S/N afforded by DNP.

Wenckenbach and co-workers originally implemented the ISE with a magnetic field sweep to improve solid effect DNP efficiency on samples with poorly resolved solid effect matching condition profiles.46 Later, Griffin and co-workers implemented the ISE with a microwave frequency sweep.42 However, we emphasize that both of these demonstrations were at field strengths < 7 T and not performed with MAS.

The matching condition for the solid effect43 is given by eq 2

graphic file with name jz-2018-016955_m002.jpg 2

where νI is the Larmor frequency of the nucleus of interest. νSeff is given by eq 3

graphic file with name jz-2018-016955_m003.jpg 3

where νS is the Larmor frequency of the electron, νmw is the microwave frequency irradiating the sample, and ν1S is the Rabi frequency (γB1) of the electrons.43Figure 2 demonstrates the energy levels involved in the traditional solid effect,29 in which νS – νmw ≫ ν1S. In this case, the effective field is essentially equal to the microwave frequency offset from the electron resonant frequency. The green circles represent the populations of the states shown at thermal equilibrium (not drawn to scale). The double-headed arrows connect the states whose populations are equalized under microwave irradiation at the frequencies shown. The lowest-energy level of the system is taken to be the zero of the energy scale.

Figure 2.

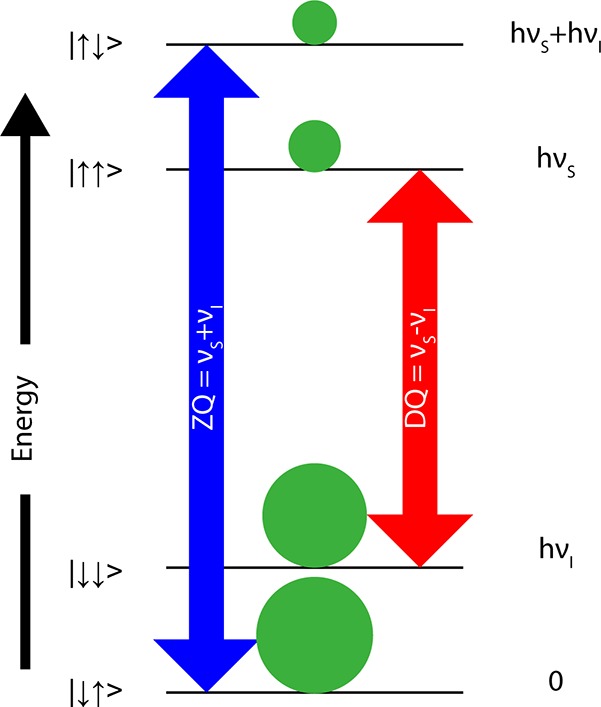
Figure 2

Open in a new tab

Microwaves drive ZQ or DQ forbidden transitions corresponding to the transitions shown. This representation of the solid effect assumes that the nucleus has a positive gyromagnetic ratio. The ket vectors are labeled as |msmI>.

Figure 3a provides an example of a solid effect enhancement profile that is not fully resolved (black), with the eDEC profile superimposed (green) to provide a guide to the position of the electron paramagnetic resonance (EPR) line shape. When the solid effect conditions are not adequately resolved, the double-quantum (DQ) and zero-quantum (ZQ) matching conditions50 given in eq 2 can be simultaneously fulfilled. In this case, the polarization rates of the DQ and ZQ conditions subtract, leading to poor enhancement in the overlapping region. 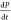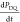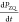This is explicitly stated in eq 4, where Inline graphic is the total rate of polarization, Inline graphic is the rate of polarization due to the DQ solid effect, and Inline graphic is the rate of polarization due to the ZQ solid effect

graphic file with name jz-2018-016955_m007.jpg 4

In the frequency-swept ISE, the microwave frequency initially fulfills either the DQ or ZQ solid effect conditions and is swept through the electron resonance condition to the other solid effect condition. This is shown in Figure 3b, which also includes pulsed eDEC during the echo detection of the NMR signal. During the ISE sweep, electron spins are adiabatically inverted, effectively reversing the direction of the ZQ or DQ contribution to the polarization rate. The rate of polarization is then given by eq 5

graphic file with name jz-2018-016955_m008.jpg 5

This improvement in the polarization rate derived from coherent control of electron spins has been used to obtain RT 1H enhancements on static samples at 0.35 T.42

Figure 3.

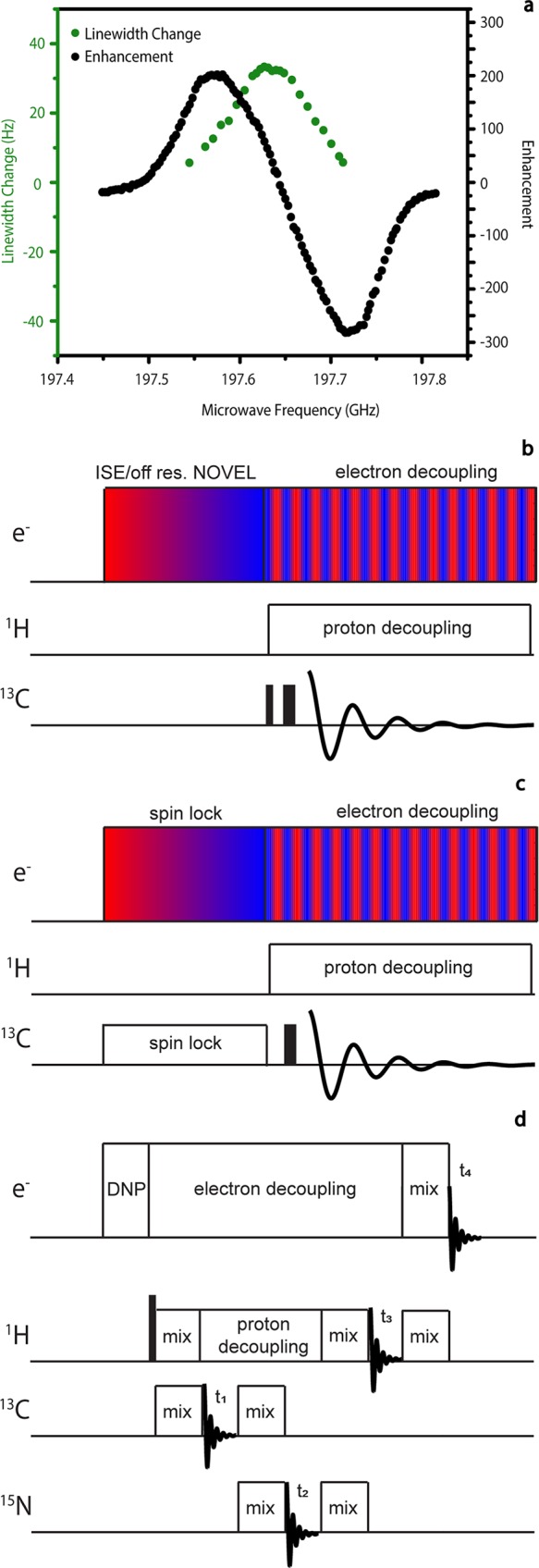
Figure 3

Open in a new tab

(a) Mildly unresolved solid effect enhancement profile for protons in 4 M [U–13C,15N] urea with 40 mM of the Finland trityl radical (black). This figure was reproduced with modification with permission from the Journal of Magnetic Resonance.53 Superimposed is the center frequency dependence of eDEC to demonstrate the location of the EPR spectrum of the radical (green). This figure was reproduced with modification with permission from the Journal of the American Chemical Society.45 (b) Possible frequency-swept ISE/off-resonance NOVEL pulse sequence. (c) eNCP. Color gradients in Figure 3b,c indicate frequency-chirped microwaves. (d) Proposed electron-detected multiple-dimensional pulse sequence.

Closely related to the ISE is off-resonance NOVEL,43 which relaxes the largely prohibitive matching condition for on-resonance NOVEL. NOVEL requires matching the electron Rabi frequency with the nuclear Larmor frequency. Even for nuclei with relatively small gyromagnetic ratios at moderate magnetic fields, such as 15N at a field strength of 7 T, an electron γB1 of 30 MHz is required for on-resonance NOVEL. NOVEL to protons at 21 T requires a 900 MHz electron Rabi frequency, which corresponds to a currently inaccessible power of >10 MW.49 In off-resonance NOVEL, the electron γB1 is made as large as possible, and the offset of the microwave frequency from the electron resonance frequency is used to reach the matching condition given in eq 2. Typically, the NOVEL experiment begins with a pulse on the electron spins to tilt their magnetization into the transverse plane, followed by a spin lock. Alternatively, a frequency chirp of the irradiating microwaves can be employed in an adiabatic half passage to generate transverse magnetization. It should be noted that the easing of the matching condition for off-resonance NOVEL over on-resonance NOVEL comes at the expense of scaling of the maximum enhancement obtainable, as derived previously in the literature.43 The expression for the corresponding scaling factor (κNOVEL) is given in eq 6

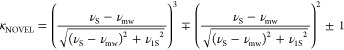graphic file with name jz-2018-016955_m009.jpg 6

The pulse sequence for a frequency-swept, off-resonance NOVEL experiment is essentially the same as the ISE shown in Figure 3b but with a larger γB1.

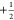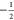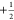eNCP (Figure 3c) is another promising time domain DNP experiment47,48 and could be implemented with readily available frequency-agile gyrotron microwave sources. 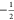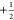Large hyperfine couplings present in a direct-transfer eNCP experiment result in differing effective fields between the Inline graphic and Inline graphic spin states of the nuclei and electrons The matching condition for eNCP is given by eq 6, where νSαeff and νSβ are the effective fields of the Inline graphic and Inline graphic electrons, respectively, and νIαeff and νIβ are the effective fields of the 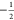Inline graphic and Inline graphic nuclei, respectively. The expressions for calculating these effective fields have been shown previously in the literature and appear in eq 7(47,48)

graphic file with name jz-2018-016955_m016.jpg 7

In magnetic resonance experiments, large gyromagnetic ratios result in more sensitive signal detection. The S/N in the experiment can therefore be optimized further by detecting the EPR signal of the electrons rather than the NMR signal of the nuclei. Electron nuclear double resonance (ENDOR)51 and electron spin echo envelope modulation (ESEEM)52 are two techniques currently used to monitor NMR transitions through EPR detection. Integration of pulsed EPR and NMR with MAS will allow for electron-detected, high-resolution multiple-dimensional NMR experiments to be performed. Figure 3d provides an example of such a sequence. Polarization could be first transferred from the electrons to the protons directly coupled with time domain DNP methods. This initial transfer could be followed by a series of mixing and evolution periods on various nuclear spins detected in indirect dimensions, as is commonly employed in high-resolution multidimensional NMR. A final mixing period could transfer magnetization back to the electrons for detection in the direct dimension. eDEC would be necessary in such experiments to maintain long nuclear spin–spin relaxation times as well as resolution in the indirect dimensions.

The time domain DNP experiments listed above will be used in conjunction with direct-transfer DNP, in which the electron spin polarizes directly to the observed nuclei. While this technique saves experimental time by removing slow nuclear spin diffusion, observed nuclei must be close to the paramagnetic radical electrons, which can have detrimental effects on the resolution of the resulting spectrum. Electron decoupling (eDEC) can be employed to partially average out hyperfine interactions and will be a crucial aspect of direct-transfer DNP.

We have successfully implemented pulsed eDEC in MAS NMR experiments.45 The pulse sequence for a 13C Hahn-Echo-detected eDEC DNP MAS experiment is shown in Figure 4a. During the polarization period, the microwave frequency is maintained at a constant value for DNP solid effect enhancement. The microwave frequency is then chirped over the electron resonance condition during the NMR signal detection.

Figure 4.

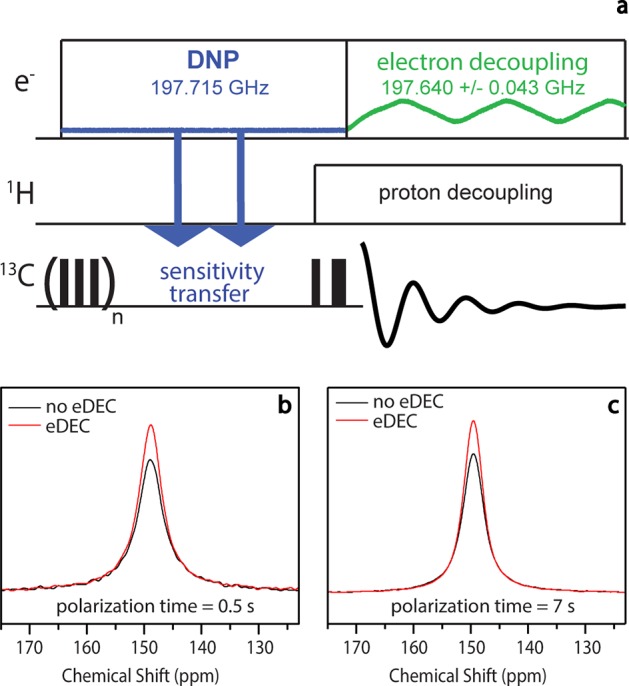
Figure 4

Open in a new tab

(a) 13C Hahn-Echo pulse sequence used to demonstrate pulsed eDEC. (b) Pulsed eDEC performed with a polarization time of 0.5 s. The line width is narrowed from 419 to 371 Hz with pulsed eDEC: a narrowing of 48 Hz. (c) Pulsed eDEC performed with a polarization time of 7 s. The line width is narrowed from 336 to 309 Hz with pulsed eDEC: a narrowing of 27 Hz. Black spectra represent the 13C signal obtained with no eDEC, while red spectra represent those obtained with pulsed eDEC. The sample is 4 M (U–13C,15N) urea and 40 mM trityl (Finland radical) in d-8 glycerol/D2O/H2O (60/30/10 by volume) at a sample volume of 30 μL in a 3.2 mm zirconia rotor. The experiments were conducted at 90 K and at a sample spinning frequency of 4 kHz. Figure reproduced with modifications by permission of the Journal of the American Chemical Society.45

Figure 4b,c displays a comparison of spectra taken with eDEC (red) and no eDEC (black) of urea frozen in a glassy matrix with trityl using DNP polarization times of 0.5 and 7 s, respectively. In both cases, the spectra obtained with eDEC show narrower resonances as well as increased intensity over those taken with no eDEC. The spectra obtained using a polarization time of 0.5 s have larger line widths than those using a polarization time of 7 s. This is expected as the nuclei that become polarized at 0.5 s of polarization time are closer to the radical electron than the polarized nuclear spins in the 7 s polarization time experiment. The effect of eDEC is greater at shorter polarization times because strongly coupled nuclei make up a larger portion of the signal in that regime, and therefore, the signal is not washed out by more weakly coupled ones that are already not as broadened.

The success of these pulsed eDEC experiments is due, in large part, to the frequency agility of the microwave source. Creating microwave chirps requires rapid frequency agility while maintaining power, as well as the ability to integrate frequency-chirped microwave irradiation into the pulse sequence of the NMR spectrometer with integrated EPR excitation capability.

Implementation of frequency-agile gyrotrons has been crucial to realizing pulsed eDEC with MAS. A high-power, frequency-agile microwave source is required to generate the requisite electron γB1 fields at the desired frequencies and to overcome extensive inhomogeneity in the microwave field irradiating the sample. The gyrotron generates microwaves by accelerating electrons into a mildly relativistic energy regime through a large magnetic field, which causes them to gyrate.54 Electrons then deposit energy in the form of microwave power into a cylindrical cavity. In the gyrotron depicted in Figure 5a,b, the rotating TE5,2 transverse electromagnetic mode was selected in the interaction cavity due to a wide-frequency excitation profile, which enables the generation of chirped microwave pulses. A helical-cut Vlasov launcher and mode converter transforms the microwave power distributed in the high-order mode into a Gaussian profile that couples efficiently to the HE11 mode supported in an overmoded waveguide (Figure 5a).49

Figure 5.

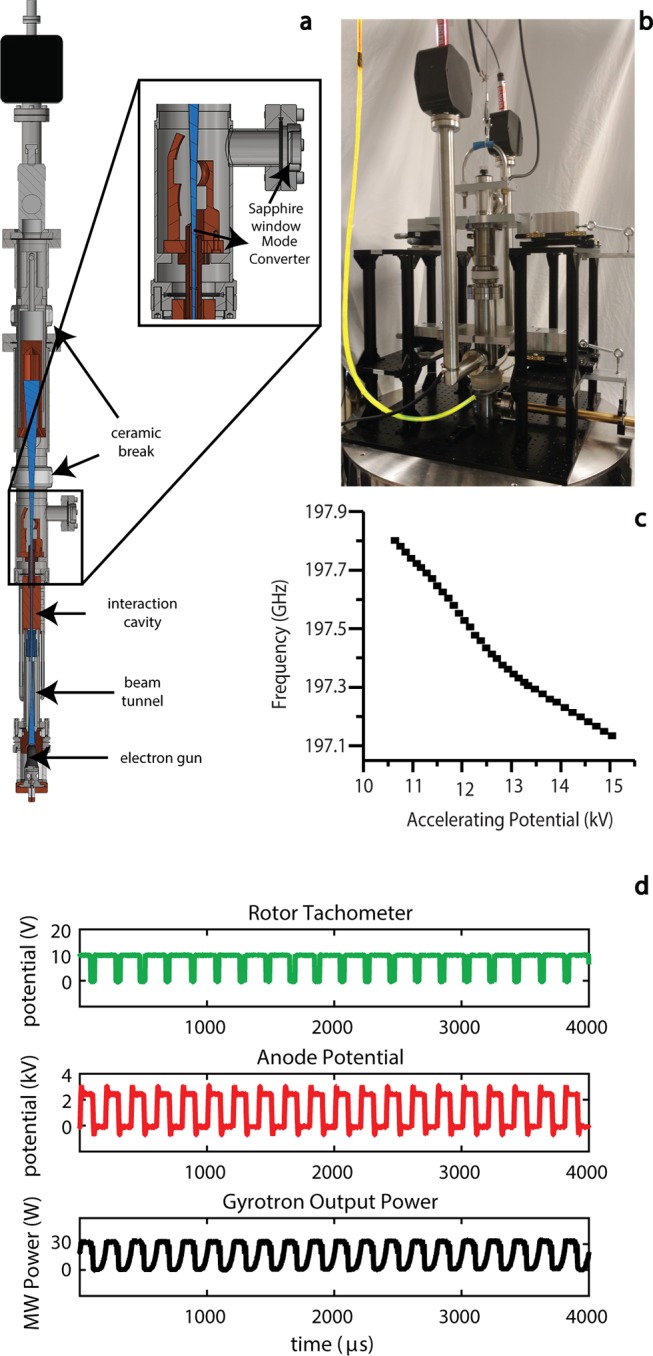
Figure 5

Open in a new tab

(a) Computer-aided design (CAD) drawing of a 198 GHz gyrotron. (b) The gyrotron is connected by the wire (highlighted in yellow) to a low-capacitance amplifier. (c) Dependence of the gyrotron output frequency on the applied accelerating voltage. (d) Rotor-synchronized microwave power output from the gyrotron. The rotor tachometer reading is shown in green, the gating voltage pulses in red, and the microwave power modulation in black. Figure reproduced with modifications by permission of the Journal of Magnetic Resonance.53

Frequency agility is achieved by quickly changing the accelerating voltage in the electron gun.53 An arbitrary waveform generator in the NMR spectrometer generates voltage sweeps that are amplified by a low-capacitance amplifier, allowing for frequency-chirped microwave irradiation to be readily implemented into the NMR pulse sequences. The amplifier output is then connected to the accelerating anode of the gyrotron (yellow cable in Figure 5b). Figure 5c shows a decrease in the output frequency when the accelerating voltage is increased.53,54

The gyrotron accelerating voltage can also be used for microwave gating. Microwave irradiation is rapidly terminated (over about 10 μs) by setting the potential to a voltage with a cyclotron frequency well outside of the resonant condition of the cavity. Microwave gating via voltage control can generate rotor-synchronized microwave power, as shown in Figure 5d. This technique could also be used to duty cycle the microwave irradiation and minimize sample heating.

We have previously calculated that 7.1% of microwave power is dissipated as heat in a frozen glycerol–water sample.49 With an input microwave power of 5 W, the 0.4 W of power deposited in the sample is easily dissipated by the large cooling capacity of the cryogenic fluid supplied by the MAS system.56 At RT, dielectric heating of aqueous samples will dramatically increase due to a higher dielectric loss tangent of liquids compared to frozen solids. Therefore, the ability to keep the microwave irradiation at a low duty cycle will be crucial to prevent excessive heating of aqueous samples. As discussed previously, more intense microwave fields will also be required to yield the required coherent electron spin control for efficient DNP at RT. Note, this microwave duty cycle is not providing true microwave “pulses” for pulsed DNP applications.

In addition to increasing the power generated by the microwave source, Teflon lenses can also increase the electron Rabi frequency by focusing the microwave irradiation into the sample.26Figure 6a is a simulation of the microwave power distribution of a Gaussian microwave beam irradiating a 4 mm outside diameter MAS rotor.26 With no lens, a considerable amount of microwave power misses the sample (indicated by the white box). However, by using a cylindrical Teflon lens that compresses the beam along the rotor short axis, a higher portion of the power is focused into the sample (Figure 6b).26Figure 6c,d shows experiments confirming the results of the simulation without and with the lens, respectively.26

Figure 6.

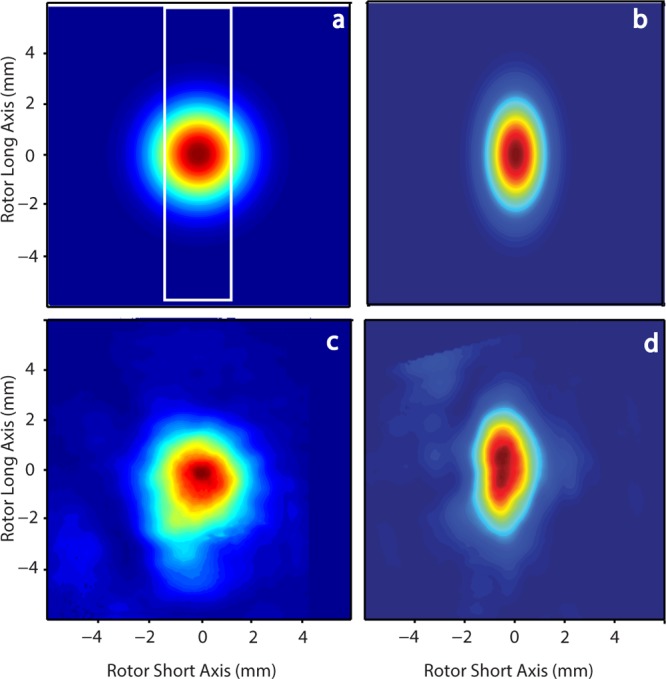
Figure 6

Open in a new tab

(a) Simulated power distribution of a Gaussian beam exiting a waveguide. The white box indicates the sample location inside of the rotor. (b) Simulated effect on the power distribution after the Gaussian beam has passed through a cylindrical lens. (c) Experimental verification of (a). (d) Experimental verification of (b). Figure reproduced with modifications by permission of the Journal of Magnetic Resonance.26

Another route to improve the electron γB1 is to construct a resonant cavity around the sample,57 as is commonly employed in EPR and static DNP instruments. However, the components required for MAS, such as the bearings and rotor, greatly complicate the implementation of microwave cavities in such a way.27 We have recently introduced a novel strategy to overcome this problem by coating the rotor with a thin layer of metal in order to form a microwave resonance structure within the rotor.57

An example of the copper-coated rotor is shown in Figure 7a. The rotor was coated by vacuum deposition to a thickness of 50 nm, with a gap to provide an iris for coupling of the microwave power into the cylindrical cavity. The metal coating is thin enough to pass radio waves but thick enough to establish a boundary condition for microwaves.57 Therefore, a Goldilocks thickness of 50 nm is just right and leverages the differences in skin depth at radio and microwave frequencies. This leads to only a mild reduction in 13C signal intensity of metal-coated rotors (Figure 7b). Additionally, the resolution of J-couplings is maintained, indicating excellent magnetic field homogeneity even with the rotor surface metalized. The 3.2 mm outside diameter rotors were also able to spin up to 5 kHz, demonstrating that the metal does not create eddy currents sufficient to prohibit MAS.

Figure 7.

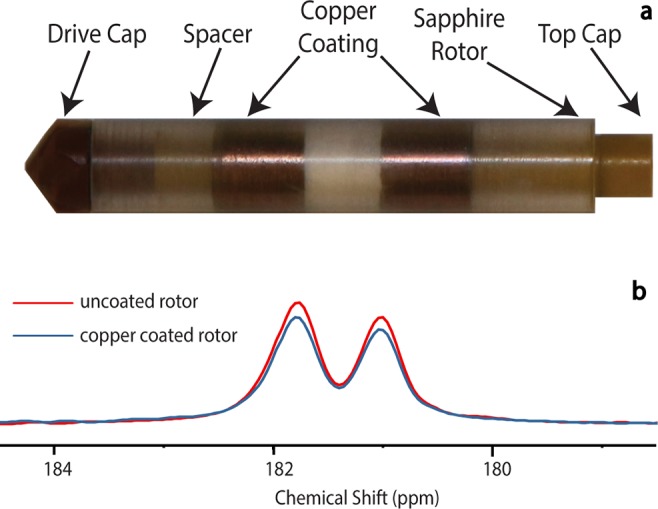
Figure 7

Open in a new tab

Metalized rotors for MAS DNP. (a) Rotor coated with copper by vacuum deposition. (b) 13C CPMAS spectrum of U–13C sodium acetate at a spinning frequency of 5.4 kHz. The spectrum is an expansion around the carboxyl peak of sodium acetate. The red curve was taken with an uncoated rotor, and a copper coating is present in the blue spectrum. Figure reproduced with modifications with permission from Magnetic Resonance in Chemistry.57

In addition to improving DNP performance at higher temperatures, access to cryogenic temperatures from 4 to 110 K is also an important avenue of technological development. Cryogenic temperatures not only yield excellent sensitivity due to higher Boltzmann polarization but also provide more accommodating sample properties to demonstrate time domain MAS DNP.

Cryogenic instrumentation for MAS DNP below 80 K has been developed by multiple groups.58−61 One method employs nitrogen gas to support (bearing) and spin (drive) the sample rotor, while cold helium gas blows directly on the center of the rotor to cool the sample to 25 K. Elongated 4 mm rotors and Teflon baffles are used to provide physical barriers between the warmer nitrogen and cooler helium regions. This configuration prevents liquefaction of the nitrogen gas and preserves spinning up to 7 kHz, with a sample temperature of 25 K.58,59,62

In our laboratory, we implemented a similar strategy but replaced the nitrogen gas used for bearing and drive with chilled helium gas at 80 K (Figure 8a).55 With this substitution, sample temperatures below 6 K are attainable while maintaining spinning of 6 kHz. Computational fluid dynamics (CFD) was used to optimize the fluid flow, minimize sample temperatures, and also provide a means to measure the sample temperature. For example, a temperature sensor is placed directly in the helium fluid path near the rotor, at which point the CFD calculations indicate the same temperature as the sample. The 79Br T1 is commonly employed to measure sample temperatures in cryogenic MAS experiments, but below 6 K, the 79Br T1 is too long (>20 min) to use as a temperature indicator. Also, in this pure helium implementation of MAS, long rotors are not required as nitrogen liquefaction is no longer an issue. Short rotors permit cryogenic sample exchange, allowing for more than five samples to be examined with MAS below 6 K within a 4 h period. The helium consumption of this apparatus is high (∼30 L/h), but because the cryogen exhaust is pure helium, a closed loop helium recirculation system could be readily implemented.60

Figure 8.

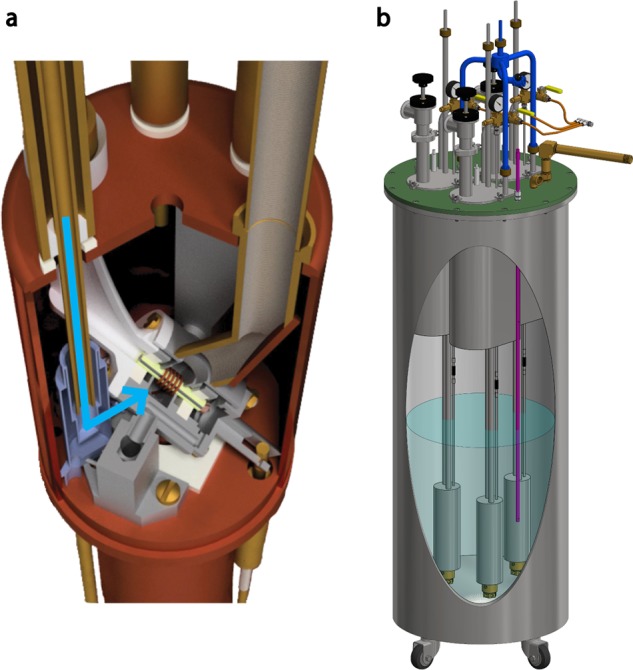
Figure 8

Open in a new tab

Cryogenic technology used in DNP MAS NMR experiments from RT to 4.2 K. (a) NMR probe head showing the path of the variable-temperature (VT) helium fluid (shown by the blue arrow) onto the sample. (b) Heat exchanger that is used to cool drive, bearing, and VT fluids to 80–100 K. These figures were reproduced with permission from the Journal of Magnetic Resonance.32,55

Cryogenic technology for MAS at temperatures > 80 K, which can be conducted with nitrogen cryogens, is important due to the expense and difficulty associated with helium cryogens for MAS. Even though nitrogen cryogens are affordable compared to helium, MAS DNP spectrometers typically require >200 L of N2(l) per day of operation.63 The heat exchanger design shown in Figure 8b makes use of a counterflow coil to reduce nitrogen consumption. This feature conserves liquid nitrogen by collecting the relatively cold exhaust gas from the probe head and using it to precool incoming warm nitrogen gas. A lower temperature of the incoming spinning gases reduces the amount of boil-off of the liquid nitrogen cooling reservoir and results in a liquid nitrogen consumption of only 90 L/day when conducting MAS experiments.32

MAS DNP is widely used to increase NMR signal intensity. The CW DNP methods currently employed in conjunction with MAS will eventually be replaced with time domain DNP and subsequent pulsed eDEC, which is a promising pathway toward efficient DNP at RT. While RT DNP has many advantages, performing experiments at temperatures below 6 K will result in unparalleled NMR sensitivity. Coherent EPR control together with MAS NMR is expected to provide a powerful experimental platform leading to many high-impact directions of research in magnetic resonance.

Frequency-chirped microwaves generated with frequency-agile gyrotron oscillators provide a direct route to coherent EPR control using currently accessible technology. Time domain DNP methods using frequency chirps have already been implemented during acquisition of the NMR signal, effectively decoupling the electrons from the nuclei. Further development of DNP instrumentation will yield significant improvements in the repertoire and performance of pulsed eDEC and MAS DNP experiments. High-power frequency-agile gyrotrons, Teflon lenses, and spinning microwave resonators will result in coherent control of electron spins in MAS experiements. Time domain DNP and pulsed eDEC will ensure that magnetic resonance continues to be a fertile field of research in the coming decades.

Acknowledgments

This research was supported by the NIH (DP2-GM119131), NSF-IDBR (CAREER DBI-1553577), and the Camille Dreyfus Teacher-Scholar Awards Program.

The authors declare the following competing financial interest(s): A.B.B. is the author of a provisional patent related to this work filed by the Washington University in Saint Louis (61/993,595 filed on 15 May 2014).

This paper was published ASAP on September 12, 2018. The paper was reposted on September 20, 2018 with a revised statement of competing financial interests.

References

  1. Rossini A. J.; Widdifield C. M.; Zagdoun A.; Lelli M.; Schwarzwälder M.; Copéret C.; Lesage A.; Emsley L. Dynamic Nuclear Polarization Enhanced NMR Spectroscopy for Pharmaceutical Formulations. J. Am. Chem. Soc. 2014, 136, 2324–2334. 10.1021/ja4092038. [DOI] [PubMed] [Google Scholar]
  2. Mak-Jurkauskas M. L.; Bajaj V. S.; Hornstein M. K.; Belenky M.; Griffin R. G.; Herzfeld J. Energy Transformations Early in the Bacteriorhodopsin Photocycle Revealed by DNP-Enhanced Solid-State NMR. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 883–888. 10.1073/pnas.0706156105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Hayes S.; Van Wüllen L.; Eckert H.; Even W. R.; Crocker R. W.; Zhang Z. Solid-State NMR Strategies for the Structural Investigation of Carbon-Based Anode Materials. Chem. Mater. 1997, 9, 901–911. 10.1021/cm960389i. [DOI] [Google Scholar]
  4. Kaplan M.; Narasimhan S.; de Heus C.; Mance D.; van Doorn S.; Houben K.; Popov-Čeleketić D.; Damman R.; Katrukha E. A.; Jain P.; et al. EGFR Dynamics Change during Activation in Native Membranes as Revealed by NMR. Cell 2016, 167, 1241–1251. 10.1016/j.cell.2016.10.038. [DOI] [PubMed] [Google Scholar]
  5. Baker L. A.; Sinnige T.; Schellenberger P.; de Keyzer J.; Siebert C. A.; Driessen A. J. M.; Baldus M.; Grünewald K. Combined 1H-Detected Solid-State NMR Spectroscopy and Electron Cryotomography to Study Membrane Proteins across Resolutions in Native Environments. Structure 2018, 26, 161–170. 10.1016/j.str.2017.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Barnes A. B.; Corzilius B.; Mak-Jurkauskas M. L.; Andreas L. B.; Bajaj V. S.; Matsuki Y.; Belenky M. L.; Lugtenburg J.; Sirigiri J. R.; Temkin R. J.; et al. Resolution and Polarization Distribution in Cryogenic DNP/MAS Experiments. Phys. Chem. Chem. Phys. 2010, 12, 5861. 10.1039/c003763j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Barnes A. B.; Andreas L. B.; Huber M.; Ramachandran R.; van der Wel P. C. A.; Veshtort M.; Griffin R. G.; Mehta M. A. High-Resolution Solid-State NMR Structure of Alanyl-Prolyl-Glycine. J. Magn. Reson. 2009, 200, 95–100. 10.1016/j.jmr.2009.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Gullion T.; Schaefer J. Rotational-Echo Double-Resonance NMR. J. Magn. Reson. 1989, 81, 196–200. 10.1016/0022-2364(89)90280-1. [DOI] [PubMed] [Google Scholar]
  9. Yang H.; Staveness D.; Ryckbosch S. M.; Axtman A. D.; Loy B. A.; Barnes A. B.; Pande V. S.; Schaefer J.; Wender P. A.; Cegelski L. REDOR NMR Reveals Multiple Conformers for a Protein Kinase c Ligand in a Membrane Environment. ACS Cent. Sci. 2018, 4, 89–96. 10.1021/acscentsci.7b00475. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Jaroniec C. P.; Filip C.; Griffin R. G. 3D TEDOR NMR Experiments for the Simultaneous Measurement of Multiple Carbon-Nitrogen Distances in Uniformly 13C,15N-Labeled Solids. J. Am. Chem. Soc. 2002, 124, 10728–10742. 10.1021/ja026385y. [DOI] [PubMed] [Google Scholar]
  11. Braunschweiler L.; Ernst R. R. Coherence Transfer by Isotropic Mixing: Application to Proton Correlation Spectroscopy. J. Magn. Reson. 1983, 53, 521–528. 10.1016/0022-2364(83)90226-3. [DOI] [Google Scholar]
  12. Castellani F.; van Rossum B.; Diehl A.; Schubert M.; Rehbein K.; Oschkinat H. Structure of a Protein Determined by Solid-State Magic-Angle-Spinning. Nature 2002, 420, 99. 10.1038/nature01070. [DOI] [PubMed] [Google Scholar]
  13. Lewandowski J. R.; Dumez J. N.; Akbey Ü.; Lange S.; Emsley L.; Oschkinat H. Enhanced Resolution and Coherence Lifetimes in the Solid-State NMR Spectroscopy of Perdeuterated Proteins under Ultrafast Magic-Angle Spinning. J. Phys. Chem. Lett. 2011, 2, 2205–2211. 10.1021/jz200844n. [DOI] [Google Scholar]
  14. Marchetti A.; Jehle S.; Felletti M.; Knight M. J.; Wang Y.; Xu Z. Q.; Park A. Y.; Otting G.; Lesage A.; Emsley L.; et al. Backbone Assignment of Fully Protonated Solid Proteins By1H Detection and Ultrafast Magic-Angle-Spinning NMR Spectroscopy. Angew. Chem., Int. Ed. 2012, 51, 10756–10759. 10.1002/anie.201203124. [DOI] [PubMed] [Google Scholar]
  15. Vasa S. K.; Janssen H.; Van Eck E. R. H.; Kentgens A. P. M. High-Resolution Solid-State 13 C ΜMAS NMR with Long Coherence Life Times. Phys. Chem. Chem. Phys. 2011, 13, 104–106. 10.1039/C0CP01929A. [DOI] [PubMed] [Google Scholar]
  16. Renault M.; Pawsey S.; Bos M. P.; Koers E. J.; Nand D.; Tommassen-Van Boxtel R.; Rosay M.; Tommassen J.; Maas W. E.; Baldus M. Solid-State NMR Spectroscopy on Cellular Preparations Enhanced by Dynamic Nuclear Polarization. Angew. Chem., Int. Ed. 2012, 51, 2998–3001. 10.1002/anie.201105984. [DOI] [PubMed] [Google Scholar]
  17. Carver T. R.; Slichter C. P. Polarization of Nuclear Spins in Metals. Phys. Rev. 1953, 92, 212–213. 10.1103/PhysRev.92.212.2. [DOI] [Google Scholar]
  18. Kubicki D. J.; Rossini A. J.; Purea A.; Zagdoun A.; Ouari O.; Tordo P.; Engelke F.; Lesage A.; Emsley L. Amplifying Dynamic Nuclear Polarization of Frozen Solutions by Incorporating Dielectric Particles. J. Am. Chem. Soc. 2014, 136, 15711–15718. 10.1021/ja5088453. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lilly Thankamony A. S.; Wittmann J. J.; Kaushik M.; Corzilius B. Dynamic Nuclear Polarization for Sensitivity Enhancement in Modern Solid-State NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 102–103, 120–195. 10.1016/j.pnmrs.2017.06.002. [DOI] [PubMed] [Google Scholar]
  20. Traficante D. D. Introduction to Transmission Lines Basic Principles and Applications of Quarter Wavelength Cables and Impedance Matching. Concepts Magn. Reson. 1993, 5, 57–86. 10.1002/cmr.1820050105. [DOI] [Google Scholar]
  21. Traficante D. D. Imepedance: What It Is, and Why It Must Be Matched. Concepts Magn. Reson. 1989, 1, 73–92. 10.1002/cmr.1820010205. [DOI] [Google Scholar]
  22. Barnes A. B.; Mak-Jurkauskas M. L.; Matsuki Y.; Bajaj V. S.; van der Wel P. C. A.; DeRocher R.; Bryant J.; Sirigiri J. R.; Temkin R. J.; Lugtenburg J.; et al. Cryogenic Sample Exchange NMR Probe for Magic Angle Spinning Dynamic Nuclear Polarization. J. Magn. Reson. 2009, 198, 261–270. 10.1016/j.jmr.2009.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Fu R.; Brey W. W.; Shetty K.; Gor’kov P.; Saha S.; Long J. R.; Grant S. C.; Chekmenev E. Y.; Hu J.; Gan Z.; et al. Ultra-Wide Bore 900 MHz High-Resolution NMR at the National High Magnetic Field Laboratory. J. Magn. Reson. 2005, 177, 1–8. 10.1016/j.jmr.2005.07.013. [DOI] [PubMed] [Google Scholar]
  24. Leavesley A.; Wilson C. B.; Sherwin M.; Han S. Effect of Water/Glycerol Polymorphism on Dynamic Nuclear Polarization. Phys. Chem. Chem. Phys. 2018, 20, 9897–9903. 10.1039/C8CP00358K. [DOI] [PubMed] [Google Scholar]
  25. Equbal A.; Li Y.; Leavesley A.; Huang S.; Rajca S.; Rajca A.; Han S. Truncated Cross Effect Dynamic Nuclear Polarization: An Overhauser Effect Doppelgänger. J. Phys. Chem. Lett. 2018, 9, 2175–2180. 10.1021/acs.jpclett.8b00751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. van der Cruijsen E. A. W.; Koers E. J.; Sauvée C.; Hulse R. E.; Weingarth M.; Ouari O.; Perozo E.; Tordo P.; Baldus M. Biomolecular DNP-Supported NMR Spectroscopy Using Site-Directed Spin Labeling. Chem. - Eur. J. 2015, 21, 12971–12977. 10.1002/chem.201501376. [DOI] [PubMed] [Google Scholar]
  27. Nanni E. a.; Barnes A. B.; Matsuki Y.; Woskov P. P.; Corzilius B.; Griffin R. G.; Temkin R. J. Microwave Field Distribution in a Magic Angle Spinning Dynamic Nuclear Polarization NMR Probe. J. Magn. Reson. 2011, 210, 16–23. 10.1016/j.jmr.2011.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Barnes A. B.; Nanni E. A.; Herzfeld J.; Griffin R. G.; Temkin R. J. A. 250 GHz Gyrotron With a 3 GHz Tuning Bandwidth for Dynamic. J. Magn. Reson. 2012, 221, 147–153. 10.1016/j.jmr.2012.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Michaelis V. K.; Smith A. a.; Corzilius B.; Haze O.; Swager T. M.; Griffin R. G. High-Field 13C Dynamic Nuclear Polarization with a Radical Mixture. J. Am. Chem. Soc. 2013, 135, 2935–2938. 10.1021/ja312265x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Maly T.; Debelouchina G. T.; Bajaj V. S.; Hu K.-N.; Joo C.-G.; Mak-Jurkauskas M. L.; Sirigiri J. R.; van der Wel P. C. a.; Herzfeld J.; Temkin R. J.; et al. Dynamic Nuclear Polarization at High Magnetic Fields. J. Chem. Phys. 2008, 128, 052211. 10.1063/1.2833582. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hu K. N.; Bajaj V. S.; Rosay M.; Griffin R. G. High-Frequency Dynamic Nuclear Polarization Using Mixtures of TEMPO and Trityl Radicals. J. Chem. Phys. 2007, 126, 044512. 10.1063/1.2429658. [DOI] [PubMed] [Google Scholar]
  32. Corzilius B.; Smith A. A.; Griffin R. G. Solid Effect in Magic Angle Spinning Dynamic Nuclear Polarization. J. Chem. Phys. 2012, 137, 054201. 10.1063/1.4738761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Albert B. J.; Pahng S. H.; Alaniva N.; Sesti E. L.; Rand P. W.; Saliba E. P.; Scott F. J.; Choi E. J.; Barnes A. B. Instrumentation for Cryogenic Magic Angle Spinning Dynamic Nuclear Polarization Using 90 L of Liquid Nitrogen per Day. J. Magn. Reson. 2017, 283, 71–78. 10.1016/j.jmr.2017.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lelli M.; Chaudhari S. R.; Gajan D.; Casano G.; Rossini A. J.; Ouari O.; Tordo P.; Lesage A.; Emsley L. Solid-State Dynamic Nuclear Polarization at 9.4 and 18.8 T from 100 K to Room Temperature. J. Am. Chem. Soc. 2015, 137, 14558–14561. 10.1021/jacs.5b08423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Chaudhari S. R.; Berruyer P.; Gajan D.; Reiter C.; Engelke F.; Silverio D. L.; Copéret C.; Lelli M.; Lesage A.; Emsley L. Dynamic Nuclear Polarization at 40 kHz Magic Angle Spinning. Phys. Chem. Chem. Phys. 2016, 18, 10616–10622. 10.1039/C6CP00839A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Afeworki M.; Schaefer J. Mechanism of DNP-Enhanced Polarization Transfer across the Interface of Polycarbonate/Polystyrene Heterogeneous Blends. Macromolecules 1992, 25, 4092–4096. 10.1021/ma00042a007. [DOI] [Google Scholar]
  37. Becerra L. R.; Gerfen G. J.; Temkin R. J.; Singel D. J.; Griffin R. G. Dynamic Nuclear Polarization with a Cyclotron Resonance Maser at 5 T. Phys. Rev. Lett. 1993, 71, 3561–3564. 10.1103/PhysRevLett.71.3561. [DOI] [PubMed] [Google Scholar]
  38. Keedy D. A.; Van Den Bedem H.; Sivak D. A.; Petsko G. A.; Ringe D.; Wilson M. A.; Fraser J. S. Crystal Cryocooling Distorts Conformational Heterogeneity in a Model Michaelis Complex of DHFR. Structure 2014, 22, 899–910. 10.1016/j.str.2014.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ni Q. Z.; Markhasin E.; Can T. V.; Corzilius B.; Tan K. O.; Barnes A. B.; Daviso E.; Su Y.; Herzfeld J.; Griffin R. G. Peptide and Protein Dynamics and Low-Temperature/DNP Magic Angle Spinning NMR. J. Phys. Chem. B 2017, 121, 4997–5006. 10.1021/acs.jpcb.7b02066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Fricke P.; Mance D.; Chevelkov V.; Giller K.; Becker S.; Baldus M.; Lange A. High Resolution Observed in 800 MHz DNP Spectra of Extremely Rigid Type III Secretion Needles. J. Biomol. NMR 2016, 65, 121–126. 10.1007/s10858-016-0044-y. [DOI] [PubMed] [Google Scholar]
  41. Sergeyev I. V.; Itin B.; Rogawski R.; Day L. A.; McDermott A. E. Efficient Assignment and NMR Analysis of an Intact Virus Using Sequential Side-Chain Correlations and DNP Sensitization. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 5171–5176. 10.1073/pnas.1701484114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Henstra A.; Dirksen P.; Schmidt J.; Wenckebach W. T. Nuclear Spin Orientation via Electron Spin Locking (NOVEL). J. Magn. Reson. 1988, 77, 389–393. 10.1016/0022-2364(88)90190-4. [DOI] [Google Scholar]
  43. Can T. V.; Weber R. T.; Walish J. J.; Swager T. M.; Griffin R. G. Frequency-Swept Integrated Solid Effect. Angew. Chem., Int. Ed. 2017, 56, 6744–6748. 10.1002/anie.201700032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Jain S. K.; Mathies G.; Griffin R. G. Off-Resonance NOVEL. J. Chem. Phys. 2017, 147, 164201. 10.1063/1.5000528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Jain S. K.; Siaw T. A.; Equbal A.; Wilson C. B.; Kaminker I.; Han S. Reversal of Paramagnetic Effects by Electron Spin Saturation. J. Phys. Chem. C 2018, 122, 5578–5589. 10.1021/acs.jpcc.8b00312. [DOI] [Google Scholar]
  46. Saliba E. P.; Sesti E. L.; Scott F. J.; Albert B. J.; Choi E. J.; Alaniva N.; Gao C.; Barnes A. B. Electron Decoupling with Dynamic Nuclear Polarization in Rotating Solids. J. Am. Chem. Soc. 2017, 139, 6310–6313. 10.1021/jacs.7b02714. [DOI] [PubMed] [Google Scholar]
  47. Henstra a.; Dirksen P.; Wenckebach W. T. Enhanced Dynamic Nuclear Polarization by the Integrated Solid Effect. Phys. Lett. A 1988, 134, 134–136. 10.1016/0375-9601(88)90950-4. [DOI] [Google Scholar]
  48. Weis V.; Griffin R. G. Electron-Nuclear Cross Polarization. Solid State Nucl. Magn. Reson. 2006, 29, 66–78. 10.1016/j.ssnmr.2005.08.005. [DOI] [PubMed] [Google Scholar]
  49. Rizzato R.; Bennati M. Cross-Polarization Electron-Nuclear Double Resonance Spectroscopy. ChemPhysChem 2015, 16, 3769–3773. 10.1002/cphc.201500938. [DOI] [PubMed] [Google Scholar]
  50. Hoff D. E. M.; Albert B. J.; Saliba E. P.; Scott F. J.; Choi E. J.; Mardini M.; Barnes A. B. Frequency Swept Microwaves for Hyperfine Decoupling and Time Domain Dynamic Nuclear Polarization. Solid State Nucl. Magn. Reson. 2015, 72, 79–89. 10.1016/j.ssnmr.2015.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Kwiram A. L. Electron Nuclear Double Resonance. Annu. Rev. Phys. Chem. 1971, 22, 133–170. 10.1146/annurev.pc.22.100171.001025. [DOI] [Google Scholar]
  52. Rowan L. G.; Hahn E. L.; Mims W. B. Electron-Spin-Echo Envelope Modulation. Phys. Rev. 1965, 137, A61–A71. 10.1103/PhysRev.137.A61. [DOI] [Google Scholar]
  53. Scott F. J.; Saliba E. P.; Albert B. J.; Alaniva N.; Sesti E. L.; Gao C.; Golota N. C.; Choi E. J.; Jagtap A. P.; Wittmann J. J.; et al. Frequency-Agile Gyrotron for Electron Decoupling and Pulsed Dynamic Nuclear Polarization. J. Magn. Reson. 2018, 289, 45–54. 10.1016/j.jmr.2018.02.010. [DOI] [PubMed] [Google Scholar]
  54. Nusinovich G. S.Introduction to the Physics of Gyrotrons; Johns Hopkins University Press, 2004. [Google Scholar]
  55. Sesti E. L.; Alaniva N.; Rand P. W.; Choi E. J.; Albert B. J.; Saliba E. P.; Scott F. J.; Barnes A. B. Magic Angle Spinning NMR below 6 K with a Computational Fluid Dynamics Analysis of Fluid Flow and Temperature Gradients. J. Magn. Reson. 2018, 286, 1–9. 10.1016/j.jmr.2017.11.002. [DOI] [PubMed] [Google Scholar]
  56. Haze O.; Corzilius B.; Smith A. a.; Griffin R. G.; Swager T. M. Water-Soluble Narrow-Line Radicals for Dynamic Nuclear Polarization. J. Am. Chem. Soc. 2012, 134, 14287–14290. 10.1021/ja304918g. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Scott F. J.; Sesti E. L.; Choi E. J.; Laut A. J.; Sirigiri J. R.; Barnes A. B. Magic Angle Spinning NMR with Metallized Rotors as Cylindrical Microwave Resonators. Magn. Reson. Chem. 2018, 56, 831. 10.1002/mrc.4744. [DOI] [PubMed] [Google Scholar]
  58. Thurber K. R.; Potapov A.; Yau W. M.; Tycko R. Solid State Nuclear Magnetic Resonance with Magic-Angle Spinning and Dynamic Nuclear Polarization below 25 K. J. Magn. Reson. 2013, 226, 100–106. 10.1016/j.jmr.2012.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Thurber K. R.; Tycko R. Biomolecular Solid State NMR with Magic-Angle Spinning at 25 K. J. Magn. Reson. 2008, 195, 179–186. 10.1016/j.jmr.2008.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Lee D.; Bouleau E.; Saint-Bonnet P.; Hediger S.; De Paëpe G. Ultra-Low Temperature MAS-DNP. J. Magn. Reson. 2016, 264, 116–124. 10.1016/j.jmr.2015.12.010. [DOI] [PubMed] [Google Scholar]
  61. Matsuki Y.; Idehara T.; Fukazawa J.; Fujiwara T. Advanced Instrumentation for DNP-Enhanced MAS NMR for Higher Magnetic Fields and Lower Temperatures. J. Magn. Reson. 2016, 264, 107–115. 10.1016/j.jmr.2016.01.022. [DOI] [PubMed] [Google Scholar]
  62. Thurber K. R.; Yau W. M.; Tycko R. Low-Temperature Dynamic Nuclear Polarization at 9.4 T with a 30 mW Microwave Source. J. Magn. Reson. 2010, 204, 303–313. 10.1016/j.jmr.2010.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Barnes A. B.; Markhasin E.; Daviso E.; Michaelis V. K.; Nanni E. A.; Jawla S.; Mena E. L.; DeRocher R.; Thakkar A.; Woskov P. P. Dynamic Nuclear Polarization at 700 MHz/460 GHz. J. Magn. Reson. 2012, 224, 1–7. 10.1016/j.jmr.2012.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES