The run-on oligomer filament enzyme mechanism of SgrAI: Part 1. Assembly kinetics of the run-on oligomer filament

Abstract

Filament or run-on oligomer formation by metabolic enzymes is now recognized as a widespread phenomenon having potentially unique enzyme regulatory properties and biological roles, and its dysfunction is implicated in human diseases such as cancer, diabetes, and developmental disorders. SgrAI is a bacterial allosteric type II restriction endonuclease that binds to invading phage DNA, may protect the host DNA from off-target cleavage activity, and forms run-on oligomeric filaments with enhanced DNA-cleavage activity and altered DNA sequence specificity. However, the mechanisms of SgrAI filament growth, cooperativity in filament formation, sequestration of enzyme activity, and advantages over other filament mechanisms remain unknown. In this first of a two-part series, we developed methods and models to derive association and dissociation rate constants of DNA-bound SgrAI in run-on oligomers and addressed the specific questions of cooperativity and filament growth mechanisms. We show that the derived rate constants are consistent with the run-on oligomer sizes determined by EM analysis and are most consistent with a noncooperative growth mode of the run-on oligomer. These models and methods are extended in the accompanying article to include the full DNA-cleavage pathway and address specific questions related to the run-on oligomer mechanism including the sequestration of DNA-cleavage activity and trapping of products.

Introduction

Phage-host systems are under intense evolutionary pressure; consequently they have developed remarkably ingenious mechanisms of attack and defense (1). The studies described herein investigate one such remarkable system: that found in Streptomyces griseus. Based on its biochemical activities, SgrAI, a nuclease from S. griseus, is postulated to be activated by binding to particular DNA sequences (primary sites) on invading phage DNA, simultaneously expanding its DNA sequence cleavage specificity and forming filaments of run-on oligomers (ROO). ² These filaments may act to protect the host DNA from its resulting off-target cleavage activity and to confer kinetic advantage in rapid DNA cleavage (2–4). Only recently has there been a growing appreciation for the widespread nature and unique attributes of enzyme mechanisms involving filament formation (5–13). Filament formation by metabolic enzymes in diverse metabolic/signaling pathways and in translation initiation have been described previously, and dysfunction in the control of such pathways is implicated in human diseases including cancer, diabetes, and developmental problems (7, 8). Being a relatively newly described enzyme mechanism (4, 14–17), several fundamental questions concerning the role of the filament in biological function and enzyme activity remain to be answered, such as filament growth mechanisms, cooperativity, sequestration of activity, and advantages over non-ROO filament mechanisms. Further, potential limitations on enzyme turnover caused by the requirement for filament assembly prior to enzyme activation and/or in potentially trapping products of the reaction within the filament have yet to be addressed. We specifically address several of these questions in the SgrAI system in this first of a two-part series, using kinetic measurements of ROO filament formation and disassembly.

SgrAI is a sequence-specific DNA enzyme and a type II restriction endonuclease with unusual allosteric properties and has been shown to form filaments we call ROO, for run-on oligomer, to describe the simple and symmetric nature of the assembly that can extend, in principle, indefinitely in either direction (3, 4). The DNA-cleavage activity of SgrAI is activated in the ROO filament by over 200-fold, and its DNA sequence specificity is also altered, allowing cleavage of an additional class of DNA sequences termed secondary sites (3, 4, 18). Only the primary site sequences stimulate SgrAI to form the ROO filaments, although SgrAI bound to secondary sites will join a ROO filament formed from SgrAI bound to primary sites (3). ROO filament formation depends on the concentration of SgrAI bound to primary site DNA, as well as the length of the bound DNA, and structural studies show a role for the DNA in stabilizing the ROO filaments through contacts to neighboring SgrAI–DNA complexes (4, 18) (Fig. 1). The ROO filament is a left-handed helix with approximately four SgrAI–DNA complexes per turn that can theoretically extend indefinitely by the addition of SgrAI–DNA complexes to either end (Fig. 1). The biological role of ROO filament formation has been speculated to be in sequestering activated SgrAI on invading phage DNA to prevent cleavage of the S. griseus host genome and may also be important in providing a rapid response to invading phage (3, 4, 18). Cleavage of the secondary sites, in addition to primary sites, expands the number of possible cleavage sites in invading phage, which could be expected to enhance the anti-phage activity of SgrAI (19–21). To explain the observed enzymatic behavior, a model has been proposed that includes an equilibrium between active and inactive conformations of SgrAI that favors the inactive conformation when bound to DNA, but more so when bound to secondary-site DNA than when bound to primary (4, 22, 23). However, only the active conformation has the propensity to assemble into the ROO filament, which in turn stabilizes this active conformation via protein–protein and protein–DNA contacts to neighboring complexes in the ROO filament (Fig. 1) (4). The activated conformation has rapid DNA-cleavage activity, and DNA is rapidly cleaved by SgrAI in the ROO filament. SgrAI cleaves secondary-site DNA appreciably only when in a ROO filament, requiring the favorable contacts between SgrAI–DNA complexes to stabilize the active conformation. In this way the primary site DNA acts as an allosteric activator of secondary-site DNA cleavage by SgrAI. The formation of the ROO filament intuitively suggests cooperativity and rapid activation; however, until the current studies, the details of these effects were not known or quantified.

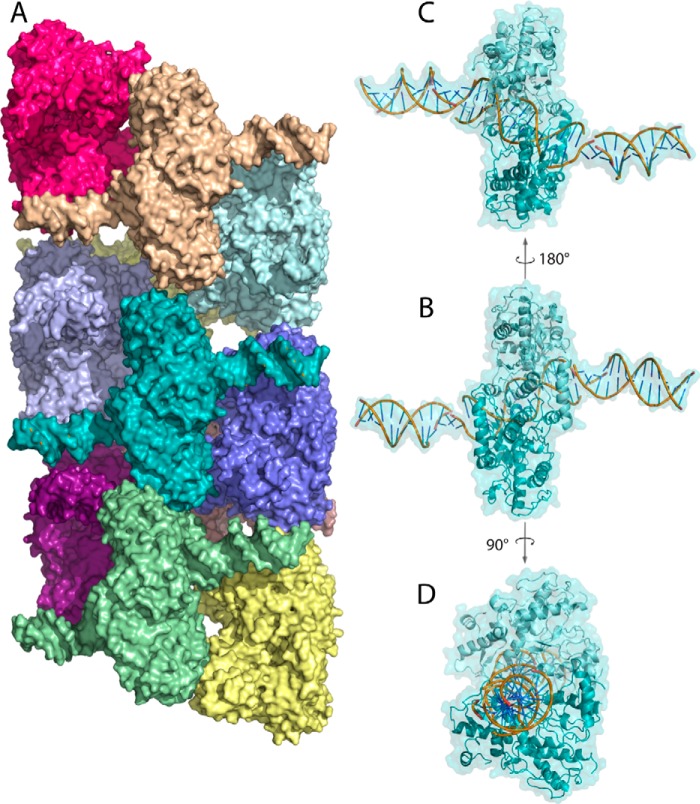
Figure 1.

A, surface rendering of oligomeric SgrAI–DNA (Protein Data Bank code 4C3G). Each SgrAI–DNA complex is colored a unique color. SgrAI is bound to two molecules of PC DNA forming a 40-bp duplex with nicks at the SgrAI cleavage sites. The oligomer has left-handed helical symmetry with approximately four SgrAI–DNA complexes per turn. B, one SgrAI–DNA complex in the same orientation as that in A, with cartoon rendering shown beneath the surface rendering (teal). Each subunit of the SgrAI dimer is shaded differently (light and dark teal). The DNA rendered in cartoon is colored yellow, green, and blue. C, the SgrAI–DNA complex shown in B, rotated 180° about the axis shown. D, the SgrAI–DNA complex shown in B, rotated 90° about the axis shown.

We use fluorophore-labeled DNA, FRET, and an approach to equilibrium method to measure the association and dissociation of SgrAI–DNA complexes into and out of the ROO filaments. Mathematically fitting the data to various models of ROO filament assembly allowed for the extraction of intrinsic rate constants for these processes, as well as measures of affinity and cooperativity of SgrAI–DNA complexes within the ROO filament. It was found that the association rate constant is approximately 3–4 orders of magnitude slower than diffusion limited and is even slower (∼10×) in the presence of divalent cations. The extracted forward and reverse rate constants and the models developed here predict nearly exactly the distribution of ROO filament sizes observed by EM (4). Models that allow for growth and disassembly of the ROO filaments at only the ends fit the experimental data as well (i.e. with similar quality of fit measures) as those that allow for breakage at any location, yet the lack of observed cooperativity in assembly, as well as the ROO filament structure, are more consistent with the latter mechanism.

We use the methods, models, and rate constants developed and derived herein to analyze the full DNA-cleavage reaction in the accompanying article (24). There, individual microscopic rate constants for each step of the reaction pathway are extracted from the DNA-cleavage kinetic data. A significant finding is that the relatively slow ROO filament association rate constant, measured in the current work, limits the assembly of ROO filaments at physiological concentrations to occur only when recognition sites are found on the same contiguous DNA (24). This sequestration limits damaging DNA cleavages away from the host genome and to only the invading phage DNA. The simulations also show that because of fast dissociation of the ROO filaments and release of the cleaved DNA product from SgrAI, no significant trapping of the reaction product occurs. Hence, the ROO filament mechanism may have evolved to solve the specific requirements of its biological niche, namely sequestration (using a rate-limiting association step into the ROO filament), and the requirement for speed (to prevent viral replication and/or DNA protection via methylation) (24).

Results

Overview of methodology

Fig. 2 illustrates the basic experimental methodology used in this work, both in the FRET titration experiment and in the time reaction data sets (Data Sets 1–3). DNA containing a single primary recognition site (CACCGGTG) embedded in a 40-bp DNA (i.e. 40-1) is labeled with either fluorescein (Flo, 6-carboxyfluorescein) or rhodamine-X (Rox, 5(6)-carboxy-X-rhodamine). Because SgrAI binds tightly both to its uncleaved recognition site, such as in 40-1, and to its cleaved version, as in PC DNA (Pre-Cleaved DNA, a synthetic version of 40-1, which mimics the product of SgrAI cleavage, including the overhanging “sticky” ends), experiments were conducted with both forms. The purpose of investigating reactions with both forms is to both investigate the effect of cleavage of the DNA on the behavior of SgrAI–DNA complexes with respect to forming the ROO filament, as well as to derive rate constants to be used in modeling the full DNA-cleavage reaction pathway (which is done in the accompanying article (24)). In those reactions, the cleaved version of 40-1 (i.e. PC DNA) acts as an activator of DNA cleavage by SgrAI in inducing ROO filament formation, which stimulates cleavage of a reporter DNA.

Figure 2.

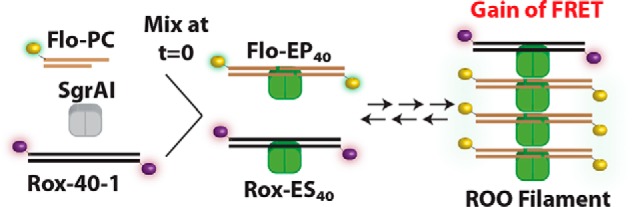
Reaction scheme used in Data Set 2. Premixed Rox–40-1 and Flo–PC are mixed with SgrAI at time = 0. SgrAI binds Rox–40-1 (to form Rox–ES₄₀) and self-annealed Flo–PC (to form Flo–EP₄₀). SgrAI–DNA complexes (Rox–ES₄₀ and Flo–EP₄₀) assemble into run-on oligomers (ROO filaments) giving a FRET signal. ROO filaments differ in number of SgrAI–DNA complexes and contain a mixture with different combinations and permutations of the two types of SgrAI–DNA complex. The FRET signal changes until equilibrium is reached between assembling SgrAI–DNA complexes and disassembling ROO filaments. The change in color of the SgrAI dimer from gray to green indicates a conformational change that activates SgrAI for DNA cleavage. Reactions of Data Set 1 differ from those of Data Set 2 in that Flo–PC is substituted with Flo–40-1. The reactions of Data Set 3 differ from those of Data Set 2 in that 10 mm CaCl₂ is present.

First, the FRET experiment was conducted to verify that increases in FRET occur with increasing concentrations of SgrAI bound to DNA, as expected. 50 nm Rox–40-1 and 2 μm SgrAI were titrated with increasing concentrations of Flo–PC DNA. Flo–PC DNA self-anneals into a contiguous 40-mer (with one nick per strand) via the overhanging four nucleotides (CCGG). SgrAI binds to Rox–40-1 and to annealed Flo–PC DNA to form SgrAI–DNA complexes, which then assemble into the ROO filament, giving a FRET signal (Fig. 2).

Next, timed reactions were carried out, and the FRET signal was measured following mixing of SgrAI and DNA. These reactions were of three types, differing in the type of DNA used (giving Data Sets 1–3) and whether or not 10 mm CaCl₂ was present (reactions of Data Sets 1 and 2 were performed in the absence of divalent cations; those of Data Set 3 were performed with CaCl₂; Table 1). The reactions were performed without Mg²⁺ (to prevent DNA cleavage), but Ca²⁺ was used in some reactions to mimic the effects on DNA binding and filament formation of Mg²⁺. Ca²⁺ binds in the active site near the Mg²⁺-binding sites; however Ca²⁺ inhibits, rather than supports, DNA cleavage by SgrAI (22, 23). The reactions of Data Set 1 utilized only uncleaved DNA (Flo–40-1 and Rox–40-1), which was done to limit the number of equilibria that must be modeled, because it does not include the self-annealing step found with precleaved DNA (i.e. PC DNA). The reactions of Data Sets 2 and 3 do include precleaved DNA, and those of Data Set 3 differ from Data Set 2 in that 10 mm CaCl₂ is present.

Table 1.

Summary of data sets

Data set	Experimental details	Number of reactions (see Table 2)
1	Only Uncleaved DNA (Rox-ES40+Flo-ES40)	5
2	Uncleaved and Precleaved DNA (Rox-ES40+Flo-EP40)	6
3	Uncleaved and Precleaved DNA with 10 mm Ca2+ (Rox-ES40+Flo-EP40 +Ca2+)	4

Multiple timed reactions were used in global fitting and collected into their relevant data sets, as defined by the type of DNA and presence or absence of Ca²⁺: five timed reactions in the case of Data Set 1, six for Data Set 2, and four for Data Set 3 (Tables 1 and 2). Global fitting utilized the software Kintek Global Kinetic Explorer (26, 27) and three different types of filament assembly models (Table 3). These models differ in the length of ROO filament modeled (the software limited this to a size of four or five SgrAI–DNA complexes maximum) and the manner of ROO filament growth and disassembly. In the “ends-only” model (5EO and 4EO; Table 3), SgrAI–DNA complexes bind and dissociate only from either end of the ROO filament. In the “breaks-in-the-middle” model (4BM; Table 3), ROO filament may break at any junction between adjacent SgrAI–DNA complexes within the ROO filament, and ROO filaments may form by the association of two ROO filaments of any size (or with individual SgrAI–DNA complexes). This is likely, because analysis of the three-dimensional structure of the ROO filament (Fig. 1) shows that most contacts within the ROO filament occur only between immediately adjacent SgrAI–DNA complexes (Fig. 3). Because of the additional equilibrium reactions necessary to be modeled in the case of the breaks-in-the-middle model, ROO filaments of only four SgrAI–DNA complexes or less could be modeled, giving the model 4BM (Table 3). Up to five SgrAI–DNA complexes were possible in the case of the ends-only mechanism, giving model 5EO (Table 3). Model 4EO was created to compare more directly to model 4BM, having the same size limit of ROO filaments as model 4EO. These limitations in ROO filament size are justified by estimating the average size of ROO filaments with a model allowing ROO filaments up to 14 in size and the rate constants derived from global fitting (see below). Given the concentrations of SgrAI–DNA complexes used in the reactions of all data sets, most ROO filaments are not greater than five SgrAI–DNA complexes long (discussed below under “Simulation of EM distribution”).

Table 2.

Reaction details and concentrations of reactions used in each Data Set

Data set	[Rox–40-1]	[Flo–40-1]	[Flo–PC]	[SgrAI]	[CaCl2]
	nm	nm		nm	mm
1	100	100	0	350	0
	100	150	0	350	0
	50	100	0	200	0
	100	50	0	200	0
	50	25	0	100	0
2	58	0	100	200	0
	50	0	50	150	0
	100	0	100	250	0
	50	0	150	250	0
	50	0	120	200	0
	50	0	150	250	0
3	50	0	100	200	10
	50	0	50	150	10
	50	0	120	200	10
	50	0	150	250	10

Table 3.

Summary of models

Filament assembly model	Distinct details of model
	Growth mechanism, DNA cleavagea	Maximum size of ROO filaments
5EO	Ends only	5
4EO	Ends only	4
4BM	Breaks in the middle	4

^a The ends-only growth mechanism is where only a single SgrAI–DNA complex (i.e. ES₄₀ or EP₄₀) adds to an ROO filament (run-on oligomer of SgrAI–DNA complexes) at a time. Dissociation similarly occurs only one SgrAI–DNA complex at a time and only from either end of the ROO filament. The breaks-in-the-middle mechanism refers to a growth mechanism where dissolution or dissociation of an ROO filament may occur at any position within the ROO filament, at any juncture between adjacent SgrAI–DNA complexes (i.e. ES₄₀ or EP₄₀). Association also may occur via the association between two ROO filaments of any size and/or single SgrAI–DNA complexes.

Figure 3.

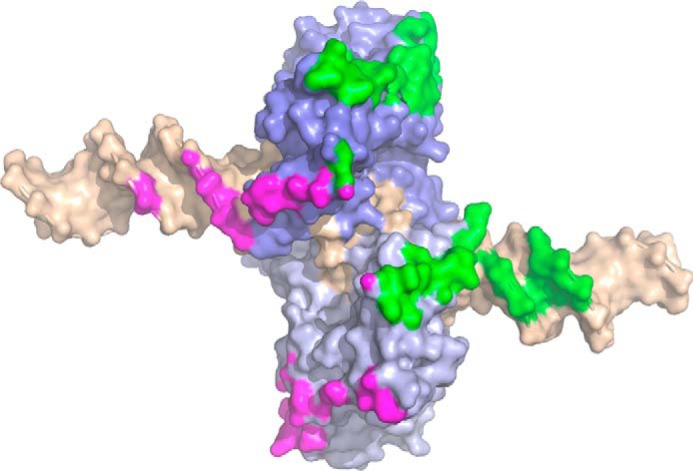
Contact surface between SgrAI–DNA complexes of the run-on oligomer, mapped onto a single SgrAI–DNA complex. The two subunits of the SgrAI dimer are colored in different shades of blue, and the bound DNA (self-annealed PC DNA) is colored in wheat. Close contacts (within 4 Å) between SgrAI–DNA complexes in the ROO filament are limited to only the SgrAI–DNA complex just before (green) and just after (magenta) and occur on both the protein and DNA components of the SgrAI–DNA complex.

All reactions of a given data set were fit together globally, with the same model (i.e. 5EO, 4EO, and 4BM) and rate constants, but each data set was fit separately from the others. The software package Kintek Global Kinetic Explorer was used (26, 27). Additional parameters, such as baseline and scaling factors, were also fit independently for each reaction of a given data set. The goal of global data fitting is to extract microscope rate constants for each step modeled and was done by simulating reactions to fit to the experimental data, namely normalized, corrected FRET signals as a function of time. The simulation software utilizes a series of equations (Tables S1, S3, and S4) and starting concentrations of SgrAI and DNA to simulate the FRET signal. In addition to the forward and reverse rate constants for each step, two constants per reaction were also fit. These constants correspond to the baseline of the FRET signal, and a scaling factor relating the simulated concentration of different species to the predicted FRET signal. To predict the FRET signal from the distinct ROO filament species (composed of two types of SgrAI–DNA complexes: one containing FRET donor fluorophore labeled-DNA (Flo) and the other containing acceptor (Rox)), the efficiency of FRET for every possible FRET pair in each ROO filament was determined using distances measured in the cryo-EM model of the ROO filament (Fig. 1). These efficiencies are shown in Table 4 and were calculated from measured distances between the 5′ ends of the DNA in the ROO filament structure (which do not take into account the linker connecting the fluorophores to the DNA). Because the simulation software predicts the concentrations as a function of time for each ROO filament, which includes all possible combinations and permutations of the two types of labeled species (i.e. SgrAI bound to Rox–DNA or to Flo–DNA), these “calculated efficiency” factors can be used to weight the predicted FRET signals for each species. Because the total signal, produced from the summed, weighted signals of each complex, is scaled using a single scaling factor to the actual FRET signal, only the relative value of each calculated efficiency factor is significant. Note also that these are first order approximations, because they do not account for fluorophore orientation (each fluorophore is linked via a 6–8-atom-long linker to the 5′ end of the DNA; Fig. S1), microenvironment, or homo-FRET. Further, a similar quality of fit to the observed FRET signal was obtained when merely scaling the concentrations of each ROO filament by the number of Rox fluorophores it contains (provided that at least one Flo is also present in the same assembly) rather than using the calculated efficiency factors (data not shown). This may be due to the averaging of signals derived from all of the different ROO filaments in the simulation; hence individual differences in FRET efficiency of each become less significant. In addition, the long and flexible linkers connecting the fluorophores to the DNA may allow for efficient FRET regardless of fluorophore positions within the ROO filament.

Table 4.

Predicted FRET efficiencies based on distances between SgrAI–(PC DNA)₂ complexes

Relationship between Rox and neighboring Floa	Distance between fluorophores	Calculated efficiencyb
	Å
N and N + 1 (or N − 1)	72.8	0.157
N and N + 1 (or N − 1)	105.6	0.020
N and N + 1 (or N − 1)	92.9	0.027
N and N + 2 (or N − 2)	76.5	0.12
N and N + 3 (or N − 3)	32	0.96

^a Rox and Flo refer to SgrAI–DNA complexes bound to Rox- or Flo-labeled DNA, respectively.

^b FRET efficiency calculated from the equation efficiency = 1/(1 + (r/R₀)⁶). A value of 51 Å was used for R₀ (44). The combined total for N to N + 1 (or N − 1) is the sum of the three values, giving 0.2.

The number of fitted parameters was reduced by constraining the reverse rate constant to the fitted forward rate constant via a known equilibrium constant. This was done in the case of the self-annealing of the precleaved DNA (PC DNA) and in the binding of SgrAI to DNA. The equilibrium constant for the self-annealing of PC DNA was calculated as described in the supporting information. The equilibrium dissociation constants for binding of SgrAI to DNA were determined by measuring the anisotropy of fluorescence emission from the fluorophore labeled DNA in the presence of increasing concentrations of SgrAI, both with and without 10 mm CaCl₂ (see supporting information). It was assumed that SgrAI bound equally tightly to the precleaved DNA (once annealed) as to the cleaved DNA. Because SgrAI is always in excess in the reactions, any differences in DNA-binding affinity are minimized, and fits show that the change in simulated FRET signal was insensitive to the DNA binding rate constants (k₂, k₋₂), provided the forward (k₂) was set to be greater than 3 × 10⁶ m⁻¹ s⁻¹ (data not shown).

Another simplification is the assumption that the forward and reverse rate constants are not impacted by the size of the ROO filament. For example, the rate constants for binding and dissociating of a SgrAI–DNA complex from a ROO filament of size 2 is considered the same as from a ROO filament of size 3, 4, or 5 (or to another SgrAI–DNA complex). This assumption was used as a first-order approximation, because otherwise many fitted rate constants would be required. An analysis described below testing this assumption was made below (see “Tests for evidence of cooperativity in models”). A final assumption made was that the state of cleavage of the DNA did not affect these rate constants for ROO filament assembly and disassembly. Hence, the total number of fitted parameters is 13 for Data Set 1 (3 rate constants and 10 for the baseline and scaling factor for each of the 5 data sets), 16 for Data Set 2, and 12 for Data Set 3 (Table 5). The high quality of fits (Table 5) and reasonable error boundaries of each rate constant (Table 6) indicated that these simplifications were justified.

Table 5.

Quality of fit values

Data set	Filament assembly model	Number of reactions fit (see Table 2)	Number of data points simulated and fit to experimental data	Number of parameters fita	χ2/DoFb	σ with respect to the fitb
1 (uncleaved DNA only)	5EO	5	425	13	1.9	0.011
	4EO				1.7	0.011
	4BM				1.4	0.010
2 (uncleaved and precleaved DNA)	5EO	6	1550	16	3.4	0.012
	4EO				5.2	0.016
	4BM				2.4	0.010
3 (uncleaved and precleaved DNA with 10 mm Ca2+)	5EO	4	1111	12	3.0	0.011
	4EO				3.9	0.013
	4BM				3.5	0.013

^a Rate constants, baseline, and scaling factors. Reverse rate constants for the self-annealing of PC DNA and for DNA binding by SgrAI were constrained by the calculated or measured equilibrium dissociation constant, respectively. Hence, only the forward rate constants were fit in these reactions. Both forward and reverse rate constants were fit for assembly and disassembly of SgrAI–DNA oligomers.

^b χ²/DoF and σ with respect to the fit are as defined by the software authors (26, 27).

Table 6.

Kintek Global Kinetic Explorer fitted forward and reverse rate constants from global fitting

Data set	Filament assembly model	Association rate constant for ROO filament assembly k4 (error boundary)a	Dissociation rate constant for ROO filament disassembly k−4 (error boundary)b
		m−1 s−1	s−1
1 (uncleaved DNA only)	5EO	4 × 106 (1.7 × 106 to 3 × 107)	0.11 (0.07–0.16)
	4EO	2 × 106 (1.1 × 106 to 6 × 106)	0.10 (0.07–0.14)
	4BM	1.7 × 106 (1.2 × 106 to 3 × 106)	0.018 (0.004–0.07)
2 (uncleaved and precleaved DNA)	5EO	3 × 106 (1.0 × 106 to 7 × 106)	0.03 (0.019–0.19)
	4EO	1.2 × 106 (1.7 × 105 to 4 × 107)	0.08 (>0.012)
	4BM	5 × 106 (3 × 106 to 1.5 × 108)	0.03 (0.02–0.9)
3 (uncleaved and precleaved DNA with 10 mm Ca2+)	5EO	4 × 105 (3 × 105 to 2 × 106)	0.03 (0.016–0.03)
	4EO	6 × 105 (4 × 104 to 5 × 106)	0.04 (0.014–0.4)
	4BM	3 × 105 (6 × 104 to 8 × 105)	0.017 (0.007–0.02)

^a The forward rate constant is the association of a SgrAI–DNA complex (or ROO filament) with another SgrAI–DNA complex (or ROO filament), and the reverse rate constant is the dissociation of a SgrAI–DNA complex (or ROO filament) from another SgrAI–DNA complex (or ROO filament).

^b Fitspace error boundaries calculated at the 0.95 χ² threshold.

FRET titration showing ROO filament formation

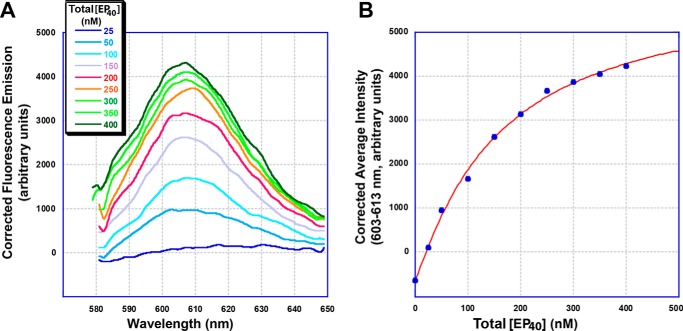
FRET between different SgrAI-bound DNAs was used to investigate the association of SgrAI–DNA complexes into ROO filaments (Figs. 2 and 3). In this case, a limiting concentration of Rox-labeled DNA (Rox–40-1 at 50 nm) was mixed with excess SgrAI (2 μm), and then PC DNA containing 10% fluorescein-labeled DNA (Flo–PC) was added (Fig. 2). The fluorescence emission (with excitation at 498 nm, the excitation maximum of Flo) was measured at 508–700 nm both before and after each addition. The emission at these wavelengths contains contributions from both the Flo and Rox fluorophores and therefore required the subtraction of the Flo emission to reveal the Rox emission (see “Experimental procedures”) (Fig. 4A; see Fig. S2 for the raw emission data and Fig. S3 for the control performed without SgrAI). This emission was further corrected for the non-FRET emission of Rox, because of Rox absorbance at the excitation wavelength. The resulting corrected Rox emission increased with increasing concentrations of Flo-labeled DNA as expected, and this increase was fit to the following Hill equation (Fig. 4B),

$$y=a+b\times \left\{\frac{{\left[\text{Flo}-{\text{EP}}_{40}\right]}^N}{\left(K_{1/2}^N+{\left[\text{Flo}-{\text{EP}}_{40}\right]}^N\right)}\right\}$$ (Eq. 1)

where y is the average corrected fluorescence intensity at 602–612 nm of the fluorescence emission at each concentration of Flo–EP₄₀ (EP₄₀ Enzyme-Product complex, where the product is a 40-bp DNA created by the self-annealing of PC DNA and contains nicks at the SgrAI-targeted cleavage sites). K_½ is the concentration of Flo–EP₄₀ where the average 602–612-nm emission is half-maximal, and N is the Hill coefficient, a measure of cooperativity. The constants a and b were also fit and correspond to the fluorescence baseline and scaling factor (to scale the term in brackets to the arbitrary fluorescence units of y), respectively. The total EP₄₀ concentration was estimated assuming complete binding of SgrAI to the Flo–PC DNA (because SgrAI is present in excess and at micromolar concentrations, and the binding affinity between SgrAI and PC DNA is in the nanomolar range). The K_½ (the concentration of total EP₄₀ at the half-maximum FRET signal) was found to be 0.16 ± 0.03 μm, with a Hill coefficient 1.1 ± 0.1. These values are interpreted as indicative of the affinity and cooperativity of the association of SgrAI/Rox–40-1 (ES₄₀, for Enzyme-Substrate complex containing 40-bp uncleaved DNA) and EP₄₀ complexes. A Hill coefficient of 1 indicates no cooperativity in ROO filament formation with respect to total EP₄₀ concentration.

Figure 4.

Titration of Rox–40-1, SgrAI, with Flo–PC DNA in the presence of 10 mm Ca²⁺. A, 50 nm Rox–40-1, 2 μm SgrAI, 10 mm CaCl₂, and buffer A (see “Experimental procedures”) with PC (1:9 Flo–PC:PC) at 25 °C. Emission spectra taken with 498-nm excitation, and corrected for Flo emission, dilution, and Rox emission caused by absorption at 498 nm. Concentration of total EP₄₀ (SgrAI bound to two Flo–PC molecules, calculated as half the concentration of total added Flo–PC and assumes complete binding of Flo–PC) shown in nm. B, average corrected intensities from A (wavelengths 603–613 nm) versus total EP₄₀ (the concentration of SgrAI bound to Flo–PC DNA) (filled blue circles). Values are fit to the Hill equation (red line, r = 0.9985) to give K_½ = 0.16 ± 03 μm and Hill coefficient = 1.1 ± 0.1.

Data Set 1: Approach to equilibrium of filament assembly containing only uncleaved DNA (i.e. Rox–ES₄₀ + Flo–ES₄₀)

Data Set 1 utilized two types of singly labeled 40-1 (Flo–40-1 and Rox–40-1), and reactions were performed in 1.5 ml of buffer at 25 °C with constant stirring. The reaction proceeds with the addition of SgrAI, which binds to the Flo- and Rox–40-1 to create Flo–ES₄₀ and Rox–ES₄₀, followed by their assembly into ROO filaments (Fig. 2). This brings the two fluorophores within proximity for FRET to occur, as evidenced by the titration shown in Fig. 4 (and described above). The change in FRET as the reaction approaches equilibrium gives information on both the forward and reverse rate constants, and repeating the reaction with different concentrations of Flo–40-1 and Rox–40-1 provides further information on these rate constants.

Global data fitting used the fluorescence emission intensities measured from the 590-nm cut-on filter after correction from intensities measured simultaneously at 585 nm (corrected filter (CF); see “Experimental procedures”) with excitation at 498 nm. Fig. S4 shows an example of intensity data measured at 585 nm (red) with the 590-nm cut-on filter (blue) and with the CF data in green. Data from five reactions were collected for this data set (Table 2).

Global data fitting proceeded by fitting each of the three filament assembly models (5EO, 4EO, and 4BM; Tables S1–S5) to the FRET signal from each of the five timed reactions. Table 5 summarizes the quality of the fits, and Table 6 gives the extracted rate constants for the association and dissociation of SgrAI–DNA complexes (or ROO filaments) into (and from) ROO filaments (k₄ and k₋₄) (please note that we use k₄ and k₋₄ to be consistent with naming of the rate constants measured in the accompanying article (24)). In addition to these two rate constants, the forward rate constant for binding of SgrAI to DNA (k₂) was also fit and found to be greater than 3 × 10⁶ m⁻¹ s⁻¹ (no upper limit was detected, and the reverse rate constant was constrained by the measured K_D, hence not fit independently).

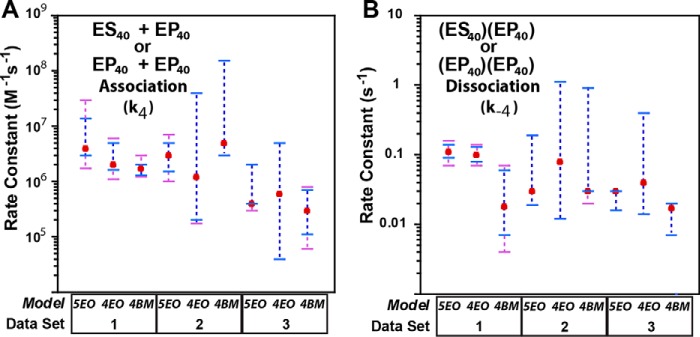
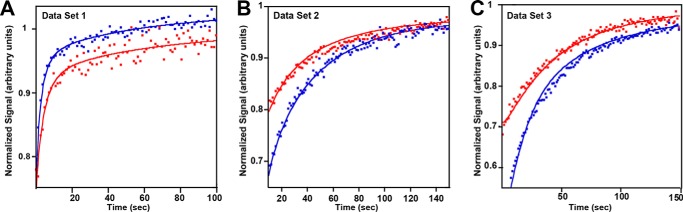
Fig. 5 plots the rate constants k₄ and k₋₄ with associated error boundaries (see “Experimental procedures” for method of error boundary calculation). Fig. 6A shows experimental data and simulated curves for select data sets of Data Set 1 using model 4BM. The model-fitting software calculates a measure of the fit in the form of χ²/DoF (28). A value near 1 indicates the best fit, and this parameter is between 1 and 2 for all three models (Table 5). The forward or association rate constant for the association of one SgrAI–DNA complex to another SgrAI–DNA complex (or to an ROO filament, or one ROO filament to another, k₄) was found to be in the range of 1 × 10⁶ to 4 × 10⁶ m⁻¹ s⁻¹ in fits using each of the three models (Table 6 and Fig. 5), and the reverse or dissociation rate constant of a SgrAI–DNA complex from another SgrAI–DNA complex (or from a ROO filament, or one ROO filament from another ROO filament, k₋₄) was found to be 0.018–0.11 s⁻¹. The error boundaries vary for each model but combined give 1.1 × 10⁶ to 3 × 10⁷ m⁻¹ s⁻¹ for the association rate constant and 0.004–0.16 s⁻¹ for the dissociation rate constant. These boundaries indicate that the association rate constants derived from the three models (5EO, 4EO, and 4BM) are indistinguishable from one another. Similarly, the error boundaries for the dissociation rate constants also overlap, although only just barely for model 4BM compared with the other two (Table 6 and Fig. 5), with this rate constant being lower in model 4BM (breaks in the middle) than the other two (ends only). It may be that to fit the same experimental data, the ends-only models (models 5EO and 4EO) require a faster dissociation rate constant because of “hold-up” time in the ROO filament. However, for the most part, the differences in the three models (maximum ROO filament size and mechanism of growth) do not significantly affect the resulting fitted rate constants, and the experimental data appear to be equally well fit by the three different models.

Figure 5.

Fitted rate constants for the fitting of each data set to each model. A, association rate constant for the association of two SgrAI–DNA complexes (i.e. k₄). Best fit values are shown as red filled circles; error boundaries from FitSpace at 0.90 χ² threshold (see “Experimental procedures”) are in purple dashed lines, and 0.95 χ² thresholds are in blue (where only blue is visible indicates complete overlap). Data set and model descriptions are given in Tables 1 and 3, respectively. B, dissociation rate constant of one SgrAI–DNA complex from another (i.e. k₋₄). Colors are as in A.

Figure 6.

Selected data (corrected and normalized FRET intensities, filled circles) and simulations from global fits (using model 4BM, lines) for Data Sets 1–3. A, blue, 350 nm SgrAI was added to 150 nm Flo–40-1 and 100 nm Rox–40-1 at time zero. Red, 200 nm SgrAI was added to 50 nm Flo–40-1 and 100 nm Rox–40-1. B, blue, 200 nm SgrAI was added to 120 nm Flo–PC and 50 nm Rox–40-1 at time zero. Red, 250 nm SgrAI was added to 100 nm Flo–PC and 100 nm Rox–40-1. C, blue, 250 nm SgrAI was added to 150 nm Flo–PC and 50 nm Rox–40-1 at time zero. Red, 150 nm SgrAI is added to 50 nm Flo–PC and 50 nm Rox–40-1.

Data Sets 2 and 3: Approach to equilibrium of filament assembly with both uncleaved and precleaved DNA (Rox–ES₄₀ + Flo–EP₄₀) and with and without Ca²⁺

Data Set 2 differs from Data Set 1 in that Flo–40-1 DNA is replaced with Flo–PC DNA, and Data Set 3 adds an additional change by including 10 mm CaCl₂; however, all else concerning the reactions and measurements is as in Data Set 1. These two data sets now introduce the self-association equilibrium of PC DNA (annealed via the sticky ends to mimic the continuous 40-1 DNA), and Data Set 3 tests the effects of Ca²⁺ on the approach to equilibrium kinetics. The same three models, including their equations (with the addition of the self-association of PC DNA) were used in global data fitting. Also, it was assumed that SgrAI bound to self-annealed PC DNA behaves just as SgrAI bound to 40-1 DNA, which is a reasonable assumption because self-annealed PC DNA is the same length and nearly the same sequence as 40-1 DNA (see “Experimental procedures”), and both stimulate DNA cleavage by SgrAI to similar degrees (3, 18). Data Set 2, along with the rate constants derived from Data Set 1, was used to derive the forward and reverse rate constants for the self-association of PC DNA and to further refine the forward and reverse rate constants for the assembly of SgrAI–DNA complexes, now including EP₄₀ (i.e. SgrAI–DNA complex with the self-annealed, precleaved PC DNA).

As with Data Set 1 data, the three models 5EO, 4EO, and 4BM (see Table 3) were used to fit the reaction data from Data Sets 2 and 3 (summarized in Tables 1 and 2), and Tables 5 and 6 provide the final quality of fit parameters for and extracted rate constants derived from each model. The χ²/DoF (a measure of the quality of the fits) were found to be 2.4–5.2 for fits to Data Set 2 and 3.0–3.9 for Data Set 3 (Table 5). Fig. 6 (B and C) shows selected experimental and simulated data using model 4BM and Data Sets 2 and 3, respectively. Rate constants for the assembly and disassembly of ROO filaments, with error boundaries for fitting of all three models (5EO, 4EO, and 4BM) using Data Sets 2–3, are shown in Fig. 5.

Because the self-annealing of PC DNA (rate constants k₁ and k₋₁; Tables S3 and S4) is the only new equilibrium added to those modeled to fit Data Sets 2 and 3, the starting values for all other rate constants (i.e. k₂, k₋₂, k₄, k₋₄) were set to those found for Data Set 1 prior to global fitting Data Sets 2 and 3. This revealed that the forward rate constant for PC DNA self-annealing (k₁) was best fit to 5 × 10⁵ to 1.3 × 10⁶ m⁻¹ s⁻¹ (Fig. S5), within the predicted range of 1 × 10⁵ to 1 × 10⁷ m⁻¹ s⁻¹ (see “Experimental procedures”; also the reverse rate constant, k₋₁, was not fit independently, being constrained to the forward rate constant by the calculated K_D). A similar result was found in global fitting of Data Set 3 (Fig. S5). The error analysis determined that the boundary of this rate constant is 7 × 10⁴ to 3 × 10⁸ m⁻¹ s⁻¹ (Fig. S5).

Global fitting of Data Set 2 revealed the forward rate constant for assembly of SgrAI–DNA complexes into ROO filaments (k₄) to be in the range of 1.2 × 10⁶ to 5 × 10⁶ m⁻¹ s⁻¹ (for the three models), but up to 10-fold slower (3 × 10⁵ to 3 × 10⁵) for Data Set 3 (Table 6). The error boundaries of these rate constants overlap (Fig. 5A); however, there is no overlap in some cases for comparable mechanisms; for example, that from fitting model 4BM with Data Set 2 does not overlap with that from fitting the same model to Data Set 3 (which differs only in the presence of 10 mm CaCl₂). Hence the association rate constant of the ROO filament assembly may actually be slower in the presence of divalent cations (please note that this is also observed in the data analyzed in the accompanying article (24), comparing experimental data with and without MgCl₂).

As for the reverse rate constant (k₋₄), which is dissociation of one SgrAI–DNA complex from another (regardless of the size of the ROO filament), a range of 0.017–0.08 s⁻¹ is found with fitting of all models (i.e. Table 6). Error analysis indicates that these differences are not significant (Fig. 5B), nor were they significantly different from those of Data Set 1. In fact, the similar forward rate constant (k₄; Fig. 5A) and the lack of a need to distinguish between SgrAI–DNA complexes with cleaved DNA and those with uncleaved DNA in modeling also support the assumption that SgrAI–DNA complexes behave similarly with respect to forming and dissociating from ROO filaments regardless of whether or not the bound DNA is cleaved.

Simulation of EM distribution

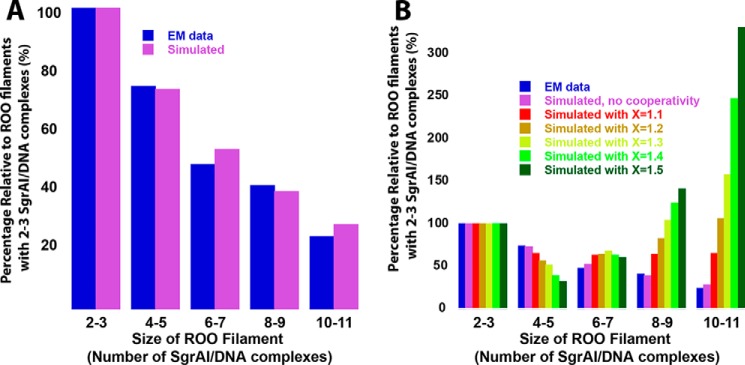
As an independent test of the methodology used in this work, a simulation with derived rate constants was performed to compare with the distribution of ROO filament sizes measured using EM (4). The model used, model EM (see “Experimental procedures”), allows ROO filaments up to 14 SgrAI–DNA complexes in size (Table S6). The rate constants for association and dissociation were taken from the fit of model 4BM to Data Set 3, and the starting concentrations of SgrAI and PC DNA were those used in the EM study (3 μm each). Fig. 7A shows the resulting distribution of ROO filament size (Fig. 7A, purple bars) and compares it to that found by EM (Fig. 7A, blue bars). As can be seen, excellent agreement between the predicted and observed size distribution is found. These simulations also showed that the mechanism of association (ends only or breaks in the middle) did not matter to the final distribution, only to the rate at which this equilibrium is achieved (data not shown).

Figure 7.

Simulation of length or size distribution of run-on oligomers, with and without cooperativity. A, distribution normalized to the value for ROO filament sizes of 1–2. EM (blue) distribution data taken from the negative stain EM histogram (4), which used 3 μm SgrAI and PC DNA. Modeling (model EM) allowing up to 14 SgrAI–DNA complexes was used with rate constants from fitting Data Set 3 to model 4BM (Table 6) and initial concentrations of 3 μm SgrAI and PC DNA (shown in purple). B, as in A, but distribution of predicted ROO filament size with different degrees of cooperativity. Also shown is the distribution of oligomers (relative to the quantity of 2–3-mers) found using EM, in blue (4). To simulate positive cooperativity, the reverse rate constant for ROO filament dissociation was serially decreased by the given cooperativity factor (X = 1.1 to 1.5) with increasing ROO filament size, up to 5-mers, after which it remained constant (see “Experimental procedures”).

As a check on methodology, the simulation shown in Fig. S6 was performed. Model EM was also used, along with the rate constants derived from fitting reactions of Data Set 1 to model 4BM. Fig. S6A shows a relative distribution of ROO filament sizes predicted by the model, and Fig. S6B shows that most ROO filaments are less than four or five SgrAI–DNA complexes long when the total SgrAI–DNA concentration is 250 nm or less. This calculation shows that models that limit the ROO filament sizes to four and five SgrAI–DNA complexes long, such as those used here, are adequate for fitting data from reactions with reactant concentrations used here (Table 2).

Tests for evidence of cooperativity in models

Cooperativity was investigated in three ways, by analysis of the FRET titration data (Fig. 4, described above) and by the introduction of cooperativity into the models and comparison to both the kinetic and EM experimental data. To model cooperative assembly of SgrAI–DNA complexes within a ROO filament, the dissociation rate constants for SgrAI–DNA complexes from the ROO filaments were made serially slower with increasing size of the ROO filament. This could be imagined to result from a greater number of favorable interactions that could be made between the incoming SgrAI–DNA complex and the other complexes already in the ROO filament (see “Experimental procedures”). In contrast, analysis of the contacts made between SgrAI–DNA complexes in the ROO filament indicates that interactions predominantly occur only with SgrAI–DNA complexes immediately before and immediately after in the left-handed ROO filament helix (Fig. 3; see also Fig. 1). The rate constants were made serially slower by a factor (X) depending on the number of SgrAI–DNA complexes per ROO filament (see “Experimental procedures”). Model EM (Table S6) was used, and values of X between 1.1 and 1.5 were tested. As can be seen in Fig. 7B, even a small cooperativity factor (e.g. X = 1.1; Fig. 7B, red) greatly alters the distribution of ROO filament sizes, predicting longer filaments than observed. The model with no cooperativity (Fig. 7B, purple) best matches the experimentally observed EM distribution (Fig. 7B, dark blue).

Discussion

Cooperativity in ROO filament formation

Although accelerated DNA-cleavage activity depends on the concentration of SgrAI–DNA complexes, filaments formed by SgrAI–DNA do not form cooperatively. This was shown in several analyses. First, the FRET titrations of EP₄₀ with ES₄₀ (Fig. 4) fit well to a Hill equation with a Hill coefficient of 1 (Fig. 4B), indicating no cooperativity in ROO filament formation on SgrAI–DNA concentration. Second, comparison of the ROO filament size distribution determined using EM (4) to predicted distributions generated with our models and rate constants indicated that the introduction of even small degrees of cooperativity are not consistent with the experimental data (Fig. 7B). Finally, the cryo-EM structure of the ROO filament where each SgrAI–DNA complex appears to contact only that before and that after it in the ROO filament suggests that a lack of cooperativity in ROO filament association would be expected (Fig. 3). We conclude that the data are most consistent with the absence of cooperativity on the concentration of SgrAI–DNA in ROO filament association of the SgrAI–DNA complexes studied here.

ROO filament growth mechanism and effect of Ca²⁺

The experimental data of Data Sets 1–3 (Table 1) have been fit globally to models differing in either maximum ROO filament size and/or in how the assemblies grow and disassemble (Table 3). The two different growth mechanisms tested have been termed either 1) ends only, indicating ROO filament growth can only occur at the ends (either end, as they are symmetrically equivalent) and only one SgrAI–DNA complex at a time; or 2) the breaks-in-the-middle mechanism, in which the ROO filaments may break via disruption of a single interface between immediately adjacent SgrAI–DNA complexes at any such junction along the ROO filament. Conversely, in the breaks-in-the-middle model, two ROO filaments of any size can come together to form one longer, continuous ROO filament. We found that either type of model fit equally well to the experimental data and gave roughly equivalent rate constants. It may be that higher concentrations of the SgrAI–DNA complex, along with models allowing ROO filaments longer than four or five SgrAI–DNA complexes (the size limitation of the simulation software), will be necessary to distinguish between these two possible growth mechanisms using this method.

Analysis of the size distribution of ROO filaments from EM data was also inconclusive on this point, because the two mechanisms led to the same final distribution. If the mechanism uses the ends-only model, it implies that the contacts between SgrAI–DNA complexes are somehow stronger in the middle than at the end. One could imagine this being the case if each SgrAI–DNA complex contacted more than just the SgrAI–DNA complex immediately ahead and immediately behind. This would also likely lead to cooperativity in forming the ROO filaments, because longer ROO filaments have more SgrAI–DNA complexes that may form favorable contacts with the new SgrAI–DNA complex being added. However, our measures (see “Tests for evidence of cooperativity in models”), indicated that such cooperativity is not likely present, and the cryo-EM structural model indicates few contacts to SgrAI–DNA complexes not immediately adjacent to each other within the ROO filament (Fig. 3). We therefore favor the breaks-in-the-middle model because it is more consistent with the observed data including the structural data (Fig. 3) and the lack of observed cooperativity (see above).

Finally, the reactions of Data Set 3 were performed to test the effect of the presence of 10 mm CaCl₂ on the association and dissociation kinetics of the ROO filaments (Table 6 and Fig. 5), because DNA-cleavage reactions require 10 mm MgCl₂, and we wish to extend these analyses to those reactions (see the accompanying article (24)). Ca²⁺ was used here as a mimic of Mg²⁺, because it binds similarly yet inhibits DNA cleavage by SgrAI (22, 23). Global data fitting and error analysis indicated similar quality of fits for the different models with Data Set 3 data, as was found for data from the other data sets, but a difference was found in the association kinetics of SgrAI–DNA complexes into the ROO filaments. This rate constant was found to be ∼10-fold slower compared with those from Data Sets 1 and 2, which did not have divalent cations (Table 6 and Fig. 5). The dissociation rate constant, however, did not seem significantly perturbed by the presence of the Ca²⁺ (Table 6). In conclusion, our analyses suggest that the breaks-in-the-middle mechanism is likely a more accurate mechanism than the ends-only mechanism and that the presence of 10 mm CaCl₂ slows (by 10×) the association rate constant of SgrAI–DNA complexes into the ROO filaments. This slowing may be due to a screening effect or alternatively in requiring dissociation of Ca²⁺ ions bound to the DNA prior to ROO filament assembly. Hence, this work favors the rate constants derived from model 4BM (Table 6), with that of Data Set 3 being most relevant to DNA cleavage studies, which are performed in the presence of divalent cations (see the accompanying article (24)).

Biological relevance

Filament formation by ATPases and GTPases such as actin and tubulin has long been known, although in those cases, the filament itself serves a necessary function that is often structural in nature, and the function of the enzymatic hydrolysis of ATP or GTP hydrolysis is merely in controlling the formation of the filament. However, filament formation in the control of activity beyond such enzymes was much less well known until relatively recently (with the exception of acetyl-CoA carboxylase (29–31)). The development of imaging technology has allowed for large-scale screening of protein localization in cells, revealing filament formation by many metabolic and other enzymes, and in some cases only during particular phases of the cell cycle, under certain stress conditions, or as part of signaling pathways (6–11, 13, 32–39). Filaments formed by various enzymes differ in total length, association into fibers or other structures, lifetime, and effects on enzyme activity, as well as conditions for their formation and disassembly. The SgrAI ROO filaments, although forming filaments as large as 30 or more SgrAI–DNA complexes in vitro (4, 40), may be more limited in size in vivo (to number of sites, usually 10–20 per phage genome including both primary and secondary types of sites), and its lifetime has not been measured but is likely to be short (see the accompanying article for estimates in the minute range (24)). In contrast, filaments formed from other enzymes can be visualized in cells with sizes of several microns in length and forming structures stable on the minutes to hours timescales (8–11, 13, 30–34). In a few cases, the effect of filament formation on enzyme function has been discerned (15–17, 37, 38, 41, 42); some inhibit enzyme activity rather than activate as is the case for SgrAI. Further, the stimulus to form filaments can differ; in the case of SgrAI, sufficient concentrations of SgrAI bound to primary site DNA (cleaved or uncleaved) result in filament formation, whereas in other enzymes, filament formation may be independent of substrate or product. However, in most cases the particular advantages of the filament forming behavior have not been identified. It has been speculated that the filaments could function in sequestration of enzyme activity, rapid activation or inhibition, storage, fine-tune buffering of metabolic activity, forming a cytoskeleton-like structure, stabilizing protein conformation, developmental switching, rapid cell proliferation, stress coping, metabolic channeling, and intracellular transportation (4, 7, 35). However, few studies have investigated the kinetics of filament or ROO filament formation and none with the level of detail here. Our detailed model building and global data fitting have produced derived association and dissociation rate constants for ROO filament formation, discovering a slow, rate-limiting association rate constant, which is sensitive to divalent cation concentration. We also test various models for ROO filament assembly and find that cooperativity is not evident. Although our data are consistent with different growth mechanisms (ends only or breaking in the middle), we find that the lack of observed cooperativity combined with structural analysis of the ROO filament is most consistent with a model allowing for disassembly at any junction within the filament.

The methods, models, and rate constants developed and derived from this first of the two-part series will be extended in the accompanying article to include the full DNA-cleavage reaction pathway (24). Therein, microscopic rate constants for each step, including DNA cleavage and dissociation from SgrAI, are determined. Given the low physiological concentration of DNA in the cell, the slow ROO filament association rate constant, determined in this work and in the accompanying article (24), is possibly the origin of the proposed sequestering effect, protecting the host genome from DNA damage by limiting activated DNA cleavage to the invading phage DNA. Sequestering of DNA-cleavage activity is necessary, because many potential cleavage sites (i.e. the secondary sites) are likely not protected in the host genome and would be otherwise cleaved by roaming, activated SgrAI (3). This is possible because recognition sites on the same DNA molecule (i.e. phage DNA, because few primary sites on the host will be unmethylated) will have a higher local concentration than sites on differing molecules (such as the host genome and phage DNA), making the association step sufficiently fast for ROO filament to form. Formation of ROO filaments by sites on different DNA molecules (such as primary sites on the phage DNA, and secondary sites on the host, which are unprotected) is far less likely given the low concentration in the cell and the slow association rate constant.

Further, because of the relatively rapid ROO filament dissociation rate constant (and rapid release of cleaved DNA from SgrAI found in the accompanying article (24)), trapping of product (cleaved DNA) in the ROO filament does not occur to any significant extent. Although relatively fast, the ROO filament dissociation rate constant (0.02–0.03 s⁻¹) is roughly 10 times slower than the DNA-cleavage rate determined in the accompanying article (24). Hence each time a SgrAI–DNA complex assembles into a ROO filament, DNA cleavage is far more likely than dissociation, making the reaction pathway efficient. ROO filaments may persist if concentrations of SgrAI–DNA complexes are sufficient; however, the ROO filaments are highly dynamic with DNA recognition sites passing in and out of ROO filaments on the order of minutes (see the accompanying article (24)). The models and rate constants determined from these studies can now be used in simulations to mimic in vivo conditions and test hypothesis of ROO filament function.

Experimental procedures

Protein preparation

SgrAI enzyme used in assays contains 13 additional C-terminal residues (ENLYFQSHHHHHH), which include 6 histidine residues to be used for SgrAI purification, as well as a cleavage site for TEV protease, and was purified using previously described methods (18). Briefly, SgrAI was expressed in BL21 (DE3) Escherichia coli (which also contain a constitutive expression system for the methyltransferase MspI.M) overnight at 17 °C. The cells were sonicated and centrifuged to remove cell debris, and SgrAI was isolated using Talon resin chromatography (Clontech), followed by further purification using heparin resin chromatography (GE Healthcare). Purified SgrAI was concentrated and stored in single use aliquots at −80 °C in buffer containing 50% glycerol. Enzyme purity was assessed using Coomassie Blue staining of SDS-PAGE and assessed to at least 99% purity.

Sequences 1–4.

DNA preparation

The oligonucleotides were prepared synthetically by a commercial source and purified using C18 reverse phase HPLC. The concentration was measured spectrophotometrically, with an extinction coefficient calculated from standard values for the nucleotides (43) and where appropriate including that for 5′ attached fluorophores. Fluorophores used include fluorescein or Flo (6-carboxyfluorescein linked to the 5′-phosphate of the first nucleotide via a trans-4-cyclohexanol linker; Fig. S1A; excitation = 495 nm; emission = 520 nm), rhodamine-X or Rox (5(6)-carboxy-X-rhodamine linked to the 5′-phosphate of the first nucleotide via a 6-aminohexan-1-ol linker; Fig. S1B; excitation = 575 nm; emission = 603 nm), and Hex or 6-(4,7,2′,4′,5′,7′-hexachloro-3′,6′-dipivaloylfluoresceinyl; excitation = 537 nm; emission = 550 nm). Equimolar quantities of complementary DNA were annealed by heating to 90 °C for 10 min at a concentration of 1 mm, followed by slow cooling to room temperature. The different DNA substrates used in binding and cleavage assays are shown in Sequences 1–4 (red indicates the SgrAI primary recognition sequence, and a vertical line indicates a cleavage site). The sequences of the DNA flanking either side of the SgrAI recognition sites in the top and bottom strands of 40-1 are designed to prevent self-association. PC DNA (the duplex formed by annealing of PC–top and PC–bot) is identical to the left half of 40-1 (the duplex formed by annealing of 40-1–top and 40-1–bot) after cleavage by SgrAI, with the exception, however, that it is missing the 5′-phosphate at the cleavage site. Two PC DNA molecules may anneal via their 5′ “overhanging” CCGG sequences to create a symmetric version of 40-1.

Rox-labeled 40-1 (Rox–40-1) was prepared by annealing single-stranded Rox–40-1–top with unlabeled 40-1–bot. Flo-labeled 40-1 (Flo–40-1) was prepared by annealing single-stranded Flo–40-1–bot with unlabeled 40-1–top. Flo-labeled PC (Flo–PC) was prepared by annealing single-stranded Flo–PC–top with unlabeled PC–bot. Hex-labeled 40-1 (Hex–40-1) was prepared by annealing single-stranded Hex–40-1 top with unlabeled 40-1–bot.

FRET titration of ROO filaments

Titrations were performed with 50 nm Rox–40-1, 2 μm SgrAI, and varied concentrations of Flo–PC DNA in buffer A (10 mm Tris-HCl, 150 mm NaCl, 10% glycerol, 1 mm DTT, pH 8.0) supplied with 10 mm CaCl₂ in 1.5 ml total and maintained at 25 °C. Excitation occurred at 498 nm, and emission spectra were collected following 2 min of incubation with constant stirring after each addition of Flo–DNA. Flo-labeled DNA was a mixture of labeled and unlabeled at 1:9 Flo–PC:PC DNA. The resulting spectra were corrected for dilution of the added DNA, for Flo emission (using a reference Flo–DNA only spectrum scaled by relative emission at 570 nm), and for Rox emission caused by absorbance at 498 nm (using the spectrum before added Flo–DNA). The resulting average emissions at 602–612 nm (or 603–613 nm) were plotted versus concentration of Flo–EP₄₀ (the concentration of SgrAI bound to Flo–PC, which is half the concentration of Flo–PC because SgrAI binds Flo–PC in a 1:2 ratio) and fit to the Hill equation (see Equation 4).

FRET kinetic measurements

Reactions were carried out in 1.5 ml in a 2-ml cuvette with constant stirring held at 25 °C and consisted of 50–150 nm Rox–40-1, 100–350 nm SgrAI, and 25–150 nm Flo–40-1 or Flo–PC in buffer A at 25 °C. The reactions of Data Set 1 (Rox–40-1 and Flo–40-1) and the reactions of Data Set 2 (Rox–40-1 and Flo–PC) were performed without any divalent cation present, and the reactions of Data Set 3 (Rox–40-1 and Flo–PC) were performed with 10 mm CaCl₂. The reactions were initiated by adding SgrAI to premixed solutions of labeled DNA in buffer. SgrAI binds 1:1 with Rox–40-1 or Flo–40-1 to create Rox–ES₄₀ or Flo–ES₄₀, respectively (an enzyme-substrate complex where the substrate is Rox- or Flo-labeled and composed of 40 bp with a single primary site), and 1:2 to Flo–PC to create Flo–EP₄₀ (an enzyme-product complex where the product is a 40-bp Flo- or Rox-labeled DNA with breaks in the backbone at the SgrAI cleavage sites).

FRET measurements were performed with a PC1 ISS spectrofluorimeter with excitation at 498 nm, the Flo excitation maximum. T format was used to monitor emissions from two different wavelength ranges to isolate the emission from Rox, where one wavelength measured Flo emission only (585 nm), and the other measured emissions from both Rox and Flo (through a 590-nm cut-on filter; ThermoOriel Inc., catalog no. 10CGA-590). Rox emits with a maximum wavelength of 605 nm, and Flo emits with a maximum at 520 nm, but because the emission from Flo is often more intense, its emission can dominate the wavelengths where the Rox emission occurs. To remove the Flo emission from the 590-nm cut-on filter data, the Flo emission contribution must be estimated. However, the Flo emission also changes during the reactions, because of increased or decreased FRET, as well as because of quenching or red shifting from other non-FRET phenomenon (e.g. SgrAI binding, ROO filament assembly). The wavelength 585 nm was chosen to monitor the Flo emission during reactions, because it best estimated the Flo emission through the 590-nm cut-on filter during reactions when scaled by a correction factor C calculated as follows,

$$\text{Correction}\hspace{0.17em}\text{factor}\hspace{0.17em}C=\frac{I_{590\text{cof}}\left(\text{Flo}-\text{PC}\right)}{I_{585}\left(\text{Flo}-\text{PC}\right)}$$ (Eq. 2)

where I_590cof(Flo–PC) and I₅₈₅(Flo–PC) are the intensities from a solution containing only Flo–PC and measured through the 590-nm cut-on filter and at 585 nm, respectively (with excitation at 498 nm).

The FRET signal used in data fitting was calculated as follows,

$$\text{Corrected}\hspace{0.17em}\text{filter}\hspace{0.17em}\text{data}\hspace{0.17em}\left(\text{reaction},\hspace{0.17em}t\right)=I_{590\text{cof}}\left(\text{reaction},\hspace{0.17em}t\right)-C\times I_{585}\left(\text{reaction},\hspace{0.17em}t\right)$$ (Eq. 3)

where Corrected filter data (reaction, t) is the corrected FRET fluorescence intensity data (i.e. CF, the signal used in global data fitting) at time t after reaction initiation and is calculated by subtracting the fluorescence intensity measured at 585 nm at time t (I₅₈₅(Flo–PC)) after scaling by the correction factor C, from the fluorescence intensity measured through the 590-nm cut-on filter at time t (I_590cof(reaction, t)).

Analytical fitting of data

The FRET titration data were fit using Kaleidagraph (Synergy Software) and the Hill equation,

$$y=a+b\times \left\{\frac{{\left[\text{Flo}-{\text{EP}}_{40}\right]}^N}{\left(K_{1/2}^N+{\left[\text{Flo}-{\text{EP}}_{40}\right]}^N\right)}\right\}$$ (Eq. 4)

where y is the average corrected fluorescence intensity at 602–612 nm of the fluorescence emission at each concentration of Flo–EP₄₀ ([Flo–EP₄₀]), K_½ is the concentration of Flo–EP₄₀ where the average 602–612-nm emission is half-maximal, and N is the Hill coefficient, a measure of cooperativity. The constants a and b are also fit and correspond to the fluorescence baseline and scaling factor (to scale the term in brackets to the arbitrary fluorescence units of y), respectively.

Global data fitting

Global data fitting was performed with Kintek Global Kinetic Explorer version 6.2.170301 (Kintek Global Kinetic Explorer Corp.) (26–28). Data fitting equations and parameters for each model and each data set used within a given model are provided in the supporting information. Global fitting was performed independently for each data set and each model. In addition, within a global fitting, the scaling and baseline parameters were fit individually for each timed reaction.

Fitting concentrations of species predicted by the simulation to the experimentally determined FRET data required scaling factors. First, a scheme was required to predict the degree of FRET between fluorophores in run-on oligomers of SgrAI–DNA complexes (ROO filaments). Distances between 5′ ends of the 40-bp DNA in the model of oligomerized SgrAI/PC DNA (4) were measured using the molecular graphics software PyMOL (PyMOL Molecular Graphics System, version 1.8.0.3, Schrödinger, LLC.), and the efficiency of FRET was calculated using the standard equation,

$$\text{Efficiency}=\frac{1}{\left\{1+{\left(\frac{r}{R_0}\right)}^6\right\}}$$ (Eq. 5)

where r is the distance between fluorophores, and R₀ is a constant for a given FRET pair (representing the distance giving 50% efficiency of FRET (25)). The R₀ for fluorescein and rhodamine-X was assumed to be 51 Å, and r was estimated as the distance between 5′ ends of DNA in the molecular model (25). The closest distances occurred between SgrAI–DNA complexes 1–3 SgrAI–DNA complexes apart in the helix (Table 4). The FRET efficiencies were then calculated to be 0.2 for the adjacent SgrAI–DNA complex (ahead and/or behind), 0.12 for that two SgrAI–DNA complexes ahead (or behind), and 0.96 for that three SgrAI–DNA complexes ahead (or behind). To predict the signal, a baseline constant plus factor was applied; then for each predicted oligomer concentration, the various FRET efficiencies were summed. For example, for the ROO filament FRFFF (where F indicates SgrAI bound to Flo-labeled DNA, i.e. Flo–ES₄₀ or Flo–EP₄₀, and R indicates SgrAI bound to Rox-labeled DNA, i.e. Rox–ES₄₀), two instances of a donor/acceptor pair occur just adjacent to each other (FRFFF and FRFFF), one instance of a donor and acceptor two SgrAI–DNA complexes apart (FRFFF), and one instance of donor and acceptor three SgrAI–DNA complexes apart (FRFFF). To predict the signal from this ROO filament, the corrected efficiency factor is used, as well as a baseline and scaling factor to relate it to the experimentally observed FRET signal.

$$\text{Signal}=\text{baseline}+\left(\text{scaling}\hspace{0.17em}\text{factor}\right)\times \left\{\left(2\right)\left(0.2\right)+\left(1\right)\left(0.96\right)\right\}\times \left[\text{FRFFF}\right]$$ (Eq. 6)

The equations used in global data fitting then require the summation of signals from each ROO filament.

$$\text{Corrected}\hspace{0.17em}\text{intensity}=\text{baseline}+\left(\text{scaling}\hspace{0.17em}\text{factor}\right)\times \left(\text{sum}\hspace{0.17em}\text{of}\hspace{0.17em}\text{signals}\hspace{0.17em}\text{for}\hspace{0.17em}\text{each}\hspace{0.17em}\text{oligomer}\right)$$ (Eq. 7)

Full equations for data fitting and fitted parameters are given in the supporting information. Although Rox–40-1 and Flo–40-1 are singly labeled, they are expected to have an equal chance of binding in either orientation, resulting in only a lessened signal relative to doubly labeled DNA and accounted for in the fitted scaling factor.

Several different models were used in the Kintek Global Kinetic Explorer (Kintek GKE) software to simulate and fit the experimental data. Because of the run-on oligomerization of SgrAI–DNA complexes, the models describing their reactions become quite complex (see Fig. S7 for combinations and permutations of the association of SgrAI complexes). All combinations and permutations of Flo- and Rox-labeled complexes were modeled explicitly (up to 4- or 5-mers) with model 5EO including up to 5-mers and models 4EO and 4BM for including up to 4-mers. Another variable to be considered in the model is whether the ROO filaments can break in the middle (as allowed in model 4BM) or whether they dissociate only single SgrAI–DNA complexes at either end, i.e. the ends-only mechanism (model 5EO and 4EO). Similarly, in models where breaking in the middle is allowed, the association of two ROO filaments of any size may occur rather than association of only single SgrAI–DNA complexes to either end of the ROO filaments as in the ends-only models. Tables S1–S5 give Kintek GKE equations for models and for simulating FRET signals.

All attempts were made to limit the number of fitted parameters. The models also assumed (unless otherwise stated) the same rate constants for association and dissociation regardless of the size of oligomers involved; hence they assume that there is no cooperativity in ROO filament formation (i.e. the binding of a SgrAI–DNA complex to a ROO filament with two SgrAI–DNA complexes is the same as adding to one with three, and so on). The forward and reverse rate constants for association of two PC DNA molecules, and binding of SgrAI of self-annealed PC DNA or 40-1, were also fit but constrained by measured or estimated K_D (which constrained the ratio of the reverse to the forward rate constant). Kintek GKE provided measures of the quality of the fit for each model in the form of the sigma with respect to the fit, the χ², and χ²/DoF.

Error analysis

The FitSpace module of Kintek GKE was used to determine boundaries (i.e. error limits) for fitted rate constants at the recommended 0.9 and 0.95 χ² threshold (28). FitSpace varies the rate constants systematically while simultaneously fitting all other parameters and recalculating χ², a measure of how well the simulated curves match the experimental data (i.e. the sum of the squares of the residuals, and a smaller number indicates a better fit). Values for the rate constants resulting in a χ² equal to or less than the minimum χ² * (0.9)⁻¹ are considered within the 0.9 χ² threshold, and χ² values equal to or less than the minimum χ² * (0.95)⁻¹ are considered within the 0.95 χ² threshold.

Simulations of ROO filament size distribution to test for cooperativity

For example, if the rate constant for dissociation is 0.017 s⁻¹, and X is 1.5, then the dissociation of a SgrAI–DNA complex from an ROO filament is 0.017 s⁻¹ when the ROO filament is composed of two SgrAI–DNA complexes, 0.017/1.5 s⁻¹ when composed of three SgrAI–DNA complexes, (0.017/(1.5)²) s⁻¹ when composed of four SgrAI–DNA complexes, and (0.017/(1.5)³) s⁻¹ when composed of five SgrAI–DNA complexes. No further reductions in rate constant were made past this number of SgrAI–DNA complexes, although ROO filaments as large as 14 SgrAI–DNA complexes were modeled using model EM (Table S6). Rate constants used in model EM are those from model 4BM with Data Set 3 (Table 6).

Author contributions

C. K. P., J. L. S., and N. C. H. supervision; C. K. P., J. L. S., C. B., L. E. B., J. S., C. H., and N. C. H. investigation; C. K. P., J. L. S., C. B., L. E. B., C. H., and N. C. H. writing-review and editing; N. C. H. conceptualization; N. C. H. resources; N. C. H. data curation; N. C. H. formal analysis; N. C. H. funding acquisition; N. C. H. validation; N. C. H. visualization; N. C. H. methodology; N. C. H. writing-original draft; N. C. H. project administration.