Bottom-Up Evolution of Vesicles from Disks to High-Genus Polymersomes

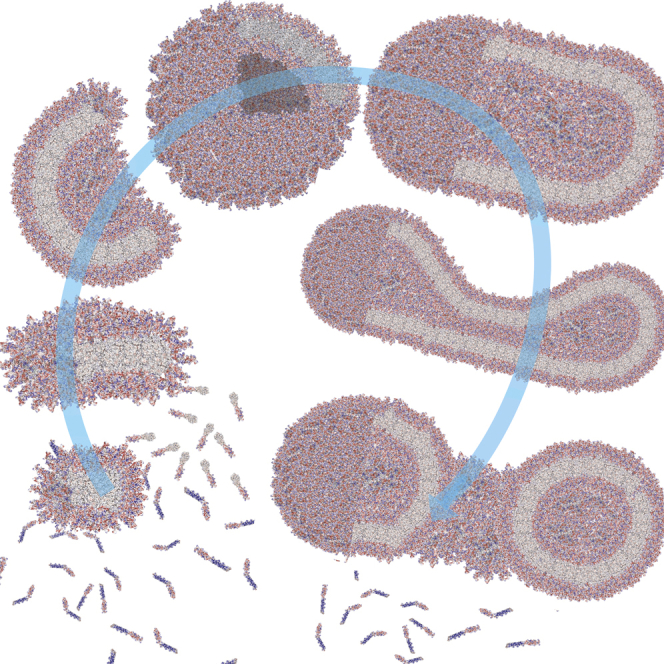
Summary

Polymersomes are vesicles formed by the self-assembly of amphiphilic copolymers in water. They represent one of the most promising alternatives of natural vesicles as they add new possibilities in the amphiphiles' molecular engineering of aqueous compartments. Here we report the design of polymersomes using a bottom-up approach wherein self-assembly of amphiphilic copolymers poly(2-(methacryloyloxy) ethyl phosphorylcholine)-poly(2-(diisopropylamino) ethyl methacrylate) (PMPC-PDPA) into membranes is tuned using pH and temperature. We report evolution from disk micelles, to vesicles, to high-genus vesicles (vesicles with many holes), where each passage is controlled by pH switch or temperature. We show that the process can be rationalized, adapting membrane physics theories to disclose scaling principles that allow the estimation of minimal radius of vesiculation as well as chain entanglement and coupling. This approach allows us to generate nanoscale vesicles with genus from 0 to 70, which have been very elusive and difficult to control so far.

Graphical Abstract

Highlights

• •Membrane-confined compartments are the most exquisite examples of self-assembly
• •We mimic compartmentalization using self-assembling polymers
• •We show that bottom-up assembly evolves from disk to vesicles to high-genus vesicles
• •We combine experiments and theory to fully elucidate vesiculation

Polymer Chemistry; Materials Chemistry; Colloids

Introduction

Amphiphiles are molecules that contain both soluble and insoluble components with respect to a given solvent. In solution, the balance of the two counteracting interactions drives one of the most exquisite examples of self-assembly processes that give rise to supramolecularly defined nanostructures. These can be spherical or cylindrical micelles, or membranes, depending on the amphiphile packing factor, which in turn is defined by the insoluble-to-soluble molar ratio (Smart et al., 2008). For spherical micelles the geometry is defined by the molecular architecture, whereas for both cylinders and membranes, the curvature of the amphiphiles decides the formation of exposed ends or edges. These regions can be protected either by the assembly of a portion of amphiphiles into more frustrated and curved structures or by the structure closing on itself to avoid any hydrophobic exposure. For cylindrical micelles, these two scenarios corresponds to either worm-like or toroidal micelles, whereas for membranes, the two options are either disk-like micelles or closed vesicles (Smart et al., 2008). The latter are a very important structure as their geometry enables the enclosure of a given solvent volume whose composition is controlled by the same amphiphilic membrane. Assembly of natural amphiphiles such as phospholipids or their progenitors (Hanczyc et al., 2003) into vesicles provides the necessary compartmentalization to house the energy pools for feeding all biochemical processes (Szostak et al., 2001, Mann, 2013) making such a structure one of the most important element of life complexity.

It is not surprising that both natural and synthetic vesicles have been the subject of several studies. Beside the obvious biophysical drive to understand natural membranes, vesicles have been proposed as reactors and energy conversion units (Peters et al., 2012, Gaitzsch et al., 2015). Also, vesicles are one of most successful drug delivery systems as they mimic nature's way of carrying molecules, enabling the encapsulation of both soluble and insoluble drugs (Guan et al., 2015, Pattni et al., 2015, Al-Jamal and Kostarelos, 2011). Vesicles can be made using either natural or synthetic amphiphilic molecules. Among these, one of the most promising is based on the use of amphiphilic block copolymers wherein each soluble and insoluble component is macromolecular and consequently bestows the vesicles (known as polymersomes) with extra interactions arising from chain entanglement (Wang et al., 2012, Smart et al., 2008). Such a macromolecular nature allows to impart responsiveness (Li and Keller, 2009), to finely control the surface properties (Photos et al., 2003), to enhance both colloidal stability (LoPresti et al., 2009) and mechanical properties (Discher et al., 1999), as well as to augment tissue penetration (Pegoraro et al., 2013). The most common vesicle shape is spherical but tubular, prolate, discocytic, stomatocytic, toroidal, and pear-shaped vesicles have all been reported (Seifert and Lipowsky, 1995, Chang et al., 2014). Vesiculation is a process that strongly depends on the methods in which amphiphiles are placed in contact with water. We classify these methods as top-down and bottom-up approaches (Messager et al., 2014). The top-down approach involves the hydration of a dry block copolymer film during which water diffusion and copolymer arrangements drive the formation of complex lyotropic liquid lamellar structures. These later break down into vesicles via unbinding of membrane-bound compartments. Such a process is complex, and its dynamics are strongly dependent on the molecular weight of the amphiphile (Battaglia and Ryan, 2006b). Moreover, the mixing of the highly viscous lamellar phase with water gives rise to finger-like instabilities, which result in the formation of tubular vesicles (Battaglia and Ryan, 2006a, Robertson et al., 2014). On the other hand, the formation of vesicles via the bottom-up approach starts with the amphiphile being fully solubilized and molecularly dispersed in solution. This can be achieved via solvent switch, tuning the amphiphile's assembly by gradually exchanging the organic solvent with water. Alternatively, the amphiphile's solubility can be controlled by pH, temperature, light, enzymatic reactions, or redox reactions (Che and van Hest, 2016, Hu et al., 2017, Liu et al., 2014, Deng et al., 2016). In all cases, the self-assembly evolves from molecularly dissolved amphiphiles to vesicles whose geometry is controlled by both thermodynamics and kinetics. This means that the final shape of the vesicle can be controlled by temperature and concentration as well as by the mixing rate. Small amphiphiles are characterized by relatively high critical assembly concentration (CAC) in water, and hence their assembly is characterized by a high exchange rate between unimers and the aggregate with consequent fast equilibration. Macromolecular amphiphiles, particularly those that assemble into membranes, have almost zero CAC, and hence once the unimer pool is depleted the assembly becomes kinetically trapped (Jain and Bates, 2003). Such a non-ergodic nature allows to access metastable phases, which are precluded for small amphiphiles. Eisenberg and colleagues noted this unique nature of polymersomes in their pioneering work (Gao et al., 1994, Zhang and Eisenberg, 1995) referring to the zoology of morphologies as crew-cut aggregates. Later on, they optimized the process controlling the final structure (Lim Soo and Eisenberg, 2004, Mai and Eisenberg, 2012) to the point that they were able to isolate complex vesicular structures. Using a similar approach, van Hest and colleagues demonstrated that the shape of polymersomes can be controlled from spherical to prolate, to disk, to stomatocytes (Meeuwissen et al., 2011, van Oers et al., 2013, Rikken et al., 2016); more recently, similar experiments were reported by Wong et al. adding extra control using aromatic groups (Wong et al., 2017). We reported a different approach using pH-sensitive poly(2-(methacryloyloxy)ethyl phosphorylcholine)-poly(2-(diisopropylamino)ethyl methacrylate) (PMPC-PDPA) (Pearson et al., 2013). Here we have shown that the PMPC-PDPA assembles into either micellar or vesicular structures depending on the kinetics of pH or temperature changes. We expanded on this study showing via a combination of different techniques that the kinetics of assembly can be controlled by either temperature or pH changes and that this allows to tune both the vesicle closing morphology and its topology.

Results and Discussion

pH-Driven Self-Assembly

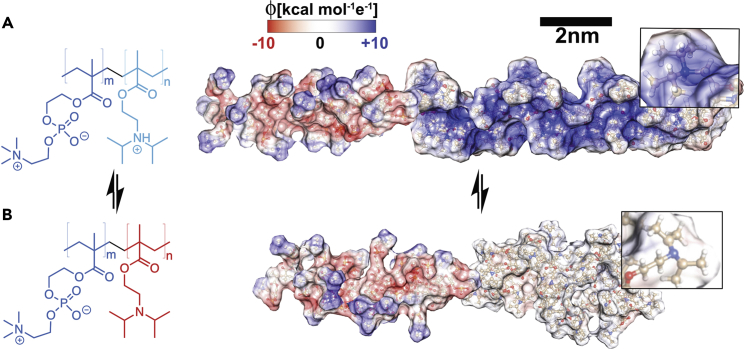
The chemical structures of PMPC-PDPA copolymers are shown alongside the corresponding molecular models with the DPA groups protonated (Figure 1A) and deprotonated (Figure 1B). The models were calculated minimizing the PMPC₂₅-PDPA₇₀ using Merck molecular force field molecular mechanics in Avogadro (Hanwell et al., 2012) (final structure rendered in Chimera [Pettersen et al., 2004]). PMPC and PDPA chains were minimized separately and joined together after calculation. No constrains were imposed on the PMPC and protonated PDPA chains, and we imposed an end-to-end distance d_AA∝N^2/3 on the deprotonated PDPA, in agreement with the scaling reported for block copolymer micelles and membranes (Battaglia and Ryan, 2005, Jain and Bates, 2003). The displayed models show the PMPC-PDPA's charge distribution and molecular size. The PDPA chain is fully soluble when protonated, whereas it is hydrophobic when deprotonated, which drives its self-assembly (Lomas et al., 2007, Pearson et al., 2013). This process is strongly dependent on the pH switch rate, as shown in Figure S1A wherein the pH change is plotted as a function of time for different flow rates of NaOH solution titration. The pH rises exponentially with time until it reaches the PDPA pK_a, which under experimental conditions (PBS 100 mM and T = 25^°C) is 6.8. The pH stabilizes for the time necessary to complete the reaction between the protonated PDPA and the hydroxyl ions in solution to form deprotonated and hydrophobic PDPA. After all the chains are deprotonated, the pH again rises exponentially with time. The graph in Figure S1B shows that the time plateau is proportional to the flow rate and changes from a few minutes to hours. In Figures S1D–S1H we show the corresponding transmission electron microscopic (TEM) images of the samples formed at different flow rates. The final morphology changes with the flow rate indicating that it is possible to modulate the formation of different architectures.

Figure 1.

Chemical Structure and Molecular Model of the PMPC-PDPA Copolymers

(A and B) The copolymers are shown with the tertiary amine group protonated (A) and deprotonated (B). Note that the molecular models were calculated for PMPC₂₅-PDPA₇₂ and the structures are represented with their solvent-accessible surface (probe distance 1.4 Å) colored as a function of the molecule electrostatic potential calculated as $\varphi \left(r\right)=\sum q_i/\mathrm{ϵ}{r}_i$ with $\mathrm{ϵ}=4r$ being the dielectric, representing screening by the water.

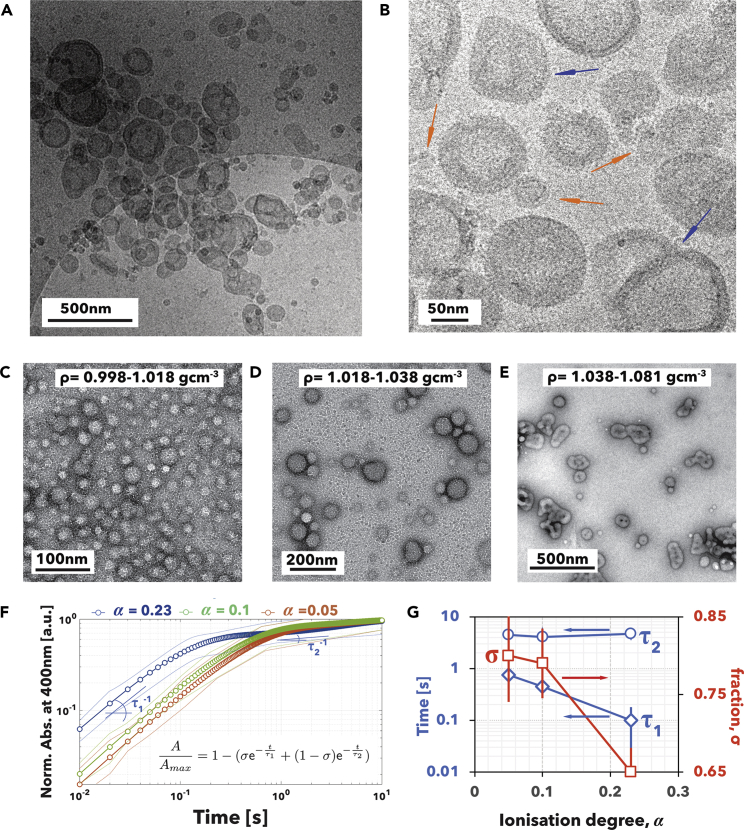
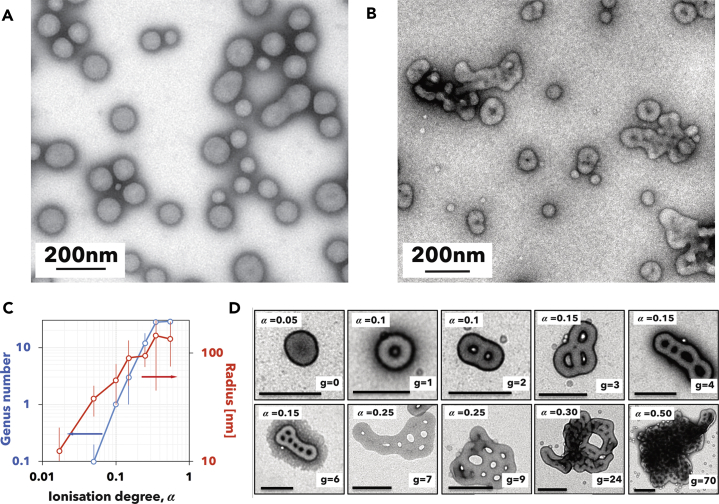
Upon more detailed inspection using cryogenic TEM imaging of the vitrified sample produced by slower rate, we observed that PMPC-PDPA assembles into a large variety of architectures, which are shown in the micrographs in Figures 2A and 2B at low and high magnification, respectively. Two populations of structures are visible, one is made of discoid micelles and the other is made of vesicles. The latter have different shapes and in some the membranes are not completely closed. We recently developed a method to separate soft particles by using density gradient fractionation (Robertson et al., 2016) and applied it to PMPC-PDPA structures made by slowest rate. At water density between 0.998 and 1.018 g cm⁻³ (as shown in the TEM image in Figure 2C), we mostly found micelles with radius varying from 10 to 20 nm. At densities between 1.018 and 1.038 g cm⁻³, the radius increases from 30 to 60 nm and the aggregates are mostly composed of spherical vesicles (Figure 2D). At higher density between 1.038 and 1.081 g cm⁻³ the sample is dominated by larger (radius from 60 to 200 nm) flattened and holed vesicles (Figure 2E). These latter structures can be described using the mathematical terminology of genus, i.e., the number of holes or handles of the vesicle (Seifert and Lipowsky, 1995), which varies from 0 for the spherical geometry to 1 for the torus to >1 for vesicles hereafter referred to as high-genus vesicles.

Figure 2.

pH-Driven Assembly of PMPC₂₅-PDPA₇₀ Copolymers

(A–E) Low- (A) and high- (B) magnification cryogenic TEM images of PMPC₂₅-PDPA₇₀ assemblies produced at 0.5 μmol min⁻¹ of NaOH solution addition. The red arrows point to disk micelles and the blue ones to high-genus vesicles. TEM images of the sample corresponding to density 0.998–1.018 gcm⁻³ (C), 1.018–1.038 gcm⁻³ (D), and 1.038–1.081 gcm⁻³ (E).

(F and G) Kinetics curves measured by stop-flow absorbance of PMPC₂₅-PDPA₇₀ copolymer at different ionization degrees (F) and the corresponding parameters (G) obtained using Equation 3.

To further elucidate the kinetics of pH switch, we studied the self-assembly of PMPC₂₅-PDPA₇₀ copolymers using stop-flow absorbance measurements following the initial 10 s of assembly at different degrees of copolymer ionization, $\alpha ={\left(1+{10}^{\left(pH-p{K}_a\right)}\right)}^{-1}$. This depends on the final solution pH and for pH = pK_a, the ionization degree α = 0.5, For any value below this, the PDPA has not sufficient charges to remain soluble and becomes hydrophobic. As shown in Figure 2F, by normalizing the absorbance as a function of time, self-assembly occurs via two steps and can be fitted by a double exponential growth as in:

$$\frac{A}{A_{max}}=1-\left(\sigma {\mathsf{e}}^{-\frac{t}{{\tau }_1}}+\left(1-\sigma \right){\mathsf{e}}^{-\frac{t}{{\tau }_2}}\right)$$ (Equation 1)

In Figure 2G, we plotted Equation 3 parameters as a function of the ionization degree showing that the first fast relaxation time, τ₁ varies from 750 to 100 ms depending on the ionization degree, whereas the second slower relaxation time τ₂ increases slightly with the ionization degree. The relative ratio between the two processes, expressed here as σ, also changes with the ionization degree and the fast dynamics dominates with σ > 0.7 for α < 0.1; the more the copolymer is charged, the more the two steps are balanced. This suggests that as α → 0.5, the unimer concentration increases.

Temperature-Driven Self-Assembly

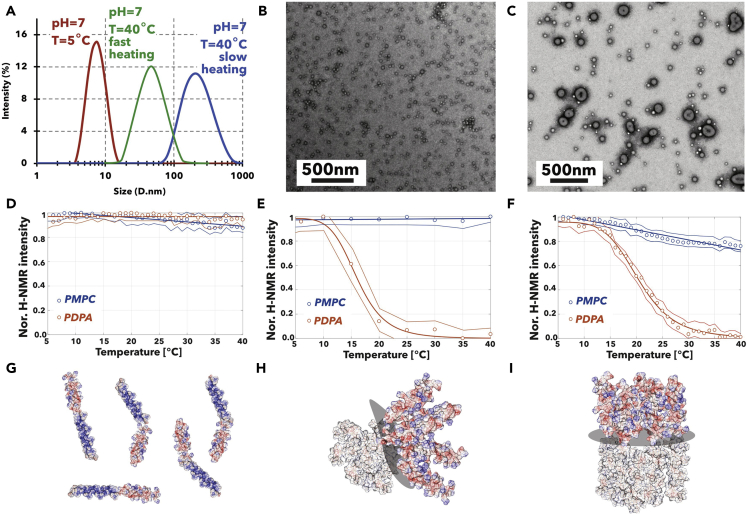
As we previously reported (Pearson et al., 2013), the PDPA pK_a varies with temperature being about 7.5 at 5^°C and going down to 5.5 at 60^°C. This means that PMPC-PDPA self-assembly can be tuned by temperature changes, as shown in Figure 3; we dissolved the copolymers at pH = 2, cooled the solution down to 5^°C, and increased the pH to 7 triggering the formation of micelles and vesicles by heating. In Figure 3A, the dynamic light scattering (DLS) of a PMPC₂₅-PDPA₇₀ dispersion confirms that the copolymer is molecularly dispersed at pH = 7 and T = 5^°C, and as we raise the temperature it self-assembles. As shown by both DLS and TEM (Figures 3B and 3C), the final structure architecture depends on the heating rate with fast rate leading to small micellar structures, whereas slow rate leading to vesicles. Such temperature sensitivity allowed us to monitor self-assembly using proton nuclear magnetic resonance (NMR) spectroscopy following chemical shift of the copolymers' hydrogens. The resulting spectra in Figure S2A show the evolution of PMPC-PDPA proton intensity as a function of the solution temperature when dispersed at pH = 2. The NMR spectra were collected every 5 min while the temperature was increased from 5°C to 40°C at a rate of 0.2^°C per minute. The spectra show no changes in the proton signal. In Figure 3D, the plot of normalized intensity of peak 1 and peaks 7–9 as a function of temperature confirms that no changes are detectable. This confirms that the PDPA is fully protonated and the copolymers are dissolved molecularly with all protons allowed to interact with the solvent (Figure 3F). However, when the solution pH is increased to 7, the NMR spectra show a decrease in several peaks. For heating rate 1^°C per minute, all the PDPA peaks decrease in intensity (Figure S2B) suggesting that the protons stop interacting with water and the PDPA tertiary amines are deprotonated. The PMPC peaks, on the other hand, seem to be unaltered, suggesting that the corresponding protons interact with the solvent in the same way as the unimers (Figure 3E). The normalized intensity of peaks 1 and 7–9 is plotted as a function of the temperature in Figure 3G and shows that the PDPA peaks decrease, whereas the PMPC peak 1 remains unchanged. This suggests an assembly structure with a fully deprotonated PDPA shielded into a hydrophobic core, whereas the PMPC chain remains in close contact with water and hence forms a curved structure that agrees with the micelles observed by TEM and shown in Figure 3H. Finally, for slower heating rate of 0.2^°C per minute, the NMR spectra collected as a function of the temperature (Figure S2C) show a similar decrease in most PDPA peaks as well as a decrease in most PMPC peaks. Such an effect is more visible in Figure 3J where peaks 7–9 decrease to almost zero and peak 1 decreases to about 75% of its starting value. Such a decrease suggests that most PMPC chains have a more packed configuration in agreement with the vesicular structure observed by TEM, as showed by the cartoon in Figure 3K. It is important to point out that the PDPA deprotonation process in D₂O used for the NMR experiments is slightly different, and indeed the transition temperature is a few degrees lower compared with our previous observations (Pearson et al., 2013). However, the scope of these experiments is to shed light on the molecular-level changes during the self-assembly and hence the shift in transition is irrelevant.

Figure 3.

PMPC₂₅-PDPA₇₀ Self-Assembly Tuned by Temperature Change

(A–F) Particle size distribution measured by dynamic light scattering (DLS) of PMPC₂₅-PDPA₇₀ polymersome dispersion at pH = 7 and at T = 5^°C and 40^°C fast and slow heating (A). Corresponding TEM images of PMPC₂₅-PDPA₇₀ polymersomes formed by fast (B) and slow (C) heating. NMR titration peaks 1 and 7–9 normalized intensity as a function of the temperature and corresponding model of PMPC₂₅-PDPA₇₀ dispersion during slow heating at pH = 2 (D) and fast (E) and slow (F) heating at pH = 7.(G–I) Schematics show the corresponding arrangements of the PMPC-PDPA copolymers under the different constionds. Images were generated using the minimized structures shown in Figure 1 packed to form either planar or curved arrangements.

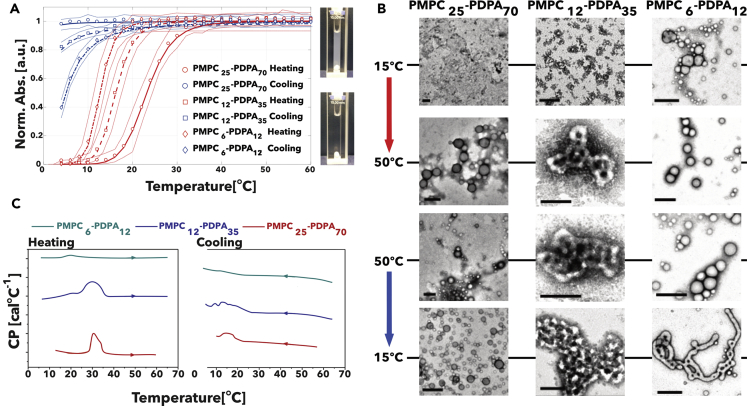
As shown in Figure 4A, the temperature-driven self-assembly, unlike the pH-driven one, is not reversible. Monitoring the solution turbidity by measuring the absorbance at 400 nm we noticed that whereas the copolymers assemble into dispersed phases going from 5°C to 60°C, with transition temperature depending on their molecular mass, the assemblies do not dissolve into unimers as the solution is cooled backed to 5^°C. The low-molecular-mass PMPC₆-PDPA₁₂ shows a hysteresis of about 8^°C and the absorbance does not go down to zero at 5^°C. As the molecular mass increases, PMPC₁₂-PDPA₃₅ displays even more hysteresis, whereas PMPC₂₅-PDPA₇₀ shows no sign of disassembly upon cooling. Upon inspection by TEM (Figure 4B), we observed that PMPC₂₅-PDPA₇₀ assemble into vesicles and micelles upon heating but the morphology of these appear unchanged upon cooling. Both PMPC₁₂-PDPA₃₅ and PMPC₆-PDPA₁₂ also assemble into vesicles and micelles upon heating, but as their solutions are cooled down the number of vesicles increases and so does their genus number. To further understand such a hysteresis in the self-assembly behavior, we performed micro-differential scanning calorimetry for the three different PMPC-PDPA copolymers, and both the heating and cooling curves are shown in Figure 4C. All the investigated copolymers showed a thermal transition starting around 20°C to 30°C indicating that PMPC-PDPA self-assembly in water is an endothermic process. We can confidently attribute such an endothermic process to the de-protonation reaction of the PDPA with water. If we compare the pH- and temperature-driven process, in the former the acid-base reaction is mostly controlled by the presence of hydrogen and hydroxyl ions in solution, whereas in the latter the concentration of these is minimal (pH = 7) and the only changing parameter is the copolymer pK_a. The thermograms show that the endothermic peak is not mirrored by an exothermic one during the reverse cooling cycle, We instead observed a shoulder typical of glass transitions indicating that the PDPA becomes an amorphous glass below 20°C. This suggests that the PDPA membrane freezes and becomes less permeable to water hence slowing down or even stopping altogether the water diffusion with consequent arrest of the copolymer disassembly.

Figure 4.

Temperature-Driven Self-Assembly of PMPC-PDPA Copolymer at Different Molecular Weight

(A–C) Turbidity measurement using UV/Vis absorbance at 400 nm of PMPC₂₅-PDPA₇₂, PMPC₁₂-PDPA₃₅, and PMPC₆-PDPA₁₂ solution during heating (red curves) and cooling (blue curves) starting from 5^°C to 60^°C; a photograph of the cuvette before and after heating is shown (A). TEM images of PMPC₂₅-PDPA₇₂, PMPC₁₂-PDPA₃₅, and PMPC₆-PDPA₁₂ structures formed during heating and after cooling. Scale bar, 200 nm (B). Micro-differential scanning calorimetry of PMPC₂₅-PDPA₇₂, PMPC₁₂-PDPA₃₅, and PMPC₆-PDPA₁₂ dispersion showing the heat exchange during heating and cooling (C).

Disk Micelles

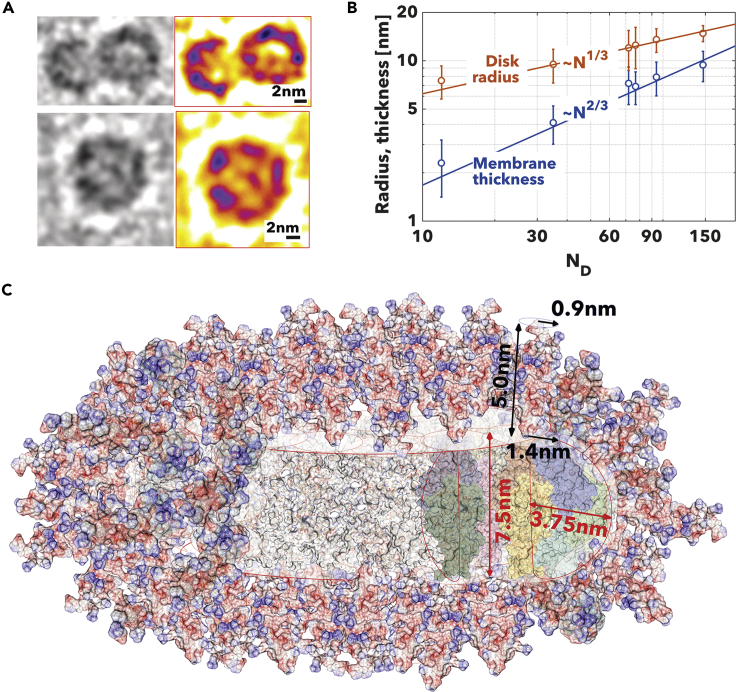
The two structures, disk micelles and vesicles formed both during pH- or temperature-driven assembly, are indeed quite unique and warrant further analysis. In Figure 5A we show two high-resolution cryogenic TEM images in grayscale and the fire palette of PMPC₂₅-PDPA₇₀ disk micelles. The PMPC chains were selectively stained by phosphotungstic acid before vitrification. The disk micelles are small and show highly curved edges with a few copolymers in the middle. We measured both the disk radius and membrane thickness for several PMPC-PDPA copolymers and plotted these as a function of the degree of polymerization of PDPA (Figure 5B). A given polymer chain has end-to-end distance scaling with its degree of polymerization according to the power law, $d\propto N^{\nu }$, where when the chains are stretched $1\ge \nu {\ge }^{3/5}$, when unperturbed (also random coil) $\nu \sim 3/5$, and when hyper-coiled $\nu \le 3/5$ (de Gennes, 1979, Battaglia and Ryan, 2005). Assuming that the PDPA chain extends as long as the disk radius or thickness, we can assess the hydrophobic chain configuration in both types of assembly. We and others reported that polymersome membranes are typically associated with a scaling exponent of 2/3 corresponding to super-segregated copolymers (Jain and Bates, 2004, Battaglia and Ryan, 2005, Pearson et al., 2013). As shown in the graph in Figure 5B, we confirm the same trend for PMPC-PDPA membranes, whereas for the disk radius the power law scales with an exponent of 1/3. This suggests a hyper-coiled configuration indicating that the interfacial energy associated with the free edges is sufficiently strong to compress the chains. Using this scaling analysis together with NMR, the density data, and the structures observed in cryogenic TEM images in Figure 5A, we conclude that the micelles are discoid with a core made of copolymers assembling into a configuration as dense as the vesicle membrane with curved edges that shield the hydrophobic chains from water. Such a structure is shown in Figure 5C where we used the minimized PMPC-PDPA copolymers to reconstruct the final geometry. As PMPC₂₅-PDPA₇₀ forms a membrane of about 7.51 nm we can assume that to stabilize the edge, few copolymers form a semi-cylindrical region with a radius of half the membrane thickness (i.e., 3.75 nm). Such a configuration is naturally frustrated, and it can only be formed when there are not enough chains to form the vesicles as all the unimers have been depleted from the solution.

Figure 5.

Disk Micelles

(A and B) High-resolution cryogenic TEM with pre-stained samples of PMPC₂₅-PDPA₇₀ disk micelles shown in gray and fire palette (A). Scaling graph between the disk radius (red) and membrane thickness (blue) and PDPA degree of polymerization (B).

(C) Schematics of the PMPC-PDPA disk shown in scale using the minimised copolymer strucutres shown in Figure 1.

High-Genus Vesicles

For both pH- and temperature-driven assemblies, the vesicles form with different topology and different genus numbers. We hypothesize that as disk micelles close into spherical (g = 0) vesicles their interior becomes inaccessible to unimers. These thus insert only onto the exterior leaflet of the vesicle membrane leading to an asymmetric growth, which in turn leads to an increase in the vesicle genus. To prove this hypothesis, we exploit the self-assembly hysteresis with the temperature, which allows the co-existence of both unimers and vesicles at low temperature. We thus dissolved PMPC-PDPA at pH = 2, cooled down the solution to 5^°C, and finally raised the pH to 7. We mixed such a unimer solution with PMPC-PDPA spherical vesicles, made using film hydration, which we established produces only g = 0 vesicles (Robertson et al., 2014) keeping the temperature at 5^°C. The TEM image in Figure 6A shows the polymersomes before mixing at 5^°C, confirming that they retain their structure, whereas the micrograph in Figure 6B shows the structure after 30 min of mixing the vesicle with unimer as stated above. The resulting structures are vesicles with an altered topology and higher genus number, confirming our initial hypothesis.

Figure 6.

High-Genus Structure

(A–D) TEM images of PMPC₂₅-PDPA₇₀ polymersomes prepared by film hydration (A) and after mixing with unimers at 5^°C at 1:1 ratio (B). Graph showing the genus number (blue) and average radius (red) as function of the PMPC₂₅-PDPA₇₀ ionization degree (C). TEM images of PMPC₂₅-PDPA₇₀ polymersomes with different genus numbers and formed with different ionization degrees (D).

A similar condition of co-existence of vesicles and unimer is achieved at pH values close to the pK_a, i.e., α > 0. We thus performed a series of experiments dissolving PMPC₂₅-PDPA₇₀ at pH = 2 and raising the pH to different values modulating its ionization degree. The graph in Figure 6C shows both the average vesicle genus number (in blue) and the radius (in red) as a function of α. It is evident that both increase with PDPA ionization degree, confirming that the longer the vesicles are allowed to grow, the higher their genus number becomes. In Figure 6D, we show the relative TEM images for the different ionization degrees further confirming the asymmetrical growth hypothesis and, moreover, demonstrating the remarkable ability to form structures with genus as high as g = 70 at pH = pK_a where α = 0.5.

Proposed Mechanism and Theoretical Considerations

Based on the data discussed above, we can conclude that both pH- and temperature-driven self-assemblies occur according to the cartoon proposed in Figure 7. As we measured in Figure 2G, we can confidently assume that the kinetics of self-assembly occurs according to two regimes, and using the model proposed by Ligoure et al. (Ligoure and Leibler, 1990), we can estimate that this occurs with a first fast nucleation time,

$${\tau }_1={\tau }_N=\simeq \frac{a^2}{D{\varphi }_u^2}$$ (Equation 2)

where a is the Kuhn statistical length of the unimer, D is the copolymer diffusion coefficient in water as unimer, and ${\varphi }_u$ is the copolymer unimer volume fraction. As shown in Figure 2G, τ_N decreases with the increase of charges on the PDPA chains, which, assuming the diffusion coefficient is unvaried, confirms that with higher α the unimer concentration ${\varphi }_u$ increases. The fast nucleation is followed by a much slower regime dominated by the activation barrier of the unimer to insert in the pre-formed assembly. Indeed, the unimer needs to diffuse through the PMPC brush and insert the PDPA chains into the preformed membrane. We adapt the Liguore-Leibler model (Ligoure and Leibler, 1990), to estimate the construction time,

$${\tau }_2={\tau }_C\sim \frac{1}{a_0}\left(N_M+\alpha N_D\right){\mathrm{e}}^{\frac{\Delta G_i}{kT}}$$ (Equation 3)

where N_M and N_D are the polymerization degree of the PMPC and PDPA blocks, ΔG_i is the free energy gain of the hydrophobic PDPA chain to insert in the membrane, k is the Boltzmann constant, and T is the temperature. From Figure 5A, we can write that the membrane thickness is $t=a{N}_D^{\frac{2}{3}}$, and we calculate for the PDPA that the Khun length a = 0.367 nm. Thus, we can derive the area per molecule of the copolymers in the assembly a₀ calculated as

$$a_0=\frac{M_D{N}_D^{1/3}}{N_A{\rho }_{P}pa}$$ (Equation 4)

where M_D is the DPA monomer molecular mass, N_A is the Avogadro number, ρ_P is the PDPA density, and p is the packing factor, which for membranes is $p\in \left[0.5,1\right]$. τ_C Is considerably slower than the nucleation time, and we measured it to increase linearly from 4.5 to 6 s together with α. Both times are also in strong agreement with previous studies that used rapid mixing techniques (Johnson and Prud’homme, 2003). In the graph in Figure 2G, we also calculated the relative fraction of the two different processes, σ, as a function of the ionization degree. This increases when the copolymer nucleation dominates the kinetics of the process, suggesting that at this stage the copolymers do not have enough time to perform insertion events to allow the disk micelles growing into vesicles.

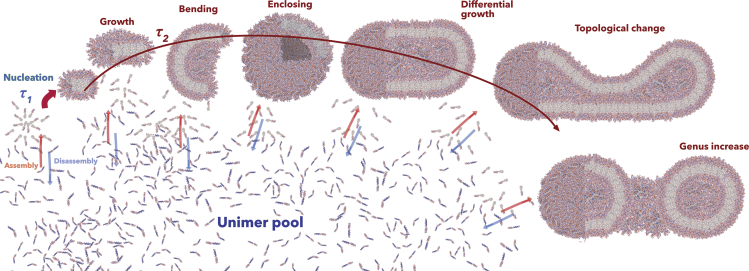
Figure 7.

Proposed Mechanism of Polymersome Formation and Topological Changes.

The blue and red arrow represent assembly and disaassembly processes.

This is very much confirmed by DLS in Figure 3A, TEM in Figures 2A and 3B, and NMR in Figures 3G and 3H, which show that the fast kinetics lead to a large number of disk micelles. NMR and cryogenic TEM image (Figure 5A) showed that these have highly curved interface with the PDPA core forming the corresponding membrane in the disk center but hyper-coiling at the edge as demonstrated by our scaling analysis in Figure 5B, which constructs a very accurate molecular model of its structure. As shown in Figure 7, provided the unimer pool is not depleted, these insert into the disk making them grow, and when these reach a critical radius (about 15 nm), the membrane starts bending and enclosing. The Hamiltonian associated with such a process is the sum of three components:

$$H=H_H+H_{ADE}+H_{edge}=\int \left[2{\kappa }_M{\left(M-c_0\right)}^2+{\kappa }_{G}G\right]dA+\frac{k_{m}a{N}_D^{5/3}{M}_D}{8N_{A}p{\int }_{A}dA}{\left(\Delta N^{\pm }\right)}^2+\frac{3N_{A}kTp{a}^2{N}_D^{2/3}}{8M_D}{\int }_{L}dL$$ (Equation 5)

The first term H_H is the membrane bending energy of Helfrich's elastic energy with A being the total surface area, ${\kappa }_M$ and ${\kappa }_G$ the bending and the Gaussian moduli, and $M=0.5\left(c_1+c_2\right)$, $G=\left(c_1{c}_2\right)$, and c₀ being the mean, Gaussian and spontaneous curvatures of a surface characterized by $c_1=R_1^{-1}$ and $c_2=R_2^{-1}$ curvatures. The second term H_ADE is the area-difference-elasticity and includes the energy contribution arising from the differential stretching and compression of the two membrane monolayers, and it depends on the membrane compression modulus k_m and the difference in copolymer numbers between the outer (+) and inner (−) layers of the membrane, $\Delta N^{\pm }=N^{+}-N^{-}$. Finally, the last term H_edge is associated with edge effect, and, as shown by the conformation of the copolymers in the disk edge (Figure 5C), we can attribute it to the entropic compression of the PDPA chain from the equilibrium end-to-end distance, i.e., the membrane thickness, t, to the radius of the disk edge, t/2.

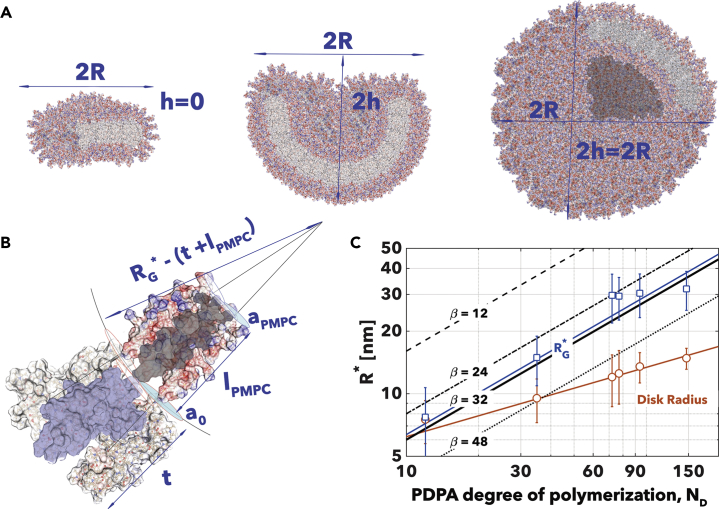
Equation 3 can be used to analyze the experimental data observed above and rationalize them in thermodynamic terms. The first transition from the disks arising from the initial fast nucleation to closed vesicle is shown in Figure 8A where the disk is characterized by its radius, R, and height $h\in [0,R]$. This is the height of the spherical cap forming from the disk bending, and it allows to measure the vesiculation as h = 0 for the planar disk and h = R for the fully closed vesicle. The very first observation is that the disk curves to limit the length of the edges with consequent membrane deformation. The spontaneous curvature, c₀, includes molecular aspects that impose a geometrical curvature, and when only one amphiphile is considered as in our case, they can be ignored. The area-difference-elasticity H_ADE term can also be ignored as long as the disk inner and outer membrane layers are equally accessible by unimers and hence $\Delta N^{\pm }\sim 0$. For most phospholipids ${\kappa }_G\simeq -{\kappa }_M$ (Huang et al., 2017), and we assume here the same for PMPC-PDPA copolymer to simplify our calculations. Finally, we define ${\kappa }_M=K_A{a}^2{N}_D^{4/3}{\beta }^{-1}$ as a function of the K_A, the area elastic modulus, which we measured for PMPC-PDPA polymersomes using atomic force microscopy (Battaglia et al., 2011), and it is invariant with the degree of polymerization (Bermudez et al., 2002). The term β is a constant that depends on the lateral pressure distribution across the membranes (Bloom et al., 1991). When the two monolayers are coupled, the repulsion can be concentrated at the interfaces, β = 4, or distributes uniformly across the membranes, β = 12. Uncoupled membranes have larger β close to the limit because the monolayers are free to slide on each other, β = 48. We can now integrate Equation 3 for the disk geometry in Figure 8A to give:

$$H\left(R,h\right)=\frac{4\pi K_A{a}^2{N}_D^{4/3}{h}^2}{\beta R^2}+\frac{3N_{A}kTp{a}^2{N}_D^{2/3}}{8M_D}\sqrt{R^2-h^2}$$ (Equation 6)

Figure 8.

Transition from Disk to Closed Vesicle

(A–C) Geometry of the transition (A). Detail of three PMPC₂₅-PDPA₇₀ copolymers packed to give the highest density possible with PMPC chains (B). The elastic minimum radius of vesiculation $R_E^{\text{*}}$ calculated from Equation 3 with β = 12, 24, 32, and 48 (black lines); the geometrical minimal radius calculated using Equation 3$R_G^{\text{*}}$ (blue line) and from the experimental data (blue square); as well as the disk radius all plotted as a function of the PDPA polymerization degree N_D (C).

The two extreme configurations are the flat disk, i.e., h = 0, where Equation 3 evolves into

$$H_{Disk}=\frac{3N_{A}kTp{a}^2{N}_D^{2/3}}{8M_D}R$$ (Equation 7)

and the closed vesicle with h = R where Equation 3 evolves into

$$H_{Vesicle}=\frac{4\pi K_A{a}^2{N}_D^{4/3}}{\beta }$$ (Equation 8)

Only for the disk radius, R, where H_Edge > H_H, i.e., for R where H_Disk > H_Vesicle vesiculation occurs spontaneously, and we thus define the elastic minimum radius of vesiculation, $R_E^{\text{*}}$, as:

$$R_E^{\text{*}}=\frac{8M_D{K}_A{N}_D^{2/3}}{3\beta N_{A}pkT}$$ (Equation 9)

In addition to this, it is important to note that the vesiculation is also limited by the amphiphile size. For amphiphilic copolymer, the hydrophilic PMPC chains are forced together within the vesicle inner leafleat. Such Using simple geometrical considerations, as shown in Figure 8B, we can thus identify a minimum geometrical radius $R_G^{\text{*}}$ as:

$$R_G^{\text{*}}=l_M\frac{2r-r_M}{r-r_M}+a{N}_D^{2/3}$$ (Equation 10)

where $r\in \left[r_D,\sqrt{a_0/\pi }\right]$, l_M is the length of the PMPC chain, and r_M and r_D are the van der Waals radii of the two monomers, which can be measured using the model in Figure 1. This is a pure molecular limit and indeed depends on the amphiphile architecture. In Figure 8C, we plot the minimum geometrical radius $R_G^{\text{*}}$, the experimentally measured average disk radius, and different $R_E^{\text{*}}$ for different β. We can conclude that β > 32 will be physically impossible for the PMPC chains to withstand. This suggests that there is some level of coupling between the two membrane leaflets and that this is in agreement with the polymersome membrane entanglement dictated by its macromolecular nature (Battaglia and Ryan, 2005, Bermudez et al., 2004). Finally, the proposed model shows again that the disks observed for fast nucleations have radius below the geometrical minimum and indeed can only be explained as disk micelles.

Most spherical vesicles have a Hamiltonian as in the Equation 3 with H_edge = 0. However, when the vesicles remain in contact with unimers and these cannot penetrate the membrane causing a larger growth of the outer layer then the inner one, we need to include the area-difference-elasticity H_ADE as well as break down the Helfrich elasticity in mean and Gaussian curvature as the latter is a topological invariant. According to the Gauss-Bonnet theorem, $\oint GdA=4\pi \left(1-g\right)$ where g is the genus number; we can thus write:

$$H_{Vesicle}=\frac{K_A{a}^2{N}_D^{4/3}}{2\beta }\left(\oint MdA+4\pi \left(1-g\right)\right)+\frac{k_{m}a{N}_D^{5/3}{M}_D}{8N_{A}p\oint dA}{\left(\Delta N^{\pm }\right)}^2$$ (Equation 11)

Equation 3 is very difficult to minimize, and for g > 1 a conformational degeneracy is often found in the ground state with consequent multiple solutions (Seifert, 1991). However, so far the theory has been applied to explain observed structures in vesicles with radius much larger than the membrane thickness using optical microscopy with several structures reported including vesicles with high genus (Noguchi, 2015). High-genus vesicles so far have been reported for micrometer-sized vesicles with radius considerable larger than the membrane thickness (Haluska et al., 2002, Noguchi et al., 2015, ichirou Akashi and Miyata, 2010) and to the best of our knowledge no example of nanoscale high-genus vesicles have been reported. Here we show that by exposing spherical vesicles to membrane-forming unimers, their topology can be considerably altered increasing the vesicle genus number. As shown in Figure 6, we can indeed control the genus by allowing longer times of contact between vesicles and unimers, in other words, by growing the outer layer and hence the term ΔN^±. Our data are in strong agreement with the simulations reported by Noguchi where an increase in genus number corresponds with an increase of area difference or ΔN^± (Noguchi, 2015). Most importantly, our data propose a very first approach to engineer the vesicle topology and indeed access structures that so far have been very elusive.

Conclusions

One of the most used top-down techniques of polymeric assembly formation is the hydration of dry polymer film with water. This mechanism often requires from days to weeks to obtain a dispersed polymersome sample. Faster approaches such as environmentally driven self-assembly, which use solvent or pH switch, are commonly exploited to accelerate the process. In this study, we have shown that the pH-responsive amphiphilic diblock copolymers PMPC-PDPA are capable of forming a range of colloidal assemblies in water via simple temperature change. This is achieved by slowly changing the temperature of the dispersion therefore modulating the DPA pKa. This novel approach allows homogeneous control of the temperature, and consequently, assembly formation within the solution, opening new mechanisms for the formation of PMPC-PDPA assemblies with different morphologies. We also demonstrate good control over the hydrodynamic diameter and the number of genus events occurring per particle by modulating the degree of copolymer ionization. The ability to generate such a range of structures in aqueous solution from a single copolymer creates exciting new avenues for exploration and extends our understanding of the formation of complex curvatures adopted by copolymers in high-genus assemblies.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: September 28, 2018