Cellular in vivo 3D imaging of the cornea by confocal laser scanning microscopy

Abstract

We present an in vivo confocal laser scanning microscopy based method for large 3D reconstruction of the cornea on a cellular level with cropped volume sizes up to 266 x 286 x 396 µm³. The microscope objective used is equipped with a piezo actuator for automated, fast and precise closed-loop focal plane control. Furthermore, we present a novel concave surface contact cap, which significantly reduces eye movements by up to 87%, hence increasing the overlapping image area of the whole stack. This increases the cuboid volume of the generated 3D reconstruction significantly. The possibility to generate oblique sections using isotropic volume stacks opens the window to slit lamp microscopy on a cellular level.

1. Introduction

Presently, a well-established method for acquiring corneal images at cellular level is the combination of the Heidelberg Retina Tomograph (HRT) and the Rostock Cornea Module (RCM; both Heidelberg Engineering GmbH, Heidelberg, Germany), which is a confocal laser scanning microscope. Since its first presentation in 2002 [1], the HRT + RCM serves as a reliable instrument [2] and plays an important role in ex vivo and in vivo studies of human or animal corneas for a qualitative and quantitative analysis based on 2D imaging and/or 3D image reconstruction, e.g. the anatomical comparison of laboratory animal corneas [3], the assessment of stromal modifications of patients with progressive keratoconus after treatment by riboflavin-UVA-induced cross-linking of corneal collagen [4], quantitative full-thickness corneal 3D imaging [5], automated quantification of morphologic features of different epithelial cell layers [6], 2D reconstruction of the subbasal nerve plexus (SNP) from volume scans in the presence of ridge-like tissue deformations [7] and large-scale image reconstruction of the SNP [8–13].

Besides confocal laser scanning microscopy based methods, the full-field optical coherence tomography (FF-OCT) [14] is a promising attempt to obtain en face corneal images. Recently, FF-OCT was demonstrated to offer in vivo human corneal images with 1.7 µm lateral resolution and 1.26 mm x 1.26 mm field of view in a non-contact measurement [15]. Nevertheless, confocal laser scanning microscopy still offers higher lateral resolution and better image quality.

Several corneal 3D reconstructions from confocal light and confocal laser scanning microscopy image stacks are published already. Image stacks through the entire cornea are presented in [16] and were acquired with a tandem scanning confocal light microscope and without image alignment, leading to lower image quality and lower resolution compared to confocal laser scanning based methods. In [7,17,18], volume imaging with a confocal laser scanning microscope (HRT + RCM) was described. The internal focus drive of the HRT was used, which allows the recording of corneal stacks with a maximum depth of only 60 µm. The full thickness corneal stacks presented in [5] were performed on a sedated rabbit to avoid eye movements. The RCM’s manual drive for focal plane control was replaced with a computer-controlled motor drive. One of the biggest flaws of this method and the RCM in general is the axial movement of the contact cap (TomoCap) for focal plane control, which inevitably changes the contact pressure on the cornea. From our experience, two major issues arise therefrom. First, the movement of the TomoCap away from the cornea during through-focusing can ultimately lead to a loss of contact. Second, when the TomoCap moves towards the cornea, the increasing applanation pressure on the cornea induces compression artifacts that manifest as ridge-like deformations in the SNP and the adjacent tissue [19–22]. These deformations are particularly detrimental for imaging thin layers such as the SNP, which cannot be kept in focus over the entire field of view once the deformation height exceeds the depth of field of the RCM.

In this study, we demonstrate our in-house developed piezo-driven cornea module (RCM 2.0), which is an improved version of the original RCM. (Please note: This RCM version is not commercially available and Heidelberg Engineering was not involved in its development. The authors do not hold any intellectual property on the device or design and are currently not planning to make it commercially available.) The integrated piezo actuator is used to move the objective lens for an axial focal plane shift of up to 500 µm without moving the TomoCap. This enables precise closed-loop focal plane control. We applied our new method to demonstrate in vivo through-focusing measurements and 3D reconstruction of a human cornea.

Furthermore, we present a new TomoCap with a concave surface to reduce involuntary eye movements (so-called saccades). The functional principle is based on the fact that the eyeball’s center of rotation differs from the cornea’s center of curvature and on the usage of a viscous contact gel. Reduced lateral eye movements result in larger fields of view of the aligned image stack. The achieved improvements, arising from the new cap design, were assessed by analyzing comparative measurements using the standard planar and the new concave TomoCap design. Additionally, we compared three image registration methods (none, rigid, non-rigid) for the alignment of the image stacks. Orthogonal as well as oblique slices through a volume data set recorded with the concave TomoCap are presented to exemplify the capabilities of the modified RCM.

2. Materials and methods

2.1 Heidelberg Retina Tomograph and Rostock Cornea Module 2.0

The HRT is a confocal laser scanning microscope primarily designed to acquire in vivo retinal images. It offers an image resolution of 384 pixels x 384 pixels with 8 bit grayscale. The RCM is a detachable extension for the HRT incorporating an immersion objective to shift the focal plane from the retina to the cornea while achieving cellular resolution [23]. Three exchangeable lenses exist to achieve a squared field of view with an edge length of 250 µm, 400 µm or 500 µm [23]. For hygienic reasons, a disposable contact element (TomoCap; Heidelberg Engineering) is used in contact with the cornea.

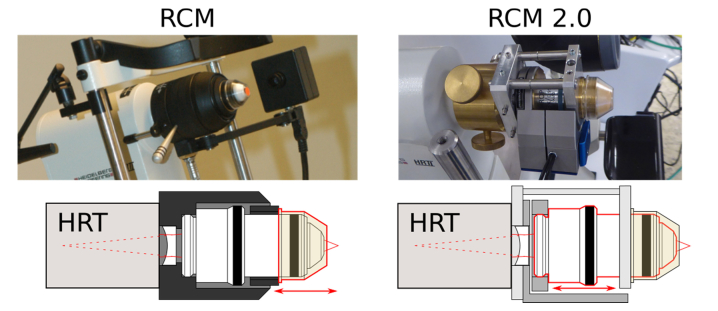
Figure 1 depicts the original and the new RCM 2.0 in the upper row and further demonstrates the modified function principle. Both modules are based on the same optical components. The plano-concave lens between HRT and objective lens is interchangeable to allow different fields of view. To realize the required high resolution, the RCM is equipped with a water immersion objective (Achroplan 63x/0.95 W; Zeiss, Jena, Germany) and hence immersion gel on either side of the TomoCap is necessary. It is also essential for the elimination of surface reflections from the cornea and the TomoCap. In order to change the focal plane within the cornea, the original RCM moves the TomoCap using a manual drive or in a modified version an electrical motor drive [5], whereas our new RCM 2.0 utilizes a closed-loop piezo system (MIPOS 600 SG OEM; piezosystem jena GmbH, Jena, Germany) with 500 µm travel range (600 µm open-loop) to move the objective lens inside the module while the TomoCap position remains fixed. Therefore, the contact pressure on the cornea is not changed by moving the focus drive. However, the contact pressure may still be influenced by the subject (eye or head movements, breathing, heartbeat, et cetera).

Fig. 1.

Left: Original RCM – focal plane adjustment by TomoCap movement (outlined in red). Right: RCM 2.0 – focal plane adjustment by objective lens movement (outlined in red), while TomoCap position remains fixed. Please note: The different TomoCaps are compatible to both RCM versions and only the planar TomoCap is shown here. The concave TomoCap is presented in Fig. 2.

Due to slightly different positions of the optical components, the RCM 2.0 has a smaller field of view of about 350 x 350 µm² instead of 400 x 400 µm² compared to the original RCM with the equivalent plano-concave lens. Since the single laser beams are not parallel when entering the objective lens, axial objective lens movements change the magnification. However, as we will show in the results section, this effect is marginal and can be neglected.

2.2 TomoCap

The standard TomoCap with a planar contact surface has been previously investigated with different surfaces modifications, for e.g. the attachment of an additional thin PMMA plain washer to prevent applanation artifacts [24]. Here we present a modified TomoCap featuring a concave surface with a diameter of 12 mm and curvature radius of (7.8 ± 0.5) mm, according to the curvature of an average human cornea. This TomoCap is in-house manufactured by cutting the concave part from a contact lens (Three-mirror single-use contact lens; SMT, Maple Valley, WA), polishing the cutting surface, and gluing it onto a modified TomoCap with the planar surface being removed. This way the new TomoCap can also be used with the standard RCM. Figure 2 shows the standard TomoCap with the planar surface and the new design with the concave surface. The goal of the new TomoCap is to avoid cornea deformation or compression artifacts and to reduce involuntary eye movements in order to obtain a larger lateral area with overlapping images throughout the whole stack. The image alignment procedures for 3D reconstruction may also potentially benefit from the reduced eye movements.

Fig. 2.

TomoCap with planar (left) and concave (right) contact surface.

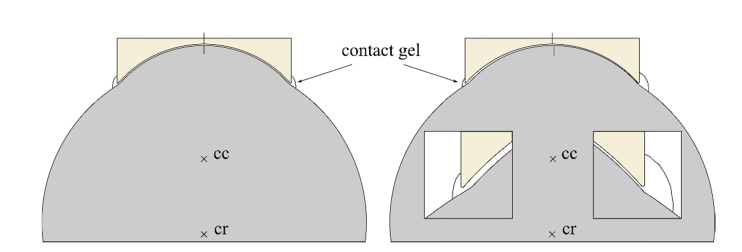
The functional principle is to approximately match the contact surface of the new TomoCap with the cornea surface offering a form closure. Since the center of rotation of the eye lies behind the center of the cornea curvature, a slight change in viewing direction mainly changes the lateral position of the cornea. In that case, lateral eye movements are confined by the form closure. The amount of possible movement depends on the thickness of the contact gel between cornea and TomoCap and the individual curvature of the examined cornea. Figure 3 shows the anterior section of an eye and a concave TomoCap both symmetrically aligned. Vertical lines mark the cornea apex and center of the concave surface. The thickness of the contact gel is 50 µm in the illustrated example. In that case, the eye’s movement is confined to about 160 µm, neglecting a potential cornea deformation. It is also restrained by the viscous gel. It stabilizes in axial direction because work is necessary to press gel out of the volume between cornea and TomoCap or to suck in surrounding gel. This effect is known for gonioscopy lenses and in that context generally referred to as suction. The gel is also responsible for laterally restrained eye movements. The effect is basically the same, but now the gel is pressed out on the one side and sucked in on the opposite side. This is depicted in the right side of Fig. 3. The eye was rotated clockwise around the eyeball’s center of rotation (cr), such that a lateral movement of the cornea of 150 µm is induced. The vertical lines on the cornea apex and center of the concave surface visualize the rotation and the induced lateral shift. The two inserts show magnified views of the limbal region with the amount of surrounding gel schematically depicted. The distance between cornea and TomoCap is now different on both sides. On the left side the distance is increased with less surrounding gel and on the right side it is decreased with more surrounding gel. Additionally, the increased contact surface leads to decreased shearing induced by the lateral forces of saccades.

Fig. 3.

True to scale sections of eyeball, cornea and concave TomoCap with a gel interface of 50 µm thickness. The cornea’s center of curvature is denoted with cc and the eye’s center of rotation with cr. Vertical lines on the cornea apex and center of the concave surface visualize the rotation of the eye. Left: no rotation; Right: Clockwise rotation around cr of 0.66 ° corresponding to a lateral corneal shift of 150 µm. Insets show the distance between cornea and TomoCap and schematically the amount of surrounding gel.

The idea of a concave contact surface for microscopy is not new. For instance, a concave applanating tip objective (7.5 mm radius of curvature) was published 25 years ago [25]. Unfortunately, the diameter of the contact surface is not specified, but it seems to be quite small. Therefore, we suppose this contact surface had no restraining effect on lateral eye movements.

2.3 Data acquisition, image alignment procedures, and stack quality parameters

To evaluate the RCM 2.0 and quantify the influences of the concave TomoCap, we acquired several cornea stacks (30 frames per second, automatic brightness control activated in HRT settings) for each TomoCap design from three healthy human volunteers. One of these data sets is visualized to demonstrate the possibility of thick corneal cuboid image stacks. All stacks were acquired with a constant scan velocity of 15 µm/s.

One image stack intended for isotropic volume reconstruction of the anterior cornea was acquired using the concave TomoCap and a focus drive velocity of 30 µm/s, resulting in an axial distance of 1 µm between two images. The axial image distance of 1 µm results in a voxel size of 0.91 x 0.91 x 1 µm³. To obtain an isotropic reconstructed volume, all images were scaled accordingly to get a voxel size of 1 x 1 x 1 µm³. However, the depth of focus of the RCM is reported to be about 8 µm [2,23]. Therefore, structures from one image are visible in the adjacent images. The reconstructed stack starts from the superficial cells of the epithelium and ends 187 µm deeper in the stroma.

Because of the differing specific reflectance, several images were under- or overexposed. Therefore in a post-processing step, the histogram of every image was scaled to the full 8 bit range excluding overexposed pixels.

Third-party software, ImageJ and Amira 3D, was used for 3D volume reconstruction of image stacks and for the imaging of sectional views. To align each image relative to the next one, we used both a rigid image registration method from Amira 3D and a specially adapted image registration algorithm developed by the Karlsruhe Institute of Technology (KIT) [7], which we term in the following as KIT-alignment. The registration method from Amira 3D uses rigid transformations (translations and rotations) to align consecutive images. In contrast, the KIT-alignment is tailored to the image generation process of the HRT and not restricted to rigid transformations. It is derived from the scanning pattern of the HRT, which scans the field of view in horizontal lines. Scanning a single horizontal scan line (i.e. image row) takes approximately 65 µs [7]. Any eye motion happening on that time scale is assumed to be negligible with regard to causing motion artifacts in the image data, hence image rows are defined as rigid units. The basic principle of the alignment algorithm is to establish the correct location for each image row of the acquired corneal confocal microscopy data set. This can be achieved by finding corresponding regions in image pairs of the recorded data set, as further detailed in [26]. This alignment technique allows the correct reversal of the characteristic motion artifacts that are induced by spontaneous eye movements, head movements or external mechanical vibrations (e.g. traffic or footsteps nearby) transferred to the HRT and that manifest as specific, non-linear distortion effects in the image data.

The TomoCap position can still be adjusted relative to the objective lens by rotating the TomoCap holder. Hence this method is not limited to the anterior part of the cornea. The stack thickness is in principle only limited by the traveling range of the piezo stage, the thickness of the gel film on the TomoCap and the preset position of the TomoCap.

After aligning all stacks of the three subjects with both TomoCaps using the KIT-alignment, we calculated the two following parameters. The first one is the mean lateral image-to-image shift of two consecutive images (MS_p for planar and MS_c for concave TomoCap), by taking the center of gravity of a registered image as a reference point. This parameter indicates the magnitude of eye movements during image acquisition. Since not all stacks could be registered entirely, we used only shift values from multiple substacks with at least ten successfully aligned consecutive images to calculate this parameter. For all combinations of subject and TomoCap the same sample size (total number of shift values) of n = 1000 was used.

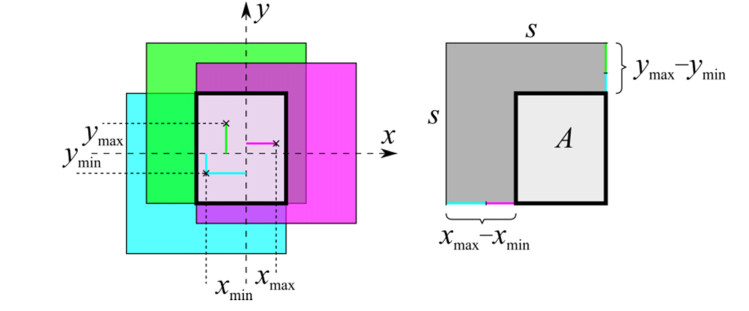
The first parameter is not sufficient to quantify the quality of a reconstructed stack. One can easily imagine an image sequence with small image-to-image shifts, but with a distinct shift direction. With increasing number of images n_im, the overlapping area of the total stack decreases. Therefore, the mean approximated overlapping area (MA_p for planar and MA_c for concave TomoCap) was calculated for all data sets as a second parameter. To calculate the approximated overlapping area A of a single stack (see Fig. 4), the coordinates of the centers of gravity for the shifted single images were calculated in both lateral directions. From these values, the maximum and minimum coordinates in both directions (x_max, x_min, y_max and y_min) related to the entire stack were determined. The distances between maximum and minimum coordinates were then subtracted from the respecting side length s of a single image to calculate the approximated area:

$$A=(s-(x_{\max }-x_{\min }))\cdot (s-(y_{\max }-y_{\min })).$$ (1)

For calculation purposes the single images are assumed to be undistorted squares, thus the area A is approximated. Figure 4 illustrates the calculation of A.

Fig. 4.

Illustration for the calculation of the approximated overlapping area A (boldly outlined area). Colored lines represent the maximum and minimum coordinate of the stack. The × -symbols mark the center of gravity of the single images with a side length s. For the sake of simplicity, the calculation is demonstrated on a strongly reduced stack with only three images.

For the calculation of the mean approximated overlapping area of several stacks, the size of the individual stacks was reduced to have a common n_im per stack. Stacks with a multiple of n_im were divided into new stacks to get a larger number of stacks n_st. This way, n_st is guaranteed to be at least 40 to ensure statistical robustness.

To verify the different performance of the planar and the concave TomoCap, the error probability p for each parameter and subject was estimated using Welch’s t-test. We also investigate the capability of the concave TomoCap regarding MA for stacks with large n_im.

3. Results

As mentioned in the method section, the magnification changes with objective lens position. Therefore, an object micrometer was imaged for various objective lens positions. The total field of view was ranging linearly from about 349 µm to 351 µm in the total closed-loop travel range of 500 µm. Hence this effect can usually be neglected.

Using the standard TomoCap, involuntary eye movements can cause the cornea to move more than the width of the field of view within the exposure time of a single frame [10]. In this case consecutive images do not overlap and therefore cannot be aligned. In general, larger eye movements lead to smaller overlapping areas, thus impeding image alignment. Qualitative visual inspection of the image streams reveals a significant reduction of lateral eye movements in the data sets recorded with the concave TomoCap. To demonstrate this issue, we included six supplementary videos showing aligned (KIT-alignment) image stacks in posterior scan direction of the three subjects with both TomoCaps (Visualization 1 ^{(12.2MB, mp4)} , Visualization 2 ^{(11.6MB, mp4)} , Visualization 3 ^{(12.1MB, mp4)} , Visualization 4 ^{(10.2MB, mp4)} , Visualization 5 ^{(4.6MB, mp4)} and Visualization 6 ^{(10.9MB, mp4)} ). Table 1 shows the determined parameters MS_p and MS_c including the standard error for the three subjects. The mean approximated overlapping area MA_p and MA_c are listed in Table 2 for n_st = 40 and the specified n_im. Furthermore, Table 3 gives MA_c for increasing n_im. For comparison, the area of a single image is 0.1219 mm².

Table 1. Comparison between TomoCaps regarding lateral image-to-image shifts.

Subject	MSp / µm	MSc / µm	p
1	18.8 ± 0.4	2.40 ± 0.14	< 0.0001
2	6.74 ± 0.19	1.34 ± 0.09	< 0.0001
3	15.0 ± 0.9	4.48 ± 0.14	< 0.0001

Table 2. Comparison between TomoCaps regarding overlapping area for n_st = 40.

Subject	MAp / mm2	MAc / mm2	p	n im
1	0.0487 ± 0.0004	0.10723 ± 0.00020	< 0.0001	32
2	0.0700 ± 0.0007	0.11010 ± 0.00020	< 0.0001	45
3	0.0583 ± 0.0007	0.10553 ± 0.00015	< 0.0001	21

Table 3. Overlapping areas using the concave TomoCap with increasing stack sizes.

Subject	n st	n im	MAc / mm2
1	40	51	0.10087 ± 0.00025
	20	98	0.10723 ± 0.00020
	10	175	0.0852 ± 0.0010
	5	294	0.0731 ± 0.0010
2	40	87	0.10569 ± 0.00024
	20	158	0.0995 ± 0.0007
	10	264	0.0943 ± 0.0014
	5	409	0.073 ± 0.004
3	40	71	0.09412 ± 0.00017
	20	139	0.0965 ± 0.0004
	10	248	0.0742 ± 0.0007
	5	497	0.0558 ± 0.0014

Comparing the parameters of both TomoCaps from Table 1, we find a reduction of 87%, 80% and 70% of the eye movements between consecutive images using the concave TomoCap for Subject 1, 2 and 3 respectively. Furthermore, Table 2 shows the mean approximated area of the stacks with the planar and the concave TomoCap. Without eye movements the stack’s field of view would be the single image field of view. Eye movements induce a loss of overlapping area, which can be calculated by subtracting the mean approximated area from the single image area. Comparing the losses of overlapping area using the different TomoCaps we find the loss is reduced by 80%, 77% and 74% for Subject 1, 2 and 3 respectively using the concave TomoCap. Table 3 presents the mean approximated area for increasing stack size for the three subjects and the concave TomoCap. As expected, the mean approximated area decreases with the number of images in the stack. But compared to Table 2, we find that MA_c is reduced to MA_p only after a few hundred images instead of a few ten images with the planar cap. That means, stacks with a high thickness particularly benefit from the concave TomoCap. Furthermore, with the concave TomoCap we achieved generally multiple times thicker stacks after the alignment compared to the planar TomoCap. This is due to involuntarily and sporadically occurring saccadic eye movements with an amplitude in the order of the side length of the FOV. They effectively prevent successful image alignment when the planar TomoCap is used but are practically absent (or occur with greatly limited amplitude) from data sets acquired with the concave TomoCap.

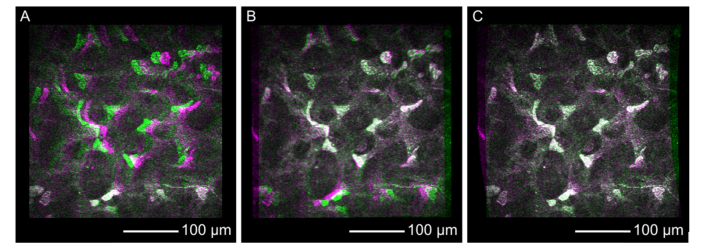
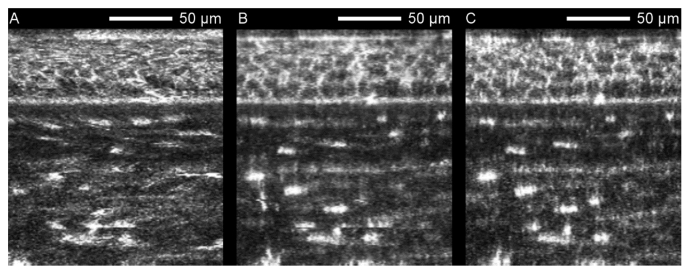
To compare the different alignment methods, Fig. 5 shows false color composites derived from two consecutive stromal images of the acquired corneal stack without alignment (Fig. 5(A)), with rigid alignment (Fig. 5(B)) and with KIT-alignment (Fig. 5(C)). These false color images can be easily calculated by setting the grayscale intensity values of one image as red and blue channel, and the grayscale intensity of the next image as green channel of a colored image. Regions without any change or in other words with same intensity are displayed in grayscale, while regions with intensity only in the first or second image are colored in magenta or green, respectively. This way, changes from one image to the next one are obvious. Despite a proper image alignment, compare Fig. 5(C), we observed spots with non-gray values resulting from noise or regions with different brightness possibly due to a structural change in axial scanning direction. However, these false color composites emphasize the misaligned regions and seem to be an intuitive representation for the comparison between alignment methods.

Fig. 5.

False color composite images derived from two single consecutive stromal images recorded with the concave TomoCap and using no alignment (A), rigid alignment (B) and KIT-alignment (C). Regions with identical intensity distribution in the first and second image are rendered in grayscales while differences are colored either magenta or green (see text for detailed explanation).

The example without any image alignment, shown in Fig. 5(A), seems to match quite well in the lower part, while the upper and middle regions exhibit a certain amount of green and magenta regions indicating eye movement from the right to the left in the order of 20 µm. The rigid alignment (Fig. 5(B)) shows good agreement in the upper and middle part of the images, but it reveals a worse alignment in the lower part due to non-linear motion distortions. We conclude that a translation and rotation of the whole image is insufficient to correct the motion induced distortions. The best alignment was achieved using the KIT-alignment (Fig. 5(C)), which corrects the motion induced distortions row-wise, leading to non-square images as seen in Fig. 5(C).

Applying the KIT-alignment to a whole stack allows a volume reconstruction and hence image slice in arbitrary directions with a high image quality as seen in an orthogonal slice in Fig. 6(A). Axial scanning artifacts are not visible in this slice, because of the stabilizing effect in axial direction. To move the eye towards the contact cap, e.g. in case of heartbeat, the contact gel has to be pressed out of the volume between cornea and TomoCap and in the opposite direction the surrounding gel has to be sucked back into this volume. The force required for these processes is counteracting to the movement force of the eye and depends on the viscosity of the contact gel.

Fig. 6.

Orthogonal slice (A) of the corneal image stack after KIT-alignment without image averaging over several slices and exemplary images from different layers: superficial cells (B), intermediate wing cells (C), basal epithelial cells (D), subbasal nerve plexus (E), Bowman’s membrane (F) and stroma (G, H, I). This image stack was recorded using the concave TomoCap.

It is also possible to measure axial sizes of corneal structures. In [27] a sub-micrometer axial resolution OCT is used to measure the epithelial and Bowman’s membrane thicknesses and in [16] they are determined by an intensity profile of an image stack along the axial direction. The latter can be applied here as well or their sizes can be measured from the orthogonal slice directly. Depending on the measurement position in Fig. 6(A), we found that the epithelial and Bowman’s membrane thickness were not perfectly constant and were determined to be 47 to 54 µm and 15 to 17 µm respectively. The axial epithelial cell diameter can be measured as well, if the cell borders are visible. For ten randomly selected cells we found axial diameters between 10 to 15 µm. Due to the depth of focus being in the order of 8 µm it is not possible to reliably measure the axial size of small structures such as keratocyte nuclei.

Additionally to Fig. 6(A), the specific en-face images of each layer ranging from the superficial cells to the stroma are presented in Fig. 6(B) to 6(I), respectively. The corresponding imaging depth is added in the bottom left corner.

The superficial cells (Fig. 6(B)) are flat, overlapping polygonal cells identified at the surface of the corneal epithelium at the depth of 0 µm. The cell borders appear clear with dark nucleus. The cytoplasm of the cells is readily visible where few cells demonstrate highly reflective cytoplasm with bright nucleus and its dark perinuclear space indicates process of cell desquamation. The superficial cells appear significantly larger than the intermediate and basal cells. Figure 6(C) demonstrates the intermediate wing cell layer at the depth of 29 µm. These cells appear more uniform and compact with bright and well-defined cell borders and dark cytoplasm. However, the cell nucleus is hardly visible. Basal epithelial cells (Fig. 6(D)) are visible as tightly packed smallest cells immediately above Bowman’s membrane. These cells have bright and clear cell borders with inhomogeneous reflectivity of cytoplasm between cells and are more uniform in shape and size similar to wing cells with uncertain cell nucleus. The SNP (Fig. 6(E)) is clearly imaged a few microns above the Bowman’s membrane. We were able to detect typical Y-shaped, thick and highly reflective nerve fibers running parallel to each other. We could also identify small highly reflective Langerhans cells with fine dendritic processes. An acellular Bowman’s layer (Fig. 6(F)), also called the anterior limiting membrane, situated between the stroma and the cellular epithelium, could be distinguished at the level of 55 µm. Anterior stroma (Fig. 6(G)) is imaged at around 64 µm close to Bowman’s membrane. This layer reveals multiple, small and highly reflective keratocyte nuclei. The lamellar collagen fibers in-between cells are not visible. The density of these nuclei seems to be significantly higher close to Bowman’s membrane and gradually decreasing towards central stroma (Fig. 6(H), 6(I)).

In Fig. 5, the alignment quality of the single confocal images was compared. Following, the impact of the different alignment methods on generating orthogonal slices will be analyzed (see Fig. 7).

Fig. 7.

Orthogonal slices of a corneal image stack captured with the concave TomoCap using no alignment (A), rigid alignment (B) and the KIT-alignment (C). Without alignment, epithelial cells cannot be resolved. Notice the increasing image quality from Fig. 7A to 7C. Image averaging was not performed.

The image distortions in the en face images induced by ocular movements are clearly demonstrated in orthogonal slices as in Fig. 7(A) where the cell layers appear wavy. Hence, it is difficult or impossible to distinguish single cells. In contrast, Fig. 7(B) and 7(C) show clear appearances of epithelial cell bodies and stroma keratocyte nuclei. Nevertheless Fig. 7(B) still exhibits some artifacts, e.g. horizontally shifted single lines in the lower region that cannot be compensated by the rigid alignment. Furthermore, Fig. 7(B) appears to be more blurry than Fig. 7(C). This is due to the type of interpolation required for the rotation of the rigid alignment. All three en face image stacks used for Fig. 7 are attached as supplementary video (Visualization 7 ^{(9.3MB, mp4)} , Visualization 8 ^{(7.7MB, mp4)} and Visualization 9 ^{(8.9MB, mp4)} ) emphasizing the lateral movements.

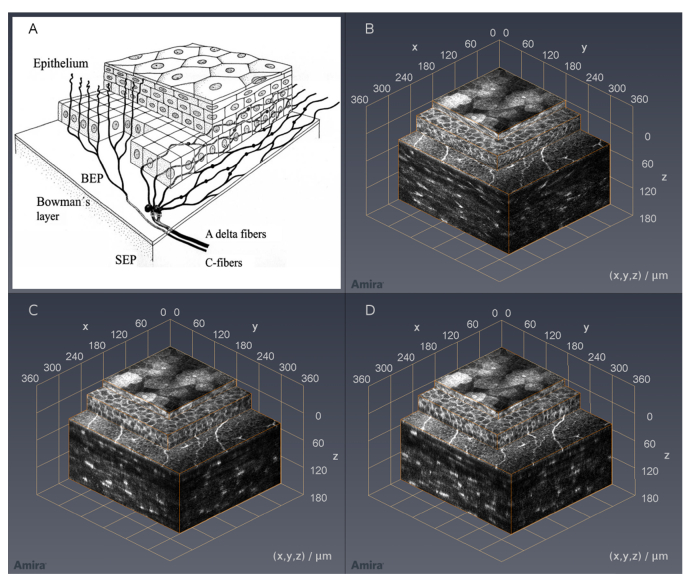
In Fig. 8, a comparison between a schematic drawing according to Guthoff et al. [28] (Fig. 8(A)) and three analogous variants of the reconstructed corneal image stack in isometric view is shown. These three variants were reconstructed by using no alignment (Fig. 8(B)), rigid alignment (Fig. 8(C)) and KIT-alignment (Fig. 8(D)) again. After aligning the corneal image stack, it was cropped in order to achieve a cuboid volume. Hence the field of view is decreased from 350 µm x 350 µm (0.123 mm²) to 273 µm x 302 µm (0.083 mm²) and 271 µm x 292 µm (0.079 mm²) for rigid alignment and KIT-alignment respectively. Compared to Table 3, the field of view reduction depends on the stack depth, but also on the subject itself. For visualization purposes, the different layers are presented in stacked boxes with increasing lateral size from top to bottom and orange highlighted edges. The topmost box shows a section of the anterior epithelium with its superficial cells on top, the middle box shows the remaining epithelium starting at the intermediate wing cells, and the last one contains the subbasal nerve plexus on top and stroma containing the keratocyte nuclei on the side. While the structures on the sides of the stack in Fig. 8(B) are distorted, the sides in Fig. 8(C) and 8(D) reveal cellular structures, especially in the epithelial layer. In this kind of presentation, the differences between the rigid alignment and KIT-alignment are less noticeable compared to Fig. 7.

Fig. 8.

Cornea sketch according to Guthoff et al. [28] (A); corneal image stack recorded with the concave TomoCap in isometric view using no alignment (B), rigid alignment (C) and KIT-alignment (D). Please note: The top surfaces in these images are, based on the imaging method, almost identical. However, the side views of (C) and (D) reveal epithelial cells whereas the stroma shows the keratocyte nuclei. Due to the different alignment methods, structures may be imaged at slightly changed positions thus leading to altered cross-sections. Image averaging was not performed.

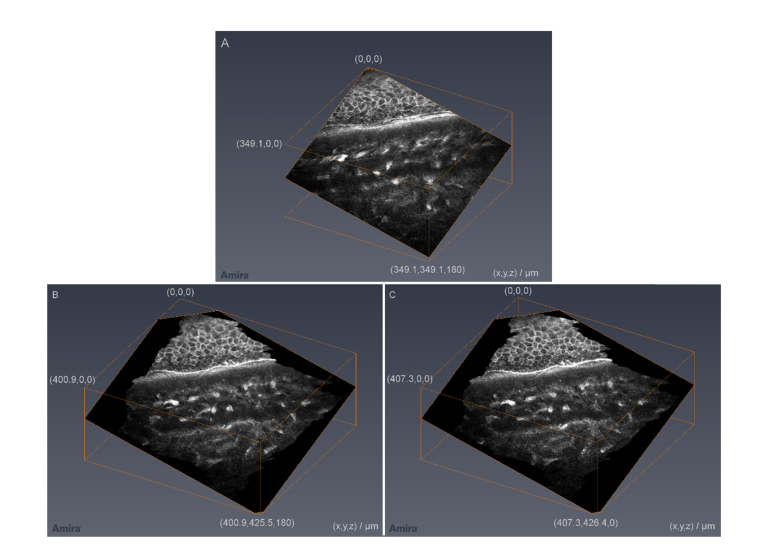
With proper alignment, it is also possible to create oblique slices through the corneal image stack, as shown in Fig. 9. Due to no alignment in Fig. 9(A), there are distortions and artifacts that are significantly reduced by rigid alignment (Fig. 9(B)) and KIT-alignment (Fig. 9(C)).

Fig. 9.

Oblique slices of a corneal image stack captured with the concave TomoCap using no alignment (A), rigid alignment (B) and KIT-alignment (C). Notice: In order to keep all information of the slice, the imaging area in B and C is increasing. Image averaging was not performed.

An example for a KIT-aligned thick corneal image stack is presented in Fig. 10. The cropped field of view of the complete stack is 266 x 286 µm² and the thickness is 396 µm. Generally, corneal image stacks with up to 500 µm are possible using this setup. The axial scan velocity was 15 µm/s resulting in an acquisition time of 26.4 s. Compared to the stack in Fig. 8, the image quality was not increased by a half scan speed. So a reasonable acquisition time for a thick image stack is in the order of 13 s using the presented setup.

Fig. 10.

Exemplary thick KIT-aligned 3D corneal image stack, originally used for the analysis of the eye movements with the concave TomoCap. It starts close to the subbasal nerve plexus and has a depth of 396 µm. (HRT automatic brightness control is deactivated and no image processing was performed)

4. Discussion and conclusions

The in-house developed RCM 2.0 in combination with the concave TomoCap performed well for in vivo corneal 3D imaging. An important, general advantage of the RCM 2.0 is the static TomoCap, reducing compression artifacts and the risk of contact loss between eye and TomoCap in e.g. through-focusing scenarios. Furthermore, in our measurements we experienced that the risk of contact loss is even smaller using the concave TomoCap compared to the planar one, which we believe is due to increased adhesion forces or the capillary effect caused by matched contact surfaces. In comparison to the planar TomoCap and depending on the investigated subject, a reduction of 70-87% in eye movements between consecutive images was achieved. Additionally, depending on the stack depth, the overlapping area loss was reduced by 74-80%, hence resulting in a larger cuboid volume. The listed data in Tables 1-3 prove the better eye fixation of the concave TomoCap. This is caused by the fact that the cornea’s center of curvature differs from the eyeball’s center of rotation and therefore the eye movements are limited. The reduction of eye movements is also due to the suction effects of the viscous contact gel as explained in detail in section 2.2.

In any case, cropping an aligned stack reduces its field of view. The reduction depends on the stack thickness and the subject. An increased field of view can be achieved by another lens inside the RCM. However, cells would appear smaller with a worse resolution. For a larger field of view with the same or even better resolution, another device with a higher sampling frequency of the detector and thus a higher image resolution than the HRT should be chosen.

Image alignment is an important step in the 3D reconstruction of axial image stacks and slices. Unaligned stacks have a number of distortions preventing analyzable orthogonal slices. The concave TomoCap with its better fixation of the cornea reduced the movement distortions in every single image. This simplified the image alignment procedures and moreover the image quality after rigid alignment is enhanced being closer to the KIT-alignment as shown in the orthogonal and oblique slices (Fig. 7 and 9) and especially in volume presentations as in Fig. 8. Even without sophisticated software routines, like the KIT-alignment, analyzable volume reconstructions can be achieved using the concave TomoCap and the new RCM 2.0. Despite that, Fig. 5 and Fig. 7 prove that the best image quality is realized with the KIT-alignment, which is tailored to the HRT.

Compared to the planar TomoCap, the image data acquired with the concave TomoCap have the same high image quality throughout all our measurements while simultaneously reducing eye movements significantly. Although expanded in vivo human corneal image stacks and arbitrary slices were presented before [16–18], the image quality of the slices is now increased by the interplay of the piezo drive, the concave TomoCap and the KIT-algorithm.

With the wide range of scanning parameters like velocity and travel distance as well as various scanning functions, the RCM 2.0 is suitable for numerous tasks. Furthermore, the maximum focus shift is increased to 500 µm and the position control is more precise while at the same time offering higher resolution and acceleration compared to the motorized RCM described in [5]. This enables a fast focal plane change with more than 800 µm/s while offering a position feedback with 12 nm accuracy. Additionally, the piezo system in combination with the fixed TomoCap provides new opportunities, for example a fast oscillating focal plane for large-scale image reconstruction of the SNP [29]. This is an elegant way to get rid of gaps and foreign tissue in large area imaging of the SNP [29,30], caused by unwanted axial shifts of this layer during examination. Without the fast oscillating focal plane shift, the focus has to be adjusted manually during image recording.

Despite the advantages of the concave TomoCap presented in this work, the usage of this cap is only recommended for investigations where the eye is supposed to remain fixed. For other tasks, e.g. mapping structures by the use of guided eye movements [13], the planar TomoCap is still the best choice. It is also not recommended to investigate the limbal region with such a concave TomoCap. Another drawback of the new TomoCap is its size. Often a camera is used to observe the reflection of the laser spot on the cornea for prealignment before contacting the cornea. This is only possible for large distances between cornea and the concave TomoCap, because otherwise the line of sight is blocked. However, a part of the scanning laser light is visible on the iris. This light can be exploited for a rough alignment. A multimodal imaging method combining confocal laser scanning microscopy and optical coherence tomography can also help in the alignment process. Sometimes the size of the TomoCap increases the setup effort. While examining subjects with a drooping eyelid, care has to be taken, that the eyelid is not between cornea and TomoCap.

Generally, the presented concave TomoCap and the RCM 2.0 enable fast and reliable recordings of expanded in vivo human corneal image stacks. Because of the reduced eye movements the cuboid volume of the 3D reconstruction is increased. Furthermore, whether a planar or concave TomoCap is used, the RCM 2.0 is preferable to the original RCM because of the computer controlled focus drive with a piezo actuator and the fixed TomoCap explained and demonstrated throughout this paper. The capability of the proposed method to create high-quality orthogonal or oblique slices through the corneal tissue presents the opportunity for in vivo slit lamp microscopy on a cellular level.

Funding

German Research Foundation (STA 543/6-1, KO 5003/1-1 and MI 1315/5-1).

Disclosures

The authors declare that there are no conflicts of interest related to this article.