Dynamic force spectroscopy of synthetic oligorotaxane foldamers

Significance

Donor–acceptor oligorotaxane foldamers are a class of molecular switches elegantly incorporating mechanical bonds in a folded molecular architecture. Such examples of foldamers are very rare, leaving the question wide open regarding what might emerge from a synergistic combination of mechanically interlocked molecules and foldamers. Here, using atomic-force-microscopy-based dynamic single-molecule force spectroscopy, we mechanically drive oligorotaxanes out of equilibrium at a wide range of loading rates and observe their exceptional refolding capabilities and the very fast dynamics of the process. The near-equilibrium pulling–relaxing cycles were exploited to determine the energy required to break one single donor–acceptor interaction from the distribution of work trajectories using fluctuation theorems. Our findings highlight the importance of molecular design on the performance of artificial molecular machines.

Abstract

Wholly synthetic molecules involving both mechanical bonds and a folded secondary structure are one of the most promising architectures for the design of functional molecular machines with unprecedented properties. Here, we report dynamic single-molecule force spectroscopy experiments that explore the energetic details of donor–acceptor oligorotaxane foldamers, a class of molecular switches. The mechanical breaking of the donor–acceptor interactions responsible for the folded structure shows a high constant rupture force over a broad range of loading rates, covering three orders of magnitude. In comparison with dynamic force spectroscopy performed during the past 20 y on various (bio)molecules, the near-equilibrium regime of oligorotaxanes persists at much higher loading rates, at which biomolecules have reached their kinetic regime, illustrating the very fast dynamics and remarkable rebinding capabilities of the intramolecular donor–acceptor interactions. We focused on one single interaction at a time and probed the stochastic rupture and rebinding paths. Using the Crooks fluctuation theorem, we measured the mechanical work produced during the breaking and rebinding to determine a free-energy difference, ΔG, of 6 kcal·mol⁻¹ between the two local conformations around a single bond.

Biological molecular machines are known to operate out of their thermodynamic equilibrium to carry out specific tasks such as cargo transport performed by single myosins (1), or cell movements driven by flagella rotary motions (2). The work performed by these natural molecular motors is related to their dynamics in solution, and to the force exerted by the molecule to drive the relevant process in one direction. The invention of synthetic routes to wholly artificial molecular machines with highly precise and controlled architectures has led to the production of amazing molecules able to perform mechanical tasks (3–7). Their integration into materials such as metal-organic frameworks (8) or polymer gels (9, 10) has been described recently. The resulting materials can experience a macroscopic change when each single machine is pulled out of its equilibrium state, as a result of an external stimulus, such as light irradiation or a change in solvent.

Collecting information about the behavior of such molecules when driven out of their equilibrium is crucial for the design of more efficient molecular devices. Atomic force microscopy (AFM)-based single-molecule force spectroscopy (SMFS) has emerged as a very elegant technique to probe inter- and intramolecular forces as well as mechanical processes (11–16). By trapping individual molecules between a mechanical probe and a substrate, it is possible to apply an external force to drive them out of the equilibrium and perform very precise and controlled operations in one direction. For 20 y, AFM-based SMFS was used to unravel the behavior of natural biomolecules under mechanical load and has led to a description of their stability, dynamics, and eventually their working processes (17–19).

Beyond standard force spectroscopy experiments, dynamic force spectroscopy, which is concerned with the influence of the loading rate on the force required to break the probed interaction, has been the subject of many theoretical and experimental studies (16, 20–24). It allows us to estimate kinetic off-rates and distances to transition states describing the involved individual bonds from out-of-equilibrium single-molecule experiments. The evolution of the rupture force against the loading rate is described by several models, namely Bell–Evans (22), Friddle–Noy–De Yoreo (23), and Dudko–Hummer–Szabo (24).

By performing successive controlled pulling–relaxing cycles on individual molecules, it is also possible to reveal their singular behaviors under various mechanical loads and to measure the work performance needed to regain their initial conformation (19). One can evaluate if molecules are effective at absorbing energy from thermal fluctuations in the environment. The stochastic behavior of small molecules in an environment governed by random thermal fluctuations forces us to use theories of nonequilibrium statistic mechanics, known as fluctuation theorems (25–29), to uncover that part of the work which is reversible and thus deduce energetics information about the probed interactions. For example, the Crooks fluctuation theorem (29) was used to correlate the work measured during the mechanical unfolding and refolding of an RNA hairpin to the free-energy difference (∆G) between both conformations (30), or to extract the free-energy differences between both conformations of a hydrogen-bonded [2]rotaxane (31).

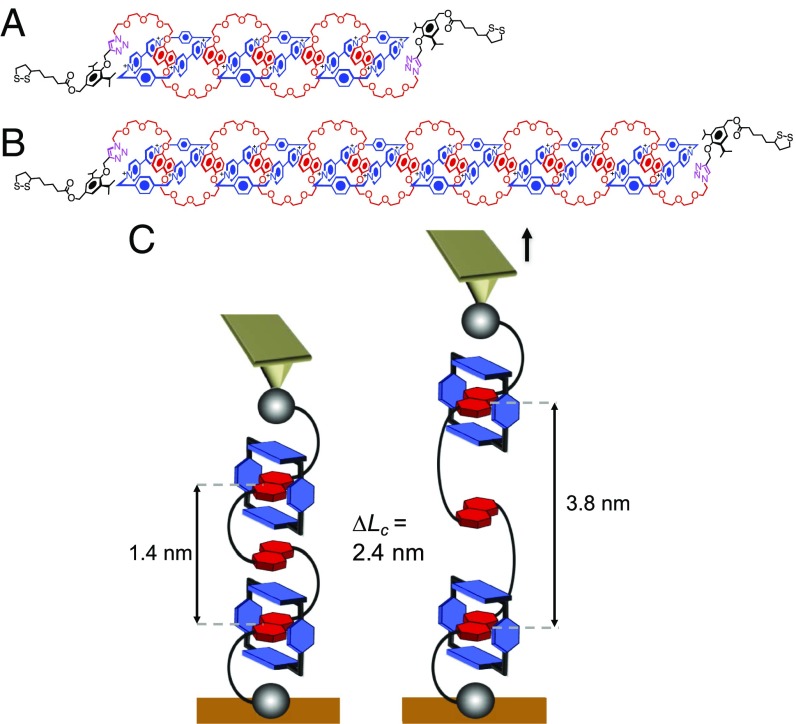
Here, we have investigated the dynamics and the stochastic behavior of single donor–acceptor oligorotaxane foldamers, prototypes of artificial molecular switches, and extracted energetics information. The molecules are made of oligomeric backbone components incorporating 1,5-dioxynaphthalene (DNP) units encircled by tetracationic cyclobis(paraquat-p-phenylene) rings (CBPQT⁴⁺, Blue Boxes) (32–34). These oligorotaxanes are known to adopt a robust serpentine-like folded conformation (as depicted in Fig. 1 A and B), stabilized by intramolecular noncovalent bonding interactions such as strong donor–acceptor π-interactions and hydrogen bonds linking the electron-donor DNP recognition sites and the electron-poor 4,4′-bipyridinium dication (BIPY²⁺) of the Blue Boxes (32–35).

Fig. 1.

Structural formulas of the oligorotaxanes and schematic description of the AFM-based single-molecule force spectroscopy experiment. (A and B) Structure formulas and coconformations of the [4]rotaxane (A) and [7]rotaxane (B) of the [0.5(n − 1) + 2] family. The terms in square brackets denote the total number of interlocked components and n is the number of DNP units present in the backbone components. In this coconformation, half of the DNP units (in red) are encircled by CBPQT⁴⁺ rings (in blue). Noncovalent intramolecular interactions such as π-interactions linking DNP units and Blue Boxes, hydrogen bonds linking α-hydrogen atoms of the Blue Boxes with tetra(ethylene oxide) chains in the backbones, and Coulombic interactions between the molecular rings and PF₆⁻ counterions stabilize the folded conformation. PF₆⁻ counterions are not shown. (C) Mechanical unfolding of individual oligorotaxanes, leading to the breaking of the intramolecular interactions maintaining the folded conformation.

Results and Discussion

Dynamic Force Spectroscopy.

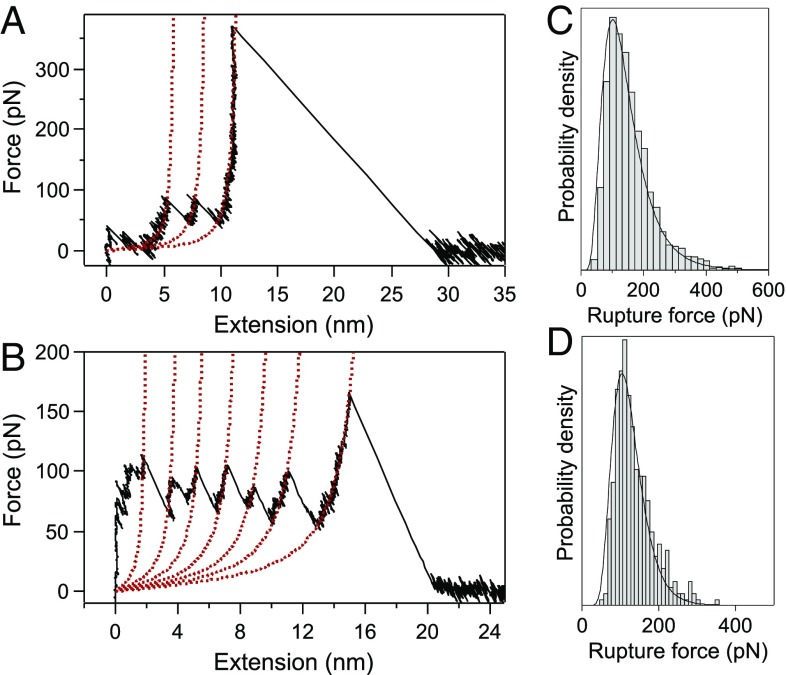
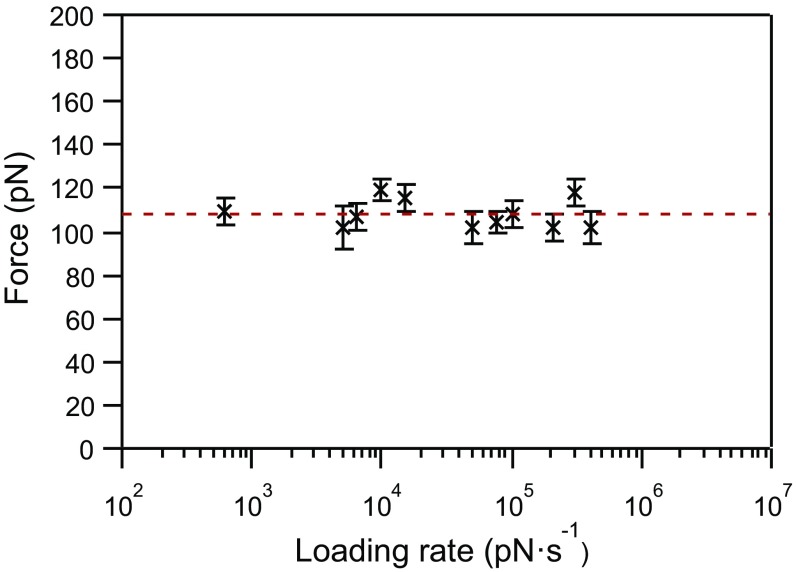
Following our previously published procedure (31), [4]- and [7]rotaxane foldamers (Fig. 1 A and B) were grafted on gold-coated substrates to obtain isolated single molecules, which were stretched mechanically using AFM-based single-molecule force spectroscopy (Fig. 1C). The force-extension curves obtained in dimethylformamide (DMF), a good solvent for the molecules, show a characteristic unfolding profile (Fig. 2) with regularly spaced force peaks, each separated by 2.4 nm on the basis of worm-like chain fits (see Supporting Information for details). The distance between the peaks nicely matches the theoretical distance expected for the sequential mechanical breaking of intramolecular donor–acceptor DNP-BIPY²⁺ interactions on both sides of the ring. Rupture force values were also compiled in histograms (Fig. 2 C and D) and show a most probable population at around 100 pN. The last peak displays a higher force, characteristic of an S–S interaction with gold (36). We performed standard SMFS experiments at 11 different loading rates, from 6 × 10² to 4 × 10⁵ pN·s⁻¹, to cover three orders of magnitude. At each loading rate, characteristic unfolding profiles were obtained and rupture force distributions were constructed (Fig. S1). The dynamic force spectrum of the [4]rotaxane, relating the evolution of the most probable rupture force (F) with the associated loading rate, is shown in Fig. 3. We observe a quasi-linearity of the rupture force with respect to the loading rate, suggesting a rate-independent rupture force in the range of loading rates investigated and thus providing evidence for the near-equilibrium regime of the experiment. Friddle et al. (23) have shown that a bond can be pulled in a near-equilibrium regime, at low loading rate, as the pulling rate approaches its natural dissociation rate. In this case, the bond is not affected by the external load and the average force required to break the interaction is constant (F_eq). On the contrary, a bond pulled at a rate higher than its dissociation rate resists this mechanical stimulus, leading to a rupture force increase. This behavior corresponds to the out-of-equilibrium regime. The Friddle–Noy–De Yoreo model has been employed successfully (23) to describe previous pulling experiments performed on numerous biomolecules and it has been shown that the rupture forces experienced at various loading rates can be described by a nonlinear fit including both the near-equilibrium (loading rate independent) and the kinetic regimes where the force is proportional to the logarithm of the loading rate, as described by Evans (22). All of the molecules studied by dynamic force spectroscopy and fitted by Friddle–Noy–De Yoreo model (Fig. 4) show a clear kinetic regime for loading rates varying from 10² to 10⁶ pN·s⁻¹ (23). Here, for the stretching of the oligorotaxanes, we do not observe an increase of the rupture force within a similar range of loading rates (Fig. 4). The kinetic regime of the oligorotaxane is not reached yet at the highest loading rates. The equilibrium force determined F_eq = 108.1 ± 1.2 pN is high in comparison with the equilibrium force measured previously on natural biomolecules, supporting the high strength of the intramolecular donor–acceptor interactions. Compared with previous dynamic force spectroscopy studies performed on the same range of loading rates, we show here that the near-equilibrium regime of this synthetic molecule persists at much higher loading rates, demonstrating the very fast dynamics of the probed interaction. We attribute this extraordinary behavior to the proximity of the binding partners and the presence of mechanical bonds (37). They keep both intramolecular partners in close proximity and favorable orientation after the breaking of the interaction, making it easier to reform the bonds rapidly.

Fig. 2.

Characteristic force-extension curves of a [4]- (A) and [7]rotaxane (B) mechanically stretched at 7.5 × 10⁴ pN·s⁻¹ in DMF, showing equally spaced force peaks, each separated by 2.4 nm. Each peak corresponds to the breaking of intramolecular interactions on both sides of the ring and the maximum peak value corresponds to the rupture force. The red dotted lines are worm-like chain fits. See Supporting Information for details. Distribution of the rupture force for the pulling of the [4]- (C) and [7]rotaxane (D) in DMF at 7.5 × 10⁴ pN·s⁻¹. The most probable values were obtained by log-normal fits and peak at 101.2 ± 1.2 pN (n = 3,338) (C) and 104 ± 4.5 pN (n = 362) (D).

Fig. 3.

Dynamic force spectrum of the mechanical unfolding of the [4]rotaxane in DMF at 11 loading rates (from 6 × 10² to 4 × 10⁵ pN·s⁻¹). Each datum (n ≥ 150) is associated with its effective loading rate and its most probable rupture force (Fig. S1). As shown by the horizontal red line (F_eq = 108.1 ± 1.2 pN), the rupture force does not increase with the loading rate, establishing the near-equilibrium regime of the experiment.

Fig. 4.

Force spectrum of the mechanical unfolding of the [4]rotaxane in DMF (in red) superimposed with force spectra of 10 data sets (in gray scale) taken from the literature and fit to the Friddle–Noy–De Yoreo model (adapted from ref. 23). The kinetic regime of the oligorotaxane is not reached yet at the highest loading rates, and the equilibrium force (F_eq = 108.1 ± 1.2 pN) is high compared with the one observed for the various molecules measured previously.

Near-Equilibrium Stochastic Behavior.

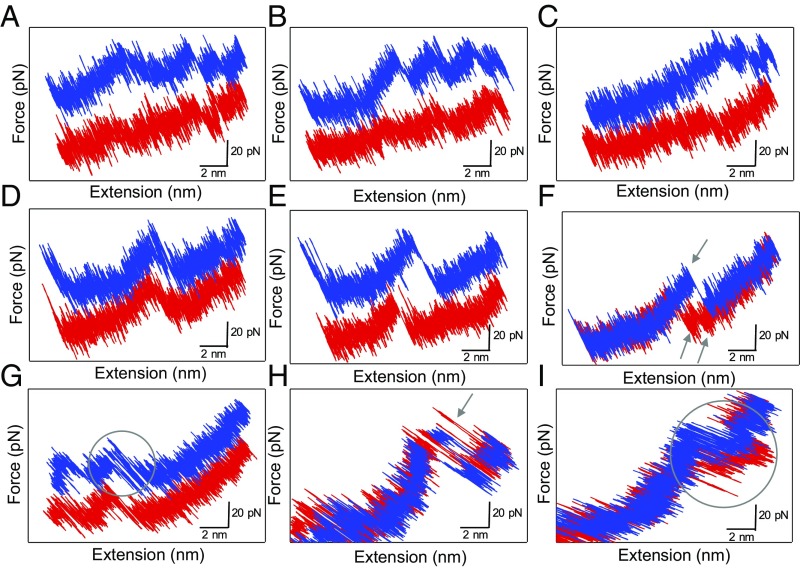
Even if the pulling experiments are performed near thermodynamic equilibrium, small molecules are always being submitted to random thermal fluctuations that constantly modify their unfolding and refolding paths (25). We performed single-molecule pulling–relaxing cycles at low loading rates (2,500 and 5,000 pN·s⁻¹). The comparison between successive pulling and relaxing force curves evidenced the stochastic behavior of individual oligorotaxanes under mechanical load (Fig. 5). The work done to unfold the molecule is not dissipated into the environment and is recovered in the refolding process to remake the broken interactions. Fig. 5 A and B shows the unfolding of several units. The relaxing curves point to the reformation of the previously broken interactions. By looking at one interaction at a time (Fig. 5 D–I), several patterns can be identified. In Fig. 5D, the relaxing curve is identical to the stretching curve without any hysteresis (quasi-static pulling), whereas hysteresis between pulling and relaxing curves can be observed in Fig. 5E. Hysteresis indicates that the work done on the oligorotaxane during pulling is not fully recovered during relaxation and was partly dissipated. Even if the dynamic force spectroscopy experiments (Fig. 3) performed on this system indicate that for most pulling experiments the near-equilibrium regime is attained on the average, we can distinguish singular stochastic behavior of individual molecules when stretched at low loading rates. Among these, we observe the simultaneous rupture of two interactions followed by the sequential reforming of each interaction separately (two peaks in the relaxing curve) (Fig. 5F). Interestingly, fluctuations between folded and unfolded states appear in some pulling and relaxing curves (Fig. 5 G–I). These fluctuations are the signature of an experiment performed near the thermodynamic equilibrium of the probed interaction. It is thus consistent with the loading-rate-independent rupture force evidenced above. In Fig. 5H, a peak in the relaxing curve, corresponding to the reformation of an interaction, appears with a “negative hysteresis” compared with the breaking peak in the pulling curve. This observation can be explained by the consumption of thermal energy by the molecule to refold back to its previous state (i.e., the surroundings do work), hence exhibiting negative dissipated work. Such nonequilibrium trajectories with W_diss ≤ 0 can indeed exist (25). Strictly speaking, this observation is not a violation of the second law of thermodynamics since it does not apply over small time scales and length scales. Nevertheless, this situation is a clear example of a molecule taking advantage of the random thermal fluctuations (k_BT) to induce a molecular movement and then recreate an intramolecular interaction.

Fig. 5.

Stochastic behavior of a single [7]rotaxane during pulling(blue)–relaxing(red) experiments in DMF (the pulling traces A–E and G are shown with a 30-pN offset for more clarity). These curves exhibit the recovery of the characteristic sawtooth pattern during the relaxation step (A–C), the reversible breaking of a single interaction without (D) and with (E) hysteresis, the simultaneous breaking of two interactions and their subsequent reforming (F), and the presence of fluctuations between folded and unfolded states during the pulling and the relaxing curves (G–I).

Determination of ∆G Between Locally Unfolded and Folded States.

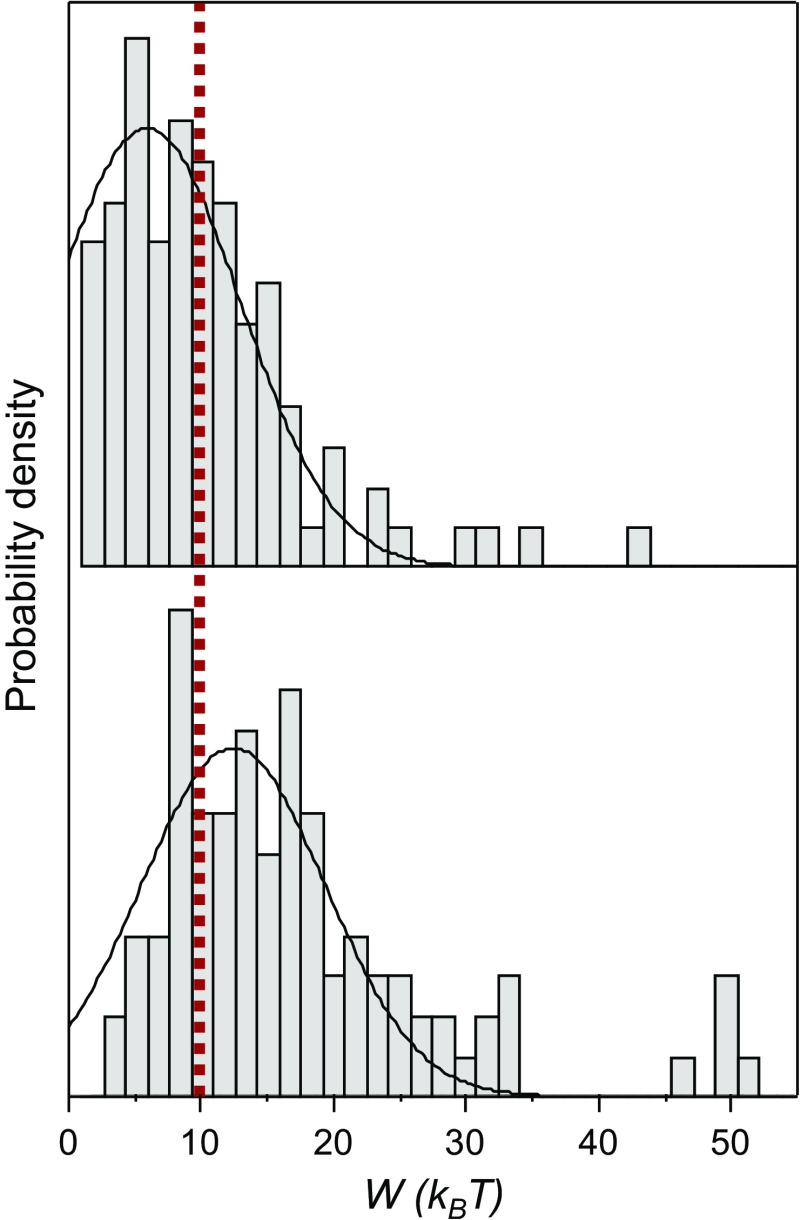
For a reversible process, the mechanical work equals the Gibbs free-energy change of the process, but the distribution of work trajectories typically results in hysteresis because of the fluctuations. Recent developments in nonequilibrium statistical mechanics enable the recovery of the reversible work, and thus the zero-force free energy, from the distribution of work trajectories in pulling–relaxing cycles (30). To evaluate the energy required to break one DNP–BIPY²⁺ interaction, the experiments were designed to probe only one interaction at a time. To measure the work performed during the breaking of a single interaction in the pulling step, we measured the area under the “force vs. distance” curve between the rupture distance and the distance where the molecule is back under tension, ∆d (Fig. S2). This area was subject to correction by withdrawing the entropic contribution resulting from the stretching of the main chain (see details in Supporting Information). The same measurement was carried out for the relaxing step to determine the work performed by the molecule to reform the interaction. The distribution of ∆d shows a main population centered at 1.1 ± 0.1 nm (Fig. S3), an observation which confirms that a single interaction is being probed. The distributions of the pulling and relaxing works are shown in Fig. 6. They reveal a large overlapping region, confirming the near-equilibrium regime in this range of loading rates and a small amount of work being dissipated during the overall process. When the work done on a system (W) is completely recovered in the reverse process (−W), the Crooks fluctuation theorem states that W = ∆G (29). Therefore, the conformational free-energy difference between locally unfolded and folded states was determined graphically where both forward and reverse works have the same value, at W = 10 ± 2 k_BT (red line in Fig. 6). Therefore, the energy required to break a single DNP–BIPY²⁺ interaction, ∆G, is equal to 6 ± 1 kcal·mol⁻¹. This value is in very good agreement with the theoretical ∆G value calculated previously (38, 39).

Fig. 6.

Distributions of forward (pulling step, Lower) and reverse (relaxing step, Upper) works corresponding, respectively, to the breaking and the reforming of a single interaction within the folded [4]rotaxane in DMF (n = 96). These distributions were obtained from pulling–relaxing experiments in the near-equilibrium regime (loading rate of 10³ pN·s⁻¹). Gaussian fits of the raw data are superimposed with the histograms (bin size = 0.5 k_BT). The forward and reverse works have the same value (red line) at W = 10 ± 2 k_BT or 6 ± 1 kcal·mol⁻¹.

Conclusion

For more than 20 y, single-molecule force spectroscopy has proved to be a powerful tool to manipulate single molecules and obtain exquisite information about their mechanical behavior. The technique has been widely used to determine equilibrium thermodynamic parameters by mechanically driving probed molecules out of equilibrium at various loading rates (16, 20–24). To date, there have been very few investigations reported on wholly synthetic small molecules (31, 40–44), mainly because of the difficulty of preparing appropriate molecules that can be interfaced with single-molecule force spectroscopy techniques, but also because the size of the molecules implies that the rupture events occur at very small distances, in the range of 1 nm. Here we have probed donor–acceptor oligorotaxane foldamers, synthetic prototypes of molecular switches, by AFM-based dynamic force spectroscopy. Our results demonstrate that the rupture force of the interactions responsible for the folding is not dependent on the loading rate over a huge range of values, from 6 × 10² up to 4 × 10⁵ pN·s⁻¹, a range at which a large variety of intramolecular systems display nonlinear force spectra. This unique behavior reveals fast bond reforming, even for very high loading rates, and provides evidence for the wide-range near-equilibrium regime of the probed interactions. We suggest that this behavior relies on the specific nature of the structure and superstructure of the oligorotaxanes. The proximity of the binding partners and the presence of mechanical bonds keep both intramolecular partners in close proximity and favorable orientations after the breaking of the interaction, making it easier to reform the bonds rapidly. Our results highlight the remarkable robustness of the intramolecular donor–acceptor interactions. The near-equilibrium conditions allowed us to use the Crooks fluctuation theorem to recover the reversible work, and thus the free energy, from the distribution of work trajectories in pulling–relaxing cycles. We determined the free-energy difference ∆G between locally folded and unfolded conformations, corresponding to the energy required to break one intramolecular DNP–BIPY²⁺ interaction.

Our findings highlight the importance of the molecular design in the synthesis of efficient molecular machines, able to compete with or even surpass the performance of natural machines.

Materials and Methods

The [4]- and [7]rotaxanes were synthesized according to protocols described previously (32). Briefly, one-pot syntheses used copper-catalyzed azide-alkyne cycloadditions to thioctic ester-functionalized stoppers at both ends of the DNP-derived polyether chains in the presence of CBPQT⁴⁺ rings. Using conventional chromatographic techniques, oligorotaxanes with half the DNP units encircled by rings were isolated. The compounds were characterized by mass spectrometry and NMR spectroscopy (32).

The oligorotaxanes were grafted onto gold-coated silicon substrates using our previously established method (31) to obtain a sparse regime of the molecule of interest. The substrates were dipped for 1 h in a solution of the oligorotaxane (2 × 10⁻⁸ mol) containing 90 mol % of dodecyl disulfide in Me₂CO at room temperature. The role of the dodecyl disulfide is to ensure a dilute distribution of the oligorotaxanes on the surface as well as passivate the substrate. All of the details are given in Supporting Information.

Single-molecule force spectroscopy experiments were carried out with a PicoPlus 5500 microscope (Agilent Technologies), equipped with a closed-loop scanner. Gold-coated tips (OBL-10 Biolever; Bruker; nominal spring constant k = 0.009–0.1 N·m⁻¹) were used for all of the force experiments. The spring constant of each cantilever was calibrated by the thermal noise and Sader methods (45, 46). The molecules were picked up for force experiments by gently pressing the AFM tip against the substrate. Pulling–relaxing cycles were realized using a custom-made routine to guide the tip. Each force curve contains 20,000 data points. All of the details are given in Supporting Information.