Structural fluctuations cause spin-split states in tetragonal (CH₃NH₃)PbI₃ as evidenced by the circular photogalvanic effect

Significance

Lead halide perovskites are successfully used in thin-film solar cells, with efficiencies on the laboratory scale exceeding 22%. The electronic structure underlying their exceptional phototransport properties is complex because of the organic–inorganic character of the materials, their mechanical softness, and the strong spin–orbit coupling induced by the constituting heavy elements. Calculations predict that a dynamical Rashba effect could enhance the lifetimes and diffusion lengths of photocarriers in perovskite solar cells. The dynamical Rashba effect is characterized by spin splittings in the band structure at elevated temperatures, induced by local structural disorder. The mechanism should be general to structurally flexible materials composed of heavy elements, making those potentially attractive for both optoelectronics and spintronics.

Abstract

Lead halide perovskites are used in thin-film solar cells, which owe their high efficiency to the long lifetimes of photocarriers. Various calculations find that a dynamical Rashba effect could significantly contribute to these long lifetimes. This effect is predicted to cause a spin splitting of the electronic bands of inversion-symmetric crystalline materials at finite temperatures, resulting in a slightly indirect band gap. Direct experimental evidence of the existence or the strength of the spin splitting is lacking. Here, we resonantly excite photocurrents in single crystalline (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ with circularly polarized light to clarify the existence of spin splittings in the band structure. We observe a circular photogalvanic effect, i.e., the photocurrent depends on the light helicity, in both orthorhombic and tetragonal (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$. At room temperature, the effect peaks for excitation photon energies $\mathrm{\Delta }E=110$ meV below the direct optical band gap. Temperature-dependent measurements reveal a sign change of the effect at the orthorhombic–tetragonal phase transition, indicating different microscopic origins in the two phases. Within the tetragonal phase, both $\mathrm{\Delta }E$ and the amplitude of the circular photogalvanic effect increase with temperature. Our findings support a dynamical Rashba effect in this phase, i.e., a spin splitting caused by thermally induced structural fluctuations which break inversion symmetry.

Lead halide perovskites (LHPs) show remarkable potential for applications in optoelectronics and especially in thin-film solar cells (1–3). Unusually long carrier lifetimes (4–6) and diffusion lengths (7–9) characterize the exceptional performance of these devices. To explain the microscopic origin of the long lifetimes two models are under discussion: on the one hand, polaronic effects (10–12), and on the other hand, a slightly indirect band gap caused by a spin-polarized band structure (13–15). Both mechanisms can separate the electron and the hole after photoexcitation and significantly reduce radiative recombination rates. Various experiments found multiple optical transitions near the band gap (16–29). The assignment of low-energy transitions to polarons (27, 28) or to spin effects (19) is difficult based on optical spectroscopy alone and relies on comparison with calculations. Moreover, low-energy transitions may arise from defects, especially due to (partial) degradation of the near-surface region (21, 30–32). Recent experiments on high-quality LHP crystals, however, indicate that low-energy transitions are intrinsic to these crystals (22, 23, 25, 27).

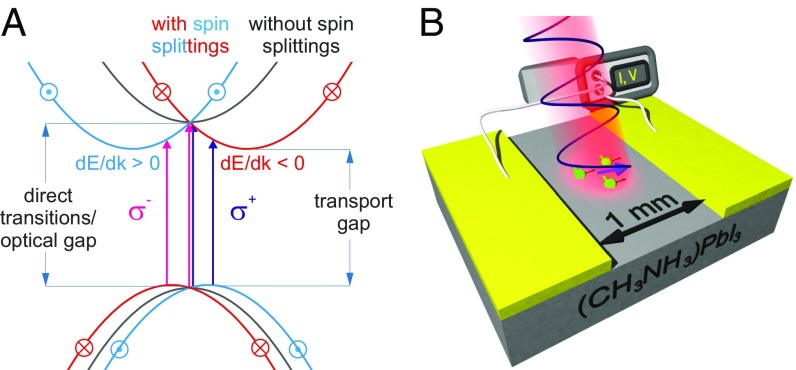
An unambiguous test for the spin-based model can be performed by addressing the spin-polarized bands with helical light. For opposite helicity of the light the group velocity of excited carriers is reversed and spin-polarized currents of opposite direction are induced (33–35) as sketched in Fig. 1A. LHPs have a direct optical band gap between single valence and conduction bands. The valence band is derived from Pb 6$s$ and halogenide $p$ orbitals, and the conduction band is from Pb 6$p_{1/2}$ states. In the absence of inversion symmetry, spin–orbit coupling causes a spin-dependent shift of the electronic bands along the k direction (36–43). This shift is typically larger for the conduction band with its strong Pb 6$p$ character than for the valence band. The band gap becomes slightly indirect and the optical transitions are spin dependent. Transitions between spin-polarized and spin-degenerate bands are indicated in Fig. 1A for a Rashba-type band structure (13, 38), which gives a minimum description of a semiconductor with spin–orbit coupling. In this complex situation, a clear-cut experiment is the excitation of photocurrents with left-handed and right-handed circularly polarized light in perovskite single-crystal devices as illustrated in Fig. 1B. Spin-polarized transverse currents are induced, which reverse their direction when the light helicity is switched (35, 44). The effect is known as the circular photogalvanic effect (CPE). It has been observed experimentally in the prototypical bulk Rashba system BiTeBr (45), in wurtzite semiconductors such as ZnO (46) and GaN (47), in GaAs/AlGaAs quantum well structures (48), in transition-metal dichalcogenides (49), and in the topological insulator ${\mathrm{B}\mathrm{i}}_2{\mathrm{S}\mathrm{e}}_3$ (50). A circular photogalvanic effect of measurable magnitude has been predicted (51, 52) for (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$. Previously, helicity dependence has been found in optical (53, 54) and electron spectroscopy (55) experiments on LHPs. A circular photogalvanic effect is hence expected if coherent spin transport takes place on a length scale large enough for spin-polarized currents to be driven through a device. We report measurements of the resulting spin-polarized photocurrents in devices made from single crystals of (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$, the most important LHP material.

Fig. 1.

Circular photogalvanic effect. Shown is a schematic illustration of the effect and the experimental setup. (A) Rashba-type spin splittings cause a shift of the bands along the k direction and lift their spin degeneracy. Excitation with left- (${\sigma }^{-}$) and right-handed (${\sigma }^{+}$) circularly polarized light creates photocarriers on opposite branches of the band structure. Since the associated group velocities d$E$/d$k$ differ in sign, a transverse spin current is induced. (B) In the experiment, a (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ single crystal with gold contacts (channel width: 1 mm) is illuminated at nonnormal incidence by light of tunable photon energy close to the band gap.

Results and Discussion

Helicity Dependence of the Photocurrent.

Fig. 2A shows the changes in the photocurrent $\mathrm{\Delta }I$ with varying light polarization, controlled via the angle $\alpha$ of a $\lambda /4$ waveplate. A polarization-independent photocurrent (several nanoamperes) was subtracted from the data; see SI Appendix, Fig. S1 for details. Data are shown for three different angles of incidence $𝜗=0^{○},\pm 50^{○}$. They show oscillations with two different periodicities of 90° and 180° which can be described by

$$\mathrm{\Delta }I=L\cdot \sin \left(4\alpha +\varphi \right)+C\cdot \sin \left(2\alpha \right),$$ [1]

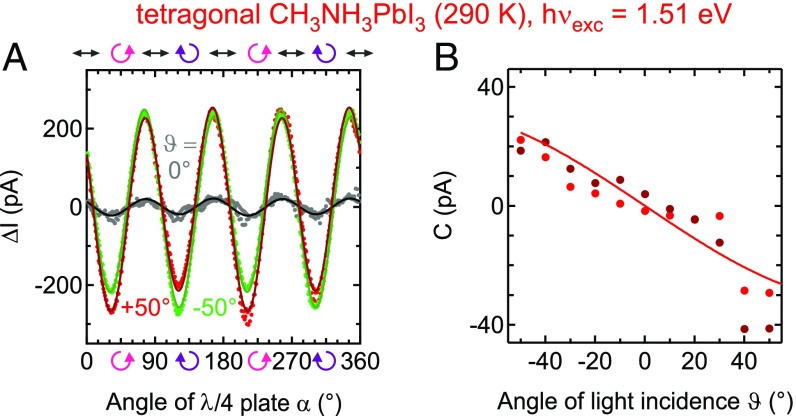
with amplitudes $L$, $C$ and phase $\varphi$. The first term describes the effect of different reflectivities for $s$- and $p$-polarized light, of the transfer of photon momentum to electrons and holes (photon drag), and of the different group velocities of the carriers after photoexcitation (linear photogalvanic effect) (56, 57). In principle, these effects can be separated when the dependencies of $L$ and $\varphi$ on $𝜗$ and the direction between the plane of light incidence and the current are known (56, 57). In practice, sample-to-sample variations, inhomogeneities, and the limited stability of (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ at room temperature hinder accurate measurements of these relationships (SI Appendix, section 1B). Instead, we focus on the more robust second term, which is the effect of the light helicity on the photocurrent. Its amplitude $C$ quantifies the difference between currents excited using left-handed and right-handed circularly polarized light. The difference represents spin-polarized photocurrents, since only those change direction when the helicity of the excitation light is reversed (56). $C$ changes sign when $𝜗$ is changed from $50^{○}$ to $-50^{○}$ and vanishes within the experimental uncertainties for $𝜗=0$. We also performed a control experiment with the sample rotated by $90^{○}$ (SI Appendix, Fig. S5). In this geometry $C$ is reduced by at least two orders of magnitude and zero within the experimental uncertainty. This behavior is indicative of the CPE and was similarly found in other measurements on devices fabricated on high-symmetry surfaces of inorganic semiconductors (46–50). As shown in Fig. 2B, $C$ changes sign and the underlying spin-polarized currents change direction for $𝜗\approx 0$, and they increase approximately linearly with $𝜗$. The angular dependence of $C$ is given for two devices, where one was fully illuminated with a parallel beam whereas the beam was focused on the other device. While the amplitude of the CPE (normalized to incident power) increases as the crystal is excited closer to the contacts, the angular dependence is the same for both samples. The experimental errors are due to the realignment of the optical setup for the different $𝜗$, which goes along with the illumination of slightly different parts of the device. The amplitude $C$ of the CPE found on different positions and devices is between 500 nA/W and 1,500 nA/W for the focused beam at $𝜗=40^{○}$. This value is larger than the one reported for the prototypical bulk Rashba system BiTeBr (100 nA/W, ref. 45) and orders of magnitude higher than in semiconductor quantum well structures ($\approx 1$ nA/W, refs. 47 and 48).

Fig. 2.

Changes in the photocurrent with light polarization. (A) The photocurrents measured as a function of light polarization for three different angles of light incidence: $+50^{○}$ (red symbols), $-50^{○}$ (green symbols), and $0^{○}$ (gray symbols). Pure linear (black arrows) and circular polarizations (pink and purple curved arrows) are indicated. Curves depict fits to the data using Eq. 1. (B) The CPE amplitudes extracted from fits to the data in A. The curve is a sinusoidal guide to the eye. Light and dark red symbols represent data recorded with a parallel beam (laser power: 5 $\mathrm{\mu }$W) and a focused beam (40 $\mathrm{\mu }$W).

Photon-Energy Dependence.

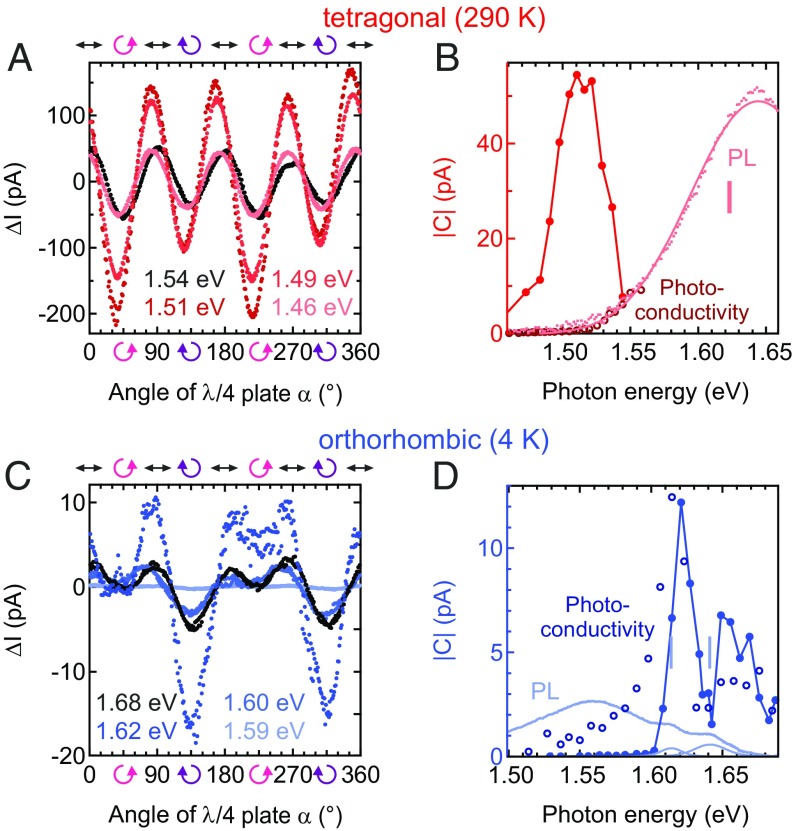
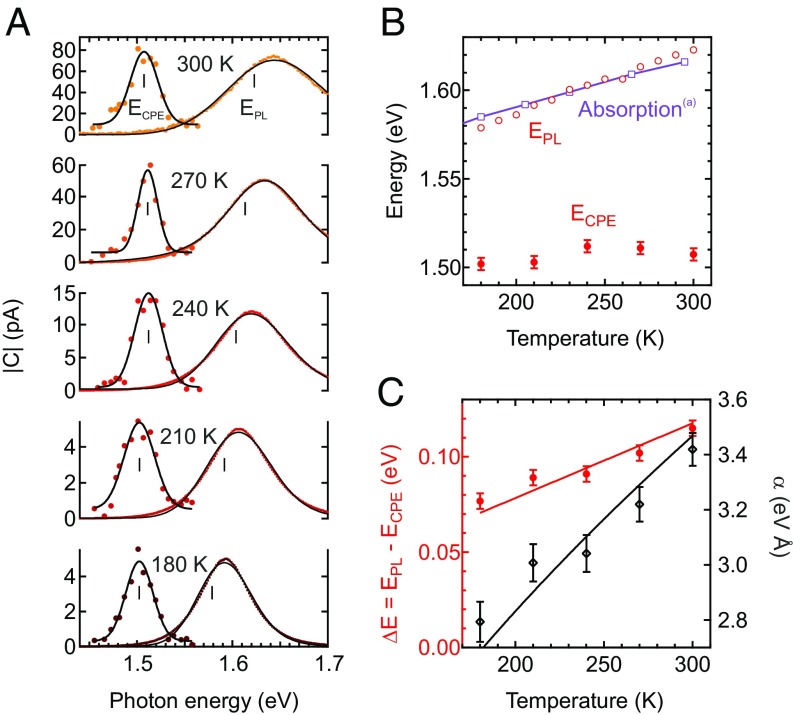
The CPE is sensitive to the excitation photon energy as illustrated in Fig. 3A, which shows the changes in the photocurrent with the light polarization for different photon energies. Fig. 3B gives the extracted CPE amplitudes $C$ together with the photocurrent spectrum and the photoluminescence spectrum of the (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ single crystals. At room temperature, $C$ peaks at 1.51 eV, well below the direct band gap which is measured as the peak position in the photoluminescence spectrum at 1.62 eV. This allows a clear assignment of the CPE to a transition between spin-polarized bands 110 meV below the direct band gap and confirms the scenario illustrated in Fig. 1A for tetragonal (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$.

Fig. 3.

Changes in the photocurrent as a function of the excitation photon energy. (A and C) Raw data for the tetragonal phase (excitation power: 40 $\mathrm{\mu }$W) and the orthorhombic phase (8 $\mathrm{\mu }$W) recorded for $𝜗=40^{○}$. Extracted CPE amplitudes $C$ are shown as solid symbols in B and D. Open symbols in B and D depict the photoconductivity. Photoluminescence (PL) spectra are given as pink and light blue dots together with fit functions (solid curves). Vertical bars indicate the positions of the PL peaks.

The direct optical gap measured for our single crystals is consistent with the literature, which reports values of 1.5–1.65 eV (7, 8, 58–63). A recent experiment on high-quality single crystals (25) resolves optical transitions at 1.48 eV and 1.58 eV, but cannot discriminate between a spin-degenerate and a spin-polarized band structure. Other authors also report a pair of direct and indirect band transitions with a spacing of 47 meV (18) and 60 meV (19) from measurements on thin films.

We note that most studies on thin films of (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ observe only a high-energy direct optical transition. Bimolecular recombination dynamics in thin films with an optical band gap of 1.65 eV and no indication of lower-energy optical transitions are well described by a Roosbroeck–Shockley analysis (64). Differences between single crystals and thin films are also evidenced by the fabrication of single-crystal solar cells with significant external quantum efficiencies for photon energies as low as 1.5 eV (23), thus giving an enhanced spectral response with respect to their thin-film counterparts. The discrepancies may arise from the small absorption cross-section of the low-energy transitions and from differences in the structural and chemical properties. Chemical modifications in the near-surface region may affect thin films more strongly than single crystals because of their higher surface-to-bulk ratio (21, 65).

Temperature Dependence.

Although our experiment clearly assigns the indirect transition to a spin-polarized band structure, it remains unclear which mechanism breaks the inversion symmetry, generating the Rashba splitting. To gain additional information on the sensitivity of the spin splitting to the crystal symmetry, low-temperature measurements are an obvious choice. Toward low temperature, the sample undergoes a phase transition from the room-temperature tetragonal phase to the low-temperature orthorhombic phase. Fig. 3C presents data obtained at a temperature of 4 K. The experiment is conducted very similarly to the one in Fig. 3A but on a different sample. A clear CPE is observed also for this sample and in this phase. In Fig. 3D the extracted $C$ for the orthorhombic phase is given together with the corresponding photocurrent and photoluminescence spectra. All three techniques find dual transitions at energies of $\approx 1.62$ eV and 1.64 eV, indicating that those are intrinsic to the orthorhombic phase. This interpretation is consistent with a recent report (25). Additional low-energy features are found in the photocurrent and photoluminescence data and dominate the latter ones, indicating that they are related to defects. The direct optical band gap, estimated from the highest-energy photoluminescence peak at 1.64 eV, is in very good agreement with literature values ranging from 1.64 eV to 1.65 eV (60, 66–68).

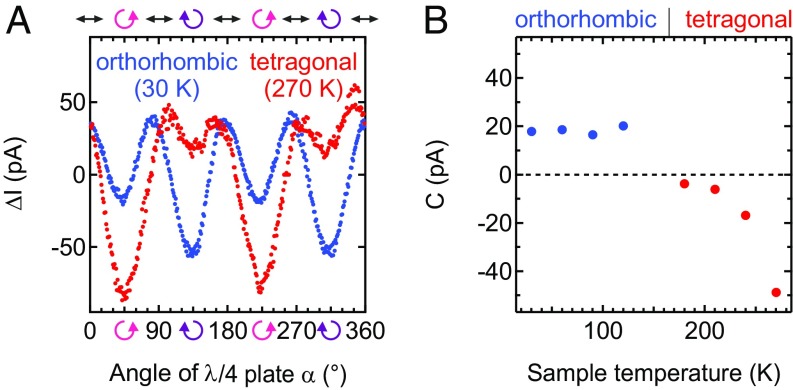
For an in-depth study we recorded photocurrents over a wide temperature range. For the tetragonal and the orthorhombic phases, excitation photon energies of 1.52 eV and 1.64 eV were chosen, matching the maxima of the CPE amplitude $C$ at 290 K and 4 K, respectively. Across the phase transition the sign of $C$ changes (Fig. 4A). Also, the temperature dependence of $C$ is different in the two phases as shown in Fig. 4B. Within the orthorhombic phase, $C$ is almost temperature independent. In the tetragonal phase, in contrast, $\left|C\right|$ increases strongly with temperature.

Fig. 4.

Temperature dependence of the CPE amplitude. (A) Data recorded for two different structural phases. (B) The extracted CPE amplitudes. Excitation photon energies are 1.52 eV for the tetragonal and 1.61 eV for the orthorhombic phase. $𝜗=40^{○}$; laser power, 40 $\mathrm{\mu }$W.

In addition, the energy difference between direct optical transition and the peak in $\left|C\right|$, which is found only in the tetragonal phase, increases with temperature as shown in Fig. 5A. The optical band gap of (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$, measured by the position of the photoluminescence peak, increases with temperature as has been reported before (25, 69, 71, 72). Photoluminescence spectra of (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ are broadened by the strong electron–phonon coupling in the material (73) and therefore not well described by models taking into account a single direct electronic transition (74); see SI Appendix, section 1E for details. We estimate the optical band gap from fitting each photoluminescence spectrum with a Gaussian peak, convolved with a Boltzmann distribution to account for the asymmetric broadening of the spectra at elevated temperature. The direct band gap determined in this way is in good agreement with the one reported from transmission measurements on (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ thin films (69) (Fig. 5B). In contrast to the photoluminescence emission, $\left|C\right|$ always has its maximum for a photon energy of $\approx 1.51$ eV. The energetic positions of both features are summarized in Fig. 5B and their energetic spacings are given in Fig. 5C. Altogether, our data indicate that the CPEs in the two structural phases of (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ must be explained by different mechanisms.

Fig. 5.

Temperature-dependent energy splitting between the direct and the spin-polarized transitions. In A, the spectral response of the CPE and the photoluminescence emission are compared for different temperatures. The peak positions extracted from fits to the data (solid red curves) are indicated by tick marks in A and summarized in B. The direct band gap of (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ thin films measured in transmission (69) is shown in purple for comparison. (C) The energy splitting between the two transitions and the estimated sum $\alpha$ of the Rashba parameters of the valence and conduction bands. Solid red and black lines depict their temperature dependences within an analytical model (70). $𝜗=40^{○}$; laser power, 4 $\mathrm{\mu }$W. ^(a) is from ref. 69.

Origin of the CPE in Orthorhombic and Tetragonal (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$.

We first discuss the CPE in the low-temperature orthorhombic phase. This phase is known to have antiferroelectric order and $Pnma$ symmetry, with the tilted inorganic octahedral cages arranged in a $\sqrt{2}\times \sqrt{2}\times 2$ superstructure with respect to the cubic building block (75–77). Because of this centro-symmetric structure, no spin splittings are expected in the bulk electronic band structure (43). We propose that the spin polarization of the optical transitions arises from the broken inversion symmetry at the surface and at interfaces. Strong spin polarizations were found in the electronic states at the surface of (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{B}\mathrm{r}}_3$ (55), in ${\mathrm{C}\mathrm{s}\mathrm{P}\mathrm{b}\mathrm{B}\mathrm{r}}_3$ nanocrystals (78), and in polycrystalline (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ thin films (79). In these the inversion symmetry is broken at surfaces or internal interfaces such as grain boundaries. The resulting surface potentials can induce significant spin polarizations of the electronic states even if those are spin degenerate in the bulk (80). The influence of the crystallinity on the CPE amplitude is also illustrated in SI Appendix, Table S3. Internal interfaces breaking the inversion symmetry of (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ single crystals at low temperature may result from twinning of orthorhombic domains and the inclusion of tetragonal (81) or disordered orthorhombic domains (82). These structural inhomogeneities are frozen in below the phase transition temperature, explaining the temperature-independent $C$ in the orthorhombic phase. The absence of a measurable bulk Rashba splitting in orthorhombic (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ is also reflected in the identical transitions observed in the CPE amplitude, in the photocurrent, and in the photoluminescence spectra recorded at 4 K (Fig. 3D). The similar spectra in the three techniques indicate that all of the electronic states involved in the transitions carry similar spin polarization, arising only from the reduced symmetry at surfaces and interfaces.

On the contrary, for (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ in the tetragonal phase we observe distinct transitions in the CPE amplitude and in the photoluminescence spectra, giving evidence of spin splittings in the band structure. The energetic spacing $\mathrm{\Delta }E$ between the two transitions increases with temperature as shown in Fig. 5C. Within the model Rashba band structure depicted in Fig. 1A, $\mathrm{\Delta }E$ serves as a measure of the sum $\alpha$ of the Rashba parameters of the valence and conduction bands as $\alpha =2\hslash \sqrt{\frac{\mathrm{\Delta }E}{m^{*}}}$. Details of the calculation are given in SI Appendix, section 3. Assuming an effective mass $m^{*}$ of 0.3 free electron masses for both electrons and holes (39, 83), we find $\alpha \approx 3$ eV Å. The temperature dependence of $\alpha$ is given in Fig. 5C. The values are taken as a rough estimate of the Rashba splitting since the actual band structure can be expected to be more complex than the one of the minimum model. Nevertheless, the continuous increase of $\mathrm{\Delta }E$ with temperature gives direct evidence of an increasing Rashba splitting. This is also reflected in the increasing CPE amplitude with temperature for tetragonal (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ (Fig. 4B). Our results imply that the CPE in tetragonal (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ is caused by thermally induced structural fluctuations which are absent in the antiferroelectrically ordered orthorhombic phase. Large-amplitude nuclear motions associated with anharmonic, soft phonon modes arising from structural bi- or multistabilities are common to (anti)ferroelectrics above the critical temperature (84). Perovskites are prototypical for this class of materials, since the ideal perovskite structure is energetically unfavorable and tends to form reconstructions with a reduced symmetry at low temperature (85, 86). These reconstructions are typically lifted at elevated temperature, resulting in an average high-symmetry structure with local disorder due to anharmonic soft phonons. Local lattice disorder has been reported for LHPs in the tetragonal and cubic phases (10, 75, 77, 87–93). In organic–inorganic perovskites like (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$, the dynamics of the inorganic lattice are coupled to the rotation of the incorporated organic ion. At room temperature, the orientation of the organic ion flips on a timescale of $\le 5$ ps (94, 95), which is slower than the inverse optical phonon frequencies [$<1$ ps (92)], implying that the movement of the inorganic cages follows the molecular rotations. Large displacements of both the ${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$ (90) and the inorganic ions (88) have been demonstrated. Details of the local structure can have a strong effect on electronic properties like band gap and Rashba splitting (14, 15). Calculations predict significant Rashba parameters even for structures which are centro-symmetric on average (14, 15, 70). As the Rashba parameter is determined primarily by the displacement of the inorganic ions from the high-symmetry sites (96), it can be influenced indirectly yet strongly by the orientation of the organic ions and their interaction with the inorganic cages. A band structure as depicted in Fig. 1A may be able to describe the instantaneous electronic properties in an adiabatic approximation, if the electronic states at the band edges remain delocalized in the disordered potential energy landscape. The latter is implied by calculations (97) and the observation of a dispersive valence band in angle-resolved photoemission (98, 99). Different models find an enhancement of the calculated spin splittings in LHPs as the temperature is increased (15, 70). In particular, an analytic model suggests an energetic splitting between the conduction band minimum and the band energy at the high-symmetry point proportional to the square root of the mean-square displacement of the atoms due to thermal fluctuations (70). In this scenario, $\alpha$ is expected to increase with temperature as $T^{\frac{1}{2}}$. A corresponding guide to the eye is shown as a black line in Fig. 5C and is consistent with our data. We also give a linear fit to $\mathrm{\Delta }E$, as the Rashba model implies $\mathrm{\Delta }E\propto {\alpha }^2\propto T$, in agreement with our data. In contrast, a negligible splitting is found in calculations which take into account only the average positions of the atoms, neglecting thermal fluctuations (96). Calculations predict thermally induced energy splittings in the conduction band of 30–100 meV at room temperature (14, 15, 70), similar to the $\mathrm{\Delta }E=110$ meV found in our experiment. Overall, our results give a strong experimental indication of the dynamical Rashba effect. It is worth noting that the effect should be general to materials with strong spin–orbit coupling as was pointed out in ref. 70.

Summary

We present a systematic study of the circular photogalvanic effect in (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$ single crystals. In the room-temperature tetragonal phase, we find a maximum in the circular photogalvanic effect for excitation 110 meV below the direct optical gap, indicating transitions between spin-polarized electronic bands below the direct gap. The amplitude of the effect is similar to the one observed for bulk Rashba systems (45). A change in the direction of the current associated with the circular photogalvanic effect at the orthorhombic–tetragonal phase transition demonstrates that the effect has different physical origins in the two phases. Within the tetragonal room-temperature phase, the energy splitting between the spin-polarized transition and the direct optical transition, as well as the amplitude of the circular photogalvanic effect, increases with temperature. These findings imply an increase of the Rashba parameter with temperature, giving experimental support for the predicted dynamical Rashba effect in tetragonal (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$. Indications of a bulk Rashba effect are absent in the low-temperature orthorhombic phase, and a temperature-independent circular photogalvanic effect in this phase is attributed to the reduced symmetry at the surface and interfaces. Our findings not only can explain the reported indirect–direct band gap (18) and thermally activated radiative recombination (100) in tetragonal (${\mathrm{C}\mathrm{H}}_3{\mathrm{N}\mathrm{H}}_3$)${\mathrm{P}\mathrm{b}\mathrm{I}}_3$. They also provide evidence for a spin-splitting mechanism at elevated temperatures that should be general to materials with inversion symmetry which contain heavy elements and exhibit soft phonon modes.

Materials and Methods

The crystals were prepared using the seed-solution growth method described in ref. 101 and contacted with 70 nm of gold at a spacing of 1 mm. Photocurrents were excited with a Ti:Sa laser. The excitation laser power ranged from 5 $\mathrm{\mu }$W to 40 $\mathrm{\mu }$W. Experiments were done with the laser in both continuous wave (cw) and pulsed (15-kHz repetition rate, 100-fs pulse duration) mode, giving similar results. Polarization-dependent photocurrents were recorded with zero bias voltage applied. The observed photocurrents are linear in laser power. The beam diameter was varied between 50 $\mathrm{\mu }$m and 1 mm. Generally, defocusing the beam results in higher photocurrents per laser power by roughly one order of magnitude, which we attribute to the generation of electron–hole pairs closer to the contacts. Photoconductivity is measured by sweeping the voltage and analyzing the resulting change in the current. Photoluminescence spectra were recorded within the same setup, using 532 nm cw excitation. Additional details of the sample growth, photoconductivity, and photoluminescence experiments are given in SI Appendix, section 1.