Defect engineering using crystal symmetry

Defects in solids can be broadly classified based on their dimensionality (1). Zero-dimensional defects (point defects) arise as a consequence of entropy considerations (configurational entropy) and thus are thermodynamically required in any material. One-dimensional defects such as dislocations are not required by thermodynamics but arise anyway as a consequence of imperfections in the synthetic environment or due to structural constraints imposed by applied stresses from a variety of sources. Dislocations arise as a consequence of stresses imposed through thermal history, processing, or structural mismatch, as in the case of heteroepitaxial thin films, which are so prevalent in modern technology. Extended defects are known to have a profound influence in achieving or impacting the desired material performance. Complex networks of dislocations are designed into alloys to enhance their mechanical properties, such as the tensile strength in steels and other technologically relevant alloys (2). In many cases, defects, such as dislocations, are harmful to the desired performance of the device (3). Volumetric defects (such as second-phase inclusions, some of which are deliberately designed into materials such as the Guinier–Preston zones in Al–Cu alloys) (4, 5) can arise as a consequence of improper processing or through deliberate materials engineering.

The characteristic length scale of such defects will depend on the physical phenomenon in question (e.g., pinning of the movement of dislocations would require second phases that are of a certain size and spacing).

We now come to 2D, surface-type defects, the designing of which is the focus of the paper by Wang et al. (6). Two-dimensional defects, such as antiphase boundaries (APBs) and domain walls in certain ferroic materials, arise primarily as a consequence of symmetry mismatch in spatial coordinates, which by themselves arise from phase transitions in materials, driven by thermodynamic fields (typically temperature, but not excluding electric, magnetic, and mechanical fields). A good example is a phase transition from a cubic structure to a tetragonal symmetry (7) (typified by the ferroelectric transition in perovskites such as BaTiO₃ and PbTiO₃) that is accompanied by the equal possibility of the tetragonal symmetry breaking occurring along the 100, 010, or 001 directions of the parent cubic phase, thus leading to three possible equivalent directions. This, combined with the fact that the polarization in the tetragonal structure can point UP/DOWN, LEFT/RIGHT, or FORWARD/BACKWARD, means that there are six possible directions for the polarization vector to point in this product tetragonal phase. Now, when one starts to pack these six “variants” in 3D space (since they arise from a 3D cubic parent phase), the final ensemble has to obey both electrostatic and elastic boundary conditions (8), with an energy Hamiltonian that contains the bulk-free energy, the elastic, electrostatic, and the gradient energy terms. The UP/DOWN domains are separated by “domain walls,” which in ferroelectric perovskites are extremely thin, of the order of a few unit cells, thus qualifying them to be considered pseudo-2D sheets. While such domain walls arise out of the finite nature of real materials, they are not required by thermodynamics, and indeed, it is possible to create materials without such “defects.”

As the term indicates, APBs are 2D defects that arise as a consequence of a structural “phase” difference between different regions of a material (9). This can happen, for example, in intermetallic alloys, such as Ni₃Al, in which the Ni and Al atoms are not randomly arranged in the cubic crystal structure but instead are ordered into specific crystallographic sites. Such an ordered arrangement arises naturally as a consequence of the electronic structure and the radius of the two atoms. It is therefore possible to create a 3D material where this ordered arrangement is not in-phase everywhere but instead goes out of phase. This leads to the formation of APBs. While such APBs are primarily evidenced in ordered alloys in metallic systems, in inorganic materials the naturally ordered arrangement of cations and anions (e.g., in NaCl) means that there is a strong prevalence for the formation of APBs in them.

In synthetic materials, such as artificially engineered heterostructures, APBs arise as a direct consequence of a change in symmetry between the underlying substrate and the overlaying thin film. The work of Wang et al. (6) is focused on creating controllable distributions of APBs using such an approach. Wang et al. demonstrate a strategy to design APBs into oxide heterostructures using the symmetry mismatch approach. Three dramatic developments over the past 5–10 y enable such exquisite control of atom placement as well as understanding of their physical properties. The first among them is the ability to synthesize materials with atomic-scale perfection, using techniques such as molecular beam epitaxy (10). This approach, which was originally pioneered for the compound semiconductor world and led to the demonstration of materials with essentially perfect physical properties (e.g., GaAs/AlGaAs heterostructures with mobilities approaching 50 million and the concomitant demonstration of quantum phenomena), has now translated into oxides and other inorganic systems. The second of the dramatic developments is the emergence of aberration-corrected electron microscopy as a pathway to image the atomic structure of materials, thus rivaling scanning tunneling microscopy in the ability to fathom the inner workings of materials at the most intimate level. The third dramatic development has been on the theoretical side, with the emergence of powerful theoretical techniques combined with equally powerful computing machines to routinely predict the properties of materials, not only in their bulk but also at such interfaces.

Armed with this three-pronged tool, Wang et al. (6) demonstrate an approach to create APBs via the combination of advanced growth, atomic-resolved electron microscopy, first-principles calculations, and defect theory. Their driving principle is to use a structural symmetry mismatch between the perovskite La_2/3Sr_1/3MnO₃ that is grown as a thin layer on a layered perovskite, Sr₂RuO₄ substrate, in which APBs in the film naturally nucleate at the step on the substrate/film interface. For a single step, the generated APBs tend to be nearly perpendicular to the interface and propagate toward film surface. They then demonstrate the formation of arrays of such APBs, driven by the pseudoperiodic array of surface steps.

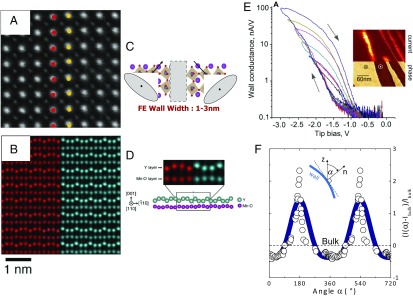
Where do we go from here? Two-dimensional interfaces, which include such APBs and domain walls as well as heterointerfaces, present a wealth of opportunities for future research to explore new physical phenomena, exemplified by the observation of electronic conduction at such atomically perfect 2D defects (Fig. 1) (11–14) in an otherwise insulating material. Can we induce metal insulator transitions at such interfaces by tuning the electronic structure precisely at such interfaces? A totally unexplored area of research is the possibility of inducing configurational changes WITHIN the interfaces: In such a scenario, the interface remains physically intact, while electronic spin, charge, and orbitals are reconstructed within the interface. Efforts are underway to demonstrate rudimentary devices such as a transistor. Of course, there are a lot of questions that remain to be answered. For example, how do we interface such 2D objects to the external world? Is the magnitude of changes that occur at such interfaces sufficient to be utilized in real applications? In the same vein, what are the limits on the changes that can occur with such interfaces?

Fig. 1.

The defect is the device: (A) An atomic-resolution scanning transmission electron microscopy (STEM) image of a 109° domain wall in the multiferroic BiFeO₃ (10). The domain wall is identified as the red–yellow stripe and is atomically sharp. C shows a schematic of the polar distortion across this wall, while E shows the electronic conduction within the wall, which has a memristive behavior (12). (B) A STEM image of an APB in the improper ferroelectric YMnO₃ (11) that also serves as a 180° domain wall; the antiphase nature of the distortion is shown in D. F shows the electronic transport within such a wall in the related improper ferroelectric, ErMnO₃ (13).

The paper of Wang et al. (6) once again highlights the immense progress that has been made in the past decade in the synthesis, probing, and theoretical understanding of such defects. The next decade will see even more dramatic advances, and one cannot wait to enable and witness them.