Striking stationarity of large-scale climate model bias patterns under strong climate change

Significance

The typical magnitude of coupled climate model biases is similar to the magnitude of the climate change that is expected on a centennial time scale. Using climate models for assessing future climate change therefore relies on the hypothesis that these biases are stationary or vary predictably. This hypothesis, however, has not been, and cannot be, tested directly. We compare the biases of individual models with respect to a multimodel mean for two very different climate states. Our comparison shows that under very large climate change the bias patterns of key climate variables do not change substantially. This provides a justification for using state-of-the-art climate models to simulate climate change and allows extending the range of climate model applications.

Abstract

Because all climate models exhibit biases, their use for assessing future climate change requires implicitly assuming or explicitly postulating that the biases are stationary or vary predictably. This hypothesis, however, has not been, and cannot be, tested directly. This work shows that under very large climate change the bias patterns of key climate variables exhibit a striking degree of stationarity. Using only correlation with a model’s preindustrial bias pattern, a model’s 4xCO₂ bias pattern is objectively and correctly identified among a large model ensemble in almost all cases. This outcome would be exceedingly improbable if bias patterns were independent of climate state. A similar result is also found for bias patterns in two historical periods. This provides compelling and heretofore missing justification for using such models to quantify climate perturbation patterns and for selecting well-performing models for regional downscaling. Furthermore, it opens the way to extending bias corrections to perturbed states, substantially broadening the range of justified applications of climate models.

Future climate projections are based on numerical simulations from global climate models that are grounded in first principles but exhibit well-documented biases in their simulation of the current climate state (1, 2), thus raising questions about their fitness for climate projections. A large body of work has assessed model biases in the context of prioritizing models for climate projections, high-resolution downscaling, and impact assessment. Such studies either implicitly assume (3–6) or explicitly postulate (7) that biases are stationary, that is, that a model’s errors should be very similar in the different climate states being examined, or that they are reproducibly linked to the state of the climate (8). However, this fundamental hypothesis has not been, and cannot be, tested directly for the obvious reason that the future climate has not been realized yet (2, 8–11). Limited stationarity of climate model biases, in particular of limited-area models, has been shown on regional scales for surface temperature and precipitation (8, 12, 13), which are certainly the most widely used climate parameters in downscaling applications for climate change impact studies. However, a global, broader assessment extending to large-scale circulation characteristics is lacking.

“Perfect model” or “pseudo-reality” experiments (e.g., ref. 14) can, in the absence of existing future climate data, provide a means of evaluating individual climate model projections or forecasts against another projection or forecast. In this case, the latter are taken as a surrogate for reality, against which perturbed model runs or other methods can be evaluated (15).

In this work, we apply a similar approach to climate model projections on the centennial time scale to test the fundamental hypothesis of climate model bias stationarity against a pseudo-reality in a coordinated CMIP5 multimodel climate change experiment. For a large set of variables that characterize tropospheric circulation, energy and water cycle (n_v = 15), we identify biases of a number of individual models (n_m = 18) against a common reference (the multimodel mean) for the preindustrial climate experiment and carry out an objective test in which, for a given variable, each model’s preindustrial bias map is compared with all models’ corresponding bias maps from the 4xCO₂ experiment. We use area-weighted pattern correlations between error maps for the two selected experiments [preindustrial control (piControl) and abrupt fourfold CO₂ concentration increase (abrupt4xCO₂)] as a metric to measure bias pattern similarity. The n_m correlation coefficients r_v,i,j for a given variable v, a given model i, and all models j ∈ {1,…,n_m} are then ranked. As there are n_v = 15 variables and n_m = 18 models, we have n_e = n_v × n_m = 270 error maps for each period, and thus n_e rankings of n_m correlations. These n_e rankings can be seen as individual, but not necessarily independent, tests of bias stationarity. If climate model bias patterns are stationary, then, among the n_m 4xCO₂ bias maps with which the preindustrial bias map of the tested model is compared, the 4xCO₂ bias of the tested model itself should in most of the cases be the one that exhibits the strongest similarity. In the following, we show that this is indeed the case to a very high extent. This provides strong support for the bias pattern stationarity hypothesis that is so crucial for the use of climate change projections.

Details on the methods used, on the selection of models, variables and experiments, and on the choice of the multimodel mean as the reference pseudo-reality are given in Methods.

Results

Bias Stationarity Under Strong Climate Change: 4xCO₂ Versus Preindustrial Climate.

In the vast majority of cases (260 out of the n_e = 270), the bias correlation coefficient r_v,i,j between the preindustrial bias map of a given model i and the 4xCO₂ bias map of any model j ∈ {1,…,n_m} is highest for i = j. That is, the abrupt4xCO₂ error pattern that most closely resembles the piControl error pattern for a given model and variable is usually the abrupt4xCO₂ error pattern of that same given model.

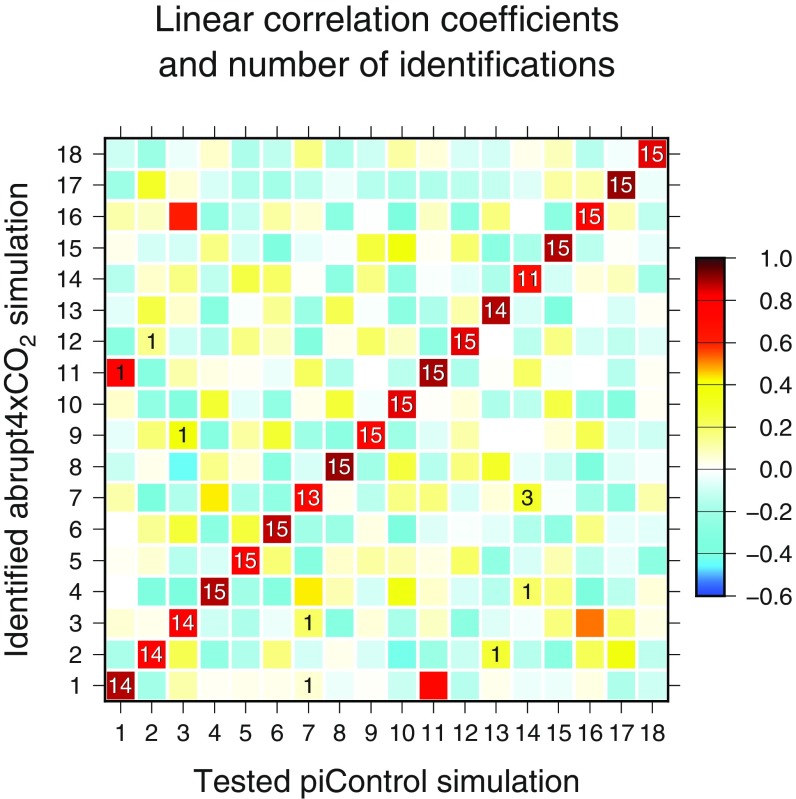
The n_m × n_m × n_v correlation coefficients r_v,i,j can be averaged over the n_v variables for each pair i,j of models, yielding n_m × n_m average correlation coefficients R_i,j. These are displayed in Fig. 1. Clearly, these average correlation coefficients tend to be highest for the diagonal elements R_i,i, with values above 0.8 in the majority of cases, and they tend to be weak (usually |r| < 0.3) for the nondiagonal elements R_{i,j ≠ i}. Because we have n_v variables, any two models i,j can be paired between 0 and n_v times, based on the ranking of their correlation coefficient r_v,i,j for a given variable and model i. This number of objective identifications of the abrupt4xCO₂ bias of model i with the piControl bias of model j, A_i,j, is also displayed in Fig. 1. For 12 models, all abrupt4xCO₂ bias maps are identified correctly (A_i,j = n_v = 15); for four models, one bias map out of 15 is identified incorrectly (A_i,j = 14); for one model, two bias maps are identified incorrectly (A_i,j = 13); and for one model (7), identification with its own piControl bias is unsuccessful for four of the 15 variables (A_i,j = 11). In total, identification of a given abrupt4xCO₂ bias pattern with the same model’s piControl bias pattern occurs therefore in 260 out of the n_e = 270 rankings; if piControl and abrupt4xCO2 biases were independent, one would expect only 15 correct identifications because the probability of correct identification for each individual test is 1/18. In a Poisson distribution, the cumulative probability of at least 260 correct identifications out of 270, given an average random success rate of 15, is vanishingly low (far below 10⁻²⁰⁰, as an upper estimate using the Chernoff bound indicates: $\text{P}\left(\text{X}\ge \text{x}\right)\le \left({\text{e}}^{-\mathrm{\lambda }}{\left(\text{e}\mathrm{\lambda }\right)}^{\text{x}}\right)/{\text{x}}^{\text{x}}\approx 2\cdot {10}^{-216}$, with x = 260 and λ = 15). We can therefore reject with extreme confidence the null hypothesis that piControl and abrupt4xCO2 biases are independent. Of course, it does not come as a surprise that piControl and abrupt4xCO2 biases are not independent; however, the exceedingly high proportion of correct identifications is a very meaningful and hence unrecognized result.

Fig. 1.

Average linear correlation coefficients R_i,j (colored squares) across all variables and number of identifications A_i,j (numbers printed on squares, not printed for A_i,j = 0) for each tested piControl/identified abrupt4xCO₂ simulation pair. Models used are as follows: 1, ACCESS1-0; 2, BNU-ESM; 3, CCSM4; 4, CNRM-CM5; 5, CSIRO-Mk3-6-0; 6, CanESM2; 7, EC-EARTH; 8, FGOALS-g2; 9, GFDL-CM3; 10, GISS-E2-H; 11, HadGEM2-ES; 12, IPSL-CM5A-LR; 13, MIROC-ESM; 14, MPI-ESM-LR; 15, MRI-CGCM3; 16, NorESM1-M; 17, bcc-csm1-1; and 18, inmcm4.

A comparison of the piControl and abrupt4xCO₂ bias maps clearly illustrates this strong similarity. The individual models’ 850-hPa temperature (T₈₅₀) error patterns for the piControl (Fig. 2A) and the abrupt4xCO₂ simulations (Fig. 2B) bear close resemblance on global to regional scales. Even if the models in the two parts of the figure were randomly shuffled, it would be easy to identify the corresponding pairs by eye because of the strong stationarity of the bias patterns. This is also the case for the other variables (SI Appendix, Figs. S1–S14). Furthermore, the comparison between these two parts of the figure shows that the magnitude of the model errors does not change much between the two periods.

Fig. 2.

T₈₅₀ error patterns (degrees celsius) with respect to the ensemble mean for the individual models. (A) piControl; (B) abrupt4xCO₂. The color scale is the same for all models and both experiments. Models are ordered from left to right and from top to bottom (model 1 at the top left, model 6 at the top right, and model 18 at the bottom right; model numbers are as in Fig. 1).

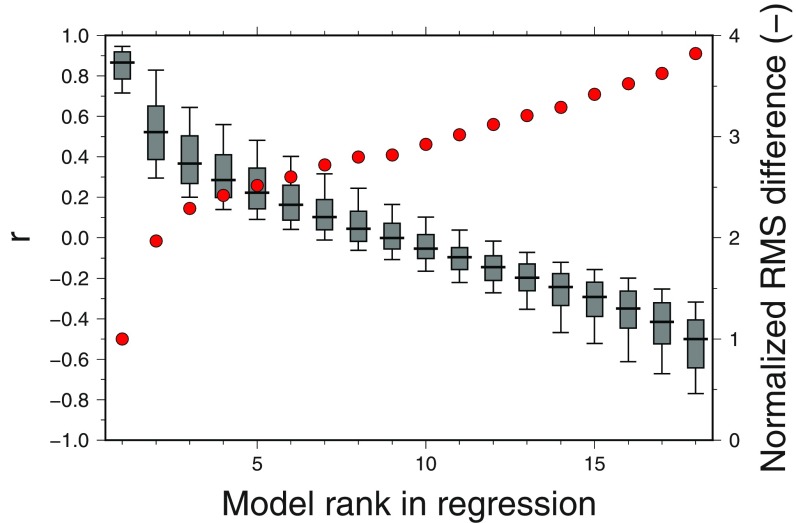
The spatial correlation between the abrupt4xCO₂ and piControl biases is naturally linked to the rms of the difference between these biases, as shown in Fig. 3 for the average rankings across all 15 variables. The correlation coefficient for the model ranked first (which, in 260 out of 270 cases, is the tested model itself) is typically much higher than for the other models (median 0.87, while the median is 0.52 for the model ranked second, and less for the models behind). The rms difference between the matched abrupt4xCO₂ and piControl biases in the same figure is on average about half the rms for the models ranked second, and less than 30% of the rms difference of the model ranked last.

Fig. 3.

Regression coefficients r between tested piControl model runs and each of the abrupt4xCO₂ model runs, in decreasing order (gray boxes and whiskers indicating the 10, 25, 50, 75, and 90% quantiles across variables; left scale). The associated mean normalized rms differences between the bias maps are shown as red circles (right scale; rms difference is normalized with respect to the rms difference of the model ranked first).

The rms of the difference between the matched abrupt4xCO₂ and piControl bias maps is on average about half the piControl bias. The average slope of the pointwise linear regression between the matched abrupt4xCO₂ and piControl bias maps tends to be slightly below 1 (between 0.7 and 0.8 for two variables, between 0.8 and 0.95 for 11 out of the 15 variables, and above 1 for only one variable). This indicates that pattern-scaled model outputs tend to slightly converge toward the multimodel mean under strong warming. A possible reason for this behavior might be that snow and ice cover is strongly reduced in the 4xCO₂ equilibrium climate, limiting the effect of strong intermodel variations in the snow and ice albedo feedback (16–18).

These results clearly show that under two very different climates the bias patterns of an individual model with respect to the multimodel ensemble mean are very similar. In CMIP-type model intercomparisons, the actual number of truly independent climate models is lower than the number of participating models because several share a common development history (19, 20). Although we only selected one model from each modeling center (Methods), our ensemble still contains such cases. Indeed, most of the rare misidentifications of bias patterns tend to occur between models that share a common development history, such as models 1 (ACCESS-1-0) and 11 (HadGEM2-ES), and similarly 7 (EC-EARTH) and 14 (MPI-ESM-LR). Such cases might have been prevented by identifying model similarity based on their output (e.g., refs. 21 and 22) instead of simply choosing only one model from each modeling center. However, this would have complicated the procedure here without adding much to the point. In any case, this further supports the finding that individual large-scale climate model bias patterns are highly stationary under climate change.

Bias Stationarity over the 20th Century.

In addition to being stationary under substantial climate change, climate model biases are also stable during the 20th century. We calculated the model biases for 1976–2005 and 1901–1930 with respect to ERA-20C (23) instead of the multimodel mean. In this case, identification of 1976–2005 biases with 1901–1930 biases is correct in 257 out of 270 cases. Most (10) of the 13 incorrect identifications in this case are due to a known spurious Southern Hemisphere extratropical sea-level pressure trend in ERA-20C during the early 20th century (23, 24). This trend leads to erroneous identification of several models’ late-20th-century sea-level pressure and 500-hPa geopotential height bias maps with the early-20th-century bias map of the GISS-E2-H model, which happens to be the only CMIP5 model that exhibits a spatiotemporal pattern of sea-level pressure change similar to the ERA-20C reanalyses. There is thus no systematic drift in the climate model biases with respect to the 20th-century reanalysis, except for the sea-level field, and in this case the drift is due to reanalysis problems. This provides confidence in the conclusion that the bias stationarity in future climate change found here is not an apparent stationarity due to a systematic bias drift common to all models.

Discussion

This analysis concerns large-scale and climatological mean tropospheric circulation, energy, and water-cycle patterns. On smaller spatial and temporal scales, the stability of bias patterns evidenced here will generally be weaker. For example, it has been shown that for hydrological climate impact studies, which concern smaller spatial and temporal scales, climate model precipitation bias stationarity is not sufficient to warrant statistical bias correction (25–27). Similarly, evaluation of paleoclimate simulations suggests that on small scales the amplitude of climate change is often underestimated (28, 29). Furthermore, feedbacks related to land-surface processes have been shown to potentially skew near-surface temperature projections on regional scales in biased models (30). However, constant surface features, such as topography, can also “pin” circulation features (e.g., katabatic winds) and thus increase local stationarity of model bias patterns.

In any case, because we address different spatial and temporal scales and variables, the results presented here cannot be seen as a direct support of statistical bias corrections of climate model output, such as quantile–quantile mapping, which are frequently used in climate change impact modeling and which usually focus on precipitation and surface air temperature (e.g., refs. 31–34). However, our results provide support for in-run bias correction of atmospheric circulation models (35). This approach consists of adding seasonally and spatially varying incremental correction terms to the prognostic equations for some of the state variables of an atmospheric model (usually temperature, wind, and humidity). These spatially and seasonally varying correction terms are propotional to the biases of these variables, but of opposite sign. We have shown here that biases of this type of atmospheric variables are stationary on the relevant spatial and temporal scales. Therefore, this bias correction method should be transferable to a different climate. Output from atmospheric circulation models that are bias-corrected using this method can then be used for impact modeling, or as an input for regional models for downscaling (which can then be used to drive impact models).

It is often argued that a biased representation of the present climate strongly reduces the credibility of projected future climate change, because it could indicate that there are fundamental flaws in climate models. Here we have shown that the climate model bias patterns are highly stationary under two climate-change regimes that have very different amplitudes of change and different combinations of forcings. This increases confidence in the basic capability of current-generation climate models to correctly simulate the climate response to a range of different drivers.

Climate models share common parameterizations, components, and, more largely, concepts. This is in particular true for climate models that share a common development history (e.g., refs. 19 and 20), but the fundamental concepts underlying the construction of climate models (e.g., which basic processes are to be represented, which ones are explicitly resolved or parameterized, etc.) are common to most, if not all, models. One might suspect that the stationarity of the climate model bias patterns shown here could be due to these structural similarities shared by all climate models, which could have led to strong similarities in the projected climate change signals. However, not all aspects of projected future climate change are robust across the CMIP5 ensemble. For example, even the sign of projected precipitation changes is uncertain in some regions (4), and yet precipitation biases as calculated here against the multimodel ensemble (SI Appendix, Fig. S2) are highly stationary. Therefore, the fundamental reason for the stationarity of the bias patterns does not seem to be that there are structural similarities among the models that could lead to quasi-identical climate change projections, but rather that there are structural dissimilarities that lead to stable intermodel differences and biases in a large range of climates.

Conclusion

In summary, the use of current-generation coupled models for projections of climate change on centennial time scales is based on the fundamental but yet unproven hypothesis that, although current climate model biases are of the same order of magnitude as the expected climate change itself (2), the simulated climate change signal as such is largely credible (34, 36). The results presented here provide altogether clear evidence for a strong and consistent stationarity of a wide range of large-scale mean tropospheric circulation, energy, and water-cycle climate model bias patterns under substantial climate change. This is a compelling and as-yet-missing justification for using current-generation coupled climate models for climate change projections. As a whole, our results open prospects for the use of climate models for improved climate projections that have until now been hampered by the uncertainties induced by inevitable biases in the representation of the present climate. In particular, our results suggest that it should be possible to empirically correct large-scale circulation errors in climate models at run time based on identification of present-day model errors with respect to observations (35, 37). These corrected global simulations could then be used as “perfect” lateral boundary conditions for limited-area, high-resolution regional climate models. However, efforts to increase the realism of climate models through improved parameterizations, higher spatial resolution, and judicious tuning (38) remain timely.

Methods

We use the last 30 y of the first ensemble members of the piControl and years 121–150 of the abrupt4xCO₂ simulation from the CMIP5 database, accessed on October 18, 2016. The global, annual mean surface air temperature difference between these two simulations varies between 3.1 and 6.3 °C for the selected models (discussed below), representing a very strong climate change signal. For these two simulations, we extracted 15 annual mean variables: precipitation rate; sea-level pressure; surface air temperature; total column water vapor; 850-, 700-, and 300-hPa air temperature; zonal mean air temperature; 850- and 200-hPa zonal and meridional wind; zonal mean zonal and meridional wind; and 500-hPa geopotential height. These variables were interpolated onto a common T42 grid. Variables that have a vertical dimension (zonal mean wind and temperature) were extracted on 17 standard pressure levels between 10 and 1,000 hPa.

These variables were available for 30 CMIP5 models. Because different versions of the same model from a given modeling center tend to share many common biases, we defined a reduced ensemble consisting of only one model version from each modeling center participating in CMIP5. This reduced ensemble consists of 18 models (see Fig. 1 legend) and is referred to as E18.

For each experiment (piControl and abrupt4xCO₂), model, and variable, we calculated the 30-y mean error with respect to the ensemble mean. For all variables except the precipitation rate p and total column water vapor v, this error is simply defined as the difference from the ensemble mean; for p and v, the error is defined via the ratio of the precipitation rate p (and total column water vapor v, respectively) of the model and the ensemble mean, that is, log(p_i/p_E18) and log(v_i/v_E18), respectively, with i indicating an individual model and E18 the multimodel ensemble mean.

While systematic biases, shared by a majority of climate models, do exist, it has been shown that the “mean model,” defined as the average output of the different models participating in CMIP-type intercomparisons, tends to exhibit weaker large-scale biases than most, if not all, models taken individually (1, 2, 39–41) and is therefore seen as the best representation of the real climate system; note that in a pseudo-reality experiment the model used as surrogate reality actually does not need to be the model that is assessed as the “best” model against some standard. Because of the large number of models (n_m = 18), the multimodel mean can be seen as virtually independent of any single model for practical purposes in the sense that an individual model will not substantially influence the multimodel mean. We carried out tests excluding the tested model from the multimodel mean; these tests yielded results very similar to those reported here.

Concentrating on bias patterns, we pattern-scaled (42, 43) the abrupt4xCO₂ model outputs, normalizing the global mean surface air temperature change with respect to the piControl value to 5 °C. This eliminates the influence of intermodel differences in climate sensitivity. The scaling with respect to a normalized global mean surface air temperature change has no effect on the correlation coefficients.

For each variable and model, the error map obtained for the piControl simulation is compared with all models’ error maps calculated for the abrupt4xCO₂ simulations for the same variable.