Linking economic growth pathways and environmental sustainability by understanding development as alternate social–ecological regimes

Significance

Our analysis shows that there are two distinct groups of national economies, roughly equating to developed and less developed countries. The economies of countries in each group are pushed toward two different equilibrium points by differences in the feedbacks between natural resource consumption, population growth, and gross domestic product. Both equilibrium points are unsustainable under population growth. The inertia that is generated by resource dependence means that extensive structural change in the economic system is required to achieve sustainable use of natural resources; it is not possible to “develop to sustainability,” and many developed countries have simply externalized costs. Our results have profound implications for aid programs, human wellbeing, and development goals.

Abstract

Scientists understand how global ecological degradation is occurring but not why it seems to be so difficult to reverse. We used national-level data and a mathematical model to provide an empirical test of the hypothesis that national economies display two distinct economic regimes that are maintained by self-reinforcing feedbacks between natural resources and society. Our results not only support previous findings that two distinct groups exist, but also show that countries move toward one of these two different equilibrium points because of their different patterns of natural resource use and responses to population growth. At the less economically developed equilibrium point maintained by “green-loop” feedbacks, human populations depend more directly on ecosystems for income. At the more economically developed equilibrium point maintained by “red-loop” feedbacks, nonecosystem services (e.g., technology, manufacturing, services) generate the majority of national gross domestic product (GDP), but increasing consumption of natural resources means that environmental impacts are higher and are often exported (via cross-scale feedbacks) to other countries. Feedbacks between income and population growth are pushing countries farther from sustainability. Our analysis shows that economic growth alone cannot lead to environmental sustainability and that current trajectories of resource use cannot be sustained without breaking feedback loops in national and international economies.

One of the most important contributions made by science to society in the last 20 y has been to show that people are changing the earth’s environment at a global scale. Research on our proximity to planetary boundaries (1, 2) suggests that we are already overexploiting (or close to overexploiting) many of the earth’s resources and documents rapid, worrying declines in diversity and ecosystem function around the world (3). This research identifies a looming crisis, but it does not explain why it seems to be so difficult to reduce exploitation and to push social, economic, and ecological systems toward global sustainability. As the consequences of global ecological change for people and ecosystems become clearer, political responses seem increasingly inadequate to escape an unsustainable pattern of resource consumption. Despite an urgent need to understand and manage the impacts of human population growth and resource use on ecosystems, the complex feedbacks between economic development, biodiversity, ecosystem services, and human wellbeing remain poorly understood and neglected in much political decision making.

Economic theories of development, following neoclassical equilibrium theories (4, 5), regard labor, capital, and technology as the foundations of growth (6–8). New growth theory adds consideration of increasing returns to knowledge as a key determinant of growth and highlights the importance of path dependency and the institutional environment for the creation, dissemination, and accumulation of knowledge (9). While the relevance of exhaustible or slowly regenerating resources for economic growth has been recognized for decades (10–13), standard theories of economic growth (14) ignore the waste products or by-products of resource use that might negatively affect human quality of life and future development potential (15). The study of economic growth remains primarily motivated by the desire to understand differences among countries and thus, to develop policies that can help individual countries achieve sustained growth and higher standards of living. This focus has deflected attention from the fact that, in a finite world with shared and globally interlinked ecosystems and in which the effects of economic activity on the environment are projected by trade across borders, national economic growth scales up to a global level at which its environmental consequences can threaten its sustainability. It is obvious that economic development can improve the quality of human life, but from an environmental perspective, it is critical to determine whether and how economic development can be made compatible with ecological sustainability. Human societies have succeeded in establishing some institutions that regulate the sustainable use of common resources (16, 17), but with a few exceptions (18), these are restricted to well-defined local resources. At the broader regional and global levels, phenomena such as collapses of fish stocks, loss of charismatic megafauna, and global climate change provide evidence of humankind’s apparent inability to care adequately for the environment.

It is well known that national economies can go through relatively fast structural transitions, during which there are fundamental shifts in the relative importance of built vs. natural infrastructure (i.e., ecosystem and nonecosystem services) (19–22), and that national economies have the potential to exist in alternate states [for example, with either high or low resource use (23–25)]. Recent work on development trajectories and economic growth focuses on “growth clubs” and the initial conditions and feedback loops that determine whether and when economies make the transition from stagnation to growth (26, 27). Here, we focus on a more ecological interpretation, the red loop–green loop (RL-GL) model (28), of the same phenomena.

Testing the RL-GL Model

The RL-GL model (28) proposes that as human populations grow, they follow one of two fundamentally different trajectories. The first trajectory, the red loop, occurs when economies industrialize and urbanize. When entering the red loop, the dominant drivers of social–ecological interactions shift from ecosystem-based production (and a strong, direct reliance on local ecosystem services) to nonecosystem-based production, an increasing demand for nonecosystem services, and spatial upscaling of resource use due to increased reliance on nonlocal ecosystem services. As shown by Cumming et al. (28), these trends are clearly visible in national-level data for industrialized countries (e.g., Sweden, Germany), many of which show constancy or declines in the numbers of workers in the agricultural sector; steep increases in employment in manufacturing and services; and continued increases in imports of food, wood, and other natural resources. All countries with highly developed economies, defined by a Human Development Index (HDI) class of one, fall into the red loop. In HDI1 countries, on average, 23% of the population is rural, and the number of rural inhabitants is declining by 0.6% per year.

The second trajectory, the green loop, occurs when the economies of countries with growing populations remain directly reliant on ecosystem goods. This situation is typical of nations in which a majority of people depend directly on natural resources (e.g., agriculture, forests, or fishing). Increasing populations and traditional cultural practices (e.g., inherited land is divided between surviving children) often lead to reduced per capita resource availability, and typical wealth-generating red-loop industries (e.g., manufacturing, service provision) remain stagnant in a less productive economy. Data presented later in the paper suggest that all countries in the lowest category of economic development, defined by an HDI class of four, fall into the green loop. In stark contrast to HDI1 nations, the average share of the rural population in HDI4 countries is 63%, and the number of rural inhabitants is growing by 1.6% per year. Countries in the two intermediate classes (HDI2 or HDI3) are harder to classify; however, in general, countries with an HDI of three are more likely to be in a red loop, while those with an HDI class of two are more likely to be in a green loop. Some additional complexity arises in the middle levels of HDI values due to the influence of geological resources, such as oil, that can create wealth without changing reliance on ecosystems.

The red and green loops represent a continuum in their early stages, but they gradually intensify and differentiate. They have different consequences for human wellbeing and offer different but interconnected pathways to ecological degradation, particularly as the drivers of economic demand increase in scale (Fig. 1). In theory, understanding and quantifying the mechanisms that lock countries into particular social–ecological regimes should lead to a stronger understanding of social–ecological transitions and the identification of alternative developmental pathways for both people and ecosystems. The nature of the developmental pathway that a nation follows and the likelihood that it tends toward a given social–ecological attractor also have consequences for intervention efforts, such as the provision of aid and the transferability of models for biodiversity conservation. Approaches that are effective in nations with HDIs of one or two are not necessarily suitable for nations that currently have HDIs of three or four.

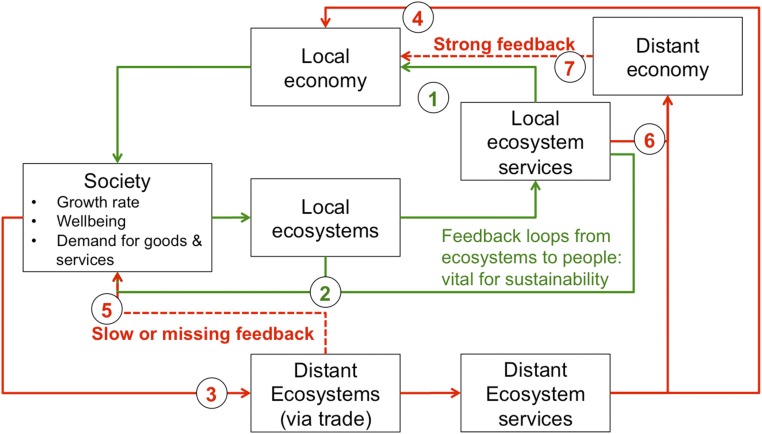
Fig. 1.

Illustration of key cross-scale relationships in the interactions between the green loop (green arrows) and the red loop (red arrows). A society that obtains ecosystem goods and services from local ecosystems (1) can directly monitor overharvesting and supply-side feedbacks (2) and develop local institutions to regulate ecosystem exploitation. A society that obtains most of its natural resources through trade (3) is locally aware of the economic impacts of trade (4) but not the ecological impacts (5) because of their remoteness. A society that primarily provides raw materials to others (6) may experience high economic pressure to harvest resources unsustainably (7).

Like many models that suggest the existence of alternate states, the RL-GL model has not been rigorously confronted with data [although its conceptual utility has been shown through application (29)]. We provide a quantitative test of the RL-GL model (and by extension, its antecedents) by confronting three central hypotheses (Table 1) with country-level data from 142 different countries. In doing so, we extend the RL-GL model from its original focus on urbanization to a more general environmental model of alternative pathways for socioeconomic development and their impacts on ecosystems.

Table 1.

The three hypotheses addressed in this analysis

Hypothesis or prediction	Test and inference
Hypothesis 1: The RL-GL model predicts not only that we should observe bimodality in economies, as shown by Vollmer et al. (26) for per capita GDP, but that the cause of bimodality (i.e., the existence of alternate attractors for development under growth) is a difference in the socioeconomic role of ecosystem services relative to nonecosystem services. As a result, population growth has different economic consequences in red-loop compared with green-loop countries.	Test for differences in the responses of HDI1 and HDI4 economies to population growth. Specifically, is there evidence for differences in natural resource use, and does the GDP–HDI relationship have a different slope or form between these two groups?
	Statistically indistinguishable responses refute hypothesis 1; contrasting forms or curve slopes with different signs support it.
Hypothesis 2: The RL-GL model predicts that red-loop countries will have disproportionately large impacts outside their boundaries, because they have externalized their dependence on ecosystems.	Test for differential impacts internally and externally, again comparing HDI1 and HDI4 countries.
	Evidence of upscaling (lower internal rents from ecosystems, greater overall consumption and/or external impacts) by HDI1 countries supports hypothesis 2; lower per capita consumption or lower ecosystem-derived rents in HDI1 countries would refute it.
Hypothesis 3: The RL-GL model predicts that feedback loops maintain two genuinely different attractors for red-loop and green-loop countries. This would mean that, under all scenarios of population growth, the economies and HDI values of countries that are caught in a particular basin of attraction will tend toward different equilibrium points rather than toward the same single point.	Model the two feedback loops (i.e., for HDI1 and HDI4 countries) between population growth, per capita GDP, and HDI as an autonomous differential equation (i.e., one that does not explicitly depend on the independent variable), in which HDI also influences population growth. Identify the number and nature of stable equilibrium points.
	Evidence of zero or one stable equilibrium point refutes hypothesis 3; evidence of two (or more) stable equilibria supports it.

Rather than referring to countries as “developed” or “undeveloped,” we use the four classes of the UNDP HDI throughout this paper. HDI1 countries score the highest on the HDI, and HDI4 countries score the lowest.

Results

Bimodality in HDI Data.

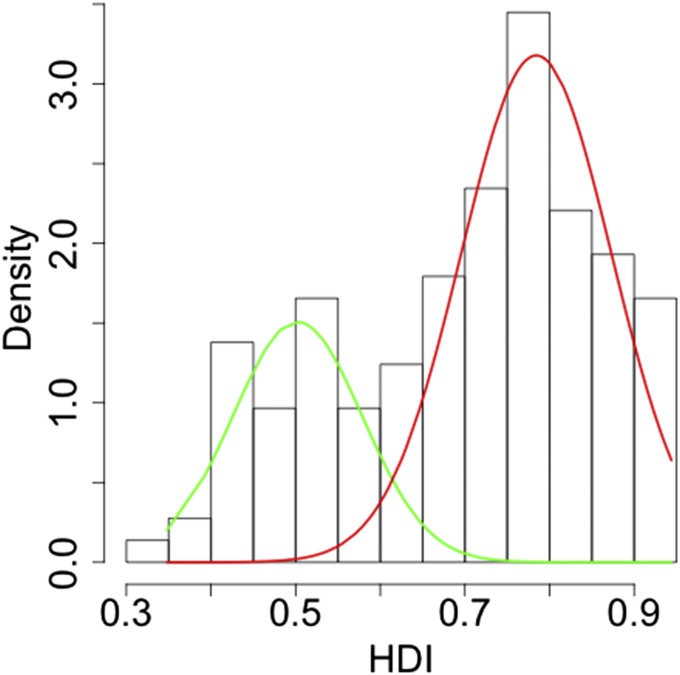
The HDI was not normally distributed across all countries (Shapiro–Wilks W = 0.95, P < 0.0001). We rejected the hypothesis of unimodality and fitted Gaussian mixed models for two and three modes. The Bayesian Information Criterion (BIC) values for these models were 134.8 and 119.9, respectively. A Kolmogorov–Smirnoff test on the two-curve model indicated a significant fit to the data (D = 0.038, P = 0.98, log likelihood 79.84). The fit of a three-curve model was poorer, and the null hypothesis could not be rejected (D = 0.83, P < 0.0001), supporting the presence of two populations within the HDI data (Fig. 2).

Fig. 2.

Density curves for the best-fit Gaussian mixed model for the HDI dataset show the presence of two different populations or clubs. The first (green) curve has a mean of 0.50 ± SD 0.07 and lambda = 0.29; the second (red) curve has a mean = 0.78 ± SD 0.09 and lambda = 0.71.

Differential Response to Growth.

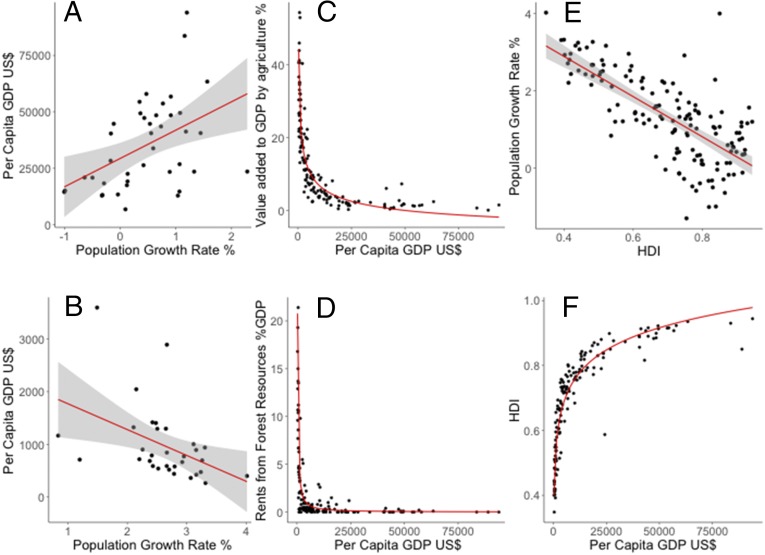
The slopes of the regressions for the two different HDI classes had different signs (Fig. 3). For HDI1 countries, there was a positive per capita gross domestic product (GDP) response to population growth (F = 9.7, df = 40, r² = 0.24, P < 0.001), while for HDI4 countries, this response was negative (F = 7, df = 30, r² = 0.19, P < 0.013). Nonlinear curves gave only minor improvements in fit, and we thus retained a linear regression.

Fig. 3.

Central relationships in understanding how alternate economic attractors arise in national economies. Red lines are fitted by regression, and gray shading shows the SE of the regression estimate; pairs of related figures are presented vertical to each other. They show the following information. Per capita GDP against population growth for (A) HDI1 and (B) HDI4 countries. The HDI1 countries seem to convert higher population growth rates into higher incomes, while the HDI4 countries seem to convert higher population growth rates into increased poverty. The contribution made to GDP by (C) agriculture and (D) rents from forest resources for all 145 countries in the analysis. (E) Population growth against the 2014 HDI for all countries in the dataset and (F) the relationship of HDI to per capita GDP.

Impacts Inside and Outside Geographical Boundaries.

Dependence on the environment is reflected by both the absolute and the relative contributions of agriculture and forestry to GDP. Although the total economic value of agricultural or forestry output may be higher in HDI1 countries than in HDI4 countries, the proportional contributions of agriculture and forestry to GDP are much lower in HDI1 countries (Fig. 3). These data show that, on average, people in HDI1 countries depend on local natural resources for a much smaller proportion of their income than people in HDI4 countries.

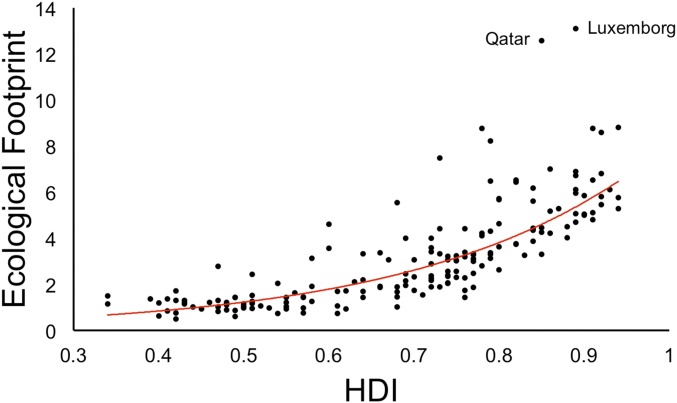
When both internal and external natural resources are considered, countries with higher HDI values also have larger ecological footprints, measured as per capita use of agricultural and grazing land (Fig. 4) (r² = 0.72, P < 0.000). There is also a significant negative correlation between the proportion of a country’s area used for agriculture and its HDI (Pearson’s r = −0.21, df = 143, P < 0.009). Since their local impacts are proportionally lower than those of HDI4 countries but their total impacts are higher, HDI1 countries must meet a higher proportion of their higher demands by importing natural resources from HDI4 countries (upscaling).

Fig. 4.

Per capita ecological footprint against HDI in 2103 for 175 countries in the EFN’s database. The ecological footprint is measured as per capita use of agricultural and grazing land both domestic and abroad.

Stable Equilibria in the Feedback Loop from Population Growth to Development.

Countries in higher HDI categories display lower population growth rates than countries in lower HDI categories (Fig. 3) (r² = 0.52, F = 151, df = 140, P < 0.00001). In addition, comparison across countries suggests that increases in GDP are associated with positive but diminishing increases in HDI (Fig. 3). For our empirically derived parameters, a model of these feedbacks has stable solutions at population growth rates of 0.4 (HDI1 countries) and 2.1 (HDI4). The HDI values associated with these two equilibrium points are 0.91 and 0.47, respectively. For HDI1 countries, 0.91 is higher than the current mean (0.78); for HDI4 countries, 0.47 is lower than the current mean HDI4 value (0.5). Bootstrap analysis of parameter uncertainty gave a mean of 0.42 ± SD 0.48 for stable population growth rates in HDI1 countries and a mean of 2.1 ± SD 0.54 for stable population growth rates in HDI4 countries. These equate to a range of equilibrium HDI values from 0.78 to 0.97 (HDI1 countries) and from 0.45 to 0.65 (HDI4 countries). Importantly, the lower and upper bounds of these HDI projections for HDI1 and HDI4 countries, respectively, do not overlap, supporting the existence of two separate equilibrium points or stable states (rather than a potential continuum of HDI values) and the likely perpetuation of two distinct growth clubs.

Discussion

We found strong empirical support for our initial hypotheses and hence, for the RL-GL model. Our results show that two distinct feedback loops between societies and natural resources are capable of causing the bimodality that has been previously described only as a pattern in distributions of per capita GDP across countries. The appearance of ecologically dissimilar outcomes between these two loops is deceptive. People in HDI1 countries have reduced their reliance on local ecosystems for income, creating an illusion of decoupling [and hence, sustainability (30)], although local ecological impacts are in many cases still high. Their high economic reliance on nonecosystem goods and services (e.g., infrastructure projects, service industries) means that population growth in these countries increases GDP, further decoupling income from local ecological change. Underpinning this “red loop,” however, is evidence that overall reliance on ecosystems has increased substantially in red-loop nations. In many cases, the environmental impacts of these activities have been exported to other countries. For example, wealthier nations eat more meat per capita, creating a wide range of knock-on environmental effects on less wealthy nations. These include increased greenhouse gas production, water use, and biodiversity loss (31).

By contrast, people in the HDI4 countries still rely heavily on local ecosystems as their primary source of income, exporting natural products (e.g., wood, fiber, crops, fish) to HDI1 countries while depending on them for manufactured goods and potentially entering a poverty trap, in which population growth reduces per capita income and leads to further reliance on ecosystems (32). These regimes are not benevolent to ecosystems; from an ecological perspective, the difference is only in the degree of upscaling and the geographic location and extent of the ecological footprint.

Our data also hint at the possible existence of a third state or growth club based on geological rather than ecological resources. Income generation by mineral extraction seems to lead to quite different relationships between people and natural resources, with several oil-producing countries (e.g., Kuwait, Oman, Lebanon) being identified as outliers during this analysis and excluded from the estimation of statistical relationships. In general, however, depending on how oil wealth translates into socioeconomic equity and internal investment, oil-producing countries seem to converge toward one of the other two models. Saudi Arabia, for example, matches HDI1 countries in its HDI and many other variables, while Equatorial Guinea is an HDI4 nation with an unusually high GDP. Several countries in the HDI2 and HDI3 groups, which we have largely excluded from this analysis, may be in the process of using resource wealth to transition from one attractor to the other. Chile, for example, depends heavily on natural resources, such as copper and agriculture, and it was removed from the official list of developing countries of the Organization for Economic Cooperation and Development’s Development Assistance Committee as of January 1, 2017 (www.oecd.org/dac/financing-sustainable-development/development-finance-standards/daclist.htm; checked March 5, 2018).

Our analysis offers three key insights. First, given current relationships between GDP, HDI, and population growth, the feedback loop between income and population growth only tends toward its equilibria in declining populations. Population growth rates at both equilibrium points (HDI1 and HDI4) are well below a typical population replacement value of ∼2.3. The relationships between GDP, HDI, and population growth thus suggest pressure toward reduced population size in both developed and developing countries. Of course, long-term population declines do not necessarily mean long-term ecological sustainability if irreversible degradation (e.g., extinction of species or loss of soil) is incurred before they are achieved.

Second, the common assumption that economic growth will eventually lead to environmental sustainability is flawed. Our analysis suggests that there is no convergence at equilibrium between the two dominant economic regimes, primarily because of (i) fundamental differences in the effects of population growth on GDP and (ii) feedbacks from economic development to population growth. Countries that are trapped in a green loop can only develop their way out of poverty through profound structural changes in the ways that they generate and use income. Also, they cannot improve wellbeing simply by regulating population growth; even at a below-replacement population growth rate of 1.15, the stable attractor is at HDI = 0.55, which closely matches the current mean value of 0.5 for nations with an HDI class of four.

Third, regardless of whether countries are able to shift from a green-loop dynamic to a red-loop dynamic, the global economic system is far from environmental sustainability. At the two estimated points of socioeconomic equilibrium, HDI1 countries have a per capita footprint of 5.15 ha (currently similar to New Zealand, 5.11; United Kingdom, 5.05; France, 5.06), and HDI4 countries have a per capita footprint of 1.48 ha (currently similar to Indonesia, 1.44; Myanmar, 1.45; Niger, 1.49). The HDI1 lifestyle is unsustainable; the HDI4 lifestyle is globally sustainable at the present time but only at a much-reduced population growth rate. The 2012 Global Ecological Footprint data indicate an average global per capita ecological footprint of 2.87 ha with a global population of 7.2 billion. If all countries were to increase their HDI to the current mean value (0.78) in the HDI1 category, predicted per capita demand would rise to 3.53 ha, which is more than double the Ecological Footprint Network’s (EFN’s) estimate of sustainability. Hypothetically, if questions of production and distribution could be resolved and assuming roughly 12 billion ha of available land globally, the world could support 3.4 billion people at 3.35 ha per person. Given the role of poorer countries as both consumers and providers of ecosystem services (presented earlier), it is unrealistic to think that a global high-development scenario would be sustainable.

Implications and Future Directions

The RL-GL model captures, in relatively simple terms, the complex social–ecological feedbacks that link ecosystems, economies, and people. For environmental scientists, recognizing that different growth clubs experience fundamentally different socioeconomic dynamics (and that the red and green loops underpinning these clubs function as attractors) has important implications for governance, for policy, and for conservation and natural resource management. Development is not a panacea for the environment. Similarly, failures in biodiversity conservation are often considered as isolated case studies rather than described or predicted from underlying theory or data (33); the RL-GL model has the potential to provide a theoretical basis for conservation interventions by predicting the key economic influences on resource management. Assumptions in forecasting and scenario planning exercises about the resilience of ecosystems and the potential for environmental feedbacks to economic development (34) will also need deeper quantitative analysis and reconsideration in light of the potential for alternative stable states.

For economists and aid agencies, our analysis highlights the need to recognize the environmental implications of the shift from a green-loop dynamic to a red-loop dynamic and the change in scale that it involves. Concerns about ecological sustainability are increasingly acknowledged in economics but seem to have little effect on development practices (35), at least at the macroeconomic level. Diamond (36) is probably the best-known proponent of the hypothesis that ecological degradation can cause socioeconomic collapse if societies become too large to cope with natural variability (the “overshoot” hypothesis). In the modern world, localized collapses resulting from overshoot and socioeconomic or ecological perturbations are frequently visible in the form of local or regional crop failures, fish stock collapses, and other reductions in ecosystem goods and services (37). These often have important economic implications (38). The adaptability of the global economy as well as trade, aid, and flows of remittances create buffers for vulnerable countries. However, the example of recently described and increasingly overwhelming impacts of climate change on coral reef ecosystems (39–41) and their potential implications for the >500 million people who depend on coral reefs for their livelihoods (42) suggest that we may soon be confronted with collapses at larger scales that challenge entire food production systems and exceed current buffering capacities.

As human societies grow, our patterns of resource use follow distinct trajectories of change. These trajectories are implicitly recognized in many research fields and invoked in models as “external drivers” or “globalization,” but too little research has connected them explicitly to conservation and natural resource use or worked through their logical consequences for ecosystems. Technological change may alter many of the relationships that we have described, but equally, socioeconomic lock in to a particular set of technologies based on fossil fuels offers a powerful example of the potential for economic development to cause disruptive environmental change. Understanding the differences between sustainable development trajectories and those that seem likely to lead to collapse is of central importance for the long-term wellbeing of our society.

Methods

Datasets and Variables.

We characterized countries as either red loop or green loop using the United Nations Development Program (UNDP) HDI data from 2014 (hdr.undp.org/en/content/human-development-index-hdi; checked July 17, 2018; at the time of analysis, the most recent available dataset). The HDI measures human socioeconomic wellbeing based on life expectancy, education, and per capita income. It correlates strongly across all countries (Pearson’s r = 0.66, t = 10.516, df = 143, P value < 2.2e-16) with the proportion of the population living in urban areas. We used the HDI in preference to the urban population (the focus of ref. 28), because the HDI offers a more widely used and accepted general measure of human socioeconomic wellbeing. It is not a personal wellbeing or happiness index but rather, a quantitative correlate of the degree to which a society fits the criteria that define the red loop (i.e., relative importance of nonecosystem goods and services).

The HDI rankings present four different categories of development: very high or HDI1 (0.8 < HDI), high or HDI2 (0.7 < HDI < 0.8), medium or HDI3 (0.55 < HDI < 0.7), and low or HDI4 (HDI < 0.55). To document general patterns and trends, many of our analyses included the entire dataset. Analyses that required explicit description of red-loop and green-loop countries used only two development categories: very high HDI corresponding conceptually to red-loop countries as explained in the Introduction and low HDI corresponding to green-loop countries. By these definitions, the data included 42 red-loop countries and 32 green-loop countries, although in a few analyses, we excluded one or two obvious outliers. We use the terms “HDI1” (highest HDI) through to “HDI4” (lowest HDI) to describe where different countries fall along the gradient suggested by the HDI.

Ecological footprint data were obtained from the Global Ecological Footprint Network (https://www.footprintnetwork.org/resources/data/; checked July 17, 2018). Data for all other variables used in the analysis were obtained from the World Bank’s World Development Indicators dataset (https://datacatalog.worldbank.org/dataset/world-development-indicators; checked July 17, 2018). To keep the total number of variables low, we used the average national population growth rate over the period 2011–2016 as a measure of population growth.

Analysis.

Testing our hypotheses included three steps: (i) testing for multimodality, (ii) quantifying and defining relationships between pairs of variables, and (iii) analysis of an autonomous differential equation of the form y′ = f(y).

We tested for multimodality using first a Shapiro–Wilks test for normality and then, both Silverman’s test and Gaussian mixed models fitted to all HDI data using the mixtools and mclust packages in R (43–45). Higher values for Silverman’s test indicate a higher likelihood that the null can be rejected; for P < 0.05, a test statistic ≥0.95 is needed (46). The test is recognized as conservative in its probability estimates, and therefore, we focused on the relative values of the statistic rather than their P values. Silverman’s tests for the number of modes gave values as follows: one mode, 0.22; two modes, 0.87; three modes, 0.64; four modes, 0.43; five modes, 0.16. Both Silverman’s test and analyses of similar data by other researchers (26) suggested that two or three modes were likely, and therefore, we used the BIC and Kolmogorov–Smirnoff test to compare alternative mixed Gaussian models with two and three modes, respectively. In the mclust implementation, higher values for the BIC indicate a better fit (in contrast to Akaike’s Information Criterion, for which lower values are better).

We quantified the relationships between variables using least squares regression estimated using the lm or nls commands in R. Outlier identification was undertaken using the residuals from fitted models and Q-Q, scale location, and leverage plots. In each case, we considered two or three alternative models, typically including at least one linear model and one nonlinear model, to determine the best-fitting curve.

We tested for a differential response to population growth by comparing the national population growth rate with per capita GDP. To remove any transitional countries (i.e., that might be moving between attractors), this analysis used only countries in the HDI1 and HDI4 categories. We also removed Kuwait and Qatar as outliers from the HDI1 dataset.

We analyzed the autonomous differential equation numerically using an iterative approach to identify stable equilibria. We initially used mean values of population growth for HDI1 countries (1.4% per year) and HDI4 countries (3.5% per year) and then tested a broader range of starting conditions to determine the stability and universality of the resulting solutions. All analyses were run in R version 1.68 (47). To quantify the uncertainty in our parameters and understand the potential impacts of uncertainty on the results, we ran a bootstrap analysis using the SEs for individual parameters. During bootstrapping, (i) the mean, (ii) the mean +1 SE, or (iii) the mean −1 SE was randomly selected 1,000 times for each parameter; and the value of y′ was calculated iteratively (i.e., updating the value of y for each successive time step) for each parameter combination until a stable population growth rate was reached. Iterations in which randomly selected parameter combinations produced negative values of per capita GDP were discarded, because the log of a negative number cannot be determined. We compared the results of the bootstrap analysis for HDI1 and HDI4 parameters to determine whether there was a clear separation between the two equilibrium points.

Fitting the Model.

If the complex relationships between GDP, HDI, and population growth remain as they currently are, we can use the statistical relationships estimated above (SI Appendix, Table S1 has parameters) to model changes in the population growth rate as an autonomous function [y′ = f(y)].

Let per capita GDP = x, population growth rate = y′, 2014 HDI = z, and the letters a–g describe parameters.

Empirically estimated equations for the relationships are as follows.

$$\mathit{x}=\mathit{a}y\prime +\mathit{c}\left(\text{GDP is a linear function of population growth}\right);$$ [1]

$$\mathit{z}=\mathit{b}\hspace{0.17em}\text{log}\left(\mathit{x}\right)+\mathit{d}\left(\text{HDI is a log function of GDP}\right);$$ [2]

$$\mathit{y}\prime =\mathit{gz}+\mathit{f}\left(\text{population growth is a linear function of HDI, either declining}\hspace{0.17em}\text{or increasing depending on the current state of development}\right).$$ [3]

By substitution,

$$\mathit{y}\prime =\mathit{gb}\hspace{0.17em}\text{log}\left(\mathit{a}y\prime +\mathit{c}\right)+\mathit{gd}+\mathit{f}\mathit{.}$$ [4]

Over time, where ay′ + c > 0, the system will converge on the solutions presented in the text from a wide range of starting conditions.