VarExp: estimating variance explained by genome-wide GxE summary statistics

Abstract

Summary

Many genome-wide association studies and genome-wide screening for gene–environment (GxE) interactions have been performed to elucidate the underlying mechanisms of human traits and diseases. When the analyzed outcome is quantitative, the overall contribution of identified genetic variants to the outcome is often expressed as the percentage of phenotypic variance explained. This is commonly done using individual-level genotype data but it is challenging when results are derived through meta-analyses. Here, we present R package, ‘VarExp’, that allows for the estimation of the percentage of phenotypic variance explained using summary statistics only. It allows for a range of models to be evaluated, including marginal genetic effects, GxE interaction effects and both effects jointly. Its implementation integrates all recent methodological developments and does not need external data to be uploaded by users.

Availability and implementation

The R package is available at https://gitlab.pasteur.fr/statistical-genetics/VarExp.git.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Many genome-wide association studies (GWAS) or genome-wide screenings incorporating gene–environment (GxE) interactions (Aschard et al., 2012) have been performed to better understand underlying mechanisms of human traits and diseases. When the analyzed outcome is continuous, a commonly used measure to judge the overall impact of the significant associations is the percentage of phenotypic variance explained. A standard way of estimating this percentage is to compare the coefficients of determination between the models including or not the significantly associated variants and/or interactions. This requires individual genotype and phenotype data which can be challenging in meta-analyses performed in big consortia as pooling data from multiple cohorts raises practical and ethical issues. However, an alternative is to use only GWAS or genome-wide GxE summary statistics. Recently, several methods (Pare et al., 2016; Shi et al., 2016) have been developed to estimate the variance explained by marginal genetic effects while taking into account linkage disequilibrium between variants, and addressing statistical issues related to finite sample size and Single Nucleotide Polymorphisms (SNP) correlation matrices. Yet, these works only focused on marginal genetic effects, while genome-wide GxE and joint effect GWAS are now commonly performed and face the same need. In this work, we address this gap by extending the methodology to GxE screening and implementing R package VarExp to rapidly and easily estimate the percentage explained by variants and/or interactions of interest using only meta-analysis summary statistics from GWAS.

2 Materials and methods

2.1 Percentage of variance explained

Consider a set of $K$ SNPs ${\left(G_k\right)}_{k=1\dots K}$, coded additively as {0, 1, 2} and a quantitative outcome Y. The marginal genetic effect ${\alpha }_{G.k}$ of SNP $G_k$ is estimated in the marginal model:

$$Y={\alpha }_0+{\alpha }_{G.k}{G}_k+\epsilon .$$

Shi et al. (2016) proposed a first naïve estimator to derive the variance explained by genetic effects, $f_G$ using summary statistics:

$$f_G={{\alpha }_G^{\mathrm{\prime }}}^{{\hspace{0.17em}}^T}{\mathrm{\Sigma }}^{\mathrm{*}}{\alpha }_G^{\mathrm{\prime }}/var\left(Y\right)$$

where ${\alpha }_G^{\mathrm{\prime }}=\left({\alpha }_{G.1}{\sigma }_1 \dots {\alpha }_{G.k}{\sigma }_k\dots {\alpha }_{G.K}{\sigma }_K\right){\hspace{0.17em}}^T$, ${\sigma }_k$ denotes the standard deviation of SNP $G_k$ and ${\mathrm{\Sigma }}^{\mathrm{*}}$ is the Moore–Penrose generalized inverse of the genotype correlation matrix. However, finite sample size implies statistical noise in both the effect sizes and the correlation matrix estimations which can induce bias in the estimation of $f_G$. Shi et al. (2016) derived a general formula that addresses this issue:

$$f_G^{\mathrm{*}}=\left[N\times {{\alpha }_G^{\mathrm{\prime }}}^{{\hspace{0.17em}}^T}{\mathrm{\Sigma }}^{\mathrm{*}}{\alpha }_G^{\mathrm{\prime }}-q\right]/\left(\left(N-q\right)\times var\left(Y\right)\right)$$

where $N$ and $q$ denote respectively the sample size and the rank of the correlation matrix.

Now consider an exposure E (either binary or quantitative). The main effect ${\alpha }_{G.k}$ of the SNP $G_k$ and the interaction effect ${\alpha }_{INT.k}$ can be estimated using a single-SNP model with an interaction term:

$$Y={\alpha }_0+{\alpha }_{G.k}{G}_k+{\alpha }_{E}E+{\alpha }_{INT.k}{G}_k\times E+\epsilon .$$

We show in Supplementary Material that, when re-parameterizing the effect estimates of the above model to obtain parameters from a fully standardized model, the percentage of variance explained by interactions effects $f_I$ or jointly by genetic and interaction effects $f_{G+I}$ can also be derived using summary statistics only:

$$f_I={{\alpha }_{INT}^{\mathrm{\prime }}}^{{\hspace{0.17em}}^T}{\mathrm{\Sigma }}^{\mathrm{*}}{\alpha }_{INT}^{\mathrm{\prime }}/var\left(Y\right)$$

$$f_{G+I}=f_G+f_I$$

where ${\alpha }_{INT}^{\mathrm{\prime }}=\left({\alpha }_{INT.1}{\sigma }_1{\sigma }_E\mathrm{ }\dots {\alpha }_{INT.k}{\sigma }_k{\sigma }_E\dots {\alpha }_{INT.K}{\sigma }_K{\sigma }_E\right){\hspace{0.17em}}^T$ and ${\sigma }_E$ is the standard deviation of E. In this model, $f_G$ is computed using effect sizes from the interaction model. However, for the reasons discussed above, we define our final estimators, $f_I^{\mathrm{*}}$ and $f_{G+I}^{\mathrm{*}}$, by applying the same corrections as proposed for the $f_G$ estimator by Shi et al. (see $f_G^{\mathrm{*}}$ equation).

2.2 Estimating the genotype correlation matrix

When the genotype correlation is not available from the data, it can be estimated using genotype data from a reference panel such as the 1000 Genomes (Abecasis et al., 2012) . We implemented a transparent function that derives this correlation matrix from 1000 Genomes Phase 3 data either through a web access for small number of SNPs or from local data files for larger number of SNPs, as computational time is dramatically reduced when querying local files (see Supplementary Material and Supplementary Fig. S3). To avoid matrix inversion issues, we also implemented an option to prune SNPs with perfect correlation of 1 with another SNP in the matrix.

3 Application example

In practice, application is performed in three main steps (see Supplementary Material and Supplementary Fig. S4): (i) estimating the SNP correlation matrix, (ii) computing mean and variance for both the outcome and the exposure in the pooled sample and (iii) finally, estimating the percentage of phenotypic variance explained by main genetic effects and/or interaction effects. To illustrate the performances of our package, we performed a simulation study (see Supplementary Material) comparing the adjusted coefficients of determination from regressions and the estimates obtained using VarExp across 1000 replicates. Figure 1 and Supplementary Figures S1 and S2 demonstrate the high accuracy of our estimator with an intraclass correlation coefficient between the coefficients of determination and their estimations equal to 0.99, 0.98 and 0.99 for the marginal genetic effects, interaction effects and joint effects, respectively.

Fig. 1.

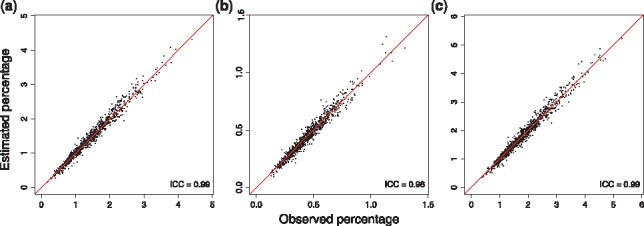
Percentage of phenotypic variance explained using summary statistics (estimated) and individual-level data (observed) for (a) main genetic (b) interaction and (c) joint effects. The line corresponds to y=x and ICC is the intraclass correlation coefficient

4 Concluding remarks

In this work, we provide R package VarExp to easily estimate the percentage of phenotypic variance explained by genetic effects, GxE interaction effects or their joint contribution using summary statistics only, making it straightforward in large-scale consortia. Importantly, several limitations of GxE screenings have previously been discussed [(Aschard, 2016; Robinson et al., 2017), see also Supplementary Material] and have to be taken into account by users before applying our approach.