Equations for O₂ and CO₂ solubilities in saline and plasma: combining temperature and density dependences

Abstract

Solubilities of respiratory gasses in water, saline, and plasma decrease with rising temperatures and solute concentrations. Henry’s Law, C = α·P, states that the equilibrium concentration of a dissolved gas is solubility times partial pressure. Solubilities in the water of a solution depend on temperature and the content of other solutes. Blood temperatures may differ more than 20°C between skin and heart, and an erythrocyte will undergo that range as blood circulates. The concentrations of O₂ and CO₂ are the driving forces for diffusion, exchanges, and for reactions. We provide an equation for O₂ and CO₂ solubilities, α, that allows for continuous changes in temperature, T, and solution density, ρ, in dynamically changing states:

$$a\left({\text{T, ρ}}_{\text{sol}}{\text{, ρ}}_{\text{ω}}\text{, γ, β}\right)=\left[1-\text{γ}\cdot {\left(\frac{{\text{ρ}}_{\text{sol}}-{\text{ρ}}_{\text{ω}}}{{\text{ρ}}_{\text{ω}}}\right)}^{\text{β}}\right]\cdot \left({\text{C}}_1\cdot e^{-k_1\text{T}}+{\text{C}}_2\cdot e^{-k_2\text{T}}\right)$$

This two-exponential expression with a density scalar γ, and a density exponent β, accounts for solubility changes due to density changes of an aqueous solution. It fits experimental data on solubilities in water, saline, and plasma over temperatures from 20 to 40°C, and for plasma densities, ρ_sol up to 1.020 g/ml with ~0.3% error. The amounts of additional bound O₂ (to Hb) and CO₂ (bicarbonate and carbamino) depend on the concentrations in the local water space and the reaction parameters. During exercise, solubility changes are large; both ρ_sol and T change rapidly with spatial position and with time. In exercise hemoconcentration plasma, ρ_sol exceeds 1.02, whereas T may range over 20°C. The six parameters for O₂ and the six for CO₂ are constants, so solubilities are calculable continuously as T and ρ_sol change.

NEW & NOTEWORTHY Solubilities for oxygen and carbon dioxide are dependent on the density of the solution, on temperature, and on the partial pressure. We provide a brief equation suitable for hand calculators or mathematical modeling, accounting for these factors over a wide range of temperatures and solution densities for use in rapidly changing conditions, such as extreme exercise or osmotic transients, with better than 0.5% accuracy.

for the application in biochemical and physiological studies, we set out to provide accurate equations for gas solubility applicable to a wide range of temperatures. The foundation for quantification and modeling of gas transport depend on the principles that determine gas solubility in liquids and defines gas concentrations in the body. Henry’s law states that gas dissolves in a solvent in proportion to the partial pressure of gas at equilibrium. O₂ and CO₂ solubilities decrease with increasing temperature and are also diminished by the presence of other solutes, ions, polymers, or proteins (12). Solute concentration, not partial pressure, drives reactions and defines diffusion gradients, so it is quantitatively important to account for changes in gas solubility as temperature increases between the inflow and outflow of heat-producing organs to define reaction rates and binding equilibria. For O₂ and CO₂, the binding and unbinding reactions with Hb are further complicated by the Bohr and Haldane effects, where increasing Pco₂ augments O₂ release in tissue and vice versa in the lung (5, 7). Alveolar temperatures are lower than heart, brain, and liver temperatures, and, as arterial blood enters these highly metabolizing organs, the rising temperature depresses gas solubility as the blood warms (1).

General equations that hold over temperatures from 15°C in skin to 44°C are needed for estimating solubilities during bypass operations with hypothermia, during dialysis where hematocrit and protein concentrations oscillate, and during intense exercise with hemoconcentration of 10–15%. The need is for the solubility in the water of solutions containing both small solutes and proteins. Hb binding of O₂ and proteins forming carbamino groups with CO₂ merely remove the gases from solution by the chemical reaction and are not to be accounted for as solubility, which is unaffected.

We took data from the literature, assessing it as best we could for accuracy of methods and reproducibility of observations, and especially for large numbers of observations over wide ranges of temperature. We found high-quality data for O₂ and CO₂ in saline and water. Data in plasma were not of equivalent quality; for example, protein concentrations were rarely measured. The plasma data were sampled from humans, and “normal human” concentrations were assumed to be all the same.

The output of this study is algebraic equations describing the solubilities of O₂ and CO₂ in pure water, saline, and acidified plasma across a wide range of temperatures. These will aid investigators using temperature-dependent reactions and exchange. In capillary beds, gases and heat exchange between blood and tissue, where the concentrations and temperatures are varied over micrometer distances. For the mathematical modeling of gas transport, it is essential to account for the changes in solubilities and partial pressures continuously. With changing metabolism and consequent osmotic transients, one needs also to account for the effects of changing blood density, as well as temperature, in defining the solubility. Reactions using or producing O₂ and CO₂ must be accounted for separately but simultaneously.

METHODS

We selected data on O₂ and CO₂ solubility at temperatures relevant to human physiology, accounting for normal and hypo- and hyperthermic conditions. We selected data we judged to be carefully obtained, rejecting data in studies with inconsistencies in observations or analyses. A prime source was the solubility data collection in Respiration and Circulation (2), referencing several sources. Investigations utilizing different techniques or methods that were inconsistent were not included (9, 12). Only data obtained by directly measuring gas solubility were used for our analyses, and we ignored interpolated estimates and observations that appeared anomalous, a somewhat arbitrary process.

Because the original data sets were imperfect in various ways and are sometimes conflicting, we advocate that new experiments be done under a uniform set of laboratory conditions to improve the accuracy of the data, the range of solution densities, and the types of solutions, and then reassess and presumably reparametrize our equations or write more accurate ones. The key thing is to provide solubility equations accounting for plasma density and temperature in space and time simultaneously, while blood circulates and the gases exchange.

The selected solubilities in water, 0.9% sodium chloride, plasma, and serum for O₂ are in Table 1 and for CO₂ are in Table 2. All measurements and estimates of gas solubility in this paper have standard units of milliliters of gas per milliliter of solvent at 1 atm pressure. The plasma samples were acidified to pH ~3.5 to block carbamino binding (11, 26).

Table 1.

Solubility coefficients for O₂ in water and physiological solutions

Temperature, °C	Water Source (15)	Water Source (4)	0.9% NaCl Source (21)	Human Plasma Source (8)
0	0.04889
1	0.04758	0.04789
2	0.04633	0.04661
3	0.04512	0.04532
4	0.04397	0.04422
5	0.04287	0.04311
6	0.0418	0.04204
7	0.0408	0.04102
8	0.03983	0.04006
9	0.03891
10	0.03802	0.03824	0.03689	0.0338
11	0.03718		0.03605	0.033
12	0.03637	0.03657	0.03524	0.0322
13	0.03559		0.03446	0.0315
14	0.03486	0.03504	0.03373	0.0308
15	0.03415	0.03432	0.03302	0.0302
16	0.03348	0.03363	0.03235	0.0296
17	0.03283		0.0317	0.029
18	0.0322		0.03107	0.0285
19	0.03161		0.03048	0.0281
20	0.03102	0.03114	0.02989	0.0277
21	0.03044		0.02931	0.0273
22	0.02988	0.03004	0.02875	0.0269
23	0.02934		0.02821	0.0265
24	0.02881	0.02903	0.02768	0.0261
25	0.02831		0.02718	0.0257
26	0.02783		0.0267	0.0253
27	0.02736	0.02763	0.02623	0.0249
28	0.02691		0.02578	0.0246
29	0.02649		0.02536	0.0242
30	0.02608	0.02638	0.02495	0.0238
31			0.02461	0.0234
32			0.02428	0.023
33		0.02529	0.02394	0.0226
34			0.02361	0.0223
35	0.0244		0.02327	0.022
36		0.02429	0.023	0.0217
37			0.02273	0.0214
38			0.02247	0.0212
39		0.02341	0.0222	0.021
40	0.02306		0.02193	0.0208
42		0.02261
45	0.02187	0.02189		0.0197
50	0.0209			0.0187
55				0.0182
60	0.01946			0.0177

Values are in standard units (ml gas/ml solvent at a partial pressure of 1 atm).

Table 2.

Solubility coefficients for CO₂ in water and physiological solutions

Temperature, °C	Water Source (15)	0.9% NaCl Source (26)	Oxygen Plasma Source (3)
0	1.713
1	1.646
2	1.584
3	1.527
4	1.473
5	1.424
6	1.377
7	1.331
8	1.282
9	1.237
10	1.194	1.177
11	1.154	1.137
12	1.117	1.1
13	1.083	1.066
14	1.05	1.033
15	1.019	1.002	0.916
16	0.985	0.968
17	0.956	0.939
18	0.928	0.911
19	0.902	0.885
20	0.878	0.861	0.787
21	0.854	0.837
22	0.829	0.812
23	0.804	0.787
24	0.781	0.764
25	0.759	0.742	0.681
26	0.738	0.721
27	0.718	0.701
28	0.699	0.682
29	0.682	0.665
30	0.665	0.648	0.601
31		0.633
32		0.619
33		0.604
34		0.59
35	0.592	0.575	0.535
36		0.563
37		0.55	0.515
38		0.538	0.503
39		0.523
40	0.53	0.513	0.482
45	0.479
50	0.436
55
60	0.359

Values are in standard units (ml gas/ml solution at a partial pressure of 1 atm).

Development of integrative equations for solubility vs. temperature.

We used simple smooth equations to fit the data on O₂ and CO₂ solubilities vs. temperature in various solutions. First, we fitted the data in water, saline, and plasma separately, obtaining excellent fits to the data. On observing that the curves for the three solution types were almost parallel to each other, we obtained the best fits for exactly parallel equations related to each other by a scalar relative to water. Such a constraint can only result in poorer fits to the data, so the minimized sums of squares are inevitably larger, but, as the results will show, the fits are still rather good. We then sought a physical basis for this good result in terms of some characteristic measurement of the particular solutions. Molar concentrations did not appeal, because of the diverse sizes of molecules in plasma. Density scaling became the next hypothesis. If the three solutions could be related by density, and if the fitted curves were indeed parallel, then one equation could serve as the descriptor for the solubilities of a gas over the whole temperature range in the three solutions given an experimental measurement of density. Such an equation would be still very simple, if the ratios of solution densities remained constant over the temperature range, and, since the solutions were all mainly water, this seemed like an hypothesis worth evaluating. The worst case would be that the equation would become more complicated if the density ratios changed with temperature.

The tabulated solubilities are monotonic with temperature and concave upward. Linear equations and polynomials are unsuitable as descriptors. We used exponential equations and found that two exponentials sufficed for the ranges covered. The solubility α(Τ) (ml gas/ml solution at 1 atm pressure) at temperature T (°C), is described by:

$$\text{α}\left(\text{T}\right)={\text{C}}_1\cdot e^{-k_1\text{T}}+{\text{C}}_2\cdot e^{-k_2\text{T}}$$ (1)

where C₁ and C₂ are scalar coefficients (ml gas/ml solution at 1 atm pressure), and k₁ and k₂ are fixed coefficients (1/°C). This function integrates the information in data set on solubility vs. temperature in a medium of constant composition.

Graphical plots of the data suggested that the solubility-temperature curves were more or less parallel for solutions of differing composition. This leads to a second, more compact way of describing the data, namely assuming a scalar relationship between pairs of solutions, scaling in proportion to the solubility in pure water by a scalar factor φ, 0 < φ < 1.

$$\text{α}\left(\text{T, φ}\right)=\text{φ}\cdot \left({\text{C}}_1\cdot e^{-k_1\text{T}}+{\text{C}}_2\cdot e^{-k_2\text{T}}\right)$$ (2)

This hypothesis is tested by our analysis. Equation 2 represents a potentially more powerful expression, describing two or more data sets. Here “more powerful” implies that the equation parameters are better constrained by virtue of using more data points to define the parameters of the equation, for 3 solutions, the 4 parameters of the 2 exponentials plus 2 φ values, for a total of 6, instead of the 12 parameters using Eq. 1 to fit each data set. The two φ values are φ_salt and φ_pl for saline and plasma, respectively.

The possible presence of scalar relationships between solubilities in water, saline, and plasma provokes one to hypothesize a basis for values of these scalars. We propose that solution density can explain differences in solubility for different solutions and can improve the modeling by incorporating a measurable parameter to replace an empirical value for φ. This idea is based on the observation that O₂ and CO₂ solubilities diminish from water to saline to plasma, in order of increasing density of the solutions. On this basis, the third quantitative hypothesis can be expressed:

$$\text{a}\left({\text{T, ρ}}_{\text{sol}}{\text{, ρ}}_{\text{w}}\text{, γ, β}\right)=\left[1-\text{γ}\cdot {\left(\frac{{\text{ρ}}_{\text{sol}}-{\text{ρ}}_{\text{w}}}{{\text{ρ}}_{\text{w}}}\right)}^{\text{β}}\right]\cdot \left({\text{C}}_1\cdot e^{-k_1\text{T}}+{\text{C}}_2\cdot e^{-k_2\text{T}}\right)$$ (3)

where ρ_sol is the density of the solution, ρ_w is the density of water at the same temperature, γ is a scalar describing a proportionality due to the difference in solution density from that of water, and β is an exponent defining the nonlinearity in the influence of density on solubility. Solution densities for water, 0.99332 g/ml, and saline, 0.99933 g/ml, were obtained at 37°C by Horlocker and Wedel (16); Hinghofer-Szalkay and Greenleaf (13) found ρ = 1.020 g/ml for human plasma. This affirmed the values found by Van Slyke et al. (27), whose observations of plasma-specific gravities (the ratio of plasma density to water) averaging 1.0268 ± 0.01 recalculate by dividing by water’s density of 0.99332, giving ρ = 1.01996 for plasma. The hypothesis that γ might be a constant over a range of solutions is to assume that charge effects might be negligible and that the nature of the space-occupying solutes is unimportant. As Van Slyke et al. (27) pointed out, this is not exactly true; if the globulin fraction of protein were increased with constant total protein, the ρ of 1.020 g/ml would increase a little.

Equation 3 is based on the density ratios, the γ, being independent of temperature even though volumes and viscosities do change with temperature. From our analyses of the data of Sharqawy et al. (22) and Iqbal and Verrall (17), the density ratios for saline to water and for plasma to water over the broad temperature ranges are almost constant: over the range from 20°C to 40°C the scalar term in parentheses in Eq. 3 ranged ±0.075% for saline and ±0.1% for plasma compared with those at 30°C. Thus error in Eq. 3 due to inconstancy of the density ratios was <0.1% over the 20°C range of physiological temperatures. In experimental studies, errors in measurement of T and ρ will be greater than this and will dominate the error.

To put these hypotheses differently, Eq. 1 expresses the temperature effect on solubility with a pair of exponentials, purely descriptive for each gas and each solution. Equation 2 tests the idea that solubilities in water can predict the solubilities in another solution over the whole range of temperatures if the scale ratio φ is determined. Equation 3 tests the broader idea that solution density is a unique determinant of gas solubility, presumably describing an excluded volume of water, reducing gas solubility.

Analysis.

We used the JSim data analysis system (6) to fit the data with models, the two-exponential equations with their adjustable curvature. The equations were fitted to the data in Tables 1 and 2, adjusting the parameters to minimize the sum of squares of the differences between model and data. Of the eight optimization routines in JSim, SENSOP and NL2SOL gave secure convergence in fitting both single data sets and multiple data sets simultaneously. In fitting model 1 (Eq. 1), each curve was fit individually. In fitting model 2 (Eq. 2), the three curves (for O₂ or CO₂) were fitted simultaneously, adjusting the coefficients, the C_i, the exponents, the k_i, that apply to all three curves, and the scalars for saline and plasma, a total of five parameters for each gas. In fitting model 3 (Eq. 3), the three curves (for O₂ or CO₂) were fitted simultaneously, adjusting the coefficients, the C_i, the exponents, the k_i, and the density coefficient, γ, and density exponent, β, a total of six parameters. The root mean sum of squares of error (RMSE) was calculated for each model fit, comparing the fit to the observed data, and then normalizing the RMSE to normal RMSE by dividing the RMSE by the average solubility. When multiple data sets were fit simultaneously, models 2 and 3, the “overall” RMSE was calculated using all the data points fitted for a given gas.

RESULTS

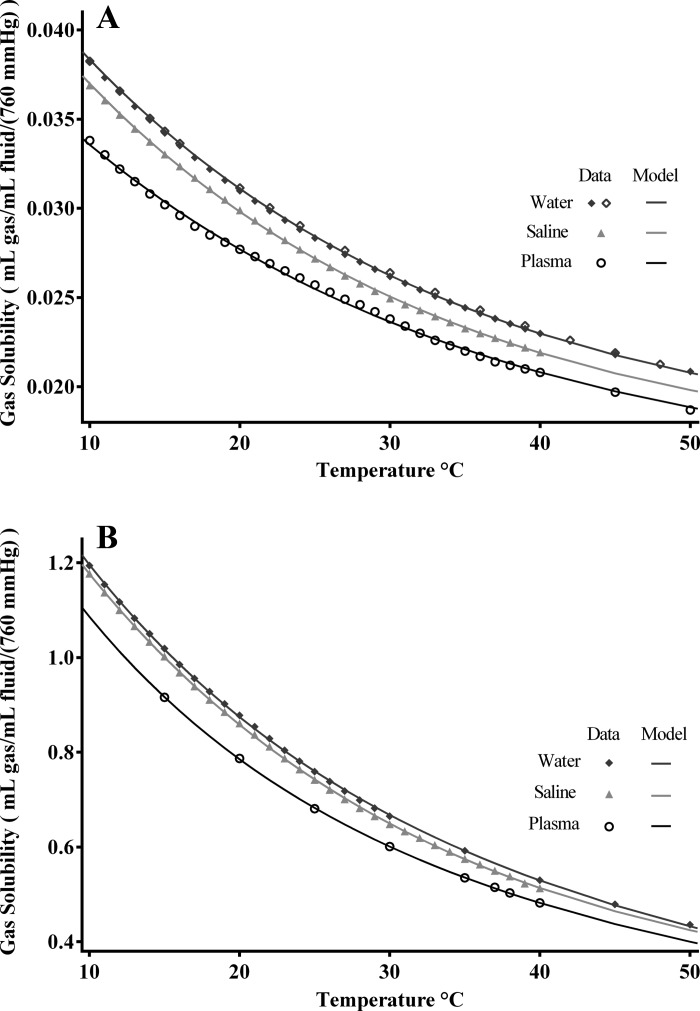
The fitting of model 1, Eq. 1, to the individual data sets are shown in Fig. 1, and the parameter are given in Table 3. These parameters give accurate estimations for gas solubilities in water and saline over the temperature ranges tabulated. The data for plasma are not as consistent as the water and saline data in that they show discernable experimental error, and the RMSE is threefold greater for O₂ in plasma than in water. The CO₂ data were somewhat noisier than for O₂, but the fits are good. Neither Eq. 1 nor Eq. 2 can handle temperature changes dynamically, but neither can handle non-homeostatic conditions when solution density changes. Equation 3 handles hemoconcentration or dilution: this would presumably be represented by changes in γ, rather than β, but, in the absence of highly accurate data, one cannot affirm that β does not change with a change in protein concentration. Further data are needed on this point.

Fig. 1.

Model 1 data sets fitted individually for O₂ and CO₂ solubilities in water, saline, and plasma vs. temperature over the range from 10 to 50°C. Data are from Table 1. The best fitting Eq. 1 and RMSEs are reported in Table 3. Top: O₂ solubilities. Water data (⧫, ◇) are from Hodgman (15) and Benson et al. (4), respectively. Saline data (▲) are from Sendroy et al. (21). Human plasma data (○) are from Christoforides et al. (8). Bottom: CO₂ solubilities. Water data (⧫) are from Hodgman (15); saline data (▲) are from Van Slyke et al. (26). O₂ plasma data (○) are from Bartels and Wrbitzky (3).

Table 3.

Model 1 (Eq. 1) temperature parameters for O₂ and CO₂ in Fig. 1

Solution	C1, ml gas·ml fluid−1·760 mmHg−1	k1, 1/°C	C2, ml gas·ml fluid−1·760 mmHg−1	k2, 1/°C	RMSE	NRMSE
Oxygen
Water (0 < t < 60°C)	0.0324	0.0405	0.0166	0.0	1.3E-04	1.1E-05
0.9% Saline (10 < t < 40°C)	0.0321	0.0411	0.0157	0.0	5.4E-05	1.9E-03
Plasma (10 < t < 60°C)	0.0276	0.0361	0.0143	0.0	1.5E-04	6.0E-03
Carbon dioxide
Water (0 < t < 60°C)	1.008	0.056	0.7046	0.0128	2.5E-03	2.5E-03
0.9% Saline (10 < t < 40°C)	1.407	0.0425	0.2565	0.0	1.7E-03	2.2E-03
Plasma (15 < t < 43°C)	0.9454	0.0625	0.6539	0.012	1.1E-03	1.8E-03

NRMSE, normal RMSE.

Model 2, Eq. 2, assuming a constant proportionality φ in solubilities over the 40° temperature range from water to saline or plasma for analyzing the same data, uses the parameters shown in Table 4. Six parameters for each gas describe the data. The two φ values are the scalars in Eq. 2, φ_salt and φ_pl, for saline and plasma, respectively. This is the most constrained of the three models, but it fails to consider density or water fraction. Because the fitting of the water data depends also on the fitting of parallel curves for saline and plasma, the water parameters must differ from those for the individual fits to the water data in Table 3. These data show that both O₂ and CO₂ solubilities in plasma are ~10% less than in water over the range of temperatures, and that, in saline, the CO₂ solubility is much less reduced by the salt than is O₂ solubility. The reason for the relatively higher CO₂ than O₂ solubility is not clear: there was no buffer, only NaCl. The fits to the data by model 2 are good, slightly better than for model 3, but not quite as good as for model 1: the fittedness, appropriately, is worse than for the least constrained model and better than for the most constrained model.

Table 4.

Model 2 (Eq. 2) scalar equations for of O₂ and CO₂

Gas	C1, ml gas·ml fluid−1·760 mmHg−1	k1, 1/°C	C2, ml gas·ml fluid−1·760 mmHg−1	k2, 1/°C	φsalt	φpl	Saline RMSE	Plasma RMSE	Overall NRMSE
O2	0.0323	0.04	0.0165	0	0.960	0.898	1.7E-04	6.0E-03	3.0E-04
CO2	1.180	0.0506	0.5305	0.0088	0.981	0.906	3.6E-03	3.6E-03	4.0E-03

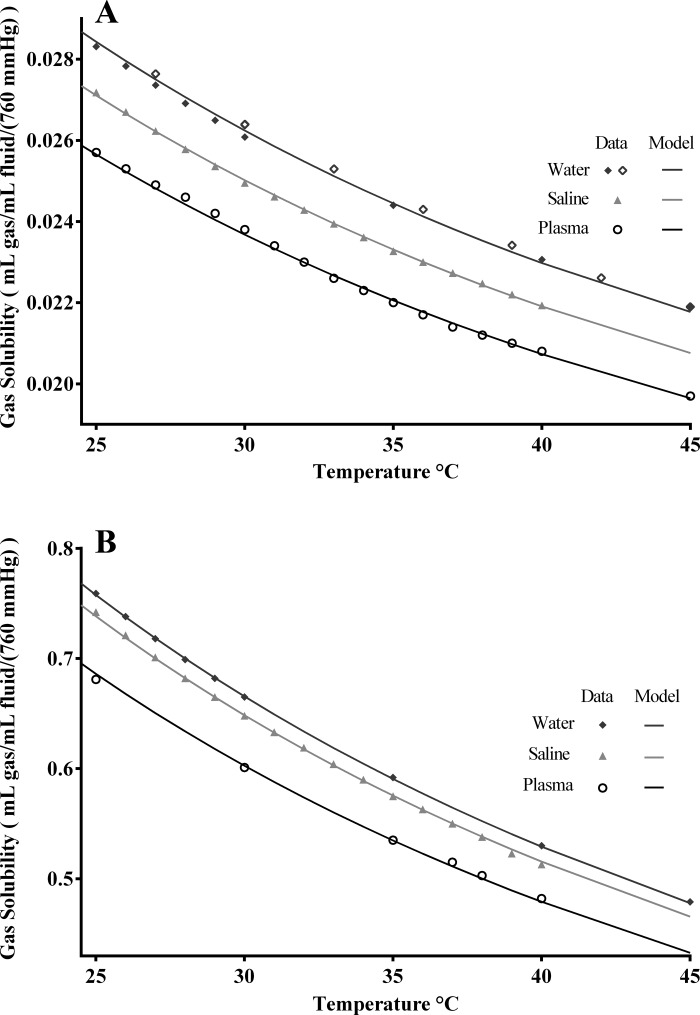
Model 3, Eq. 3 tests the idea of basing the saline and plasma model curves on the water curve and the densities of the solutions compared with water density. The data sources for the solubilities did not provide the densities, so we used 1.020 g/ml, the average plasma densities reported by Van Slyke et al. (27) and Hinghofer-Szalkay and Greenleaf (13). Six free parameters are optimized to fit the three sets of data, fewer than for model 1, but the same as for model 2, and are reported in Table 5. The density scaling parameter γ, combined with the density exponent β, allows almost as much freedom in positioning the curves as did using individual scalars of model 2 (Eq. 2), so the normalized sums of squares are similar to those for model 2. The estimates for γ for O₂, 0.59, and CO₂, 2.26, are dissimilar, as are the β values. The overall density scalars in the eighth column of Table 5, the parenthetic phrase in Eq. 3, are similar to those from model 2, but, due to the constraint by the known densities, are not identical. There is actually some positive covariance between γ and β, so this overlap is, in effect, a reduction in flexibility in the fitting.

Table 5.

Model 3 (Eq. 3) density effects on O₂ and CO₂ solubility over 25–45°C using ρ_w = 0.99332 g/ml, ρ_s = 0.99933 g/ml, and ρ_pl = 1.020 g/ml at 37°C

Gas/Solution	C1, ml gas·ml fluid−1·760 mmHg−1	k1, 1/°C	C2, ml gas·ml fluid−1·760 mmHg−1	k2, 1/°C	γ	β	Density Scalar $\left[1-\text{γ}\cdot {\left(\frac{{\text{ρ}}_{\text{sol}}-{\text{ρ}}_{\text{w}}}{{\text{ρ}}_{\text{w}}}\right)}^{\text{β}}\right]$	Overall RMSE	Overall NRMSE
O2
Water	0.0328	0.0398	0.0163	0.0	0.59	0.497	1	1.4E-04	2.5E-05
Saline							0.9534	3.7E-05
Plasma							0.9023	8.8E-05
CO2
Water	1.052	0.0571	0.6821	0.012	2.256	0.877	1	8.7E-04	1.4E-03
Saline							0.974	1.7E-03
Plasma							0.905	3.2E-03

Fits of the density model 3 are shown in Fig. 2. The two sets of O₂ solubility data are slightly different, but systematic. For the analysis, we took the water densities, ρ_w, from Sharqawy et al. (22). The saline densities, ρ_s, from Sharqawy et al. (22) were validated by van Lopik et al. (24). Plasma densities, ρ_pl, are from Van Slyke et al. (27) and Hinghofer-Szalkay and Greenleaf (13). Plasma densities in normal humans have an almost 1% SD, and in abnormal humans range from 1.009 to 1.027, as taken from the specific gravities of Van Slyke et al. (27), times 0.99332, water density. The plasma data determine the γ, the scaling from one density to another. The β modifies the nonlinear curvature in the density relationships among water, saline, and plasma: β is <1.0, having a plateauing effect on dα/dρ.

Fig. 2.

Fitting of model 3, density-defined parallel curves, to O₂ and CO₂ solubilities in water, saline, and plasma vs. temperatures in the physiological range. Data are from Table 1 and are the same data as in Fig. 1, omitting the data at temperatures <25°C and >45°C. The model fits use Eq. 3 with the parameters reported in Table 5. Top: O₂ solubilities. Densities at 37°C were water 0.99332 g/ml, 0.9% saline 0.99933 g/ml, and human plasma 1.020 g/ml. Bottom: CO₂ solubilities. The higher β for CO₂ than for O₂ reflects the fact that the gap between water and saline curves for CO₂ is smaller than the gap between water and saline of the O₂ curves.

DISCUSSION

Methodology.

The observed solubilities listed in Tables 1 and 2 were all obtained with similar methods: gas determination in each solutions was measured manometrically with a Van Slyke apparatus (25). Error is <2% in manometric methods when triply repeated estimations are made. Using equations to interpolate through a whole set of observations reduces the error further, probably to the order of 1/2%. Benson et al. (4) describes more accurate methods for equilibrating gas and fluids and mass spectrometry for the fluid concentrations to estimate gas solubilities in water with accuracy of 0.01–0.02%. For O₂ solubilities in water, the results are indistinguishable from those in our selected data sets and provide further confidence in our data selection process.

The utility of a solubility descriptor, including temperature and plasma density.

The amount of dissolved O₂ in the blood is commonly taken to be 3 ml/l whole blood; it is at 37°C more correctly 2.816 ml/l whole blood, a 5.5% error. Such error is not acceptable for scientific studies or exercise models. Exercise can hemoconcentrate blood ~10–15% and permit differences between skin and core temperatures, rising as high as 12°C (18). Hemoconcentration alone drops gas solubility by at least the amount of water displaced, and temperature increasing at exercising muscle can reduce solubility at the working muscle by as much as 25% compared with the cooler peripheral tissues. Because temperatures vary widely between cooled skin, lung alveoli, and metabolically warmed organs, we need accurate solubilities for quantitative analysis of metabolic reactions and fluxes.

The model equations describing solubilities as functions of temperature and solution density serve two purposes. First, they provide an integrated description that smooths through data that contain experimental error, reducing the error when estimating the solubility at a particular temperature. Second, they summarize the data to give quantitative measures that can be computed for non-steady-state conditions, such as the increase in temperature that occurs when blood passes through metabolizing tissues. Equations that estimate the solubility of respiratory gases are necessary to calculate the gas’s molar concentration, the driving force for diffusional exchanges and reaction rates. Undoubtedly, our Eq. 3 will be superseded, perhaps by more comprehensive equations accounting for more refined understanding of the relationship between solutes, temperature, density, and other factors influencing gas solubility, and the parameters must be revised as better data are acquired.

Gas solubilities are highest in pure water, decreasing with increasing concentrations of other solutes Binding or chemical buffering, for example, O₂ binding to Hb, or CO₂ being buffered as bicarbonate, augments their total blood content for the same gas tension. Other nonspecific binding can occur, as reported by Power (19) for O₂ and CO₂ in lung tissue. In experimental conditions in which the Hb hemeporphyrin site for O₂ was ostensibly blocked by NaNO₂ or ferricyanide, Power noted that as much as 17% of the O₂ is loosely bound in blood. Christoforides and Hedley-White (9) found apparent increases in O₂ solubility with increasing concentrations of seemingly NaNO₂-blocked Hb. We think it is likely that the apparent increase in O₂ solubility in their studies is really due to the binding of the O₂ to the heme site, despite the partial block, rather than nonspecific protein binding.

The influences of temperature on gas solubility are needed, particularly in mathematical models in exercise physiology. Metabolism in tissues produces heat, reducing gas solubility, thus augmenting the Bohr effects of CO₂ and pH in fostering increased O₂ release in tissues. At rest, the liver, brain, and heart have the highest heat-generating rates per gram, while during whole body exercise, skeletal muscle becomes the primary heat generator (20).

The effect of temperature on the oxyhemoglobin saturation curve is greater than the effects of pH, Pco₂, and 2,3-diphospho-d-glycerate. Increases in each of these increase the P₅₀, the Po₂ at which the hemoglobin binding sites for O₂ are half filled, as does a rise in temperature. The summed effects are significant and make up the basis for the Bohr and Haldane effects (23). Gas solubilities are dependent also on the concentrations of ions and solutes in the blood. At 37°C, 9 g of NaCl/l H₂O depresses O₂ solubility by 5% and CO₂ by 3%, as seen in Figs. 1 and 2. In plasma, O₂ and CO₂ solubilities are diminished by ~10%. These numbers represent the diminution in aqueous diffusive transport between bloodstream and cell fluid. The large plasma proteins, albumins and globulins, displace water and increase viscosity, as well as leave less space for gas to diffuse (14). The oxyhemoglobin and carboxyhemoglobin saturation curves are driven by the partial pressures and are not changed by plasma solution densities.

The need for a single equation for the solubility of a gas over a large range of temperatures and solution densities (or other factors) is for accurate accounting of the circulatory exchanges in different tissues in normal and exercising humans. By accounting for both density and temperature, we can account for changes in affinities of Hb for O₂ and CO₂ along the length of a capillary in a metabolizing organ using the Hb binding equations of Dash et al. (10). These account for the changing gas tensions (O₂ and CO₂) simultaneously with temperature and pH, which change markedly in single capillary passage. Having a single equation for both temperature and density effects also allows for the consideration of solubilities in transient situations: a provocative example is sudden strenuous exercise in which the heart and skeletal muscle, and probably the brain, heat rapidly by 2–4°, and the circulating blood is concentrated by 10–15% by virtue of osmotic forces pulling water into the muscle cells. Blood density and muscle temperatures change rapidly before the skin warms. In computational modeling, the concentrations, temperatures, blood densities, and blood and tissue osmolarities need to be calculated at every time step and at each space step along the capillary. The hemoconcentration during exercise is a measure of the density and can be used to provide relatively accurate, continuously changing calculated solubilities and gas tensions in space and time.

The parameterized versions of Eq. 3 for the O₂ and CO₂ solubilities in practical applications, using the values in Table 5, are:

$${\text{a}}_{{\text{O}}_{\text{2}}}=\left[1-0.59\cdot {\left(\frac{{\text{ρ}}_{\text{sol}}-{\text{ρ}}_{\text{w}}}{{\text{ρ}}_{\text{w}}}\right)}^{0.497}\right]\cdot \left(0.0328\cdot e^{-0.0398\text{T}}+0.0163\right)$$ (4a)

$${\text{a}}_{{\text{CO}}_{\text{2}}}=\left[1-2.256\cdot {\left(\frac{{\text{ρ}}_{\text{sol}}-{\text{ρ}}_{\text{w}}}{{\text{ρ}}_{\text{w}}}\right)}^{0.877}\right]\cdot \left(1.052\cdot e^{-0.0571\text{T}}+0.6821\cdot e^{-0.012\text{T}}\right)$$ (4b)

with ρ_w = 0.99332 g/ml and ρ_sol = 0.99933 g/ml for saline or 1.020 g/ml for plasma at 37°C. The plasma value is a normal population average, but can vary from 1.017 to 1.034 (27). The 1.020 is van Slyke’s specific gravity of 1.0268 multiplied by water density of 0.99332 g/ml.

The equations are for the solubility of the gases in the water of the solution. Additional O₂ is bound to Hb within erythrocytes, and additional CO₂ is bound as bicarbonate or as carbamino groups. All of these are separate calculations to account for their total masses. Since normally over 99% of O₂ is bound, it is the dissolved O₂ that is the poor neglected cousin. However, for CO₂, it is the opposite: the carbamino content can be high enough that the total CO₂ curve summing the carbamino-CO₂ bound to plasma protein and the dissolved CO₂ is higher than the curve for pure water; in this case, the bound CO₂ more than makes up for the excluded CO₂. The CO₂ data reported here were all on plasma acidification to prevent the carbamino binding; thus there is a need for sets of data to characterize the total CO₂, summing dissolved carbamino and bicarbonate CO₂ at varied temperatures.

We recommend using Eqs. 4a and 4b for O₂ and CO₂ solubilities somewhat tentatively: they are based on approximations to density effects and are based on data obtained from a variety of laboratories and experimental measures. We are particularly insecure about the plasma equation parameters since few investigators have reported the composition of plasma or serum when measuring solubility or density at different temperatures. Their exact composition is unknown. Consequently, we recommend new solubility studies in which plasma protein composition and densities are measured; this will improve the accuracy of the plasma equations.

Using water fraction instead of density.

Another approach is to replace the accounting for solution density with a scalar based on the water fraction of the solution. The water fraction of plasma is ~0.94, but is heavily dependent on protein levels. An equation like Eq. 3 can be used similarly for water fraction instead of density, replacing density by water mass per unit volume, using values of water = 1.0 g/ml, saline = 0.991 g/ml, and plasma = 0.935 g/ml. Coefficients for O₂ become C₁, 0.0324; C₂, 0.0165; k₁, 0.0402; k₂, 0; γ, 0.292; and β, 0.395, and for CO₂ become C₁, 1.167; C₂, 0.543; k₁, 0.0509; k₂, 0.0092; γ, 0.871; and β, 0.8063. This allows for a second method for estimating solution solubility where there is limited information provided on the solvent. The advantage over density might be that it may be simpler to measure water content than density. Either density or water fraction will work. In either case, more and more accurate data are needed for plasma and plasma constituents.

Conclusions.

Our observations leave us with the practical equations for gas solubilities as functions of temperature and density, Eqs. 4a and 4b for O₂ and CO₂ and two recommendations. First, to improve the accuracy of gas solubility data in physiological solutions and to improve the understanding of solution density effects vs. the ionic or other chemical influence on solubility, new experiments should be undertaken. Second, when making measurements of gas solubility, the densities and the exact composition of the solution should be described in detail. These equations for solubilities as functions of temperature and plasma density or water content are practical for quantitative analysis of gaseous exchange in continuously changing states and in integrative modeling or analyzing such data.

GRANTS

This research was supported by National Heart, Lung, and Blood Institute Grant NHLBI T15 088516 and U01-HL122199 and National Institute of Biomedical Imaging and Bioengineering Grant EB08407.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

K.M.C. performed experiments; K.M.C. and J.B.B. analyzed data; K.M.C. and J.B.B. interpreted results of experiments; K.M.C. and J.B.B. prepared figures; K.M.C. and J.B.B. drafted manuscript; K.M.C. and J.B.B. edited and revised manuscript; K.M.C. approved final version of manuscript; J.B.B. conceived and designed research.