Expectancy Effects in Feedback Processing are Explained Primarily by Time-frequency Delta not Theta

Abstract

The roles of outcome valence and expectancy in feedback processing have been investigated as important factors modulating event-related potential (ERP) measures including the feedback negativity (FN) and P300, but results have been inconsistent. Recent work from our group has shown that processes underlying the FN and P300 are better represented as separable processes in the theta (3–7 Hz) and delta (0–3 Hz) ranges using time-frequency analysis. The current study evaluated the modulation of time-domain FN and P300 and time-frequency theta and delta to outcome valence and expectancy in a gambling feedback task paradigm. Results revealed that the FN was sensitive to valence but not expectancy, and that valence effects were driven by loss-sensitive theta and gain-sensitive delta. Alternatively, the P300 was sensitive to the expectedness of outcomes but only for gain trials, and these expectancy differences were explained by time-frequency delta not theta. These results add to a growing body of research showing that time-frequency measures reflect separable processes underlying time-domain components, where theta is more sensitive to primary task features and less sensitive to secondary features while delta is sensitive to primary and more complex, secondary task features.

Introduction

The current study evaluated valence- and expectancy-related processing in a gambling feedback task. Many characteristics of gambling feedback processing, including outcome valence (Bernat, Nelson, & Baskin-Sommers, 2015; Gehring & Willoughby, 2002; Miltner, Braun, & Coles, 1997; Proudfit, 2015 (review); San Martín, 2012 (review); Wu & Zhou, 2009; Yeung & Sanfey, 2004), outcome magnitude (Bernat et al., 2015; San Martín, 2012 (review); Wu & Zhou, 2009; Yeung & Sanfey, 2004), relative outcome (Bernat et al., 2015), outcome context (Holroyd, Larsen, & Cohen, 2004; Kujawa, Smith, Luhmann, & Hajcak, 2013), and outcome expectancy (Cohen, Elger, & Ranganath, 2007; Hajcak, Holroyd, Moser, & Simons, 2005; Holroyd & Coles, 2002; Holroyd, Krigolson, & Lee, 2011; Holroyd, Pakzad-Vaezi, & Krigolson, 2008; Oliveira, McDonald, & Goodman, 2007; San Martín, 2012; Wu & Zhou, 2009), have been investigated as important factors modulating event-related potential (ERP) measures. Gambling outcome valence (i.e., monetary gains and losses) has been widely examined as a key factor modulating time-domain ERP components, including the feedback negativity (FN) and P300. Outcome expectancy, or the degree to which one event is anticipated over others, has also been evaluated as an important feature of feedback processing. Previous work has demonstrated increases in P300 amplitude when an event is unexpected, but FN findings have been more inconsistent (Hajcak et al., 2005; Holroyd & Coles, 2002; Holroyd et al., 2008; Oliveira et al., 2007; Proudfit, 2015; Wu & Zhou, 2009; Yeung & Sanfey, 2004). Substantial work has revealed that ERPs generally contain delta (0–3 Hz) and theta (3–7 Hz) activity which overlap partially in time (Başar, Başar-Eroglu, Karakaş, & Schürmann, 2001; Bernat, Malone, Williams, Patrick, & Iacono, 2007; Cavanagh, Zambrano-Vazquez, & Allen, 2012; Cohen et al., 2007; Demiralp, Ademoglu, Istefanopulos, Başar-Eroglu, & Başar, 2001). Recent research from our group has demonstrated that delta and theta underlying ERP components, such as the N2 or FN and the P300, index separable processes, which can be obscured in conventional time-domain measures (Bernat et al., 2015; Bernat, Nelson, Steele, Gehring, & Patrick, 2011; Harper, Malone, Bachman, & Bernat, 2016; Harper, Malone, & Bernat, 2014). With regard to gambling feedback more specifically, when outcome stimuli provide multiple pieces of information, we have recently demonstrated that theta activity is modulated by the most salient, or primary stimulus features (such as outcome valence), while delta is sensitive to both primary characteristics and a range of higher-level processing related to secondary stimulus attributes (such as comparisons with alternative outcomes not chosen, and the magnitude of the outcome; Bernat et al., 2015). The current study assessed modulation of time-domain ERPs, and associated time-frequency delta and theta measures, to outcome valence and expectancy. We hypothesize that time-frequency theta and delta will be differentially sensitive to valence- and expectancy-related processes: theta will be most sensitive to outcome valence, the most salient stimulus characteristic, and less sensitive to expectancy, while delta will be similarly sensitive to valence as well as expectancy. Given inconsistent findings regarding modulation of the FN and P300 to outcome valence and expectancy as described in the sections below, we predict that these distinct feedback processes in delta and theta will account for modulation in the time-domain measures.

Outcome valence

The FN has been extensively studied as a marker of outcome valence, differentiating negative from positive feedback (Gehring & Willoughby, 2002; Miltner et al., 1997). Miltner et al. (1997) provided the first evidence of the FN component, a negative-going deflection at medial-frontal recording sites that peaks approximately 250 ms after negative feedback. Converging evidence from source localization techniques, fMRI, and single-unit recordings have identified medial frontal regions, and likely the anterior cingulate cortex (ACC), as the neural generator of the FN (Foti, Weinberg, Bernat, & Proudfit, 2014; Gehring & Willoughby, 2002; Hauser et al., 2014; Holroyd & Coles, 2002; Miltner et al., 1997; Potts, Martin, Burton, & Montague, 2006) .

Conventional FN measures have traditionally been associated with negative feedback because the component is diminished or absent following positive feedback; however, more recent work has suggested modulation of the FN by positive feedback. Bernat, Nelson, Holroyd, Gehring, & Patrick (2008) and Holroyd et al. (2008) provided early evidence of a reward positivity (RewP) component, which is increased for positive relative to negative feedback. This work, along with other recent findings, has shown that smaller FN amplitude on positive feedback trials is partially explained by the superposition of an increase in positive-going amplitude, the RewP (Bernat et al., 2008; Foti, Weinberg, Dien, & Hajcak, 2011a; Holroyd et al., 2008; Kujawa et al., 2013; Proudfit, 2015). Recent efforts based on temporal-spatial principal components analysis (PCA) of the FN have indexed positive amplitude activity, which is heightened for gains relative to losses (Carlson, Foti, Mujica-Parodi, Harmon-Jones, & Hajcak, 2011; Foti et al., 2014, 2011a; Weinberg, Riesel, & Proudfit, 2014). Based on time-frequency decomposition, work from our group now indicates that the RewP is indexed in delta activity, not in theta (Bernat et al., 2015, 2011). Approaches based on multiple techniques suggest that the RewP has primary sources in the striatum of the basal ganglia, including EEG/ERP source localization (Foti et al., 2014, 2011a), and combined EEG/fMRI (Becker, Nitsch, Miltner, & Straube, 2014; Carlson et al., 2011). Using simultaneous fMRI-EEG recordings, Becker et al. (2014) found increased activation in the ventral striatum, midcingulate, and midfrontal cortices to positive feedback during the FN time window, and suggested that the activation of these brain regions during reward is driving the ERP differences during the time range of the FN. Conventional fMRI analysis corroborates these findings and also implicates the ACC, amygdala, and the orbital frontal cortex in reward processing (Carlson et al., 2011; Foti et al., 2014).

To bring clarity to opposing views of the FN, the FN as an error signal or a reward signal, time-frequency analytic approaches have been used to separate electrophysiological signals that are distinct in frequency band. Regression analyses using time-frequency components as predictors have shown that theta and delta frequency bands contribute unique sources of variance to the FN, with increases in theta activity reflecting loss outcomes and increases in delta activity reflecting gain outcomes (Bernat et al., 2008; Nelson, Patrick, Collins, Lang, & Bernat, 2011), leading to the conclusion that separable neural activity indexing losses and gains contributes to the FN. Foti et al. (2014) extended this work by applying source localization to time-frequency measures of the FN, where two distinct neural generators were identified. Loss-related theta activity was localized in the ACC, while gain-related delta activity was focused in the striatum (Foti et al., 2014). These results indicate that discrepancies regarding the FN and outcome valence can be clarified by time-frequency analytic approaches.

Results implicating the P300 and outcome valence are more consistent. The majority of studies have shown no relationship between P300 amplitude and outcome valence (Foti, Weinberg, Dien, & Hajcak, 2011b; Hajcak et al., 2005; Pfabigan, Alexopoulos, Bauer, & Sailer, 2011; Yeung & Sanfey, 2004), but there is some evidence showing increases to positive feedback (Bellebaum & Daum, 2008; Hajcak, Moser, Holroyd, & Simons, 2007; Zhou, Yu, & Zhou, 2010). Work from our group has supported the idea that significant, but opposite, effects in theta and delta are often responsible for suppressing effects in time-domain P300 measures (Bernat et al., 2015, 2008, 2011).

Outcome expectancy

Outcome expectancy has been investigated as an important secondary stimulus characteristic of feedback processing, but findings implicating the FN as a marker of expectancy are inconsistent. Holroyd and Coles (2002) presented a reinforcement learning theory (RL-theory) of the FN, stating that FN amplitude is monotonically related to the size of the reward prediction error (RPE), which depends on the difference between expected and actual feedback. Specifically, heightened FN amplitude reflects phasic decreases in mesencephalic dopamine signals to the ACC for a negative RPE (i.e., when outcomes are worse than expected; Holroyd & Coles, 2002). According to the RL-theory, several regions of the brain are involved in reinforcement learning: (1) the basal ganglia is the adaptive critic, which hones ongoing predictions, (2) the motor controllers (e.g., amygdala, dorsolateral prefrontal cortex, and orbitofrontal cortex) are used to update state-action mappings, and (3) the ACC is the control filter, which selects a plan according to state-action associations and communicates with the motor cortex for execution (Holroyd & Coles, 2002).

Later work by the Holroyd group and others has indicated that a reward positivity (RewP) component during the FN time window is sensitive to unexpected outcomes, and in particular, unexpected positive outcomes (Holroyd et al., 2011, 2008). As outlined in the previous section, evidence suggests the superposition of the RewP, composed primarily of delta activity during the FN time window, partially accounts for FN amplitude differences between positive and negative feedback (Bernat et al., 2008; Foti et al., 2011a; Holroyd et al., 2008; Kujawa et al., 2013; Proudfit, 2015). Results have shown that the RewP is sensitive to outcome expectancy, such that unexpected feedback produces a larger RewP compared to expected feedback, and positive relative to negative unexpected feedback produces the largest RewP (Holroyd et al., 2011, 2008).

Several studies now indicate that there is an interaction between outcome valence and expectancy on FN and RewP amplitude, where the FN is largest for unexpected negative feedback and the RewP is largest for unexpected positive feedback (Bellebaum & Daum, 2008; Bismark, Hajcak, Whitworth, & Allen, 2013; Cohen et al., 2007; Hajcak et al., 2007; Holroyd & Coles, 2002; Holroyd, Krigolson, Baker, Lee, & Gibson, 2009; Holroyd et al., 2011, 2011, 2008; Pfabigan et al., 2011; Potts et al., 2006; Walsh & Anderson, 2012). Conversely, some evidence has revealed that the FN is sensitive to unexpected outcomes regardless of valence (Alexander & Brown, 2011; Oliveira et al., 2007; Wu & Zhou, 2009). The predicted response-outcome (PRO) model proposed by Alexander and Brown (2011) presents a unifying computational model of the FN relative to ACC function. They suggest that the ACC encodes multiple independent action-outcome predictions in parallel, and ACC activity is suppressed when the predicted outcome occurs and elevated when an expected outcome fails to occur (i.e., negative surprise), regardless of outcome valence (Alexander & Brown, 2011).

Yet another study has found no difference in FN amplitude between expected and unexpected negative feedback, suggesting that the FN may not be sensitive to expectancy (Hajcak et al., 2005). However, in response to this study’s findings, Holroyd et al. (2009) showed that expectancy is evoked in tasks where the optimal response can actually be learned (as opposed to random feedback delivered independently of the participant’s behavior), a parameter lacking in the task utilized in Hajcak et al. (2005). In a follow-up study, Hajcak et al. (2007) demonstrated that FN amplitude was related to participants’ belief that they would receive a reward on the previous trial, suggesting a relationship between the FN and participants’ confidence in action-outcome associations. Taken together, these findings suggest that modulation of the FN to outcome expectancy is dependent on whether participants believe that their behavior affects outcomes.

Discrepancies in FN findings may be due, in part, to the difference wave approach utilized by many studies (i.e. where FN amplitudes are taken from loss – gain difference waveforms), which can complicate inferences about unexpected losses verses gains. Additionally, the FN calculated from the difference wave, like the regular time-domain waveform, contains mixtures of separable delta and theta band activity (Bernat et al., 2011). Given inconsistencies in the FN literature, including results showing an interaction between outcome valence and expectancy, findings revealing a main effect of expectancy regardless of valence, and research suggesting no relationship with expectancy at all, additional research using time-frequency analysis is needed to resolve difficulties quantifying time-domain FN amplitude and clarify the relationship between neural processes and outcome expectancy.

Results implicating the P300 in outcome evaluation are more consistent, where the P300 has long been shown to be sensitive to stimulus probability (Courchesne, Hillyard, & Courchesne, 1977; Duncan-Johnson & Donchin, 1977; Johnson & Donchin, 1980) and more recently, outcome expectancy (Hajcak et al., 2005, 2007; Luu, Shane, Pratt, & Tucker, 2009; Wu & Zhou, 2009; Yeung & Sanfey, 2004). These studies have demonstrated that the P300 is larger for unexpected relative to expected outcomes, regardless of valence. However, a few studies have found opposing evidence showing a larger P300 for unexpected gains relative to expected gains but either no difference between unexpected and expected losses (Cohen et al., 2007) or a difference in the opposite direction (Kreussel et al., 2012). Cohen et al. (2007) found that these P300 effects were largest over anterior electrode sites, indicating that the findings may be related to modulation of the FN as well. Research showing that the P300 is sensitive to unexpected outcomes, a secondary stimulus feature, supports the well-established theory that the P300 reflects more evaluative processing necessary for updating working memory about the task context (Donchin, 1981; Polich, 2007) However, alternative evidence showing that the P300 is modulated by the interaction between expectancy and valence suggests the need for a time-frequency approach that better indexes primary and secondary feedback attributes through theta and delta frequency bands, respectively.

A few studies have investigated outcome expectancy using time-frequency analysis. Cohen et al. (2007) found that expectancy modulated EEG power in the theta and gamma frequency bands following gains but not losses. Cavanagh (2015) showed that delta activity is sensitive to positive reward prediction errors (+RPEs), or unexpected gains. Sambrook and Goslin (2016) demonstrated that theta was sensitive to negative reward prediction errors (-RPEs), or unexpected losses, and delta was larger for +RPEs. Furthermore, there was an interaction between the size and valence of the RPE in delta, where delta was largest for high magnitude +RPEs.

Current study

The current study was designed to assess for differential valence- and expectancy-related theta and delta processing in a gambling feedback task. Additionally, the study aimed to evaluate valence- and expectancy-related modulations in time-domain FN and P300 and assess contributions of delta and theta to these effects. The study utilized time-frequency principal component analysis of EEG data recorded during a modified gambling task, in which outcome probabilities were presented with each gambling choice on every trial. Recent research has revealed that the FN and P300 contain mixtures of separable activity in the theta and delta frequency bands using these methods (Bernat et al., 2015, 2011). These frequencies have been demonstrated to be sensitive to differing stimulus features: theta activity is modulated by primary stimulus features while delta is sensitive to both primary and multiple secondary attributes (Bernat et al., 2015). Therefore, evaluation of feedback processing through time-domain analysis combines separable underlying processes indexed by theta and delta, making time-domain FN and P300 results difficult to interpret. Rather, when these ERPs are decomposed into distinct frequency bands, we expect theta and delta to be modulated as suggested by Bernat et al. (2015): theta will be most sensitive to valence, the most salient stimulus feature, while delta will be sensitive to secondary features, i.e., expectancy, in addition to valence. Furthermore, we predict that delta activity will better explain differences in expectancy among the time-domain components. If these hypotheses are confirmed, this would bolster the notion that time-frequency analysis is beneficial in understanding the role of valence and expectancy in feedback processing.

Methods

Participants

Participants (n = 34) were recruited from undergraduate students at Florida State University. Four participants were excluded due to an excessive number of EEG artifacts (>50% of trials rejected using methods described below) and four participants were removed for choosing the riskier option fewer than two times over the course of the full experiment (explained below under Procedure and Data Averaging). A total of 26 participants remained for analysis (12 females; M age = 19.38, SD = 1.92). All participants were 18 years of age or older and were screened for neurological conditions, visual impairments, and/or traumatic brain injuries. Participants were provided informed consent before starting the study and were offered monetary compensation ($10/hr) or course credit for participation.

Procedure

Data collection was conducted in a dimly lit, sound-attenuated room. Experimental stimuli were presented on a 21-inch Dell high-definition CRT color monitor, centrally placed at a viewing distance of 100 cm, subtending a visual angle of 3.5°. E-Prime version 2.0 was used to present the stimuli, and a PST Serial Response Box (Psychology Software Tools, Inc.) was used to collect responses to the task.

Participants performed a modified version of a two-choice gambling task, as shown in Figure 1 (Gehring & Willoughby, 2002). Similar to the original task, each trial consisted of two adjacent choices. After choosing between the left or right option, participants received feedback indicating whether their choice resulted in a monetary gain or loss, as well as the outcome of the unchosen option. However, our version of the task included several additional parameters, designed to modulate the riskiness of each choice, and consequently the participant’s expectation of their choice’s outcome. Each option contained a bet amount and a win amount. To choose a side, participants spent the bet amount from the total points they had accumulated. In the event of a win, the win amount was added to their total points. If the choice resulted in a loss, then only the bet amount was deducted. Each side showed a percentage that represented the likelihood of a gain. These percentages ranged in increments of 12.5%, ranging from 50%/50%, where both sides had an equal likelihood of winning, up to 87.5%/12.5%. The ratio of the bet amount to the win amount scaled with the percentage of risk, where the riskiest options resulted in the largest possible net gains. Outcome probabilities reflected the probabilities presented to the participants. Thus, participants learned that their choices affected the outcomes, a key task parameter necessary for evoking expectancy (Holroyd et al., 2009).

Figure 1.

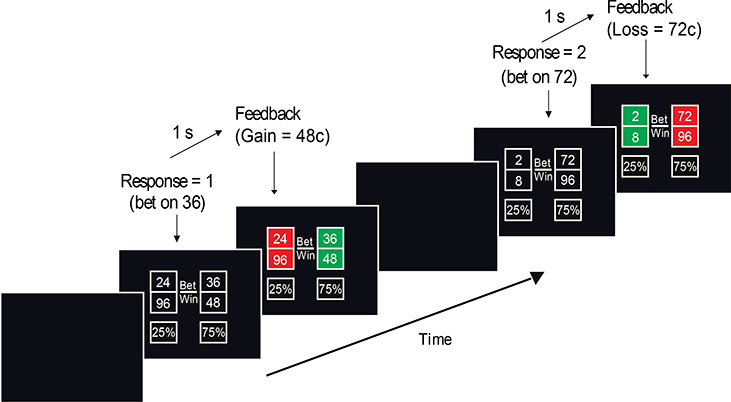
Sequence of stimulus and outcome events in the gambling task. Participants were instructed to chose between options ranging in probability of winning. Participants were given bet, win, and probability amounts (ranging from 50/50 to 87.5/12.5) for each option on every trial. One second after the participant made a choice, each square turned green or red to indicate winning or losing, respectively. If the chosen square turned green, then the win amount was awarded, and if the chosen square turned red, then the bet amount was deducted. The square that the participant did not chose also turned red or green to indicate how much money the participant would have won if (s)he had chosen that square instead. The first trial in the sequence shows an expected win and the second shows an unexpected loss.

Each trial proceeded once a choice was made, followed by feedback indicating the outcome. Feedback was displayed 1000ms after a choice was made and was shown for 1000ms. Each trial was additionally separated by a 1000ms inter-trial interval consisting of a black screen. Feedback was indicated by changing both options to different colors, either green or red, signaling a win or loss. The task consisted of two blocks of 96 trials, resulting in a total of 192 trials. Each combination of percentage was equally distributed across the task, and winning trials were counterbalanced between the left and right sides. The color associated with winning (green or red) was also counterbalanced across participants. All of the participants were given 50 points to use at the beginning of the task. Before the task began, participants completed a brief practice.

Six different outcomes were identified: outcomes that were correctly expected to result in a win or loss (i.e., choosing a high probability win and winning or a low probability win and losing), outcomes that unexpectedly resulted in a win or loss (i.e., choosing a low probability win and winning or a high probability win and losing), and outcomes that could not be predicted to result in a win or loss (50/50% percentage.) As participants knew that some choices were much riskier than others, many participants developed strategies of choosing the safer choices with smaller rewards rather than the riskier choices with larger rewards. Participants chose the safer side an average of 104.46 times (SD = 20.60) and the riskier side an average of 39.54 times (SD = 20.60).

Gambling Task

Psychophysiological Data Acquisition

Data were recorded using a Neuroscan 128-channel Quik-Cap (sintered Ag-Ag/Cl; non-frequent layout) as well as a 128-channel Synamps RT amplifier (Neuroscan, Inc.). Ten electrodes around the ears were removed from analysis due to inconsistent connection to the scalp across participants, leaving a total of 113 EEG channels. Horizontal electrooculogram (EOG) activity was recorded from electrodes placed on the outer canthus of both eyes, while vertical EOG activity was recorded from electrodes placed above and below the left eye. Impedances were kept below 10 kΩ. EEG signals were vertex referenced during recording (directly between Cz and CPz), and re-referenced to averaged mastoid signals offline, collected using an analog 0.05 to 200 Hz bandpass filter, and digitized at 1000 Hz using a Neuroscan Synamps2 system and Acquire software (Neuroscan,Inc.).

Data Preprocessing

Epochs of three seconds were then taken from 1000ms pre to 2000ms post-stimulus onset with a 150ms pre-stimulus baseline, and were re-referenced to averaged mastoid sties. Data were corrected for ocular artifacts using an algorithm developed by Semlitsch, Anderer, Schuster, & Presslich (1986), as implemented in the Neuroscan Edit 4.5 software (Neuroscan, Inc.), and downsampled to 128 Hz using the Matlab resample function (Mathworks, Inc.), which utilizes an anti-aliasing filter before resampling. Then, two methods of data cleaning were used. In the first method, trials were rejected if activity at F3 or F4 exceeded ±100 µV in either the pre-stimulus period of −1000 to −1 ms or the post stimulus period of 1 to 2000 ms, relative to the median of the other, and trials were rejected if activity in any electrode exceeded ±150 µV during the same pre-and post-stimulus time periods. This removed 20.6% of all trials from analysis. Visual analysis of the averaged waveforms indicated that 27 electrodes out of 2938 were disconnected during recording and were replaced with the mean of the nearest neighbors. After preprocessing, data were averaged according to the six different outcomes specified above under Procedures.

Data Averaging

Due to the parameters given by the task, certain outcomes were far less likely to be encountered than others. To minimize the impact of this difference, each of the six outcomes categories underwent resampling during ERP averaging. This was particularly useful because computed averages were based on the same number of trials, despite varying numbers of trials per participant (e.g. depending on the number of risky choices, number of artifacts, etc.). This was achieved by computing the average of two random trials for each outcome, 20 times, with replacement. Next, these sets of 20 resampled averages were then bootstrapped 100 times. Integrity of each waveform was preserved during bootstrapping by retaining all time points together in each step of the resampling and bootstrapping process. Despite these approaches, there were still four participants whose choices resulted in fewer than two trials in at least one outcome category, and they were removed from analysis.

Data Reduction

Time-Domain Amplitude Components.

Time-domain (TD) amplitude measures were extracted for both the FN and P300. The FN was defined as a negative deflection ranging between 203 to 352 milliseconds post stimulus, and the P300 was defined as a positive deflection ranging from 250 to 500 milliseconds. These time ranges were converted into bins of the 128 Hz resampled signal. For statistical analyses, activity for both of these components was reduced to a group of 9 electrodes (shown in Figure 2) clustered around Cz.

Figure 2.

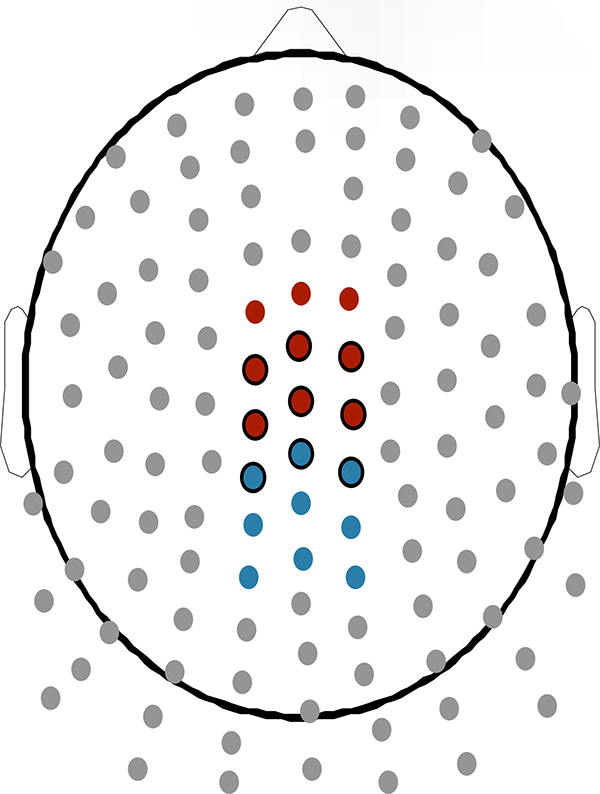
Electrode clusters for analysis of delta (blue), theta (red), and time-domain components (black border).

Time-Frequency Evoked Power.

Time-frequency transforms were next applied to the computed condition averages in the same manner as a number of other reports from our group (Bernat et al., 2011; Harper et al., 2016, 2014; Nelson et al., 2011). First, 3^rd order Butterworth filters were used to isolate activity within delta and theta frequency ranges. For delta, a 4 Hz lowpass filter was employed. For theta, a 3 Hz highpass filter in conjunction with an 8 Hz lowpass filter was used. A 1 Hz overlap was included between theta and delta (3–4 Hz), with the goal of allowing the PCA to separate out relevant activity, as detailed below. TF decompositions were produced using the binomial reduced interference distribution (RID) variant of Cohen’s class of time-frequency transformations on each epoch of the filtered signals, producing a TF representation with resolution of 32 time bins per second and 2 frequency bins per Hz. The RID was chosen to better represent low-frequency activity and avoid smearing the representation of such activity in time, consistent with our previous work. Principal component analysis (PCA) was then conducted separately on the TF decomposition from theta and delta filtered signals, using a post-stimulus time window of 0–1000ms and a 0–12 Hz frequency window. The data matrix consisted of TF points as vectors and subject/electrode/trial-averaged scores as rows (a more detailed explanation of this process can be found in Bernat, Williams, & Gehring (2005)).

One principal component (PC) was extracted from both delta and theta as the best representation of their respective frequencies. The grand-averaged TF-PCA decomposition is displayed in Figure 3. The delta PC, explaining 64.9% of the total variance, represented centro-parietal activity in the FN and P300 time-range at the 1 to 1.5 Hz range. The theta PC, explaining 55.1% of the variance, represented fronto-central activity in the FN and P300 time-range between 5 and 6 Hz. The mean PC-weighted TF amplitude of these two PCs were averaged for a subset of 9 electrodes each, shown in Figure 2, with delta clustered around a centro-parietal electrode and theta clustered around a fronto-central electrode. These clusters served as the units for analyses.

Figure 3.

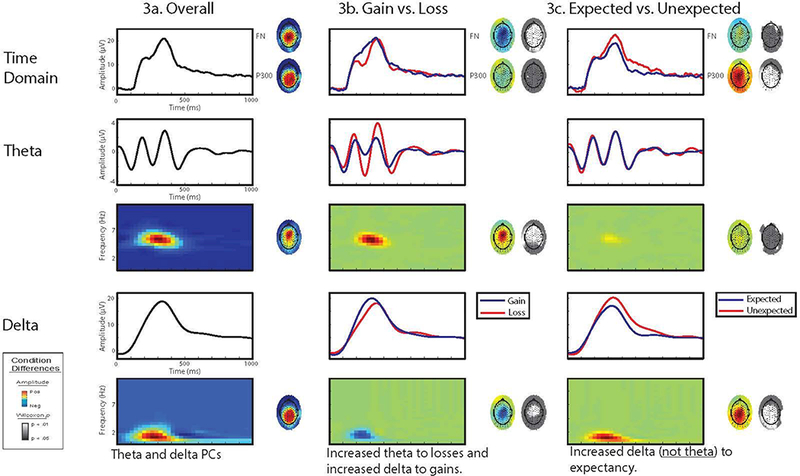
For overall, gain vs. loss, and expected vs. unexpected comparisons: average waveforms and topomaps for FN and P300 and average waveforms, time- frequency

Electrode Clusters

Data Analysis Plan

The primary analyses assessed valence- and expectancy-related processes indexed by two ERP components, the FN and P300, and how these processes were indexed using time-frequency techniques. Four measures were analyzed: the TD components of the FN and P3 and the TF principal components for delta and theta. First, each of the four measures were analyzed in separate 2 × 3 repeated measure ANOVAs: valence (gain vs. loss) by expectancy (expected, equal expectation, or unexpected). Additionally, the bivariate relationships within and between the time-domain and time-frequency measures were evaluated using Pearson correlations. Correlations were conducted for the component grand averages across condition and each condition difference. Fisher’s z-test was used to assess whether the time-domain measures (FN and P300) were significantly more related to each other than the time-frequency measures (theta and delta). These correlations were also used to assess multicollinearity in the multiple regression models. Multiple regression models with simultaneous entry of predictors were used to assess the unique contributions of delta and theta to valence and expectancy differences in the FN and P300. Regression models were only conducted for dependent variables that showed significant valence and/or expectancy differences in the ANOVAs, thus allowing for the evaluation of delta and theta’s contribution to these differences. In order to assess how delta and theta contributed to processes differences in time-domain measures, expectancy and valence difference scores were calculated. Expectancy differences were calculated by subtracting unexpected and expected outcomes and valence differences were calculated by subtracting gain and loss outcomes. The two extremes of the expectancy spectrum (unexpected and expected outcomes, not the 50/50 outcome) were chosen because they reflect the largest difference in expectancy-related processing.

Additionally, Bayesian posterior probabilities were calculated for an estimate of the probability of the null (H₀) and the alternative (H₁) hypotheses given the observed data (Masson, 2011; Wagenmakers, 2007). Whereas null-hypothesis significance only allows you to reject or fail to reject the null hypothesis, the Bayesian method allows for the quantification of evidence in favor of the alternative hypothesis and in favor of the null hypothesis. Posterior probability values range from 0 (i.e., no evidence) to 1 (e.g., very strong evidence; (Raftery, 1995))¹. The posterior probability in favor of the null hypothesis will be presented as p(H₀|D) and the posterior probability in favor of the alternative hypothesis will be presented as p(H₁|D).

Results

Time-domain FN and P3.

The first row of Figure 3 displays the average outcome-locked ERP waveform for the average of nine electrodes (see Figure 2). The overall waveform is shown as well as the gain vs. loss comparison and the expected vs. unexpected comparison. The FN is evident as the negative deflection peaking approximately 240 milliseconds after feedback onset, while the P300 is the positive deflection following the FN, peaking about 340 milliseconds after feedback onset. The scalp distribution of the FN is central while the distribution of P300 is parietal.

To test for the effects of valence (gain vs. loss) and expectancy (expected, equal expectancy, and unexpected) on the FN and P300, a repeated-measures 2 X 3 ANOVA was performed on each component. For the FN, a main effect of valence (F(1,25) = 22.74, p < 0.001, ηp² = .48, p(H₁|D) = .999) but not expectancy (F(2,50) = .25, p = .78, ηp² = .01, p(H₀|D) = .98) was found, where the negative amplitude of the FN was larger for loss relative to gain outcomes; no interaction was found. For the P300, a repeated measures 2 X 3 ANOVA with a Greenhouse-Geisser (ε = .82) correction showed an interaction between valence and expectancy (F(1.64, 41.00) = 5.56, p = .01, ηp² = .18, p(H₁|D) = .78), where the P300 was sensitive to expectancy for gains but not losses. Post hoc comparisons using t-tests indicated that P300 amplitude to unexpected gain outcomes (M = 28.83, SD = 2.14) was significantly greater than expected gain outcomes (M = 20.24, SD = 1.78, t(25) = −5.67, p < .001). Significant differences were also seen between expected gains and 50/50 gains (t(25) = −4.47, p < .001) and 50/50 gains and unexpected gains (t(25) = −2.83, p = .009).

Time-frequency component scores.

Figure 3 depicts the time-frequency (TF) decomposition of the outcome-locked ERP. For each comparison, the average waveforms and TF principal components are displayed for theta and delta. Consistent with our prior research using this approach (Bernat et al., 2015, 2011) theta activity mirrored the FN in terms of latency, medial frontal scalp distribution, and enhanced amplitude to loss relative to gain feedback. Similarly, delta activity paralleled P300 activity in terms of latency and parietal scalp distribution. Furthermore, it is apparent that negative polarity activity in theta contributes to enhanced negative FN amplitude while positive delta activity counteracts the negative amplitude of the FN. Conversely, the positive polarity of both theta and delta during the P300 time-window contribute towards enhanced positive amplitude of the P300.

To test for the effects of valence and expectancy on theta and delta, we again utilized a repeated measures 2 X 3 ANOVA design. For theta, a main effect of valence (F(1,25) = 9.60, p = .005, ηp² = .28, p(H₁|D) = .93), but not expectancy (F(2,50) = 3.08, p = .06, ηp² = .11, p(H₀|D) = .81) was found, mirroring the findings of the FN (see Figure 4); no interaction was found. For delta, a repeated measures 2 X 3 ANOVA with Greenhouse-Geisser corrections for the main effect of expectancy (ε = .74) and the interaction (ε = .77) revealed a main effect of valence (F(1,25) = 5.29, p = 0.03, ηp² = .17, p(H₁|D) = .69) and expectancy (F(2,50) = 12.19, p < .001, ηp² = .33, p(H₁|D) = .998)². However, these main effects were qualified by an interaction between valence and expectancy (F(1.54,38.50) = 4.46, p = .03, ηp² = .15, p(H₁|D) = .61). This finding emulated the P300 results, where expectancy effects were stronger in gains compared to losses. The relationship between expectancy and valence in delta is represented in the mean plots in Figure 4. Descriptive statistics reveal that delta scaled with the expectedness of the outcome, where unexpected gains showed the largest delta (M = 1.31, SD = .22) and expected gains showed the smallest delta (M = .75, SD = .12). Significant differences were seen between expected gains and unexpected gains (t(25) = −4.02, p < .001) as well as expected gains and 50/50 gains (t(25) = −3.28, p = .003).

Figure 4.

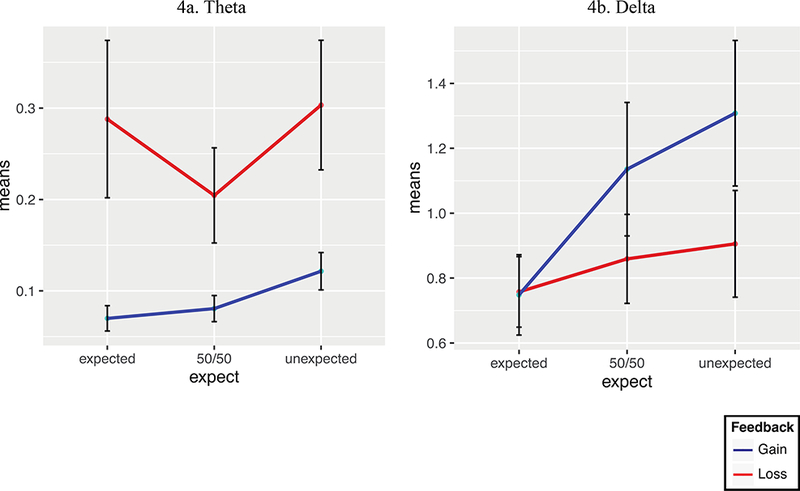
Theta (4a) and delta (4b) mean plots showing expectancy (expected, 50/50, unexpected) by valence (gain, loss) relationships.

Correlations: Within Time-Domain and Time-Frequency Measures.

In order to evaluate whether time-domain FN and P300 component measures could be understood as a mixture of more functionally distinct theta and delta processes, the correlations between FN and P300 and between theta and delta were conducted. Consistent with previous research (Bernat et al., 2015, 2011), the overall FN and P300 component average measures were significantly correlated, while the overall theta and delta measures showed a small, non-significant correlation (see Table 1). Fisher’s z-test confirms that these correlations are significantly different (z = 2.15, p = .03). Additionally, unexpected-expected differences between FN and P300 were significantly correlated while these expectancy differences between theta and delta were not. Together, these correlations support the inference that theta and delta index more independent processes than FN and P300.

Table 1.

Pearson correlations within and between time-domain measures and time-frequency measures. Gain-loss differences were calculated by subtracting overall loss from gain outcomes, and unexpected-expected differences were calculated by subtracting overall expected from unexpected outcomes.

	Component averages r	Gain-loss difference scores r	Unexpected-expected difference scores r
FN and P300	.68***	.24	.39*
Theta and Delta	.2	−.18	.25
FN and Theta	−.02	−.52**	−.37
FN and Delta	.80***	.81***	.45*
P300 and Theta	.44*	.49**	.28
P300 and Delta	.87***	.46*	.82***

Note:

^*p < .05,

^**p < .01,

^***p < .001;

N = 26

Correlations: Between Time-Domain and Time-Frequency Measures.

Correlations between time-domain FN and P300 measures and time-frequency theta and delta measures were also conducted (see Table 1). For theta, significant correlations were seen with P300 and FN for gain-loss differences but not expectancy differences. For delta, significant correlations were seen for gain-loss differences and expectancy differences.

Table 2 presents two multiple regression models with theta and delta predicting time-domain FN or P300, a technique used in previous research (Bernat et al., 2015, 2011). Regression models were only conducted for dependent variables that showed significant valence and/or expectancy differences, thus allowing for the evaluation of delta and theta’s contribution to these differences. Because a main effect of valence but not expectancy was found in the FN, one regression model assessed the contributions of gain-loss differences in theta and delta to gain-loss differences in the FN. As previous research has shown, gain-loss differences in theta and delta accounted for unique sources of variance in the FN, revealing that valence differences in the FN can be understood as a mixture of separable contributions from theta and delta. Because an interaction between valence and expectancy in the P300 was found, where expectancy effects were only seen in gain outcomes, a second regression model evaluated the contributions of unexpected-expected differences within gains in theta and delta to unexpected-expected differences within gains in the P300. Results showed that expectancy differences within gains in delta significantly predicted expectancy differences within gains in the P300, but theta did not. Thus, expectancy differences to gain feedback seem to be partially driven by contributions from delta but not theta.

Table 2.

Multiple regression models of: 1) delta and theta gain-loss differences predicting FN gain-loss differences, and 2) delta and theta unexpected-expected differences predicting P300 expectancy differences. Standardized beta coefficients are reported. No problems with multicollinearity were found (variance inflation factors were less than or equal to 2.0 and tolerance values were greater than .10).

		Delta		Theta		Overall
		Beta	t	Beta	t	F	Adj. R2
FN	Gain-loss difference across expectancy outcomes	.74	7.69***	−.38	-4.01***	44.51***	.78
P300	Unexpected-expected difference within gain outcomes	.52	2.62*	.28	1.44	14.67***	.52

Note:

^*p < .05,

^**p < .01,

^***p < .001;

N = 26

Discussion

In the current study, we analyzed brain responses to feedback stimuli in a modified gambling task where outcome valence and expectancy were of key interest. The main goals were to: (1) assess modulation of time-domain and time-frequency delta and theta to outcome valence and expectancy (2) clarify inconsistent time-domain ERP findings related to outcome valence and expectancy by utilizing time-frequency analysis, and (3) build on previous research (e.g. Bernat et al. (2015)) proposing that theta and delta are differentially sensitive to a range of stimulus characteristics.

Analysis of the FN and P300 components revealed a main effect of outcome valence on FN amplitude and an interaction between outcome valence and expectancy on P300 amplitude. The FN findings are consistent with some previous work showing enhanced amplitude to loss relative to gain feedback (Gehring & Willoughby, 2002; Hajcak et al., 2005, 2007; Luu et al., 2009; Miltner et al., 1997; Sato et al., 2005; Wu & Zhou, 2009; Yeung & Sanfey, 2004) but not other research showing sensitivity to expectancy (Alexander & Brown, 2011; Oliveira et al., 2007; Wu & Zhou, 2009) or an interaction between valence and expectancy (Bellebaum & Daum, 2008; Bismark et al., 2013; Cohen et al., 2007; Hajcak et al., 2007; Holroyd & Coles, 2002; Holroyd et al., 2009, 2011, 2008; Pfabigan et al., 2011; Potts et al., 2006; Walsh & Anderson, 2012). Similarly, some evidence has shown an interaction between outcome valence and expectancy on P300 amplitude (Cohen et al., 2007), but a large body of work had reported main effects of valence and/or expectancy (Hajcak et al., 2005, 2007; Luu et al., 2009; Wu & Zhou, 2009; Yeung & Sanfey, 2004).

We endeavored to resolve these inconsistencies by overcoming the problem of time-domain component overlap in the FN and P300 with time-frequency representations of the signals based on principal component analysis. Results revealed that theta band activity was sensitive to outcome valence, where increased theta activity was present on loss relative to gain trials. These findings are consistent with recent work from our group indicating that theta is mainly modulated by the most salient or primary stimulus attributes (Bernat et al., 2015). Delta activity was modulated by an interaction between outcome valence and expectancy, such that delta was more sensitive to expectancy for gain outcomes than loss outcomes. This interaction is also in line with previous work showing that delta is sensitive to primary and secondary stimulus characteristics (Bernat et al., 2015) and that the RewP is largest for positive relative to negative unexpected feedback (Holroyd et al., 2011, 2008).

These results suggest very strong support for the hypothesis that delta is sensitive to expectancy (p(H₁|D) = .998) and some evidence (albeit weak) that delta gains are more sensitive to expectancy than delta losses (p(H₁|D) = .61). Notably, the expectancy main effect in theta was close to significance (F(2,24) = 3.08, p = .06, η²_partial = .11). However, this was driven by the reduction in theta to the 50/50 outcome relative to the expected and unexpected outcomes (see Figure 4), rather than by differences between expected and unexpected outcomes. Perhaps theta activity was diminished for the 50/50 outcome because participants were less invested in the outcome when they had an equal likelihood of winning or losing. In any case, the posterior probability (p(H₀|D) = .81) indicates that the data more strongly favor the null hypothesis that theta is not related to expectancy overall.

Previous research has shown that the FN and P300 contain separable theta and delta activity, as described above. Correlations revealed that the FN and P300 were more strongly related than theta and delta, demonstrating that time-frequency measures reflect more independent processes. To better elucidate the impact of these separable processes indexed by time-frequency measures on FN and P300, regression analyses were employed predicting time-domain measures with time-frequency delta and theta. Regression models were only conducted for dependent variables that showed significant valence and/or expectancy differences, thus allowing for the evaluation of delta and theta’s contribution to these differences. Because a main effect of valence but not expectancy was found in the FN, one regression model assessed the contributions of gain-loss differences in theta and delta to gain-loss differences in the FN. As previous research has shown, gain-loss differences in theta and delta accounted for unique sources of variance in the FN, demonstrating that valence differences in the FN are driven by separable contributions from loss-sensitive theta and gain-sensitive delta. Since an interaction between outcome valence and expectancy was found in P300 amplitude, multiple regression was used to assess the contributions of theta and delta expectancy differences within gains to P300 expectancy differences within gains. Results revealed that P300 expectancy differences within gain outcomes were significantly predicted by delta but not theta. Thus, the P300 was shown to be a sensitive index of expectancy-related processing differences, driven primarily by underlying delta activity indexed with time-frequency approaches.

Time-frequency results from the current study are consistent with recent theories about stimulus processing more broadly, notably about the processes underlying the P300 ERP component. A growing body of evidence suggests that the P300 is composed of two spatiotemporally overlapping components, a more fronto-central P3a and a more centro-parietal P3b (Debener, Makeig, Delorme, & Engel, 2005; Spencer, Dien, & Donchin, 1999, 2001). Recent models of these two processes propose that the early fronto-central component reflects a simple response involving attention and salience processing, and the later centro-parietal component involves more complex processing (Polich, 2007). This work suggests that these two processes are combined in conventional time-domain measures of P300 components, and that the relative weight of these processes will determine the amplitude and topographical distribution of an observed P300 component (e.g. P3a and P3b). There is widespread support for the contention that fronto-central theta and centro-parietal delta activity occurs during oddball tasks generating conventional P300 component activity (Kolev, Demiralp, Yordanova, Ademoglu, & Isoglu-Alkaç, 1997; Spencer & Polich, 1999; Sirel Karakaş, Erzengin, & Başar, 2000; S. Karakaş, Erzengin, & Başar, 2000; Yordanova, Devrim, Kolev, Ademoglu, & Demiralp, 2000; Demiralp, Ademoglu, Istefanopulos, et al., 2001; Demiralp, Ademoglu, Comerchero, & Polich, 2001; Porjesz et al., 2005; Bernat et al., 2007; Başar et al., 2001; Bachman & Bernat, in review), and recent work from our group has extended this observation to gambling feedback (Bernat et al., 2015, 2011) and go/no-go tasks (Harper et al., 2016, 2014). The present results contribute to this body of information by demonstrating the P300 is partially modulated by expectancy-sensitive, central-parietal delta activity.

Limitations and future directions.

One main limitation that must be acknowledged is small sample size. The final sample size was 26 participants, after four were removed for excessive EEG artifacts and four were removed for choosing the riskier choice less then two times throughout the task. By reducing the sample to 26 participants, we retained all outcome iterations, including the less probable outcomes associated with unexpected gains and expected losses. Alternative approaches, such as tasks in which choices are made for the participants, would not involve the same sense of expectation, as participants’ behavior would not be causally related to the outcomes, a task component necessary for inducing expectancy (Holroyd et al., 2009). Indeed, variations in the tendency to chose the risker, high reward option is an important topic for future research investigating individual differences in risk-averse choice behavior. Furthermore, the current task did not employ a training portion in which participants learned to associate cues with certain outcomes; instead, probabilities were explicit and participants learned that they were linked to outcomes. The effect of our non-traditional probabilistic learning task on expectancy results is unclear.

Future work should evaluate the brain regions and networks associated with valence- and expectancy-related delta activity. Gain-related delta activity has been shown to have contributions from the striatum in the basal ganglia (Foti et al., 2014), but considering the widespread topography of delta activity, source localization methods and fMRI approaches would be helpful in order to identify the brain regions and networks implicated in expectancy-related delta. Future research could also expand upon our methods by utilizing single trial analysis in order to assess behavioral adaptation associated with reinforcement learning and how delta and theta are related to performance. Cavanagh, Frank, Klein, & Allen, (2010), for example, found that medial frontal theta reflected reaction time slowing to errors and lateral frontal theta reflected reaction time speeding for the correct choices.

Importantly, results from the current study show that expectancy effects are only found within gain outcomes and not loss outcomes. This effect is seen in the time-domain P300 and is partially driven by delta activity, but not theta. These findings build on previous work showing that loss processes are more basic or simple, whereas gain processes are more sensitive to complex task features, such as reward magnitude (Bernat et al., 2015) and now expectancy. These results could have important implications for the factors that drive learning and might suggest that gains or positive outcomes are more integral to the reinforcement learning system. Future work investigating outcome expectancy and reinforcement learning should assess the role of rewarding feedback using time-frequency delta.

Conclusions

Results indicate that the FN is primarily sensitive to outcome valence and not expectancy, and reflects contributions from delta-gain activity and theta-loss activity. The P300, on the other hand, indexes expectancy differences for gain outcomes only, and these effects are driven by delta activity, not theta. Taken together, these findings further bolster work in the field suggesting that theta is mainly sensitive to primary/salient stimulus features while delta is sensitive to primary as well as more complex secondary features, now including expectancy.

Highlights:

• FN is sensitive to outcome valence but not expectancy; valence effects are driven by loss-sensitive theta and gain-sensitive delta

• P300 is sensitive to outcome expectancy for gain outcomes only; expectancy effects are driven by delta, not theta

• Theta band activity is sensitive to the most salient stimulus feature, outcome valence

• Delta band activity is modulated by valence as well as a more complex characteristic: outcome expectancy