On quantification of geometry and topology of protein pockets and channels for assessing mutation effects

Abstract

Geometric and topological features of proteins such as voids, pockets and channels are important for protein functions. We discuss a method for visualizing protein pockets and channels based on orthogonal spheres computed from alpha shapes of the protein structures, and how metric properties of channel surfaces can be mapped. In addition, we discuss how structurally prominent sites, such as constriction sties in channels, can be computed, which may help to understand protein functions and mutation effects, with implications in developing novel therapeutic interventions.

I. INTRODUCTION

Geometric and topological properties of protein structures, including voids, pockets and channels are of fundamental importance for proteins to carry out their functions. Understanding the geometric basis of the mechanism of protein functions and predicting effects of mutations at specific sites through characterization of these geometric and topological properties can provide useful information for understanding the mechanism of diseases, and may help to characterize drug-protein interactions and for developing additional therapeutic intervention strategies.

A number of computational methods have been developed to detect voids and pockets in protein and to relate their roles in biochemical functions [1–4]. Among these methods, geometric and topological techniques, such as CASTp [5, 6] based on the alpha shape theory [7], can provide accurate characterization of topological and geometric properties of proteins. However, current identification and visualization of pockets and channels are cumbersome, as the detection of the most prominent feature depends on pre-specified threshold related to size, which may differ among different proteins and may not be known a priori. Moreover, current methods in visualization of pockets and channels do not contain mapping between pocket surface and metric information of individual atoms and residues. In addition, detection of potentially multiple constriction sites and residues involved remains a difficult task.

Using the alpha complex techniques, one can detect voids, pockets and channels from a given protein structure, and determine the relevant atoms and residues of each geometric feature [7]. Here we briefly revisit the alpha complex techniques, and show that these can be visualized using the orthogonal spheres to the set of Delaunay tetrahedra that form the pockets or channels. The metric contributions of atoms on the wall of the pockets or channels can also be mapped to the orthogonal spheres.

II. ALPHA COMPLEX TECHNIQUES

A. Voronoi diagram

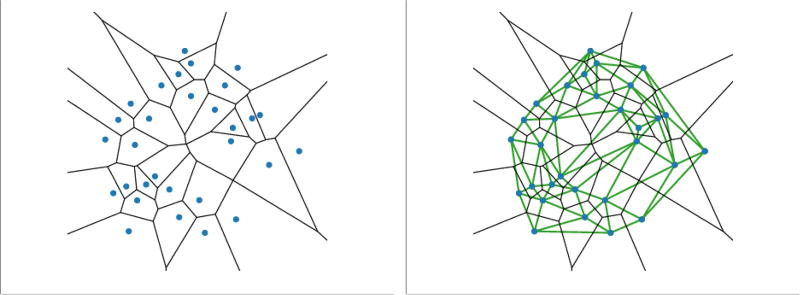
The Voronoi diagram of a set of points S in ℝ³ is formed by the collection of Voronoi cells that cover the ℝ³ space. Fig 1 shows a set of points and the corresponding Voronoi diagram in ℝ². All the features of the description in ℝ², which we will discuss in this paper, have more complex counterparts in ℝ³. We will use the 2D point set in Fig 1 for all figures of this paper for the sake of simplicity. A Voronoi cell V_s of a point s is a convex polyhedron that contains all points in ℝ³, distance of which to the point s is no longer than the distances to the other points:

$$V_s=\{x\in {ℝ}^3|\Vert x-s\Vert \le \Vert x-t\Vert ,\forall t\in S\},$$ (1)

where ‖·‖ stands for the Euclidean distance.

Fig. 1.

The Voronoi diagram of a set of points and the corresponding Delaunay triangulation. A simplified case of points in ℝ² is used here. The blue dots are the points in S. The black polygons are the Voronoi cells, while the green ones are the Delaunay triangulation.

Given the Voronoi diagram generated by S, we can obtain the dual Delaunay tetrahedralization by connecting two points by a straight edge whenever the corresponding two Voronoi cells share a plane (Fig 1). Three Voronoi regions may share an edge, which is then the interaction of the three planes formed by taking pairwise intersections. Correspondingly, the three points form a triangle in the Delaunay tetrahedralization. Similarly, one intersecting point of four Voronoi cells corresponds to a tetrahedron in the Delaunay tetrahedralization. We assume that the point of S are in general position, meaning that no 4 points lie on a common plane, and no 5 points lie on a common sphere. As a result, there will be no intersection point formed by more than 4 Voronoi planes. The Delaunay tetrahedralization is a division of the convex hull of S.

B. Alpha shape

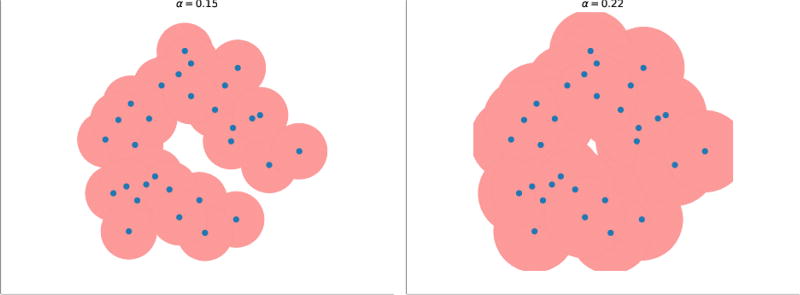
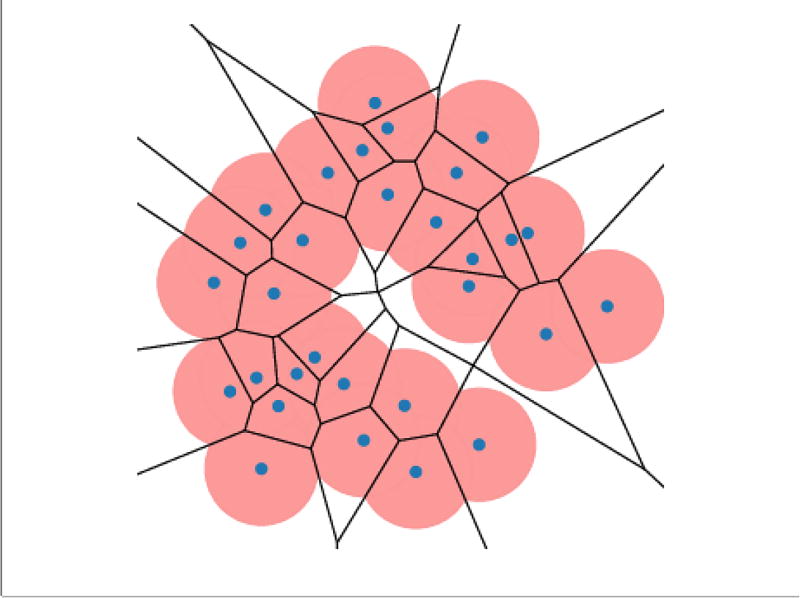
To obtain the shape of S, we place balls B_s (α) with radius α centered on each point s of S. With different radius α, different subspace of ℝ³ is covered by the union of the balls (Fig 2). To define the alpha-shape, we overlay the union of balls with the Voronoi diagram (Fig 3). To formalize this idea, we write

$$R_s(\alpha )=V_s\cap B_s(\alpha ),$$ (2)

$${𝕌}_S(\alpha )=\underset{s\in S}{\cup }{R}_s(\alpha ).$$ (3)

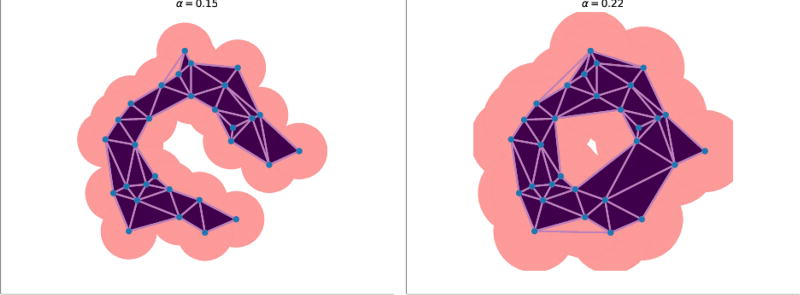
We construct the alpha-complex A_S (α) following the procedure of Delaunay tetrahedralization (Fig 4). For example, whenever two regions R_s (α) intersect in a common plane, we draw an edge connecting the two corresponding points.

Fig. 2.

The union of alpha-balls with different α values. Left: α = 0.15; right: α = 0.22. The pink region is the union of the alpha-balls (−disks in this 2D case).

Fig. 3.

The superimposition between the Voronoi diagram and the union of alpha-balls.

Fig. 4.

The alpha-complex with different values of α. Left: α = 0.15; right: α = 0.22. The dark purple triangles and the light purple are the simplexes form the alpha-complex of the specific value of α. As the α increases, the number of simplexes that from the alpha-complex increases.

C. Filtration

A_S(α) is a generalization of Delaunay tetrahedralization. When α varies from 0 to ∞, the corresponding alphacomplex varies from the set of points without any additional structure (A_S(0)) to the Delaunay tetrahedralization of S (A_S(∞)). For α ≤ α′, B_S (α) ⊆ B_S(α′) and therefore R_S(α) ⊆ R_S(α′). Thus R_S(α) ⊆ R_S(α′) For each vertex, edge, triangle, and tetrahedra σ in the Delaunay tetrahedralization, denote α_σ as the smallest value of α for which σ belongs to A_S(α). We can construct the alpha-complex by collecting all vertices, edges, triangles, and tetrahedron that have a value not larger than α:

$$A_S(\alpha )=\{\sigma \in K|{\alpha }_{\sigma }\le \alpha \},$$ (4)

where K is the Delaunay tetrahedralization of S. We can easily find α_σ for every vertex, edge, triangle and tetrahedra in the Delaunay tetrahedralization, which can be sorted such that

$${\alpha }_{{\sigma }_1}\le {\alpha }_{{\sigma }_2}\le \cdots \le {\alpha }_{{\sigma }_n}.$$ (5)

The corresponding increasing sequence of complexes is

$$S=A_S(0)\subseteq A_S({\alpha }_{{\sigma }_1})\subseteq A_S({\alpha }_{{\sigma }_2})\subseteq \cdots \subseteq A_S({\alpha }_{{\sigma }_n})=K.$$ (6)

D. Voids, pockets, channels, and their orthogonal sphere representation

When we vary the value of α, voids in the corresponding alpha-complex appear and disappear. Using the filtration technology, we can keep track of the voids. For example, Fig 2 shows how a void in the center of a set S of points forms, while Fig 4 shows how the corresponding alpha-complex changes. If we keep increasing α, the void in the center will eventually disappear, and the alpha-complex will become the Delaunay tetrahedralization of S. A pocket can be defined as a subset of the complement of the alpha-complex that becomes a void before it disappears. A channel may be cut from the outside at two or more places when increasing α, defining the space enclosed by these openings as a pocket with more than one mouth. We refer to [3] for more details about detection and representation of voids, pockets, and channels.

For each tetrahedra constructed by four point s₁, s₂, s₃, and s₄, denote τ as the intersecting point of the four corresponding regions R_si, where i = 1 ⋯ 4. By definition of Voronoi diagram, the distance of τ from the points is the same:

$$r_{\tau }=\Vert \tau -s_1\Vert =\Vert \tau -s_2\Vert =\Vert \tau -s_3\Vert =\Vert \tau -s_4\Vert$$ (7)

τ is thus refered as orthogonal center. The orthogonal sphere centering at τ with radius r_τ has the four points on its boundary (surface), but no other point inside it. The orthogonal spheres can be used to represent and visualize the voids, pockets, and channels of the alpha-complex.

E. Weighted alpha-complex

The representation of space-filling balls is similar to the van der Waals diagram of a protein, where the difference is that different types of atoms affecting neighboring atoms differently, thus leads to different weights or radii. Using this insight, we can assign different weight w_s to each point s in S. Using a corresponding metric of power distance,

$$d(s,x)=\Vert x-s\Vert -w_s,$$ (8)

we can construct the weighted Voronoi diagram, Delaunay tetrahedralization, and thus the weighted alpha-complex. We refer [3] for more details about these constructions using power distance. By assigning the van der Walls radius as the weight to each atom, we can detect voids, pockets, and channels of the protein.

F. Topological persistence

Betti numbers that count holes of different dimension of simplicial complexes can be used to characterize the topological properties of the complex. During the filtration process of the weighted alpha-complex of a protein, geometric features appear and disappear. For example, with the increase of α, a channel may appear, break into subpockets, and disappear eventually. In practice, there is no need to simulate the process of increasing the alpha value. Instead, a sorting of each simplexes according to their alpha value will be enough. We can track these geometric features during the filtration process by calculating the Betti numbers. The topological persistence can be used to detect critical geometric features, for example constriction sites, of proteins. More details of filtration and topological persistence can be found in [8].

III. Map of pocket region controlled by each atom

In addition to detection of pockets, the properties of different region of a pocket is important in determining the function of the pocket. It is therefore essential to map the physicochemical properties, including electrostatics, hydrogen bonding, hydrophobicity, polarity, and rigidity of each atom or residue onto to the surface of the pocket. However, there is currently no method that can do this mapping. Here, using the properties of weighted alpha-complex and the power distance, we show that different pocket region can be mapped to each atom that controls this region.

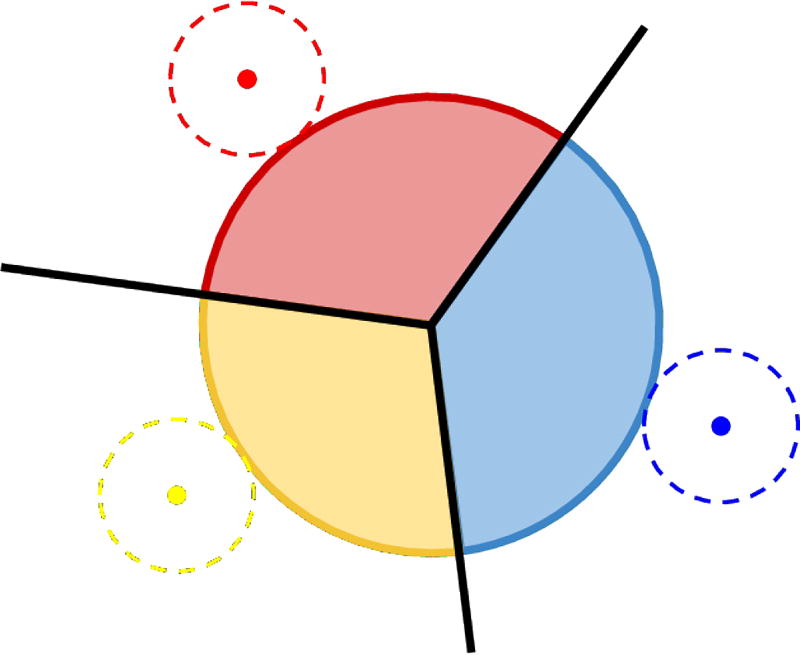
An orthogonal sphere Orth_s1,s2,s3,s4 (α) can be divided using weighted Voronoi diagram (Fig 5)

$${\text{Orth}}_{s_i}(\alpha )={\text{Orth}}_{s_1,s_2,s_3,s_4}(\alpha )\cap R_{s_i}(\alpha ),i,\cdots ,4.$$ (9)

This division gives a map of region controlled by each atom under the definitions of power distance, which can be further used to guide the mapping of the physicochemical properties of atoms/residues to the pocket.

Fig. 5.

Map of area controlled by atoms. The multiple colored disk in the middle is the orthogonal circle formed by 3 weighted atoms (3 atoms instead of 4 in this 2D illustration). The 3 dashed circles stands for the atoms. The black vertex and edges show Voronoi diagram constructed using these atoms. The orthogonal circle is colored according to the closest atom using the Voronoi diagram.

IV. Detecting pockets, channels and prominent sites

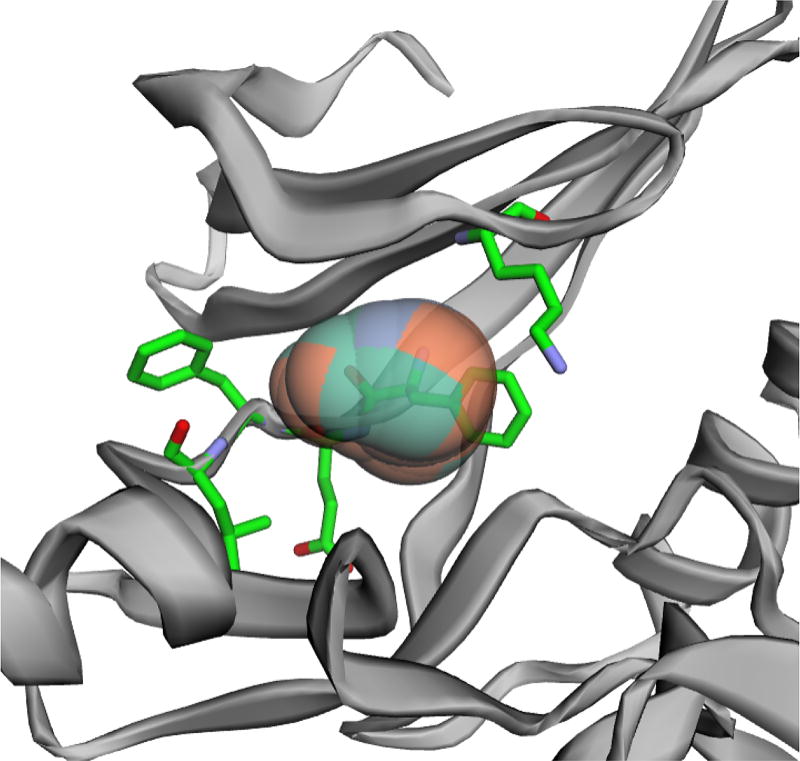
With the orthogonal spheres to the set of weighted alpha-complex, we can detect and visualize protein pockets and channels and the map of area controlled by each atom/residue. Fig 6 shows a pocket of human cyclin-dependent kinase 2 (CDK2) for ATP binding, which is an important target for design of antitumor agents [9]. Mutation or modification of the residues that form the pocket, namely K33, F80, E81, F82, and L83 (shown in sticks in Fig 6), could affect the interaction between the pocket and ATP. Study has shown that acetylation of K33 inhibits CDK2 activity [10]. For each orthogonal sphere of the pocket, the surface is colored according to the type of the closet atom quantified by the power distance, which is useful in further mapping the physiochemical properties of atoms/residues. These information will facilitate the structure-based drug design.

Fig. 6.

A potential druggable pocket detected in CDK2 (PDB id 1e9h [9]). Important residues that form the pocket are shown as sticks.

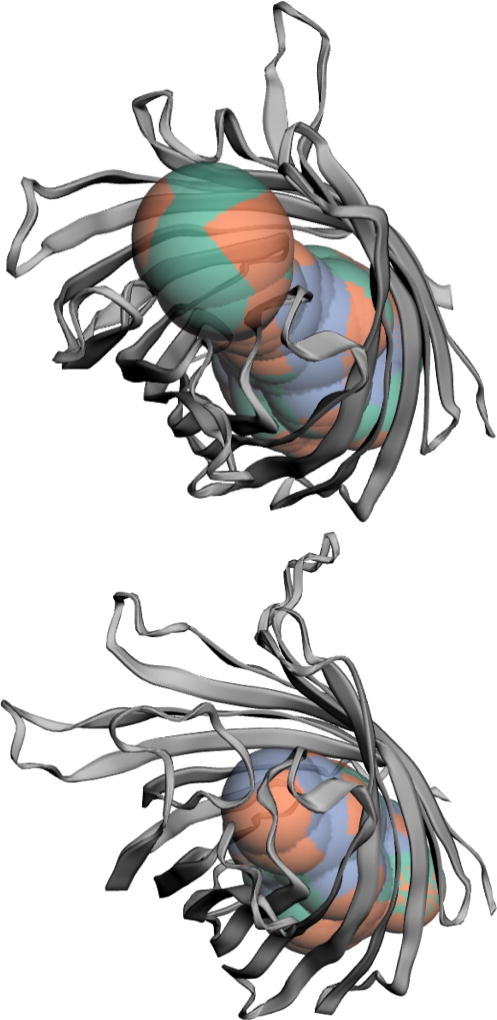
Bacterial outer membrane porins have important effects in several pathogenic mechanisms. Outer membrane protein G (OmpG) is a porin with gating behaviors. We can detect the channels in the open and closed states (Fig 7), which shows how the loops affect geometry and conductance of the channel.

Fig. 7.

Change of the channel of OmpG. Top: open state (PDB id 2iwv [11]); bottom: closed state (PDB id 2iww [10]).

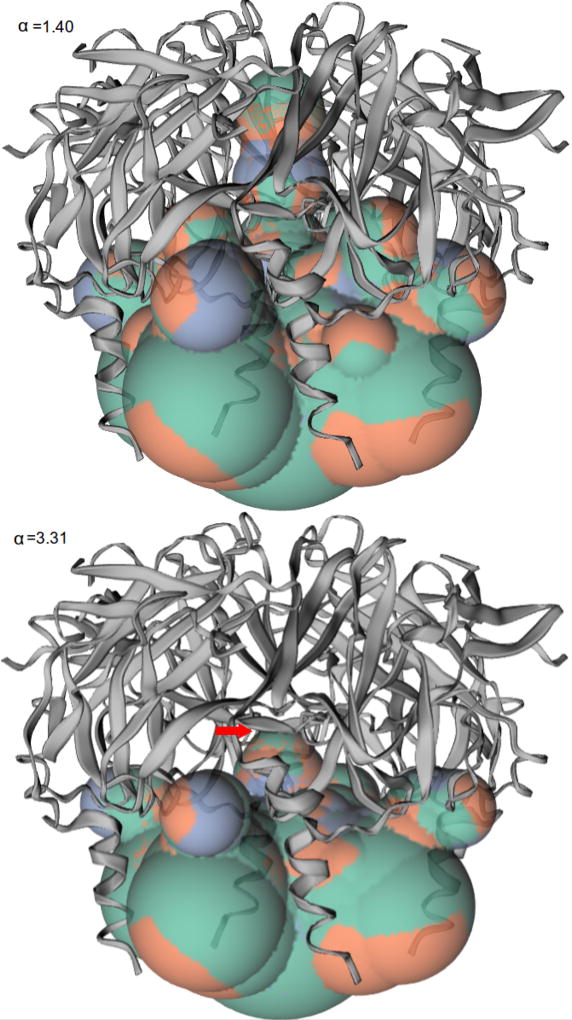
Based on the computation of topological persistence using the filtration of the computed alpha complexes, we can find structurally prominent sites of proteins independent of any pre-specified threshold or a priori knowledge. For example, the G protein-coupled inwardly-rectifying potassium channel 1 (GIRK1) participates in a wide range of physiologic responses. When we increase the value of α, the channel detected keeps narrowing until it breaks at α = 3.31, indicating a constriction site of the channel at the breaking position (Fig 8).

Fig. 8.

Channel detected with different values of α of GIRK1 (PDB id 1u4e [12]). The red arrow points to the constriction site.

V. Conclusion

In this paper, we discuss the alpha-complex techniques and how they can be applied in analyzing protein structures. For a protein channel, we have constructed the map of area controlled by each atom which forms the channel using the power distance. This can be used to map the physicochemical properties of atoms/residues onto the channel, which is helpful in understanding its functions and properties. we also show how residues that are likely important in maintaining the topological properties can be located. This will help us to identify key atoms and residues important for selectivity and specificity, and aid in finding potential druggable regions for novel interventions.