Acoustic Denoising using Dictionary Learning with Spectral and Temporal Regularization

Abstract

We present a method for speech enhancement of data collected in extremely noisy environments, such as those obtained during magnetic resonance imaging (MRI) scans. We propose an algorithm based on dictionary learning to perform this enhancement. We use complex nonnegative matrix factorization with intra-source additivity (CMF-WISA) to learn dictionaries of the noise and speech+noise portions of the data and use these to factor the noisy spectrum into estimated speech and noise components. We augment the CMF-WISA cost function with spectral and temporal regularization terms to improve the noise modeling. Based on both objective and subjective assessments, we find that our algorithm significantly outperforms traditional techniques such as Least Mean Squares (LMS) filtering, while not requiring prior knowledge or specific assumptions such as periodicity of the noise waveforms that current state-of-the-art algorithms require.

I. Introduction

Technological applications using speech are ubiquitous, and include speech-to-text systems [1], emotional-state detection [2], and assistive applications, such as hearing aids [3]. The presence of background noise usually degrades the performance of these systems, thus limiting their use to confined environments or scenarios. Researchers are actively developing speech denoising methods to overcome these barriers. Such methods include signal subspace approaches [4], model-based methods [5], and spectral subtraction algorithms [6]. These different techniques make specific assumptions about the noise or SNR levels, and give a certain trade-off between noise suppression and speech distortion. This trade-off is particularly important when denoising speech for speech science analysis.

This paper focuses on denoising speech audio obtained during magnetic resonance imaging (MRI) scans, a major motivation arising from speech science and clinical applications. Speech science researchers use a variety of methods to study articulation and the associated acoustic details of speech production. These include Electromagnetic Articulography [7] and x-ray microbeam [8] methods that track the movement of articulators while subjects speak into a microphone. Data from these methods offer excellent temporal details of speech production. Such methods, however, are invasive and do not offer a full view of the vocal tract. On the other hand, methods using real-time MRI (rtMRI) offer a non-invasive method for imaging the vocal tract, affording access to more structural details [9]. Unfortunately, MRI scanners produce high-energy broadband noise that corrupts the speech recording. This affects the ability to analyze the speech acoustics resulting from the articulation and requires additional schemes to improve the audio quality. Another motivation for denoising speech corrupted with MRI scanner noise arises from the need for enabling communication between a patient and a provider during scanning.

The Least Mean Squares (LMS) algorithm is a popular technique for signal denoising. The algorithm estimates the filter weights of an unknown system by minimizing the mean square error between the denoised signal and a reference signal. This approach removes noise from the noisy signal very well, but severely degrades the quality of the recovered speech [10]. Bresch et al. proposed a variant to the LMS algorithm in [11] to remove MRI noise from noisy recordings. This method, however, uses knowledge of the MRI pulse sequence to design an artificial reference “noise” signal that can be used in place of a recorded noise reference. We found that this method outperforms LMS in denoising speech corrupted with noise from certain types of pulse sequences. Unfortunately, it performs rather poorly when the noise frequencies are spaced closely together in the frequency domain. Furthermore, the algorithm creates a reverberant artifact in the denoised signal, which makes speech analysis challenging. The LMS formulation assumes additive noise, so these algorithms may not perform well in the presence of convolutive noise in the signal, which we encounter during MRI scans.

Recently, Inouye et al. proposed an MRI denoising method that uses correlation subtraction followed by spectral noise gating [12]. Correlation subtraction finds the temporal shift that maximizes the correlation between the noisy signal and a reference noise signal, and subtracts this shifted reference noise from the noisy signal. The residual noise from this procedure is removed by spectral noise gating, which uses the reference noise to calculate a spectral envelope of the noise and attenuates the frequency components of the noisy speech that are below the noise spectral envelope. Their method showed a high level of noise suppression and low distortion, both desirable properties of a denoising algorithm. A drawback to their approach is manual setting of the threshold in the spectral noise gating. Furthermore, their algorithm assumes access to a reference noise recording. As such, their algorithm would not be suitable for use in single-microphone setups and would perform poorly if speech leaks into the reference microphone.

We propose an algorithm for removing MRI scanner noise using complex non-negative matrix factorization with intra-source additivity (CMF-WISA) [13] with additional spectral and temporal regularizations. CMF-WISA learns the dictionaries and their associated time activation weights for the speech and noise, which enables separation of the noisy signal into speech and noise components. Unlike non-negative matrix factorization (NMF), CMF-WISA also estimates the phases of the speech and noise components, which improves source separation and reconstruction quality of the speech and noise components. The initial version of the denoising algorithm and preliminary results were presented originally in [14]. This paper extends the original algorithm in three important ways:

• We switch from a sequential two-step algorithm of dictionary learning and wavelet packet analysis to a single-step dictionary learning-only method. This switch can enable the development of a real-time version of the algorithm.

• We use CMF-WISA instead of NMF to use magnitude and phase information about the signal when learning speech and noise dictionaries.

• We incorporate spectral and temporal regularization in the CMF-WISA cost function to better model spectro-temporal properties of the MRI noise during speech production.

A MATLAB implementation of this algorithm is available at github.com/colinvaz/mri-speech-denoising.

This paper is organized as follows. Section II discusses properties of MRI noise. After providing a synopsis of the notations we will use in this article in Section III and a brief overview of NMF in Section IV, we describe the denoising algorithm in Section V. Section VI discusses the experiments we conducted and the evaluation metrics we used to evaluate the denoising performance. Section VII gives insight into the parameter settings for the proposed algorithm and Section VIII shows the results of our method on data acquired from MRI scans and artificially-created noisy speech. Finally, Section IX offers our conclusions and directions for future work.

II. MRI Noise

MRI scanners produce a powerful magnetic field that aligns the protons in water molecules with this field. The MRI operator briefly turns on a radio frequency electromagnetic field, which causes the protons to realign with the new field. After the electromagnetic field is turned off, the protons relax back their alignment with the scanner’s magnetic field. The on and off switching pattern of the electromagnetic field is called a pulse sequence. The pulse sequence constantly realigns the protons, which causes a changing magnetic flux, and which in turn generates a changing voltage within the receiver coils.

During each pulse, the MRI scanner samples these changing voltages in the 2-dimensional Fourier space (called k-space). In real-time MRI (rtMRI), the pulses are repeated periodically to get a temporal sequence of images. The period between each repetition is called the repetition time (TR). Typically, the readout from multiple successive pulses are combined to form one image because it improves the SNR and spatial resolution of the image. The number of pulses that are combined to form one image is called the number of interleaves. The number of interleaves gives a trade-off between spatial and temporal resolution of the images; a higher number of interleaves increases the spatial resolution but decreases the temporal resolution.

A primary source of MRI noise arises from Lorentz forces, due to the pulse sequence, acting on receiver coils in the body of an MRI scanner. These forces cause vibrations of the coils, which impact against their mountings. The result is a high-energy broadband noise that can reach as high as 115 dBA [15]. The noise corrupts the speech recording, making it hard to listen to the speaker, and can obscure important details in speech.

MRI pulse sequences typically used in rtMRI produce periodic noise because the pulse is repeated every TR. The fundamental frequency of this noise, i.e., the closest spacing between two adjacent noise frequencies in the frequency spectrum, is given by:

$$f_0=\frac{1}{\text{TR}\times \text{number}\text{of}\text{interleaves}}\text{Hz}$$ (1)

The repetition time and number of interleaves are scanning parameters set by the MRI operator. Choice of these parameters inform the spatial and temporal resolution of the reconstructed image sequence, as well as the spectral characteristics of the acoustic noise generated by the scanner.

Table I provides a summary of the pulse sequences that we will consider in this article and their properties. Importantly, the periodicity property of the noise allows us to design effective denoising algorithms for time-synchronized audio collected during rtMRI scans. For instance, the algorithm proposed by Bresch et al. [11] relies on knowing f₀ to create an artificial “noise” signal which can then be used as a reference signal by standard adaptive noise cancellation algorithms. This algorithm has been shown to effectively remove noise from some commonly-used rtMRI pulse sequences, such as Sequences 1–3 (seq1, seq2, seq3), and the multislice (mult) sequence listed in Table I.

TABLE I.

Description of common rtMRI (seq1, seq2, seq3, ga21, ga55, mult) and static 3D (st3d) pulse sequences.

Pulse sequence usage	Pulse sequence	TR (ms)	Number of interleaves	f0 (Hz)
Real-time (dynamic) MRI (rtMRI)	seq1	6.164	13	12.48
	seq2	6.004	13	12.81
	seq3	6.028	9	18.43
	ga21	6.004	21	7.93
	ga55	6.004	55	3.03
Multislice rtMRI	mult	6.004	13	12.81
Static 3D MRI	st3d	4.22	N/A	N/A

However, there are pulse sequences that do not exhibit this exact periodic structure. In addition, there are other useful sequences that are either periodic with an extremely large period, resulting in very closely-spaced noise frequencies in the spectrum (i.e. f₀ is very small), or are periodic with discontinuities that can introduce artifacts in the spectrum. To handle these cases, it is essential that denoising algorithms do not rely on periodicity. One example of such sequences which we will consider in this article is the Golden Angle (GA) sequence [16], which allows for retrospective and flexible selection of the temporal resolution of the reconstructed image sequences (typical rtMRI protocols do not allow this desirable property). We will consider the ga21 and ga55 Golden Angle sequences in this article. These two sequences, along with seq1, seq2, seq3, and mult, constitute the rtMRI pulse sequences that this article focuses on.

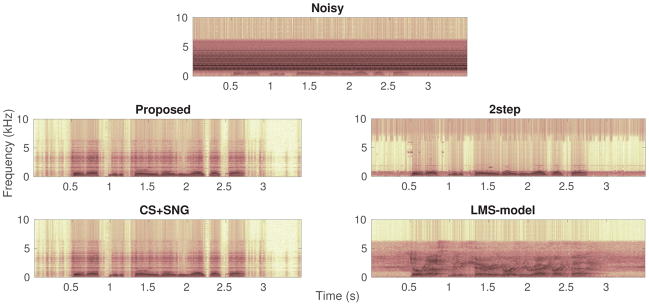
In addition to using rtMRI for imaging speech dynamics, one can use 3D MR imaging to capture a three-dimensional image of a static speech posture. 3D pulse sequences scan the vocal tract in multiple planes simultaneously. Such sequences can be highly aperiodic, and like the GA sequences require a denoising algorithm that does not rely on periodicity for proper denoising. We will consider the st3d static 3D pulse sequence in this article (see Table I). For further reading about MRI pulse sequences and their use in upper airway imaging, see [16], [17], [18]. For an example spectrogram of speech recorded with the seq3 pulse sequence, see the top panel in Figure 2.

Fig. 2.

Noisy and denoised spectrograms of the sentence “Don’t ask me to carry an oily rag like that” in the MRI-utt dataset. The noise is seq3.

III. Notation

Prior to introducing the algorithm, we lay out the notation conventions and variables we will use throughout the paper for clarity.

We denote scalars by lower case letters (eg. m, t), vectors by bolded lower case letters (eg. x, μ), and matrices by upper case letters (eg. V, W). [V]_ij, [V]_j, and [V]_i,: denote the (i, j)th entry, jth column, and ith row of V respectively. We use ⊙ to denote element-wise product between two matrices and a fraction involving two matrices (eg. $\frac{A}{B}$) to denote element-wise division. We define ${[A]}^{+}=\frac{1}{2}(\mid A\mid +A)$ as a matrix containing only the positive values of A and ${[A]}^{-}=\frac{1}{2}(\mid A\mid -A)$ as a matrix containing only the absolute value of the negative values of A. The notation diag (x) is used to form a diagonal matrix with the diagonal elements from vector x.

ℝ, ℝ^m×t, and ${ℝ}_{+}^{m\times t}$ denote the sets of real numbers, m × t real-valued matrices, and m × t non-negative matrices respectively. Similarly, ℂ and ℂ^m×t denote the sets of complex numbers and complex-valued matrices respectively.

Table II shows the key variables we will use consistently throughout the manuscript as well as a brief description for quick reference.

TABLE II.

Key variables.

Variable	Meaning
ks, kd	Number of basis elements in the speech and noise bases
td, tn	Number of spectrogram frames of the noise-only and noisy speech signals
Vs, Vd, V	Complex-valued spectrograms of speech, noise-only, and noisy speech signals
Ws, Wd, Wn	Speech basis, noise basis learned on noise-only signal, and noise basis learned on noisy speech
Hs, Hd, Hn	Speech time-activation matrix, noise time-activation matrix learned on noise-only signal, and noise time-activation matrix learned on noisy speech
Ps, Pd, Pn	Speech phase matrix, noise phase matrix learned on noise-only signal, and noise phase matrix learned on noisy speech

IV. Non-negative Matrix Factorization Background

NMF is a commonly-used dictionary learning algorithm and was first proposed by Paatero and Tapper [19], [20] and further developed by Lee and Seung [21]. NMF factors a m × t non-negative matrix X into a m × k basis matrix W and k × t time-activation matrix H by minimizing the divergence between X and the product WH. Typical cost functions measure the Frobenius norm [21], generalized Kullback-Leibler (GKL) divergence [21], or Itakura-Saito (IS) divergence [22] between X and WH. For audio, X is the magnitude or power of the short-time Fourier transform (STFT) of the audio signal (also known as a spectrogram), W is a dictionary of different spectral patterns found in the spectrogram, and H indicates when and how strongly the spectral patterns occur in the spectrogram. NMF has two attractive properties: the factorization is interpretable and its cost function can be minimized with multiplicative updates. Unfortunately, using the magnitude or power spectrogram discards phase information, which is useful for separating multiple sources, particularly if the sources have energy at similar frequencies. Because the phase is discarded, NMF methods are required to use the phase of the original mixture when reconstructing the individual sources, which introduces distortion in the reconstructed sources.

Kameoka et al. introduced complex non-negative matrix factorization (CMF) to be able to use the complex-valued STFT as the input V [23]. In addition to learning a basis matrix W and time-activation matrix H, CMF also learns a phase matrix P_i ∈ ℂ^m×t corresponding to the ith basis vector and ith row in H. CMF approximates the input as $V\approx {\sum }_{i=1}^k{[W]}_i{[H]}_{i,:}\odot P_i$. Thus, one uses the phase matrices corresponding to the elements in the basis and time-activation matrix rather than the phase of the original noisy signal. King and Atlas showed that reconstructed sources from CMF have lower distortion and artifacts than those from NMF [24]. One drawback of CMF is that it has significantly more parameters than NMF because it estimates a phase matrix for each basis vector. This results in high computational load and memory requirements.

King et al. overcame this drawback with CMF-WISA [13]. Instead of estimating a phase matrix for each basis vector, CMF-WISA calculates a phase matrix for each source (which is represented by multiple basis vectors). In this case, an input with q sources is approximated as $V\approx {\sum }_{j=1}^q\left({\sum }_{i\in \mathcal{Q}(j)}{[W]}_i{[H]}_{i,:}\right)\odot P_j$, where 𝒬(j) is the set of indices of basis vectors and time-activation rows corresponding to source j. Since the number of sources is typically much less than the number of basis vectors ( $q<{\sum }_{j=1}^q\mid \mathcal{Q}(j)\mid$), CMF-WISA has much fewer parameters than CMF without sacrificing the advantages of CMF over NMF. It should be noted that if the input contains only one source (q = 1), then CMF-WISA is equivalent to NMF because the phase matrix P₁ will be the same as the phase of the input. In this case, CMF-WISA learns W and H from the magnitude spectrogram and returns the phase of the input matrix.

V. Denoising Algorithm

We propose a denoising algorithm that uses CMF-WISA to model spectro-temporal properties of the speech and noise components. We also add spectral and temporal regularization terms to better model the noise component. The following subsections provide an overview of the algorithm, introduce the regularization terms, and show the update equations used in the algorithm.

A. Algorithm Overview

We propose a denoising algorithm that uses CMF-WISA to model spectro-temporal properties of the speech and MRI noise and to faithfully recover the speech. We first use NMF on the MRI noise to learn a noise basis $W_d\in {ℝ}_{+}^{m\times k_d}$ and its time-activation matrix $H_d\in {ℝ}_{+}^{k_d\times t_d}$. We obtain the noise-only recording from the beginning 1 second of the noisy speech recording before the speaker speaks (it is usually the case that the speaker speaks at least 1 second after the start of the recording). Alternatively, one can obtain a noise-only recording using a reference microphone placed far away enough from the speaker so that it does not record speech. We convert the noise signal to a spectrogram $V_d\in {ℝ}_{+}^{m\times t_d}$ by taking the magnitude of the STFT of the noisy speech with a 25-ms Hamming window shifted by 10 ms. NMF will approximate V_d by W_dH_d. NMF uses iterative updates to learn the basis and time-activation matrix, so we initialize W_d and H_d with random matrices sampled from the uniform distribution on [0, 1].

After learning the noise basis, we use CMF-WISA with the noisy speech complex-valued spectrogram V ∈ ℂ^m×t_n as the input to separate into speech and noise components. We initialize the basis matrix with $W_0=[\begin{array}{cc}{W}_s& W_d\end{array}]$, where W_s is a random m × k_s matrix from the uniform distribution and W_d is the noise basis learned from the noise-only signal. We initialize the time-activation matrix with $H_n=\left[\begin{array}{c}{H}_s\\ H_d\end{array}\right]$, where $H_s\in {ℝ}_{+}^{k_s\times t_n}$ and $H_d\in {ℝ}_{+}^{k_d\times t_n}$ are random matrices from the uniform distribution. We initialize the phase matrices for speech P_s ∈ ℂ^m×t_n and noise P_n ∈ ℂ^m×t_n with the phase of the noisy spectrogram: exp (j arg (V)). After initialization, we run the CMF-WISA algorithm for a fixed number of iterations, which approximates V with V̂ = V̂_s+V̂_n, where V̂_s = W_sH_s ⊙ P_s and V̂_n = W_nH_n ⊙ P_n. We will show the update equations for the basis, time-activation, and phase matrices in Section V-D. For convenience, we define $W=[\begin{array}{cc}{W}_s& W_n\end{array}]$ as the concatenation of the learned speech and noise dictionaries. Similarly, we define $H=\left[\begin{array}{c}{H}_s\\ H_n\end{array}\right]$ as the concatenation of the learned speech and noise time-activation matrices.

Once CMF-WISA terminates, we reconstruct the speech component. Generally, we have a better estimate of the noise component than the speech component because we learn the noise model from a noise-only signal, whereas we learn the speech model from the noisy speech. Moreover, we apply regularization terms (discussed in Sections V-B and V-C) to improve the noise model. Consequently, we reconstruct the speech by reconstructing the noise component and subtracting it from the noisy speech. We form the complex-valued spectrogram V̂_n = W_nH_n ⊙ P_n and take the inverse STFT to reconstruct the time-domain noise signal d̂. We subtract d̂ from the noisy signal x to obtain the denoised speech ŝ = x − d̂.

B. Temporal Regularization

After running NMF on the noise-only signal, we have a noise dictionary W_d and time-activation matrix H_d that models the noise-only signal. We will use W_d and H_d for initializing the noise dictionary W_n and time-activation matrix H_n that models the noise in the noisy speech. In order to model the noise for the entire duration of the noisy speech, we assume that the columns of H_d are generated by a multivariate log-normal random variable. Then ln(H_d) consists of t_d samples drawn from the normal distribution with mean μ ∈ ℝ^k_d and covariance Σ ∈ ℝ^k_d×k_d. Suppose that the columns of the log time-activation matrix ln(H_n) ∈ ℝ^k_d×t_n for the noise component of the noisy signal consist of t_n samples drawn from the normal distribution with mean m ∈ ℝ^k_d and covariance S ∈ ℝ^k_d×k_d. In a slight abuse of notation, we write H_n (m, S) to indicate the dependence of H_n on m and S. We add a regularization term J_temp (H_n (m, S)) to the CMF-WISA cost function that measures the Kullback-Leibler (KL) divergence between ln (H_d) and ln (H_n):

$$J_{\text{temp}}(H_n(\mathit{m},S))=D_{KL}(ln(H_d)\Vert ln(H_n(\mathit{m},S)))=\frac{1}{2}\left(\text{tr}(S^{-1}\mathrm{\sum })+{(\mathbf{m}-\mathit{\mu })}^T{S}^{-1}(\mathbf{m}-\mathit{\mu })-k_d+ln\left(\frac{det(S)}{det(\mathrm{\sum })}\right)\right)$$ (2)

This regularization term will try to learn H_n such that the second-order statistics of H_n match the second-order statistics of H_d. In this article, we assume that the covariance matrices Σ and S are diagonal; i.e., each row of H_d and H_n is generated independently.

C. Spectral Regularization

The bore of the MRI scanner acts as a resonance cavity that imparts a transfer function on the MRI noise prior to being recorded. When we learn a noise model from the noise-only signal, we implicity capture the Fourier coefficients of the transfer function in the noise dictionary W_d. When a subject speaks inside the scanner, they open and close their mouth and vary the position of their articulators, which changes the volume of the resonance cavity. This results in slight but noticable changes in the transfer function. Consequently, there can be a slight mismatch between the noise dictionary W_d and the noise component during speech production. The mismatch is most noticeable at frequencies where the noise has high energy.

To address the mismatch, we allow entries in W_d corresponding to frequencies with high noise energy to change when updating the noise dictionary W_n on the noisy speech. We achieve this by introducing a regularization term J_spec (W_n) to the CMF-WISA cost function:

$$J_{\text{spec}}(W_n)={\Vert \mathrm{\Lambda }(W_d-W_n)\Vert }_F^2.$$ (3)

$\mathrm{\Lambda }\in {ℝ}_{+}^{m\times m}$ is a diagonal matrix that specifies how closely the entries in W_n must match the entries in W_d for the frequency bins 1, …, m. High values in Λ enforce less change while lower values allow for greater change, so we set entries in Λ corresponding to frequencies with low noise energy to a high value λ₀ and entries corresponding to frequencies with high noise energy to values lower than λ₀.

D. Update Equations

We now present the update equations with the regularization terms incorporated and pseudo-code for the denoising algorithm. When learning the noise-only model, we minimize the following cost function:

$$C_{\text{noise}}(W_d,H_d)={\Vert V_d-W_d{H}_d\Vert }_F^2+{\alpha }_d\sum _{j=1}^{t_d}{\Vert {[H_d]}_j\Vert }_1,$$ (4)

where α_d trades reconstruction error for sparsity in H_d. The update equations for the noise model on the noise-only signal are as follows:

$$W_d\leftarrow W_d\odot \frac{V_d{H}_d^T}{W_d{H}_d{H}_d^T}$$ (5)

$$H_d\leftarrow H_d\odot \frac{W_d^T{V}_d}{W_d^T{W}_d{H}_d+{\alpha }_d}$$ (6)

These update equations are derived in [21].

When learning the speech model and updating the noise model on the noisy speech, we minimize the following cost function:

$$C_{\text{noisy}}(W_s,W_n,H_s,H_n,P_s,P_n)={\Vert V-(W_s{H}_s\odot P_s+W_n{H}_n\odot P_n)\Vert }_F^2+{\alpha }_s\sum _{j=1}^{t_n}{\Vert {[H_s]}_j\Vert }_1+\gamma J_{\text{temp}}(H_n(\mathit{m},S))+J_{\text{spec}}(W_n),$$ (7)

where α_s trades reconstruction error for sparsity in H_s, γ controls the amount of temporal regularization, and Λ controls the amount of spectral regularization. We will discuss parameter settings of γ and Λ in Section VII. Minimizing Equation 7 directly is difficult, so we minimize an auxiliary cost function, shown in Equation 31 in Appendix A. The auxiliary function has auxiliary variables V̄_s and V̄_n that are calculated as

$${\overline{V}}_s={\widehat{V}}_s+B_s\odot \left(V-\widehat{V}\right)$$ (8)

$${\overline{V}}_n={\widehat{V}}_n+B_n\odot \left(V-\widehat{V}\right),$$ (9)

where

$$B_s=\frac{W_s{H}_s}{WH}$$ (10)

$$B_n=\frac{W_n{H}_n}{WH}$$ (11)

The update equations for the speech model on the noisy speech are

$$P_s=exp(jarg({\overline{V}}_s)),$$ (12)

$$W_s\leftarrow W_s\odot \frac{\frac{\mid {\overline{V}}_s\mid }{B_s}{H}_s^T}{\frac{W_s{H}_s}{B_s}{H}_s^T},$$ (13)

$$H_s\leftarrow H_s\odot \frac{W_s^T\frac{\mid {\overline{V}}_s\mid }{B_s}}{W_s^T\frac{W_s{H}_s}{B_s}+{\alpha }_s{1}_{k_s\times t_n}}.$$ (14)

The derivation of these update equations can be found in [24]. Finally, the update equations for the noise model on the noisy speech are

$$P_n=exp(jarg({\overline{V}}_n)),$$ (15)

$$W_n\leftarrow W_n\odot \frac{\frac{\mid {\overline{V}}_n\mid }{B_n}{H}_n^T+{({\nabla }_{W_n}{J}_{\text{spec}}(W_n))}_{\text{num}}}{\frac{W_n{H}_n}{B_n}{H}_n^T+{({\nabla }_{W_n}{J}_{\text{spec}}(W_n))}_{\text{den}}},$$ (16)

$$H_n\leftarrow H_n\odot \frac{W_n^T\frac{\mid {\overline{V}}_n\mid }{B_n}+\gamma {({\nabla }_{H_n}{J}_{\text{temp}}(H_n(\mathit{m},S)))}_{\text{num}}}{W_n^T\frac{W_n{H}_n}{B_n}+\gamma {({\nabla }_{H_n}{J}_{\text{temp}}(H_n,(\mathit{m},S)))}_{\text{den}}},$$ (17)

where

$${({\nabla }_{W_n}{J}_{\text{spec}}(W_n))}_{\text{num}}={\mathrm{\Lambda }}^T\mathrm{\Lambda }{W}_d,$$ (18)

$${({\nabla }_{W_n}{J}_{\text{spec}}(W_n))}_{\text{den}}={\mathrm{\Lambda }}^T\mathrm{\Lambda }{W}_n,$$ (19)

$${({\nabla }_{H_n}{J}_{\text{temp}}(H_n(\mathit{m},S)))}_{\text{num}}=\frac{1}{H_n}\odot [\frac{1}{t_n}{S}^{-1}\left({[U]}^{+}+{[M]}^{-}\right)1_{k_d\times t_n}+\frac{1}{t_n-1}(S^{-2}\mathrm{\sum }+{(M-U)}^T{S}^{-2}(M-U))\left({[ln(H_n)]}^{+}+{[M]}^{-}{1}_{k_d\times t_n}\right)+\frac{1}{t_n-1}{S}^{-1}\left({[ln(H_n)]}^{-}+{[M]}^{+}{1}_{k_d\times t_n}\right)],$$ (20)

and

$${({\nabla }_{H_n}{J}_{\text{temp}}(H_n(\mathit{m},S)))}_{\text{den}}=\frac{1}{H_n}\odot [\frac{1}{t_n}{S}^{-1}\left({[U]}^{-}+{[M]}^{+}\right)1_{k_d\times t_n}+\frac{1}{t_n-1}(S^{-2}\mathrm{\sum }+{(M-U)}^T{S}^{-2}(M-U))\left({[ln(H_n)]}^{-}+{[M]}^{+}{1}_{k_d\times t_n}\right)+\frac{1}{t_n-1}{S}^{-1}\left({[ln(H_n)]}^{+}+{[M]}^{-}{1}_{k_d\times t_n}\right)].$$ (21)

In the above equations, U = diag (μ) and M = diag (m). We show the derivation of these update equations in Appendix A. Algorithm 1 shows the pseudo-code for the denoising algorithm.

VI. Experimental Evaluation

The following sections describe the datasets we tested our algorithm on, the other denoising algorithms we compared against, and the evaluation metrics we used.

Algorithm 1.

Denoising Algorithm

1:	Initialize parameters num_iter, ks, kd, αs, αd, γ, Λ
2:	Create spectrograms Vd from noise-only signal and V from noisy speech x {Learn noise model from noise-only signal}
3:	Initialize Wd and Hd with random matrices
4:	Initialize Pd = exp(j arg (Vd))
5:	for iter = 1 to num_iter do
6:	Update Wd using Equation 5
7:	Update Hd using Equation 6
8:	end for
9:	Calculate second-order statistics μ and Σ from Hd {Learn speech model and update noise model from noisy speech}
10:	Initialize Ws, Hs, and Hn with random matrices
11:	Initialize $W=[\begin{array}{cc}{W}_s& W_d\end{array}]$ and $H=\left[\begin{array}{c}{H}_s\\ H_n\end{array}\right]$
12:	Initialize Ps, Pn = exp(j arg (V))
13:	Initialize V̂ = WsHs ⊗ Ps + WnHn ⊗ Pn
14:	Calculate second-order statistics m and S from Hn
15:	for iter = 1 to num_iter do
16:	Update Bs, Bn with Equations 10, 11
17:	Update V̄s, V̄n with Equations 8, 9
18:	Update Ps, Pn with Equations 12, 15
19:	Update Ws, Wn with Equations 13, 16
20:	Update Hs, Hn with Equations 14, 17
21:	Update second-order statistics m and S from Hn
22:	end for
23:	Estimate noise d̂ from inverse STFT of WnHn ⊗ Pn
24:	return Estimated speech ŝ = x − d̂

A. Datasets

MRI-utt dataset

The MRI-utt dataset contains 6 utterances spoken by a male in an MRI scanner. The utterances include 2 TIMIT sentences [25] and various standard vowel-consonant-vowel utterances that can be used to verify how well the denoising preserves the spectral components of these vowels and consonants. We recorded these utterances with seq1, seq2, seq3, ga21, ga55, and mult pulse sequences (we refer to these sequences as the real-time sequences). In the case of the static 3D pulse sequence (st3d), the utterances consist of a vowel held for 7 seconds because this sequence can only be used to capture static vocal tract postures. We obtained a noise-only signal of the real-time sequences from the start of the noisy speech before the subject speaks, while the st3d noise-only signal came from a recording of the st3d pulse while the subject remained silent. The drawback with using recordings in the MRI scanner for denoising evaluation is the lack of a clean reference signal.

Aurora 4 dataset [26]

The Aurora 4 dataset is a subset of clean speech from the Wall Street Journal corpus [27]. We added the 7 pulse sequence noises to the clean speech with an SNR of −7 dB, which is similar to the SNR in the MRI-utt dataset. We note that even though the static 3D noise would occur with a held vowel rather than continuous speech in a real-world scenario, we still added this noise to the clean speech to evaluate how well our algorithm removes this noise. Aurora 4 is divided into train, dev, and test sets. We used the dev set to determine optimum parameter settings for our algorithm (see Section VII) and report denoising results on the test set.

B. Other Denoising Algorithms

We compared the performance of our proposed algorithm to the two-step algorithm (denoted 2step) we previously proposed in [14], the correlation subtraction + spectral noise gating algorithm (denoted CS+SNG) [12], and the LMS variant (denoted LMS-model) proposed in [11].

2step [14]

The 2step algorithm sequentially processes the noisy speech through an NMF step then a wavelet packet analysis stage. The NMF step estimates the speech and noise components in the noisy speech and passes the estimated speech to a wavelet packet analysis step for further noise removal. Wavelet packet analysis thresholds the estimated speech wavelet coefficients in different frequency bands based on the wavelet coefficients of the reference noise signal [28]; speech wavelet coefficients below the threshold are set to zero. The resulting thresholded coefficients are converted back to the time domain with the inverse wavelet packet transform to give the final denoised speech.

CS+SNG [12]

The CS+SNG algorithm is also a two-stage algorithm. The first stage, correlation subtraction, determines the best temporal alignment between the noisy speech and noise reference using the correlation metric. The time-aligned noise reference is subtracted from the noisy speech to get the estimated speech. The estimate speech is then passed to a spectral noise gating algorithm which thresholds the estimated speech Fourier coefficients in each frequency band based on the noise reference Fourier coefficients, similar to wavelet packet analysis. The thresholded coefficients are converted back to the time domain, resulting in the final denoised speech.

LMS-model [11]

LMS-model creates an artificial noise reference signal based on the periodicity of the MRI pulse sequence (see f₀ in Table I). Using the noisy speech and reference noise signals, LMS-model recursively updates the weights of an adaptive filter to minimize the mean square error between the filter output and the noise signal. The residual error between the filter output and the noise signal is the final denoised speech.

LMS-model is known to perform well with seq1, seq2, and seq3 noises and is currently used to remove these pulse sequence noises from speech recordings. However, its performance degrades with golden angle and static 3D pulse sequence noises, preventing speech researchers from collecting better MR images using golden angle pulse sequences or capturing 3D visualizations of the vocal tract during speech production. On the other hand, the other denoising methods are agnostic to the pulse sequence and can be used for removing a wider range of pulse sequence noises, including the golden angle sequences.

C. Quantitative Performance Metrics

We used the following 5 objective measures for evaluating the denoising performance.

1. Noise suppression (NS): To quantify the amount of noise the denoising algorithms remove, we calculated the noise suppression, which is given by

   $$\text{NS}=10log\left(\frac{P_{\text{noise}}}{{\widehat{P}}_{\text{noise}}}\right),$$ (22)

   where P_noise is the power of the noise in the noisy signal and P̂_noise is the power of the noise in the denoised signal. We used a voice activity detector (VAD) to find the noise-only regions in the denoised and noisy signals. We calculated the noise suppression measure instead of SNR because we do not have a clean reference signal for the MRI-utt dataset.

2. Log-likelihood ratio (LLR): Ramachandran et al. proposed the log-likelihood ratio (LLR) and distortion variance (DV) measures in [29] for evaluating the amount of distortion introduced by the denoising algorithm. The LLR calculates the mismatch between the spectral envelopes of the clean signal and the denoised signal. It is calculated using

   $$\text{LLR}=log\frac{{\mathit{a}}_{\widehat{s}}^T{R}_s{\mathit{a}}_{\widehat{s}}}{{\mathit{a}}_s^T{R}_s{\mathit{a}}_s},$$ (23)

   where a_s and a_ŝ are p-order LPC coefficients of the clean and denoised signals respectively, and R_s is a (p+1) × (p+1) autocorrelation matrix of the clean signal. An LLR of 0 indicates no spectral distortion between the clean and denoised signals, while a high LLR indicates the presence of noise and/or distortion in the denoised signal.

3. Distortion variance (DV): The distortion variance is given by

   $$\text{DV}=\frac{1}{N}\sum _{n=0}^{N-1}{\mid s[n]-\widehat{s}[n]\mid }^2,$$ (24)

   where s[n] and ŝ[n] are the clean and denoised signals respectively, and N is the length of the signal. A low distortion variance is more desirable than a high distortion variance.

4. Perceptual Evaluation of Speech Quality (PESQ) score: The PESQ score is an automated assessment of speech quality [30]. It gives a score for the denoised signal from −0.5 to 4.5, where −0.5 indicates poor speech quality and 4.5 indicates excellent quality. The score models the mean opinion score (but with a different scale), so the PESQ score provides a way to estimate the speech quality quantitatively without requiring listening tests. We calculated the PESQ score using C code provided by ITU-T.

5. Short-Time Object Intelligibility (STOI) score: Similar to the PESQ score, the STOI score is an automated assessment of the speech intelligibility [31]. Unlike several other objective intelligibility measures, STOI is designed to evaluate denoised speech. The STOI score ranges from 0 to 1, with higher values indicating better intelligibility. We calculated the STOI score using the Matlab code provided by the authors in [31].

D. Qualitative Performance Metrics

To supplement the quantitative results, we created a listening test on Amazon Mechanical Turk to compare the denoised signals from our proposed algorithm, 2step, CS+SNG, and LMS-model. We selected 4 Aurora sentences and added the 7 pulse sequence noises to these with −7 dB SNR. For each clean/noisy pair, we denoised the noisy signal with the denoising algorithms and presented the listeners with the clean, denoised, and noisy signals. We refer to these 6 clips (clean, denoised with proposed, 2step, CS+SNG, LMS-model, and noisy) as a set. We asked the listeners to rate the speech quality of each of the clips on a scale of 1 to 5, with 1 meaning poor quality and 5 meaning excellent quality. Additionally, we asked them to rank the clips within each set from 1 to 6, with 1 being the least natural/worst quality clip to 6 being the most natural/best quality. We also included 2 clips of TIMIT sentences from the MRI-utt dataset with the rtMRI pulse sequences and 2 clips of held vowels with the st3d static 3D sequence. For these clips, we only provided the noisy and denoised clips in the set because we don’t have a clean recording of the speech. The listeners had to rate these clips from 1 to 5 as before, but only provide rankings from 2 to 6 because there are only 5 clips in these sets. 40 Mechanical Turk workers evaluated each set and assigned a rating and ranking to each clip as described.

During the experiment, we rejected any sets where the rating or ranking was left blank and allowed someone else to provide ratings and rankings for those sets. After the experiment concluded, we processed the results to remove bad data. If an annotator rated a noisy clip from a set as a 4 or 5, or ranked it as a 5 or 6, then we discarded the results for that set. Table III shows the total number of data points for each dataset and pulse sequence noise after processing the results. The values in Table III reflect the fact that we used 2 clips from MRI-utt and 4 clips from Aurora per noise in the listening test. Thus, on average, we retained 35 unique ratings and rankings for the clips in each dataset and sequence noise after processing the results.

TABLE III.

Number of data points for the listening test for each data set and pulse squence noise.

Dataset	seq1	seq2	seq3	ga21	ga55	mult	st3d
MRI-utt	73	70	73	75	69	70	60
Aurora 4	144	139	141	136	140	134	137

VII. Analysis of Regularization Parameters

The proposed algorithm contains two parameters that control the spectral and temporal regularization during the multiplicative updates. Generally, analysis of the noise can inform proper selection of these parameters. In this section, we will analyze these parameters and provide insight into choosing good values for these parameters.

A. Spectral Regularization

The weight of the spectral regularization term in the cost function (Equation 7) is controlled by Λ. In this article, we explore spectral regularization weightings of the form Λ = diag ([c ⋯ c λ ⋯ λ c ⋯ c]), where c ∈ ℝ₊ controls the regularization of the DFT bins corresponding to low and high frequency bins and λ ∈ ℝ₊ controls the regularization of the DFT bins corresponding to the middle frequencies. Higher values of c and λ result in less change in W_n relative to W_d at the corresponding frequencies.

In our datasets, most of the MRI noise energy is concentrated between 600 Hz and 6 kHz for the rtMRI sequences and 700 Hz to 8 kHz for the st3d sequence. Thus, we let λ regularize the frequency bins for 600 Hz to 6 kHz for the realtime sequences and 700 Hz to 8 kHz for the st3d sequence, while c controls the remaining frequency bins. We set c = 10⁸ and varied λ from the set λ ∈ {0, 10¹, 10², 10³, 10⁴, 10⁵}.

B. Temporal Regularization

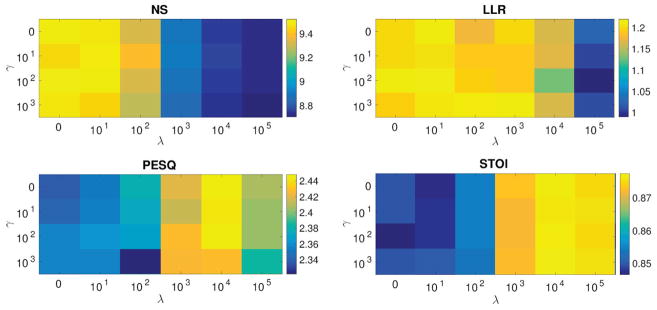
The influence of the temporal regularization term on the cost function (Equation 4) is controlled by γ. Higher values of γ enforce greater adherence to the statistics calculated from H_d. Temporal regularization also implicitly affects how the noise basis W_n is updated; by incorporating prior knowledge about the time-activations, W_n is forced to model parts of the noisy speech (i.e., noise) that results in time-activation statistics matching the learned statistics. To explore the effect of temporal regularization on the denoising performance, we varied γ from the set γ ∈ {0, 10¹, 10², 10³} and measured the noise suppression, LLR, PESQ scores, and STOI scores for the Aurora 4 dev set with ga55 noise added.

C. Discussion

Figure 1 shows the noise suppression, LLR, PESQ scores, and STOI scores for the Aurora 4 dev set with ga55 noise added at −7 dB SNR when varying λ and γ. From the figure, we see a trade-off between noise suppression and signal distortion as we vary λ. Noise suppression, LLR, and distortion variance decrease as λ increases. This makes sense because higher λ results in less changes to the noise dictionary, which causes less noise to be removed but also reduces the chance of removing speech. The PESQ score indicates that the denoised speech quality increases slightly when increasing λ from 10¹ to 10³, but decreases beyond 10³. Similar to the spectral regularization, we see a trade-off between noise suppression and signal distortion as we vary γ, though the effect is not as pronounced as when we varied λ. Higher values of γ lead to less noise suppression, greater distortion, and lower speech quality. In the interest of space, we only show results with ga55 noise, but the trends are similar for the other pulse sequence noises.

Fig. 1.

Quantitative metrics for different spectral regularization weights λ and temporal regularization weights γ.

When we do not use any regularization in the cost function (Equation 7) (i.e. λ = 0 and γ = 0), we see that the performance is generally worse than when regularization is used. Without these regularization terms, the cost function only contains the reconstruction error and the ℓ₁ penalty on the speech time-activation matrix. In this case, the algorithm will learn a noise model that maximally minimizes the reconstruction error, which leads to maximal noise removal. This result is reflected in the noise suppression values in Figure 1. However, the unregularized cost function does not take into account the temporal structure of the noise and the filtering effects of the MRI scanner bore and vocal tract shaping, as discussed in Sections V-B and V-C. This means that the algorithm does not properly account for the presence of speech when learning the noise model, and subtracting the estimated noise component from the noisy speech leads to distortion in the speech. This results in a higher LLR and lower PESQ and STOI scores, as shown in Figure 1.

VIII. Results and Discussion

Based on our discussion in Section VII, we optimized the parameters of our proposed algorithm for each pulse sequence noise. We chose λ = 10³ and γ = 100. Additionally, we set the number of speech dictionary elements k_s = 30 and number of noise dictionary elements k_d = 50 for the real-time sequences in the MRI-utt dataset and for all sequences in the Aurora 4 dataset. For the st3d sequence in the MRI-utt dataset, we used k_s = 5 and k_d = 100 because a held vowel requires fewer speech dictionary elements than running speech, which has a wider range of sounds. We ran the update equations for 300 iterations. The parameters used for the 2step algorithm [14] are shown in Table IV. These parameters were determined in the same manner we used to select the parameters for the proposed algorithm. For the CS+SNG method [12], we optimized the noise reduction coefficient parameter for the 5 objective metrics. We found the best value to be 0.3. The LMS-model algorithm [11] does not require parameter tuning; its parameter is based on f₀, which is noise-dependent (see Table I).

TABLE IV.

Parameter settings for the number of speech dictionary elements (n_s) and wavelet packet depth (D) in the 2step algorithm. The number of noise dictionary elements was set to 70 and the window length for wavelet packet analysis was set to 2048 for all noises. See [14] for more information about the 2step parameters.

Parameter	seq1–3	ga21	ga55	mult	st3d
ns	30	30	30	30	10
D	7	8	9	7	9

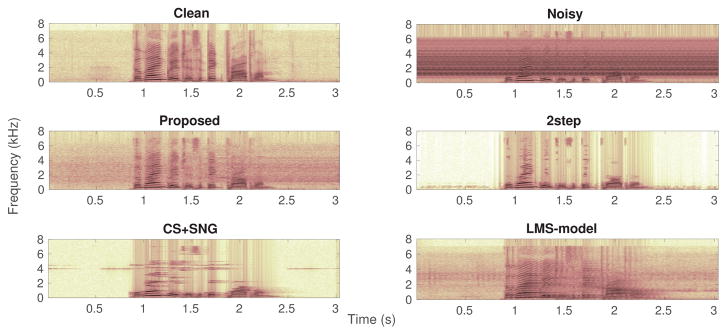
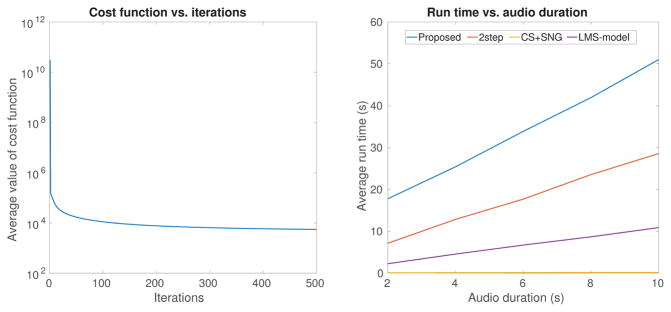
Figures 2 and 3 show spectrograms of removing seq3 noise from an audio clip in the MRI-utt and Aurora 4 datasets using the different denoising algorithms. Figure 4 shows the average value of the cost function (Equation 7) at each iteration when denoising files in the Aurora 4 dev set. The cost function monotonically decreases and reaches convergence after roughly 300 iterations for both datasets. Additionally, the figure shows the average run time for the denoising algorithms when processing files of different durations in the Aurora 4 dev set. We either chopped or zero-padded the files to achieve the desired duration. Unfortunately, we see that the proposed algorithm has the longest run time among the denoising algorithms. Finding ways to improve computation efficiency will be one of our priorities in improving the algorithm.

Fig. 3.

Clean, noisy, and denoised spectrograms of the sentence “The language is a big problem” in the Aurora 4 dataset. The noise is seq3.

Fig. 4.

Average values of the noisy cost function (Equation 7) as a function of iteration number and average run times for the denoising algorithms as a function of audio durtaion for the Aurora 4 dev set.

A. Objective Results

Table V lists the average noise suppression across each utterance in the MRI-utt dataset. We used the nonparametric Wilcoxon Rank-Sum Test to determine if the medians of the noise suppression (and the other metrics) are significantly different between the different denoising methods. In Table V and subsequent tables, a bolded value indicates the best-performing algorithm and an asterisk denotes statistically significant performance with p < 0.05. Table VI shows the noise suppression, LLR, distortion variance, PESQ, and STOI results for the Aurora 4 test set.

TABLE V.

NS results (dB) for the MRI-utt dataset.

Sequence	Proposed	2step	CS+SNG	LMS-model
seq1	30.18	25.52	33.51	13.90
seq2	29.42	14.71	31.87*	15.04
seq3	29.55	13.65	31.79*	16.70
ga21	29.26	15.47	31.57*	13.81
ga55	30.34	14.74	33.19*	10.30
mult	29.22	12.69	32.87*	0.47
st3d	10.82	7.99	10.12	−1.69

TABLE VI.

NS, LLR, DV, PESQ scores, and STOI scores for the Aurora 4 dataset.

Metric	Sequence	Proposed	2step	CS+SNG	LMS-model
NS (dB)	seq1	15.42	11.17	18.08*	9.52
	seq2	15.78	11.38	17.49*	9.62
	seq3	15.61	11.38	18.24*	10.33
	ga21	15.39	11.29	16.57*	8.71
	ga55	14.96	10.95	16.36*	7.16
	mult	14.93	10.51	16.61*	0.21
	st3d	14.78	11.98	17.12*	−1.80
LLR	seq1	1.004	3.676	2.462	0.987*
	seq2	1.058	3.666	2.046	0.931*
	seq3	1.012	3.650	2.065	0.850*
	ga21	1.018*	3.329	1.987	1.058
	ga55	1.020*	3.179	1.882	1.497
	mult	1.098*	3.486	2.480	2.839
	st3d	0.676*	2.522	2.265	2.094
DV (×10−5)	seq1	1.933*	2.502	2.512	3.105
	seq2	1.919*	2.484	2.401	3.094
	seq3	1.846*	2.342	2.428	3.013
	ga21	1.635*	2.149	1.909	2.941
	ga55	1.497*	1.908	1.769	3.043
	mult	1.552*	1.897	1.941	4.187
	st3d	0.971*	2.919	1.683	4.217
PESQ	seq1	2.20	2.49*	1.95	1.91
	seq2	2.23	2.60*	2.09	1.97
	seq3	2.30	2.67*	2.06	2.03
	ga21	2.36	2.65*	2.07	1.94
	ga55	2.43	2.71*	2.14	1.97
	mult	2.30	2.70*	2.08	1.56
	st3d	3.01*	2.12	2.02	1.97
STOI	seq1	0.907*	0.781	0.785	0.869
	seq2	0.910*	0.778	0.800	0.873
	seq3	0.920*	0.795	0.788	0.883
	ga21	0.920*	0.782	0.828	0.861
	ga55	0.922*	0.798	0.836	0.825
	mult	0.907*	0.792	0.790	0.714
	st3d	0.964*	0.705	0.812	0.765

We see that our proposed algorithm consistently has the least signal distortion compared to the other denoising methods, except for the LLR measurement in seq1, seq2, and seq3 noises, where the LMS-model performs the best. Unfortunately, this comes at a cost of less noise removal, as indicated by the better noise suppression performance of CS+SNG for all of the pulse sequence noises in the Aurora 4 datasets. However, as we discussed in Section VII, minor changes in parameter settings can vary the trade-off between noise suppression and distortion, depending on the user’s needs. We also see that our algorithm always gave the best STOI scores and the best PESQ score in st3d noise. The low distortion coupled with good speech intelligibility indicates that our proposed algorithm produces denoised speech that can be used reliably for speech analysis and subjective listening tests. We observe that the proposed algorithm improves upon our previous approach (2step algorithm) in all measures except the PESQ score in real-time pulse sequences. This observation suggests that incorporating phase information results in better separation of speech and noise, particularly at frequencies where there is overlap between speech and noise.

For the st3d noise, we see that our algorithm far outperforms the other denoising methods in terms of signal distortion, speech quality, and intelligibility. This encouraging result suggests our denoising approach is better suited for removing aperiodic noise, such as st3d pulse sequence noises, than other denoising approaches. One reason why our algorithm shows better results for st3d compared to the real-time sequences is that our algorithm had access to the st3d noise-only signal while it extracted the real-time sequence noises from the start of the noisy speech. Meanwhile, CS+SNG had access to the noise-only signal for all sequences. We performed the experiment in this way because we wanted to mimic how these algorithms function in the wild; CS+SNG requires a reference noise signal while our algorithm can handle having partial information about the noise signal.

It is interesting to note that the 2step algorithm gives a better PESQ score for the real-time sequence noises while the proposed algorithm gives a better STOI score. These results suggest that the 2step approach preserves properties of the speech that lead to better perceptual quality while the proposed method retains speech properties important for conveying speech content. This finding warrants further investigation into the specific speech properties required for good speech and quality and intelligibility, and understanding how the proposed and 2step algorithms preserve these properties. Incorporating these properties in the optimization framework of the proposed algorithm can further improve the denoised speech quality.

B. Listening Test Results

Table VII shows the mean rankings obtained from the listening test for the 3 datasets corrupted by the pulse sequence noises. A higher value indicates a better ranking. In this table, we highlight the best rank in bold and statistically significant results, marked with an asterisk, are computed by comparing the rankings among the denoising methods only; not surprisingly, the rankings for the clean speech are always significantly better than the denoised speech. Table VIII shows the mean ratings of speech quality obtained from the listening test. As with the ranking results, we highlight the best statistically significant results when comparing the ratings from the denoising methods.

TABLE VII.

Mean rankings of the audio clips for each dataset corrupted with different pulse sequence noises.

Dataset	Sequence	Clean	Proposed	2step	CS+SNG	LMS-model	Noisy
MRI-utt	seq1	—	3.85	3.63	4.47*	3.47	1.63
	seq2	—	4.13	3.57	4.10	3.44	1.70
	seq3	—	3.56	3.47	3.81	3.71	1.66
	ga21	—	3.81	3.25	4.21	3.48	1.64
	ga55	—	3.54	3.65	3.94	2.70	1.65
	mult	—	3.44	3.39	4.10*	1.94	1.99
	st3d	—	2.78	3.17	2.72	2.35	1.92
Aurora 4	seq1	5.74	4.10*	3.74	2.99	3.07	1.29
	seq2	5.66	4.17*	3.58	3.09	3.30	1.29
	seq3	5.60	4.06*	3.64	3.48	3.28	1.33
	ga21	5.71	4.46*	3.94	2.95	2.87	1.28
	ga55	5.63	4.34*	3.82	3.20	2.33	1.30
	mult	5.69	4.18	4.28	3.22	1.59	1.66
	st3d	5.72	4.26*	3.62	3.57	1.39	1.93

TABLE VIII.

Mean ratings of the audio clips for each dataset corrupted with different pulse sequence noises.

Dataset	Sequence	Clean	Proposed	2step	CS+SNG	LMS-model	Noisy
MRI-utt	seq1	—	3.07	2.99	3.60*	2.78	1.26
	seq2	—	3.30	2.77	3.24	2.69	1.29
	seq3	—	2.82	2.66	3.07	3.00	1.19
	ga21	—	2.93	2.65	3.36*	2.80	1.29
	ga55	—	2.99	2.94	3.14	2.09	1.32
	mult	—	2.44	2.40	3.14*	1.20	1.36
	st3d	—	1.73	2.07	1.78	1.53	1.27
Aurora	seq1	4.78	3.58	3.39	2.75	2.85	1.33
	seq2	4.78	3.68*	3.17	2.75	2.98	1.35
	seq3	4.73	3.59*	3.28	3.17	2.99	1.45
	ga21	4.82	3.83*	3.44	2.75	2.70	1.36
	ga55	4.75	3.74*	3.44	2.93	2.16	1.34
	mult	4.79	3.66	3.66	2.90	1.50	1.57
	st3d	4.77	3.63	3.24	3.14	1.44	1.61

We see from Tables VII and VIII that listeners compared the denoised speech from our algorithm favorably with the denoised speech from CS+SNG. In all cases in the Aurora dataset, listeners ranked and rated our output as the best denoised speech. More interestingly, we see that our algorithm ranked and rated the best among the denoising algorithms for removing st3d pulse sequence noise in the Aurora dataset. Though the ratings are poor for the MRI-utt dataset, they are a promising indicator that our algorithm is a step in the right direction for handling aperiodic, high-power noise corrupting a speech recording. Another observation is that the rankings and ratings for the LMS-model algorithm decreases when going from Sequence 1–3 noise to Golden Angle noise and finally to multislice and static 3D noise. In contrast, the proposed algorithm performs consistently well in the different noises, giving speech researchers greater flexibility in choosing an MRI sequence to study the vocal tract.

IX. Conclusion

We have proposed a denoising algorithm to remove noise from speech recorded in an MRI scanner. The algorithm uses CMF-WISA to model spectro-temporal properties of the speech and noise in the noisy signal. Using CMF-WISA instead of NMF allowed us to model the magnitude and phase of the speech and noise. We incorporated spectral and temporal regularization terms in the CMF-WISA cost function to improve the modeling of the noise. Parameter analysis of the weights of the regularization terms gave us optimum ranges for the weights to balance the trade-off between noise suppression and speech distortion and also showed that having the regularization terms improved denoising performance over not having the regularization terms. Objective measures show that our proposed algorithm achieves lower distortion and higher STOI scores than other recently proposed denoising methods. A listening test shows that our algorithm yields higher quality and more intelligible speech than some other denoising methods in some pulse sequence noises, especially the aperiodic static 3D pulse sequence. We have provided a MATLAB implementation of our work at github.com/colinvaz/mri-speech-denoising.

To further extend our work, we will improve the contribution of the temporal regularization term by modeling the distribution of the noise time-activation matrix in a data-driven manner rather than assuming a log-normal distribution. Additionally, we will incorporate STFT consistency constraints [32] and phase constraints [33] when learning the speech and noise components to reduce artifacts and distortions in the estimated components. In our current work, we made strides towards addressing convolutive noise in the MRI recordings by using spectral regularization to account for filtering effects of the scanner bore, but a more rigorous treatment of convolutive noise might further improve results. Given that the primary motivation behind recording speech in an MRI is for linguistic studies, we will evaluate how well our algorithm aids speech analysis, such as improving the reliability of formant and pitch measurements. However, we will also target clinical use of this algorithm by developing a real-time version that facilitates doctor-patient interaction during MRI scanning. Finally, we will evaluate the performance of our algorithm in other low-SNR speech enhancement scenarios, such as those involving babble and traffic noises to generalize its application beyond MRI acoustic denoising.

Appendix A. Derivation of Update Equations

When learning the speech basis and updating the noise basis from the noisy speech, we used the following cost function:

$$C(\theta )=J_{\text{error}}\left(V,\widehat{V}\right)+{\alpha }_s{J}_{\text{spars}}(H_s)+\gamma J_{\text{temp}}(H_n(\mathit{m},S))+J_{\text{spec}}(W_s,\mathrm{\Lambda })$$ (25)

where

$$J_{\text{error}}\left(V,\widehat{V}\right)={\Vert V-\widehat{V}\Vert }_F^2,$$ (26)

$$J_{\text{spars}}(H_s)=\sum _{j=1}^{t_n}{\Vert {[H_s]}_j\Vert }_1,$$ (27)

$$J_{\text{temp}}(H_n(\mathit{m},S))=D_{KL}(ln(H_d)\Vert ln(H_n(\mathit{m},S))),$$ (28)

and

$$J_{\text{spec}}(W_n)={\Vert \mathrm{\Lambda }(W_d-W_n)\Vert }_F^2.$$ (29)

θ = (W_s, W_n, H_s, H_n, P_s, P_n) is the set of parameters we seek when optimizing the cost function, and V̂ = W_sH_s ⊙ P_s +W_nH_n ⊙ P_n.

In this work, we assume that ln (H_d) ~ 𝒩(μ, Σ) and ln (H_n (m, S)) ~ 𝒩(m, S), with diagonal covariance matrices Σ and S. In this case,

$$J_{\text{temp}}(H_n(\mathit{m},S))=\frac{1}{2}\left(\text{tr}\left(S^{-1}\mathrm{\sum }\right)+{(\mathbf{m}-\mathit{\mu })}^T{S}^{-1}(\mathbf{m}-\mathit{\mu })-k_d+ln\left(\frac{det(S)}{det(\mathrm{\sum })}\right)\right).$$ (30)

We estimate μ with the sample mean $\frac{1}{t_d}{\sum }_{t=1}^{t_d}ln({[H_d]}_t)$ and Σ with the sample covariance $\frac{1}{t_{d-1}}{\sum }_{t=1}^{t_d}(ln({[H_d]}_t)-\mathit{\mu }){(ln[{(H_d]}_t)-\mathit{\mu })}^T$ and keeping only the diagonal elements in Σ. Similarly, we estimate m with the sample mean $\frac{1}{t_n}{\sum }_{t=1}^{t_n}ln({[H_n]}_t)$ and S with the sample covariance $\frac{1}{t_n-1}{\sum }_{t=1}^{t_n}(ln({[H_n]}_t)-\mathit{m}){(ln[{(H_n]}_t)-\mathit{m})}^T$ and keeping only the diagonal elements in S.

When minimizing the primary cost function is difficult, an auxiliary function is introduced.

Definition 1

C⁺ (θ, θ̄) is an auxiliary function for C (θ) if C⁺ (θ, θ̄) ≥ C (θ) and C⁺ (θ, θ) = C (θ).

It has been shown in [23] that C (θ) monotonically decreases under the updates θ̄ ← argmin_θ̄ C⁺ (θ, θ̄) and θ ← argmin_θ C⁺ (θ, θ̄).

We form the auxiliary function as

$$C^{+}(\theta ,\overline{\theta })=J_{\text{error}}^{+}\left(V,\overline{V},V\right)+{\alpha }_s{J}_{\text{spars}}^{+}(H_s,{\overline{H}}_s)+\gamma J_{\text{temp}}^{+}(H_n(\mathit{m},S),{\overline{H}}_n(\overline{\mathit{m}},\overline{S}))+J_{\text{spec}}(W_s),$$ (31)

where

$$J_{\text{error}}^{+}\left(V,\overline{V},\widehat{V}\right)=\sum _{f=1}^m\sum _{t=1}^n\frac{{\left|{\left[{\overline{V}}_s\right]}_{ft}-{\left[{\widehat{V}}_s\right]}_{ft}\right|}^2}{{[{\beta }_s]}_{ft}}+\sum _{f=1}^m\sum _{t=1}^n\frac{{\left|{\left[{\overline{V}}_n\right]}_{ft}-{\left[{\widehat{V}}_n\right]}_{ft}\right|}^2}{{[{\beta }_n]}_{ft}},$$ (32)

$$J_{\text{spars}}^{+}(H_s,{\overline{H}}_s)=\sum _{k=1}^{k_s}\sum _{t=1}^n\left(\rho {\mid {[{\overline{H}}_s]}_{kt}\mid }^{\rho -2}{[H_s]}_{kt}^2+2{\mid {[{\overline{H}}_s]}_{kt}\mid }^{\rho }-\rho {\mid {[{\overline{H}}_s]}_{kt}\mid }^{\rho }\right),$$ (33)

and

$$J_{\text{temp}}^{+}(H_n(\mathit{m},S),{\overline{H}}_n(\overline{\mathit{m}},\overline{S}))=\frac{1}{2}\left(\text{tr}(S^{-1}\mathrm{\sum })+{(\mathbf{m}-\mathit{\mu })}^T{S}^{-1}(\mathbf{m}-\mathit{\mu })-k_d+\text{tr}({\overline{S}}^{-1}S)+ln\left(\frac{det(\overline{S})}{det(\mathrm{\sum })}\right)-k_d\right),$$ (34)

where ln (H̄_n (m̄, S̄)) ~ 𝒩(m̄, S̄). θ̄ = (V̄, H̄_s, H̄_n) are the auxiliary variables. 0 < ρ < 2 is a parameter for ${\sum }_{k=1}^{k_d}{\sum }_{t=1}^{t_n}{\mid {[H_s]}_{kt}\mid }^{\rho }$ to promote sparsity in H_s. In our work, we measure the ℓ₁ norm of H_n, so ρ = 1. Proofs that $J_{\text{error}}^{+}$ and $J_{\text{spars}}^{+}$ are auxiliary functions for J_error and J_spars respectively can be found in Appendix A of [24], so we will focus on proving that $J_{\text{temp}}^{+}$ is an auxiliary function of J_temp. For simplicity, we write H_n := H_n (m, S) and H̄_n := H̄_n (m̄, S̄).

Since we assume that each row of H_d and H_n are independent, we will consider each row separately. In this case, Equation 30 simplifies to

$$J_{\text{temp}}({\mathit{h}}_n)=\frac{1}{2}\left(\frac{{\sigma }^2+{(m-\mu )}^2}{s^2}-1+ln\left(\frac{s^2}{{\sigma }^2}\right)\right)$$ (35)

and Equation 34 simplifies to

$$J_{\text{temp}}^{+}({\mathit{h}}_n,{\overline{\mathit{h}}}_n)=\frac{1}{2}\left(\frac{{\sigma }^2+{(m-\mu )}^2}{s^2}-1+\frac{s^2}{{\overline{s}}^2}+ln({\overline{s}}^2)-1-ln({\sigma }^2)\right).$$ (36)

Theorem 1

$J_{\mathit{temp}}^{+}({\mathit{h}}_n,{\overline{\mathit{h}}}_n)$ is an auxiliary function for J_temp (h_n).

Proof

If h̄_n = h_n, then m̄ = m and s̄² = s².

In this case, $J_{\text{temp}}^{+}({\mathit{h}}_n,{\mathit{h}}_n)=J_{\text{temp}}({\mathit{h}}_n)$.

$$\begin{gathered} J_{\text{temp}}^{+}({\mathit{h}}_n,{\overline{\mathit{h}}}_n)-J_{\text{temp}}({\mathit{h}}_n) \\ =\left(\frac{s^2}{{\overline{s}}^2}+ln({\overline{s}}^2)-1\right)-ln(s^2) \\ =ln({\overline{s}}^2)+\left(\frac{s^2}{{\overline{s}}^2}-1\right)-ln(s^2) \\ \ge ln({\overline{s}}^2)+ln\left(\frac{s^2}{{\overline{s}}^2}\right)-ln(s^2)\because ln(x)\le x-1\forall x>0 \\ =0 \end{gathered}$$ (37)

Hence $J_{\text{temp}}^{+}({\mathit{h}}_n,{\overline{\mathit{h}}}_n)\ge J_{\text{temp}}({\mathit{h}}_n)$ and $J_{\text{temp}}^{+}({\mathit{h}}_n,{\mathit{h}}_n)=J_{\text{temp}}({\mathit{h}}_n)$.

$\therefore J_{\text{temp}}^{+}({\mathit{h}}_n,{\overline{\mathit{h}}}_n)$ is an auxiliary function for J_temp (h_n).

The optimum value of the auxiliary variable h̄_n can be found by setting the gradient of $J_{\text{temp}}^{+}({\mathit{h}}_n,{\overline{\mathit{h}}}_n)$ w.r.t. h̄_n equal to zero:

$$\begin{gathered} {\nabla }_{{\overline{\mathit{h}}}_n}{J}_{\text{temp}}^{+}({\mathit{h}}_n,{\overline{\mathit{h}}}_n)=\frac{ln({\overline{\mathit{h}}}_n)-\overline{m}{\mathbf{1}}_{t_n}}{(t_n-1){\overline{s}}^2{\overline{\mathit{h}}}_n}-\frac{s^2(ln({\overline{\mathit{h}}}_n)-\overline{m}{\mathbf{1}}_{t_n})}{(t_n-1){({\overline{s}}^2)}^2{\overline{\mathit{h}}}_n}=0 \\ ln({\overline{\mathit{h}}}_n)-\overline{m}{\mathbf{1}}_n=\frac{s^2}{{\overline{s}}^2}(ln({\overline{\mathit{h}}}_n)-\overline{m}{\mathbf{1}}_{t_n}) \\ \left(1-\frac{s^2}{{\overline{s}}^2}\right)ln({\overline{\mathit{h}}}_n)=\left(1-\frac{s^2}{{\overline{s}}^2}\right)\overline{m}{\mathbf{1}}_n \\ ln({\overline{\mathit{h}}}_n)-\overline{m}{\mathbf{1}}_{t_n} \end{gathered}$$ (38)

$J_{\text{temp}}^{+}({\mathit{h}}_n,{\overline{\mathit{h}}}_n)$ can be rewritten for all rows of H_d and H_n as Equation 34 and the auxiliary variable H̄_n can be updated as H̄_n = diag (m̄) 1_kn×tn.

We did not create an auxiliary function for J_spec (W_n) because it is already quadratic in W_n, so minimizing J_spec w.r.t. W_n is not difficult. Indeed, ∇_WnJ_spec (W_n) = Λ^TΛ(W_n − W_d).

A. Basis update equations

To find the update for W_s, we need to find ∇_WsC⁺ (θ, θ̄). Since the regularization terms we added do not contain W_s, they do not affect gradient. Hence, we use the update equation derived in [24], which results in Equation 13.

To find the update for W_n, we calculate ${\nabla }_{W_n}{C}^{+}(\theta ,\overline{\theta })={\nabla }_{W_n}\left(J_{\text{error}}^{+}\left(V,\overline{V},\widehat{V}\right)+J_{\text{spec}}(W_n)\right)$. ${\nabla }_{W_n}{J}_{\text{error}}^{+}\left(V,\overline{V},\widehat{V}\right)=\frac{W_n{H}_n-\mid {\overline{V}}_n\mid }{{\beta }_n}{H}_n^T$ is derived in [24] and ∇_WnJ_spec (W_d,W_n,Λ) = Λ^TΛ(W_n − W_d). So,

$${\nabla }_{W_n}{C}^{+}(\theta ,\overline{\theta })=\frac{W_n{H}_n-\mid {\overline{V}}_n\mid }{{\beta }_n}{H}_n^T+{\mathrm{\Lambda }}^T\mathrm{\Lambda }(W_n-W_d).$$ (39)

The update equation for W_n is

$$W_n\leftarrow W_n\odot \frac{{[{\nabla }_{W_n}{C}^{+}(\theta ,\overline{\theta })]}^{-}}{{[{\nabla }_{W_n}{C}^{+}(\theta ,\overline{\theta })]}^{+}},$$ (40)

which leads to the update equation given in Equation 16.

B. Time-activation update equations

To find the update for H_s, we need to find ∇_HsC⁺ (θ, θ̄). As in the case with W_s, the added regularization terms do not contain H_s so they do not affect the gradient. Hence, we use the update equation derived in [24], which results in Equation 14.

To find the update for H_n, we calculate ${\nabla }_{H_n}{C}^{+}(\theta ,\overline{\theta })={\nabla }_{H_n}\left(J_{\text{error}}^{+}\left(V,\overline{V},\widehat{V}\right)+\gamma J_{\text{temp}}^{+}(H_n,{\overline{H}}_n)\right)$.

${\nabla }_{H_n}{J}_{\text{error}}^{+}\left(V,\overline{V},\widehat{V}\right)=W_n^T\frac{W_n{H}_n-\mid {\overline{V}}_n\mid }{{\beta }_n}$ is derived in [24]. Define U = diag (μ) and M = diag (m).

$${\nabla }_{H_n}{J}_{\text{temp}}^{+}(H_d,H_n,{\overline{H}}_n)=\frac{1}{H_n}\otimes [\frac{1}{t_n}{S}^{-1}(M-U)1_{k_n\times t_n}-\frac{1}{t_n-1}(S^{-2}\mathrm{\sum }+{(M-U)}^T{S}^{-2}(M-U))(ln(H_n)-M{1}_{k_n\times t_n})+\frac{1}{t_n-1}{S}^{-1}(ln(H_n)-M{1}_{k_n\times t_n})]$$ (41)

The update equation for H_n is

$$H_n\leftarrow H_n\odot \frac{{[{\nabla }_{H_n}{C}^{+}(\theta ,\overline{\theta })]}^{-}}{{[{\nabla }_{H_n}{C}^{+}(\theta ,\overline{\theta })]}^{+}}.$$ (42)

Note that U, M, and ln (H_n) are mixed-sign matrices. A mixed-sign matrix A can be rewritten in terms of nonnegative matrices as A = [A]⁺ −[A]⁻. Rewriting the mixedsign matrices leads to the update equation for H_n given by Equation 17.