Multiple surface segmentation using convolution neural nets: application to retinal layer segmentation in OCT images

Abstract

Automated segmentation of object boundaries or surfaces is crucial for quantitative image analysis in numerous biomedical applications. For example, retinal surfaces in optical coherence tomography (OCT) images play a vital role in the diagnosis and management of retinal diseases. Recently, graph based surface segmentation and contour modeling have been developed and optimized for various surface segmentation tasks. These methods require expertly designed, application specific transforms, including cost functions, constraints and model parameters. However, deep learning based methods are able to directly learn the model and features from training data. In this paper, we propose a convolutional neural network (CNN) based framework to segment multiple surfaces simultaneously. We demonstrate the application of the proposed method by training a single CNN to segment three retinal surfaces in two types of OCT images - normal retinas and retinas affected by intermediate age-related macular degeneration (AMD). The trained network directly infers the segmentations for each B-scan in one pass. The proposed method was validated on 50 retinal OCT volumes (3000 B-scans) including 25 normal and 25 intermediate AMD subjects. Our experiment demonstrated statistically significant improvement of segmentation accuracy compared to the optimal surface segmentation method with convex priors (OSCS) and two deep learning based UNET methods for both types of data. The average computation time for segmenting an entire OCT volume (consisting of 60 B-scans each) for the proposed method was 12.3 seconds, demonstrating low computation costs and higher performance compared to the graph based optimal surface segmentation and UNET based methods.

1. Introduction

Segmentation of object boundaries is essential in various medical image analysis applications. Segmentation identifies surfaces that separate organs, tissues and region of interests in an image and is crucial in quantification of medical images and management of disease. Since manual segmentation of surfaces or object boundaries is time consuming and subjective, it is attractive to develop automated surface segmentation algorithms. Over the last several decades, many such automated surface segmentation methods have been developed. State-of-the-art surface segmentation methods can be broadly classified into three categories. (i) Graph based methods - optimal surface segmentation methods which convert the segmentation problem into an optimization problem subject to surface smoothness and interrelation constraints [1–3] or shortest-path based approach which detects boundaries by searching the shortest-path with respect to assigned node costs [4,5] - where node costs can be generated using machine learning. Graph-cut [6] is also used for surface segmentation where regions are segmented using an optimizing framework and surfaces are recovered as a post processing step by finding the boundary of segmented regions. (ii) Contour modeling approaches [7,8] - use an adaptive model based on prior shape information of the target structure in input images. In addition to prior target structure information, iterative models have also been used to consider weighted functions of image intensity and gradient properties [9]. (iii) Machine learning based methods, which formulate the segmentation problem as a classification problem based on features extracted from target surfaces [10] or employ machine learning as component of a hybrid system [11] for learning features and parameters to aid graph based/contour modeling approaches. These methods have been successfully employed for various medical image analysis and segmentation applications [12–20]. However, most of these methods rely on expert designed or hand-crafted application specific parameters and features based on their respective techniques. For example, graph based optimal surface segmentation method [1] uses expert designed cost images, various surface constraints, and region of interest extraction schemes [21], while active contour modeling based approaches require hand crafted models and shape priors. Generation of such parameters and features may be difficult, especially for cases with pathology.

In recent years, deep learning [22] based methods have shown to achieve significant results in numerous computer vision [23–25] and medical image analysis applications [26, 27]. For image based applications, these methods are typically implemented as Convolutional Neural Nets (CNNs) [28] which learn highly complex features and models at various levels of abstractions from training data without any explicitly expertly-designed feature extraction process. CNNs have been successfully used for various object segmentation application [29–32] where the problem is modeled as a pixel or voxel classification problem but has not been used for direct surface / boundary segmentation of the object.

In this paper, we propose a CNN based deep learning approach for direct multiple surface segmentation, where both features and models are learned from training data without expert designed features, models and transformations. Further, we demonstrate the application of the proposed method on retinal layer segmentation in Optical Coherence Tomography (OCT) images.

OCT is a 3-D non-invasive [33] imaging technique that is widely used in the diagnosis and management of patients with retinal diseases [35]. OCT technology is based on the principle of low-coherence interferometry, where a low-coherence light beam is directed on to the target tissue and the scattered back-reflected light is combined with a second beam (reference beam). The resulting interference patterns are used to reconstruct an axial A-scan, which represents the scattering properties of the tissue along the beam path. Moving the beam of light along the tissue in a line results in a compilation of A-scans, from which a two-dimensional cross-sectional image (B-scan) of the target tissue is reconstructed. An OCT volume of an eye consists of multiple such B-scans of a given cross-section of the retina.

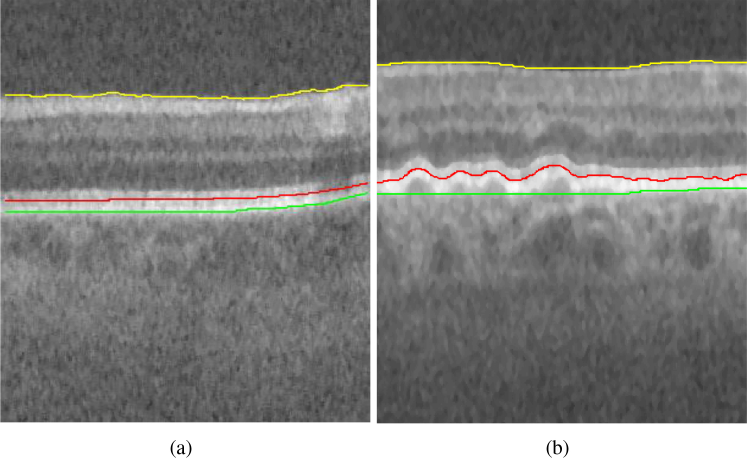
The tissue boundaries in OCTs vary by presence and severity of disease. An example is shown in Fig. 1(a)(b) to illustrate the difference in profile of the Inner Retinal Pigment Epithelium (IRPE) and outer aspect of the Bruch membrane (OBM) in a normal eye and in an eye with Age-related Macular Degeneration (AMD) [36]. Accurate quantification of layer thicknesses based on retinal layer segmentations in OCT images is crucial for the study of many retinal diseases.

Fig. 1.

Example B-scan from an OCT image volume of (a) normal eye (b) eye with pathology (intermediate AMD). Yellow = Internal limiting membrane (ILM), red = Inner retinal pigment epithelium (IRPE) and green = outer aspect of the Bruch membrane (OBM). It can be seen that IRPE and OBM in the B-scan with intermediate AMD exhibits more changes in surface smoothness and surface distance between the two surfaces compared to the B-scan of normal eye.

A plethora of OCT retinal layer segmentation algorithms [13,34] have been developed and applied to various applications. State-of-the-art graph based global optimization methods [1,35] have been developed and used for different applications including normal eyes [37] and eyes with various disease manifestations [21,38]. Each application may require construction of new constraints such as hard constraint [37], soft constraints [2] and shape priors [3, 39, 40] while also requiring different hand crafted schemes for region of interest extraction and cost image generation [21,38]. Generation of various constraints, features, transformations and models for these methods is especially difficult for the use on a multitude of applications relating to the kind of pathology present in the OCT image. For example, such methods have separate set of models and parameters for normal cases and disease specific cases. By employing a CNN based approach one of the goals is to eliminate the requirement of expert designed transforms, constraints and features for each specific pathology and non-pathology based application.

Recently, CNN based methods have also been studied to perform surface segmentation in OCT images [41–44]. These methods do not segment the retinal surfaces directly but instead employ a hybrid approach where the CNN is used as a module to learn the data consistency cost to be used by various graph based optimization methods. Herein, after learning the data term through the CNN, the method requires expert designing of various constraints and parameter settings. The methods show improvement over the traditional graph based approach but suffer from similar deficiencies regarding requirement of separate set of parameters and constraints for normal and disease specific applications. UNET [29] is another method that can be potentially employed to directly perform surface segmentation [45]. A UNET performs voxel wise classification, thus labeling each voxel as belonging to a certain class. The method has been shown to produce highly accurate results for object and region segmentation but has not been specifically used to perform surface segmentation directly.

Our main contribution in this paper is the development of a CNN based approach which performs multiple surface segmentation directly. We demonstrate the applicability of the method by segmenting retinal surfaces in OCT volumes at the B-scan level in one single shot. A key aspect of the method is modeling of the surface segmentation problem in a similar manner as optimal surface segmentation method [1] and exploiting the voxel column structure as developed in Ref. [1]. The proposed method encodes the target surface segmentations into a vector and the CNN is trained to learn inferring the surface segmentation vector from training data. The method allows for training of a single CNN to infer on OCT images of both normal eyes and eyes with pathology (intermediate AMD). To show the improved performance of the method, we compare our proposed method to state-of-the-art optimal surface segmentation method [39] and two UNET based methods to directly infer the target surface segmentations.

2. Method

We present the method to perform segmentation in 2-D at a B-scan level, to avoid computationally expensive 3-D convolutions [46]. The method can be readily extended to perform segmentation in 3-D as is briefly described in Section 5.4. We formulate the problem in a similar manner as our previous patch based approach [47] while extending the approach to segment the entire B-scan in a single pass. The patch based approach may have problem to segment the Outer Aspect of Bruch Membrane (OBM) due to presence of Drusen in intermediate AMD data. The method [47] requires much larger patches to estimate the OBM due to absence of local intensity information for the surface. Hence, we segment the entire B-scan in one pass instead of using patches. Segmenting the entire B-scan directly also encourages smoother surface modeling.

We model the problem in a similar manner as the optimal surface segmentation method [39] to exploit the column structure in the formulation. Consider a B-scan image I(x, z) of size X × Z. A surface is defined as a function S(x), where x ∈ x = {0, 1, ... X − 1}, and S(x) ∈ z = {0, 1, ...Z − 1}. Each (x) corresponds to a pixel column {(I(x, z)|z = 0, 1, . . ., Z − 1}. The function S(x) can be viewed as labeling for (x) with the label set z (S(x) ∈ z). We denote such kind of surface S(x) as a terrain-like surface. Herein, the method is explained for a terrain like surface. However, the method can be adapted to segment non terrain-like surfaces and is discussed in Section 5.5. For simultaneously segmenting λ(λ ≥ 2) distinct but interrelated surfaces, the goal of the problem is to seek surfaces S_i(x), where i = 1, 2, ...λ in I.

To train the network, the entire B-scan is used to create input samples and the manual tracings for the respective B-scans are used to create the output labels. Most of the CNN based methods have been used for classification or region segmentation while the proposed method aims to segment the boundary/surfaces directly using a CNN. Therefore, we encode the consecutive target surface positions for a given input image as a vector while maintaining a strict order with respect to the consecutiveness of the target surface positions based on the inherent column ordering. For example, m consecutive target surface positions are represented as an m-D vector, which may be interpreted as a point in the m-D space. The ordering of the target surface positions also encapsulates the smoothness of the surface.

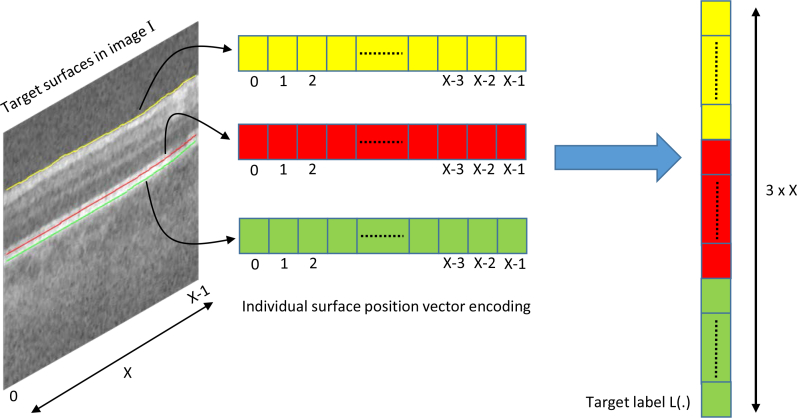
The input sample is a B-scan image while the label for the respective sample corresponds to the target surfaces encoded in a vector. For a single surface S(x), there exists X surface positions in the order x ∈ x = {0, 1, ... X − 1}. The label L for the input sample is therefore a vector of length X with L(x) = S(x) for x ∈ x = {0, 1, ... X − 1}. For multiple surfaces, the target surface positions for each surface is encoded into the label vector according to the order in which surfaces appear from top to bottom in the B-scan image. Therefore, for λ surfaces, the label vector is of size λ × X and is defined as L((i − 1) × X + x) = S_i(x), where i ∈ {1, 2, ... λ}. The vector encoding for multiple surfaces is shown in Fig. 2.

Fig. 2.

Label vector encoding for a given image sample I with λ = 3 target surfaces. The indexes of vector positions are shown below each cell. The target label L(.) used in network training is the ordered concatenation of each surface encoded vector.

2.1. Network architecture

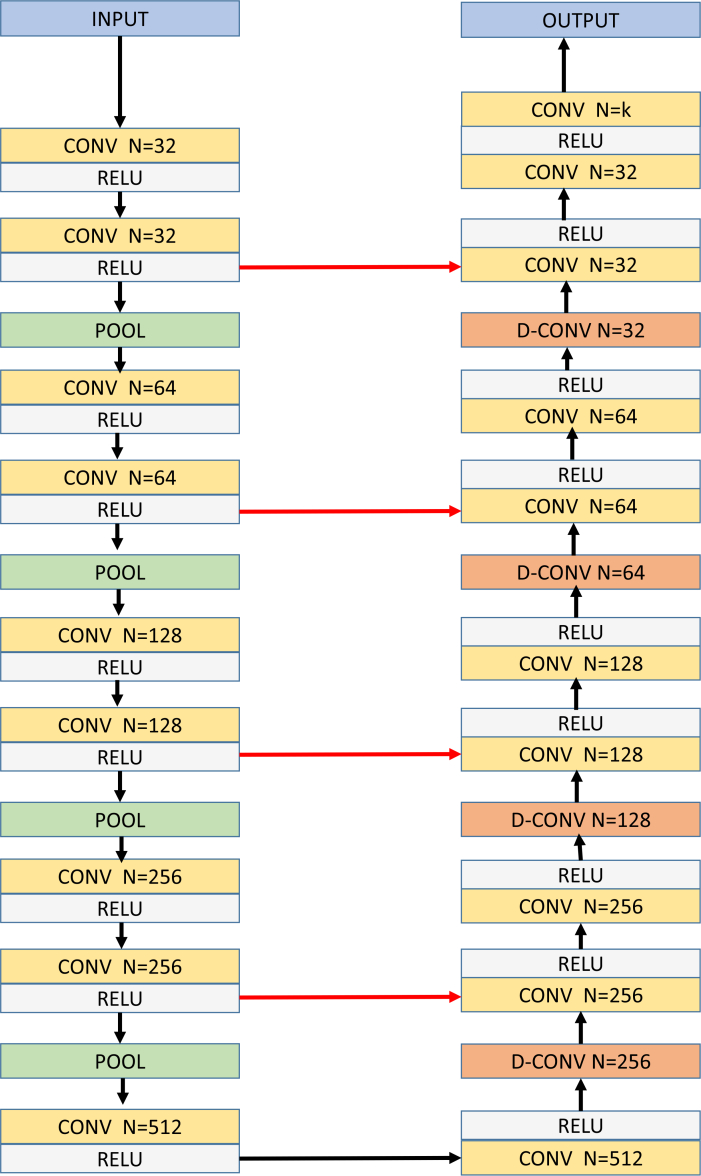
The proposed network architecture (CNN-S) is closely inspired by the AlexNet architecture [28]. Herein, the network is described for image size of input samples used in this study and can be adapted in a straight forward manner for different input sample sizes. The network consists of blocks of single convolution layer and a pooling layer [28], with specified number of convolution kernels, thus resulting in decreasing levels of abstractions. The last block is then followed by two fully connected layers where the number of neurons in the last fully connected layer is equal to λ × X (number of surfaces × number of columns in B-scan). Herein, the convolution layer kernel size used was 3 × 3 with a stride of 1, the pooling layer employed was max pooling with kernel size 2 × 2 and ReLU [28] non-linearity activation function was used. The architecture for the proposed method is shown in Fig. 3.

Fig. 3.

Network architecture for CNN-S with number of columns in B-scan = 400 and 3 target surfaces. N=number of kernels used in the convolution layer, CONV=Convolution Layer, FC=Fully connected layer, n=number of neurons in the FC layer.

One hallmark of the proposed method and network architecture is to attain highly accurate segmentations while maintaining surface monotonicity for terrain-like surfaces compared to UNET [29] based approaches while encoding significantly lesser network weights/parameters. Therefore, it is important to adequately design the network architecture configuration, especially the input to the fully connected layers and the number of neurons in the first fully connected layer to avoid an explosion in the number of network weights.

2.2. Loss function

The error (loss) function utilized in CNN-S to backpropagate the error is a Euclidean loss function (used for regressing to real-valued labels) as shown in Eq. 1, wherein the network adjusts the weights of the various nonlinear transformations within the network to minimize the Euclidean distance between the CNN-S output and the target surface positions in the (λ × X)-D space (size of the label vector L).

Unsigned mean surface positioning error [37] is one of the commonly used error metric for evaluation of surface segmentation accuracy, especially for terrain like surfaces. The Euclidean loss function (Eq. 1), in fact computes sum of the squared unsigned surface positioning error between the consecutive surface positions of the CNN-S output for each surface and manual tracings encoded in the label vector L, thereby reflecting the exact squared surface positioning error to be used for back propagation during training the network. In other words, the loss function can be interpreted as enforcing a quadratic penalty on the exact difference in the surface positions between the CNN-S output and the reference tracings. Therefore, the training/validation loss for CNN-S method provides a direct approximation of the unsigned mean surface positioning error.

$$E=\sum _{i=1}^{\lambda }\sum _{x=0}^{X-1}{\left(S_i(x)-L((i-1)\times X+x)\right)}^2$$ (1)

3. Experiment

The proposed CNN-based surface segmentation method was applied to Spectral domain OCT (SD-OCT) volumes of normal eyes and eyes with intermediate AMD, to demonstrate its utility and effectiveness. It was compared to two UNET [29] based methods and one graph search method.

3.1. Data

380 SD-OCT volumes (115 normal eyes and 265 eyes with intermediate AMD) and their respective expert manual tracings were obtained from the publicly available repository of datasets Ref. [48]. Each 3-D volume had a size of 1000 × 100 × 512 (horizontal × vertical × axial) voxels with voxel size 6.54 × 67 × 3.23 μm³. The OCT volume size was 6.7 × 6.7 × 1.66 mm³. Since the manual tracings were only available for a 5mm diameter region centered at the fovea [48], subvolumes of size 400 × 60 × 512 were extracted around the fovea for training, testing and evaluation purposes. The dataset was randomly divided into 3 sets. 1) Training set - comprising of 264 SD-OCT volumes (72 normal, 192 intermediate AMD) utilized in training the CNN based methods. 2)Validation set - comprising of 66 SD-OCT volumes (18 normal, 48 intermediate AMD) used to optimize CNN weights during the training phase, make decisions on changing the learning rates and stopping the training process. 3) Testing set - comprising of 50 SD-OCT volumes (25 normal, 25 intermediate AMD) to evaluate the segmentation performance of the proposed and compared methods. Three surfaces were simultaneously segmented in this study. The surfaces are S₁- Internal Limiting Membrane (ILM), S₂- Inner Aspect of Retinal Pigment Epithelium Drusen Complex (IRPE) and S₃- Outer Aspect of Bruch Membrane (OBM) as shown in Fig. 1.

3.2. Compared methods

As discussed in Section 1, CNN based methods have been used to segment surfaces at a B-scan level in 2-D where the UNET [29] or a modified version of the UNET forms the basis of the network architecture. While some of these methods [41–43] employ the CNN to generate a cost which is used by surface segmentation algorithms (where user has to optimize various constraints and model parameters for a given application) to compute the segmentation, the UNET may also be used to directly perform the surface segmentation via a classification approach. Direct segmentation using UNET based CNN methods is typically performed in either of the following two ways: The UNET is used to directly classify voxels into respective target surface segmentation classes or the UNET is employed to classify voxels into regions between the target surfaces and the final surface segmentation is attained from the region segmentation by application of a user defined post processing step [45]. The proposed method (CNN-S) was therefore compared to two UNET based methods. Specifically, we trained two UNETs. UNET-1 which directly classifies the voxel into surface labels and UNET-2 similar to [45] which segments the region between the target surfaces via voxel classification, where the target surface segmentation is obtained using a post processing step. We also compared our proposed method to state-of-the-art 3-D optimal surface segmentation method (OSCS) [39]. We used the OSCS method in 3-D because it has been shown that the method outperforms its 2-D counterparts [1].

3.3. CNN based methods implementation

All CNN based models were implemented with the publicly available deep learning toolkit CAFFE [49]. We used a single NVIDIA Titan X GPU for training the CNNs. A Linux workstation (3.4 GHz, 16 GB memory) without GPU support was used for segmenting the images in the testing dataset using each of the CNN based methods and the OSCS method. For all the CNN based method a single CNN was trained to segment the three surfaces in both normal and intermediate AMD volumes. All the CNN based methods used the same data augmentation scheme as described in Section 3.3.3 and the same training and validation sets.

3.3.1. Network architectures and loss functions for UNET based methods

The network architectures for UNET-1 and UNET-2 is designed using the standard UNET [29] configuration. The architectures for UNET-1 and UNET-2 are exactly the same with the difference being in the final output convolution layer [28]. The network consists of blocks of two convolution layers and a pooling layer [28], with increasing number of convolution kernels, thus resulting in decreasing levels of abstractions and increasing of feature maps. The architecture uses four such blocks. Then, it is followed by blocks of deconvolution layers [29] followed by two convolution layers, where the output of the deconvolution layer is concatenated with output of the parallel abstraction level convolution layer output, finally resulting in the exact same resolution of the input sample with k = 4 and k = 3 output channels for UNET-1 and UNET-2 respectively. In the UNET architectures, the convolution layer kernel size used was 3 × 3 with a stride of 1, the pooling layer employed was max pooling with kernel size 2 × 2, deconvolution kernel size was 2 × 2 with a stride of 2 and ReLU [28] non-linearity activation function was used. The architecture for the UNET based methods are shown in Fig. 4.

Fig. 4.

Network architecture for UNET based methods. N=number of kernels used in a given layer, CONV=Convolution Layer, D-CONV=Deconvolution Layer, k=4 for UNET-1 and k=3 for UNET-2. Red arrows indicate concatenation operation.

The output of the network is an image with the same size as the input B-scan. The truth labels for the training and validation set are generated as follows:

• UNET-1 - Each pixel is given an integer class label between 0 to 3, where 0 indicates background, 1 indicates S₁, 2 indicates S₂ and 3 indicates S₃.

• UNET-2 - Each pixel is given an integer class label between 0 to 2, where 0 indicates background, 1 indicates the region between S₁ and S₂ and 2 indicates the region between S₂ and S₃.

The loss function utilized in these networks during training is the pixel-wise Mean Square Error (MSE) loss which minimizes the predicted segmentation and the ground truth. Finally, the output image is quantized to integer values. For UNET-2, further post processing is conducted to extract the target surfaces from the region segmentations by using gradient filters. No post-processing is applied to the UNET-1 segmentation solution. The standard UNet architecture [29] was used in this work. The UNet architectures were not optimized for retinal layer segmentation by investigating multiple configurations of various numbers of convolution kernels or regularized layers to attain best performance.

3.3.2. Training scheme

The network weights are initialized using xavier initialization [49]. The network parameters are updated via back-propagation and Adam optimization process with the infinity norm [50] and a momentum of 0.9 was used. The training process is started with an initial learning rate of 10⁻³ and is reduced by a factor of 10 if the loss does not improve for 10 consecutive epochs. The learning rate is reduced down to a minimum of 10⁻⁹. The validation set is utilized to evaluate the loss and adaptively set the learning rate. At the end of the training process, network weights with the lowest validation loss is used to perform segmentation of the testing dataset for quantitative evaluation.

3.3.3. Data augmentation and batch size

Data augmentation was performed to increase the power of the training and validation datasets. For each B-scan, four additional training samples were created. First, a random translation value was chosen between −120 and 120 such that the translation was within the range of the B-scan size. The training sample and the corresponding manual tracings for the surfaces were translated in the z dimension accordingly. Second, a random rotation value was chosen between −45 degrees and 45 degrees. The training sample and the corresponding manual tracings for the surfaces were rotated accordingly. Third, a combination of rotation and translation was used to generate another training sample. Last, a horizontal flip was performed across the middle column of the training sample and the respective manual tracings were updated accordingly. Thus, we increased the power of the training and validation datasets by a factor of 4, resulting in a training set of 79,200 and a validation set of 19,800 B-scan samples.

In the training phase, CNN-S method had a mini batch size of 80 samples with 990 mini batches in 1 epoch, while for UNET-1 and UNET-2, the mini batch size was 50 samples with 1584 mini batches in 1 epoch. In the validation phase, CNN-S method had a mini batch size 180 of samples with 110 mini batches in 1 epoch, while for UNET-1 and UNET-2, the mini batch size was 100 samples with 200 mini batches in 1 epoch.

3.4. Cost function design and parameter setting for the OSCS method

The cost function image volumes encode the data term required for the energy function in [39]. To detect surfaces S₁, S₂ and S₃, a 3-D Sobel filter of size 5 × 5 × 5 voxels is applied to generate respective cost volumes wherein the vertical edges for dark to bright transitions and bright to dark transitions are emphasized.

50 randomly selected volumes (25 normal, 25 intermediate AMD) from the training set were used to optimize parameters to achieve best performance for the OSCS method including the weight co-efficients for the surface smoothness constraints. Two different set of parameters were selected: OSCS-1 parameters for normal data and OSCS-2 parameters for pathological (intermediate AMD) data, since it has been shown previously [47] that for the entire dataset, a single set of parameters results in inferior performance for the OSCS method. The minimum surface distance constraint [39] between S₁ and S₂ was set to 30 voxels for OSCS-1 and 20 voxels for OSCS-2. The minimum surface distance constraint between S₂ and S₃ was set to 3 voxels for both OSCS-1 and OSCS-2. A linear convex function was employed to model the surface smoothness constraint [39].

4. Results

The segmentation accuracy was estimated using unsigned mean surface positioning error (UMSP) and unsigned average symmetric surface distance error (UASSD). The UMSP error for a surface was computed by averaging the vertical difference between the manual tracings and the automated segmentations for all the B-scans in the testing dataset. The UASSD error for a surface was calculated by averaging the closest distance between all surface points of the automated segmentation and those of the expert manual tracings. Statistical significance of the observed differences was determined using 2-tailed paired t-test for which p values of 0.05 were considered significant.

As discussed in Section 3.2, the UNET-1 and UNET-2 method, may require user defined post processing steps to clean the solution, since surface monotonicity is not explicitly enforced, hence there may be instances where a given column has multiple instances of the same surface. Therefore for UNET-1 and UNET-2, it is not feasible to compute the UMSP and the segmentation accuracy is compared using only the ASSD metric. It is to be noted, that the goal of the segmentation problem is to directly segment the target surfaces, hence no comparisons are conducted for the region segmentation between the two consecutive surfaces. For UNET-2, the surface segmentation is extracted by computing the edges of the resulting region segmentation.

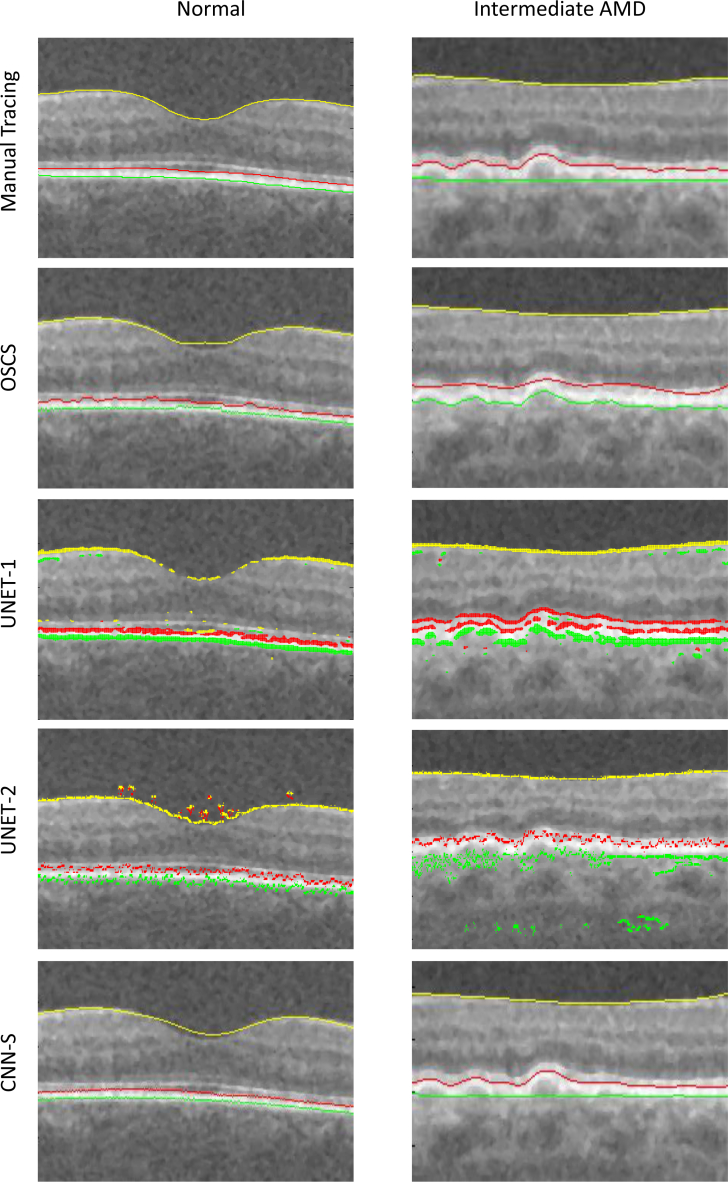
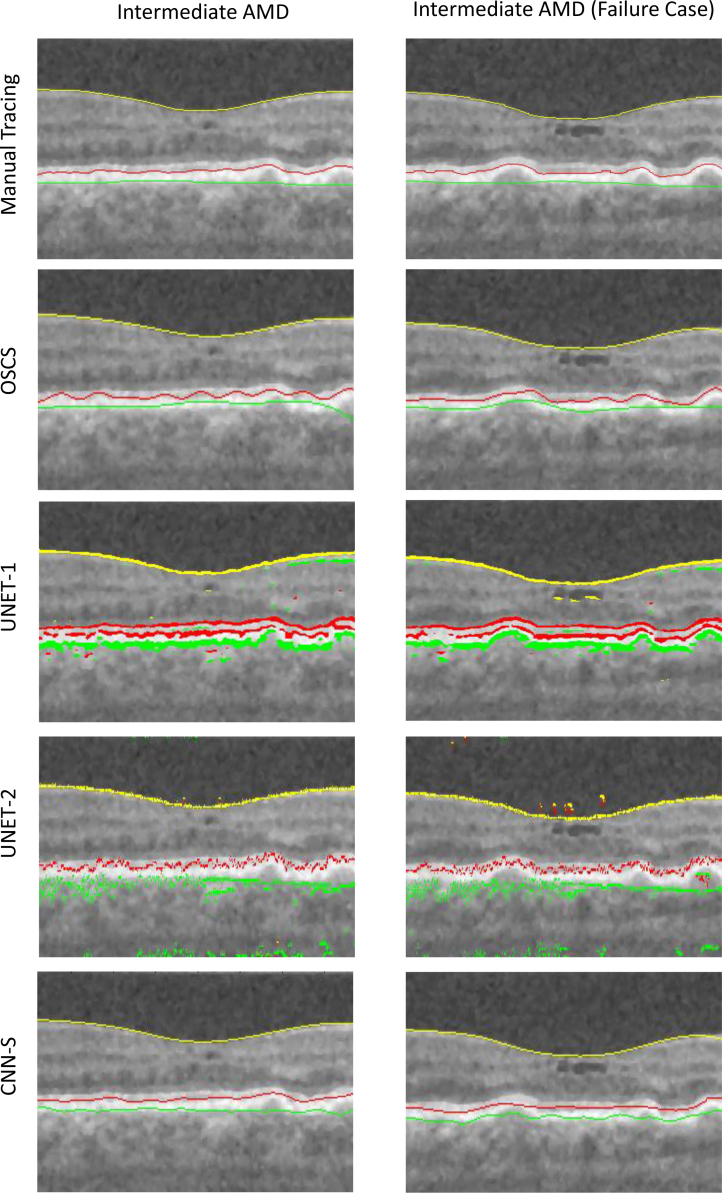
The qualitative results are shown in Fig. 5 and Fig. 6. Herein, the left column shows a B-scan from normal data while the right column shows the a B-scan from intermediate AMD data. The automated segmentation for each of the compared methods is shown in each column. Note, results shown for the OSCS method, is indeed from OSCS-1 for the normal B-scan and OSCS-2 for the intermediate AMD B-scan. It can be seen from Fig. 5, that the graph based OSCS methods struggles to segment the OBM surface in both types of B-scans and segmentation results are inaccurate for IRPE surface due to oversmoothing with the surface smoothness constraints. For UNET-1 and UNET-2, it is evident that the absence of any surface monotonicity results in many false instances for each surface in a given column. Moreover, UNET-2 fails to enforce any smoothness of the surface segmentations since it is primarily trained to segment regions without any explicit smoothness enforcement. Thus, surface extraction from the segmented regions results in discontinuous and erroneous segmentations. Qualitatively, the CNN-S method produced very good and consistent segmentations. The CNN-S method, results in more accurate segmentations in comparison with OSCS, UNET-1 and UNET-2 methods. It can also be seen that the surface segmentations from the CNN-S method enforces surface monotonicity like the OSCS method while also producing smooth surface segmentations.

Fig. 5.

The left column shows the same B-scan from a SD-OCT volume of a normal eye. The right column shows the same B-scan form a SD-OCT volume of an eye with intermediate AMD. Yellow = ILM, red = IRPE, green = OBM.

Fig. 6.

Each column shows the same B-scan from a SD-OCT volume of an eye with intermediate AMD. The right column illustrates an encountered failure case for the proposed CNN-S method. Yellow = ILM, red = IRPE, green = OBM.

The UMSP errors for the CNN-S and the OSCS method are summarized in Table 1. The results for the OSCS methods are based on OSCS-1 and OSCS-2 results for normal and intermediate AMD data respectively. Our proposed method CNN-S, produced significantly lower UMSP for S₁ (p<0.05), S₂ (p<0.01) and S₃ (p<0.01) for both types of data compared to the OSCS method. It is to be noted that while the CNN-S method was trained using a single CNN to infer on both normal and intermediate AMD data, but the OSCS method was used with two different set of parameters for each type of data to obtain best performance.

Table 1.

Unsigned mean surface positioning error (UMSP) (mean ± standard deviation) in μm. Obsv - Expert manual tracings.

Surface	Normal		Intermediate AMD
	OSCS vs. Obsv	CNN-S vs. Obsv	OSCS vs. Obsv	CNN-S vs. Obsv
S 1	3.84±0.16	3.36±0.23	4.43±0.71	3.71±0.77
S 2	4.55±0.36	3.84±0.58	9.30±1.74	6.07±1.84
S 3	5.59±1.20	4.97±1.01	10.14±5.30	5.85±1.80
Overall	4.65 ±0.61	4.07±0.55	7.95±2.68	5.20±1.58

The UASSD errors for the CNN-S, OSCS, UNET-1 and UNET-2 method are summarized in Table 2,3. Our proposed method CNN-S, produced significantly lower UASSD for S₁ (p<0.05), S₂ (p<0.01) and S₃ (p<0.001) for both types of data compared to the OSCS, UNET-1 and UNET-2 method.

Table 2.

Unsigned average symmetric surface distance error (UASSD) (mean ± standard deviation) in μm for normal case. Obsv - Expert manual tracings.

Surface	Normal
	OSCS vs. Obsv	CNN-S vs. Obsv	UNET-1 vs Obsv.	UNET-2 vs Obsv.
S 1	4.04±0.19	3.45±0.26	38.11±16.47	30.52±11.78
S 2	4.94±0.52	4.10±0.68	11.98±1.26	10.36±5.97
S 3	5.78±1.26	5.14±1.03	12.43±6.69	11.11±6.33
Overall	4.90 ±0.71	4.23±0.71	20.83±8.33	17.31±8.10

Table 3.

Unsigned average symmetric surface distance error (UASSD) (mean ± standard deviation) in μm for intermediate AMD case. Obsv - Expert manual tracings.

Surface	Intermediate AMD
	OSCS vs. Obsv	CNN-S vs. Obsv	UNET-1 vs Obsv.	UNET-2 vs Obsv.
S 1	4.52±0.74	4.01±0.87	62.34±43.79	45.99±35.88
S 2	9.72±1.87	6.36±1.97	18.89±3.42	15.63±6.84
S 3	10.30±5.33	5.91±1.81	48.09±31.36	29.87±15.14
Overall	8.17±2.68	5.43±1.68	42.44±26.36	30.49±19.51

The CNN-S method with average computation time of 12.3 seconds (for entire OCT volume) was much faster than the UNET based methods (24.8 seconds) and OSCS method (2746.7 seconds) for the segmentation of a complete 3D OCT volume. Herein, the OSCS method was applied in 3-D to obtain more accurate segmentation than the 2-D version of the method, thus resulting in much higher computation time compared to the CNN-S and UNET methods. Note, as discussed in Section 3.1 the CNN methods were not trained on entire B-scans due to availability of manual tracings only for a 5mm diameter region. Thus, the segmentation performance in the leftover regions were not investigated and may result in less accurate segmentations in such regions because they were never included in training. However, due to the generalization ability of the CNN and the homogeneity in retinal SD-OCT B-scans, the networks are expected to provide comparably accurate segmentations in the leftover regions.

5. Discussion

5.1. Current network architecture

The architecture used for the CNN-S method can be extended and improved upon for various retinal layer segmentation applications. First, the network architecture is closely inspired by the AlexNet [28] architecture. The idea behind the network architecture was to add blocks of convolution and pooling layers to eventually bring the output feature map to a size ≤ 5 × 5, which is fed into the fully connected layers. This, is the simplest way of creating a network architecture similar to the AlexNet architecture. The number of kernels in each convolution layer was increased by a factor of 2 after every pooling layer and then reduced by a factor of 2 in a similar manner to reduce the input size to the first fully connected layer, to prevent explosion of network parameters at the first fully connected layer. During the experiment we simultaneously trained two similar architectures and used the architecture with best performance (presented in Fig. 3) on the validation set, to perform quantitative analysis on the test set. Therefore, there are multiple variation of similar feasible architectures which may result in better accuracy. Second, the network architecture does not utilize any batch normalization [52] or drop out layers. The use of such layers in the architecture could result in faster convergence due to better regularization and the reduction in overfitting the training data. It may marginally increase the segmentation accuracy while the number of training samples in the network is comparable to or not greater than the network capacity. Thus, in our current application, addition of batch normalization layers before every pooling layer in the presented network architecture may result in better accuracy. Third, the presented network architecture will need to be modified for different input sizes. The modifications should ensure correctness of the network and presence of sufficient number of network parameters for adequate training. Additionally, the final fully connected layers should be modified to accommodate the number of target surface positions in the given application.

5.2. Training data

One of the important requirements for deep learning algorithms is availability of adequate amounts of training data with good quality truth. Although deep learning algorithms have recently shown improved performances for segmentation purposes, various such medical image segmentation applications require ample amounts of training data which contain an adequate heterogeneity of disease manifestations with manually segmented truth by experts. Creation of or acquiring such kind of datasets may be infeasible and, in most cases, costly. Therefore, such a deep learning method as presented in this paper, comes with a training data overhead compared to unsupervised/semi-supervised segmentation methods like graph search, which do not necessarily require a large amount of data and expert manual segmentation truth.

5.3. Number of parameters

CNN based methods naturally have a substantially larger number of parameters (network weights) to optimize compared to the graph based optimal surface segmentation method (OSCS). The typical parameters required for the OSCS method are surface distance constraints, surface smoothness constraints and weight co-efficients for the modeled constraints. Thus, the total number of parameters is a small factor multiple of the number of target surfaces. However as discussed previously, these parameters have to be defined by an expert user or require repeated qualitative/quantitative evaluations which results in separate sets of parameters for normal scans, each type of pathological scans and also the type of scan (macula centered or optical nerve head centered). Additionally, data cost functions/features (which require their own set of parameters) are to be designed by expert users for application of the OSCS method. In contrast, the CNN based methods are aimed toward learning the segmentation through training data.

The CNN-S method required approximately 3 million parameters with the majority of parameters in the fully connected layer; the UNET required approximately 7.5 million parameters. Thus, the CNN-S method requires 2.5 times lesser number of parameters than the UNET while achieving significantly better segmentation accuracy for the given application. A smaller number of parameters is crucial with respect to the computational resources and time required for training these algorithms. In spite of the larger number of parameters in the UNET methods, the surface segmentation suffers from surface monotonicity issues because the problem formulation for UNET has no inherent mechanism to enforce surface monotonicity. However, the number of parameters for the proposed CNN-S architecture is associated to the number of target surfaces.

5.4. Non terrain-like surfaces

In this study, we demonstrated terrain-like surface segmentation using the proposed method. However, numerous applications exist where the target surfaces are non-terrain like. The problem formulation for the proposed method, thus does not allow for non terrain-like surface segmentation in the current configuration. On the other hand, UNET based methods can segment non terrain-like surface (since there is not enforcement of surface monotonicity based on voxel columns) but shall require post processing operations to extract the surface from the region segmentation or to suppress false/discontinuous classified surface pixels. However, since the proposed method exploits the column structure used in the graph based methods, the input images can be resampled to generate columns normal to the target surface profiles [51], allowing adoption of the proposed method to segment the non terrain-like surfaces. In many cases, resampling requires a pre- segmentation which may be difficult to attain. Therefore, the proposed method and UNET can be used together, wherein the UNET is used to get an approximate regional pre-segmentation, allowing resampling of columns in the images and then the proposed method can be applied for segmentation without any post-processing step.

5.5. 2-D vs 3-D

Majority of the CNN based surface segmentation algorithms including the proposed method have been demonstrated in 2-D. Due to the image acquisition process, wherein each B-scan is acquired separately without a guaranteed global alignment, the methods opt to segment retinal layers at the B-scan level. This avoids the need for computationally intensive 3-D convolutions and volumetric pre-processing like registration and alignment. However, state-of-the-art graph based methods segment the surfaces in 3-D and have demonstrated superior performance over 2-D segmentations but suffer from high computational times. The graph based method [21] reduces the computation time by region of interest extraction using a series of pre-segmentations and image processing operations which results in a variety of application specific region of extraction schemes. Although, the study shows that the proposed CNN-S implemented at the 2-D level results in higher segmentation accuracy compared to the OSCS method which was used in 3-D, it is reasonable to assume that segmentation of surfaces using CNN-S method in 3-D may result in more accurate segmentation compared to 2-D. The proposed method can readily be extended to segment the surfaces in 3-D by encoding the target surface positions in the following manner. Assume, an input volume I(x, y, z), the surface is defined as S(x, y) ∈ z = {0, 1, ... Z − 1}, where x ∈ x = {0, 1, ... X − 1}, y ∈ y ={0, 1, ... Y − 1}. Therefore, for a single surface the label vector is of size X × Y and is defined as L(t) = S(x, y) where t = (j × X) + x, where j ∈ y ={0, 1, ... Y − 1}. Multiple surfaces for the 3-D case can similarly encoded as discussed in Section 2. However, the proposed extension will result in a significant increase in the number of network weights.

5.6. Future work and limitations

The proposed method has certain limitations. First, the proposed method was validated on three target surfaces while retinal OCTs have eleven clinical significant surfaces. The target three surfaces were chosen based on their relevance with disease case (intermediate AMD) used in the study. Furthermore, the method requires ample amounts of data for training the CNN and expert annotated truth was only available for the three respective surfaces in the given dataset. Future work would include validating the performance and robustness of the algorithm on larger number of target surfaces and various other pathologies present in the eye. Second, the method requires significant amount of data as compared to UNet based methods. UNet based method have been shown to attain high performance for multiple surfaces with smaller amounts of training data. However, UNet based methods involve certain post processing steps or a hybrid approach as discussed previously unlike the proposed method. Third, the amount and type of augmentation used on the training data was limited. Future work would perform the augmentations online and increase the type of augmentations at the training phase during batch generation. Thus, increasing the power of training data, instead of creating the augmentations offline as performed currently in the experiments.

6. Conclusion

We have presented a method for performing multiple surface segmentation using CNNs and applied it to retinal layer segmentation in normal and intermediate AMD OCT scans at the B-scan level in a single pass. The experiments demonstrated the qualitative improvements in segmentation accuracy of the proposed method compared to the state-of-the-art baseline methods. The proposed method requires training of a single CNN to infer on both normal and intermediate AMD data while maintaining computational efficiency to the order of seconds, thus demonstrating applicability of the proposed method in a clinical setting. Given the robustness of this approach on pathological and normal cases, the method is suitable for further investigation into training a single CNN-S for surface segmentations in OCTs of normal eyes and eyes with a variety of different pathologies. Our approach is obviously not limited to the modality, for which the experiments were conducted. The proposed method is readily extensible to higher dimensions.

Disclosures

Abhay Shah: IDx LLC, Coralville, IA, USA (E), Michael D. Abrámoff: IDx LLC, Coralville, IA, USA (I, E, C, P, R), Xiaodong Wu: IDx LLC, Coralville, IA, USA (P)