Comparison of speckleplethysmographic (SPG) and photoplethysmographic (PPG) imaging by Monte Carlo simulations and in vivo measurements

Abstract

Noncontact photoplethysmography (PPG) is limited by a poor signal-to-noise ratio (SNR). A solution to this limitation is the use of alternate sources of optical contrast to generate a complementary pulsatile waveform. One such source is laser speckle contrast, which is modulated in biological tissues by the flow rate of red blood cells. Averaging a region of interest from a speckle contrast image over time allows for the calculation of a speckleplethysmogram (SPG). Similar to PPG, SPG enables monitoring of heart rate and respiratory rate. A gap in the knowledge base exists as to the precise spatiotemporal relationship between PPG and SPG signals. We have developed an eight-layer tissue model to simulate both PPG and SPG signals in a reflectance geometry via Monte Carlo methods. We modeled PPG by compression of the upper and lower blood nets due to expansion of the larger arterial layer below. The in silico PPG peak-to-peak amplitude percent was greater at 532 nm than at 860 nm (5.6% vs. 3.0%, respectively), which matches trends from the literature. We modeled SPG by changing flow speeds of red blood cells in both the capillaries and arterioles over the cardiac cycle. The in silico SPG peak-to-peak amplitude percent was 24% at 532 nm and 40% at 860 nm. In silico results are similar to in vivo results measured with a two-camera set up for simultaneous imaging of PPG and SPG. Both in silico and in vivo data suggest SPG has a much larger SNR than PPG, which may prove beneficial for noncontact, wide-field optical monitoring of cardiovascular health.

1. Introduction

In the United States, an estimated 92.1 million adults have one or more types of cardiovascular disease (CVD) [1]. Invasive monitoring procedures for CVD are undesirable because they may cause additional complications and trauma to patients, especially those that are already in critical condition. Ideally, measurements relevant to CVD will be noncontact but as accurate as invasive systems.

A photoplethysmogram (PPG) is an optical measurement that monitors blood volume changes. It may be utilized in a transmittance or reflectance geometry to monitor the cardiac cycle. Analyzing increases and decreases in blood volume within a region of interest (ROI) enables extraction of heart rate and respiratory rate. The pulsatile PPG waveform can be used to monitor anesthesia depth [2], detect hypovolemia [3], detect arrhythmia [4], and approximate a patient’s blood pressure [5]. Recently, photoplethysmographic imaging (PPGI) has been developed as a noncontact method to measure spatial information of the pulsatile PPG waveform using a camera and incoherent source with near-homogeneous illumination to measure intensity in a reflectance geometry [4]. However, PPGI is limited by the signal-to-noise ratio (SNR), defined in this paper as the ratio of the AC-to-DC components (AC/DC) within the measured signal, of the system setup and the need for extensive signal processing to extract the desired waveforms [6].

We hypothesize that laser speckle imaging (LSI) will increase the SNR of the pulsatile waveform as compared to PPGI. The pulsatile waveform from LSI data is based on increasing and decreasing flow rates of red blood cells [7]. Averaging a ROI from each laser speckle image over time allows for the calculation of a speckleplethysmogram (SPG). Similar to the PPG, the SPG signal enables monitoring of the heart rate and respiratory rate variability. A comparison of the SPG and PPG frequency content has been performed [8–11], but analysis has not been performed concerning the reflectance SPG waveform and its relationship to the reflectance PPG waveform.

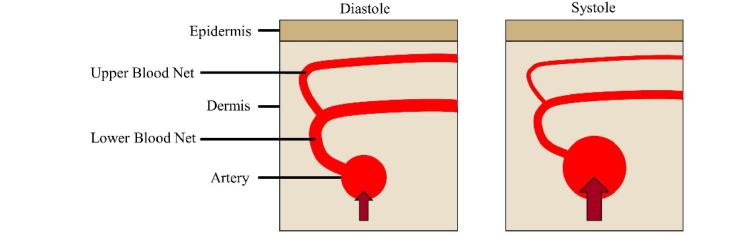
In particular, there is a gap in knowledge regarding the spatiotemporal relationship of the PPG and SPG signals. A model for PPG was proposed that suggests the reflectance signal originates from the compression of tissue components due to arterial expansion and the resulting changes in the dermal optical properties (Fig. 1) [12]. Capillary size does not change in a pulsatile manner, but the increased density of capillaries in the upper blood net because of underlying arteries could explain the origin of green PPG signals [13]. However, Monte Carlo methods have not successfully simulated how these phenomena result in improved signal with green light compared to near-infrared (NIR) light in experimental data while also looking at speckle contrast [14,15].

Fig. 1.

During systole, the flow speed through the artery increases when compared with diastole. This increased speed causes the artery to expand, which in turn compresses the upper and lower blood nets. SPG is sensitive to the change in flow speed, and PPG is sensitive to the change in optical properties due to compression.

Regan et al. [16] recently reported on a momentum-transfer Monte Carlo model to simulate speckle contrast in a six-layer tissue model and study the spectral and depth dependence of speckle contrast. In the present study, we adapt this modeling framework to perform in silico study of reflectance PPG and SPG signals. We demonstrate that the model produces data that correspond to in vivo experimental results. Both the simulations and experimental results demonstrate that the SPG signal has a much higher SNR than the PPG signal and improved synchronization between adjacent ROIs [17].

2. Theoretical model

We tracked photon scattering by discrete absorption weighting using a version of the C# Command Line Monte Carlo model developed by the Virtual Photonics Initiative at Beckman Laser Institute and Medical Clinic, University of California, Irvine [18–22]. Rice et al. [23] modified the model to calculate speckle contrast using the field correlation function, g₁(τ), for a two-flow system:

$$g_1\left(\tau \right)={\displaystyle \underset{0}{\overset{\infty }{\int }}P\left(Y\right){\displaystyle \underset{0}{\overset{1}{\int }}P\left(y\right)\left[\frac{-Y{k}^2\left(y\right)〈\Delta r_1^2\left(\tau \right)〉+\left(1-y\right)〈\Delta r_2^2\left(\tau \right)〉}{3}\right]}}dydY$$ (1)

where <∆r₁²(τ)> and <∆r₂²(τ)> are the mean-squared displacements associated with two flow types, Y is the dimensionless momentum transfer, P(Y) is the normalized probability distribution of momentum transfer, y is the fraction of Y for one flow type, and P(y) is the normalized probability distribution of total momentum transfer associated with the respective flow type [23]. The Siegert relation is employed to calculate speckle contrast (K) using the following equation:

$$K^2=\frac{2\beta }{T}{\displaystyle \underset{0}{\overset{T}{\int }}\left(1-\frac{\tau }{T}\right)}{\left|\frac{g_1\left(\tau \right)}{g_1\left(0\right)}\right|}^{2}d\tau$$ (2)

where T is the camera exposure time and β an empirical constant that accounts for experimental factors such as laser coherence. Note that the value of β is trivial for our in silico measurements because of the normalization process used for data analysis (discussed below). With knowledge of the blood volume fraction, each scattering event is defined probabilistically as dynamic (resulting in reduction of speckle contrast) or static.

The six-layer model for speckle contrast used by Regan et al. [16] did not incorporate vessels such as the ulnar and radial arteries in the wrist, which are common locations for PPG measurements due to the relatively high SNR [12]. To adapt the speckle contrast model, we added an arterial layer of 2.3 mm in thickness within the lipid layer at a depth of 3.0 mm to represent the radial artery in the subcutaneous tissue (Table 1) [24–26]. We used the “makeTissue” function and corresponding spectral library by Jacques [27] to estimate tissue optical properties at 532, 660, and 860 nm. We simulated an epidermis corresponding to fair skin (3% melanin content) [28] and semi-infinite geometry.

Table 1. Eight-layer model with initial layer thickness and blood volume fraction.

Layer	Thickness (um)	Blood Volume Fraction (%)
Epidermis	75	0
Papillary Dermis	150	0.4
Upper Blood Net	150	4
Reticular Dermis	800	0.4
Lower Blood Net	400	4
Lipid	1,425	0
Arterial Layer	2,300	100
Lipid	4,700	0

Virtual detectors in the Monte Carlo model track the reflectance of the simulated photons for PPG intensity calculations. The arterial layer is expanded and contracted (details below) to simulate the pulsatility of arteries due to contractions of the heart throughout the cardiac cycle. When the arterial layer expands, the lower and upper blood nets are compressed, increasing the blood volume fraction in those two layers (Table 1) [13]. A change in blood volume fraction is associated with adjusted optical properties.

Furthermore, virtual detectors in the Monte Carlo model track the reflected momentum transfer for the speckle contrast calculation. We assigned to the static scatterers a Brownian diffusion constant of 2x10⁻⁶ mm²/s [29]. We varied the flow speed of dynamic scatterers within a range reasonable for smaller, more superficial vessels such as arterioles and capillaries [30].

3. Materials and methods

3.1 In-silico experiments

For in silico experiments, we used one million photons for each simulation. The photons were distributed over a 15mm x 15mm square at the surface of the modeled tissue, and the intensity and speckle contrast were calculated over the central 7mm x 7mm region to avoid edge inconsistencies. Simulations were run at wavelengths of 532, 660, and 860 nm. We varied movement of dynamic scatterers over the range of 1.00 to 3.68 mm/s in 0.67 mm/s increments [30]. The thickness of the arterial layer was varied by ± 5% and ± 10%, and then the upper and lower blood nets were compressed or expanded accordingly to compensate for the change in thickness such that the simulated tissue maintained a total thickness of 10 mm. For example, when the arterial layer thickness was increased in size by 10%, the upper and lower blood net thicknesses were decreased such that they had an increase in blood volume fraction to 6.9% in order to maintain the same total blood volume in these two layers as before the change in arterial thickness. To calculate speckle contrast, an exposure time of 5ms was used for all wavelengths. Each simulation was run twice to test model stability, and the difference in values was less than 0.3%, suggesting that one million photons were sufficient.

The amplitude of the PPG signal was calculated from the simulations as the percent difference of reflected photons at an arterial thickness from 2.07 mm to 2.53 mm compared to the percentage of reflected photons at an average arterial thickness of 2.3 mm. The simulated amplitude of the SPG was calculated as the percent difference of the speckle contrast at the various flow speeds (1.00 to 3.68 mm/s) compared to the speckle contrast at a mean flow speed of 2.34 mm/s [30]. All results were multiplied by −1 to align the signals with blood pressure orientation [12].

3.2 In-vivo experiments

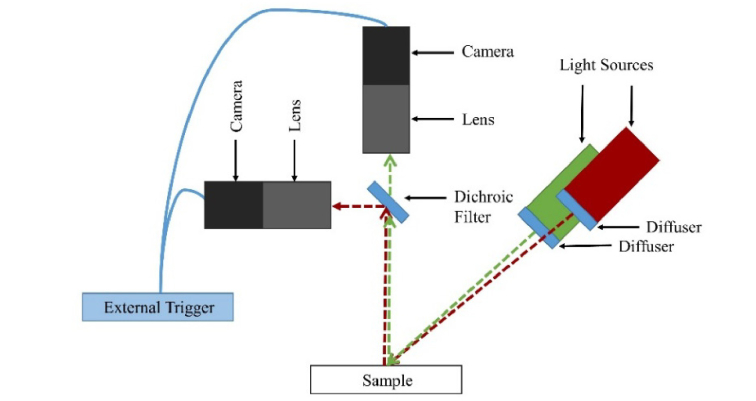
To simultaneously measure the PPG and SPG signals, we used two Grasshopper3 cameras (GS3-U3-41C6NIR-C, FLIR, Wilsonville, Oregon) with macro 10X lenses (MLH-10X, Computar, Cary, North Carolina) for image acquisition (Fig. 2). We used an 860 nm laser (HPM135(860-150)G36/A960, Power Technology, Alexander, Arkansas) with an aspheric lens (C330TMD-B, Thorlabs, Newton, New Jersey) and diffuser (DG10-220, Thorlabs) for the NIR SPG measurements and a 532 nm laser (M-Series 100 mW, Dragon Lasers, China) with an aspheric lens (C330TMD-A, Thorlabs) and diffuser (DG10-220, Thorlabs) for the green SPG measurements. The lens and diffuser were used to achieve near-homogeneous illumination of the tissue. We switched the green SPG laser with a broadband source with a 530 nm excitation filter (MF530-43, Thorlabs) for the incoherent green PPG measurements. To split the multispectral light to the two cameras, we placed an 805 nm dichroic mirror (DMSP805L, Thorlabs) between the cameras. To simultaneously acquire images with both cameras, we used an external trigger (cDAQ-9171, National Instruments, Austin, Texas). Images were acquired and saved using a laptop (i7-7500U, 8GB DDR4 RAM, 512GB SSD, 80VD000KUS, Lenovo, Morrisville, North Carolina). When using the coherent sources, the Nyquist sampling criterion was met with both setups at 2.35 pixels per speckle [31]. Measurements were taken and analyzed from the wrists of four different subjects. All measurements were done in accordance with the human subjects protocol approved by the Institutional Review Board at University of California, Irvine.

Fig. 2.

The experimental setup used two cameras and two light sources for imaging. The coherent NIR source remained constant, while the green source was switched between a coherent and incoherent source for PPG and SPG measurements.

Subjects placed their wrists within the camera field of view and remained still during the data acquisition. The cameras for the NIR and green coherent sources were set to 5 ms exposure time to match the simulations. When using the green incoherent source, the camera was set to an exposure time of 20 ms to increase camera signal, which is essential for reflectance PPG measurements [32]. In silico PPG results were not affected by exposure time. We acquired images with pixel resolution of 1800 x 1312 for 20 seconds at 30 fps. Two measurements were taken from each subject. The first measurement used the NIR coherent source to measure NIR SPG and the incoherent source to measure green PPG, and the second measurement used two coherent sources to measure NIR SPG and green SPG.

We calculated the 532 nm PPG signal by averaging the intensity of a 50x50 pixel ROI, an ~2.3x2.3 mm² region, from the incoherent green source. We converted raw speckle images to speckle contrast images by running a 7x7 sliding window filter with the equation σ/<I> over the raw images, where σ is the standard deviation of gray level values over the window and <I> is the mean gray level over the window [33]. We then determined the SPG signal by averaging a 50x50 pixel ROI from the speckle contrast image of the coherent sources. To select the specific ROI on the subject’s wrist, we tested regions located over the radial and ulnar arteries for representative waveforms [12]. The experimental normalized PPG and experimental normalized SPG were calculated by using a 30-point moving average to determine the DC signal and then the percent different from the AC signal to the DC signal [12]. We determined that we could observe the heart rate after applying a low-pass filter of 6 Hz, well above the Nyquist rate for the standard human heart rate [34]. Results were multiplied by −1 to align the signals with blood pressure orientation [12]. Effectively, the amplitude plotted is equivalent to −100(AC/DC).

4. Results

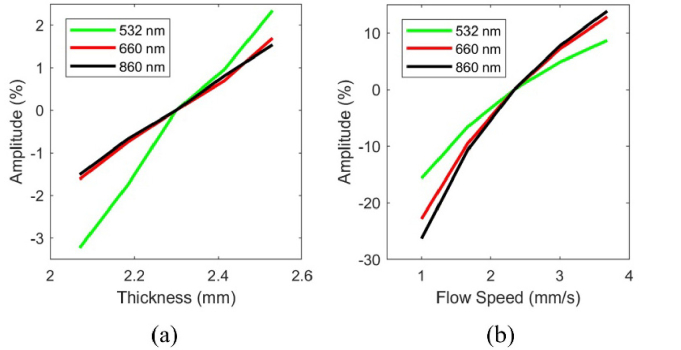
Simulation data (Fig. 3) illustrate the theoretical spectral sensitivity of PPG and SPG to cutaneous hemodynamics. Figure 3(a) shows that as the arterial thickness increases, the percentage of reflected photons decreases, which causes an increase in amplitude. This suggests that the PPG signal at the green wavelength is more influenced by the compression of the dermal blood nets than at the red and NIR wavelengths.

Fig. 3.

(a) The simulated results for PPG and (b) SPG. The PPG signal increases in amplitude percent as the arterial layer thickness increases, with the green wavelength having the highest sensitivity. The SPG signal at the three wavelengths increases in amplitude percent as the flow speed increases, and the NIR wavelength has the largest dynamic range. The SPG signals at all wavelengths have a much larger range than the PPG signals at all wavelengths.

Figure 3(b) shows that as flow speed increases, the SPG signal increases in amplitude. An increase in flow speed corresponds to an increase in vessel diameter. All simulations for SPG were taken at the arterial layer thickness of 2.3 mm, since the change in speckle contrast was less than 2% different at any of the other arterial layer thicknesses that we evaluated in this work. The results of the SPG simulations suggest the SPG signal has the largest dynamic range at the NIR wavelength, a slightly smaller range at red wavelengths, and an even smaller range at green wavelengths.

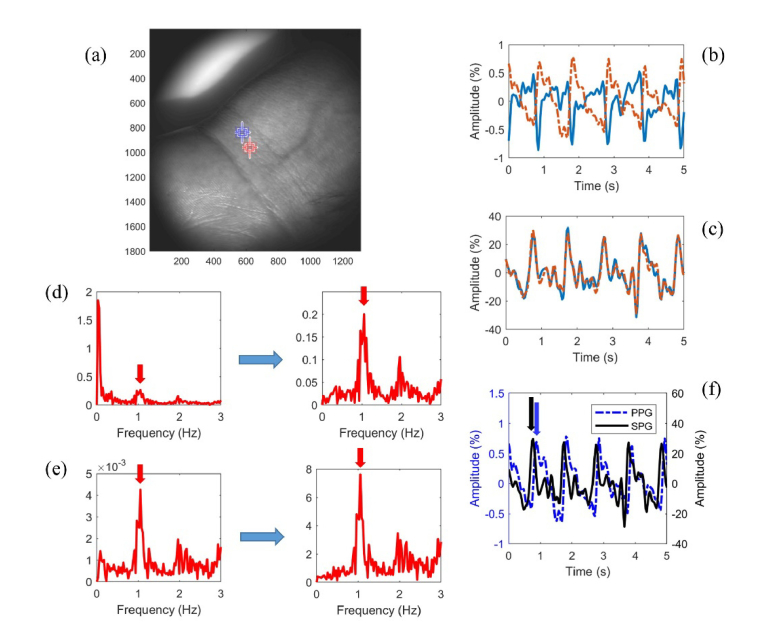
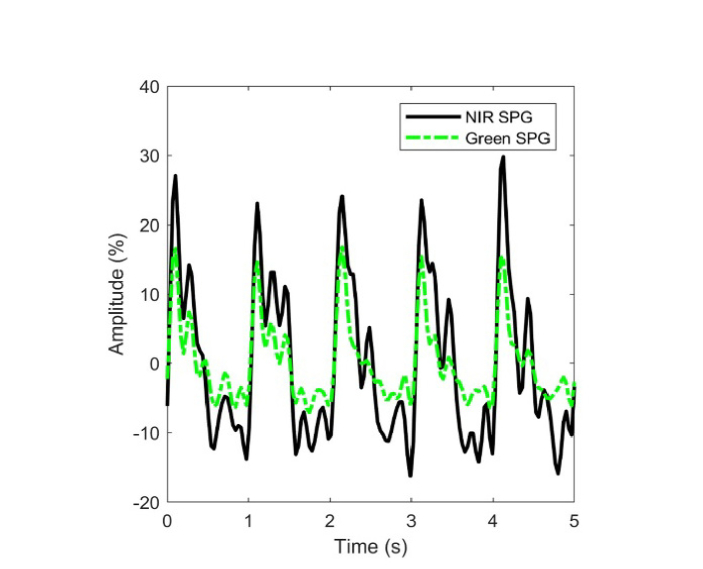
In vivo data show that the normalized NIR SPG data from a representative subject has a much larger amplitude percent than the normalized green PPG data from the same subject (Fig. 4). A phase shift between neighboring ROIs is seen in the PPG signal (Fig. 4(b)) but not in the SPG signal (Fig. 4(c)). The heart-rate frequencies have an over tenfold increase in amplitude in the frequency spectrum of SPG as opposed to PPG after AC/DC processing (Fig. 4(d) and 4(e)). The PPG signal peak has a time delay on the order of 100 ms with respect to the SPG signal peak (Fig. 4(f)). The SPG data has a larger amplitude percent at NIR wavelengths than green wavelengths (Fig. 5). However, even at green wavelengths the SPG signal (Fig. 5) has a larger amplitude percent than the PPG data (Fig. 4(b)).

Fig. 4.

(a) Green PPG and NIR SPG results from a representative subject from the two neighboring ROIs. (b) The green PPG signal experiences a 180° phase shift from one region to the next, while (c) the NIR SPG signal does not. In the corresponding frequency spectrums for the orange ROI before (left) and after (right) AC/DC processing, the heart rate peak has a smaller amplitude in the (d) PPG spectrum than the (e) SPG spectrum after processing. (f) The SPG has a much larger amplitude and peaks before the PPG from the same orange ROI.

Fig. 5.

SPG results taken from the same ROI simultaneously using the green and NIR coherent sources. The amplitude of the NIR source is larger. The two wavelengths peak at the same time.

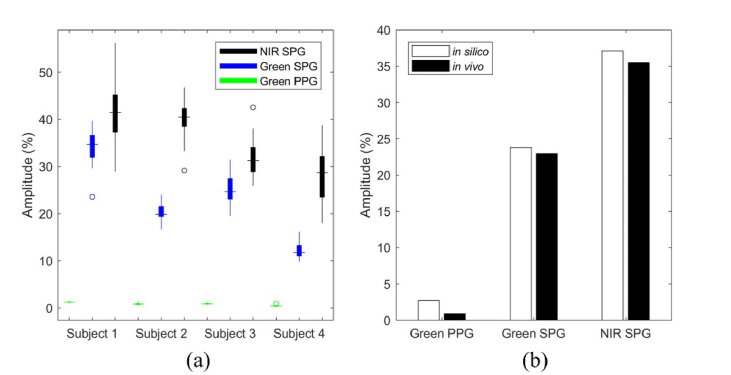
In the four subjects, the NIR SPG has a larger peak-to-peak amplitude percent than the green SPG peak-to-peak amplitude percent (p<0.001) using the Wilcoxon signed rank test (Fig. 6(a)). Both the NIR SPG and green SPG have a larger peak-to-peak amplitude percent than the green PPG peak-to-peak amplitude percent (p<0.001 and p<0.001, respectively) using the Wilcoxon ranked sum test.

Fig. 6.

(a) NIR SPG amplitude percent is larger than the green SPG amplitude percent (p<0.001) and the green PPG amplitude percent (p<0.001). The green SPG amplitude percent is larger than the green PPG amplitude percent (p<0.001). (b) The in silico amplitude percent ranges closely match the corresponding values across the subjects measured in vivo. For in silico green PPG, the peak-to-peak amplitude was 2.7%, compared to the in vivo peak-to-peak amplitude for green PPG of 0.88%. The in silico green SPG peak-to-peak amplitude was 24%, compared to the in vivo peak-to-peak amplitude of 23%. The in silico peak-to-peak amplitude for NIR SPG was 37%, compared to the in vivo peak-to-peak amplitude of 35%.

We computed the in vivo values in Fig. 6(b) by taking the average of the median values from each of the four subjects. The experimental data is in good agreement with the simulated data (Fig. 6(b)). At a 5% expansion and contraction of the arterial layer for in silico green PPG, the peak-to-peak amplitude was 2.7%, compared to the in vivo peak-to-peak amplitude for green PPG of 0.88%. The in silico peak-to-peak amplitude for green SPG was 24%, compared to the in vivo peak-to-peak amplitude of 23%. The in silico peak-to-peak amplitude for NIR SPG was 37%, compared to the in vivo peak-to-peak amplitude of 35%.

5. Discussion

Monte Carlo modeling of the PPG signal supports the model Kamshilin et al. [12] proposed of upper layer compression due to arterial expansion and matches previous trends in PPG experimental data [13]. The greater penetration depth of the NIR light versus green light in the skin reduces its interaction with the capillaries, which have a greater impact on the PPG dynamic range for intensity values. Monte Carlo modeling of the SPG signal suggests it has a much larger dynamic range as compared to the PPG signal. The experimental data support the premise that SPG at multiple wavelengths has improved signal-to-noise ratio over PPG. PPG has been noted to invert and change shape in the same subject in neighboring ROIs, but we did not observe such an inversion or change in shape for SPG extracted from the same ROIs. It is believed the PPG waveform inverts at neighboring ROIs near the radial artery due to ballistocardiography (BCG) motion artifacts [35,36]. The results suggest the larger SNR of the SPG signal makes it less susceptible to BCG artifacts.

As demonstrated by in silico and in vivo results, the NIR SPG has a larger peak-to-peak amplitude than the green SPG. This is in line with previous work that shows that NIR wavelengths have greater speckle contrast sensitivity than green wavelengths due to the increased depth penetration of NIR light [16].

The SPG waveform reaches local peaks before the PPG signal, likely due to changes in flow speed (to which SPG is sensitive) preceding expansion and contraction of blood vessels (to which PPG is sensitive). The lack of phase shift in SPG versus PPG may be attributed to its emphasis on flow speed instead of intensity. The time delay between the peaks of the two signals may provide insight into patient health and risk of future cardiovascular events [37].

Motion artifact can play a major role in signal accuracy for both PPG and SPG. The current processing techniques did not account for motion artifact, but motion artifact has been addressed in both SPG [38] and PPG [39] acquisition through the use of alignment. The ideal ROI for each individual varied slightly and representative waveforms were used. Further enhancements can be made with the use of algorithms for peak amplitude identification in the images [40].

In the PPG simulations, the epidermal layer is assumed to be stationary in its location, which is physiologically inaccurate. This assumption may account for the in silico PPG results having a larger amplitude percent than the in vivo results. Kamshilin et al. [12] previously demonstrated that increased contact of the skin’s surface against a glass table increases the PPG amplitude percent by holding the epidermal layer stationary and further compressing the upper blood nets. Filtering of the SPG signal for visualization of the heart rate frequency may help explain why in silico peak-to-peak amplitudes for SPG are slightly larger than in vivo peak-to-peak amplitudes at both green and NIR wavelengths.

Additional limitations of this study include the assumptions made in the modeling of cutaneous hemodynamics (i.e., only two flow speeds were used, one for dynamic scatterers and one for static scatterers, and vessels approximated as layers), and the small number of subjects. Future work should address each of these limitations.

6. Conclusion

We developed an eight-layer model for simulating both PPG and SPG reflectance measurements. The Monte Carlo simulations support the PPG model proposed by Kamshilin et al. [12,13]. The modeling data suggests that SPG has a considerably larger dynamic range at multiple wavelengths than does the corresponding PPG. The experimental data confirm the modeling results.

This work provides a new method of monitoring cardiovascular health via SPG, which we demonstrated has a larger SNR than the more common PPG. SPG allows for noncontact monitoring of blood flow in the extremities. This provides opportunities for monitoring heart rate, peripheral arterial disease, and other cardiovascular-related diseases. For example, the earliest manifestations of cardiovascular disease occur in the microcirculation, and SPG in a reflectance geometry provides an opportunity for monitoring the microcirculation [41]. Furthermore, the use of PPG and SPG to monitor the brain in models of focal and global ischemia [42] and Alzheimer’s disease [43] may lead to a better understanding of the role pulsatile cerebral hemodynamics have on neurological function and injury.

In the future, increased analysis of SPG is necessary to determine the benefits of this signal for monitoring cardiovascular health. Additional clinical studies from subjects with and without cardiovascular disease are required to better understand the utility of SPG alone and a combined SPG/PPG measurement protocol.

Funding

National Institutes of Health (NIH) (P41 EB015890); Seed Grant Award from University of California; Cardiovascular Applied Research and Entrepreneurship Fellowship through the Edwards Lifesciences Center for Advanced Cardiovascular Technology’s NIH/NHLBI T32 Training (5T32HL116270); NIH-funded Institute of Clinical and Translational Science Fellowship (TL1 TR001415); National Science Foundation Graduate Research Fellowship Program (DGE 1321846).

Disclosures

The authors declare that there are no conflicts of interest related to this article.