Abstract
Age-related macular degeneration (AMD) is the leading cause of blindness in the elderly (over the age of 60 years) in western countries. In the early stages of the disease, structural changes may be subtle and cannot be detected. Recently it has been postulated that the mechanical properties of the retina may change with the onset of AMD. In this manuscript, we present a novel, non-invasive means that utilizes synchronized acoustic radiation force optical coherence elastography (ARF-OCE) to measure and estimate the elasticity of cadaver porcine retina. Both regions near the optic nerve and in the peripheral retina were studied. An acoustic force is exerted on the tissue for excitation and the resulting tissue vibrations, often in the nanometer scale, are detected with high-resolution optical methods. Segmentation has been performed to isolate individual layers and the Young’s modulus has been estimated for each. The results have been successfully compared and mapped to corresponding histological results using H&E staining. Finally, 64 elastograms of the retina were analyzed, as well as the elastic properties, with stiffness ranging from 1.3 to 25.9 kPa in the ganglion to the photoreceptor sides respectively. ARF-OCE allows for the elasticity mapping of anatomical retinal layers. This imaging approach needs further evaluation but has the potential to allow physicians to gain a better understanding of the elasticity of retinal layers in retinal diseases such as AMD.
1. Introduction
The retina is a light sensitive layer at the posterior section of the eye that is responsible for converting visual images and sending visual signals to the brain. Although the retina is thin, it has many well organized sublayers that contribute to its function. In people over 60 years of age, age-related macular degeneration (AMD) is the leading cause of vision loss in the United States [1-2]. Early stage AMD is marked by accumulation of drusen, which are focal deposits of acellular polymorphous debris that accumulate in the retinal pigment epithelium under the macula and the peripheral retina. In the late stage progression of AMD, the drusen can be accompanied by neovascularization and/or atrophy of the retinal pigment epithelium and also the overlying retina [1-2].
In order to diagnose AMD, fundus imaging, fluorescein angiography, and optical coherence tomography are some of the commonly used techniques in the clinic [3]. The structure of the retina has been studied extensively. For further analysis of the retina, there have been many segmentation methods that have been used to separate the different layers within the retina [4–6]. Many of these features are built into commercial imaging systems, and automated detection is possible. The thickness of the layers and other anatomical structures can be analyzed in-vivo and correlated with pathology. Although, this structural information is very helpful in mid to late stage AMD, often it is not sufficient for very early diagnosis of AMD.
As a precursor to neovascularization and disease progression, the elasticity of the tissue will change [7–10]. Friedman et al. demonstrated that increased scleral rigidity might be a precursor to the onset of AMD, which brought to attention the possibility of using mechanical properties as a diagnostic tool [8]. Shahbazi et al. used ultrasound to show that the posterior ocular elasticity of patients with AMD is indeed different than that of healthy humans, but did not offer retinal layer analysis [9]. Recently, Chen et al. presented the possibility of retinal elastin decreases during the early onset of AMD [10]. Since these cellular level changes are expected to precede structural abnormalities that can be detected with current imaging techniques, we believe that there is significance in studying the mechanical properties of the retina. In addition, elasticity changes in the retina and choroid can also occur when the microvasculature changes or when drusen forms. Optical coherence elastography (OCE) may offer an alternate method to detect the environmental changes that occur when alteration of cellular properties begin to take place. Measuring the elasticity will give scientists and physicians a better understanding on the disease mechanism in the early stages, and possibly provide a powerful diagnosis tool.
In order to study the mechanical structure of the retina, several studies attempted to provide elastic properties by performing mechanical strain testing in vitro [11-12]. However, strain testing is not possible for tissues in vivo. In addition, the entire retina is extracted as a single unit, which means that individual layer information cannot be obtained. Although mathematical modeling of the retina to determine the Young’s modulus has been reported, in vivo determination remains a challenge [13]. In order to perform in vivo imaging with information of different layers, a high resolution system functional imaging system is necessary.
OCE is a relatively new method of providing elasticity mapping with high resolution and sensitivity [14]. Several different applications have been studied using this technique, including the study of corneal elasticity [15–18]. However, the mechanical properties of the retina are still not well defined since the retina is inaccessible to many elastography methods or is limited by low resolution. We recently reported on an acoustic radiation force (ARF) OCE method that can map out the elasticity of the cornea both axially and laterally with high resolution [19].
In this manuscript, we present the quantified retinal layered elasticity map for the first time in a porcine model. The instrumentation has been updated, including a mechanical stage to increase the field of view and synchronization to generate a spatial elasticity map. In this way, the phase cycle of the tissue vibration is uniform in the direction parallel to the mechanical stage. First, structural optical coherence tomography (OCT) and functional OCE imaging were performed on a healthy pig retina near the optic disc and in the periphery of the retina after isolation of the posterior portion of the eye. Then the OCE phase information was analyzed along the axial direction. Then segmentation was performed on the retinal layers using OCT and the corresponding layer was matched on the OCE and histology. Nanometer displacement differences were observed between the layers. Finally, the relative stiffness was analyzed over 64 B-scan samples and statistical analysis was performed. The Young’s moduli are estimated for each layer using the experimental stiffness ratios and average elasticity obtained from literature.
2. Results
2.1 System design
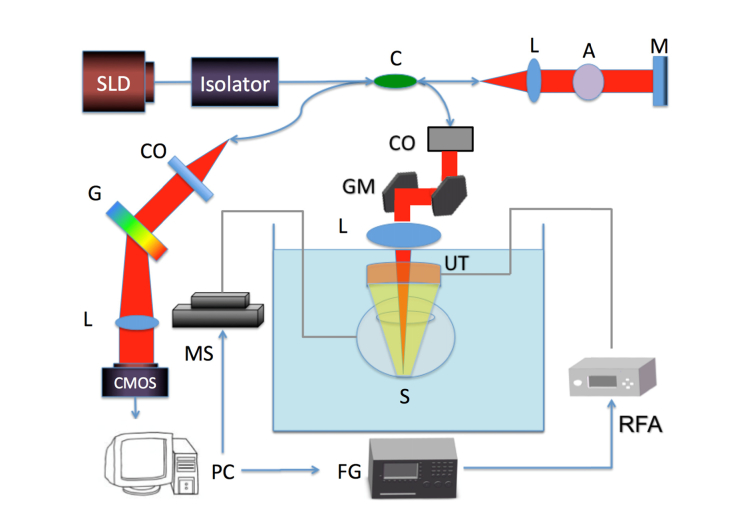
In this elastography study, an ultrasonic focused ring transducer was used for excitation while a spectral domain OCT system was used for detection of the tissue response. The acoustic and optical signals are all synchronized using the computer in order to obtain images with synchronized vibrational responses. A schematic diagram of the system set up is illustrated in Fig. 1.
Fig. 1.
Schematic diagram of system setup. SLD: superluminescent diode, L: lens, G: diffraction grating, CMOS: camera, C: coupler, A: attenuator, M: mirror, MS: mechanical stage, GM: galvo mirror, UT: ultrasound transducer, S: sample, RFA: radio-frequency amplifier, FG: function generator, CO: collimator. Red beam: light path. Yellow beam: ARF path.
The function generator first outputs a modulated square wave signal, which is amplified by approximately 170 times and fed to a ring ultrasound (US) transducer with a focal distance of 3 cm. The ring transducer has an outer diameter of 4.5 cm and inner aperture of 9 mm. The driving frequency is 4.5 MHz and the function generator modulates a square wave signal with a frequency of 833 Hz. The signal is continuously modulated to form many ARF pushes so that the tissue response can be tracked consistently. The electrical impedance at the driving frequency has been experimentally determined to be 42 Ohms at the driving frequency while the acoustic power output is approximately 1.0 MPa. The small impedance mismatch will cause a relatively lower power output, but is sufficient for this application. ARF using approximately 40V post-amplification is induced on the sample and vibrations are generated. A modulation frequency of 833 Hz, which is much higher than the resonance frequency of retinal tissue, was chosen so that the mechanical contrasts of the layers are not skewed by resonance vibrations. On the detection side, the optical set up highly resembles that of previous publications [19]. The axial resolution has been experimentally measured to be 3 μm while the lateral resolution is 27 μm in air. The power from the sample arm is measured to be 0.89 mW, which is well below the safety limit determined by the American National Standards Institute. In order to optimize imaging conditions, especially to maximize imaging range, a mechanical stage has been incorporated into the system to move the sample. The sample is fastened to the mechanical stage via metal posts and the sample is mobilized in discrete steps during imaging. In this way, the limitation set forth by the 500 μm uniform focal diameter of the transducer can be bypassed. One galvanometer mirror is used for scanning in one lateral dimension while the motorized stage provides scanning in the other lateral direction. This increases our imaging range from 500 μm to over 3 mm and at the same time provides more uniform excitation across B-scans. A 20 kHz A-line rate is used and a volumetric scan in these experiments consists of 500 by 500 A-lines.
The ring ultrasonic transducer is coupled to the porcine eye via a PBS bath. The transducer is submerged in the bath while the OCT lens is just above the liquid interface. The OCT light travels through the center aperture of the ring transducer to focus confocally with the ARF beam. In Fig. 1, the ring transducer is shown in orange with a yellow focused ARF beam, while the OCT lens is shown in blue with the light path depicted in red, and both focus on the posterior eye tissue. In other words, the bearing angle is 0 degrees so that we can ensure that the ARF and the OCT beams are co-aligned.
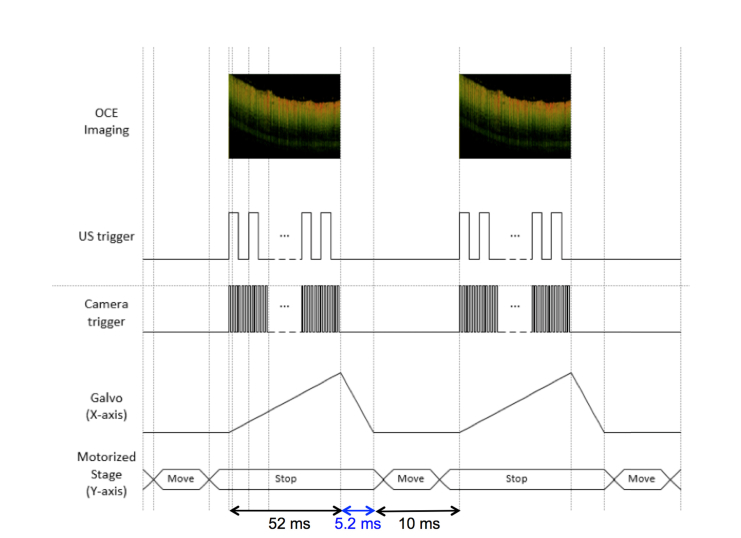
Synchronization between the acoustic excitation and optical detection was performed as shown in Fig. 2. In this way, it is possible to control the phase of the modulation cycle at different spatial locations on the sample. A 0.1 ms pause was incorporated into the system to minimize noise caused by the movement of the motorized stage. The galvo sweeping, camera acquisition, and ultrasound modulation signals are triggered at the same time when the motorized stage is stationary to produce a single B-scan. Then the motorized stage shifts in a preset increment smaller than the lateral resolution of the system, and another B-scan is acquired. The scanning time is 52 ms for a B-scan image with 1000 A-lines, the recovery step of the Galvo back to the origin is 5.2 ms, and the rest step where the motorized stage moves is 10 ms as shown on the timing diagram. For the results shown here, a 6 μm displacement is achieved for each step.
Fig. 2.
Timing diagram of system showing excitation and detection.
2.2. Retina and optic disc imaging
A porcine eyeball was isolated within 24 hours of death and the anterior of the eye was removed so that only the vitreous fluids and the retina/sclera remained. The eyeball was then fixed using agar gel and mounted to the imaging stage in the water bath. The optical disc was identified on the retina by its diameter of approximately 1.7 mm. Using the synchronized system, a region of 3 mm by 3 mm was scanned near the optical disc. Previously [19], only the middle 500 μm by 500 μm region can be assumed to have uniform excitation, but with the addition of the mechanical stage, a region of 500 μm by 3 mm is able to achieve uniform force. This expands our imaging region by 6 fold in this figure.
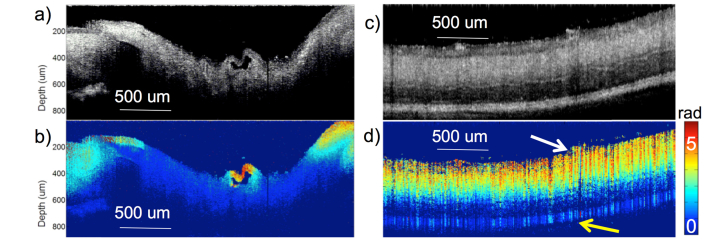
The OCT cross-sectional image showing the optical disc region is displayed in Fig. 3(a), while the corresponding OCE phase map is displayed in Fig. 3(b). The B-scan shown is in the same direction as the movement of the mechanical stage. Within this B-scan, an accurate uniform acoustic field is guaranteed for elastography since synchronization allows for phase cycle uniformity in the direction perpendicular to the galvo scanning.
Fig. 3.
Optical disc and peripheral retina imaging. a) OCT cross-section of optical disc. b) OCE phase cross-section of optical disc. c) OCT cross-section of peripheral retina. d) OCE phase cross-section of peripheral retina. Phase is measured in radians from 0 to 5. White arrow indicates ganglion side and yellow arrow points to the photoreceptor side.
The OCT and OCE images of the peripheral retina are shown in Figs. 3(c) and 3(d), respectively. The same scanning mechanism was used over a 3 mm by 3 mm region after shifting the focus to the peripheral retina, and then extracting the phase information, , from the raw OCT data. Then using the Doppler principle, the change in displacement of the tissue response can be calculated according to the following equation: , where is the central wavelength, is the Doppler angle, n is the refractive index, is the exposure time of the detector. The Young’s modulus is inversely related to the change in displacement as depicted in the following relationship: , where is the stress and z is the axial depth. It is clear that the optic disc region had a much smaller vibrational response, indicating a stiffer tissue, than the peripheral retina and the retinal regions closer to the optic disc. The pocket structure in the middle of Fig. 3(b) had a very high vibrational response, which indicates a softer tissue that is concluded to be a collapsed blood vessel. This figure portrays the elasticity of the optic nerve relative to the peripheral retina and demonstrates the feasibility of using ARF-OCE in the mapping of retinal elasticity. It was also noted that the relative stiffness of the retina changes in the axial direction, suggesting the separation of different layers, with the top layer indicating the softest structure.
Previously, we have shown that the ARF field is uniform across the imaging axial depth, and verified the ability of OCE to separate the stiffness of individual axial and lateral components in a connected agar phantom with inclusions [19]. OCE was able to extract the stiffness of the 2 layers of different elasticity accurately according to verification with compression testing methods [19]. In addition, we have also demonstrated that the vibrational response is uniform within the axial imaging range for a uniform phantom [20], which means that the material attenuation is minimal within the 1 mm imaging range. Therefore, according to the phase map, we conclude that the stiffness of the retina increases from the inner ganglion side (white arrow) to the outer photoreceptor side (yellow arrow).
2.3. Segmentation and histology correlation
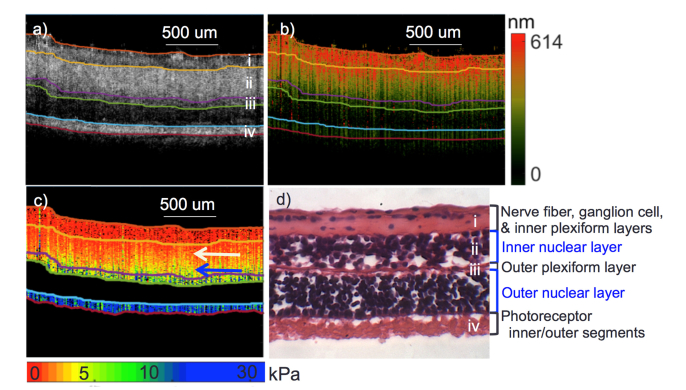
Since different layers were observed both in the OCT intensity images and the OCE phase images, segmentation was performed on the OCT images based on a graph-based method presented previously by our group [21]. From experimental results, 5 different axial layers could be isolated as shown in Fig. 4(a). The OCE small interval displacement image in Fig. 4b was also segmented using the same boundaries. Segmentation was not performed on OCE directly since we have yet to validate the stiffness contrast corresponding to the boundaries between layers. Figure 4(c) shows the corresponding elastogram with Young’s modulus values, which were derived from the frequency sweeping experiments. According to porcine retinal anatomy, there are ideally 7 layers that can be separated, but were not visible in these results. Therefore, histology using H&E staining was performed shown in Fig. 4(d) to match the imaging layers to anatomy. The top three layers, including the nerve fiber layer, ganglion cell layer, and inner plexiform layer, were compressed into a single detected layer. This is probably caused by the deterioration of the tissue after harvest, also as indicated by the collapsed blood vessel near the optic disc in Fig. 3(b). Experiments were performed approximately 40-48 hours after tissue harvest, and it is likely that degradation occurred during storage and transport.
Fig. 4.
Retina segmentation and elastogram. a) OCT segmentation. b) Corresponding segments of OCE displacement mapping. c) Corresponding elastogram. d) H&E staining of porcine retina with the anatomical layers labeled. White arrow point to outer nuclear layer region with low elasticity. Blue arrow point to outer nuclear layer portion with high elasticity.
The boundaries for the inner nuclear layer was highly distinguishable from the OCT images, and the mechanical elasticity also showed contrast between upper and lower layers. Within the inner nuclear layer, there seems to be a elasticity gradient in the axial direction, with a redder color or lower elasticity on the inside as denoted by the white arrow and a green color or higher elasticity on the outside, shown by the blue arrow. This is due to the connective boundaries between the layers that vibrate together. Unfortunately, it is not possible to completely segregate the layers due to the interdependent motion and response. The outer plexiform layer is relatively thin and displacement values continue to decrease. The outer nuclear layer is difficult to visualize on the OCT image, since its properties allow for low scattering of optical light. Therefore, it was omitted in the quantitative analysis. The outermost layer of the retina is the photoreceptor region, which had high scattering contrast, but low displacement values. The average imaging or penetration depth is approximately 400 μm for the porcine retinal tissue.
From analysis of Fig. 4, it can be concluded that the OCE displacement map is not affected by the difference in OCT intensity. As long as there is some scattering, the relative displacement can be measured. In this case, the depth penetration was enough to capture the retina. In the onset of AMD, drusen can form in the retinal pigment epithelium (RPE) layer, which is directly underneath the photoreceptor layer shown. A higher output power or a longer central wavelength can be used to increase imaging depth.
2.4 Statistical analysis
In order to verify the consistency of the relative layered stiffness over the entire retina, 64 cross-sectional OCT and OCE B-scans were obtained at different spatial locations on 2 retina samples. Segmentation was performed on OCT images and the respective OCE segments were analyzed. Five different retinal layers were isolated and the thickness of each layer was estimated by counting the axial pixels and averaging over the lateral direction. The results are summarized in Table 1. The entire thickness of the retina was approximately 400 μm.
Table 1. Analysis of 64 B-scan locations on the retina.
| Retinal Layer | Mean Thickness (μm) | Normalized Displacement | Young’s Modulus (kPa) |
|---|---|---|---|
|
Nerve fiber layer
Ganglion cell layer Inner plexiform layer |
67 | 0.99 | 1.33 ± 0.37 |
| Inner nuclear layer | 132 | 0.48 | 2.73 ± 0.82 |
| Outer plexiform layer | 37 | 0.17 | 7.7 ± 2.26 |
| Outer nuclear layer | 84 | N/A | N/A |
| Photoreceptor inner/outer segments | 72 | 0.06 | 25.9 ± 7.36 |
Since each of the 64 images varies in their phase cycle, it is necessary to normalize all the displacement values to a relative scale so direct comparisons can be made according to the ratios. In this case, the value of the highest displacement was set to be 1, and the other displacement values are portrayed as a fraction of the maximum. As shown from previous publications [22], the Young’s modulus is inversely proportional to the displacement values, but only relative displacement ratios are available. Therefore, the elasticity estimations are based on the resonance frequency theory where the Young’s modulus is proportional to the square of the resonance frequency [23]. After measuring the displacement response under different excitation frequency similar to previous experiments [23], the highest tissue response was observed at 21 Hz. We experimentally calibrated the squared relationship between the resonance frequency and the Young’s modulus using silicone phantoms. The relationship was determined to be , where is the resonance frequency and is the Young’s modulus. The Young’s modulus of the entire retina was calculated to be 13 kPa. The retinal elasticity measurement is similar to the ones reported in literature using a mathematical model [13]. A weighted average approach was used to provide individual layer elasticity, where the weight contribution was dependent on the thickness of the respective layers, and the mean was set to 13 kPa. The results are shown in Table 1, where the Young’s modulus was estimated anywhere from 1 to 26 kPa. The outer nuclear layer was omitted from this estimation since scattering signal was too low for proper detection of OCE. According to previous literature, the bulk elasticity of the retina has been determined to be 20 kPa with mathematical modeling methods [24], while the layered elasticity has been shown to increase from the ganglion to the photoreceptor sides, ranging from approximately 10 to 30 kPa using shear wave OCE methods [25]. The results from the ARF-OCE study closely agree with the reported values, and the increasing elasticity trend from the ganglion layer has also been similarly observed. The advantages of this ARF-OCE system lies in the capability to non-invasively access the posterior eye and the high-speed mechanical mapping using a continuous modulated excitation. In addition, this ARF-OCE technology has nanometer scale displacement sensitivity, which allows us to minimize the ARF power [26].
According to the results for 4 retinal layers, it seems that the inside layer on top of the retina is much softer than the bottom layers, which is getting closer to the sclera. This is expected since the sclera, which is the protective outer layer, is much stiffer than the retina. A total of 64 B-scans were analyzed to correspond to 80% confidence level with 8% confidence interval. However, further analysis is necessary to accurately measure the retinal layers between several different samples.
Since the ARF-OCE measurements are based on the sample displacement, it is less accurate for stiff samples that correspond to a low tissue displacement. The reason is that the measurements are often at the ten-micron level, meaning that a small amount of noise or motion will create a larger percentage of error. Therefore, in Table 1, the error increases with the stiffer layers of the retina as expected.
3. Discussion and conclusion
This study using ARF-OCE technology is the first to visualize the mechanical properties of individual retinal layers, where 4 distinct layers were quantified. An ARF-OCE system was set up with synchronized excitation, detection, and scanning for better control of the modulation phase cycle. By analyzing the cross-sectional images perpendicular to the galvanometer scanning direction, it can be guaranteed that the B-scan shows a synchronized vibration in a uniform phase cycle. Using this approach, elasticity maps were obtained for the peripheral retina and the optic disc regions. Segmentation was performed on the OCT images and the corresponding layers were separated in the OCE, and both were matched to histology results using H&E staining. Further analysis was performed on 64 B-scans to estimate the thickness of the 5 layers as well as the relative displacement values. Using a weighted average method, the Young’s moduli for 4 different retinal layers were estimated.
Since this is a feasibility study to demonstrate the ARF-OCE method to generate quantified elasticity maps, only results from 1 sample is analyzed, and the sample was not very fresh as can be seen by the collapse of the top three layers. We are currently doing work on more samples in order to study the consistency between different subjects. However, freshness of the samples remains a problem. Since the porcine eyeball deteriorates at a rapid rate, and retinal structure is highly correlated with perfusion and freshness, it is difficult to obtain ex-vivo data. In addition, the anterior of the eye is always clouded, making the removal of the cornea and lens a necessity. However, since the procedure itself is non-invasive, it has a very optimistic outlook in in-vivo animal studies. There are a few issues that must be addressed in advance.
The imaging region of the sample must be further expanded in order to decrease imaging time and complexity during the procedure. This can be solved by using an ultrasound transducer with a wider focus or no focus. Scanning can be performed over the entirety of the retina within 12.5 seconds. This also indirectly helps to address the problem of the safety of the acoustic excitation. In order to adhere to the mechanical index limit of 0.23 for human ocular tissue, it is necessary to lower the excitation power per unit area. The current MI was estimated to be around 0.9. Since OCE has nanometer displacement sensitivity, it would be sensitive enough to detect smaller vibrations that adhere to the MI.
Since ARF is used for excitation, a transmission medium is necessary for the propagation of the ultrasound force. While it is sufficient to use a PBS bath in ex vivo settings, the current setup would not be feasible for in vivo imaging. In clinical ultrasound for ophthalmic applications, ocular ultrasonic gel can be directly applied to the eye and serve as the medium between the probe and the eye. Another solution is a steridrape setup, which involves a transparent drape that comes into contact with the eye and the probe is submerged into fluid on the other side. Both these setups can easily be adapted for use with the ARF-OCE system.
Another observation we made was the blending of the OCE information at the boundaries between layers. This is caused by the bulk vibrations of the entire sample, where each of the connected layers affect each other. In addition to the visible layers, the sclera is relatively a much stiffer medium that can also affect the lower layers of the retina. If there is a stiff layer connected to a soft layer, the boundary shows a gradient [16]. This relationship must be taken into account when analyzing the mechanical properties of the layers. Modeling of the viscoelastic phenomenon can help us better understand this issue and make more accurate parameter estimations.
The ARF-OCE technology was used to quantify retinal layered elasticity and is adaptable to in-vivo applications. We believe that this initial demonstration in the porcine eye is a stepping stone to the translation of the technique, which can potentially provide a powerful tool for the clinical diagnostic management of AMD.
Funding
National Institutes of Health (NIH) (R01HL-125084, R01HL-127271, R01EY-026091, R01EY-028662, P41EB-015890, T32HL116270, F31EY027666); Air Force Office of Scientific Research (FA9550-17-1-0193).
Disclosures
Dr. Zhongping Chen has a financial interest in OCT Medical Inc., which, however, did not support this work.
References and links
- 1.Bressler N. M., Bressler S. B., Fine S. L., “Age-related macular degeneration,” Surv. Ophthalmol. 32(6), 375–413 (1988). 10.1016/0039-6257(88)90052-5 [DOI] [PubMed] [Google Scholar]
- 2.Jager R. D., Mieler W. F., Miller J. W., “Age-related macular degeneration,” N. Engl. J. Med. 358(24), 2606–2617 (2008). 10.1056/NEJMra0801537 [DOI] [PubMed] [Google Scholar]
- 3.Chakravarthy U., Evans J., Rosenfeld P. J., “Age related macular degeneration,” BMJ 340, 526–530 (2010). [DOI] [PubMed] [Google Scholar]
- 4.Huang S., Piao Z., Zhu J., Lu F., Chen Z., “In vivo microvascular network imaging of the human retina combined with an automatic three-dimensional segmentation method,” J. Biomed. Opt. 20(7), 076003 (2015). 10.1117/1.JBO.20.7.076003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Garvin M. K., Abràmoff M. D., Kardon R., Russell S. R., Wu X., Sonka M., “Intraretinal layer segmentation of macular optical coherence tomography images using optimal 3-D graph search,” IEEE Trans. Med. Imaging 27(10), 1495–1505 (2008). 10.1109/TMI.2008.923966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ishikawa H., Stein D. M., Wollstein G., Beaton S., Fujimoto J. G., Schuman J. S., “Macular segmentation with optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 46(6), 2012–2017 (2005). 10.1167/iovs.04-0335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Krishnan L., Hoying J. B., Nguyen H., Song H., Weiss J. A., “Interaction of angiogenic microvessels with the extracellular matrix,” Am. J. Physiol. Heart Circ. Physiol. 293(6), H3650–H3658 (2007). 10.1152/ajpheart.00772.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Friedman E., Ivry M., Ebert E., Glynn R., Gragoudas E., Seddon J., “Increased scleral rigidity and age-related macular degeneration,” Ophthalmology 96(1), 104–108 (1989). 10.1016/S0161-6420(89)32936-8 [DOI] [PubMed] [Google Scholar]
- 9.Shahbazi S., Mokhtari-Dizaji M., Mansori M. R., “Noninvasive estimation of the ocular elastic modulus for age-related macular degeneration in the human eye using sequential ultrasound imaging,” Ultrasonics 52(2), 208–214 (2012). 10.1016/j.ultras.2011.08.004 [DOI] [PubMed] [Google Scholar]
- 10.Chen K., Weiland J. D., “Discovery of retinal elastin and its possible role in age-related macular degeneration,” Ann. Biomed. Eng. 42(3), 678–684 (2014). 10.1007/s10439-013-0936-x [DOI] [PubMed] [Google Scholar]
- 11.Chen K., Rowley A. P., Weiland J. D., “Elastic properties of porcine ocular posterior soft tissues,” J. Biomed. Mater. Res. A 93(2), 634–645 (2010). [DOI] [PubMed] [Google Scholar]
- 12.Friberg T. R., Lace J. W., “A comparison of the elastic properties of human choroid and sclera,” Exp. Eye Res. 47(3), 429–436 (1988). 10.1016/0014-4835(88)90053-X [DOI] [PubMed] [Google Scholar]
- 13.Jones I. L., Warner M., Stevens J. D., “Mathematical modelling of the elastic properties of retina: a determination of Young’s modulus,” Eye (Lond.) 6(6), 556–559 (1992). 10.1038/eye.1992.121 [DOI] [PubMed] [Google Scholar]
- 14.Khalil A. S., Chan R. C., Chau A. H., Bouma B. E., Mofrad M. R., “Tissue elasticity estimation with optical coherence elastography: toward mechanical characterization of in vivo soft tissue,” Ann. Biomed. Eng. 33(11), 1631–1639 (2005). 10.1007/s10439-005-6766-3 [DOI] [PubMed] [Google Scholar]
- 15.Wang S., Larin K. V., “Noncontact depth-resolved micro-scale optical coherence elastography of the cornea,” Biomed. Opt. Express 5(11), 3807–3821 (2014). 10.1364/BOE.5.003807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nguyen T. M., Arnal B., Song S., Huang Z., Wang R. K., O’Donnell M., “Shear wave elastography using amplitude-modulated acoustic radiation force and phase-sensitive optical coherence tomography,” J. Biomed. Opt. 20(1), 016001 (2015). 10.1117/1.JBO.20.1.016001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liang X., Crecea V., Boppart S. A., “Dynamic optical coherence elastography: a review,” J. Innov. Opt. Health Sci. 3(4), 221–233 (2010). 10.1142/S1793545810001180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhu J., Qu Y., Ma T., Li R., Du Y., Huang S., Shung K. K., Zhou Q., Chen Z., “Imaging and characterizing shear wave and shear modulus under orthogonal acoustic radiation force excitation using OCT Doppler variance method,” Opt. Lett. 40(9), 2099–2102 (2015). 10.1364/OL.40.002099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Qu Y., Ma T., He Y., Zhu J., Dai C., Yu M., Huang S., Lu F., Shung K. K., Zhou Q., Chen Z., “Acoustic radiation force optical coherence elastography of corneal tissue,” IEEE J. Sel. Top. Quantum Electron. 22(3), 1–7 (2016). 10.1109/JSTQE.2016.2524618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Qi W., Li R., Ma T., Kirk Shung K., Zhou Q., Chen Z., “Confocal acoustic radiation force optical coherence elastography using a ring ultrasonic transducer,” Appl. Phys. Lett. 104(12), 123702 (2014). 10.1063/1.4869562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huang S., Piao Z., Zhu J., Lu F., Chen Z., “In vivo microvascular network imaging of the human retina combined with an automatic three-dimensional segmentation method,” J. Biomed. Opt. 20(7), 076003 (2015). 10.1117/1.JBO.20.7.076003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Qi W., Chen R., Chou L., Liu G., Zhang J., Zhou Q., Chen Z., “Phase-resolved acoustic radiation force optical coherence elastography,” J. Biomed. Opt. 17(11), 110505 (2012). 10.1117/1.JBO.17.11.110505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Qi W., Li R., Ma T., Li J., Kirk Shung K., Zhou Q., Chen Z., “Resonant acoustic radiation force optical coherence elastography,” Appl. Phys. Lett. 103(10), 103704 (2013). 10.1063/1.4820252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jones I. L., Warner M., Stevens J. D., “Mathematical modelling of the elastic properties of retina: a determination of Young’s modulus,” Eye (Lond.) 6(6), 556–559 (1992). 10.1038/eye.1992.121 [DOI] [PubMed] [Google Scholar]
- 25.Song S., Le N. M., Huang Z., Shen T., Wang R. K., “Quantitative shear-wave optical coherence elastography with a programmable phased array ultrasound as the wave source,” Opt. Lett. 40(21), 5007–5010 (2015). 10.1364/OL.40.005007 [DOI] [PubMed] [Google Scholar]
- 26.Zhang J., Rao B., Yu L., Chen Z., “High-dynamic-range quantitative phase imaging with spectral domain phase microscopy,” Opt. Lett. 34(21), 3442–3444 (2009). 10.1364/OL.34.003442 [DOI] [PMC free article] [PubMed] [Google Scholar]