To hover effectively, hummingbirds invert their wings further to increase upstroke lift, while small bats rely on larger wings.
Abstract
Hummingbirds and nectar bats are the only vertebrates that are specialized for hovering in front of flowers to forage nectar. How their aerodynamic performance compares is, however, unclear. To hover, hummingbirds consistently generate about a quarter of the vertical aerodynamic force required to support their body weight during the upstroke. In contrast, generalist birds in slow hovering flight generate little upstroke weight support. We report that nectar bats also generate elevated weight support during the upstroke compared to generalist bats. Comparing 20 Neotropical species, we show how nectarivorous birds and bats converged on this ability by inverting their respective feathered and membrane wings more than species with other diets. However, while hummingbirds converged on an efficient horizontal wingbeat to mostly generate lift, bats rely on lift and drag during the downstroke to fully support their body weight. Furthermore, whereas the ability of nectar bats to aerodynamically support their body weight during the upstroke is elevated, it is much smaller than that of hummingbirds. Bats compensate by generating more aerodynamic weight support during their extended downstroke. Although, in principle, it requires more aerodynamic power to hover using this method, bats have adapted by evolving much larger wings for their body weight. Therefore, the net aerodynamic induced power required to hover is similar among hummingbirds and bats per unit body mass. This mechanistic insight into how feathered wings and membrane wings ultimately require similar aerodynamic power to hover may inform analogous design trade-offs in aerial robots.
INTRODUCTION
Hovering flight evolved independently in insects, birds, and bats to adapt to the ecological constraints of a nectarivorous diet (1). The power required to hover increases via a power law with body mass and cannot exceed the maximum power density of vertebrate muscle (1). This physiological constraint not only limits the scale of the largest vertebrate that can hover on Earth (1) but also, for the smallest hovering vertebrates, necessitates abundant floral resources with high spatiotemporal predictability, habitat types found primarily in the Neotropics (2). Adaptation to this ecological niche may have required several evolutionary innovations in vertebrate morphology and behavior to generate an average aerodynamic force equal to body weight during slow hovering flight while foraging for nectar (1). For example, research during the past decade has revealed how aerodynamic constraints resulted in the convergent evolution of a prominent tornado-like vortex that is formed along the leading edge of the wing during the downstroke of insects (3), hummingbirds (4) (5), and nectar bats (6), to generate lift. However, the unsteady aerodynamic force that all these taxa generate to support their body weight during the downstroke and upstroke remains to be fully resolved in vivo.
Robot fly models demonstrated that flies (Drosophila hydei) can support up to half their body weight during the upstroke (7). In contrast, hummingbirds (Selasphorus rufus) generate about a quarter of their weight support during the upstroke according to in vivo flow measurements (4). Similar flow measurements in hovering nectar bats (Leptonycteris yerbabuenae) did not give reliable force estimates for the downstroke versus upstroke because the complex wake structures cannot be reliably associated with each stroke phase (8, 9). Complexities in the wing shape of bats during wing tip reversal and the upstroke (1, 10) make it difficult to compare force production between half-strokes using kinematics alone (11), although scientists hypothesized that there may be additional lift generated during the upstroke resulting from an observed backwards flick (12). Furthermore, at low flight speeds, Muijres et al. (13) found that nectar bats generate a leading-edge vortex on both the dorsal and ventral side of the wing with opposite spin. However, a direct measurement of the aerodynamic force generated by freely flying animals was not possible until recently with the invention of the aerodynamic force platform (14). This new instrument revealed how a Neotropical generalist bird, the Pacific parrotlet (Forpus coelestis), generates little upstroke weight support during slow hovering flight (15). While previous biomechanical studies have measured and compared aerodynamics of forward flight across generalist birds and bats (16), no study has made a one-to-one comparison among hovering taxa. Such a comparison across Neotropical hummingbirds and bats can help clarify why, and to which degree, vertebrates evolved to support body weight during the upstroke.
To determine how Neotropical hummingbird and bat species support their body weight when they hover slowly, we traveled to Costa Rica (Fig. 1) and deployed a new high-resolution aerodynamic force platform with a three-dimensional (3D) high-speed camera rig (Fig. 2). Costa Rica’s ecology includes more than 10% of the world’s bat species (17) and more than 15% of the New World’s hummingbird species (18, 19). On the basis of a 10-week field study (January 2016 to March 2016) at the Las Cruces Biological Station in Coto Brus, we compared how N = 17 hummingbird species (n = 88), N = 2 nectarivorous bat species (n = 12), and N = 1 frugivorous bat species (n = 4) perform during slow hovering flight (Fig. 1). Our sample is representative of the local ecosystem because we sampled the most prevalent hummingbird, nectar bat, and fruit bat species (20, 21). By combining instantaneous in vivo vertical force measurements (movie S1) (14) with digitized 3D wing kinematics (movie S2) (22), we determined the similarities and differences in how birds and bats lift their body weight during slow hovering flight in the same ecosystem.
Fig. 1. Neotropical hummingbird and nectarivorous bat species converged on hovering while foraging from flowers.
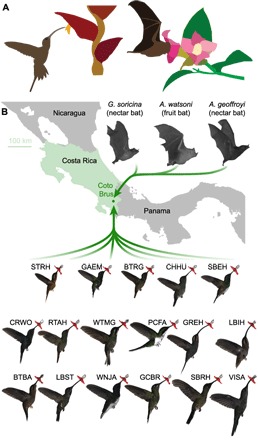
(A) A long-billed hermit (Phaethornis longirostris) hovers in front of a lobster claw (Heliconia), and a Geoffroy’s tailless bat (Anoura geoffroyi) sticks its head in a ring-gentian (Symbolanthus) to drink nectar and eat pollen (illustrations based on photos from C. Jiménez and N. Muchhala). (B) We studied hummingbird species (N = 17), nectarivorous bat species (N = 2), and frugivorous bat species (N = 1) living in the same habitat in Coto Brus, Costa Rica (species acronyms explained in table S1).
Fig. 2. Time-resolved vertical aerodynamic force measurements in freely flying hummingbirds and bats in vivo.
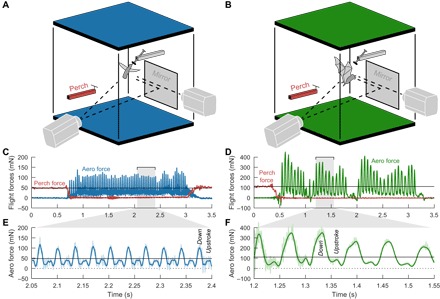
(A) A rufous-tailed hummingbird (Amazilia tzacatl) hovers at an artificial feeder, while high-speed cameras record wing kinematics. A mirror below the feeder allows a third perspective of the hovering bird for more accurate 3D reconstruction. A perch (red) instrumented with custom capacitive force sensors measures takeoff and landing forces for accurate weight measurements between each flight. Carbon fiber force plates (blue) mechanically integrate the pressure field generated by the bird and allow us to resolve the instantaneous vertical aerodynamic force. (B) A nectar bat (Glossophaga soricina) hovers in the same aerodynamic force platform but does not drink from the artificial feeder. Full flight recordings from the hummingbird (C) and bat (D) show how body weight is supported by the perch before takeoff and by the aerodynamic force generated with the wings in flight. Hummingbirds landed back on the perch or feeder after each flight, while bats often landed inverted perching on small screw heads on the side walls, which results in zero measured force after the flight. By zooming in to a 0.35-s window, we can see the large downstroke humps and smaller upstroke humps in each wingbeat for hummingbirds (E) and nectar bats (F). Unfiltered forces are shown in light blue and green.
RESULTS
Wingbeat-resolved 3D kinematics
Hummingbirds flap their wings more symmetrically during the downstroke and upstroke compared to bats, which use highly asymmetrical wing kinematics to hover (Fig. 3). Hummingbirds beat their wings back and forth in an almost horizontal stroke plane that is tilted downward 7° on average (Fig. 3, A, B, and G). They twist their wings (Fig. 3C) to angles of attack below 45° at the radius of gyration on the downstroke and upstroke (Fig. 3, E and F) while keeping their wings mostly extended (Fig. 3D). In contrast, bats beat their wings back and forth in a stroke plane with a downward inclination of 24° on average (Fig. 3G). Simultaneously, bats beat their wings down at very high angles of attack, beyond 50°, after which they twist their wings rapidly (Fig. 3C) and beat them up at even higher angles (Fig. 3, E and F). On the upstroke, bats also retract their wings up to 35% (Fig. 3D). In addition, bats hover at a Reynolds number two times higher than that of hummingbirds (fig. S1). How do these differences in wing kinematics translate into differences in aerodynamic weight support?
Fig. 3. Hummingbirds primarily rely on lift to support body weight, and bats increase wing angle of attack and stroke plane angle to include drag.
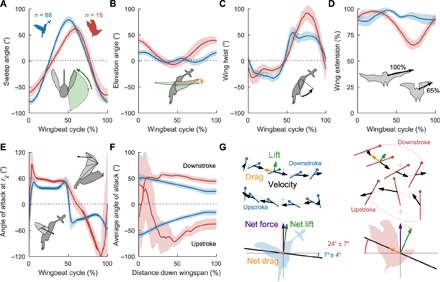
(A) The hummingbird (blue; n = 88 individuals from 17 species) stroke is sinusoidal, while bats (red; n = 16 individuals from three species) have a longer downstroke period, followed by a faster upstroke (shaded areas are SD across individuals). (B) With a larger vertical elevation amplitude, bats produce an oval “O”-shaped wing tip trace, while hummingbirds generate a classic “U” trace with a double harmonic. (C) Hummingbirds twist their wings during both the downstroke and upstroke, while bat wings have less twist during the downstroke and much more twist during the upstroke. (D) Bats retract their wings during the upstroke, reducing their wingspan up to 35%. (E) Hummingbirds operate their wings at lower angles of attack than bats, at the wing radius of gyration r2 (25) where the center of pressure acts. (F) Radial angle-of-attack distribution from the base (0%) to the wing tip (100%) averaged over the high dynamic pressure phase of the stroke [thickened lines in (E); see Materials and Methods and fig. S6]. Bat wings operate at much higher angles of attack along their wingspan than hummingbirds (ill-defined near the root where chord velocity approaches zero; inverted wings have negative angles). (G) Wing stroke path (at r2) and chord angles of attack show that bats tilt the stroke plane and increase angle of attack to orient relatively more drag (orange) upward to support body weight (purple) in addition to lift (green), explaining the wingbeat-averaged vector magnitudes in the avatars (1) (lift and drag are shown as unit vectors on airfoil, and velocity vectors are shown as proportionally scaled black vectors; small gray cross, shoulder; cross width and height represents 10° wing sweep and elevation).
In vivo aerodynamic forces and power
Bats support their weight less during the upstroke than hummingbirds, which they compensate for by generating more force during an extended downstroke. The associated aerodynamic losses are offset by sweeping their relatively larger wings over a wide area. This reduces their induced power per unit body mass to values similar to hummingbirds. Pooling all the hummingbirds (N = 17, n = 88) versus bats (N = 3, n = 16) in our vertical aerodynamic force measurements (Fig. 4A), we find that bats prolong weight support during the downstroke, whereas hummingbirds make use of a more active upstroke. Consequently, hummingbirds accelerate air through the stroke plane more evenly over the downstroke and upstroke, which makes their induced power cost more balanced over the wingbeat (Fig. 4B) and improves aerodynamic efficiency. The elevated efficiency stems from the lower temporal cost factor for induced power (see Materials and Methods) compared to bats (Fig. 4D). Nevertheless, bats are on par with hummingbirds when it comes to maintaining a low stroke-averaged induced power (Fig. 4C) because their greatly reduced actuator disk loading saves energy (Fig. 4E).
Fig. 4. Bats compensate aerodynamic inefficiency due to weight support asymmetry with low disk and wing loadings, which help minimize aerodynamic power.
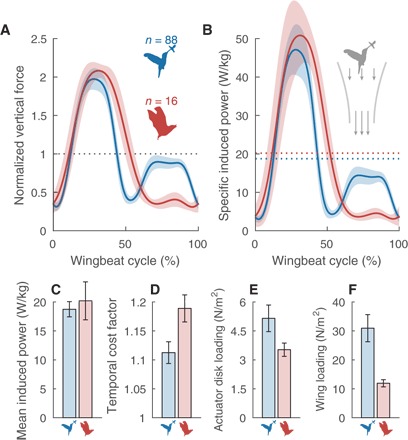
(A) Hummingbirds (blue) support more of their body weight during the upstroke compared to the inactive upstroke of bats (red). (B) Body weight is supported by accelerating air downward through the stroke plane, which requires induced power (1). The hummingbird’s ability to support body weight more uniformly over the upstroke and downstroke reduces induced power asymmetry, which makes them more efficient than bats (see the “Induced power calculation” section). (C) Regardless, hummingbirds and bats need similar induced power per unit body mass to hover. (D) Bats accomplish equivalent induced power by compensating for their higher temporal induced power cost factor with a lower (E) actuator disk loading (body weight per swept wing area). (F) Similarly, bats have a much lower wing loading due to their disproportionally larger wing lengths (fig. S5C; shaded areas and error bars are SD across individuals).
How diet relates to upstroke weight support
Despite marked differences in flower specialization, hummingbirds converged on generating similar elevated weight support on the upstroke. The 17 hummingbird species that we studied span six clades (fig. S2) and have diverse beak shapes (Fig. 1B) that adapted to the different flowers foraged (23). Therefore, we wondered whether the hover pose required for each flower angle (24) would modify upstroke support. To test how the flower angle affects upstroke force production, we made aerodynamic force recordings for horizontal (45°) and vertical flower orientations. Comparing a hummingbird with a specialist (green hermit) versus generalist (rufous-tailed hummingbird) beak shape, we observed no pronounced dependence of stroke plane angle, wingbeat frequency, or vertical force on flower angle (Fig. 5). Instead, hummingbirds seem to combine both body angle (Fig. 1B) and an extraordinarily supple neck to feed from flowers regardless of the angles at which they point (Fig. 5). When we compare all the hummingbird species (Fig. 1B), we find that hummingbirds converged on generating similar vertical force during the wingbeat (Fig. 6A) with a substantial amount during the upstroke (Fig. 6B).
Fig. 5. Hummingbirds accommodate flower angle with their body angle and supple neck, keeping wingbeat frequency and vertical force distribution nearly consistent.
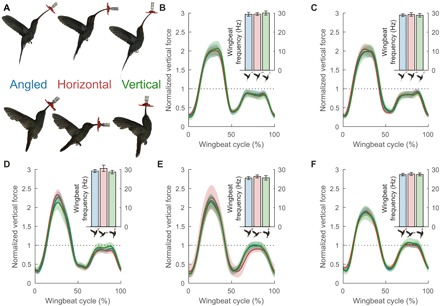
(A) A green hermit (Phaethornis guy; top) and rufous-tailed hummingbird (A. tzacatl; bottom) hover at a feeder in three orientations: 45°, 0°, and 90°. Comparison of the average wingbeat frequency and normalized vertical force for two green hermits (B and C) and three rufous-tailed hummingbirds (D to F) reveals that these parameters are not substantially modulated by hummingbirds to accommodate a flower angle. Across all individuals, and relative to the angled (45°) feeder, the stroke plane angle only decreased by 1° ± 2° for the horizontal (0°) feeder and only increased by 2° ± 4° for the vertical (90°) feeder. Shaded areas and error bars represent SD across the hundreds of wingbeats recorded during three flights per individual for each feeder orientation.
Fig. 6. Nectarivorous bats generate more upstroke weight support than fruit bats during slow hovering flight by inverting their wing further.
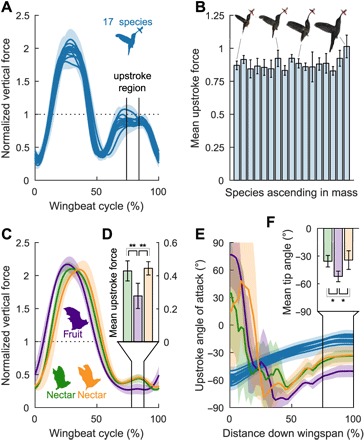
(A) All 17 hummingbird species converged on generating similarly elevated weight support during the upstroke. (B) The amplitude of upstroke weight support averaged over a 10% wingbeat interval (74 to 84% of the wingbeat cycle) confirms this (see table S1 for species names sorted by mass). (C) In contrast, nectar bats produce noticeably more vertical force during the upstroke than the fruit bat. (D) The vertical force amplitude is significantly different (78 to 88% of the wingbeat cycle). (E) This difference is explained by the radial angle-of-attack distribution for the upstroke (based on Fig. 3F), which shows pronounced differences in the angle of attack (<0%, inverted wing) of the wing tip (75 to 100% span). (F) At the wing tip, hummingbirds use angles around −15° to generate lift efficiently. Nectar bats (G. soricina, green; A. geoffroyi, orange) flick their wing tips back at around −35°, generating significant lift and drag, whereas fruit bats (Artibeus watsoni, purple) operate at −52°, generating more drag. Shaded areas and error bars represent SD across individuals. *P < 0.05, **P < 0.01 (light gray comparison bar; nonsignificant; see the “Statistical analysis” section).
Although all three bat species generate much less upstroke support than the hummingbirds, both nectar bat species generate significantly more upstroke support than the fruit bat. By comparing two Neotropical nectivore bat species with one frugivore bat species (Fig. 6C), we find that the nectarivorous bats, Glossophaga soricina (P = 0.0038) and Anoura geoffroyi (P = 0.0018), generate a significantly elevated weight support during the upstroke compared to the frugivore bat, Artibeus watsoni, while we could not detect a difference between the two nectarivorous bats (P = 0.8886). When comparing the kinematic parameters (Fig. 3) that describe the upstroke for all three bat species (fig. S3), we only found substantial differences in the average radial angle-of-attack distribution (Fig. 6E). The nectarivorous bats, G. soricina (P = 0.0166) and A. geoffroyi (P = 0.0105), invert their wing tip significantly more during the upstroke than the frugivore bat, A. watsoni. We could not detect a difference between the wing inversion amplitude of the two nectarivorous bats (P = 0.9593; Fig. 6F), which fall between the frugivore bat and hummingbirds (Fig. 6E; see the “Statistical analysis” section). In concert, all these findings are mechanistically consistent with how lift is generated in relation to wing angle of attack (1).
DISCUSSION
Neotropical hummingbirds hover aerodynamically more efficiently than small bats in the same ecosystem by generating more upstroke weight support (Fig. 4D). However, bats compensate for this limitation with larger wings (Fig. 4, E and F), such that the mass-specific induced power required to hover is similar for both groups (Fig. 4C). Furthermore, both Neotropical hummingbirds and nectarivorous bats generate more upstroke weight support than generalist Neotropical foragers [parrotlets (15) and fruit bats (Fig. 6, C and D)]. The nectar bats achieve this by inverting their wings further during slow hovering flight, as hummingbirds do (Fig. 6, E and F). This behavior is consistent with flow visualizations of leading edge vortices during the upstroke of slow hovering nectar bats (13). In contrast, flow-based lift calculations in nectar bats do not resemble our upstroke force measurements (Fig. 4A), supporting the hypothesis that complex wake structures confound force calculations in slow hovering bats (9). Flow-based lift calculations for hovering hummingbirds (4, 5), on the other hand, do agree with our measured upstroke support (Fig. 4A and fig. S4). Finally, because the relative increase in upstroke support is modest in nectar bats, their overall weight support trace is still more similar to fruit bats than hummingbirds (Fig. 6, A and C).
Hummingbirds achieve high upstroke weight support by beating their wings nearly symmetrically back and forth, so they can efficiently generate net lift (Fig. 3). This can be understood based on quasi-steady aerodynamic theory (25); lift is approximately perpendicular to local wing velocity, while drag opposes it. By maintaining angles of attack below 45° (at the radius of gyration; Fig. 3, E and F) with a nearly horizontal stroke plane (Fig. 3G), hummingbirds can orient lift forces mostly upward, which reduces the drag and thus the power required to support their bodyweight (25). To maximize upstroke lift, hummingbirds keep their wings nearly fully extended throughout the wingbeat (Fig. 3D). Our finding that the way hummingbirds support their body weight does not vary substantially with flower angle (Fig. 5) and species (Fig. 6A) suggests that this may be a conserved trait.
Bats offset their lower upstroke weight support by using highly asymmetrical wing kinematics during the downstroke and upstroke, so they can harness both net lift and drag to support body weight (Fig. 3). Bats achieve this by beating their wings down at much higher angles of attack, beyond 50°, after which they twist and beat them up at even higher angles (Fig. 3, C, E, and F), which generates a lot of drag. Because the stroke plane is inclined downward at 24° on average, drag has an upward component during the downstroke that opposes weight (26). To benefit from this, bats retract their wings up to 35% (Fig. 3D) during the upstroke, which much reduces drag pointing downward. This explains how bats support body weight with net lift and drag (Fig. 3G). This mechanism of weight support based on combining lift and drag was recently observed in parrotlets as well (27). During takeoff, they also beat their wings at angles of attack beyond 50° along a downward inclined stroke plane. This maximizes the total aerodynamic force coefficient to combat gravity during the downstroke by vectorially combining lift and drag (27).
In addition to minimizing the induced power required for hovering with their reduced actuator disk loading (Fig. 4E), bats can also offset their lower aerodynamic efficiency by reducing inertial and profile power. Wingspan retraction during the upstroke reduces wing inertia and thus inertial power (10). Although it remains to be determined how much (unsteady) profile power bats incur in hover (26, 28), the much lower wing loading in bats (Fig. 4F), as well as their much lower wing tip velocity (fig. S5H), greatly reduces the profile power per unit weight required to hover (1), particularly because aerodynamic power reduction is proportional to wing velocity cubed (29). In concert, all these findings illustrate the extent to which the wing kinematics and morphology of vertebrates adapted to feed from flowers on the wing.
The smaller upstroke weight support in nectarivorous bats versus hummingbirds can also be understood through the lens of evolution. Phylogenetic analyses suggest that bats evolved a nectarivorous diet (21, 30) when hummingbirds started to speciate (18) roughly 20 million years ago (phylogenetic trees shown in fig. S2). Notwithstanding the fact that hummingbirds evolved earlier than nectarivorous bats, the differences in their ability to generate vertical aerodynamic force during the upstroke probably stem from specific adaptations in the avian versus mammalian bauplan (1). Whereas hummingbirds have evolved specialized limb functions, using their forelimbs solely to fly and their legs to perch, bats use both their forelimbs and legs to tension their membrane wing in flight and to locomote over substrates (1, 31). This bimodal function of bat forelimbs may have slowed down, or limited, the adaptation of upstroke weight support. Instead of high upstroke weight support, bats evolved much larger wings for their body mass than hummingbirds (fig. S5, A and F) (1), which allows bats to flap their wings more slowly in support of their body weight and to save energy. The evolution of aerodynamic performance in hummingbirds and nectar bats, foraging in the same Neotropic ecosystem, thus appears to be guided by different trade-offs that ultimately required similar induced power per unit body mass to forage nectar. Further studies using our new field-deployable aerodynamic force platform can assess which role these trade-offs play in Old World nectivore birds, which have been observed to also hover briefly (32). If the analysis we performed here can be automated and expanded to broadly sample across all ~1200 bat and ~10,000 bird species, then a phylogenetic least-squares analysis may show how hovering flight evolved across ecosystems in the world more generally. Finally, our findings can shed new light on trade-offs in flapping robot designs such as the Nano Hummingbird (33) and the Bat Bot (34) because it currently remains unclear which specific advantages each bioinspired design offers over the other.
MATERIALS AND METHODS
Experimental design
Hummingbirds were captured in various locations around Coto Brus, Costa Rica in collaboration with the Stanford Center for Conservation Biology (20). After banding, selected hummingbirds (up to six per day) were transported to the Las Cruces Biological Station where they were trained to feed from a syringe containing sugar water (3:1 water/sugar). Once sufficiently trained, hummingbirds were placed in a 50 cm × 50 cm × 50 cm flight chamber with a perch and feeder, as shown in Fig. 2. The perch and feeder were instrumented with force sensors to measure animal weights before and after each flight. Acrylic side walls enclosed the flight chamber, while the top and bottom consisted of carbon fiber aerodynamic force plates (498 and 496 g, respectively; KVE Composites Group) attached to three force sensors each. The custom-made force sensors consisted of an aluminum flexural spring with a known stiffness. Capacitive sensors [MicroSense model 8800 electronics module with model 2805 probes (resolution, ~0.8 nm), National Instruments USB-6210 DAQ, Lenovo ThinkPad T440s, and MATLAB R2015b] sampled spring displacements at 10 kHz, which were then converted into forces using the respective spring stiffness. The instantaneous sum of forces on the top and bottom force plates is equal to the instantaneous vertical aerodynamic force generated by the hovering animals (14, 35, 36). Hummingbird flights were recorded at 2000 frames per second (fps) using Phantom Miro M310 and LC310 cameras. The color camera (LC310) captured the right-side hummingbird view, while the grayscale camera (M310) captured both an angled-up view from behind and in front of the bird with the help of a mirror (Fig. 2). Each flight recording consisted of a hummingbird taking off, drinking from the feeder, and then landing. Forces were sampled during the entire duration, while high-speed cameras recorded up to ~4 s (8310 frames) of hovering at the feeder. After three successful flight recordings, birds were transported back to their location of capture and released. For three nights, bats were captured and flown in the same flight chamber. We were not able to train these wild bats to feed from the feeder within the time constraints of a catch-and-release field study. Coincidentally, this made the comparison between the nectar bats and fruit bat fairer because fruit bats are not known to be trainable to feed on the wing. Accordingly, recordings were made while bats hovered around the flight chamber (advance ratio of 0.069 ± 0.036) between successful and unsuccessful attempts to perch on the feeder, perch, or screw heads on the side walls (without attempting to escape). Bat flights were recorded at 1000 fps (~8 s of flight) using two Phantom Miro M310 cameras and infrared lights (CMVision Wide Angle IRD50). After three successful recordings, bats were released. For five hummingbirds and two bat individuals, the number of recordings was less than three (see table S1). All procedures were approved by the Stanford Administrative Panel on Laboratory Animal Care and carried out under permits from Sistema Nacional de Áreas de Conservación (SINAC) and Ministerio de Ambiente y Energía (MINAE) of Costa Rica.
Individual selection criteria
Because we could not know the exact number of species and individuals that we would be able to catch, we applied the following data selection criteria after the field study before we performed the data analysis. We captured only one Platyrrhinus helleri bat and one ruby-throated hummingbird (Archilochus colubris), which were excluded from the analysis. We also capped the number of individuals per species to seven. We gathered data on 18 rufous-tailed hummingbirds (Amazilia tzacatl) and 10 green hermits (Phaethornis guy), which were randomly down-selected to seven before analysis. In addition, we attempted to measure hovering forces from the white-tipped sicklebill (Eutoxeres aquila) with a curved beak, but we could not train it to hover in front of the feeder, as its natural behavior is to perch while drinking from specific flowers (during its flight before perching, we observed an active upstroke similar to the other hummingbirds). Overall, we analyzed the 3D kinematics and forces from 88 hummingbirds and 16 bats across 17 and 3 species, respectively (see table S1).
Hummingbird wingbeat selection criteria
Hummingbird wingbeat transitions were calculated by automatically tracking the centroid of the bird’s silhouette in the side view camera (MATLAB R2015b; see movie S1). This definition allowed for an objective wingbeat transition criteria, with the beginning of the downstroke starting when the area centroid reached a maximum distance behind the bird. This automated image processing technique also allowed us to determine when the bird’s beak was touching the feeder. All feedings longer than 12 wingbeats were included in the aerodynamic force analysis while excluding the first three and last three wingbeats at the feeder (see table S1 for number of wingbeats per individual). While the transitions from upstroke to downstroke were determined for all these wingbeats, only one representative wingbeat was selected for kinematic tracking (to limit the total manual tracking effort to 6 months of full-time effort). We first visually ranked each flight on a scale of 1 to 3 based on orientation (yaw angle) of the bird to the feeder. A score of 1 corresponded to a flight where the right wing was not fully visible over the full wingbeat due to high body yaw relative to the feeder, while a score of 2 and 3 corresponded to slight yaw and no yaw, respectively. We then determined the number of frames that comprised each wingbeat period, based on which we calculated the average wingbeat period for each individual. We then automatically selected all wingbeats (excluding highly yawed flights) that matched the average wingbeat period within one frame (0.0005 s) and randomly selected one of these wingbeats for manual 3D tracking.
Bat wingbeat selection criteria
Bat wingbeats were segmented for each individual by cross-correlating a template force trace. We first noted all wingbeats for which the bat was hovering and away from the flight chamber surfaces. The aerodynamic forces of all these wingbeats were included in the analysis, allowing us to determine an average representative force trace. Wingbeats were manually ranked on the basis of visibility in all three camera views. The wingbeat that most closely resembled hovering (low body roll and forward speed), and was visible in all views, was selected for kinematic tracking to minimize variability in hovering kinematics while not feeding. We excluded bats from the analysis for which we could not identify reasonably trackable wingbeats (three individuals). As not all noted bat wingbeats included a visible wing tip in every camera view, exact wingbeat transitions were calculated by extracting the vertical force trace of the single template wingbeat that was tracked kinematically. The maximum vertical position of the bat wing tip (37) was used to define the start of this wingbeat. The corresponding vertical force trace template for that kinematically tracked wingbeat was then cross-correlated with the full flight force trace. The maximum cross-correlation values defined the start and end of each bat wingbeat for aerodynamic force segmentation.
Digitizing kinematics
A single wingbeat was digitized from each hummingbird and bat individual using direct linear transformation calibrations (22). Nine points along the outline of the wing planform were tracked for each hummingbird (one on wing tip, four on leading edge, and four on trailing edge; see overlaid purple dots in movie S2), while seven points were tracked for each bat [shoulder, wrist, tip of digit 2, tip of digit 3 (wing tip), tip of digit 4, tip of digit 5, and ankle; see overlaid purple dots in movie S2]. We used these points to accurately calculate wing length and area (and thus aspect ratio) using the frame in which the bats attained maximum wing extension. Similarly, for hummingbirds, we tracked 25 points around the wing perimeter during the first frame of the downstroke to calculate wing length and area (and thus aspect ratio). In addition, we located the flower position for hummingbirds during each wingbeat we analyzed and tracked the nose position for bats during each wingbeat we analyzed. To keep the average number of tracked frames per hummingbird wingbeat consistent, subsamples of the recorded frames (at 2000 fps) were tracked. Wing outline digitization and 3D reconstruction were performed at every other frame, or every third frame depending on the species, resulting in 27 to 42 frames tracked per hummingbird wingbeat. As bats have much more complex wingbeat kinematics, every frame at 1000 fps was tracked, resulting in 69 to 100 frames per wingbeat.
Wing and body kinematics
The wingbeat kinematics of both hummingbirds and bats were analyzed in a similar way for fair comparison. First, the wing perimeter was extracted, and a midspan vector (from the wing tip through the center of wing planform) was calculated for each tracked frame. Then, the local coordinate system origin was placed at the best fit intersection of all midspan vectors over each wingbeat. The positive z axis was aligned up against the direction of gravity and calculated in easyWand5 (22) by dropping a small sphere through the volume. The positive x axis was aligned to the right of the animal (centered between maximum and minimum sweep angles, as shown in Fig. 3A), leaving the positive y axis pointing in front of the animal (when a bat’s left wing was tracked, kinematics were reflected to match a right wing). Next, the sweep angle (Fig. 3A) was defined as the angle of the wing tip with respect to the shoulder projected into the horizontal xy plane (normal to gravity). The wing motion in this horizontal plane shapes the (projected) actuator disk area associated with the vertical force (29). Similarly, the elevation angle was defined as the vertical elevation of the wing tip with respect to the shoulder (Fig. 3B). Finally, the instantaneous wing extension was defined as the distance from the shoulder to the wing tip, normalized by the maximum distance during the wingbeat (Fig. 3D).
We also measured and compared morphological and wingbeat-averaged variables. First, the wing length was defined as the distance from the wing tip to the shoulder (the shoulder was defined as the proximal tracked point on the leading edge; fig. S5C), while the wing area was calculated by summing the triangular patches (23 for hummingbirds and 4 for bats) that defined the wing surface (fig. S5F). Consequently, the mean chord length was defined as the wing area divided by the wing length (fig. S5D). Next, the aspect ratio was defined as the wing length divided by the mean chord length (fig. S5G). Finally, the swept area was calculated by projecting the wing outline to the horizontal plane over the whole wingbeat. The perimeter of this projected wing area was found using the alpha hull method with a 5-cm probe radius to account for concave features in the tracked points (fig. S5E). In addition to these standard kinematics variables, a 3D wing reconstruction was used to calculate the spanwise twist and angle of attack.
For each tracked frame, 50 equally spaced chord segments down the wing were calculated. Each chord intersected the leading and trailing edge but did not necessarily hold a constant length over the wingbeat (see movie S2). All chords were aligned perpendicular to the midspan vector, starting at the most proximal tracked point (on either the leading or trailing edge) and ending at the wing tip. First, the wing twist rate per meter of wingspan (degrees per meter) was found by calculating the angle of each chord relative to the root chord. A best fit twist rate down the wing’s span was calculated and multiplied by the wing’s length to get a measure of wing twist (Fig. 3C). Then, the angular velocity of each wing panel (single panel for hummingbird wing and five triangular panels for bat wing) with respect to the wing origin was numerically differentiated (38). Next, to find the local velocity of each chord, the position to each chord was vectorially crossed with the angular velocity of its closest panel. Then, the angle of attack of each chord segment was calculated by measuring the angle toward the wing’s leading edge relative to the component of the chord’s velocity perpendicular to the midspan (see movie S2 and Fig. 3E). The angle of attack was defined as negative when the wing was inverted on the upstroke. The angles of attack that we found are higher than in previous studies (4, 25) because we computed them more precisely based on the local chord velocities from wing root to wing tip (see movie S2). Next, the stroke-averaged angle of attack at each chord during the downstroke and upstroke (Figs. 3F and 6E) was averaged over the portion of the respective stroke when the wing tip speed exceeded the mean tip speed (see fig. S6). Finally, the wingbeat-resolved Reynolds number at the radius of gyration was calculated (fig. S1) using the average air density and dynamic viscosity.
Atmospheric conditions
To calculate the Reynolds number and induced power required to hover, we determined the average atmospheric conditions at the Las Cruces Biological Station based on the available on-site recordings (https://archive.tropicalstudies.org/meteoro/default.php?pestacion=1). The barometric pressure (880 ± 2 mbar), temperature (21.4 ± 7.4°C), and relative humidity (70.5 ± 18.8%) were averaged over the research period (4 February 2016 through 15 March 2016). We then calculated the average air density (1.04 kg m−3) and dynamic viscosity (1.79 × 10−5 kg m−1 s−1) using the ideal gas law and Sutherland’s law (25).
Hummingbird vertical force processing
Aerodynamic forces were averaged across hundreds (see table S1) of wingbeats to obtain representative normalized vertical force traces of each individual (see movie S1). First, step responses from the perch and feeder during takeoff and landing were used to determine hummingbird weights. Next, aerodynamic forces were filtered offline at 180 Hz (about six times their wingbeat frequency) using an eighth-order digital low-pass Butterworth filter to isolate animal frequencies from structural frequencies of the setup (35). Temperature drift caused flexural springs to slowly expand and contract during recordings. To account for this, a linear drift model was applied to process the hummingbird recordings, which assumes that the bird generates a vertical force equal to their weight on average (mean drift per wingbeat was 0.98% of bird weight). Normalized vertical force profiles were calculated by dividing the force trace from each wingbeat by the bird’s weight during that flight (resulting in 100% weight support on average due to linear drift model). All normalized vertical force profiles for each individual were interpolated to 1000 points, starting at the beginning of the downstroke (0%) and ending at the end of the upstroke (100%). These interpolated traces were then averaged to find a representative normalized vertical force for each hummingbird, as shown in fig. S4. Follow-up experiments with Anna’s hummingbirds helped determine the effect of sensor drift and air leakage through the 5-mm gaps between the plates and side walls (fig. S7). Linear drift corrections to our capacitive sensors (fig. S7A) match the force traces from a setup using ATI Nano43 sensors with negligible drift (fig. S7B). Placing a thin strip of Saran Wrap along the gaps prevented air leakage (fig. S7C). The air leakage seemed to filter the force amplitude of the downstroke and valleys but did not result in differences between the five flights of an individual within each treatment, and the upstroke amplitude was basically unaffected (fig. S7D). This demonstrates consistency and our ability to fairly make comparisons within the Costa Rica field experiment with the air gap and the capacitive sensor drift correction. If future comparisons with our study require higher accuracy than achieved in this study, then we recommend considering the minor filter effect due to the air gaps in our vertical force recordings.
Bat vertical force processing
Bat forces were processed in a manner similar to that used for hummingbirds. First, individual bat weights were determined by measuring step responses from the perch and feeder during takeoff and landing. Next, aerodynamic forces were filtered offline at 100 Hz (about seven times their wingbeat frequency) using an eighth-order digital low-pass Butterworth. Drift was corrected in bat recordings by applying a linear drift model from (before) takeoff to (after) landing. Normalized vertical force profiles were then calculated by dividing the vertical force during each wingbeat by the mean force during that wingbeat. As bats tended to generate more than 100% weight support on each wingbeat (fig. S3D), this normalization method helps compare the relative magnitude of force generated throughout the wingbeat.
Induced power calculation
As birds and bats flap their wings to hover, they accelerate air downward. The induced power required to accelerate this air can be calculated as follows (29)
| (1) |
where κ is the induced power factor that accounts for tip losses, nonuniform inflow, and other nonideal effects; ρ is the density of air (1.04 kg m−3); A is the area swept by the rotors or wings; and W is the weight of the animal. Lighthill (39) noted that, for animals, this ideal induced power must be a minimum, as animals do not generate a jet of uniform velocity below. Ellington (40) broke down this κ value into a spatial correction factor to account for downwash profile (σ) and a temporal correction factor for wake periodicity (τ)
| (2) |
While Ellington estimated this spatial correction factor (σ) to be about 0.1 and the temporal correction factor (τ) to be around 0.05 for horizontal stroke planes and 0.5 for inclined stroke planes, we can determine the temporal factor precisely using our directly measured time-resolved force trace. When we decouple the correction factors into a spatial cost factor, κσ (which equals 1 for a uniform wake), and temporal cost factor, κτ (which equals 1 for a constant wake), we can calculate the stroke-averaged induced power as
| (3) |
By substituting the time-varying vertical aerodynamic force [F(t)] for the constant vertical aerodynamic force equal to weight (W) and integrating over the wingbeat, we can account for power losses due to temporal force fluctuation
| (4) |
where T is the wingbeat period. This allows us to calculate the temporal cost factor based on our directly measured instantaneous vertical force as follows
| (5) |
Because the time-varying normalized vertical force is raised to the power 1.5, the animal takes an extra penalty when it generates a fluctuating force unequal to its weight. We calculate temporal cost factors of 1.11 and 1.19 for hummingbirds and bats, respectively, as shown in Fig. 4D. The instantaneous induced power [Pind(t)] can be calculated by
| (6) |
where we will use a spatial cost factor of κσ = 1.1 from Ellington (40). To compare across species, the average body mass–specific induced power () is calculated as
| (7) |
where m is the mass of the animal, and g is the gravitational acceleration. While the asymmetric weight support of bats leads to a higher temporal cost factor, they reduce body mass–specific induced power by lowering the actuator disk loading (W/A), as shown in Fig. 4E.
Feeder angle comparison
To test the influence of the feeder angle on hummingbird hovering, we performed further experiments with five individuals. In addition to the three recordings, with the feeder angled at 45° as in the experiment, we also recorded three flights for a horizontal (0°) feeder and three for a vertical (90°) feeder for two green hermits (P. guy) and three rufous-tailed hummingbirds (A. tzacatl). Figure 5 shows the wingbeat frequency and normalized vertical force generated over each wingbeat at each feeder orientation for each individual. There does not seem to be any noticeable difference in either metric across these experimental treatments. As hummingbirds drink from a diversity of flowers in various orientations, they benefit from the ability to contort their neck to reach the nectar while minimally affecting their flight strategies. This further supports the idea that the hovering technique is a very conservative trait in hummingbirds with low variation across physical circumstances or species.
Statistical analysis
We performed statistical tests (MATLAB R2015b) on the mean normalized upstroke (Fig. 6D) and upstroke wing tip angle of attack (Fig. 6F) to compare the differences between bat species. First one-way analyses of variance (ANOVAs) was run to compare the means of the three species (G. soricina, n = 6; A. watsoni, n = 4; A. geoffroyi, n = 6). These tests showed that there is indeed a difference between the three species, with P = 0.0014 (F = 11.3145, 2 df) for the mean normalized upstroke and P = 0.0082 (F = 7.1017, 2 df) for the wing tip angle of attack. A post hoc Tukey-Kramer multiple comparisons test (with α = 0.05) was then run to see what species were statistically different in these two parameters. For the mean normalized upstroke, the fruit bat (A. watsoni) was statistically different from the nectar bats [G. soricina (P = 0.0038) and A. geoffroyi (P = 0.0018)], while the two nectar bats were not significantly different from each other (P = 0.8886). For the upstroke wing tip angle of attack, the fruit bat (A. watsoni) was also statistically different from the nectar bats [G. soricina (P = 0.0166) and A. geoffroyi (P = 0.0105)], while the two nectar bats were not significantly different from each other (P = 0.9593).
Supplementary Material
Acknowledgments
We thank G. Daily, C. Mendenhall, A. Zheng, N. Hendershot, J. Smith, J. Sandí, P. Cabezas, A. Rodriguez, M. Sandí, B. Gomez, the field assistants and Costa Rican landowners, Las Cruces Biological Station, and the Organization for Tropical Studies, who all helped us with this study. Finally, we thank D. Chin for helping proofread our manuscript. Funding: This research was supported by the NSF CAREER Award 1552419 and the King Abdulaziz City for Science and Technology Center of Excellence for Aeronautics and Astronautics at Stanford. Author contributions: R.I. and D.L. conceived the experimental design and contributed equally to the drafting of the manuscript. R.I. designed and constructed the experimental apparatus, performed the experiments, and processed the data with advice from D.L. L.H. digitized wing kinematics. All authors contributed to data interpretation and manuscript preparation. Competing interests: The authors declare that they have no competing interests. Data and materials availability: Data is available at https://doi.org/10.6084/m9.figshare.6411125. All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/9/eaat2980/DC1
Fig. S1. Bats hover at two times higher Reynolds numbers than hummingbirds.
Fig. S2. Phylogenetic tree of the hummingbirds and bats in the study.
Fig. S3. Beyond the radial angle-of-attack distribution, kinematic parameters do not vary much across bat species.
Fig. S4. Hummingbirds generate substantially more vertical force during the upstroke than bats, and the nectar bats outperform the fruit bat.
Fig. S5. Morphological and kinematic parameters of the sampled species.
Fig. S6. Definition of the wing tip speed range associated with high lift production during the downstroke and upstroke.
Fig. S7. Aerodynamic force platform verification.
Table S1. Overview of wingbeats analyzed for force processing.
Movie S1. Force measurements and wingbeat segmentation.
Movie S2. Wing tracking and kinematic parameters.
REFERENCES AND NOTES
- 1.U. M. Norberg, Vertebrate Flight: Mechanics, Physiology, Morphology, Ecology and Evolution (Springer Science & Business Media, 2012). [Google Scholar]
- 2.Fleming T. H., Muchhala N., Nectar-feeding bird and bat niches in two worlds: Pantropical comparisons of vertebrate pollination systems. J. Biogeogr. 35, 764–780 (2008). [Google Scholar]
- 3.Ellington C. P., van den Berg C., Willmott A. P., Thomas A. L. R., Leading-edge vortices in insect flight. Nature 384, 626–630 (1996). [Google Scholar]
- 4.Warrick D. R., Tobalske B. W., Powers D. R., Aerodynamics of the hovering hummingbird. Nature 435, 1094–1097 (2005). [DOI] [PubMed] [Google Scholar]
- 5.Warrick D. R., Tobalske B. W., Powers D. R., Lift production in the hovering hummingbird. Proc. R. Soc. Lond. B Biol. Sci. 276, 3747–3752 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Muijres F. T., Johansson L. C., Barfield R., Wolf M., Spedding G. R., Hedenström A., Leading-edge vortex improves lift in slow-flying bats. Science 319, 1250–1253 (2008). [DOI] [PubMed] [Google Scholar]
- 7.Muijres F. T., Elzinga M. J., Melis J. M., Dickinson M. H., Flies evade looming targets by executing rapid visually directed banked turns. Science 344, 172–177 (2014). [DOI] [PubMed] [Google Scholar]
- 8.Hedenström A., Johansson L. C., Wolf M., von Busse R., Winter Y., Spedding G. R., Bat flight generates complex aerodynamic tracks. Science 316, 894–897 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Håkansson J., Hedenström A., Winter Y., Johansson L. C., The wake of hovering flight in bats. J. R. Soc. Interface 12, 20150357 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Riskin D. K., Bergou A., Breuer K. S., Swartz S. M., Upstroke wing flexion and the inertial cost of bat flight. Proc. Biol. Sci. 279, 2945–2950 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dudley R., Winter Y., Hovering flight mechanics of neotropical flower bats (Phyllostomidae: Glossophaginae) in normodense and hypodense gas mixtures. J. Exp. Biol. 205, 3669–3677 (2002). [DOI] [PubMed] [Google Scholar]
- 12.Wolf M., Johansson L. C., von Busse R., Winter Y., Hedenström A., Kinematics of flight and the relationship to the vortex wake of a Pallas’ long tongued bat (Glossophaga soricina). J. Exp. Biol. 213, 2142–2153 (2010). [DOI] [PubMed] [Google Scholar]
- 13.Muijres F. T., Johansson L. C., Winter Y., Hedenström A., Leading edge vortices in lesser long-nosed bats occurring at slow but not fast flight speeds. Bioinspir. Biomim. 9, 025006 (2014). [DOI] [PubMed] [Google Scholar]
- 14.Lentink D., Haselsteiner A. F., Ingersoll R., In vivo recording of aerodynamic force with an aerodynamic force platform: From drones to birds. J. R. Soc. Interface 12, 20141283 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chin D. D., Lentink D., How birds direct impulse to minimize the energetic cost of foraging flight. Sci. Adv. 3, e1603041 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Muijres F. T., Johansson L. C., Bowlin M. S., Winter Y., Hedenström A., Comparing aerodynamic efficiency in birds and bats suggests better flight performance in birds. PLOS ONE 7, e37335 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.F. Reid, A Field Guide to the Mammals of Central America and Southeast Mexico (Oxford Univ. Press, 1997). [Google Scholar]
- 18.McGuire J. A., Witt C. C., Remsen J. V. Jr, Corl A., Rabosky D. L., Altshuler D. L., Dudley R., Molecular phylogenetics and the diversification of hummingbirds. Curr. Biol. 24, 910–916 (2014). [DOI] [PubMed] [Google Scholar]
- 19.R. Garrigues, R. Dean, The Birds of Costa Rica (Comstock Publishing Associates, 2007). [Google Scholar]
- 20.Mendenhall C. D., Karp D. S., Meyer C. F. J., Hadly E. A., Daily G. C., Predicting biodiversity change and averting collapse in agricultural landscapes. Nature 509, 213–217 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Frank H. K., Frishkoff L. O., Mendenhall C. D., Daily G. C., Hadly E. A., Phylogeny, traits, and biodiversity of a neotropical bat assemblage: Close relatives show similar responses to local deforestation. Am. Nat. 190, 200–212 (2017). [DOI] [PubMed] [Google Scholar]
- 22.Hedrick T. L., Software techniques for two- and three-dimensional kinematic measurements of biological and biomimetic systems. Bioinspir. Biomim. 3, 034001 (2008). [DOI] [PubMed] [Google Scholar]
- 23.Snow B. K., Snow D. W., Feeding niches of hummingbirds in a Trinidad valley. J. Anim. Ecol. 41, 471–485 (1972). [Google Scholar]
- 24.Sapir N., Dudley R., Implications of floral orientation for flight kinematics and metabolic expenditure of hover-feeding hummingbirds. Funct. Ecol. 27, 227–235 (2013). [Google Scholar]
- 25.Kruyt J. W., Quicazán-Rubio E. M., van Heijst G. F., Altshuler D. L., Lentink D., Hummingbird wing efficacy depends on aspect ratio and compares with helicopter rotors. J. R. Soc. Interface 11, 20140585 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Norberg U. M., Aerodynamics of hovering flight in the long-eared bat Plecotus auritus. J. Exp. Biol. 65, 459–470 (1976). [DOI] [PubMed] [Google Scholar]
- 27.Deetjen M. E., Biewener A. A., Lentink D., High-speed surface reconstruction of a flying bird using structured light. J. Exp. Biol. 220, 1956–1961 (2017). [DOI] [PubMed] [Google Scholar]
- 28.Hedenström A., Johansson L. C., Bat flight: Aerodynamics, kinematics and flight morphology. J. Exp. Biol. 218, 653–663 (2015). [DOI] [PubMed] [Google Scholar]
- 29.G. J. Leishman, Principles of Helicopter Aerodynamics (Cambridge Univ. Press, 2006). [Google Scholar]
- 30.R. J. Baker, O. R. P. Bininda-Emonds, H. Mantilla-Meluk, C. A. Porter, R. A. Van Den Bussche, Molecular time scale of diversification of feeding strategy and morphology in New world leaf-nosed bats (Phyllostomidae): A phylogenetic perspective, in Evolutionary History of Bats: Fossils, Molecules and Morphology, G. F. Gunnel, N. B. Simmons, Eds. (Cambridge Univ. Press, 2012), pp. 385–409. [Google Scholar]
- 31.A. A. Panyutina, L. P. Korzun, A. N. Kuznetsov, Flight of Mammals: From Terrestrial Limbs to Wings (Springer, 2015). [Google Scholar]
- 32.Wester P., Feeding on the wing: Hovering in nectar-drinking Old World birds—More common than expected. Emu - Austral Ornithology 114, 171–183 (2014). [Google Scholar]
- 33.M. Keennon, K. Klingebiel, H. Won, A. Andriukov, Development of the nano hummingbird: A tailless flapping wing micro air vehicle, in 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, Tennessee, 9 to 12 January 2012. [Google Scholar]
- 34.Ramezani A., Chung S.-J., Hutchinson S., A biomimetic robotic platform to study flight specializations of bats. Sci. Robot. 2, eaal2505 (2017). [DOI] [PubMed] [Google Scholar]
- 35.Hightower B. J., Ingersoll R., Chin D. D., Lawhon C., Haselsteiner A. F., Lentink D., Design and analysis of aerodynamic force platforms for free flight studies. Bioinspir. Biomim. 12, 064001 (2017). [DOI] [PubMed] [Google Scholar]
- 36.Lentink D., Accurate fluid force measurement based on control surface integration. Exp. Fluids 59, 22 (2018). [Google Scholar]
- 37.S. M. Swartz, J. Iriarte-Diaz, D. K. Riskin, A. Song, X. D. Tian, K. Breuer, Wing structure and the aerodynamic basis of flight in bats, in 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 8 to 11 January, 2007. [Google Scholar]
- 38.Eilers P. H., A perfect smoother. Anal. Chem. 75, 3631–3636 (2003). [DOI] [PubMed] [Google Scholar]
- 39.M. J. Lighthill, Introduction to the scaling of aerial locomotion, in Scale Effects in Animal Locomotion, T. J. Pedley, Ed. (Academic Press, 1977), pp. 365–404. [Google Scholar]
- 40.Ellington C. P., The aerodynamics of hovering insect flight. VI. Lift and power requirements. Philos. Trans. R. Soc. Lond. B Biol. Sci. 305, 145–181 (1984). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/9/eaat2980/DC1
Fig. S1. Bats hover at two times higher Reynolds numbers than hummingbirds.
Fig. S2. Phylogenetic tree of the hummingbirds and bats in the study.
Fig. S3. Beyond the radial angle-of-attack distribution, kinematic parameters do not vary much across bat species.
Fig. S4. Hummingbirds generate substantially more vertical force during the upstroke than bats, and the nectar bats outperform the fruit bat.
Fig. S5. Morphological and kinematic parameters of the sampled species.
Fig. S6. Definition of the wing tip speed range associated with high lift production during the downstroke and upstroke.
Fig. S7. Aerodynamic force platform verification.
Table S1. Overview of wingbeats analyzed for force processing.
Movie S1. Force measurements and wingbeat segmentation.
Movie S2. Wing tracking and kinematic parameters.


