The same but different: cell intercalation as a driver of tissue deformation and fluidity

Abstract

The ability of cells to exchange neighbours, termed intercalation, is a key feature of epithelial tissues. Intercalation is predominantly associated with tissue deformations that drive morphogenesis. More recently, however, intercalation that is not associated with large-scale tissue deformations has been described both during animal development and in mature epithelial tissues. This latter form of intercalation appears to contribute to an emerging phenomenon that we refer to as tissue fluidity—the ability of cells to exchange neighbours without changing the overall dimensions of the tissue. Here, we discuss the contribution of junctional dynamics to intercalation governing both morphogenesis and tissue fluidity. In particular, we focus on the relative roles of junctional contractility and cell–cell adhesion as the driving forces behind intercalation. These two contributors to junctional mechanics can be used to simulate cellular intercalation in mechanical computational models, to test how junctional cell behaviours might regulate tissue fluidity and contribute to the maintenance of tissue integrity and the onset of disease.

This article is part of the Theo Murphy meeting issue ‘Mechanics of development’.

1. Planar cell intercalation and the role of cell–cell junctions

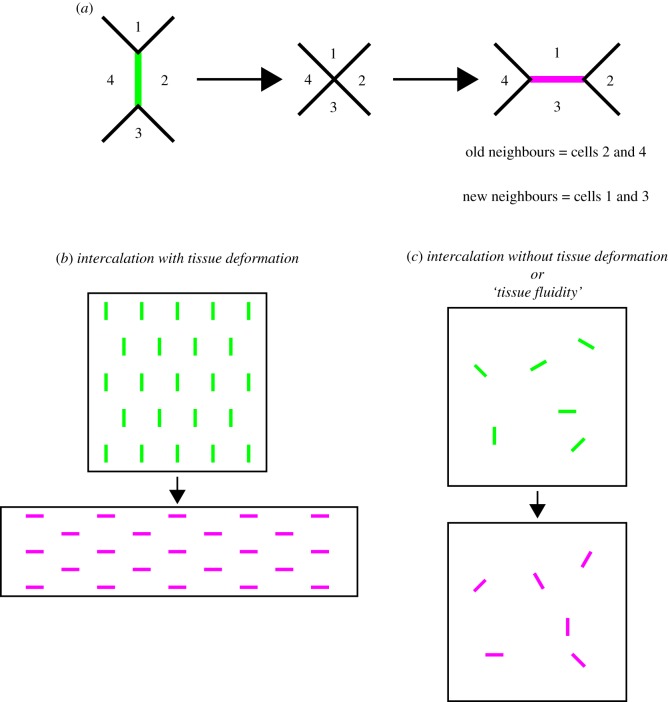
Cell intercalation (here referred to purely as intercalation) is the process through which cells within an epithelium exchange neighbours (figure 1a). While intercalation can occur perpendicular to the plane of an epithelium (termed radial intercalation), for instance when producing a stratified epithelium from a monolayered precursor, this review will focus exclusively on planar intercalation. Furthermore, although there are multiple mechanisms through which intercalation can occur (cell protrusive activity [1,2], tissue stress [3–5]), we will focus on intercalation that is mediated by the dynamics of intercellular junctions. Specifically, we will discuss the contribution of adhesion at adherens junctions and contractility to intercalation. Adherens junctions are the predominant sites of intercellular adhesion (mainly through cadherin homophilic adhesion molecules) and are coupled to the contractile cortical actomyosin cytoskeleton [6]. Therefore, adherens junctions represent a region within the cell that both generates and integrates mechanical forces across cells and tissues [7].

Figure 1.

Cell intercalation is associated both with tissue deformation and with tissues having static boundaries. (a) During an intercalation event, a junction shared between two cells (green) shrinks to a single point creating a four-way vertex. This vertex then resolves in the orthogonal direction as a new junction (magenta) grows. This results in an exchange of neighbours. In a tissue, there are often multiple intercalation events associated with either (b) tissue deformation or (c) no tissue deformation (old shrinking and new growing junctions are coloured as in (a)). We refer to the latter example (c) as ‘tissue fluidity’.

An emerging picture is that cell intercalation can act in two ways in a tissue. The first is to deform a tissue, resulting in morphogenesis, which involves a change in the dimensions of the tissue (figure 1b). The second is to allow cells to exchange neighbours without a change in the size or shape of the tissue (figure 1c). In such a situation, cell intercalations are analogous to the rearrangement of molecules in a fluid in a container that does not change its dimensions. We therefore refer to this as ‘tissue fluidity’. A common feature of these examples is that intercalation behaviours can be explained at the level of cell–cell junctions. In this review, we aim to discuss how intercalation is regulated to achieve these two functions and how computational modelling approaches can be used to understand the mechanical basis of intercalation at the level of cell–cell junctions.

2. Intercalation can deform developing tissues

A conserved element of animal development is the extension of a tissue in one axis, concomitant with a narrowing of the tissue in the orthogonal axis. This process is termed convergent extension (or convergence and extension) and is driven by polarized intercalation in many examples. The contribution of intercalation to convergent extension can be clearly illustrated by two developmental morphogenetic processes—axis extension and tubule elongation.

(a). Axis extension

Perhaps, the most striking example of convergent extension in animal development is the extension of the embryonic body axis (figure 2a). Classically, embryos will extend along their anteroposterior (AP) axis and converge along the orthogonal axis (referred to as dorsoventral (DV) or mediolateral depending on the system).

Figure 2.

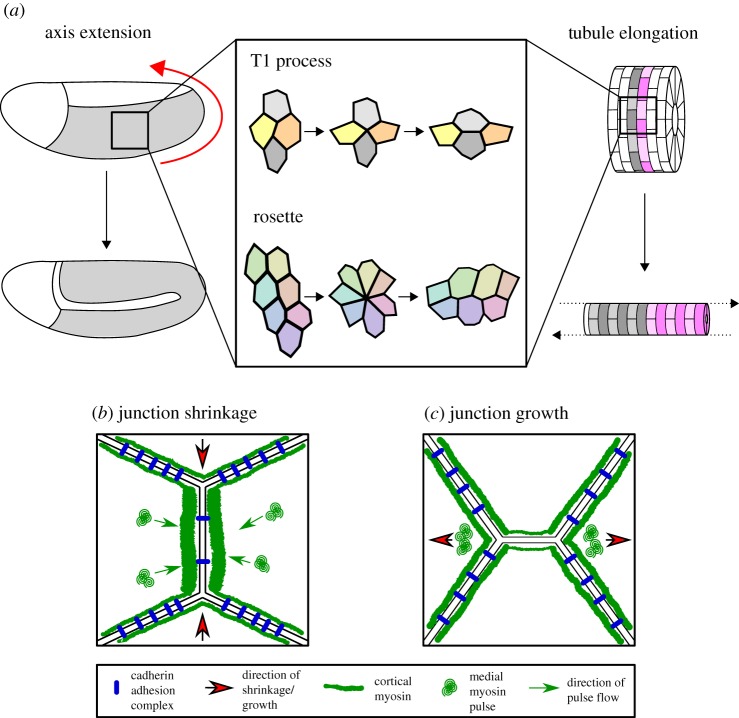
Polarized intercalation deforms tissues during morphogenesis. (a) Morphogenesis, particularly examples of convergent extension such as axis extension (here shown Drosophila GBE, germband in grey, direction of elongation shown by red arrow) and tubule elongation, is often driven by polarized cell intercalation. Intercalation can take the form of either a T1 process in a tetrad of cells or the formation and resolution of a multicellular rosette. In Drosophila, junction shrinkage (b) is driven by planar polarized distributions of myosin II and cadherin adhesion complexes. Cortical junctional myosin is enriched at DV-oriented shrinking junctions, while cadherin adhesion complexes are enriched at stable AP-oriented junctions. Junction shrinkage is further driven by pulsatile flows of medial myosin, which flow into shrinking junctions. To achieve new junction growth (c), junctional myosin II activity must be reduced in the growing junction. Junctions then grow owing to cell non-autonomous forces generated by medial myosin pulses in adjacent cells, close to the ends of the new junction.

Arguably, the most thoroughly studied example of axis extension is in the embryonic germband in Drosophila (germband extension, GBE). As intercalation is a dynamic process, it is best studied through live imaging and the simple epithelium of the germband in Drosophila embryos is particularly well suited to this technique. It is likely that this is the reason that the majority of our understanding of intercalation comes from work in Drosophila, as is reflected in this review. During GBE, the germband extends roughly twofold along its AP axis, while narrowing by the same magnitude along its DV axis (figure 2a). This process is characterized by many polarized intercalation events [8], in which DV-oriented cell–cell junctions preferentially shrink and a new junction grows along the AP axis [9].

GBE intercalation can take two forms. The first involves a tetrad of cells and is often described as a ‘T1 process’ using terminology from dynamics within foams [10]. A DV junction shared between two neighbouring cells (much like a wall shared between two bubbles within a soap foam) initially shrinks to a single point, producing a four-way junction in which all four cells of the tetrad come into contact (figure 2a). Subsequently, a new junction grows along the AP axis, resulting in an exchange of neighbours within the tetrad [9]. The T1 mode of intercalation predominates early during GBE, but later a second form of intercalation is initiated. This involves the shrinkage of multiple connected DV-oriented junctions shared by more than four cells, which ultimately produces a multicellular structure known as a rosette [11]. This rosette is then resolved along the AP axis, again resulting in exchanges of neighbours (figure 2a).

GBE intercalation has a mechanical basis, as it relies on the combined activity of the contractile actomyosin cytoskeleton and intercellular adhesion. Cell surface mechanics predicts that a contractile junction will shrink, while an adhesive junction will be prone to grow [12]. Indeed, there is a striking polarization of both actin and myosin II in the germband, which are both preferentially enriched at shrinking DV-oriented junctions in both T1s [9,13] and the multi-cellular cables generating rosettes [11,14]. Myosin II activity is required for both active intercalation and axis extension [9]. Moreover, myosin II and its activity must be planar polarized, otherwise again both intercalation and axis extension fail [11,13,15,16]. Furthermore, components of cell–cell adhesion complexes such as E-cadherin (E-cad) and β-catenin are polarized in the opposite orientation [11]. Interestingly, planar polarized endocytosis of E-cad is required to downregulate adhesion at DV-oriented junctions [17]. When endocytosis is blocked, intercalation fails almost entirely, leading to a drastic reduction in GBE. Therefore, increased contractility and decreased adhesion act in concert to permit junction shrinkage (figure 2b).

Polarized junctional myosin not only promotes junction shrinkage during Drosophila GBE, but also drives intercalation in chordate systems undergoing axis extension. During convergent extension of the chordate notochord, cells intercalate mediolaterally [18–20]. This process is most often described as being driven by polarized protrusive activity and directed cell crawling [1,2]. However, more recently, a role for polarized junction dynamics has emerged in Xenopus. Phosphorylated myosin localizes strongly to mediolaterally oriented junctions in the notochord, which are also under increased tension, suggesting an additional role for junction shrinkage in notochord convergent extension [21].

In chick embryos, myosin cables form perpendicular to the direction of primitive streak formation and drive polarized junctional shrinkage [22]. Similarly, mediolaterally oriented actomyosin cables form in the neural plate of chick embryos. These are required for shrinkage of mediolateral junctions, leading to the convergent extension of the neural tube [23]. Relatively, little is understood about the contribution of junctional adhesion to axis extension in vertebrate systems. There is some evidence that cadherins play a role in Xenopus axis extension [24,25]; however, it will be interesting to see whether reciprocal roles of contractility and adhesion are conserved.

Although myosin is strongly polarized at the level of cell–cell junctions, during GBE a second pool of myosin also has a role in generating the forces required for DV junction shrinkage. Myosin also localizes in a medial pool, in the centre of cells, away from junctions. During GBE, the medial pool of myosin coalesces into ‘pulses’ that appear to flow into DV-oriented junctions (figure 2b) and these flows are temporally correlated with a reduction in junction length [26]. Interestingly, it appears that these pulses are required to shorten the junctions, while the pool of myosin tightly associated with the junctions stabilizes this length reduction [26], apparently through scission of Rab35 compartments and membrane removal [27]. The flows are dependent on planar polarized distributions of E-cad [26], which display transient asymmetries (due to E-cad endocytosis) that permit the flow of myosin towards regions of strongest anchoring of the actomyosin meshwork where E-cad concentration is highest [28].

Historically, the GBE field has been dominated by work focusing on apical cell behaviours. However, cells are polarized along their apicobasal axes and, more recently, a role for basal cell behaviours in GBE intercalation has emerged. In the majority of cases, rosettes resolve basally first, suggesting basal dynamics are the main driving force of intercalation. Basal cell protrusions are observed during GBE, and when they are abolished many rosettes fail to resolve and GBE is reduced [29]. However, when either basal protrusions or myosin activity throughout the cell are abolished, a subset of rosettes still resolve apically and basally [29], suggesting mechanical cooperativity between apical and basal sides of the same cell.

So far, we have focused on the early stages of intercalation, when junctions decrease in length to produce vertices shared by more than three cells. For cells to acquire new neighbours, however, this multicellular vertex must be resolved to produce two or more tricellular junctions (figure 2a). This is achieved by the formation of a new cell–cell junction, a process that, like junction shrinkage, is dependent on actomyosin contractility. Unlike junction shrinkage, new junction growth is a cell non-autonomous process driven by myosin activity in the cells that were previously neighbours [30,31] (figure 2c). Pulses of actomyosin, much like those contributing to junction shrinkage, form at regions within these cells close to the newly formed tricellular junctions [32] and this is coupled with transient contractions of apical cell area [30]. The activity of myosin causes these cells to exert a local pulling force on the new junction, which in turn is thought to promote junction elongation, initially independently of E-cad in the growing junctions [32]. Local cell non-autonomous forces are also required for junction elongation in the Drosophila amnioserosa [33], suggesting that this may be a general mechanism of junction growth. In the germband, an additional tissue scale pulling force from the invagination of the posterior midgut [32,34] aligns new junction growth along the AP axis [32].

For intercalation to be successful, there must therefore be tight spatiotemporal regulation of junction shrinkage and new junction growth. If there is no temporal separation between the two processes, they will antagonize each other (as a junction cannot both grow and shrink at the same time), resulting in a failure of cell intercalation. Evidence that this is true comes from work performed in the pupal wing of Drosophila. The pupal wing displays significant intercalation when undergoing morphogenesis to produce the shape of the adult wing blade [3,35]. Timely removal of myosin II (and its activator Rho kinase (Rok)) from new junctions is crucial to allow multicellular vertices to resolve and for these new junctions to grow [31]. Myosin II removal from new junctions in the pupal wing is controlled by phosphatase and tensin homologue, which drives the conversion of PIP3–PIP2 [36]. When this pathway is disrupted, myosin II remains concentrated in the new junctions and cells fluctuate back and forth through four-way vertices. Therefore, it appears that dissipation of tension in growing junctions is required for their growth (figure 2c), which was supported by computational modelling of pupal wings [31]. The same is likely to be true during GBE, as when a constitutively active, phosphomimetic form of myosin regulatory light chain (MRLC) is expressed in place of wild-type MRLC, there is an increase in the number of junctions that fail to resolve correctly [16].

(b). Tubule elongation

While axis extension is a key process driven by convergent extension, there are other developmental processes that require the simultaneous elongation and narrowing of a tissue. Tubule elongation is one such example where intercalation can contribute to organogenesis.

Tubule elongation can involve oriented growth and cell shape changes among other mechanisms; however, often the process instead relies on the rearrangement of cells [37]. Again, much work has been performed on the role of intercalations in tubule elongation in Drosophila embryos, particularly in the Malpighian tubules (which form the fly's renal system) and tracheal network (which is the site of gaseous exchange). The Malpighian tubule lumen is initially lined by up to 12 cells when viewed in cross-section [38]. However, at later stages of development, only two cells contact the lumen in cross-section, which is achieved by cells intercalating between each other in the circumferential axis (figure 2a). This reduction in luminal cell number is associated with a vast proximodistal elongation and concomitant circumferential convergence. Circumferential intercalation in the tubule is, as in Drosophila GBE, driven by polarized pulses of myosin II. However, unlike during GBE, these pulses are localized to the basal surface of the tubule cells [38]. Intercalation in the Malpighian tubules is therefore cell autonomous, as evidenced by intercalation and extension of Malpighian tubules cultured externally to the embryo [39]. This is in contrast with intercalation in the tracheal network, which is a cell non-autonomous process [40]. In the developing dorsal branches of the tracheal network, the distal-most cells (known as tip cells) mechanically pull on the tubules to generate a proximodistally oriented force. Intercalation in the tracheal branches can be entirely suppressed by ablation of the leading tip cell.

Interestingly, intercalation in the trachea still relies on junction dynamics to some extent, but in terms of adhesion [41] rather than actomyosin-based contractility [42]. Intercalation can be suppressed genetically in the trachea [43] and this appears to be due to a reduction in E-cad turnover. It is thought that this may render junctions fixed in one conformation, unable to remodel to allow intercalation to proceed [41]. Despite a lack of intercalation in this situation, trachea are still able to elongate to a large extent [40]. Therefore, elongation drives intercalation, rather than the reverse being true as in GBE.

Cell intercalation in tubule elongation is not a peculiarity of Drosophila, as similar observations have been made during vertebrate tubulogenesis. In the developing renal tube of Xenopus, rosette-based intercalations are prevalent and associated with tubule elongation [44]. Furthermore, both elongation and rosette formation are dependent on polarized distributions of myosin II, arguing that cell rearrangements are vital for elongation. Multicellular rosettes can also be found in developing mouse kidney collecting ducts [44] and cochlea [45], suggesting that this mechanism of tubule elongation may be conserved throughout vertebrates.

3. Intercalation without tissue-level deformation

It is clear from the examples above that cell intercalation has the capacity to drive tissue morphogenesis. More recently, however, evidence has emerged that intercalation can equally be associated with tissues that are comparably static in nature. In these examples, although cells exchange neighbours, the overall boundaries, and therefore the shape of the tissue, remain unchanged. As we described earlier, we term this phenomenon ‘tissue fluidity’.

(a). Non-morphogenetic intercalation in the Drosophila notum

The pupal notum of Drosophila is an example of a tissue undergoing intercalation events that do not contribute to tissue deformation (figure 3). In this tissue, although intercalations are frequent, the tissue itself does not undergo any overall deformation [46]. In other words, its overall boundary conditions do not change significantly. Instead of highly deterministic changes in junction length, intercalations appear to occur as a consequence of stochastic fluctuations in junction length. Long junctions can shrink and grow without inducing an intercalation event. However, when a short junction shrinks completely, the resulting four-way vertex can sometimes resolve in the orthogonal direction, leading to an exchange of neighbours. The non-deterministic nature of these intercalations is particularly highlighted by a subset of intercalations that only result in a transient neighbour exchange, something that appears to be shared by the larval wing imaginal disc of Drosophila [47].

Figure 3.

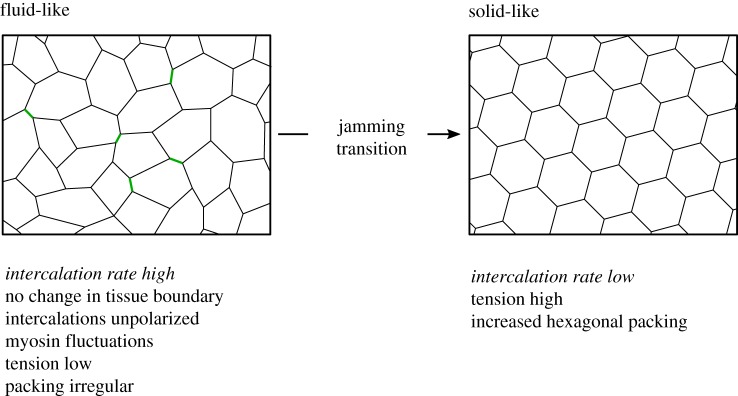
Regulation of tissue fluidity in the Drosophila notum. A summary of experimental observations relating to the regulated tissue fluidity of the Drosophila notum (see text below schematics). This tissue can undergo a jamming transition from a fluid-like regime characterized by many intercalation events (left, shrinking junctions shown in green) and irregular packing to a solid-like regime with little intercalation and more regular hexagonal packing (right).

The non-deterministic nature of intercalations not only applies to the length of junction changes, but also to the orientation of these changes. Surprisingly, given what is known about intercalation in the systems described above, notum intercalations are not polarized and are not driven by highly polarized distributions of actomyosin. Instead, these intercalations occur because of stochastic variations in junctional myosin levels, which occur in random orientations. The importance of fluctuations in myosin has been demonstrated through computational modelling [46] (see section below).

As well as being controlled by local stochastic fluctuations in myosin concentration, the rate of intercalation in the notum is controlled by the global average level of junctional tension [46]. Early in notum development, myosin concentration and junctional tension are low, which is associated with a high intercalation rate. Later in development, the concentration of myosin and junctional tension are much higher and this correlates with a reduction in the rate of intercalation. The notion that myosin contractility might in fact be inhibitory to cell intercalation in the notum was confirmed by genetically perturbing myosin activity throughout the notum. Hyperactivation of myosin led to a decrease in intercalation, while inactivation of myosin increased the rate of intercalation (figure 3). The increase in junctional tension over time, and the corresponding decrease in intercalation rate, are associated with a gradual improvement in cell packing [46]. As tension gradually increases, so too does the proportion of hexagonal cells (also verified by computation modelling, see later), suggesting that the regulation of tissue fluidity in the notum has a role in tissue patterning.

The role of myosin II in intercalation in Drosophila therefore appears to be highly context-dependent. In polarized systems such as the germband and Malpighian tubule, myosin II directs the selective shortening of junctions along a single axis. In an unpolarized system, global tissue properties dominate; however, this must be coupled with fluctuations in myosin activity.

The gradual decrease in tissue fluidity in the notum is reminiscent of an epithelial fluid-to-solid jamming transition [48,49]. Jamming terminology is derived from the physics of particulate matter where a fluid-to-solid jamming transition occurs when particles can no longer move past each other owing to increased density [50]. In a cell layer, a fluid-to-solid jamming transition occurs when cells can no longer exchange neighbours through intercalation. The latter is distinct from jamming in particulate matter, as it is independent of the density of cells [48]. The theory that explains unjamming, which sheds light on tissue fluidity in certain contexts, will be explored in the following sections.

(b). Tissue fluidity and disease

Epithelial jamming transition has recently been implicated in disease, specifically asthma. Cultured monolayers of differentiated human bronchial epithelial cells (HBECs) undergo a transition from a solid-like jammed phase to a fluid-like unjammed phase when subjected to an apicobasal compression of a magnitude that mimics that encountered during asthmatic bronchospasm [49]. Furthermore, during HBEC layer maturation after reaching confluency, a fluid-to-solid jamming transition is observed. Cell fluidity is high on early culture days but decreases with age of the culture, until the cell monolayer is almost completely static. This may be a general property of maturing epithelial cell layers, as recently the same has been observed in epidermal progenitor cell monolayers [51]. It is unclear what drives this jamming transition during maturation at the cellular level; however, it is likely to be related to cell–cell adhesion and cortical contractility (and this will be explored in the following section).

Intriguingly, the fluid-to-solid jamming transition is delayed in monolayers of HBECs derived from asthmatic donors. What the functional significance of this is remains to be seen; however, it suggests that hyperfluidity of epithelial layers might contribute to pathogenesis. Furthermore, it remains to be tested whether HBEC layers derived from asthmatic patients respond in the same way to compression.

Like in the Drosophila notum, the induced fluidity does not contribute to changes in the dimension of the cell layer. For HBEC layers, the confines of the culture dish provide a clear physical boundary to the cell layer that cannot be deformed. This then raises the question of whether static boundaries (meaning the tissue does not change size or shape) contribute to fluidity or whether the stochastic nature of intercalations maintains the boundary's dimensions. This is challenging to test, as by removing a boundary one creates a free edge in the cell layer which is likely to induce effects independent of intercalation, such as an increase in boundary contractility [52]. One possible method that could be used to explore this question is computational modelling, which will be discussed in the following section.

This potential contribution of unregulated tissue fluidity to disease is, to our knowledge, a first. With the advent of more physiological culturing systems such as lung-on-a-chip [53] and organoid technology [54], both amenable to live cell imaging, it will be fascinating to see if tissue fluidity might relate to underlying causes of other epithelial diseases.

(c). Why do tissues regulate their fluidity?

In the Drosophila notum, it appears that the regulation of tissue fluidity is connected to the preservation of cell shape, patterning and packing. As junctional tension increases through development, the notum becomes increasingly hexagonally packed (figure 3) [46]. Another striking example of tissue fluidity is that of the chick epiblast [55]. During gastrulation, many intercalation events occur, which are associated with cell divisions. Epiblast fluidity shares parallels with the Drosophila notum, as reduced cortical tension facilitates cell division-mediated intercalation [55]. Fluidity in the epiblast appears to have a clear role in patterning gastrulation movements, possibly by relaxing forces generated by cell behaviours in the neighbouring primitive streak. When fluidity is inhibited by blocking cell division (and subsequently the majority of intercalations), the characteristic ‘Polonaise movements’ of chick gastrulation are strongly disrupted [55]. However, why the bronchial airway epithelium should undergo an unjamming transition in response to compression remains unclear. Future work investigating the fluidity of other tissues in contexts such as development and tissue homeostasis will hopefully begin to shed more light on the function of tissue fluidity. On the other hand, the regulation of tissue fluidity during cell layer maturation raises the intriguing possibility that the ability of a mature tissue to be fluid under certain conditions might be linked to tissue robustness. A specific example is after tissue wounding. Tissues may need to fluidize after injury, explore new configurations, then resettle into a new solid-like state.

When an epithelial tissue is wounded, a gap is created that the existing cells need to fill. One possible way cells could ‘flow’ into this gap is to rearrange relative to each other in a directional manner, similar to intercalation during convergent extension. Such an observation has been made in the Drosophila embryonic ectoderm. Here, the strategy for intercalation during GBE appears to be ‘redeployed’ to allow these epithelial wounds to close [56]. Cells a few rows from an ectodermal wound edge undergo intercalation events driven by pulsatile flows of myosin that are qualitatively identical to those seen during GBE. The role of these intercalations appears to be to allow the wound edge to move forwards, as when intercalation is inhibited by reducing myosin activity, wound healing is slower [56]. Strictly speaking, while these wounds are healing and cells are intercalating, the outer boundaries of the ectoderm do not change. Therefore, this represents an example where tissue fluidity is driven by polarized localizations of myosin. Interestingly, this is reminiscent of another situation where a polarized tissue is challenged by introducing new static boundaries in the germband [32]. With static boundaries, the tissue can no longer extend along the AP axis; however, the rate of cell intercalation is unchanged and cells readily exchange neighbours [32], meaning that the tissue has become fluid by the terms of our definition of tissue fluidity. Therefore, it appears that the presence of unchanging tissue boundaries can induce tissue fluidity even in situations where intercalation is polarized.

It will be interesting to see whether actively driven polarized intercalation events, when combined with fixed tissue boundaries, have a role in driving fluidity in other contexts. In particular, it remains to be seen whether polarized intercalation is used to induce fluidity during wound closure in more mature epithelia (and not just embryos), or whether stochastic junctional fluctuation-induced tissue fluidity might have a role. Certainly, there are other indications that tissue fluidity might contribute to wound closure. Maturation of a cultured cell monolayer shares parallels with wound closure, in that a functional barrier needs to be formed during the process. It is fascinating that asthmatic patients have impaired wound healing in the lung [57] and that asthmatic HBEC monolayers are fluid for longer during maturation [49]. One might hypothesize that if an unjamming or jamming transition is delayed, this might be connected to failures in wound healing. However, this remains to be tested.

Adhesions also play a role in wound closure. Eph–ephrin signalling is upregulated in wounded mouse and human skin, and this is required to downregulate cell–cell adhesion at tight junctions and adherens junctions [58]. In keratinocyte culture scratch wound assays, removal of Eph–ephrin signalling reduces the ability of cells to move into the wound, although it is unclear whether this is due to increased migration or through increased intercalation. However, increased Eph–ephrin signalling appears to downregulate tension in cells surrounding the wound by dissolving actomyosin stress fibres [58], which is consistent with the notion that decreased epithelial tension is associated with increased tissue fluidity. On the other hand, hyperactivation of Eph–ephrin signalling in wounded skin appears to lead to defective healing as a result of an almost total loss of adhesion between cells [58]. This highlights that a delicate balance between cell cohesiveness and fluidity is probably key for intercalation-mediated events, both in development and disease.

4. Understanding intercalation using vertex-based models

Above, we have described examples of experimental work that has furthered our understanding of intercalation in many contexts. However, dissecting the relative roles of tissue mechanics and biochemical signalling experimentally remains challenging. For this reason, the field is increasingly turning to computational models to understand how intercalation contributes to morphogenesis and how the mechanical properties of a tissue can contribute to fluidity.

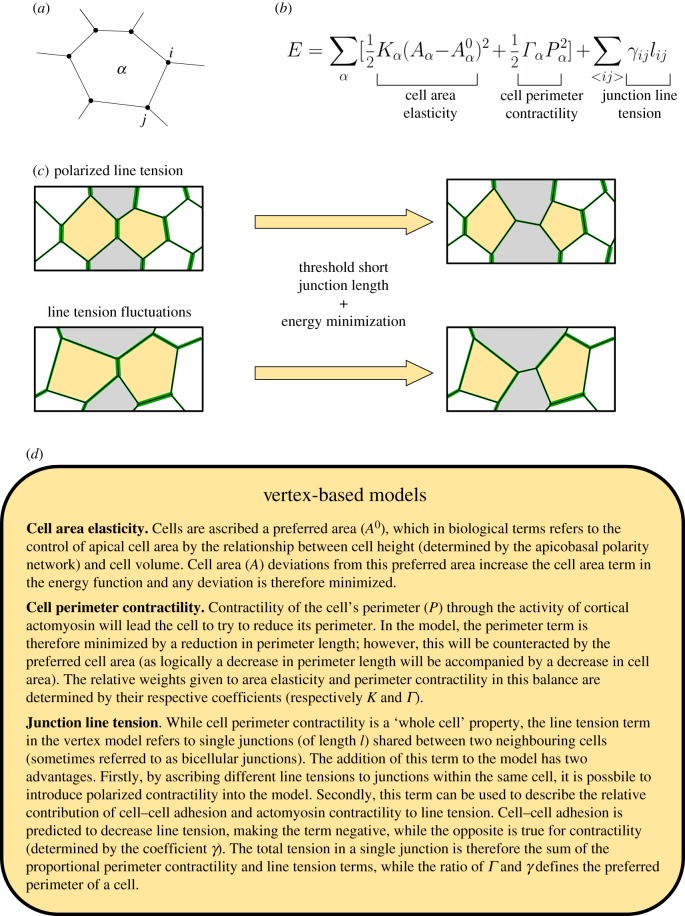
While a number of models exist (for instance, the cellular Potts [59], ‘cell-centre’ [60] and ‘finite-element’ [61] models), vertex-based models have arguably increased our understanding of intercalation the most. Vertex models [62] describe a layer of epithelial cells as a network of vertices (which represent tricellular junctions and vertices at the centre of higher-order structures, such as rosettes) connected by junctions (representing bicellular junctions) (figure 4a). Vertex modelling of an epithelium relies on the relationship between three key properties of cells that determine the movement of vertices: cell area elasticity, cell perimeter contractility and the line tension of individual junctions (described in detail in figure 4d). In combination, these define an energy function that the model aims to minimize (figure 4b) [62].

Figure 4.

Vertex modelling of intercalation. (a) Schematic representation of vertex model cells (α) and junctions (ij). (b) Vertex model behaviours are determined by an energy function comprising three key terms: cell area elasticity, cell perimeter contractility and junction line tension. (c) Implementation of intercalation in vertex models. Intercalation can arise either by polarized line tension (top) or by fluctuations in line tension around a global mean (bottom). Line tension magnitudes are indicated by the thickness of green junctions. Old neighbours are in yellow, new neighbours in grey. Intercalations occur when junctions reach a threshold short length and the rearrangement induced by an intercalation reduces the total energy. (d) Summary of vertex model terms and parameters.

Vertex modelling has been used to understand how intercalation contributes to convergent extension during GBE in more detail. Key to modelling GBE is to use the line tension term to introduce polarity into the simulated system. In such models, intercalation events occur when junctions shorten to a threshold length and are then allowed to resolve orthogonally, provided this reduces the energy in the model [63–65] (figure 4c). Taking this approach, vertex modelling has demonstrated that intercalation driven by polarized junctional tension can explain the convergent extension of two-dimensional fields of cells [63], three-dimensional aggregates and tubes [65]. Interestingly, modelling suggests that polarized junction contraction only allows tissues to extend up to roughly 2.5 times their original length [65]. This may indicate that there is an inherent property of the germband that prevents it from attempting to extend continuously.

A further vertex model of GBE was used to investigate the interaction between patterning of the germband and intercalation [64]. The germband is patterned along its AP axis by a hierarchical cascade of spatially restricted genes into discrete domains [66]. These ‘AP patterning genes’ are required to polarize myosin activity to DV-oriented junctions [8,13] at the boundaries of domains through local cell–cell interactions [64] mediated by Toll receptors [67]. In the model, line tension was increased at boundaries between spatial domains, to mimic myosin polarization. Myosin concentration increases at junctions as they shrink during GBE; therefore, length dependency was introduced to the line tension term in the model. This model demonstrated that myosin polarity, like those above, could drive convergent extension of the germband. However, it also predicted that restricting myosin contractility to junctions between AP spatial domains was sufficient to maintain the order of these predefined AP domains along the body axis [64].

The above examples demonstrate that intercalation can be successfully modelled by introducing polarized contractility into vertex models to explain morphogenesis and the maintenance of tissue order. However, vertex models have hugely furthered our understanding of how tissue mechanics might contribute to tissue fluidity in the context of tissue unjamming. Again, fluidity through unjamming can be explained theoretically by the mechanical properties of cell–cell junctions. Vertex modelling has been particularly useful to explain the transition from a jammed, immobile epithelium to an unjammed, fluid epithelium.

In contrast with modelling polarized intercalation, when modelling intercalations associated with tissue unjamming, vertex model parameters do not vary across cells or between junctions. The relative contributions of perimeter contractility (determined by the sum of perimeter contractility and cell–cell junction line tension) and cell area interact to give cells a preferred cell shape. This can be described by a cell shape parameter (p₀) which is the ratio between the preferred perimeter and square root of the preferred area (p₀ = P/√A) [48]. Therefore, the energy function of the vertex model can be phrased in terms of how far a cell's shape deviates from its preferred shape. Inherently, cells must change shape to allow an exchange of neighbours. Thus, the magnitude of the energy cost of cell shape changes (specifically how easily a cell can deviate from its preferred shape) determines how easily cells can intercalate [49]. This energy barrier is determined by p₀ itself and, as p₀ increases, the energy barrier decreases. When p₀ reaches a threshold value of 3.81, the energy barrier to cell shape changes becomes vanishingly small [48], meaning that such a system can readily undergo intercalation and therefore is in a fluid regime. Accordingly, the shear modulus vanishes at this transitional p₀ value [48].

This apparent link between cell shape and fluidity has been probed using the HBEC monolayers described earlier. When p₀ in jammed and unjammed HBEC monolayers was quantified, it was on average closer to the theoretical threshold value of 3.81 in unjammed layers than jammed layers [49]. This therefore supports the notion that the increased ability of cells to change shape promotes tissue fluidity.

One failing of this model is that it does not describe a dynamic epithelium, but instead reaches steady state and infers fluidity from cell shape. Therefore, intercalation rate, per se, cannot be quantified from the model. Vertex modelling of the Drosophila notum introduced dynamics by having an additional term describing stochastic fluctuations in edge tension [46]. In this model, edge tension fluctuations are derived from spatiotemporal quantification of myosin intensity from live imaging. This approach was able to recapitulate the fluidity of the notum. Moreover, increasing the average magnitude of line tension in this model was sufficient to increase the proportion of hexagonal cells in simulations. This was also observed in the more mature notum and is a hallmark of a jammed epithelium undergoing fewer intercalations (figure 3) [46].

On the basis of data from the Drosophila notum vertex model, it is possible that non-deterministic fluctuations in cell edge tension (either through changes in contractility or adhesion) also contribute to the fluidity of HBEC monolayers in the same manner as the Drosophila notum. However, to confirm this, quantitative analysis of myosin and cell–cell adhesion must be performed in HBEC layers.

5. Conclusion

In this review, we have discussed the contribution of intercalation to morphogenesis and tissue fluidity. The key difference between these two functions appears to be associated with whether the tissue undergoes a deformation or not. Much is understood about the role of intercalation in morphogenesis and how it is driven by a combination of regulated cortical contractility and cell–cell adhesion. Comparatively little is known about intercalation in tissue fluidity. However, it appears that it can similarly be explained by the properties of cell–cell junctions. The regulation of tissue fluidity may have more far-reaching consequences, as it appears that the induction of a jammed state is important for both inducing cell differentiation and delamination from the embryonic mouse epidermis, to drive stratification [51]. It will be fascinating to understand in more detail how tissue fluidity contributes to development, homeostasis and disease.

Data accessibility

This article has no additional data.

Authors' contributions

R.J.T. and Y.M. conceived and wrote the article.

Competing interests

We have no competing interests.

Funding

R.J.T. is funded by a Medical Research Council Skills Development Fellowship (MR/N014529/1). Y.M. is funded by a Medical Research Council Fellowship MR/L009056/1, a UCL Excellence Fellowship and a NSFC International Young Scientist Fellowship 31650110472. This work was also supported by MRC funding to the MRC LMCB University Unit at UCL, award code MC_U12266B.