Tissue self-organization underlies morphogenesis of the notochord

Abstract

The notochord is a conserved axial structure that in vertebrates serves as a hydrostatic scaffold for embryonic axis elongation and, later on, for proper spine assembly. It consists of a core of large fluid-filled vacuolated cells surrounded by an epithelial sheath that is encased in extracellular matrix. During morphogenesis, the vacuolated cells inflate their vacuole and arrange in a stereotypical staircase pattern. We investigated the origin of this pattern and found that it can be achieved purely by simple physical principles. We are able to model the arrangement of vacuolated cells within the zebrafish notochord using a physical model composed of silicone tubes and water-absorbing polymer beads. The biological structure and the physical model can be accurately described by the theory developed for the packing of spheres and foams in cylinders. Our experiments with physical models and numerical simulations generated several predictions on key features of notochord organization that we documented and tested experimentally in zebrafish. Altogether, our data reveal that the organization of the vertebrate notochord is governed by the density of the osmotically swelling vacuolated cells and the aspect ratio of the notochord rod. We therefore conclude that self-organization underlies morphogenesis of the vertebrate notochord.

This article is part of the Theo Murphy meeting issue on ‘Mechanics of development’.

1. Introduction

In essence, all morphogenetic processes are the result of one or more self-organized events governed by physical principles. This is illustrated by the fact that a properly proportioned and physiologically active embryo, with all its organs, can be generated from an externally fertilized egg. Identifying the key features and understanding the underlying principles that guide specific morphogenetic processes constitutes one of the major challenges in biology. The discovery of oscillations in simple chemical systems and the formal description of reaction–diffusion processes paved the way for the understanding of the physical principles governing many sub-cellular processes (reviewed in [1]). The celebrated and highly influential theoretical work of Turing [2], who predicted the emergence of stable patterns via reaction–diffusion mechanisms, has been the conceptual basis of much of the work on biological modelling. This has been applied initially to describe signalling and patterning cues [3–5], and more recently to the emergence of tissue and organ level structures [6–8]. However, it is clear that other conceptual frameworks can also reach similar conclusions [9]. The main difficulties for modelling morphogenetic processes lie in the identification of the key components and the most relevant physical parameters. One successful approach to these problems has been to take the perspective of the engineer, using geometric [10] and continuum mechanical modelling [11], as well as macroscopic physical models [12]. These studies have inspired us to build a physical model to capture key elements controlling the organization of the zebrafish notochord.

The zebrafish notochord is a rod that spans most of the antero-posterior (AP) axis and serves as a hydrostatic scaffold for embryonic axis elongation and later on for spine assembly [13]. It is composed of a core of large vacuolated cells surrounded by an epithelial sheath that is encased in a thick extracellular matrix [14,15]. Both cell types differentiate from a common precursor via a Notch-dependent mechanism [16]. Each vacuolated cell nucleates a single fluid-filled vacuole, which is a lysosome-related organelle, that occupies most of the cellular volume [13]. As the vacuoles inflate by accumulating water, the vacuolated cells expand within the confinement created by the cylindrical notochord sheath, resulting in an expansion of the AP axis [13,17]. Loss of vacuolated cells or fragmentation of vacuoles leads to shortening of the AP axis and kinking of the spine [13]. The sheath also plays important structural roles [18–20] and forms a template for patterning the segmented vertebrae [21–23]. Sheath cells are also able to regenerate vacuolated cells following collapse or injury [24,25].

Once notochord morphogenesis is completed, the vacuolated cells are arranged in a stereotypical staircase pattern [15]. While such arrangement could result from interactions with other tissues such as the bilateral paraxial mesoderm, we reasoned that being surrounded by another cell layer and a thick matrix would make that scenario unlikely. Instead, we hypothesized that vacuolated cells are arranged via a self-organized process. Here, we identify key physical and geometric parameters to build a simple physical model whose main predictions we tested in vivo in zebrafish. Our results indicate that vacuolated cells are organized by simple packing rules that are governed by cell density and the aspect ratio of the notochord rod.

2. Material and methods

(a). Animals

Zebrafish: Danio rerio stocks were maintained at 28°C and bred as previously described [26]. Zebrafish stocks were healthy and of normal immune status, not involved in previous procedures, and were drug test naive. Male and female breeders from three to nine months of age were used to generate fish for all experiments. In total, zebrafish larvae from Ekkwill background at 1–8 days post-fertilization were used in this study. The Tg(rcn3:QF2)^pd1190 strain was generated for this study using a Tol2 construct [27] in which the rcn3 promoter [13] drives expression of QF2 [28]. Previously published strains were as follows: cavin1b^bns110 [24], Tg(col9a2:mcherry)^pd1150 [24], Tg(col8a1a:GFPCaaX)^pd1152 [24], Tg(rcn3:GFPrab32a)^pd1153 [24], Tg(QUAS:nlsVenus-V2a-notch1aICD)^pd1164 [21], Tg(QUAS:nVenus-V2a-SuHDN)^pd1165 [21].

Xenopus: Xenopus laevis tadpoles (stages 33–34) fixed in para-formaldehyde were kindly provided by the laboratory of Nanette Nascone-Yoder.

(b). Physical models

Silicone tube models were made with clear silicone tubing (OCSparts.com) and sodium polyacrylate gel beads (JBs) (Jelly BeadZ, jellybeads.com). The silicone tubes had a length of either 29 cm (figures 1 and 2) or 30.48 cm (figure 5) with an inner diameter of 12.7 mm, an outer diameter of 15.9 mm and a wall thickness of 3.2 mm. Circular tube models were made using clear polycarbonate tubing and elliptical tube models were made using clear vinyl tubing (OCSparts). Polypropylene tube caps, punctured to allow water flow, were placed on one end of the silicone tube and then sealed with parafilm. Dry JBs were placed inside empty and dry silicone tubes, which were then capped and sealed with parafilm. Tubes were then submerged in a distilled water bath and allowed to completely fill with water. Then, JBs were given at least 3.5 h to grow and distribute throughout the tube before being scored for patterns. For sectioning, silicone tubes were frozen and cut into cross sections using a hacksaw. Images of the tubes and the patterns generated were taken using a cell phone camera. Time-lapse videos of the JBs growing and arranging in the tubes were taken using a Go Pro HERO 3 camera.

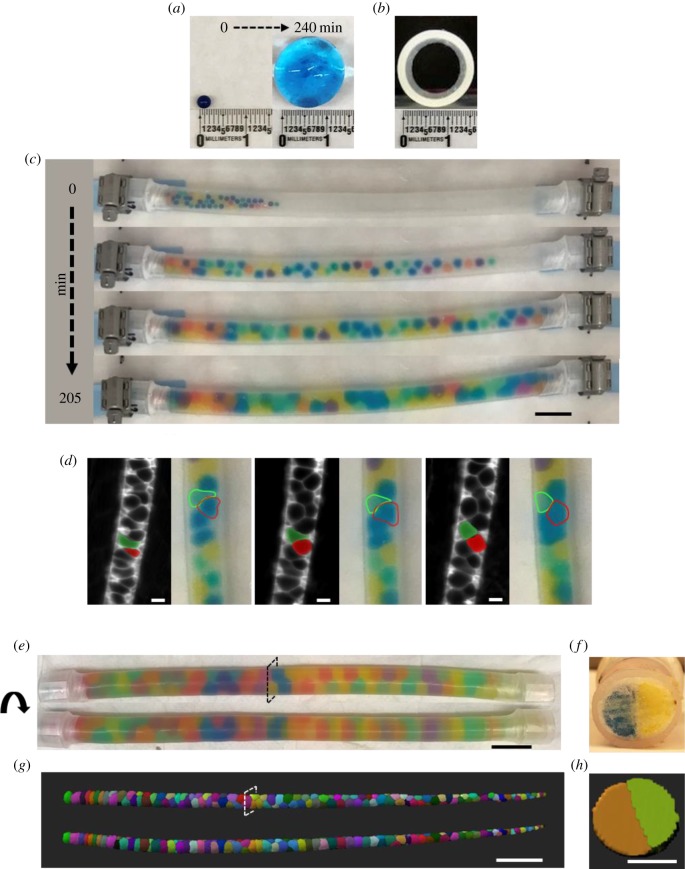
Figure 1.

A physical model recapitulates the organization and key behaviours of the zebrafish notochord. (a) A single JB before (left panel) and after (right panel) being placed in a water bath to grow unrestricted. (b) Cross-section image of an empty circular silicone tube (inner diameter, 12.7 mm). (c) Time-lapse images of JBs swelling in a capped silicone tube. Scale bar, 2.5 cm. (d) Still images from time-lapse movies of vacuolated cells in the notochord of a zebrafish embryo starting at the 20-somite stage and JBs as they settle in their final arrangement. Two cells wedging into a staircase arrangement are pseudo-coloured in green and red. A similar behaviour is highlighted for JBs traced with dotted lines. Scale bar, 20 µm. (e) Rotating views of a silicone tube filled with 80 JBs. (f) Cross section of the tube shown in (e) taken at the indicated level. Scale bar, 2.5 cm. (g) Dorsal (top) and lateral (bottom) views of a three-dimensional rendering of a 48 h post-fertilization (hpf) wild-type (WT) zebrafish expressing plasma-membrane-targeted green fluorescent protein (GFP) in vacuolated cells of the notochord. Note similarities between the arrangement of vacuolated cells, mainly in a ‘staircase’ pattern, and the JB tube shown in (e). (h) Orthogonal view of the notochord shown in (g). Scale bars, (g) 200 µm, (h) 50 µm.

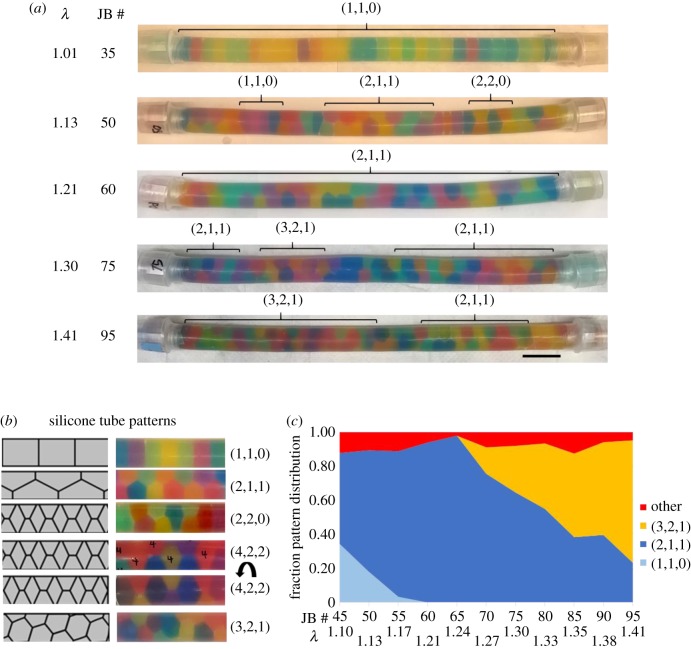
Figure 2.

JB arrangement in capped silicone tubes depends on bead density. (a) Images of capped silicone tubes filled with a range of JBs (30–95) that swelled to fill the available space. JB numbers and their respective calculated λ values are indicated on the left. Brackets mark regions of specific patterns. Scale bar, 2.5 cm. (b) Schematic (left) and images (right) of JB patterns observed in capped silicone tubes. (c) Quantification of the fraction of JB pattern observed for various JB densities (n = 3). Corresponding λ values and JB numbers are shown at the bottom.

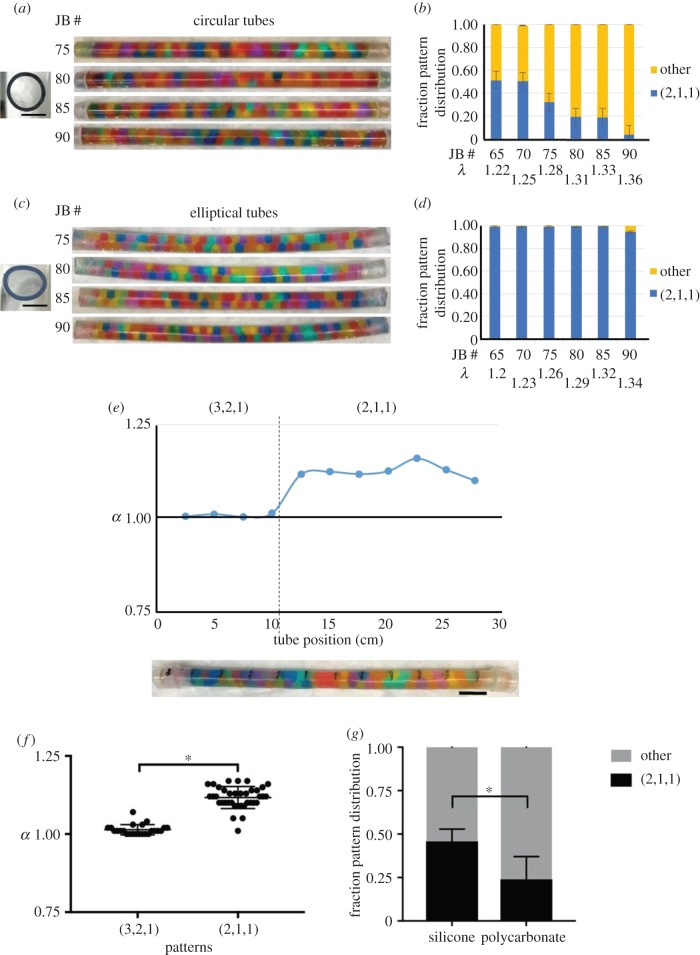
Figure 5.

Bead arrangement and tube aspect ratio are interrelated. (a) Cross section of an empty hard polycarbonate circular tube, aspect ratio 1.00 (left). Images of a range of JBs (75–90) swollen in capped polycarbonate tubes (right). (b) Quantification of the fraction pattern distribution in the polycarbonate tubes shown in (a). The other category includes the (3,2,1), (2,2,0) and (4,2,2) patterns. (c) Cross-sectional image of an empty hard vinyl elliptical tube, aspect ratio 1.25 (left). Images of a range of JBs (75–90) swollen in capped vinyl tubes (right). (d) Quantification of the fraction pattern distribution in the vinyl tubes shown in (c) as in (b). Note that almost all JBs are arranged in the (2,1,1) staircase pattern. (b,d) λ values differ for equal JB number owing to unequal cross-sectional areas of round polycarbonate and elliptical vinyl tubes. Error bars correspond to s.e. (e) Correlation between the JB pattern and the local aspect ratio (α) measured at 11 points along the length of a silicone tube after 80 JBs (λ = 1.31) have swollen. Scale bar, 2.5 cm. (f) Quantitation of α in areas of silicone tubes with the (2,1,1) or (3,2,1) pattern of JB arrangement after 80 JBs have swollen (n = 6 tubes, *p < 0.0001, Welch's t-test). Note the deformation into a more elliptical shape associated with the (2,1,1) pattern. Scale bars, 1 mm for circular and elliptical tube cross sections. (g) Staircase (2,1,1) pattern fraction in silicone versus polycarbonate tubes at (λ = 1.33). Unpaired t-test, *p = 0.011 (n = 5).

Aspect ratio was measured for all tubes using a digital calliper (Fine Science Tools, Foster City, CA, USA) at 11 points, equally spaced 2.54 cm apart, along the length of the tube. For the silicone tube deformation experiment (figure 5e), the aspect ratio was measured before and after JB swelling.

(c). Simulations

For circular cylinders, sphere centres are confined within a cylinder of radius 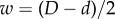, where D is the inner diameter and d is the sphere diameter. In other words, sphere centres must lie no further than 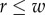from the central axis of the cylinder. For elliptic cylinders, the corresponding boundary condition does not have a simple analytical form, but for sufficiently small D ( 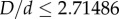for circular cylinders [29]) all spheres are in contact with the cylindrical wall at close packing. We can thus reformulate the problem as identifying the densest packing of sphere centres set on the surface of an elliptic cylinder. This approximation is valid in the limit of small eccentricity. The semi-major axis and semi-minor axis are such that ad > bd. In order to more easily compare our results with experiments, we define two diameters, 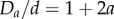and 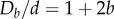, and hence the aspect ratio .

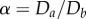We follow the sequential linear programming (SLP) scheme described before [30–32] to identify the densest sphere packing for a fixed cylinder geometry. At each optimization step, N particles on the surface of the elliptic cylinder move with small angular and axial displacements 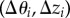, and the unit cell height, h_z, changes by a relative shrinkage factor, 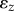. The coordinates of the sphere i before and after the movement are thus

where 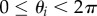and 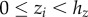. Finding the maximum packing density is then equivalent to minimizing h_z, subject to

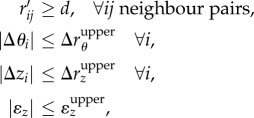where r_ij denotes the distance between neighbouring pairs, which can be linearized by Taylor expansion if the upper bound (denoted by the superscript ‘upper’) for a single step is sufficiently small. Here we set 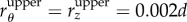and 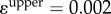and sequentially conduct optimization steps until convergence, i.e. 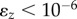. Because the number of spheres in the unit cell (N) for dense packing is not known, we scan N from 6 to 50 and repeat 100 times with different initial structure to identify potential densest structure for each pair of D_a/d and D_a/d considered.

(d). Microscopy

Three-dimensional renderings were generated from whole-mount confocal live images obtained on a Fluoview FV3000 (Olympus) confocal microscope equipped with 30×/1.05 silicone oil objective (Olympus) and Fluoview software (Olympus). Fish were mounted onto glass-bottom dishes in a 3% methylcellulose mixture of egg water and 1× tricane. Digital stitching of confocal images used for Imaris renderings was done in the Fluoview software. Time-lapse movies of notochord morphogenesis were recorded on a Lightsheet Z.1 microscope (Carl Zeiss) as previously described [24].

(e). Image processing

Notochord renderings were created using the Imaris v. 9.0.0 and 9.1.2 software (Bitplane USA, Concord, MA). Notochord renderings were created using both the surface and cells features (Imaris software, v. 9.0.0 and 9.1.2, respectively). Centroids, volumes and diameters were obtained for each vacuolated cell using the detailed statistical analysis function for the reconstructed notochords in the Imaris software v. 9.0.0 and 9.1.2.

(f). Morphometric analyses

(i). Notochords

Centroid locations were obtained from image processing software (Imaris) in (x, y, z) coordinates corresponding roughly to (AP, DV and LR) axes, in micrometre units. Notochord tube diameter was determined by two methods. (a) Creating a running sum of cell volumes V(x) from head to tail, such that the local cross-sectional area A(x) is dV/dx. Diameters in the LR and DV directions D_LR(x) and D_DV(x) were determined either on the assumption that the cross section was circular, or on the assumption that it was elliptical, with the same aspect ratio measured by method (b). (b) Measuring major and minor axes in Fiji 1.50a from cross sections every 100 µm. Methods (a) and (b) were verified to measure statistically equal area values for wild-type (WT) zebrafish. Aspect ratio was defined for notochords as D_LR(x)/D_DV(x).

Diameter ratios λ(x) = D(x)/d(x) were determined from smoothed tube diameters and smoothed cell volumes, using the diameters of equivalent spheres of the same volume as the cells. For each fish, we created a local coordinate system (X, Y, Z), normalizing cell centroid positions so that (1) the head was at X = 0; (2) the centreline was at (Y, Z) = (0, 0); (3) each cross section had radius 1. Patterns were classified on the basis of the vector defined by connecting two adjacent centroids, and this vector's angle relative to the XY and XZ axes in the normalized coordinate system (X, Y, Z). For each centroid, vectors were created between them and the following centroids, and the angle between each of these vectors and the X axis was calculated sequentially until a vector was found to be parallel to the X axis. The periodicity of a centroid C was then defined as the number of centroids examined in this process, and all centroids examined were assigned the same periodicity as C. Cell arrangement patterns were classified for each centroid by categorizing sub-sequences within the sequence of periodicities in Matlab using the code PatternInterpreter.m. Cells in transitional patterns were flagged in this program and then assessed manually based on the surrounding cell patterns. Transitional cells were counted as half a cell in each pattern. Sphere figures were created for each fish by plotting a sphere with the same volume as each cell at each cell's normalized position. These were then colourized using the pattern classifications previously determined, using Maple 2017.

(ii). JB tubes

JB patterns were classified visually. In order for a JB to count towards a pattern, we required there be at least three sequential JBs in this pattern. We counted JBs in transitions between patterns, where a JB could be considered in either pattern, as half a JB for each pattern. Regular hopscotch was defined to be two JBs in staircase alternating with one in bamboo. Any pattern that was a mixture of staircase and bamboo, but did not have a sequence of three JBs in the same pattern, was classified as irregular hopscotch.

To calculate λ, the volume of the tube, calculated as the volume of a cylinder with height and diameter equal to the measured height and interior diameter of the tube, was divided by the number of JBs to obtain the volume of each JB. From this, the diameter of a JB was calculated as the diameter of a sphere with equivalent volume. Because the tubes lack a distinguished orientation, aspect ratios for tubes were defined as D_M(x)/D_m(x) where D_M(x) is the largest diameter at location x and D_m(x) is the smallest.

(g). Statistical analyses

Statistical analysis was performed in JMP^® Pro v. 13.0.0 (SAS Corp., Cary, NC, USA) and GraphPad Prism v. 7.0c for Mac (GraphPad Software, La Jolla, CA, USA).

3. Results

(a). A physical model of the zebrafish notochord

In the zebrafish, notochord vacuolated cells are organized in a consistent staircase pattern [15]. To investigate the mechanism that controls the arrangement of vacuolated cells during morphogenesis, we built a physical model. We conceptualized the notochord as a cylinder containing liquid-filled spheroids. This is reminiscent of the arrangement of hard spheres or detergent foam cells (soap bubbles) in cylinders, which have both been extensively studied using theory and experimental approaches in soft matter physics. In those systems, spheres or foam cells arrange in progressively more complex patterns as the ratio (λ = D/d) of the diameter of the cylinder (D) over that of the spheres or cells (d) increases [33–35]. The range of patterns observed as λ increases follows a progression from a row of single units, called ‘bamboo’ and noted as (1,1,0) using the nomenclature derived from phyllotaxis [35,36], to a ‘staircase’ or ‘zigzag’ (2,1,1), and then to more complex helical and chiral patterns such as (3,2,1) [35,36]. For a given λ value different patterns have been observed to coexist, separated by transitional arrangements (‘defects’ in the terminology of crystallography). While these patterns are generally reminiscent of the arrangement of vacuolated cells in the notochord there are important differences that limit the applicability of the established models. First, unlike the existing physical models, vacuolated cells do not have a constant nor uniform size and shape. Second, unlike hard sphere models, vacuolated cells completely fill their available space. While this property is also present in cylindrical foams, these resemble epithelia and their interaction is completely driven by surface tension. By contrast, vacuolated cells are not epithelial and do not, at least during morphogenesis, establish junctions between neighbouring vacuolated cells or with sheath cells. Third, in cylindrical foams and hard sphere packing templating effects can bias pattern formation [36,37]. Therefore, we wanted to generate a physical model that resembles the properties of notochord vacuolated cells more closely.

Because the arrangement of vacuolated cells in the notochord during morphogenesis occurs as the cells inflate by drawing in fluid [13], we initially tried to emulate vacuolated cells using starch beads (tapioca pearls) and the notochord sheath using collagen sausage casing or silicone tubes. Alas, the high softness of the starch beads and their relatively rapid disintegration made this set-up unsuitable to analysis. After a brief survey of other common materials, we found sodium polyacrylate beads (a.k.a. JBs) to be suitable. These beads are deformable hydrogels, comprising a polymer network that absorbs a significant amount of water to swell in aqueous solutions. Thus, these beads mimic the polymeric nature of the cytoskeleton and exhibit large shape changes through swelling like the vacuolated cells.

When placed in water, dry JBs swell from approximately 1.5 mm to approximately 15 mm in a span of 4 h at room temperature and assume a spherical shape (figure 1a), similar to vacuolated cells isolated from the zebrafish notochord [24]. When placed at one end of a capped silicone tube JBs swelled and distributed throughout the tube in about 3.5 h (figure 1c), mimicking the expansion of the embryonic axis driven by notochord vacuolated cell expansion [13]. If one cap is removed from the tube the expanding JBs extrude from the open end, similar to what occurs with vacuolated cells when the tail of a 24 h post-fertilization (hpf) embryo is cut (electronic supplementary material, video S1). Interestingly, when compared with the behaviour of vacuolated cells during morphogenesis (electronic supplementary material, video S2) we observed that JBs exhibited similar movements as they locked into their final arrangement (figure 1c). We then tested different types of tubes of varying diameters and a range of JB numbers. We found that placing an appropriate number (see next section) of JBs in a capped 12.7 mm-wide silicone tube (a diameter slightly smaller than that of a fully swollen JB) results in a staircase arrangement that closely resembles that of vacuolated cells in the notochord of a 48hpf WT zebrafish (figure 1d).

Next, we explored JB arrangement at increasing λ values in capped tubes of constant length in which JBs swell to fill the available space. In this simple set-up, the final size each JB acquires is progressively reduced as the number of JBs per tube increases, thereby increasing λ. To calculate λ values, we simply divided the internal volume of the tubes by the number of JBs to obtain an equivalent sphere volume that we used to calculate the average JB diameter. As λ increased from 1 to 1.41, we observed bamboo (1,1,0), staircase (2,1,1), ‘hopscotch’ (2,2,0) and helical patterns (e.g. 3,2,1) appearing (figure 2a). Of note, the arrangement observed for each λ value was independent of the speed at which the JBs swelled and the initial distribution of the dry JBs (data not shown). The order of transitions from one pattern to the next and the λ values at which they occurred were consistent with those reported for hard spheres and cylindrical foams [30,35]. Similar to other packing models, we also observed the coexistence of different patterns within a tube (marked with brackets, figure 2a). However, unlike what has been reported for cylindrical foams [36], in our JB tubes the different patterns were intermixed and not sharply separated in large domains. We also observed the generation of mixed ‘hopscotch’ irregular arrangements (figure 2b) at the transitions between patterns. This may be comparable to the ‘line slip’ structures identified in the packing of wet foams, a model of soft sphere packing [38].

Together, these data show that a simple physical model composed of JBs swelling inside capped silicone tubes can reproduce the arrangement and even some of the behaviours of zebrafish notochord vacuolated cells. These results also generate testable quantitative and qualitative predictions about the arrangement of vacuolated cells in the notochord.

(b). Vacuolated cell arrangement in the zebrafish notochord is influenced by the aspect ratio of the rod

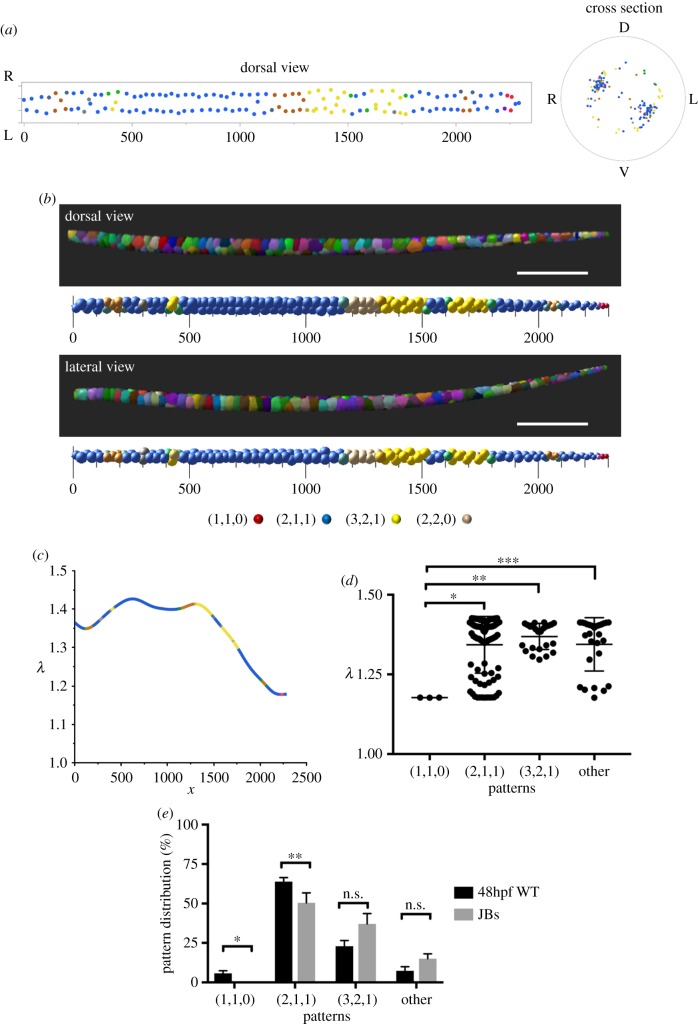
We next used confocal microscopy to image the entire notochord of 48hpf WT embryos expressing a plasma membrane marker in vacuolated cells and generated three-dimensional renderings. Using quantitative analyses, we obtained the position of each cell's centroid and plotted them in dorsal view and in cross section. As expected, the centroids were clustered along two areas that were consistent with a staircase pattern (figure 3a). However, a fraction of cells seemed to deviate from that pattern. To visualize arrangements, we generated three-dimensional renderings in which we placed a sphere of volume proportional to that of each vacuolated cell at the position of the respective centroid. We found that while most of the notochord length corresponds to the staircase pattern (2,1,1), some areas contain helical patterns, particularly (3,2,1) (figure 3b). Other patterns including (4,2,2), bamboo (1,1,0), which was often found at the rostral and caudal ends of the notochord, and hopscotch (2,2,0) were also present (electronic supplementary material, figure S1).

Figure 3.

The organization of vacuolated cells in the zebrafish notochord and the aspect ratio of the notochord rod are interrelated. (a) Dorsal (left) and cross-sectional (right) centroid plots of notochord vacuolated cells for a 48hpf WT zebrafish embryo. Orientation labels D (dorsal), V (ventral), L (left) and R (right). Units are in micrometres. (b) Lateral and dorsal views of three-dimensional renderings (top) and corresponding sphere plots (bottom) depicting the morphology and arrangement of vacuolated cells in a 48hpf WT zebrafish embryo. Colours in the sphere plots indicate patterns observed: blue (2,1,1), yellow (3,2,1), red (1,1,0), orange (4,2,2), tan (2,2,0), grey (uncertain), green (transition between 2,1,1 and 3,2,1). Scale bars, 300 µm (c) λ values of vacuolated cells along the length of the notochord of a 48hpf WT embryo. Line colours reflect patterns as in (b). (d) λ values for different patterns in the notochord of a 48hpf WT embryo. One-way ANOVA, Tuckey's test, *p = 0.0037; **p = 0.001; ***p = 0.005. (e) Distribution of patterns in 48hpf WT embryos (n = 6) and JB tubes (n = 3, λ=1.33). Paired t-test, *p = 0.047; **p = 0.045.

To compare the type and frequency of pattern occurrence between notochord vacuolated cells and JBs in silicone tubes, we first determined the λ value along the notochord of six 48hpf embryos. To do this, we took the local average volume of each cell and calculated the diameter based on a sphere of the same volume. We found that the λ value was on average 1.33 ± 0.14, and that it varied along the length of the AP axis, tapering towards the caudal region (figure 3c). As expected, the λ value was significantly higher in areas of staircase and complex arrangements compared with the linear bamboo pattern (figure 3d). Overall, the frequency of each pattern observed in vivo in 48hpf embryos closely followed the distribution of JB tubes of the same λ value (figure 3e). However, we observed a significantly higher proportion of bamboo (1,1,0) and staircase (2,1,1) arrangements in vivo compared with the JB tubes (figure 3e). To identify what might explain this discrepancy, we first analysed the transverse aspect ratio (α) of the notochord in 48hpf embryos and found it is significantly elliptical with an average value of 1.07 ± 0.03. Interestingly, when we analysed α values during notochord morphogenesis we found that the notochord rod is highly elliptical at the ‘stack of coins’ (chrodamesoderm) stage and that it becomes more circular as the vacuolated cells inflate (electronic supplementary material, figure S2). These data suggest that the aspect ratio of the notochord rod influences the arrangement of the vacuolated cells.

(c). Elliptical cylinders favour staircase arrangement of hard spheres in simulations

To test whether the discrepancy between the notochord and the physical model can be explained by the geometry of the notochord rod, we conducted numerical simulations of hard sphere packing in cylinders with a variable aspect ratio between 1 and 2. Specifically, we wanted to determine whether elliptical cylinders favour the (2,1,1) staircase arrangements. To this end, we used the SLP method, previously used to simulate hard sphere packing in circular cylinders up to a λ value of 4 [30], and adapted it to the case of elliptic cylinders.

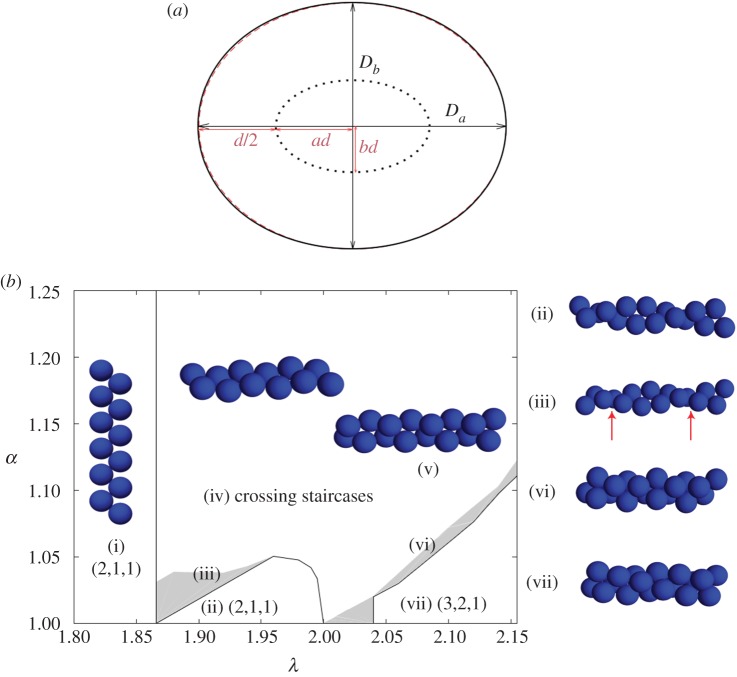
Figure 4 shows the densest structures identified by SLP for different 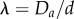up to 2.15 and 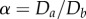. For λ < 1.866, next-nearest-neighbour contacts are impossible, hence the densest packings have a staircase morphology. A twisted staircase regime appears at λ < 1.866, and persists for a relatively small ellipticity, i.e. λ < 1.05. For larger α, hard spheres form a crossing staircase structure. Specifically, two staircase structures intersect every other sphere. The angle between the two planes of these two staircase structures increases with α. This helical regime diminishes upon approaching λ = 2, which in circular cylinders is achiral. For λ > 2.039, a triple helical structure, (3,2,1), appears. This helical structure also transforms into the crossing staircase structure as α increases. Similarly, between these two regimes complex intermediate structures with both discontinuous helical strands and bend crossing staircases appear. The crossing staircase structures generally become preferred as α increases.

Figure 4.

Elliptical cylinders favour the staircase arrangement of hard spheres in simulations. (a) Cross section of elliptical cylinder model. During the SLP optimization, hard sphere centres of diameter d evolve on the surface of an elliptical cylinder (dotted curve) with semi-major axis ad and semi-minor axis bd. The resulting boundary confinement (black solid curve) is approximately elliptical (red dashed curve) with major and minor diameters D_a and D_b, respectively, when α = D_a/D_b is small. The case α = 1.25 is depicted here. (b) Diagram of the densest packings of hard spheres in cylinders of width up to λ = 2.15 and an elliptical aspect ratio α. Sharp transitions (solid lines) are observed between certain structures. Because of the competition between packing helicity and cylinder ellipticity, however, helicity is lost in two steps. It becomes discontinuous (solid line), before slowly vanishing (grey zones). Sample structures of (i) staircase (2,1,1) and (ii) twisted staircase (2,1,1); (iii) transitional defective (red arrows) structure between staircase and twisted staircase; (iv) and (v) crossing staircase (see text); (vi) triple helix (3,2,1); and (vii) transitional structure between (3,2,1) and crossing staircase regimes. The regime of staircase and twisted staircase is markedly enlarged for α > 1. Note, however, that in this model the bamboo structure is only stable at λ = 1, and the hopscotch structure is always unstable. (Online version in colour.)

(d). Reciprocal control of tube aspect ratio and local cell arrangement in physical models

The analysis of vacuolated cell arrangement suggested that the aspect ratio (α) of the notochord rod strongly influences the pattern these cells achieve. This notion was supported by numerical simulations indicating that elliptical cylinders strongly favour the (2,1,1) staircase arrangement. Because hard spheres impose constraints that limit their possible arrangements, we decided to test in physical models the effect of tube aspect ratio on JB arrangement. To this end, we procured relatively inflexible vinyl tubes of elliptical section (α = 1.25) and hard polycarbonate tubes of circular section (α = 1.00) and filled them with dry JBs which were allowed to swell as before. We tested a range of λ values close to those of the WT notochord and found that in the circular tubes the helical and chiral patterns were the most prominent, particularly at higher λ values (figure 5a,b). By contrast, in elliptical tubes JBs were arranged almost completely in a staircase (2,1,1) pattern (figure 5c,d).

Next, we re-visited the silicone tube model and took into account their aspect ratio and the material properties. We first measured the aspect ratio before the addition of JBs and found α = 1.02 throughout its length. Then, we added 80 JBs and allowed them to swell as before, reaching a λ value of 1.31, before scoring JB arrangement and the local aspect ratio. Interestingly, we found that the tubes deformed locally from α = 1.00 up to 1.17 and that the areas with (2,1,1) staircase pattern were significantly more elliptical than those presenting the chiral pattern (3,2,1) (figure 5f). We then compared the fraction of staircase (2,1,1) arrangement present in silicone and hard polycarbonate tubes at a λ value of 1.33 and found it is significantly higher in the deformable silicone tube (figure 5g).

Together, these data indicate that the aspect ratio of the cylinder strongly influences the local arrangement of JBs in our physical model. Conversely, the local arrangement of JBs also modifies the aspect ratio of the tube, indicating these two key variables are interdependent. These data also explain why in the largely elliptical WT zebrafish notochord rod vacuolated cells are arranged mostly in a staircase pattern while λ values are relatively high.

(e). The density of vacuolated cells determines their organization and influences the aspect ratio of the notochord rod

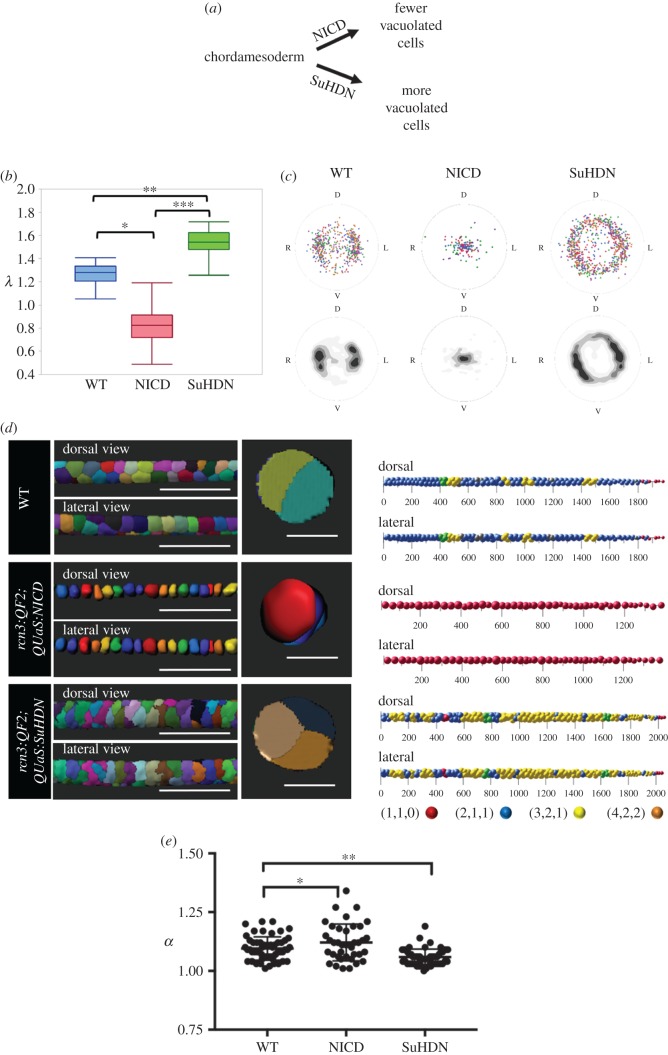
The experiments with our physical model of the notochord and our theoretical model generated two important predictions: (1) the arrangement of vacuolated cells within the notochord is dictated by cell density, which in turn defines the λ value as cells swell to occupy the available space; (2) vacuolated cell arrangement and the aspect ratio of the notochord rod are mutually regulated. To test these predictions in vivo, we first took a genetic approach to alter vacuolated cell density in the zebrafish notochord. Previous work in zebrafish has shown that differentiation of chordamesoderm cells, the notochord primordium, into vacuolated and sheath cells is controlled by the Notch pathway [16]. Activation of the Notch pathway in the early notochord leads to the generation of more sheath cells at the expense of the vacuolated cells. Conversely, Notch inhibition leads to more vacuolated cells (figure 6a). To manipulate Notch activation specifically in the zebrafish notochord, we generated a new driver line, Tg(rcn3:QF2), to drive expression of either constitutively active Notch intracellular domain (NICD) or a dominant negative form of suppressor of hairless (SuH-DN) from QUAS lines we previously established [21].

Figure 6.

Vacuolated cell density determines their arrangement in the zebrafish notochord. (a) Schematic showing the effect of expressing NICD or SuH-DN in the early notochord (chordamesoderm). (b) Average λ values obtained from three-dimensional reconstructions of notochords in 48hpf WT, NICD and SuHDN embryos (n = 4, p < 0.0001, one-way ANOVA). (c) Centroid plots and heat maps of vacuolated cells from 48hpf WT (left), NICD (middle) and SuHDN (right) (n = 4). Orientation labels D (dorsal), V (ventral), L (left) and R (right). (d) Left panel, three-dimensional renderings of vacuolated cells showing dorsal, lateral and orthogonal (right panels) views of an approximate 500 µm segment of notochord from 48hpf WT (top), NICD (middle) and SuHDN (bottom) zebrafish. Right panel, Sphere plots of notochord vacuolated cells of the 48hpf WT (top), NICD (middle) and SuHDN (bottom) zebrafish embryos shown in (b). Patterns of vacuolated cell arrangement are colour coded as follows: blue (2,1,1), yellow (3,2,1), red (1,1,0), orange (4,2,2), green (transition between 2,1,1 and 3,2,1) and grey (uncertain). (e) Aspect ratio (α) of 500 µm regions, same as in (d), of the notochord rod in 48hpf WT (n = 5), NICD (n = 4) and SuHDN (n = 5) embryos (*p = 0.043, **p = 0.001, Dunnett's multiple comparisons test). Scale bars are 200 µm for three-dimensional rendering lateral and dorsal views and 50 µm for cross-sectional views.

When we expressed NICD the number of vacuolated cells was sharply reduced (69%, n = 4). This produced a significantly lower λ value and drastically different arrangement of vacuolated cells respect to WT controls, producing a bamboo (1,1,0) pattern throughout most of the notochord, which was readily recognized in centroid plots that collapsed at the centre of the notochord (figure 6c). In three-dimensional renderings, vacuolated cells clearly arranged in a linear arrangement that was completely composed of the bamboo (1,1,0) pattern (figure 6d). Interestingly, the aspect ratio of the notochord rod was also significantly more elliptical in NICD when compared to WT (figure 6e). This is similar to what we observed during morphogenesis (electronic supplementary material, figure S2). We also observed an increase in notochord aspect ratio after a tail cut (electronic supplementary material, figure S3), resulting in a local increase in the formation of staircase and transitional patterns at the expense of the chiral (3,2,1) pattern close to the posterior end of the notochord (proximal to the cut), suggesting that the shape of notochord rod is kept by the internal pressure of the structure and opposed by surrounding tissues.

By contrast, when we inhibited Notch in the early notochord we generated an average of 25% (n = 5) more vacuolated cells of smaller size, with λ values raising with respect to WT controls to about 1.60 (figure 6b). The increased λ value was accompanied by a change in vacuolated cell arrangement as visualized by three-dimensional renderings and centroid plots, which showed a fairly even distribution around the whole periphery of the notochord (figure 6c,d). Remarkably, and similar to our physical models (figure 5), the dramatic shift towards the (3,2,1) chiral pattern was also associated with a significant increase in circularity (reduced aspect ratio) in comparison to WT controls (figure 6f). Together, these data demonstrate that vacuolated cell arrangement in the zebrafish notochord is determined by cell density, which in turn defines λ. Our data also reveal that the local aspect ratio of the rod and the arrangement of vacuolated cells are interdependent.

Next, we wanted to examine a regeneration response that also alters the number and size of notochord vacuolated cells. Recently, we and others showed that in cavin1b mutants lacking functional caveolae, vacuolated cells collapse in specific areas under the mechanical stress of locomotion [24,39]. Then, sheath cells invade the inner notochord and trans-differentiate into new vacuolated cells [24]. If the extent of the lesion is large many sheath cells invade, eventually generating more, but smaller, new vacuolated cells [24]. To determine whether the arrangement of vacuolated cells changes during this injury and regeneration response, we placed WT and cavin1b mutant embryos in methylcellulose to increase the incidence of large notochord lesions and tracked fish over time during the regeneration response. Interestingly, we found that upon collapse of several vacuolated cells, the remaining nearby vacuolated cells occupied part of the vacant space and adopted locally a bamboo (1,1,0) arrangement (electronic supplementary material, figure S4). Then, over the course of 7 days the invading sheath cells trans-differentiated and expanded to fill the available space. However, these newly generated vacuolated cells were more numerous and smaller compared with the primary vacuolated cells (larger local λ) and were arranged in a complex pattern (electronic supplementary material, figure S4c) similar to that found for fish expressing SuH-DN in the notochord (figure 6d). These data reveal that the arrangement of vacuolated cells is not fixed and is able to re-settle according to the prevailing tissue constraints during injury and regeneration.

4. Discussion

Altogether, our data show that the organization of vacuolated cells within the zebrafish notochord follows packing rules that can be recapitulated in a simple physical model. This model is also able to recapitulate the path vacuolated cells follow as they settle into their final arrangement within the zebrafish notochord. Thus, the morphogenesis of the zebrafish notochord can be considered a self-organizing process [1] in which the osmotic swelling of vacuolated cells, an energy consuming process [13], within the boundaries of a semi-flexible notochord sheath leads to a stereotypical arrangement.

Using water swelling JBs to emulate notochord vacuolated cells provided two important advantages over cylindrical foams and hard sphere packing models. First, the JBs settle into their position as they swell and thus are not influenced by a pre-existing pattern as is the case with cylindrical foams and hard spheres. Second, because the volume JBs reach is variable, within the range covered by our experiments, it is easy to change λ continuously simply by changing bead number for any given length of tube, which can also be of variable geometry. If we add to these features the possibility of replacing JBs by highly customizable hydrogels, it would be possible to address the effect of the material properties of the packing beads. This may allow for easier physical modelling of soft spheres and other related problems. However, further development of the theoretical framework will be needed to incorporate variables of biological relevance such as tube wall elasticity and geometry, medium viscosity, bead properties (i.e. soft spheres) and combinations of these variables.

Our data demonstrate that the particular arrangement vacuolated cells achieve and the aspect ratio of the notochord rod are largely determined by cell density (figure 6), which defines λ. Therefore, it is basically a geometry-driven process. With a notochord rod aspect ratio that is initially highly elliptical (electronic supplementary material, figure S2), probably because of the effect of surrounding tissues, vacuolated cells are prone to arrange in a staircase pattern. However, osmotic swelling of the vacuolated cells tends to counter this effect, making the structure more circular. This effect is also patent in the mirroring changes that α and λ exhibit along the length of the notochord, i.e. as λ increases α diminishes (electronic supplementary material, figure S5), suggesting a mechanical buffering mechanism. The final α value the notochord eventually reaches (approx. 1.07) is at the boundary where the staircase pattern is strongly favoured in hard sphere-simulations, but close to what allows chiral patterns to exist, thus explaining the bias in vacuolated cell arrangement observed in the notochord with respect to what is seen in circular tubes, as well as the presence of chiral patterns which are basically not found in hard elliptical tubes. However, establishing exact boundary points is challenging because the λ values for vacuolated cells are low estimates that do not take into account the role cell shapes irregularities (e.g. λ < 1 for NICD in figure 6). Conversely, it is also expected that a soft sphere theoretical model would be closer quantitatively to the JB and in vivo models with a lower effective λ value. Nevertheless, the trends and responses to variations in tube geometry are all in good agreement.

One way to establish a closer quantitative comparison between the hard sphere models and the notochord vacuolated cell is to obtain effective λ values using the longitudinal centroid plots by calculating each cell's diameter as twice the distance from the perimeter to the centroid. This approximation is valid for the notochord because all vacuolated cells are in contact the surrounding sheath. Using this method, we obtained average 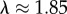for WT, which is close the boundary where helical patterns are generated for a hard tube with an λ ∼ 1.866 in simulations.

Clearly, the material properties of the sheath and the mechanical coupling of surrounding tissues [40] also influence the local aspect ratio (α) of the notochord rod, thereby modulating the local arrangement of vacuolated cells. In this context, the initial allocation of vacuolated cells and the starting morphology of the notochord rod, which are defined during gastrulation [41], probably determine the internal organization of the notochord. These notions may also help explain the variability in size and arrangement that are seen across vertebrates. For example, the large notochord rod of Xenopus laevis is filled with more vacuolated cells, but of roughly the same size compared with zebrafish. As a result, their organization is more complex, with internal cells that are not in contact with the sheath, yet still similar to that achieved by silicone/JB tubes of similar proportions (electronic supplementary material, figure S6). It will be interesting to explore whether the mammalian notochord also follows the same organizational principles.

During morphogenesis, vacuolated cells are able to slide past each other as they settle into their final arrangement (figure 1), which later (around 96 hpf) is stabilized by the formation of desmosomes between vacuolated cells [24,42]. However, this arrangement is not fixed, as illustrated by the dynamic changes that occur following vacuolated cell collapse and regeneration (electronic supplementary material, figure S2). This provides a robust mechanism ensuring the mechanical integrity of the axis and safeguarding normal spine development when more vacuolated cells are generated [24]. However, it remains unclear whether the production of more but smaller vacuolated cells impacts the mechanical properties of the spine, particularly the intervertebral discs, later in life. By contrast, when fewer vacuolated cells are produced (e.g. NICD expression) the axis kinks during spine formation [13], suggesting that the allocation of a minimum number of vacuolated cells during embryogenesis is crucial.

Ethics

Experiments were performed at Duke University. Research using zebrafish was conducted adhering to protocols approved by the Duke University Institutional Animal Care Use Committee.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material. Original scripts used for data analysis and the data have been archived; they can be accessed at our website https://sites.duke.edu/bagnat/tools/.

Authors' contributions

M.B. designed the study; J.N., J.B., V.S. and J.G. performed experiments with physical and in vivo models; J.N., J.G. and M.B. interpreted experimental data; E.L.S. and S.R.L. developed quantitative methods and analysed data; Y.H. and P.C. developed the theory and performed the numerical simulations for hard spheres; M.B. wrote the manuscript with input from the other authors.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by National Institutes of Health (NIH) grant no. AR065439 and a Howard Hughes Medical Institute Faculty Research Scholar grant to M.B.; by Simons Foundation grant no. 524764 to S.R.L.; J.G was supported by NIH fellowship F31GM122422. P.C. and Y.H. were supported by National Science Foundation grant no. DMR-1749374. Our light sheet microscopy was supported by NIH Shared Instrumentation grant no. 1S10OD020010-01A1.