Signatures of proprioceptive control in Caenorhabditis elegans locomotion

Abstract

Animal neuromechanics describes the coordinated self-propelled movement of a body, subject to the combined effects of internal neural control and mechanical forces. Here we use a computational model to identify effects of neural and mechanical modulation on undulatory forward locomotion of Caenorhabditis elegans, with a focus on proprioceptively driven neural control. We reveal a fundamental relationship between body elasticity and environmental drag in determining the dynamics of the body and demonstrate the manifestation of this relationship in the context of proprioceptively driven control. By considering characteristics unique to proprioceptive neurons, we predict the signatures of internal gait modulation that contrast with the known signatures of externally or biomechanically modulated gait. We further show that proprioceptive feedback can suppress neuromechanical phase lags during undulatory locomotion, contrasting with well studied advancing phase lags that have long been a signature of centrally generated, feed-forward control.

This article is part of a discussion meeting issue ‘Connectome to behaviour: modelling C. elegans at cellular resolution’.

1. Introduction

Undulatory locomotion, or movement via the propagation of mechanical waves along a body, is a remarkably old and successful strategy, and one that is prevalent across all scales of life—from microorganisms to monster prehistoric snakes [1–7]. While each life form is unique, the generation of whole-body undulations resulting in directional movement necessarily emerges from the coupling among the components of the system, including the nervous system and muscles in animals, other body tissue and the physical environment. Understanding the separate and combined roles that these components play can elucidate the constraints imposed on the neuromechanical system.

The small, compact anatomy and fully mapped nervous system of the nematode Caenorhabditis elegans along with its undulatory repertoire make it an ideal organism for linking neural control with behaviour [8]. Like other organisms [2,9], C. elegans exhibits gait modulation when swimming through media characterized by different viscosities or viscoelasticities. Higher resistance due to external drag forces results in slower undulations with shorter wavelength and lower wave amplitude [8,10,11]. While internal neural modulation can also affect the locomotion speed and waveform within homogeneous environments [12–15], the coupling between internal (neural and neuromuscular) and external (biomechanical) modulation of gait has received little attention. This question is particularly interesting in systems where proprioception—the sensing of the position or movement of different parts of the body—plays a crucial role in the generation, coordination or entrainment of different motor patterns [16–20]. The importance of proprioception has long been conjectured in C. elegans [21,22] and supported by the identification of proprioceptive neurons [23–25] and by direct evidence linking body curvature to neuronal activation [26]. Proprioception has been postulated to contribute to pattern generation itself [22,26–28], to mediate the propagation of undulations down the body [29–31], to underpin gait modulation [10,11,26,28] and even to mediate turning behaviours [25,32].

This leaves a major open question: what is the extent and role of proprioceptive control of locomotion in C. elegans and by what mechanism does it act? To pin down this question, we sought a minimal, biologically grounded explanatory model that we could use to simulate realistic locomotion with a view to stating the minimal requirements for proprioceptive control and signatures of such a control mechanism that can be translated to experimental behavioural predictions. Here, we use a neuromechanical computational model to address this question. The model combines biomechanical realism, seamless integration of biomechanics with neuromuscular control and high computational efficiency, allowing us to study a range of hypotheses and gain understanding and mechanistic insight about both the neural control and neuromechanical coupling.

The neural circuit explored here lacks central pattern generators (CPGs) and instead relies on proprioceptive feedback to generate undulations. In what follows, we first show that this model qualitatively reproduces the swim–crawl transition, previously observed experimentally in different Newtonian and viscoelastic media [10,11] and theoretically captured by Boyle et al. [28] in an articulated neuromechanical framework with proprioceptive control. We then perform a more systematic analysis of mechanical and neural properties of the system to obtain a holistic understanding of their interplay and to derive signatures of proprioceptive control.

2. Model overview

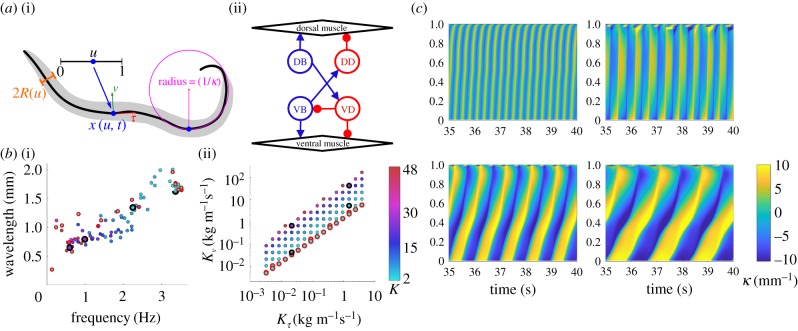
Our model consists of a continuous incompressible viscoelastic shell [33]. At each point along the body, we assume the width of the nematode's body is fixed in time, which allows us to collapse all internal and external forces onto the midline (figure 1a and electronic supplementary material, §S1). Four free parameters modulate the biomechanical properties of the body and its interaction with the environment.

Figure 1.

A continuum neuromechanical model reproduces the swim–crawl transition. (a) Model schematic describing (i) geometry and (ii) neural circuit. (b) Frequency–wavelength relationship (i) plotted for a wide set of drag coefficients, K = K_ν/K_τ, as shown in (ii), including Newtonian environments (red circles). Parameters used for sample kymograms (black circles) span the swim–crawl transition. (c) Curvature kymograms (showing the curvature along the body along the vertical axis from head, at u = 0, to tail, u = 1, and in time) in environments from water (top left) through intermediate fluids (top right to bottom left) to agar (bottom right).

Environmental forces are modelled by resistive force theory and parametrized by two drag coefficients, K_ν and K_τ, that act to resist motion normal, ν, and tangential, τ, to the local body surface [1,10,28]. This allows us to model both Newtonian and linear viscoelastic environments in the low Reynolds number regime. In the viscoelastic case, we interpolate between reported parameter sets for swimming in water (buffer solution) [1] and crawling on agar [3,10,22,28] to model intermediate environments.

The passive body is parametrized by a Young's modulus, E (the elastic resistance to bending or body stiffness), and an internal viscosity, η (the body damping in response to bending). Note that nematodes modulate their muscle stiffness as a function of activity [34]. For parsimony, we assume that at any point in time, opposite dorsal and ventral muscles along the body contract and relax in anti-phase, such that the sum of their Young's moduli is approximately constant. Thus, our choice of E represents an effective elasticity associated with the mean Young's modulus of the body during undulatory locomotion.

Our neural control consists of a binary activation function acting continuously along the body, loosely representing on/off activation of B-type excitatory motor neurons (figure 1a). At every point along the body, B-type neurons receive proprioceptive input, which corresponds to the mean body curvature integrated over their receptive range, posteriorly to the muscle coordinate. Posteriorly facing proprioception has long been conjectured in B-type neurons, owing to these neurons' extended and undifferentiated processes [21,22,27,28]. Wen et al. [26] have shown that anterior, but not posterior, bending of C. elegans appears to activate B-type neurons, and suggested a proprioceptive range of 100 μm. Anteriorly facing proprioception is considered in the electronic supplementary materials (figure S1). In the model, we use the simplest form of posterior proprioception to alternate the activation of ventral B-type (VB) and dorsal B-type (DB) neurons: a single bistable switch with only two free parameters—the proprioceptive range and an activation threshold, switching neurons on or off when crossing the corresponding proprioceptive input threshold (see electronic supplementary materials, §S1 for details). Command interneuron input and D-type neurons are implicitly treated assuming D-type neurons instantaneously react to excitation from B-type neurons on the opposite side of the body [28]. In our model, the neural circuit controls the muscles, modelled by a leaky integration equation that converts a current input at every point along the body u to a mechanical torque β(u, t); the muscle model contains two free parameters, corresponding to a muscle time scale (set to 100 ms) and an amplitude or maximum curvature (set to 10 mm⁻¹; see table 1 and electronic supplementary materials for details). The model equations balance internal and external forces and torques subject to mass conservation within the nematode's body [33].

Table 1.

Default values for model parameters. See the electronic supplementary materials for details. Using the values below and equation (2.1) yields a default value e = 0.02.

parameter	label	default value	reference
body length	L	1 mm	[35]
second moment	I	2.0 × 10−19 m4	[33]
undulation period (agar)	T0	3.3 s	[11]
Young's modulus	E	100 kPa	[33]
normal drag (agar)	Kν	128 kg m−s s−1	[28]
tangential drag (agar)	Kτ	3.2 kg m−s s−1	[28]
drag ratio (agar)	Kagar	40	[22]
drag ratio (water)	Kwater	1.5	[1]
proprioceptive threshold	θ	3	[10]
proprioceptive range	δ	0.5	[28]
muscle time constant	τm	100 ms	[11,28]
curvature amplitude	β0	10 mm−1	[11,28]

To gain a fundamental understanding of the dynamics of this system, we formulate the model in non-dimensional form. Non-dimensionalization, typically performed around a physical regime or point of interest, is a powerful approach for representing the minimum number of independent parameters of a system, thus abstracting over a variety of phenomena. The representation of physical parameters as dimensionless control parameters of the system allows, on the one hand, the extraction of the key determinants of a system's behaviour, and on the other the identification of regimes where some parameters may be neglected [36].

In our earlier non-dimensionalization of the biomechanical model, performed for C. elegans on agar-like conditions and described in Cohen & Ranner [33], the internal viscosity η was found to be negligible and the remaining mechanical parameters K_τ, K_ν and E were related through two dimensionless parameters:

2.1

where I and L are constant geometrical factors representing the cross-sectional shape and length of the nematode and T₀ is a characteristic period of undulation (see electronic supplementary material, §S1).

In addition to being a result of the non-dimensionalization, neglecting viscosity offers us a better understanding of the contribution of elasticity to the dynamics, and allows us to identify the limits of elastic models of C. elegans. The variable K represents the ratio of drag coefficients resisting the bending action of the nematode. Increasing K corresponds to an increase in the strength of lateral resistive forces that arise from the viscoelasticity of the fluid (e.g. on the surface of an agar gel), whereas e represents the ratio of internal elastic forces to environmental drag forces. In ideal Newtonian fluids, K is fully determined by the geometry of C. elegans, such that e becomes the key control parameter of the biomechanics.

3. A proprioceptively driven elastic shell model reproduces the swim–crawl transition

It has long been observed that C. elegans smoothly adapts its gait in response to changes in the resistivity of the surrounding environment [10,11,37]. Gait modulation was first demonstrated in different concentrations of highly non-Newtonian gelatin solution and characterized as a function of the ratio of drag coefficients 1.5 ≲ K ≲ 40 [10]. Other studies demonstrated gait modulation in near-Newtonian media with fluid viscosities ranging over six orders of magnitude [11]. Gait modulation both as a function of fluid viscosity and as a function of effective viscoelasticity K was reproduced in the neuromechanical model of Boyle et al. [28] using an articulated body comprised of springs and dampers. That model demonstrated how the proprioceptive feedback acts as the key ingredient coupling the neural activation and biomechanics and hence mediating the modulation of kinematic parameters of the locomotion. And yet, we lack a combined understanding of the coupling between fluid viscosity, its non-Newtonian properties and body elasticity.

To determine the minimal model requirements for gait modulation, we simulated our model nematode in a variety of model environments that mimic water-like, agar-like and intermediate Newtonian and viscoelastic fluids [10,28]. We found that our model simulations (figure 1b,c) quantitatively reproduce the relationship between the frequency and wavelength of undulations previously observed experimentally [10,11], confirming that these kinematic parameters are tightly coupled under proprioceptively driven control. Boyle et al. [28] required some damping (internal viscosity) to reproduce the experimentally observed gait modulation, especially in low viscosity solutions. In our model, neglecting the internal viscosity of the body results in realistic undulations in agar-like conditions but unrealistically high frequencies as we approach water indicating the significance of internal viscosity in this regime.

It is worth noting that two models, presented here and in Boyle et al. [28], have now demonstrated similar proprioceptively facilitated gait modulation, suggesting that these results emerge from the model assumptions rather than from the implementation (e.g. using continuous elastic shells versus articulated bodies). We conclude that proprioceptive feedback, bistability in the neuromuscular activation and alternating dorsoventral muscle contractions are sufficient to produce gait adaptation in different physical environments. We further conclude that gait modulation in the form of decreasing frequency and wavelength of undulations with increasing environmental drag is a strong signature of feedback control.

4. Towards a universal picture of gait modulation

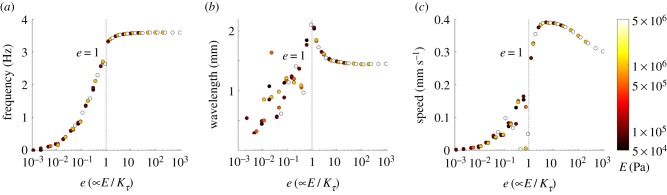
To gain a deeper understanding of the relationship between environment and body mechanics, we examined the effect of the body's elasticity on gait adaptation. From equation (2.1), we expect an inverse relationship between the effect of the nematode's effective elasticity E and the external viscosity (parametrized here by K_τ for Newtonian media). We first ask whether this inverse relationship holds in an integrated neuromechanical control system dominated by a strong feedback loop. We then characterize the kinematics of locomotion as a function of our dimensionless parameter e using environmental drag parameters used in figure 1b with a Young's modulus which spans the experimentally predicted values.

The results (figure 2) neatly collapse the interplay between internal and external forces into a single function of e, confirming that this is the control parameter of interest. In this way, they reveal a more general picture of the determinants of elastic undulations subject to feedback driven control, extending beyond a simple modulation of external drag. We find that undulatory locomotion dynamics falls into two dynamical regimes separated by e = 1 (figure 2). For e < 1, the external drag dominates and gait modulation ensues from the competition between external drag and internal elasticity. This result relies on the accuracy of predicted drag coefficients given in the work of Niebur & Erdös [22] and Boyle et al. [28]. Karbowski et al. [38] give a slightly lower estimate of drag in agar (K = 9 − 14), which we note still produces considerable gait adaptation in our model (figure 1). In summary, we associate the key signature of gait modulation with the regime e < 1. Gait modulation (between water and agar, or high viscosity alternatives) requires e ≪ 1 in the high viscosity or agar-like environment.

Figure 2.

The effect of environmental drag on (a) undulation frequency, (b) wavelength and (c) the speed of the nematode in Newtonian environments (K = 1.5). Simulation results spanning E-K_τ space are plotted against the non-dimensional parameter e. Outliers represent simulations exhibiting uncoordinated locomotion.

For e > 1, internal time scales dominate so the undulation dynamics are bounded by the balance between the elastic modulus and the slowest internal time scale (in this model, emerging from the wave propagation, as determined by proprioceptive threshold and range, combined with the muscle time scale). Reinterpreting e in terms of physical variables (see electronic supplementary material, figure S2) can provide insight into the effective elasticity required to reproduce the observed kinematics of the swim–crawl transition. For the parameters used in our simulations, the requirement e ≲ 1 implies that E ≲ 500 kPa and a value in the range 50–100 kPa captures the full range of gait modulation observed. Naively, this reasoning rules out the peak speed (achieved around e ≈ 10). However, we know that C. elegans can modulate its muscle tonus with a dramatic effect on stiffness. Using an estimate of E = 380 MPa from Park et al. [39] would easily allow the nematode to reach this maximal speed and thrust (see also electronic supplementary material, figure S4).

Our estimated Young's modulus coincides with our default parameter value of E = 100 kPa for typical forward locomotion in spontaneous free behaviour, which is consistent with our previously estimated value based on a purely mechanical model subject to rhythmic forcing [33] but falls below experimentally measured estimates of Young's modulus [11,39].

5. Internal neural modulation produces an inverse frequency–wavelength relationship

Like all animals, C. elegans is capable of adapting its gait in a context-dependent manner within a homogeneous medium. This must be achieved by some internal mechanism. Candidate mechanisms include descending neural control (e.g. a modulation of the current input from locomotion command neurons [27]), a modulation of the motor circuit (e.g. the excitability of motor neurons [40]), and a modulation of the proprioceptive field (though no such mechanism has been documented to date). Although the neural model used here is idealized, the feedback mechanism allows us to investigate two fundamental parameters: (i) the proprioceptive threshold and (ii) the range over which stretch is perceived. An increased threshold could correspond to a reduced excitability of B-type motor neurons, reduced sensitivity to stretch, or a reduced tonic input current, for example from AVB command interneurons.

Figure 3a (and electronic supplementary material, figure S3) shows the effect of threshold modulation in different environments. For even lower threshold values than shown here, undulations cease to occur, and for higher values the initial transient becomes very long (≳40 s). Our first observation is that undulations are robust for a wide range of thresholds over a wide range of environments (parametrized by K). As expected, increasing the proprioceptive threshold (or lowering the neural sensitivity to stretch) results in a lower undulation frequency. However, unlike external modulation, the increased threshold manifests in an increased wavelength of undulation. Thus, the model predicts that the direct or indirect modulation of the proprioceptive threshold should lead to an inverse relationship between wavelength and frequency (wavelength increases but frequency decreases with threshold). Importantly, in the model, this inverse frequency–wavelength relationship is maintained across a wide range of environmental resistances, suggesting that the nematode's ability to internally modulate its waveform does not depend on environmental resistance. This presents a novel key signature of proprioceptive control.

Figure 3.

Internal modulation of proprioceptive pathways gives rise to an inverse frequency–wavelength relationship. Internal neural modulation of (a) proprioceptive threshold and (b) proprioceptive range, for K = 7.5 (circles), K = 12 (squares), K = 18 (diamonds), K = 30 (triangles) and K = 45 (stars), with E = 100 kPa.

For any fixed environmental resistance K, threshold modulation appears to yield at most a twofold change in frequency and wavelength, as contrasted with the multi-fold increase in frequencies and more than twofold increase in wavelengths arising from external gait modulation. The lower the external resistance K, the stronger the resulting modulation due to a change in the proprioceptive threshold. Finally, the speed of the nematode in these simulations roughly matches observed locomotion velocities across the entire range of thresholds tested (electronic supplementary material, figure S3). In other words, for the vast range of parameters, the speed is proportional to the frequency, such that the modulation of thrust is negligible.

The inverse frequency–wavelength relationship obtained under threshold modulation begs the question of its generality. Will other forms of neural modulation yield a similar relationship? By construction, in our proprioceptive model of control, there are only two fundamental targets of modulation, threshold and range of proprioception. Naively, however, if our intuition is drawn from our past experience of gait modulation, increasing the proprioceptive range may yield a different trend. Under external modulation, an increased proprioceptive range facilitates longer undulation wavelengths, which in turn allow the animal to reach the threshold more quickly (hence speeding up the undulations). To understand the role of sensory range in locomotion, and to better understand the link between sensory range and kinematics, we varied the proprioceptive range from an effectively local range of 5% to a maximum of 90% of the body length, posteriorly from the action of the muscle moment.

Following our intuition above, we find that the higher the proprioceptive range, the longer the undulatory wavelength (figure 3b, and electronic supplementary material, figure S4). However, unlike the wavelength–frequency coupling that results from external gait modulation, we find that an increased range suppresses the undulation frequency. Thus, we find that range modulation also gives rise to an inverse relationship between wavelength and frequency, qualitatively mirroring that of threshold modulation. However, under range modulation, the extent of the modulation of both frequency and wavelength is more significant.

The model of Boyle et al. [28] required an extended proprioceptive range spanning half of the nematode's body length to achieve the long-wavelength undulations observed during swimming. While the extended proprioceptive range is probably unrealistic, we find that, for instantaneous and linear proprioception, a similarly long effective range is required to generate the desired range of kinematic parameters across water and agar. We note that the form of proprioceptive current incorporated in our model is minimal by construction and could be loosely interpreted as an effective range that may be estimated by a more sophisticated, possibly nonlinear integration of stretch over a more limited range of the body.

Finally, in our model, reversing the direction of the proprioceptive range to face anteriorly reverses the direction of locomotion (electronic supplementary material, figure S1). Reversing the polarity of the proprioceptive input current (either by detecting contraction, or by polarizing, rather than depolarizing the corresponding B-type neuron in response to stretch) would reinstate forward locomotion with anteriorly facing proprioceptive input.

6. Proprioceptive feedback suppresses neuromechanical phase lags

In the previous section, we identified signatures of proprioceptive behaviour arising from the modulation of the proprioceptive signal in terms of kinematic quantities, such as undulation frequencies and wavelengths. Here, we turn our attention inwards to the coupling between neuromuscular activity and body posture as it manifests in neuromechanical phase lags. Our aim is to identify signatures of proprioceptive control that can be directly compared and distinguished from signatures of feed-forward (CPG) control, and to pin down experimental conditions under which such signatures may be distinguished.

One manifestation of the coupling between neural circuits and the body, which is evident in a variety of swimming animals, is an advancing neuromechanical phase [6,41,42]. When a retrograde undulation is generated, a neuromechanical wave propagates from head to tail, resulting in forward thrust of the body. Typically, the wave of neuromuscular activation travels faster down the body than the physical wave of body undulations, resulting in an advancing neuromechanical phase lag: a phase lag between the neural and muscle activation on the one hand and the mechanical action of the body on the other, which grows from head to tail. The wide range of animal sizes and conditions in which neuromechanical phase lags arise suggests that such phase lags are fundamental to undulatory locomotion. In a recent study, Butler et al. [43] reported musculo-mechanical phase lags of approximately π/4 (or 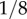of an undulation cycle) across a wide range of external fluid viscosities, and conjectured that the maintenance of a constant lag is indicative of a proprioceptive mechanism. To our knowledge, however, little is known about the propagation of neuromechanical phase lags along the nematode's body. Our intuition is that whereas the wave speed of neural activation and of muscle activation are largely decoupled under feed-forward control, the entrainment of the neural activation by the curvature, as observed under gait modulation, should impose a constant phase lag along the body.

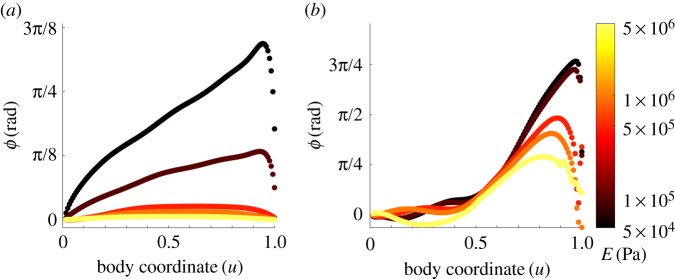
To address this question, we compared neuromechanical phase lags under feed-forward and feedback-driven control. To mimic CPG control, we imposed a neural activation function in the form of a travelling sine wave that drives our model of the body muscles and mechanics (see electronic supplementary material, §S1). We set the period of undulations to T_f = 2 s with a wavelength of λ_f = 0.6 mm. As expected, simulations of feed-forward control yield linearly advancing neuromechanical phase lag (figure 4a), but the rate of increase depends strongly on the body stiffness. For a Young's modulus of 0.5 MPa or above, the phase lags (and corresponding time lags, see electronic supplementary material, figure S5a,b) are effectively negligible. For intermediate values of Young's modulus, around 50–100 kPa, the advancing phase is clearly significant, with the phase lag growing to almost a fifth of an undulation period towards the tail; hence, the corresponding time lags should be directly measurable. At lower values of Young's modulus, the phase lag in our feed-forward simulations rapidly grows, and below 20 kPa it exceeds a sixth of an undulation at the tail and the nematode becomes too flaccid to generate a coordinated undulatory gait (not shown).

Figure 4.

Neuromechanical phase lag along the body, simulated in agar, over the same range of Young's modulus shown in figure 2. (a) Under feed-forward control, lag is negligible for E ≳ 0.5 MPa but increases approximately linearly for lower E. Note that for a constant undulation period T_f the phase lag ϕ and time lag Δ are related by ϕ = 2πT_f/Δ. (b) Under proprioceptive control, the lag is negligible in the anterior half of the body and increases dramatically towards the tail (u = 1).

To determine how proprioceptive control affects the magnitude and spatial profile of neuromechanical phase lag, we ran simulations of our proprioceptively driven model using the same values of Young's modulus and drag coefficients. In line with our intuition, in the anterior, phase lags appear strongly suppressed, with muscles preceding body curvature by under 5% of a cycle midway down the body, for all values of Young's modulus. These lags are notably smaller than observed by Butler et al. [43]. As in the case of feed-forward control, we also observe that the stiffer the body, the smaller the phase lag, though this effect seems small in the anterior, owing to the clamping of the neuromechanical lag. However, unexpectedly, and for all values of Young's modulus, phase lags advance rapidly in the posterior part of the body, such that the curvatures towards the tail are retarded by up to a third of a full cycle behind the driving muscle torque.

We note that, unlike our model of CPG control, the frequency of undulations is an emergent property of the system and its interactions with the environment. Therefore, a significant phase lag does not necessarily imply an experimentally measurable time lag. To better understand the implication of these results, we considered the corresponding (measurable) time lags (electronic supplementary material, figure S5a,b). In our simulations, higher body stiffness leads to faster undulations (figure 2a) and hence shorter time lags (electronic supplementary material, figure S5b). We find that time lags in the anterior part of the body appear negligible for intermediate and high values of E; for lower Young's moduli of 50–100 kPa, time lags under feedback control are still considerably smaller than we observe in our CPG model (figure 5 and electronic supplementary material, figure S5). Recall that a modulation of Young's modulus is directly analogous to a modulation of viscosity in Newtonian media. Therefore, our results for the anterior of the body are expected to hold for a wide variety of external drag coefficients (electronic supplementary material, figure S5).

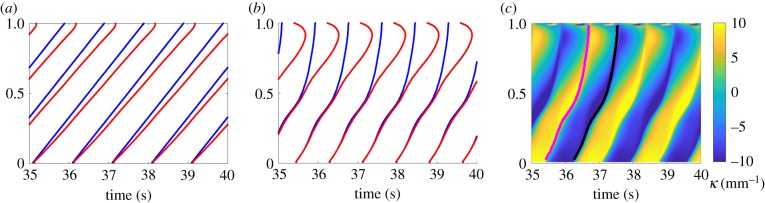
Figure 5.

Zero contours of the muscle torque, β(u, t) (blue), and body curvatures, κ(u, t) (red), obtained from simulations in an agar-like medium and E = 100 kPa. Both positive and negative zero-crossings are included. (a) Under a model of feed-forward (CPG) control, the latency between activation and body bend grows linearly along the body. (b) Under a model of proprioceptive control with a diminishing proprioceptive range in the posterior half of the body, the curvature and muscle activation are tightly coupled in the anterior half; the increasing phase lag towards the tail arises from an accelerated neuromuscular wave speed of muscle torque in the posterior half of the body. (c) Kymograms of the body curvature corresponding to (b). Black and magenta lines show peak negative and positive values of muscle activation β(u, t), along the body, respectively.

To interpret our results, we asked how the posteriorly advancing phase lags relate to the propagation of bends along the body. Figure 5 demonstrates the advancing phase lags for simulations of feed-forward and feedback-driven control with default parameters. Under feed-forward control, zero contours of both the muscle activation and the body curvature show a characteristic and consistent wave speed along the body. By contrast, under feedback control, the wave speed of the muscle activation sharply increases midway along the body. This pattern of muscle activation is consistent with our model of proprioceptive feedback: the dorsoventral switching of the neural activation closely follows the peak curvature of the opposite side all along the body. Unlike the muscle activation, the curvature maintains an approximately fixed wave speed. The corresponding curvature kymogram with superimposed contours of peak (positive and negative) excitation confirms this observation: the body elasticity is too weak (relative to the mechanical load by the environment) for the tail to respond as promptly as the anterior of the nematode.

While our results for the posterior part of the body may not match the curvature dynamics in the nematode, they highlight the sensitivity of the system to the exact form of sensory input. In fact, the rich dynamics in the tail demonstrate the tight coupling among kinematic parameters of curvature, wavelength, wave speed and thrust under feedback control. It is striking that the point along the body at which the phase lag emerges under feedback control coincides with the range of the proprioceptive field (L/2 in this case, see electronic supplementary material, §S1). In our model, the proprioceptive range gradually vanishes in the posterior half of the body. Indeed, with different ranges of the proprioceptive field, the phase lag emerges consistently at the point along the nematode at which the receptive field begins to decrease (electronic supplementary material, figure S5e). Thus, we conclude that, regardless of the proprioceptive range, feedback control leads to a strong clamping of proprioceptive feedback at least along the anterior of the body. We note that further work would be required to better understand the origin and physiological significance, if any, of the observed posterior phase lags. In particular, in our model, we find that they strongly depend not only on the receptive field but also on the form of the proprioceptive sensory input (not shown).

We further conclude that while feed-forward and feedback control architectures generate qualitatively very different signatures, the time scales involved (≲100 ms) may make it challenging to experimentally distinguish proprioceptive from feed-forward control based on neuromechanical phase lags. If our estimates of the nematode's Young's modulus are accurate, it should nonetheless be possible to resolve advancing phase lags in agar-like or higher viscosity conditions.

7. Discussion

Understanding neural circuits that allow animals to orchestrate and fine tune their locomotion behaviours is a long-standing endeavour. A variety of behaviours studied to date, from invertebrates to humans, are controlled by CPG circuits that are subject to activation and modulation by descending control and ascending sensory information, often in the form of proprioception [44,45]. Indeed in a number of cases, sensory neurons are embedded within the pattern generating circuit itself, such that a meaningful description of the behaviourally relevant pattern generation mechanism invariably combines the two [46]. Whatever the rhythm generating mechanism, however, all motor behaviour is ultimately generated by the combined action of neural circuits and the body. It stands to reason, therefore, that an integrated understanding of neural circuits and biomechanics can provide a much more complete understanding of the control of motor behaviour [9,41,47].

While the importance of proprioception is well established in controlling posture and locomotion in a variety of limbless and legged species [4,48–51], the roles of proprioception in shaping motor patterns in peripheral and central nervous systems is not well understood. In C. elegans, proprioception has been studied primarily with a focus on posture or locomotion [22–28,52]. Although the neural circuitry of C. elegans is fully mapped, the precise pattern generating mechanism responsible for locomotion remains undetermined. The evidence to date suggests a number of complementary proprioceptive pathways and functions. Previous computational models as well as experimental studies suggest that, within the ventral nerve cord, proprioception may be sufficient for pattern generation and is necessary for coordinating dorsoventral anti-phase contractions as well as for imposing the appropriate wave speed along the body [26,28,30]. Recent experimental [29,30] and theoretical [53] papers also present support for CPGs within this circuit.

Here, we follow a modelling approach to study neuromechanical coupling in C. elegans forward locomotion. In doing so, we seek experimental signatures of proprioceptive control that may shed light on the mechanisms and characteristics for pattern generation in C. elegans. In particular, our analysis points to a more universal description of gait modulation that unifies our description of viscous and viscoelastic media and allows for a better understanding of the interplay between body stiffness and environmental drag. Furthermore, we observe a qualitative distinction between mechanical and neural modulation. On the one hand, the model captures the correlation between frequency and wavelength as a function of mechanical load [10]. On the other hand, increasing either the activation threshold or the proprioceptive field yields the opposite relationship: the higher the frequency, the lower the wavelength. Finally, we characterize the neuromechanical phase lags in this system and find that while proprioception can serve to suppress such lags along the body, the actual lags are likely to be small and difficult to resolve experimentally.

In the nematode's neural circuit, multiple neuron classes associated with proprioceptive function contain processes that extend along the rostro-caudal body axis, suggesting an extended receptive field [23–26]. Here, and in previous studies, we have followed this conjecture. We note that, in other species, stretch receptors in neurons and muscles have been found to respond to deformation, muscle tension or length [4]. If stretch receptors integrate length along their body, it is essential to identify their receptive field in order to better understand the sensory motor loop.

While most conjectured proprioceptive neurons have posteriorly facing axons, Wen et al. [26] have reported behaviours consistent with anteriorly facing proprioceptive fields, with a range of under 200 μm. Here, our model requires an extensive proprioceptive range of approximately half the body length to generate the experimentally observed ranges of frequency and wavelength; these results are consistent with Boyle et al. [28] although our model incorporates only a toy model of proprioception. Shorter ranges, while still generating frequency modulation, exhibit a much reduced wavelength modulation. Simulations using feed-forward control of the same mechanical framework previously suggested [33] that gait modulation may be needed by C. elegans to maximize its speed in different media. If so, the nematode's effective proprioceptive range places important constraints on the mechanical and sensory coupling mechanisms required for robust locomotion. Our model therefore begs for a proposed mechanism by which such an effective proprioceptive range may be achieved in the nematode.

Neuromechanical phase lags are known to contribute to locomotion in a variety of swimmers, and yet, have not been characterized or modelled in detail in C. elegans [43]. Here, we find that, unlike in fish [47], the relatively low beat frequencies of the nematode combined with the relatively high effective Young's modulus preclude the existence of any significant neuromechanical phase lags in water and low viscosity fluids. In environments with sufficiently high external drag (sufficiently low e), we found that neuromechanical phase lags can arise but depend strongly on the nature of the pattern generation. In a model of CPG control, we observe potentially significant linearly advancing phase lags along the body. When the rhythm is entrained by the body curvature, however, as in our model of proprioceptive control, we observe that neuromechanical phase lags are strongly suppressed, over a wide range of values of body stiffness. In practice, experiments directly measure time, rather than phases. For our estimated values of Young's modulus, and conditions ranging from water to agar, our results suggest that neuromechanical time lags are very small and therefore unlikely to be useful in discerning between feed-forward and feedback-driven coordination of undulations. These results therefore suggest that future experiments should focus on high viscoelasticity and characterizing the advance of phase lags along the body.

Estimates for Young's modulus in C. elegans range over five orders of magnitude [39,54]. The methods used to obtain these estimates vary considerably and address complementary aspects of the nematode's material properties (see the discussion in Cohen & Ranner [33], for example). We have previously considered the role of Young's modulus in C. elegans locomotion in a mechanical framework driven by feed-forward (CPG-like) control [33], finding that a Young's modulus of at least 50–100 kPa is required to produce observed locomotion speeds. Revisiting this question in the context of a proprioceptive control has allowed us to take advantage of drag-dependent undulation time scales in order to check for consistency in our estimates while potentially adding an upper estimate for E. Furthermore, by recasting the model in dimensionless form, we are able to express our experimental estimates more generally, since any estimated Young's modulus is dependent on other parameter choices in the model (equation (2.1)). We find that, within our model, a dimensionless modulus of e ≈ 0.02 (corresponding, with the above caveat, to a Young's modulus of 100 kPa under agar-like conditions) is consistent with experimentally observed gait modulation. By contrast, a dimensionless parameter of 1 (corresponding to a Young's modulus of 5 MPa under the same assumptions) would not give rise to discernible gait modulation.

In this study, we have focused our consideration on a proprioceptive control mechanism to better understand sensory–motor coupling effects subject to proprioceptive entrainment. To maximize the explanatory power of our investigation, we have simplified the sensory–motor coupling to a minimal model. This investigation therefore paves the road for further studies that may include a more detailed description of the neural circuitry and neuronal properties. In particular, we anticipate the fundamental insights gained here to extend to models in which a proprioceptive mechanism is superimposed on centrally generated patterns, a scenario not examined in this work.

Data accessibility

Additional methods and figures are available online as electronic supplementary material at rs.figshare.com; the model source code is available at https://bitbucket.org/leedswormlab/curve-worm-royal-society-paper.

Competing interests

We declare we have no competing interests.

Funding

This work was funded by the EPSRC (EP/J004057/1). T.R. is funded by a Leverhulme Trust Early Career Fellowship. Part of this work was undertaken on ARC3, part of the High Performance Computing facilities at the University of Leeds, UK.