Nonlinear averaging of thermal experience predicts population growth rates in a thermally variable environment

Abstract

As thermal regimes change worldwide, projections of future population and species persistence often require estimates of how population growth rates depend on temperature. These projections rarely account for how temporal variation in temperature can systematically modify growth rates relative to projections based on constant temperatures. Here, we tested the hypothesis that time-averaged population growth rates in fluctuating thermal environments differ from growth rates in constant conditions as a consequence of Jensen's inequality, and that the thermal performance curves (TPCs) describing population growth in fluctuating environments can be predicted quantitatively based on TPCs generated in constant laboratory conditions. With experimental populations of the green alga Tetraselmis tetrahele, we show that nonlinear averaging techniques accurately predicted increased as well as decreased population growth rates in fluctuating thermal regimes relative to constant thermal regimes. We extrapolate from these results to project critical temperatures for population growth and persistence of 89 phytoplankton species in naturally variable thermal environments. These results advance our ability to predict population dynamics in the context of global change.

1. Introduction

Organisms live in variable environments. Demographic rates and outcomes that integrate temporal or spatial environmental variation may differ substantially from what might be predicted based on short-term physiological responses to constant, non-varying experimental environments. For example, population growth rates are predicted to vary with temperature as described by their thermal performance curve (TPC). The minimum and maximum temperatures that allow population growth can be estimated from TPCs, and these ‘critical temperatures' are important thermal traits used in the large and growing body of synthesis research that links physiological processes with projected population responses to climate change [1,2].

One factor that complicates the application of thermal traits derived from TPCs to natural environments is that TPCs are usually generated from physiological assays in constant-temperature laboratory experiments, in contrast to the thermal variation organisms would experience in the field. Thermally variable environments can lead to population growth rates over time that differ substantially from estimates based on the average temperature over the same time period, a problem known as the ‘fallacy of the averages’ [3,4]. This difference complicates projections of population performance based on experiments in constant conditions, prompting calls for ecologists to explicitly incorporate environmental variation into predictions of performance in the field [5–7]. Because temporal patterns of environmental variability differ across regions and the lifespans of organisms, an approach that allows quantitative scaling from TPCs of population growth generated under constant-temperature conditions to population performance in variable environments may be particularly useful for understanding systematic variation in patterns of abundance and distribution, and species' responses to climate change [8].

Biological responses to environmental variation depend on whether the relationship between performance and an environmental gradient is linear or nonlinear [4,9,10], and if nonlinear, whether it is accelerating with increasing temperature or decelerating (figure 1a). When performance, P, changes nonlinearly with environmental conditions, E, time-averaged performance in a variable environment 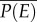does not necessarily equal performance at the mean environmental condition 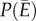. This fact, captured by the well-known mathematical rule ‘Jensen's inequality’ leads to clear predictions about how environmental variability should affect performance over time [9,11,12]. Jensen's inequality states that if P is a nonlinear function of E, then 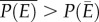where P(E) is accelerating (i.e. positive second derivative) and 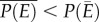where P(E) is decelerating (i.e. negative second derivative; figure 1b). In the context of temperature, the relationship between organismal or population performance and temperature, captured in the TPC (figure 1a), is almost always nonlinear [12–14]. Yet the relationship between temperature and population growth is often implicitly assumed to be linear in commonly used demographic models and degree-day analyses [15], making these approaches inadequate to describe population dynamics over wide temperature gradients [16]. The potential ecological and evolutionary effects of Jensen's inequality have been shown in several recent studies [2,12,17]. Yet, ecologists struggle to incorporate thermal variability when making predictions about the effects of temperature on growth, abundance and distributions of species in nature, often assuming that species' thermal experiences are well represented by the mean temperature of their environment.

Figure 1.

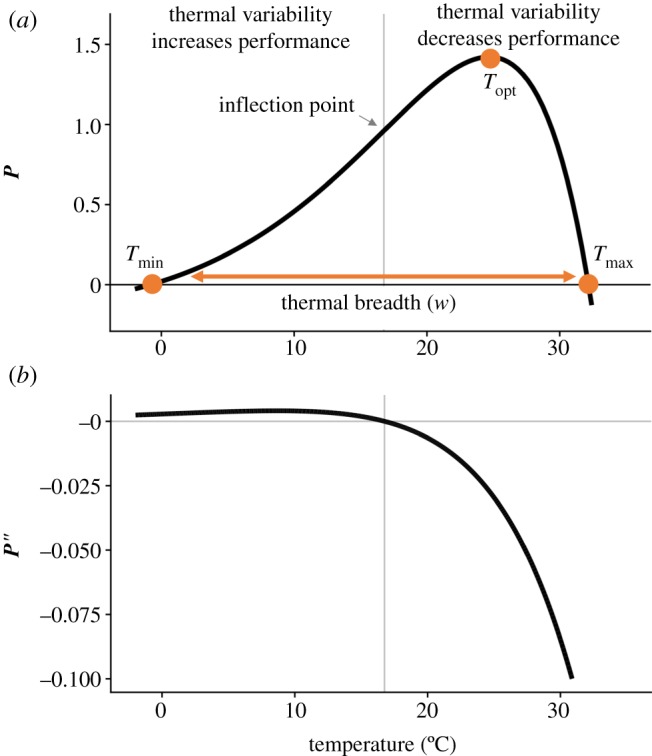
(a) A TPC and its critical temperatures (T_min, T_max, T_opt; dots) and thermal breadth, w. The critical temperatures are not fitted parameters of the TPC, but are estimated by numerical optimization. This negatively skewed curve shows an exponential increase typical of processes following an Arrhenius function, with an accelerating region to the left of the inflection point (grey vertical line), followed by a decelerating region to the right of the inflection point. Notice that the accelerating region corresponds to the region with a positive second derivative (b). Figure adapted from [5], but parametrized with T. tetrahele data from this study. (Online version in colour.)

The typical shapes of TPCs (figure 1a) [18], with an accelerating phase at lower temperatures and a decelerating phase at higher temperatures, suggest positive effects of thermal variation at low temperatures and negative effects at high temperatures [5,17]. Current estimates of the consequences of temporal thermal variability for population growth rates have assumed a certain shape to the curve (i.e. a Gaussian rise and a parabolic fall [2]), thus forcing certain outcomes of temporal variability. The shape and skew of the TPC can vary substantially among phenotypes and ecological contexts, including predation risk or resource supply levels [12,19,20], leading to more nuanced responses to environmental variation than may be predicted from empirical TPCs generated in the laboratory under highly simplified conditions. To date, empirical tests of how temporal temperature variability affects population growth rates have been done at only two mean temperatures [21], and have not made quantitative predictions for population growth in fluctuating conditions based on the curvature of the TPC under constant conditions.

Here, using a fast-growing green alga with a short generation time, we tested whether population growth in a diurnally fluctuating thermal environment reflects the effects of nonlinear averaging of performance at each temperature experienced. We hypothesized that population growth rates would be accurately predicted by Jensen's inequality and the instantaneous effects of time-averaging of acute thermal responses in population growth. Under this hypothesis, performance at a given temperature in a fluctuating environment is no different than performance at that temperature in a constant environment, such that time-averaged performance in fluctuating conditions would be directly predictable based on temperature-dependent performance under constant conditions. Alternatively, if time-dependent stress or acclimation effects that depend on recent thermal history modify growth rates in fluctuating environments [8,22,23], then population performance in naturally variable environments may not be predicted directly from TPCs generated under constant laboratory conditions and would require a more detailed understanding of the mechanisms and time-course of thermal niche plasticity.

2. Methods

To test our hypothesis that performance in variable environments is predictable based on Jensen's inequality and nonlinear averaging, we experimentally estimated population growth in constant and fluctuating thermal environments. First, we used experimental populations of Tetraselmis tetrahele grown in the laboratory at nine constant temperatures to generate a TPC for population growth rate (electronic supplementary material, figure S1, steps 1–2). Then, we expressed expectations for how population growth in fluctuating environments varies with mean temperature using two approaches: nonlinear averaging and scale transition theory (electronic supplementary material, figure S1, step 3). Finally, we tested these predictions against observed population growth rates from experimental populations of T. tetrahele reared under fluctuating thermal conditions over six mean temperatures (electronic supplementary material, figure S1, steps 4–5). Then, having identified an approach for linking laboratory performance to fluctuating field conditions, we drew on a global dataset of empirical TPCs for phytoplankton population growth rates, which vary in shape and geographical origin, and used nonlinear averaging to estimate in situ population growth rates, given in situ environmental variation at each species's isolation location (electronic supplementary material, figure S1, step 6). We estimated the extent to which predicted growth rates differ when they are predicted using nonlinear averaging of varying temperatures over time, as compared to when they are predicted based on mean temperatures only. By including a range of phytoplankton TPC shapes from a global distribution, we explored the consequences of considering thermal variability in projections of population growth rates, with implications for patterns of abundance and distribution.

(a). Using nonlinear averaging to predict population growth in variable environments

We described how population growth rate, r, varies with temperature using a TPC, r = f(T). We described the expected growth rate, E(r), for a population over time, t, by taking the average observed growth rate over time,

2.1

where t indexes time. While this approach allows for population growth rates to be negative, the time-averaging approach assumes that the sequence of temperatures does not make population growth rate negative for long enough to drive a population to extinction nor to produce irreversible damage that alters how individuals perform at more benign temperatures.

Empirical time series of environmental or body temperatures required to use equation (2.1) are often not available; however, mean and variance of the distribution of temperatures over a period of time may be more readily accessible. In cases when only the mean and variance of the temperature distribution are available, expected performance can be estimated using a Taylor approximation of the TPC (electronic supplementary material, equation S5), an approach that has been incorporated into scale transition theory [5,17,24]. Scale transition theory makes predictions for how nonlinear dynamics change over spatial and temporal scales. We compare results using both approaches (equation (2.1) and electronic supplementary material, equation S5) to increase the toolkit for ecologists with different kinds of temperature data available (electronic supplementary material, appendix A, figures S2–S4).

(b). Experimental quantification of thermal performance curves in constant and fluctuating environments

We experimentally quantified TPCs in constant and varying thermal environments for T. tetrahele, a globally distributed coastal marine phytoplankton species. We used acute TPCs estimated directly from experimental populations newly exposed to a temperature gradient (i.e. with no acclimation period), rather than longer-term acclimated TPCs, to match the time scale of temperature exposure under constant and fluctuating conditions and to simulate the effects of temperature variability in real time. The cultured strain used here was obtained from the Canadian Centre for the Culture of Microorganisms (UW418) and was originally isolated off the coast of Vancouver Island, British Columbia, Canada. Tetraselmis tetrahele was maintained in laboratory culture in ESAW medium (Enriched Seawater, Artificial Water) [25] at 16°C on a 16 L : 8 D cycle under nutrient- and light-saturated conditions for 1 year (approx. 300 generations) before the start of the experiments.

We initiated 20 replicate experimental populations of T. tetrahele in 30 ml glass test tubes containing 20 ml of 10 µM nitrate ESAW medium at a density of approximately 700 cells ml⁻¹ under constant-temperature conditions at 0°C, 5°C, 10°C, 15°C, 20°C, 24°C, 27°C, 29°C and 32°C (electronic supplementary material, figure S1, step 1) and under fluctuating temperature conditions, with the same mean temperatures as the constant conditions, but fluctuating ±5°C (i.e. 0–10°C, 5–15°C, 10–20°C, 15–25°C, 19–29°C and 22–32°C; electronic supplementary material, figure S1, step 4). We created fluctuating temperature treatments by programming temperature-controlled incubators (Panasonic MR 154) to switch between low and high temperatures once per day (i.e. approx. 11.5 h at each of the high and low temperatures, with 30 min of transition time in between). This period corresponds to approximately half a generation time of T. tetrahele at 20°C. We verified that the rates of heating and cooling were the same in the experimental populations by measuring water temperatures inside the test tubes at 1-min intervals with iButton temperature loggers (Maxim/Dallas Semiconductor). To avoid confounding the temperature cycles with daily light cycles, we grew all experimental populations under continuous light at saturating intensities of 150 µmol m⁻² s⁻¹ (electronic supplementary material, figure S5). The source population was acclimated to continuous light for four months prior to the experiment during which time we observed no detrimental effects on population growth rates. Continuous light regimes are often used in algal physiological studies to simplify sampling [26] and have been shown to induce rapid growth with no detrimental effects in coastal algae [27]. We sampled four replicate populations destructively at each of five time points over the period corresponding to the exponential growth phase (i.e. when resources were not limiting) at each temperature. Population abundances were estimated from 250 µl samples using a FlowCAM (flow rate = 0.3 ml min⁻¹; FlowCAM VS Series, Fluid Imaging Technologies).

(c). Estimating the temperature dependence of population growth in constant and variable conditions

We estimated the temperature dependence of population growth directly from the observed time series of population abundance over the temperature gradient [28] (electronic supplementary material, figure S1, step 2, and figure S6). We modelled the temperature-dependent intrinsic rate of population growth, r, during the exponential growth phase as

2.2

where N(t) is the number of individuals at time t and r(T) is given by [19],

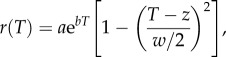2.3

using nonlinear least-squares regression with the nls.LM function in the minpack.LM package in R [29]. Population growth rate, r, is a function of temperature, T, a and b are parameters from the Eppley curve [30] that together describe the increase in maximum observed population growth rates with temperature, z determines the location of the maximum of the quadratic portion of the function and w is the range over which the growth rate is positive (i.e. the thermal breadth). Equation (2.3) allows the TPC to have any combination of accelerating and decelerating portions and allows for population growth rates to be negative at thermal extremes. We favoured this TPC over others, such as the modified Gaussian, which do not permit negative population growth rates at cold temperatures, and because it is parametrized with biologically meaningful parameters for phytoplankton [19,31]. For comparison, we fitted several other functional forms to the experimental dataset but did not find any better fits when we compared models via AIC. In addition to estimating the temperature dependence of r directly from the time series at all temperatures simultaneously, we also estimated the temperature dependence of r via an ‘indirect’ approach [28] (electronic supplementary material, appendix A), a traditional way of fitting TPCs, in which we first estimated growth rates at each temperature separately, and then fit equation (2.3) to the growth estimates at each temperature (electronic supplementary material, figures S7 and S8).

(d). Estimating thermal traits

To facilitate comparisons of thermal performance in constant and fluctuating environments, we estimated four thermal traits derived from the TPC (figure 1a): the optimal temperature for population growth, T_opt, the minimum and maximum temperatures for positive population growth, T_min and T_max, and thermal niche breadth, w [32]. Here we use T_min and T_max to denote the lower and upper limits of the thermal niche (w) for positive population growth, respectively (figure 1a). T_opt, T_min and T_max are not parameters of equation (2.3), but rather features of the curve defined because they are understood to be important for the ecology of populations. We identified T_opt via numerical optimization using the optim function in R, and T_min and T_max by finding the roots of the TPC (i.e. the intercepts of the TPC with the x-axis) using the uniroot function in R. We quantified the analogues of these critical temperatures under thermally variable conditions and refer to them as the minimum mean and maximum mean temperatures for positive population growth under fluctuating conditions, 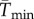and 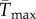, respectively, the mean temperature for optimal growth under fluctuating conditions, 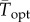and thermal niche breadth under fluctuating conditions, 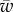. Because T_min from the estimated curve could be below the freezing point of seawater, −1.8°C, we used an additional metric of thermal breadth, w_s, which assumes that T. tetrahele cannot maintain positive population growth below the freezing point of seawater. We defined w_s as the difference between T_max and −1.8°C if T_min was estimated to be below −1.8°C. If T_min was estimated to be above −1.8°C, then we defined w_s as the difference between T_max and T_min.

To generate estimates of uncertainty in TPC fits, we determined confidence intervals around fitted TPCs using non-parametric bootstrapping of mean-centred residuals using the nlsBoot function with 999 iterations in the nlstools package [33] in R. We calculated 95% confidence intervals as the range between the 2.5th and 97.5th quantiles.

To test our hypothesis that performance in varying conditions can be explained by nonlinear averaging of performance at each temperature experienced, we generated an expected TPC for T. tetrahele under thermally fluctuating conditions (electronic supplementary material, figure S1, step 3). We evaluated equation (2.1) with f(T) equal to the TPC fitted using equation (2.3), for all values of T between 0°C and 33°C (i.e. the entire TPC), assuming that experimental populations spend half their time at 5°C above and below each mean temperature. We generated confidence intervals around the expected TPC under variable conditions by evaluating equation (2.1) for each of the 999 bootstrapped constant-environment curves and calculating 95% confidence intervals as the range between the 2.5th and 97.5th quantiles (figure 2a, dashed band). This predicted TPC demonstrates the effects of Jensen's inequality: we expected temperature variability to increase population growth in the accelerating phase of the TPC and decrease population growth rate in the decelerating phase of the TPC [9] (figure 1), and to shift 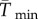and 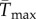to lower temperatures because the TPC is left-skewed (figure 2a). Time-averaged maximum growth rate, 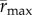, should decrease under variable temperature conditions relative to constant conditions because T_opt is always in a decelerating portion of the TPC. Finally, we expected the thermal breadth under fluctuating conditions, 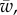to also decrease under fluctuating conditions if T_min is close to freezing, thus preventing 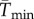from shifting to lower temperatures to compensate for decreased 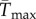_. Ultimately, the predicted balance between positive and negative effects of temperature variability depends on whether the range of variable temperatures is above or below the inflection point, the shape of the curve and the amount of variability.

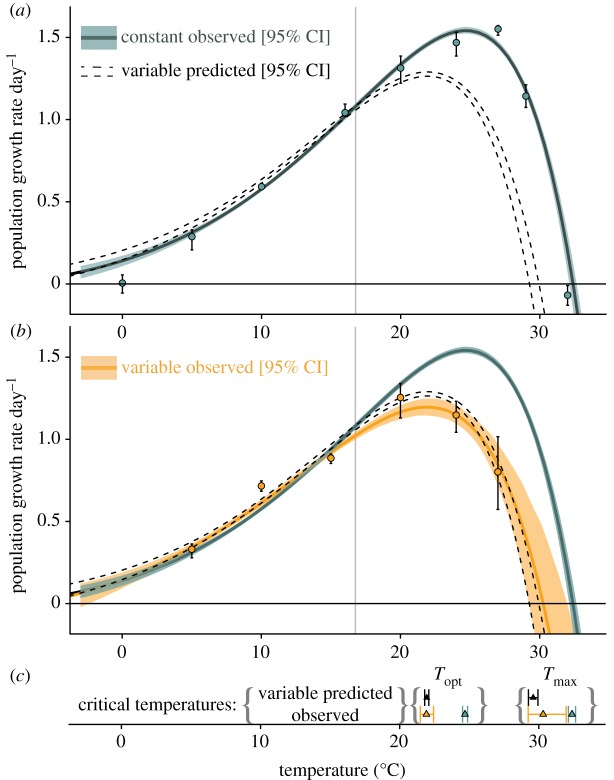
Figure 2.

TPCs for T. tetrahele populations growing under constant and variable temperature conditions. (a) Exponential growth rates under constant-temperature conditions; green line is the fitted TPC and green shading corresponds to 95% CI generated from non-parametric bootstrapping. The dashed curve represents predicted mean growth rate and 95% CI under thermally variable conditions (±5°C) based on nonlinear averaging (equation (2.1)). Points and error bars are observed mean growth rates generated by estimating exponential growth rates at each mean temperature separately (‘indirect’ approach described in the electronic supplementary material, appendix A; error bars represent 95% CI). (b) Exponential growth rates under thermally fluctuating conditions (±5°C); dashed curve is predicted based on panel (a) and equation (2.1), orange line is the fitted TPC under fluctuating conditions, orange shading corresponds to 95% CI generated from non-parametric bootstrapping. Orange points and error bars are observed mean growth rates in the fluctuating temperature regime (estimated via the ‘indirect’ approach, electronic supplementary material, appendix A; error bars represent 95% CI). (c) Predicted and observe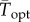d and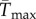 were statistically indistinguishable (predicted: black triangles and 95% CI error bars, observed: orange triangles and 95% CI error bars), and lower than observed T_max and T_opt in constant conditions (green triangles and 95% CI error bars).

We then compared these predictions to observed population growth rates estimated in fluctuating thermal environments, which we estimated by fitting equations (2.2) and (2.3) to the time series of population abundance in the variable experimental treatments (electronic supplementary material, figure S1, step 5). For this, we used 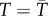, the mean temperature in each treatment, to characterize the thermal experience of populations in thermal regimes that we know varied over time. By doing this, we explicitly and empirically tested whether the ‘fallacy of the averages' is sufficient to explain how TPCs from fluctuating environments differ from TPCs in constant environments.

(e). Applying nonlinear averaging to estimate in situ phytoplankton population growth rates

We estimated time-averaged population growth rates in thermally variable environments for a diverse set of phytoplankton species using nonlinear averaging (equation (2.1); electronic supplementary material, figure S1, step 6) and scale transition theory (electronic supplementary material, equation S5). We estimated TPCs for 89 species by fitting equation (2.3) to published phytoplankton growth rates [31] measured in the laboratory at arrays of constant temperatures. We fit the TPCs using maximum-likelihood estimation with the mle2 function in the bblme package in R [34] (electronic supplementary material, appendix A).

For each of these 89 species, we used historical reconstructed sea surface temperature (SST) data to characterize thermal regimes at isolation locations reported in the original studies. For each species’s isolation location, we extracted daily average SSTs from the closest point in NOAA's Optimum Interpolation Sea Surface Temperature dataset, Advanced Very High Resolution Radiometer (AVHRR) and Advanced Microwave Scanning Radiometer on the Earth Observing System (AMSR-E) AVHRR+AMSR, which uses additional data from AMSR-E, available from 2002 to 2011 [35]. This dataset has 0.25° spatial resolution.

(f). Statistical estimation of ‘realized’ thermal performance curves

For each species and isolation location, we generated a ‘realized TPC’ which represents expected growth rates, given natural patterns of temperature variability (electronic supplementary material, figure S1, Step 6). We compared the expected in situ growth rate, r, at each species's isolation location using a mean annual temperature only, such that T = mean annual SST at the isolation location, with a time-averaged growth rate using two approaches: first using equation (2.1) where T_t is daily temperature at the isolation location and where f(T) is the TPC fit using equation (2.3); and second using the scale transition theory (Taylor approximation) approach (electronic supplementary material, equation S5) where f(T) is the TPC fit using equation (2.3), 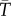and 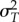are the mean and standard deviation of daily temperatures over the period 1981–2011 (electronic supplementary material, figures S3 and S4). Our purpose in using these two approaches was to compare the predictions made with empirical time series of temperature versus only the mean and standard deviation of the temperature distribution. We then extrapolated these approaches over the entire TPC to generate an expected ‘realized TPC’, given in situ thermal variability. To do this, we first generated a synthetic temperature distribution around each mean temperature from −2°C to 40°C by taking the distribution of temperatures over the historical time series at each isolation location, subtracting the mean and then adding each temperature from −2°C to 40°C. From these ‘realized TPCs’, we compare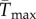d and 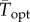to the T_opt and T_max estimated in constant laboratory environments.

Given that predicted effects of thermal variability depend on curve shape and temperature variance (electronic supplementary material, equation S5), we tested how the effects of thermal variability on estimated critical temperatures and population growth rates depend on the TPC skew and standard deviation of SST using OLS regression. We used a curve skewness metric developed by Thomas et al. [31] (electronic supplementary material, eqn 5 in [31]), which standardizes the absolute skewness of the curve by the niche width, w. All analyses were conducted in R version 3.4.1 [36]; data and code for these analyses are available at https://github.com/JoeyBernhardt/thermal-variability.

3. Results

(a). Does population growth in a thermally variable environment reflect the effects of nonlinear averaging over the thermal performance curve?

Population growth in fluctuating conditions differed from that in constant thermal conditions over the thermal gradient, and the differences were predicted quantitatively by nonlinear averaging of temporal variation in temperature-dependent performance (95% CI of the growth rate estimates under fluctuating conditions overlapped with predicted growth rates from equation (2.1); orange curve and dashed band in figure 2b). Consistent with expectations based on Jensen's inequality and nonlinear averaging, experimental populations of T. tetrahele had higher population growth rates under fluctuating temperature conditions compared with constant conditions over accelerating portions of the TPC, but lower growth rates under fluctuating temperature conditions compared with constant conditions over decelerating portions of the TPC (figure 2b). Notably, population growth was lower under fluctuating conditions relative to constant conditions at 24°C, which is close to T_opt in this population of T. tetrahele (figure 2b). Populations had negative growth rates at 32°C. The shift between positive effects of temperature fluctuations on population growth at low temperatures and negative effects of fluctuations at warmer temperatures aligned with the inflection point of the constant-temperature TPC (16.76°C, 95% CI: 16.76°C, 16.81°C), providing strong empirical support for nonlinear averaging in predicting population growth in thermally variable environments.

Thermal variation altered estimated parameter values and thermal traits of the realized TPC, effectively shifting the height of the curve down and the position of the curve to lower temperatures. The maximum exponential growth rate 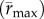was lower under variable conditions than constant conditions, 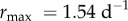(95% CI: 1.52 d⁻¹, 1.56 d⁻¹) versus 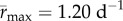(95% CI: 1.15 d⁻¹, 1.25 d⁻¹) (figure 2a,b). Estimated mean optimal temperatures for growth rate were lower under variable conditions: T_opt = 24.69°C (95% CI: 24.52°C, 24.88°C) versus 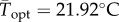(95% CI: 21.48°C, 22.43°C). Maximum mean temperatures for positive growth rates were lower under variable conditions T_max = 32.39°C (95% CI: 32.13°C, 32.64°C) versus 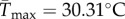(95% CI: 29.24°C, 31.97°C). All estimated critical temperatures under fluctuating conditions 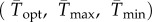were quantitatively consistent with theoretical predictions from equation (2.1) (i.e. had 95% CI overlapping the predicted values from equation (2.1); figure 2b,c). The range of temperatures associated with positive growth rates, accounting for the freezing point of seawater, w_s, was 34.19°C (95% CI: 33.93°C, 34.44°C) under constant conditions and 32.11°C (95% CI: 31.04°C, 33.77°C) under variable conditions. The estimated thermal breadth, w, was also lower under variable conditions, but not statistically distinguishable from constant conditions (i.e. had overlapping 95% CI): 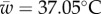, 95% CI: 33.57°C, 45.52°C, versus w = 41.23°C, 95% CI: 37.31°C, 47.41°C).

(b). How different are predicted ‘realized’ thermal performance curves in variable natural environments from predictions based on thermal performance curves generated under constant conditions?

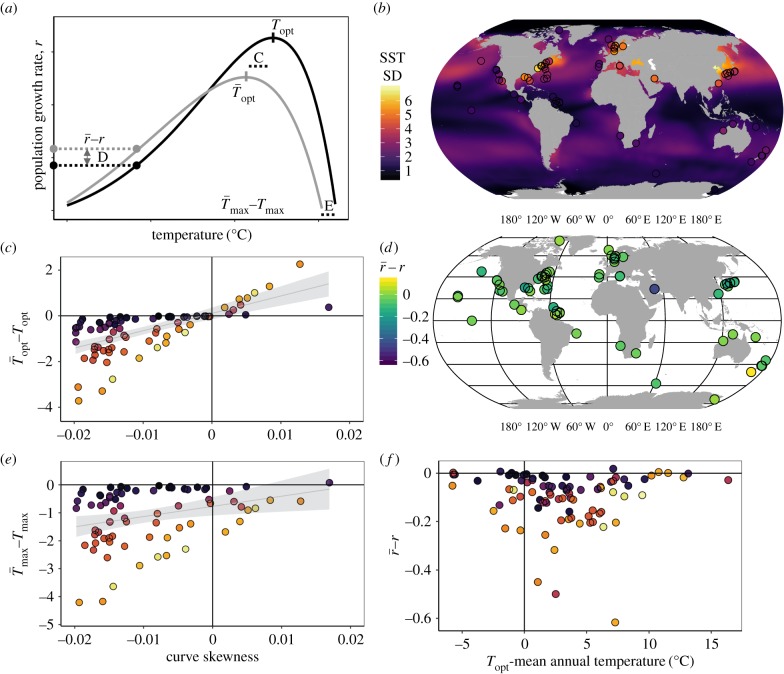
When we estimated the TPCs of the 89 phytoplankton species for constant and varying temperature regimes, we found that for the 90% of species that show negative skew (i.e. mean < median), 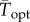in variable environments is lower than T_opt in constant environments (figure 3c), while for the remaining 10% of species which show a positive skew (electronic supplementary material, table S1), thermal variability is expected to increase 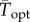relative to T_opt. The magnitude of the difference between 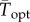and T_opt increased with increasing standard deviation of SST and was well explained by curve skew (slope = 85.98, 95% CI: 70.13, 101.82) and the standard deviation of SST (slope = −0.32, 95% CI: −0.40, −0.24; adjusted R² = 0.66, F_2,86 = 85.32, p < 0.001; figure 3c). Phytoplankton growth rate estimates that included the effects of thermal variability, 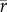, differed from those that did not account for in situ thermal variability, r (figure 3d,f). Generally, predicted growth rates under variable conditions were lower than predicted growth rates assuming constant conditions (i.e. 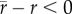, data points below the line y = 0 in figure 3f), and the majority of species (84%) were isolated at locations with mean daily temperatures that were colder than their T_opt (on average 4.26°C lower than T_opt). Importantly, the differences between r and 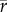were greatest for species whose isolation locations have mean temperatures that are close to their T_opt. Of the species that were isolated at locations warmer than their T_opt, 64% had a positively skewed TPC. Predicted upper thermal limits for population growth were almost always lower under variable conditions 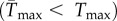(figure 3e), and the difference between 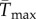and T_max increased with increasing skewness (positive slope = 53.31, 95% CI: 39.77, 66.85) and standard deviation of SST (negative slope = −0.50, 95% CI: −0.57, −0.43; Adjusted R² = 0.77, F_2,75 = 132.8, p < 0.001).

Figure 3.

Curve skew and environmental variability predict differences between performance under constant and variable conditions. (a) Diagram showing predicted differences in key features of a TPC under constant (black line) and variable (grey line) environmental conditions. The distances labelled ‘C’, ‘D’ and ‘E’ illustrate the distances between curve features, plotted in the panels (c–e). (b) Map of all phytoplankton isolation locations used in the analysis. The colour of the ocean and the points corresponds to standard deviation of daily SST over the time period 1981–2011 [34]. (c) The difference between predicted 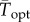and T_opt generated under constant lab conditions. (d,f) Predicted differences in phytoplankton growth rates that do not incorporate in situ temperature variation (r) versus predicted growth rates based on equation (2.1) 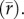(e) The difference between 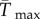and T_max. Colour coding in panels (c, e and f as in b).

For all 89 species in the global dataset, the nonlinear averaging approach (presented here) and the scale transition theory approach (electronic supplementary material, appendix A) resulted in similar ‘realized’ TPCs in variable environments (electronic supplementary material, figure S3). Predicted critical temperatures, 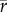estimates and relationships shown in figure 3 were all qualitatively consistent between the two approaches (electronic supplementary material, figures S3 and S4) indicating that scale transition theory, which makes use of parameters of environmental variation rather than detailed time series, leads to similar predictions in the datasets considered here.

4. Discussion

As climate changes worldwide, how temperature affects population growth is a critical link between climate and species persistence in a changing world. One common approach to project population abundance, persistence or fitness under future climate conditions is to apply mathematical curves describing population growth rate over a range of temperatures (a TPC) generated from controlled laboratory studies at constant temperatures (e.g. [37]). This approach relies on the assumption that TPCs do not vary systematically with thermal variation and that performance in naturally variable environments is well approximated by performance in constant-temperature environments [38]. Here we tested this important assumption and found that natural levels of environmental variability systematically change how population growth depends on temperature. In our analysis of globally distributed phytoplankton TPCs, we found that a variable thermal environment reduced critical upper mean temperatures 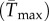for population persistence by up to 4°C, meaning that population growth in variable conditions was much lower at warmer temperatures than would be predicted based on a TPC generated under constant conditions. This thermal differential is substantial—the 4°C difference in T_max is on a par with the magnitude of predicted temperature changes over the next 100 years [39], suggesting that projections of TPCs used for future conditions may overestimate population performance in warming climates. Other work has compared acute thermal physiological limits (e.g. CT_max, CT_min) to environmental temperatures at range limits to assess relative sensitivities of range edges to warming (e.g. [1]), yet the underlying nonlinear negatively skewed TPC expected for these ectotherms suggests that variability at warm range edges will have a stronger effect on population persistence than variability at cold range edges. Specifically, our findings suggest that approaches based on direct applications of laboratory-determined critical temperatures may under-predict range edges at boundaries defined by cold temperatures and over-predict range edges at boundaries defined by warm temperatures.

We have shown experimentally that realized TPCs in variable environments differ from those in constant environments, and that these differences are predicted qualitatively by Jensen's inequality [9,17] and quantitatively from nonlinear time-averaging of performance over the TPC. Fluctuating temperatures changed several aspects of the ‘realized’ TPC including 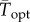and 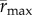—effectively shifting the TPC towards lower temperatures and lower population growth rates overall. Consistent with the argument that ‘suboptimal’ is optimal [12], we show both experimentally (figure 2b) and theoretically (using empirical TPCs and in situ temperatures; figure 3d,f) that population growth rates are often lower under variable thermal conditions relative to constant ones, and this negative effect of temperature variation is greatest for populations living close to their thermal optima. However, in contrast to the common assumption that environmental variation is always detrimental for population growth rates [16], our results suggest that populations living at mean temperatures in an accelerating part of the TPC will benefit from environmental variation. Indeed, the T. tetrahele isolate used here was collected at a location where mean annual temperatures are far colder than its 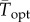in the accelerating portion of the negatively skewed TPC (at mean temperature = 11.69°C) [34]. In this way, when TPCs have accelerating portions at the edges of the thermal niche, thermal variation may allow population persistence in environments that would be too hot or cold under constant conditions.

When we applied nonlinear averaging to estimate the growth rates of globally distributed phytoplankton species, we found that the effect of variability on predicted phytoplankton thermal performance depended strongly on the shape and skew of the TPC and the degree of thermal variability in the oceans from which the phytoplankton originated. Previous approaches have, in the absence of more complete datasets, assumed a certain shape to the TPC, thus forcing certain outcomes of variability. Here, we used a model that does not prescribe a shape, enabling a more complete exploration of the effects of temperature variability on population performance. Importantly, empirical TPCs varied in skew, and whether the TPC was positively or negatively skewed determined the direction of the predicted shifts in thermal optima. The majority of the curves in the dataset were negatively skewed, and in these cases variability shifted 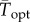to colder temperatures. Negatively skewed TPCs are widely observed across ectothermic taxa [18], suggesting that the direction of the effects of thermal variability observed in our experiment may be general across ectothermic taxa. Because the shape of the TPC determines performance in variable environments, the mechanisms that determine TPC shape can have an important influence on the outcome of thermal variability on population persistence. More studies of the diversity of TPC shapes among species and the phenotypic plasticity of TPCs within species will elucidate the extent to which environmental variability increases or decreases performance optima relative to constant laboratory conditions.

Our results suggest that TPCs derived from constant thermal conditions yield systematically biased estimates of thermal traits such as T_opt and T_max. Although this has been noted before, our empirical results provide support for mathematical approaches that can bridge the gap between laboratory-derived TPCs and their associated estimates of thermal traits and projections of species' performance in the field in varying environments. It is possible that additional variation in resource environments, such as light or nutrient conditions, could further complicate extensions of thermal traits to biogeographic patterns. Still, even in the absence of empirical temperature time series, as is often the case, predictions made based on the mean and standard deviation of a temperature distribution may provide a more accurate estimate of population growth or persistence in the field than thermal traits based on a TPC that does not consider thermal variability. We predicted similar effects of thermal variability on population growth rates when these predictions were made using empirical time series of in situ SST (equation (2.1)) and when using a Taylor approximation approach from scale transition theory, which relies on the mean and standard deviation of the temperature distribution only.

Our results, that performance in fluctuating environments can be predicted from TPCs generated in constant conditions, differ from two previous attempts to predict individual somatic growth rates in fluctuating environments based on TPCs generated in constant conditions [8,22]. Previous observations showed that short-term acute responses to diurnal temperature variation were not predictable based on TPCs generated from chronic exposure to constant temperatures over the course of development of an insect [8] and amphibian [22]. These contrasting results highlight the importance of the time scale of temperature exposures used to measure and predict performance in constant and fluctuating conditions. Biological responses to temperature, including acclimation and thermal stress are inherently time-dependent and may accrue over the course of development in longer lived species [14,38,40], thus precluding the ability of TPCs generated over longer terms (i.e. entire lifespans of individuals) to predict temperature responses over relatively short time spans (small fractions of lifespans corresponding to daily temperature variation). In our experiments, using a fast-growing phytoplankton with short overlapping generations, we maintained the time frames of temperature exposure comparable under both constant and fluctuating conditions. We matched the time scales of thermal acclimation and the time scale over which we measured population growth rates (i.e. multiple generations) in both the constant and fluctuating temperature treatments, thus keeping the time frames for prediction and observation comparable. This approach allowed us to avoid mismatches in time scale and time-dependent effects and instead test the nonlinear effects of temperature variation.

Our predictions of in situ phytoplankton population growth rates should be interpreted as first-order predictions, which do not incorporate long-term phenotypic responses to thermal variability. Organisms may be able to acclimatize or adapt to fluctuating conditions over longer-term exposures [40], with the potential to alter the shape and limits of the TPC. The global predictions we make here should be viewed as null models which do not incorporate long-term biological responses to environmental variability and should be tested empirically [5]. To extend our predictions of time-averaged growth rates over the whole thermal niche, i.e. our visualization of a ‘realized TPC’, we had to assume a particular distribution of temperatures around each hypothetical mean and used the variation observed at each isolation location as the residual variation around each putative mean temperature. This assumption about temperature distributions is a simplification of real thermal regimes, which likely show more complex patterns of variability and temporal autocorrelation, which can further modify the effects of variability on populations [3]. Resource supply may also covary with temperature, potentially altering the outcomes of thermal variability on population growth. Nevertheless, even in the simplest scenario of environmental variability, we predict significant changes in realized thermal traits.

Understanding population responses to temperature now and into the future involves understanding biological responses to changes in the full suite of temperatures experienced (i.e. all the variation). Omitting the effects of environmental variation from population and species distribution models may limit our ability to predict species' responses, particularly at the extreme edges of their ranges, even if variability patterns remain unchanged. We show that the effects of environmental variation can be predicted based on the shape of the functional relationship between population growth and the environment, adding another tool to the kit for forecasting species’ responses to the environment in a changing world.

Data accessibility

All code and data for analyses are available at Dryad Digital Repository: https://doi.org/10.5061/dryad.5kt4j51 [41].

Authors' contributions

J.R.B. conceived the study and designed the experiments, with help from J.M.S., P.L.T. and M.I.O. J.R.B. carried out the experiments, analysed the data and wrote the first draft of the manuscript. All authors contributed to writing and gave final approval for publication.

Competing interests

We have no competing interests.

Funding

Funding was provided by Vanier Canada Graduate Scholarship (J.R.B.), the Biodiversity Research Centre (J.M.S.), a Killam Postdoctoral Fellowship (P.L.T.), the Natural Sciences and Engineering Research Council (J.M.S. and M.I.O.) and Eawag (M.I.O.).