Diffusion of ring-shaped proteins along DNA: case study of sliding clamps

Abstract

Several DNA-binding proteins, such as topoisomerases, helicases and sliding clamps, have a toroidal (i.e. ring) shape that topologically traps DNA, with this quality being essential to their function. Many DNA-binding proteins that function, for example, as transcription factors or enzymes were shown to be able to diffuse linearly (i.e. slide) along DNA during the search for their target binding sites. The protein's sliding properties and ability to search DNA, which often also involves hopping and dissociation, are expected to be different when it encircles the DNA. In this study, we explored the linear diffusion of four ring-shaped proteins of very similar structure: three sliding clamps (PCNA, β-clamp, and the gp45) and the 9-1-1 protein, with a particular focus on PCNA. Coarse-grained molecular dynamics simulations were performed to decipher the sliding mechanism adopted by these ring-shaped proteins and to determine how the molecular properties of the inner and outer ring govern its search speed. We designed in silico variants to dissect the contributions of ring geometry and electrostatics to the sliding speed of ring-shaped proteins along DNA. We found that the toroidal proteins diffuse when they are tilted relative to the DNA axis and able to rotate during translocation, but that coupling between rotation and translocation is quite weak. Their diffusion speed is affected by the shape of the inner ring and, to a lesser extent, by its electrostatic properties. However, breaking the symmetry of the electrostatic potential can result in deviation of the DNA from the center of the ring and cause slower linear diffusion. The findings are discussed in light of earlier computational and experimental studies on the sliding of clamps.

INTRODUCTION

DNA processing reactions, such as transcription, translation, duplication and repair, involve a variety of essential proteins. These processes, as well as others involving regulatory events, are performed by diverse DNA-binding proteins (DBPs) that differ in their structure, number of domains, and oligomeric states. Many DBPs bind specifically and with high affinity to a unique stretch of DNA sequence, which they identify through an extensive search that includes facilitated diffusion throughout the genomic DNA (1,2). A smaller fraction of DBPs shows a lower degree of specificity and functions by interacting nonspecifically with any DNA sequence. Among these DPBs are the sliding clamps, which are toroidal ring-shaped proteins that encircle the DNA. During their nonspecific interactions with DNA, toroidal clamps serve as processivity factors (3) that assist other proteins to stay bound to DNA through multiple catalytic turnovers. The sliding clamps bind their respective DNA polymerase partner to template DNA, allowing it to replicate several bases without dissociation (3). Sliding clamps are now known to be used in many processes beyond replication, including repair, cell cycle control, and chromatin remodeling (4,5). The dynamics of sliding clamps along DNA is expected to be essential for all these crucial processes. The toroidal form is also adopted by some other proteins that have catalytic activity (e.g. GroEL, proteasomes, F1-ATPase) or that engage in DNA interactions (e.g. helicases, topoisomerases, and some DNA repair proteins), which suggests that the ring shape may provide functional advantages or even be vital to their mobility along DNA (6).

Sliding clamps are present in all organisms: in eukaryotes, archaea, prokaryotes, and viruses. The sliding clamps of eukaryotes and archaea are called PCNA (Proliferating Cell Nuclear Antigen) (7), those of bacteria are the β-clamps (i.e. the β subunit of pol III) (8,9), and the clamp of bacteriophage T4 is called gp45 (10). All clamps are homomers: the PCNA and gp45 are trimers while the β-clamp is a dimer. The sliding clamps do not have specific DNA-binding sites, but the circular assembly creates a positively charged channel in which duplex DNA can bind and slide freely. The three sliding clamps are structurally superimposable despite little sequence conservation (11). The 3D structure of sliding clamps consists of six domains that form an outer layer of six β-sheets and an inner layer of 12 α-helices lining the central channel. The inner diameter of the clamp is ∼30 Å, compared to the 20 Å diameter of duplex DNA. The sliding clamps are unique in their symmetry, however not all ring-shaped proteins are symmetric homomers. For example, the heterotrimer formed from the proteins Rad9, Hus1 and Rad1 (here called 9-1-1) resembles the sliding clamps in structure, however 9-1-1 does not function as a sliding clamp, but coordinates checkpoint activation and DNA repair (12).

The sliding clamps are only a small part of a large family of proteins that interact with DNA and are able to slide. A question was raised—how different is the sliding of the sliding clamps from that of non-toroidal DBPs? It is well accepted that non-toroidal DBPs find their target sequence by a combination of sliding and hopping (13). During sliding, the DBPs have high DNA affinity dominated by nonspecific electrostatic interactions that are quite uniform along the DNA backbone, and thus linear diffusion is possible. During hopping, the DBP may dissociate from the DNA and reattach at a different site located a few base pairs away from the initial location (namely, the DBPs perform in hopping linear diffusion but in a rotation-uncoupled translation manner). Salt concentration is one of the main factors affecting the linear diffusion search mode, mostly via modulation of electrostatic strength. At low salt concentrations, the electrostatic interactions between the DBP and the DNA are stronger, so the protein slides more and hops less. At higher salt concentrations, the probability that a DBP will adopt the hopping search mechanism increases at the expense of sliding. Thus, it is interesting to investigate whether the diffusion of ring-shaped proteins that cannot dissociate from the DNA is faster or slower than the diffusion of non-toroidal DBPs and whether their movement is affected by salt concentration.

The clamps have a net negative charge, with the solvent-exposed outer ring being negatively charged, while the inner ring, which topologically traps the negatively charged double-stranded DNA, is positively charged. The microscopic details of the interactions between the inner ring and the DNA may dictate the sliding mechanism. Following the symmetry of the sliding clamps, their electrostatic properties are also symmetric and depend on whether the sliding clamps are homodimeric or homotrimeric. The combined consequences of the topological constraints imposed on the DNA by its localization within the inner ring together with the extensive and symmetric electrostatically attractive forces are not trivial. The positive residues of the inner ring, which are well conserved, are essential to facilitate loading of the clamp on the DNA (14). Special enzymes called ‘clamp loaders’ load the generally negatively charged protein onto the negatively charged DNA (15). The role of the positively charged residues in the dynamics of the protein–DNA interface is still not entirely clear. On the one hand, their role might be to create a general electrostatic potential that complements that of the DNA. On the other hand, they may play a more active role in direct interaction with the DNA. In addition, the extensive electrostatic interface between the inner ring and the DNA it encircles, together with the diameter of the inner ring being larger than that of the DNA, complicate our understanding of the interaction between the surface of the inner ring and the DNA. One may also ask why the whole clamp has a net negative charge. Given that the negative electrostatics frustrate the migration of clap monomers to the DNA and the camp loading process, the electrostatics may be important for clamp dynamics on the DNA.

So far, few studies have been conducted to assess the unique diffusion modes adopted by clamps moving along DNA, and these few have focused on PCNA as a case study using simulations (16) and single molecule imaging (17,18). It has been suggested that PCNA moves in two distinctive modes: one that is coupled with its rotation along the helical dsDNA, following its major and minor grooves, and another that is a purely linear translocation along the DNA (17). A recent study of PCNA sliding using X-ray crystallography, NMR spectroscopy, and molecular dynamics simulations supports the existence of rotation-coupled translation, which occurs when the ring-shaped PCNA protein is tilted relative to the DNA axis (19,20). The strength of the coupling between the rotation and translation of sliding clamps as they diffuse along DNA, as well as other molecular determinants that govern their diffusion, require further quantification. Extensive molecular dynamics simulations using coarse-grained models provide the opportunity to directly observe the simulated movement of sliding clamps along DNA and so shed light on the mechanism of their dynamics.

PCNA is the most-studied sliding clamp, and was therefore the major focus of the current study. For comparative and control purposes, we also investigated two other sliding clamps (β-clamp, and the gp45) and one ring-shaped protein that mediates DNA damage response (the 9-1-1 protein). All four proteins were studied using coarse-grained molecular dynamics simulations, which allow the simulation of long time-scale biomolecular processes. The computational study aimed to characterize the molecular determinants affecting the diffusion of toroidal proteins along DNA. For example, the properties of both the inner and outer rings may affect sliding, as may the two different faces of the toroidal proteins. Different aspects of the sliding were analyzed, including the direction of sliding, rotation around the DNA, the tilt of the clamp, and the location of the DNA inside the inner ring of the toroidal protein. The coarse-grained simulations were used here to characterize the mechanism of linear diffusion employed by the sliding clamps and particularly to address the existence of coupling between translocation and rotation. Furthermore, the coarse-grained simulations allowed us to study mutants of the sliding clamps with modified electrostatic potentials.

MATERIALS AND METHODS

Coarse-grained molecular dynamics simulations

The dynamics of sliding clamps on DNA was studied using coarse-grained molecular dynamics simulations that enable the investigation of long time scale processes that are very challenging for high-resolution models. The proteins were modeled by a single bead per amino acid, located at the geometrical center of the Cα carbon. The DNA in the simulations was 200 bp double stranded DNA in a canonical B form (the DNA geometry was adopted from a DNA composed of poly C and poly G single-stranded chains). The dsDNA was modeled with three beads per nucleotide, representing the sugar, phosphate, and base groups.

Two different DNA models were used. In the first model, given the high persistence length for DNA of ∼50 nm, it was represented as a rigid and static molecule. It was modeled in its canonical B-form and was centered on and aligned with the Z-axis. To incorporate flexibility into the DNA, the second model used a three sites per nucleotide (3SPN.1) approach, which has been shown to capture the thermodynamic properties of various DNA sequences under different conditions (21).

The proteins were modeled using a structure-based model in which internal flexibility was represented by native interactions (22,23). The interaction between the protein and the DNA was modeled using the Debye-Hückel approximation (24,25). The beads representing DNA phosphates and the Asp and Glu residues were negatively charged, while those of Lys and Arg were positively charged (13). The charged beads can participate in any non-specific charge–charge interactions. Given that sliding clamps interact nonspecifically with DNA, electrostatic interactions are the main force driving their linear diffusion along DNA (26), whereas the contribution of hydrogen bonds, which may increase energetic ruggedness (27) and thereby slow down linear diffusion, is negligible. Excluded volume interactions are introduced between all the protein and the DNA beads.

The dynamics of the ring-shaped proteins along the dsDNA was simulated with the Langevin equation. Hydrodynamic forces that can affect diffusivity (28) were included in this study. The simulation temperature was maintained at 0.6 (reduced units), which is lower than the folding temperature of PCNA (T ∼ 1.0) so that during the diffusion along the DNA the toroidal proteins are stable and do not undergo unfolding. The dielectric constant was 70 and the salt concentration was 0.05 M (if not stated otherwise). Note that, because of the coarse-grained representation, the simulated salt concentrations were ∼2-fold lower than physiological salt concentrations. The system was confined in a box with periodic boundary conditions (PBC) and dimensions of 850 × 850 × 1250 Å where the DNA was aligned along the longer axis. For all variants, we performed 10–100 simulations of 10⁷ time steps to achieve equilibrium sampling. For some systems, we examined the equilibrium sampling by comparing the convergence of two different sets of simulations. This coarse-grained model was applied to various protein–DNA systems (13,29,30) and was shown to capture some of their major experimental characterization (31–33).

Studied natural ring-shaped proteins

Four naturally occurring ring-shaped proteins were studied diffusing on nonspecific dsDNA using the coarse-grained model. The proteins and their corresponding protein database codes were: eukaryotic yeast PCNA (PDB code: 3K4X, 756 residues), β-Clamp (PDB code: 3BEP, 732 residues), gp45 (PDB code: 1CZD, 684 residues), and the 9-1-1 (PDB code: 3GGR, 821 residues). Each protein was threaded on a 200 bp dsDNA. These four proteins were studied in two charge configurations: with their natural charges and following neutralization of all their charges. The neutralized variants of these four proteins were simulated for comparative purposes.

The contribution of electrostatic interactions to the binding free energy between each ring-shaped protein and a nonspecific DNA molecule was calculated as ΔG^el_binding = ΔG^el_complex - (ΔG^el_prot + ΔG^el_DNA). In this equation, ΔG^el_prot, ΔG^el_DNA and ΔG^el_complex are the electrostatic energies of the protein, the DNA strand, and the protein–DNA complex, respectively, which are the work of charging up the solute molecule as estimated by solving the Poisson-Boltzmann equation using the atomistic models of the proteins. A negative value for ΔG^el_binding indicates that electrostatic interactions are stabilizing for protein–DNA binding. The electrostatic binding energies were evaluated using the APBS software package (34). In all electrostatic calculations, the parameters of charges and bond radii were adopted from the AMBER force field. The temperature was set to 298.15 K, and the solute and solvent dielectric constants were 4 and 80, respectively. The solvent was modeled with an ionic strength of 150 mM. The dielectric boundary was set to the van der Waals surface. The calculation began using a coarse grid with 2.0 Å spacing, and then moved to a finer grid with 1.2 Å spacing, both centered at the geometric center of the solute molecule. The dimensions of all grids were 97 × 97 × 97 Å.

Design of mutants

To investigate the effect of electrostatics on the dynamics of clamps sliding on DNA, neutral variants were generated by neutralizing all the positively and negative charged residues of the four wild type (WT) toroidal proteins. The resulting sets of variants comprised: (1) WT gp45 (charge –21) and neutralized gp45; (2) WT β-clamp (charge –22) and neutralized β-clamp and (3) WT 9-1-1 (charge –10) and neutralized 9-1-1. For the PCNA clamp, many additional variants were also created, with (4) the PCNA set described in detail below.

The PCNA variants were designed using WT yeast PCNA and had the same structure as the original clamp, but differed in the charges of some of the amino acid beads. Native PCNA molecules comprise 26 positively and 46 negatively charged residues per subunit, so the net charge of PCNA is −60 [ = 3·(26 – 46)]. All the variants were generated by manipulating some or of all the 216 [ = 3·(26 + 46)] charged residues of PCNA. Most of the simulated variants are not realistic, because they vary greatly from the protein's native sequences and may even prevent folding. Nevertheless, these variants are useful for investigating the role of electrostatics in clamp diffusion along DNA and for characterizing this diffusion. Overall, four sets of homotrimeric PNCA clamps (wild type, negatively charged,and positively charged sets together with a neutral variant) were designed to produce ring-shaped proteins with a symmetric geometry but sometimes asymmetric electrostatic potential.

The first PNCA set contained three WT variants. One variant in the set was the WT PCNA (WT^1,2,3), another variant included two WT subunits while the third subunit had no charged residues (WT^1,2), and the last variant had only a single subunit with WT properties while the remaining subunits had no charged residues (WT¹). WT^1,2,3, WT^1,2 and WT¹ had net charges of −60, −40 and −20, respectively.

The second set comprised three negatively charged (Neg) variants, in which all the 78 positively charged residues of PCNA were set to be neutral. One variant had three identical negatively charged monomer subunits, each bearing a charge of −0.33 (Neg^1,2,3). Another variant had two identical negatively charged subunits, each bearing a charge of −0.66, and one subunit that was rendered uncharged by setting its negatively charged residues to neutral (Neg^1,2). The third variant contained a single negatively charged subunit bearing a charge of −1.0, while its remaining two subunits were uncharged (Neg¹). Thus, the Neg^1,2,3, Neg^1,2 and Neg¹ variants all bore the same overall charge of −46.

The third set comprised three positively charged variants (Pos), in which all 138 negatively charged amino acids were set to neutral. One variant was designed to have three identical subunits, with a charge of +0.33 on the positive residues so that the total charge of the PCNA trimer was +26 (Pos^1,2,3). Another variant had two identical positively charged subunits, with the third subunit carrying zero net charge after setting the positive residues to neutral as well. In this variant, the charge of the positively charged residues in the non-neutral monomers was set to be +0.66 to achieve the same total charge of +26 (Pos^1,2). The third variant in this set had two subunits with zero charge and one positive subunit bearing a charge of 1 (Pos¹).

Whereas neutralization in the previous three PCNA sets was limited to one or two subunits, the fourth set involved neutralization of all three subunits or neutralization across subunits. In the entirely neutral clamp (Neu), all 138 negatively and 78 positively PCNA charged residues were set to neutral. The two other variants were neutralized by eliminating all the charged residues on either the inner or outer rings, Neuⁱⁿ and Neu^outer, respectively. The Neuⁱⁿ variant was created by neutralizing 24 positively and 12 negatively charged residues on the helices located at the surface of the inner ring, resulting in a net charge of –63. The Neu^out variant was created by neutralizing all charges on PCNA, except for the 36 charges on the helices that surround the DNA, resulting in a net charge of +12.

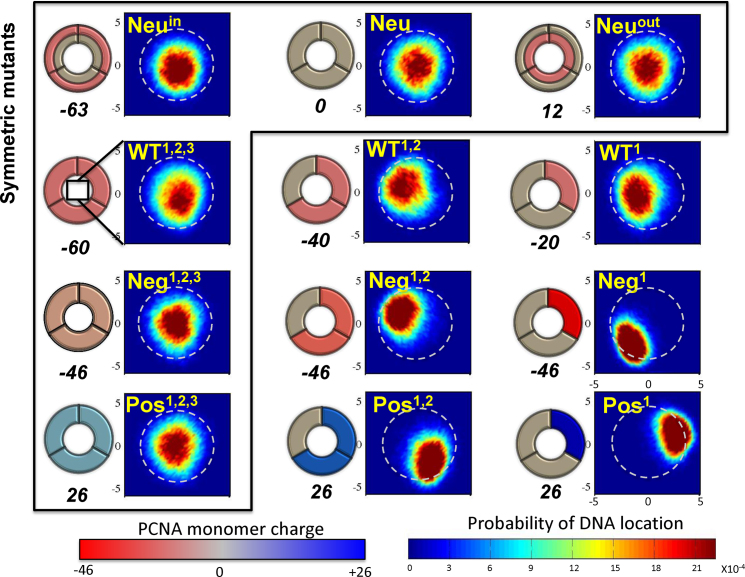
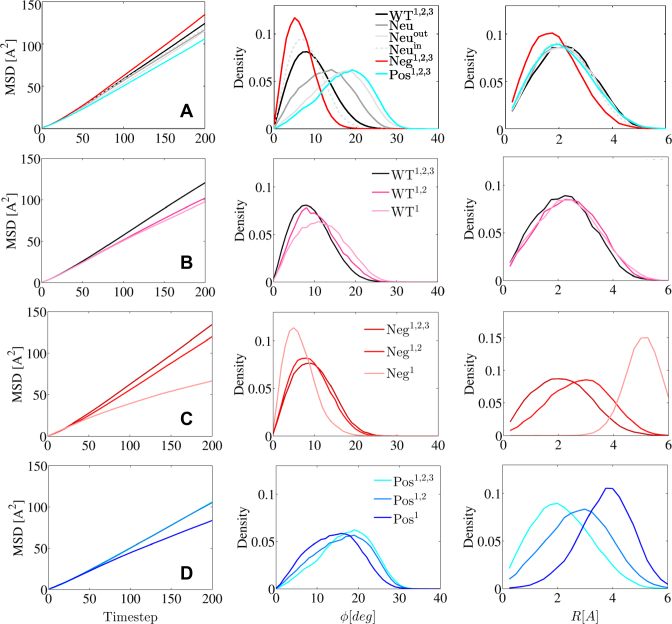
The four designed PCNA sets resulted in 12 variants of PCNA with different charge patterns. Figure 5 schematically presents these variants. In Figure 5, the variants are arranged in columns by increasing electrostatic strength. Each of the four rows corresponds to a different set (Neu, WT, Neg and Pos). This arrangement also emphasizes that six variants (enclosed in a frame) maintain the original symmetry of PCNA while the symmetry of the other six variants is broken. The variants were designed to enable us to investigate the role that coupling between geometric and electrostatic symmetry plays in protein diffusion along DNA. We sought to understand how breaking the electrostatic symmetry by redistributing the charges of these symmetric ring-shaped proteins could affect their sliding along DNA. Although electrostatic symmetry is broken in both the negatively and positively charged sets, they were designed to ensure that, within each set, all members bore the same net charge. Some diffusion properties may be affected by the net charge itself, and therefore keeping the net charge fixed enabled us to control this potentially confounding variable. As described above, keeping the net charge constant was achieved by changing the charge load on the charged subunits. In addition to the variants of ring-shaped proteins, we studied the interactions of a single monomer of PCNA with DNA.

Figure 5.

Schematics and localization probability maps for the DNA center of mass inside the inner rings of the PCNA variants. The Neu set includes variants in which different regions were neutralized by reparametrizing the charges of charged amino acids: the whole protein (Neu), the inner ring (Neuⁱⁿ), or the outer ring (Neu^out). The differences within each of the other three sets (WT, Neg, Pos) were achieved by manipulating zero, one, or two subunits of the trimeric PCNA. The WT set includes variants whose monomers bear the same charges as the WT PCNA on three, two, or one subunit(s). The Neg and Pos sets include variants in which the positive or negative charges were neutralized, respectively. Thus, the charge on charged residues becomes more negative (decreasing from –0.33 to –1.0) across the Neg row and similarly becomes increasingly positive (from +0.33 to +1.0) across the Pos row. This is indicated by the increasingly intense shade of the charged subunit in the schematic drawings of the PCNA rings. The colors of the subunits in the schematics are based on the monomer net charge (red to blue color bar) and the overall net charge of each variant appears under its diagram. The variants inside the frame are symmetric whereas those outside the frame are asymmetric. The WT^1,2,3 variant corresponds to wild-type PCNA. A probability map for DNA localization within the PCNA ring is shown to the right of each schematic, with probability indicated by the rainbow color bar. A direct interaction between the DNA and PCNA is expected to occur at R ∼ 4 Å (deduced from the interaction of variant Pos¹ with DNA), as indicated by the dashed circular line on each probability map.

Trajectory analysis

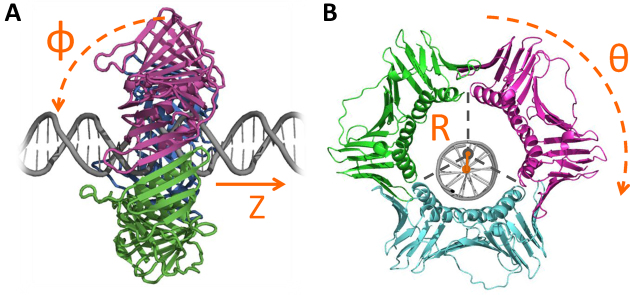
In all the simulations, the DNA was aligned along the Z axis. The rotation angle of the clamps around the DNA, θ, was calculated as the rotation angle of one bead in the X–Y plane (this definition is allowed because the protein does not undergo conformational changes during the simulations) (see Figure 1). The tilt angle, ϵ, is the angle between the DNA and protein ring (see Figure 1). The tilt angle was calculated as the angle between the Z axis and a plane spanned by three beads on the clamp. The three beads of the plane were chosen so that the plane would be parallel to the protein ring.

Figure 1.

Geometric characterization of the linear diffusion of sliding clamps along DNA. (A) side view of PCNA, indicating the translocation distance along the Z axis and the tilt angle, φ. A perpendicular orientation of the ring relative to the DNA axis corresponds to a tilt angle of φ = 0°. (B) Front view of PCNA, showing the distance between the centers of mass of the PCNA ring and the DNA molecule, R, and the rotation angle θ.

The D₁ coefficient of one-dimensional (1D) diffusion was calculated from the mean square displacement (MSD) of the center of mass of the protein moving along the DNA double helix:

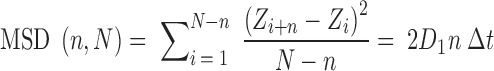where N is the trajectory length in time steps, n is the measurement window ranging from 1 to N, Δt is the time interval between two time steps and Z is the location of the sliding clamp along the DNA.

The localization of the DNA inside the clamp was quantified by the distance R between the centers of mass of the DNA and the ring (Figure 1). The center of mass of the ring-shaped protein is the geometric center of 12 beads: 1 bead on each helix. The dynamics of the ring throughout the simulations was visualized by calculating the probability of finding the DNA at any location inside the ring. The plane inside the clamp was gridded and each grid cell was annotated with the probability that the DNA center would lie in it during the trajectory.

RESULTS

Characterization of PCNA diffusion along dsDNA

Various studies conducted using different approaches showed that globular (non-toroidal) DBPs slide along DNA in a translation-coupled rotation manner in which the protein follows the track defined by the DNA’s major groove (13,24,25,35–38). However, the detailed biophysical features of the sliding dynamics can be different for different globular DBPs. The diffusion of non-toroidal proteins along DNA may vary, for example, with respect to the durations of the sliding events (which are interrupted by hopping or dissociation events), by the lengths of DNA that are scanned in each sliding event, and by the 1D diffusion coefficients (13,24).

Ring-shaped proteins are expected to search DNA differently from globular proteins for various reasons. Given their ring-shaped structures, these proteins cannot dissociate from the DNA simply by weakening the strength of the nonspecific interactions, but only by breaking the protein–protein interface between the constituent subunits. Furthermore, for symmetric ring-shaped proteins, it is unclear whether non-specific association with the DNA, and thus a coupled translation–rotation dynamics, is likely. Some earlier efforts endeavored to quantitatively characterize the diffusion of PCNA along DNA from the experimental and computational (16) perspectives. In this study, we aimed to explore the dynamics of PCNA using coarse-grained simulations that may shed light on various molecular and biophysical aspects of its diffusion.

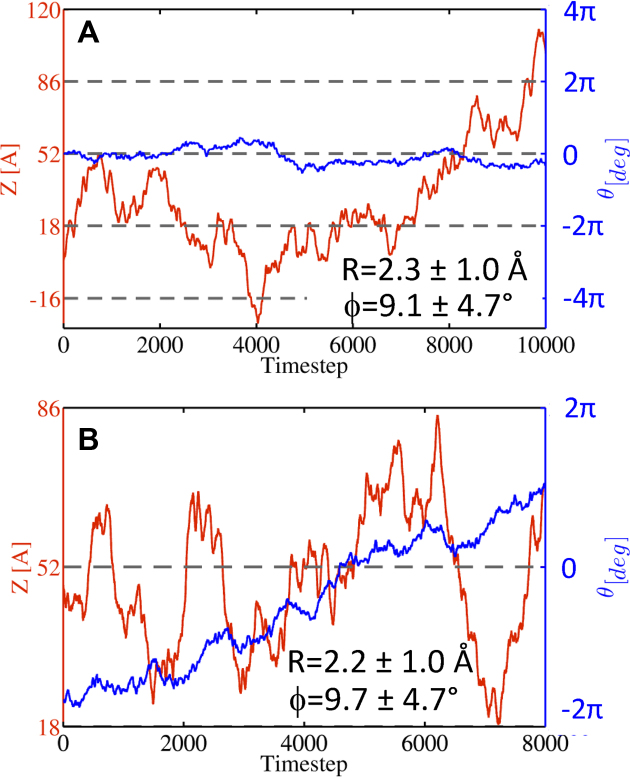
Figure 2 shows two typical trajectories of the diffusion of PCNA along DNA. The simulations were analyzed by following the location of the protein along the DNA axis (Z), the protein's rotation and tilt angles (θ and ϕ, respectively), and the distance between the centers of mass of the DNA and of the protein that encircles it (R), see Figure 1. The two simulations show large translocations of the ring protein along the DNA (Figure 2A and B, red line). The protein can rotate around the DNA and, while diffusing, the PCNA is tilted by ∼10 ± 5° relative to the DNA axis (Figure 2A and B). Our simulations indicate that, during diffusion along DNA, the DNA is located close to the center of the inner ring (R ∼ 2 Å, see Figure 2A and B). Given that the radius of the inner ring is 50% larger than the radius of the DNA molecule, this central location suggests that the ring does not interact directly with DNA phosphates, however, fluctuations of the location of the DNA in the inner ring indicate that transient PCNA–DNA interactions are possible.

Figure 2.

Representative trajectories for the linear diffusion of PCNA along nonspecific DNA simulated using coarse-grained molecular dynamics simulations (A and B). The trajectories show the translocation distance Z (red, left y axis) and the rotation angle θ (blue, right y axis) as a function of time. The mean values of R and ϕ (as defined in Figure 1) in each simulation are also indicated for each trajectory. The gray dashed lines indicate complete turns of the DNA (i.e. a distance of 34 Å along the DNA axis and a rotation of 2π).

The coupling of translocation and rotation of PCNA is weak

Translation-coupled rotation dynamics, which is a hallmark of 1D diffusion by DBPs when they search DNA via sliding, was observed computationally and experimentally for various proteins of different structures (13,25) and different oligomeric states (30,31,39,40). The existence of coupling between translation and rotation for a ring-shaped protein is less obvious. The helical form of the DNA may suggest that the PCNA could slide on it like a nut on a screw, completing 360° at every turn of the DNA (10 bp, corresponding to 34 Å). However, our finding that the DNA sits about equidistant from the sides of the DBP suggests that rotation and translation may not be tightly coupled. Figure 3B shows the distributions of the distance (R) between the centers of mass of the DNA and PCNA. The distribution of R distances is quite broad relative to the size of the inner ring and the DNA radius. This distribution suggests that the DNA does not form a tight interface with PCNA and that their distance from each other varies during the simulation.

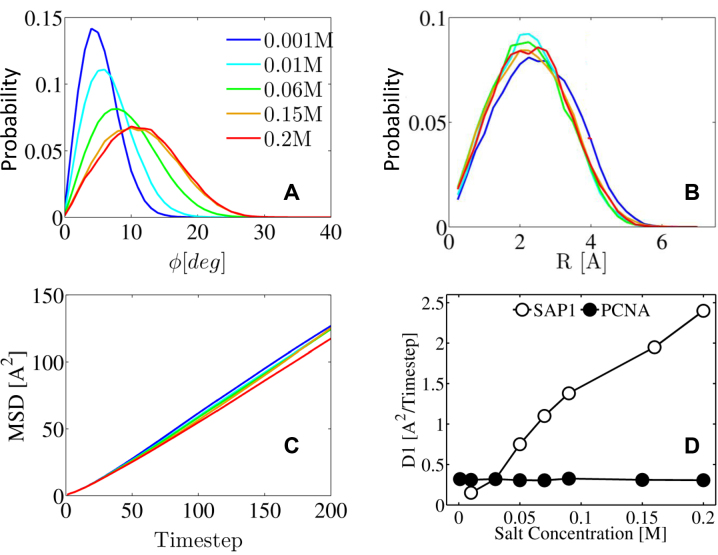
Figure 3.

The effect of salt concentration on the diffusion of PCNA along DNA. The dynamics of the center of mass of the PCNA as it moves along the DNA double helix is quantified by plotting the probability (y-axis) against: (A) the tilt angle ϕ; and (B) the distance (R) between the center of mass of the ring and that of the DNA. (C) The mean square displacement (MSD) of the center of mass of the protein moving along the DNA double helix plotted against simulation timestep. Panels A, B and C, show this information for five different salt concentrations in the range 0.001–0.2 M, designated by different colors. (D) The linear diffusion coefficient, D₁, is compared for PCNA (black circles) and the non-ring Sap1 transcription factor (white circles) by plotting both against salt concentration. The D₁ values for the Sap1 protein were taken from ref. (13).

A previous study based on single molecule imaging data suggested that PCNA moves in two distinctive modes: one that is coupled with its rotation along the DNA helix, following its turns, and another that is described by simple translocation (17). The coarse-grained simulations over long time-scales that were performed in the current study showed that the translocation of PCNA along DNA is much faster than its rotation along the DNA axis. For example, Figure 2A shows that in a typical trajectory of 10⁴ time steps, the PCNA slides back and forth along a distance of 136 Å (from Z = –16 to Z = 120), which corresponds to four DNA turns, however the protein does not complete even a single full rotation around the DNA (measured by the θ angle). This suggests that the translocation of PCNA along the DNA is not coupled with its rotation, although the PCNA is freely rotating. If the rotation were coupled with translation, during translocation in the ‘3→’5 direction, there would be more clockwise than counter clockwise rotation, because the DNA helix is right-handed. However, the simulations showed no effect of translocation direction on the direction of rotation.

One may explain the lack of strong coupling between the translocation and rotation of PCNA diffusing along DNA using simple energetic arguments. The ring shape of PCNA means that, at any location along the DNA and at any rotation angle, it interacts with both minor and major grooves. Consequently, the protein–DNA interface is large and includes both favorable and less favorable interactions, such that there is no optimal path for moving along DNA such as can be visualized easily for single domain DBPs. Thus, if the DNA is located at the center of the symmetric ring-shaped protein, a non-biased interface guarantees a smooth energy landscape for linear diffusion. In the next sections, we will address whether other locations within the ring may be more stable energetically than the central position while still guaranteeing smooth linear diffusion. We note that uncoupled translation-rotation diffusion of PCNA along DNA was observed also when using the flexible model of DNA (data not shown).

Diffusion of PCNA is insensitive to salt concentration

Translation (i.e. 1D diffusion) of a protein along DNA can be described as sliding, hopping, or their combination. In the sliding mode, the protein follows the major groove track while the interface it forms with the DNA resembles that found in the crystal structure, although it is expected to be much more hydrated (41). In the hopping mode, the protein is still close to the DNA but the geometric properties of the protein–DNA interface deviate from that of the specific complex (13). Previous studies showed that D₁ is strongly affected by salt concentration (see, e.g. the dependence on salt concentration of the value of D₁ for the Sap1 transcription factor, Figure 3D). The origin of the increase in D₁ with salt concentration is the greater usage the globular protein makes of the hopping mode at the expense of the sliding mode as the salt concentration increases (13).

The dynamics of PCNA on DNA was simulated at salt concentrations varying from 0.001 to 0.2 M. These simulations showed that the tilt angle ϕ increases with increasing salt concentration (Figure 3A), however, the distribution of distance R is hardly affected by salt concentration (Figure 3B). Figure 3C shows that the mean square displacement (MSD), and therefore the D₁ (Figure 3D) to which it is directly proportional_, is not sensitive to salt concentration. The result shown in Figure 3D is consistent with previous single molecule imaging data results that showed only a mild increase in the diffusion coefficient of PCNA under increasing salt concentration (18). More specifically, the diffusion coefficient increased 2.2-fold over a 13-fold change in concentration, while the diffusion coefficient of another non-ring DBP (UL42) increased by 4-fold over a 5-fold change in salt concentration (17). As for the UL42 protein, a similar strong dependence of D₁ on salt concentration was observed experimentally for other transcription factors, such as p53 (42) and the TALE protein (43) as well as computationally in the current study for the non-toroidal nucleotide-binding SAP1 protein (Figure 3D). The weaker dependence of D₁ on salt concentration for PCNA compared with transcription factors or other non-toroidal proteins might be because its unique geometry restricts its dissociation, such that switching between the sliding and hopping search modes is not modulated by increasing salt concentration.

Given that the PCNA does not follow the DNA major groove, we conclude that the linear diffusion is performed mostly via hopping. This conclusion is supported by the high K_D of PCNA–DNA (0.7 mM) compared with the K_D of other nonspecific protein–DNA systems (of a few μM), which also suggests that the DNA mostly diffuses using a hopping mode, even at low salt concentrations. The use of hopping can be explained by the extensive electrostatic surface between the DNA and PNCA’s inner ring, which may introduce competition between subunits and thereby prevent strong interaction between DNA and any one of the PCNA subunits, even at low salt concentrations. Nonetheless, some sliding events may take place via direct interactions between the positively charged residues located at the helices of PCNA and the DNA phosphates. Such nonspecific binding was observed in all-atom simulations of PCNA with a nonspecific DNA sequence (16,19), however the short time-scale of those simulations does not permit conclusions to be drawn with respect to the relative population of the sliding and hopping modes of linear diffusion. We note that our simulations of a single PCNA monomer with DNA did not reveal sliding such as is common to non-toroidal DBPs. We observed that an isolated PCNA monomer performs neither sliding nor hopping movements on the DNA, but rather dissociates from the DNA and performs 3D diffusion in the simulation box (data not shown). This may be explained by the net negative charge of the monomer, which repulses the negative charge of the DNA. PCNA, therefore, must be in a toroidal geometry to be able to diffuse linearly along the DNA.

The effect of PCNA electrostatics on its linear diffusion on DNA

The electrostatic properties of proteins govern their linear diffusion along nonspecific DNA. This is manifested by the strong effect salt concentration has on the D₁ diffusion coefficient (13,25). A previous study predicted that the absence of attractive forces between the PCNA clamp protein and DNA would make the PCNA move faster, such that the diffusion coefficient would be 3 orders of magnitude higher (18). To check that prediction, a variant of PCNA was constructed in which all the 216 charged residues were neutralized (variant Neu, see Materials and Methods section). The completely electrostatically neutral PCNA exhibited no interactions with DNA, however, simulations showed that the MSD (which is proportional to D₁) of Neu was similar to that of WT PCNA (Figure 4A, left, where WT PCNA refers to the WT^1,2,3 variant).

Figure 4.

Characterization of the linear diffusion of the PCNA variants along nonspecific DNA. Analysis for the symmetric PCNA variants is compared in (A). Panels (B), (C) and (D) show the diffusion for all the WT, Neg and Pos variants, respectively. The colors correspond to the color of each variant in Figure 5. The diffusion of the 12 variants of PCNA is analyzed in terms of: (left) mean square displacement (MSD) versus timestep, (middle) probability versus the tilt angle ϕ and (right) probability versus distance R (as defined in Figure 1).

PCNA is a very acidic protein with a net charge of -60e, and previously it was suggested that the negative charge prevents nonspecific interactions with DNA (15) and that it creates electrostatic repulsion with the DNA and therefore contributes to ‘frictionless’ diffusive motion. To investigate the role of the negative charges, all 138 negative charges were set to neutral, resulting in a positively charged PCNA with net charge of 26 (variant Pos^1,2,3, see Materials and Methods, Figure 5). This positively charged PCNA had a lower D₁ than the native PCNA (Figure 4A, left; D₁ represented by MSD), supporting the previously mentioned suggestions that net negative charge on PCNA contributes to faster movement.

PCNA has a positively charged inner ring. It has been suggested that these positive residues are important for clamp loading¹⁵ and for the sliding mechanism¹⁸. To investigate the role of the positive residues in sliding dynamics, a third variant was constructed, in which the 78 positive charges were set to neutral, resulting in a net charge of –46 (variant Neg^1,2,3, Figure 5). This negative variant moved faster and its diffusion coefficient was 16% higher than that of native PCNA, although of the same order of magnitude (Figure 4A). To further dissect the effect that the distance of charged DNA residues has on PNCA dynamics, we created two additional variants of PCNA whose inner or the outer ring was neutralized (variants Neuⁱⁿ and Neu^out with net charges of –63 and 12, respectively). Despite having such different net charges, the D₁ of these variants is similar to that of WT PCNA (i.e. WT ^1,2,3) (Figure 4A, left). We may conclude from these PCNA variants that the negative charge on PCNA, especially on the inner ring, plays an important role in its translocation mode whereas the total charge affects the diffusion coefficient.

To further analyze the effect of the net charge of PCNA on the mechanisms that underlie its diffusion along DNA, we analyzed the tilt angle, ϕ, of the PCNA relative to the DNA. Figure 4A (middle) presents the distribution of ϕ for six symmetric PCNA variants with different charge distributions. The tilt is correlated with the net charge, but not completely explained by it, since, for example, the negative variant, which has a net charge of −46, is less tilted than the WT PCNA, which has a net charge of –60. The correlation between tilt and total net charge can be explained by simple energetic considerations, since increased tilt reduces the distance between the PCNA residues and the negatively charged DNA phosphate residues. This increase is energetically favorable in the case of positively charged PCNA and energetically unfavorable in case of negatively charged PCNA. We suggest that the cases where the net charge is not correlated with tilt angle are the result of different charge distribution. Accordingly, the variants Neg^1,2,3 and Neuⁱⁿ have similar tilt angles, suggesting that the negative electrostatic potential of the outer ring is responsible for a small ϕ angle. Similarly, the variants Pos^1,2,3 and Neu^out have similar tilt angles, indicating that the absence of the negative charges in the outer ring produce a greater ring title angle having a wider distribution.

The effect of the net charge of PCNA on the diffusion mechanism was also studied by estimating the localization of the DNA within the inner ring of PCNA. Figure 4A (right panel) shows the distribution of the distance, R, between the centers of mass of the DNA and PCNA. The distributions of R are very similar for all the variants except for the negatively charge variant Neg^1,2,3 that is shifted to shorter distances. The DNA is centered within the inner ring of the PCNA variants. The width of the distributions indicates that the center of mass of the DNA is quite mobile and it changes its location relative to the PCNA center of mass. Another perspective on the location of the DNA within the inner ring of PCNA is presented in Figure 5. It shows two-dimensionally the probabilities of the center of mass of the DNA being located at various points within the inner rings of different PCNA variants. For the WT^1,2,3, Neu, Neuⁱⁿ, Neu^out, Pos^1,2,3 and Neg^1,2,3 variants, the DNA is centered in the ring, however, for the Neg^1,2,3 variant exhibits greater central localization.

Diffusion of various ring-shaped proteins along nonspecific DNA

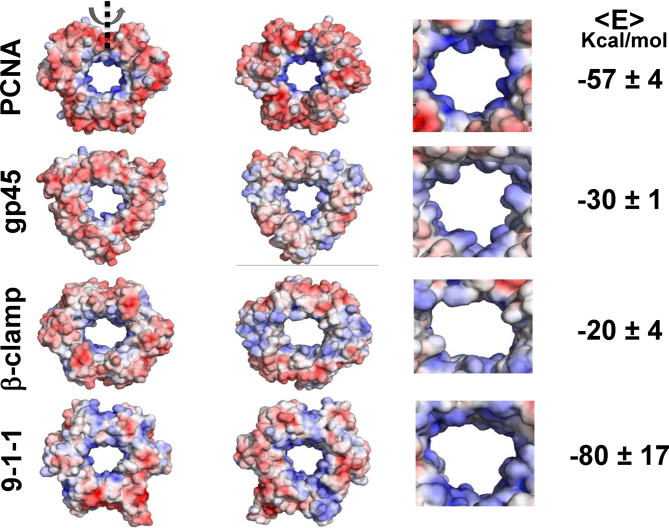
Sliding clamps are present in all organisms: bacteria, eukaryotes and viruses (10). In this study, we looked for similarities and differences in the dynamics of four different but similarly structured ring-shaped proteins on DNA: sliding clamps from three different organisms (the eukaryotic PCNA, the prokaryotic β-clamp, and the virus gp45 protein) and the 9-1-1 repair protein (see Figures 6 and 7). Despite the similar function of these proteins and their similar need to diffuse along DNA, they have substantially different electrostatic properties (Figure 6), as revealed by the binding electrostatic energies of these proteins with DNA as calculated with the APBS software (34). The nonspecific electrostatic energy of the four toroidal proteins ranges from –20 for the β-clamp to -80 Kcal/mol for the 9-1-1 protein, which is a 4-fold difference (see Figure 6). Furthermore, although these ring-shaped proteins have very similar 3D structure (regardless of whether they have 2- or 3-fold symmetry) (Figure 7), the geometries of their inner rings differ (Figure 6). For example, while the inner rings of PCNA and gp45 are more circular, that of β-clamp has a more elliptic shape.

Figure 6.

Electrostatic maps for the toroidal proteins PCNA, gp45, β-clamp and the 9-1-1 complex. From left to right, the electrostatic maps of the ring-shaped proteins are shown from the front, the back, and enlarged (back view). The number on the right corresponds to the average electrostatic free energy of the protein–DNA complex at a salt concentration of 0.125 M (the energy was calculated using APBS (34) and was averaged for different protein positions that were generated by their translocations along nonspecific DNA).

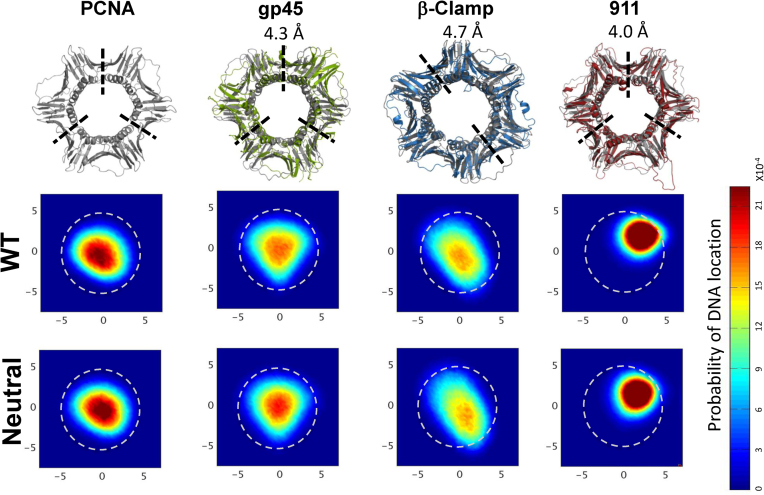
Figure 7.

Linear diffusion of four ring-shaped proteins (PCNA, β-clamp, gp45 and the 9-1-1 protein) along DNA. Each protein is structurally aligned with PCNA (shown in gray) and the root-mean-square deviation (RMSD) is shown on top. The localization probability maps of the DNA’s center of mass within the inner rings of the four proteins are shown for their wild-type (WT) sequence as well as for their neutral variants. A direct interaction between the DNA and PCNA is expected to occur at R ∼ 4 Å (deduced from the interaction of variant Pos1 with DNA, Figure 5D) and is indicated by the dashed circular line.

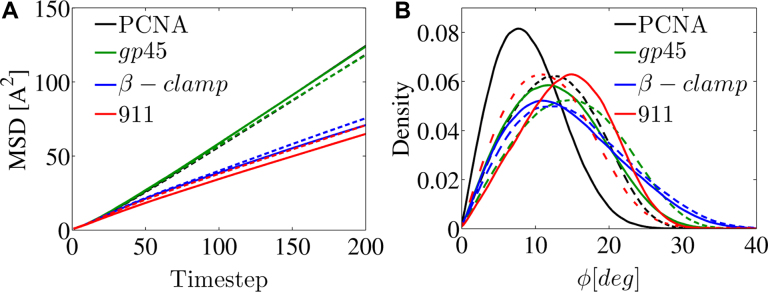
The linear diffusion of each protein was simulated along DNA at a salt concentration of 0.06 M and the D₁ value was estimated. Each of the toroidal proteins was studied also when all its charged residues were neutralized. Comparing the diffusion coefficients of each of the four proteins might be useful to quantify the effects of electrostatic potential and geometry on linear diffusion. Figure 8A shows the MSD of the four proteins and illustrates that PCNA and gp45 have the highest D₁ diffusion coefficient, and β-clamp and 9-1-1 have much lower diffusion coefficients. Interestingly, the D₁ values of the four ring-shaped proteins do not correlate with their electrostatic affinity to DNA. For example, the electrostatic energies of β-clamp and gp45 with DNA are of very similar strength, yet their D₁ values are very different. Also, based on the weak electrostatic energy of β-clamp with the nonspecific DNA (only –20 kcal/mol), which indicates the formation of a weak interface, one might expect fast sliding, however its low D₁ value reflects slow diffusion (Figure 8A).

Figure 8.

Characterization of the linear diffusion of PCNA, β-clamp, gp45 and the 9-1-1 proteins along DNA. For each wild type ring-shaped protein (solid line) and its neutralized variant (dashed line), the mean squared displacement (MSD) versus time step is shown as well as the of the tilt angle, ϕ. The color of each of the four proteins matches their coloring in Figure 7. In this plot, the black and green lines overlap.

Additional support for the notion that electrostatic interactions play a relatively minor role in the diffusion speed was obtained from examining the D₁ of the electrostatically neutral variants of the four proteins. Eliminating electrostatics forces between the four ring-shaped proteins and DNA affects D₁ by only about 6% (Figure 8A). A difference between the proteins with higher D₁ (i.e. PCNA and gp45) and the proteins with lower D₁ (i.e. β-clamp and 9-1-1) is the location of the DNA within the inner ring of the toroidal proteins. During the trajectory, if the DNA is more likely to be in the geometrical center of the clamp, the electrostatic interactions between the clamp and the DNA will be weaker and the diffusion will be faster. The probability of DNA localization inside the clamps is presented in Figure 7 for the four proteins. The DNA molecule is mostly symmetrically centered within the PCNA and gp45 proteins, while its localization probability within the β-clamp is elliptic, and within the 9-1-1 ring it is shifted toward one of the monomers. The location of the DNA in the inner ring is similar for WT and neutral variants of the four studied proteins (Figure 7), although some differences (such as the movement of the DNA toward the center of the inner ring of the neutralized 9-1-1 protein) are observed, again suggesting that the electrostatic interaction between the ring proteins and the DNA does not play a major role.

All four WT proteins show a tilt angle when diffusing along DNA (Figure 8B). The tilt angle is affected by the neutralization of the proteins. For PCNA and gp45, larger tilt angles are measured for the neutral proteins compared with their WT counterparts. For the 9-1-1 protein, a smaller tilt angle is seen for the neutral protein, whereas for the β-clamp the tilt angle hardly changes upon neutralization. The charges on the surface of the outer ring of the proteins may be the key to understanding these findings. For example, PCNA is negatively charged on both sides, thus repelling the negatively charged DNA, so resulting in a low tilt angle that increases upon neutralization. For the 9-1-1 protein, the larger tilt angle of the WT variant can be explained by the positively charged patches on its surface that can be attracted by the DNA and increase the tilt angle. In addition to the electrostatic features, the geometry of the inner ring and its electrostatics are also expected to influence tilt angle. One may note that, consistently with the results for the PCNA variants (Figure 4), a larger tilt angle following neutralization (PCNA and gp45) is associated with lower D₁, whereas a smaller tilt angle (9-1-1) is associated with larger D₁ (Figure 8).

The effect of symmetry breaking on sliding dynamics

A comparison of the diffusion coefficients of the toroidal clamp proteins (PCNA, β-clamp and gp45) with the toroidal but non-clamp 9-1-1 protein suggests that the symmetry of the protein affects the speed of their linear diffusion along DNA. Ring symmetry is reflected in the geometry of the toroidal protein as well as in the distribution of the electrostatic potential (i.e. of the charged residues) on the inner and outer rings.

To study the influence of the distribution of charges on the diffusion speed and mechanism, we designed three sets of PCNA variants in which the symmetry of the electrostatics was modified. One set was designed by neutralizing all the charges in none, one, or two of the PCNA subunits. These variants (designated as WT^1,2,3, WT^1,2 and WT¹, respectively (see Figure 5)) had net charges of –60, –40 and –20, respectively. Positive (Pos) and negative (Neg) sets of PCNA mutants were also designed by neutralizing either the negatively or positively charged residues, respectively, in three (Pos^1,2,3 and Neg^1,2,3), two (Pos^1,2 and Neg^1,2), or one (Pos¹ and Neg¹) of the three monomer subunits. Mutating one or two of the three subunits produced variants with broken electrostatic symmetry (Figure 5). Although the variants differed with respect to their charge distribution, they all bore the same net charge of either +26 (Pos variants) or -46 (Neg variants) and they all retained the geometric symmetry of the wild type.

A comparison of the linear diffusion of variants WT^1,2,3, WT^1,2 and WT¹ (Figure 4B) reveals faster diffusion (greater MSD) and a smaller tilt angle (Figure 4B) as the net charge becomes more negative (Figure 5). A similar relationship between net charge, tilt angle and D₁ was observed for all the electrostatically symmetrical variants of PCNA (variants WT^1,2,3, Neg^1,2,3, Pos^1,2,3, Neu, Neuⁱⁿ and Neu^out; Figure 4A). A comparison of the interactions between the three Neg variants (Neg^1,2,3, Neg^1,2 and Neg¹) and DNA shows that breaking the symmetry of the electrostatics results in slower diffusion, although the variants have the same net charge (Figure 4C). The different D₁ values for the diffusion of these negatively charged variants along DNA are not linked to a change in the tilt angle, ϕ (Figure 4C). Similar results were observed for the Pos^1,2,3, Pos^1,2 and Pos¹ variants (Figure 5), which again do not correlate with a change in the tilt angle (Figure 4D).

Figure 5 shows the localization of the DNA in the inner ring of the 12 PCNA variants studied to examine the effect of electrostatic symmetry breakage. Symmetry breaking of the electrostatic potential causes the DNA to shift from the center. In the case of the negatively charged variants, the DNA moves toward the neutralized subunits to minimize the repulsion. In the case of the positively charged variants, the DNA is attracted from the center toward the positively charged subunits. In both sets, the symmetry breaking results in a restricted volume for diffusion and higher friction at the PCNA–DNA interface. The D₁ is, therefore, higher and diffusion is faster for the PCNA with the symmetric electrostatic potential.

DISCUSSION AND CONCLUSIONS

In this study, the interactions between four ring-shaped proteins sharing a very similar architecture and dsDNA were investigated and compared. The proteins studied were the eukaryotic PCNA and 9-1-1 protein, the bacterial β-Clamp, and the T4 bacteriophage gp45. These four proteins have very similar 3D structures although they deviate in their length by up to 20% and their sequence identity is low. Furthermore, some of them are homotrimeric (PCNA and gp45), one of them is homodimeric (β-clamp), and one is a hetero-trimer (the 9-1-1 protein). These proteins are known for their ability to diffuse on non-specific DNA molecule sequences during gene regulation and DNA polymerization. We show that these ring-shaped proteins slide differently from transcription factors, as they do not necessarily follow the DNA major groove. The toroidal proteins can rotate around the DNA, however, the speed of their translocation along the DNA is much faster than the speed of their rotation. Accordingly, the sliding of the ring-shaped proteins is not necessarily rotation-coupled translation. The uncoupled rotation-translation dynamics is not linked to the degree of DNA flexibility.

Analyzing the linear diffusion of the four toroidal proteins allows the molecular ingredients that affect their linear diffusion along DNA to be deciphered. We found three major molecular properties of the toroidal proteins that govern the speed of their sliding along DNA. These molecular determinants are: (i) the shape of the inner ring; (ii) the overall electrostatic potential of the protein and (iii) the electrostatic and geometric symmetry of the protein. Despite the overall high similarity between the 3D structures of the four studied toroidal proteins, there are considerable differences between the shapes of their inner rings. We found that the inner ring of β-clamp is more elliptical than those of PCNA and gp45, which are more circular. The elliptic shape imposes constraints on the DNA dynamics that slow down diffusion. Neutralizing the positively charged residues in the inner ring of β-clamp increases its D₁ diffusion coefficient, but only to a small extent. This suggests that the electrostatic potential has a smaller effect on diffusion rate than the geometry and therefore the β-clamp is characterized by an intrinsically slow diffusion rate. The experimentally measured D₁ value for β-clamp is 10⁻¹⁴ m²/s, (18) which is 50-fold lower than the measured D₁ of PCNA (17).

Although the inner rings of the four studied toroidal proteins are positively charged and therefore attracted to the negative electrostatic potential of the DNA, this interaction does not seem to govern their sliding speed. Similarly, the negatively charged surface of the outer ring does not affect significantly the linear diffusion rate, but it does affect the tilt angle. The minor role electrostatic interactions between the sliding clamps and the DNA have on the linear diffusion is illustrated by the weak dependence of the linear diffusion coefficient on salt concentration. We show that a PCNA variant that lacks any charged residues slides similarly to WT PCNA. However, a negatively charged PCNA slides faster than WT PCNA and vice versa for positively charged PCNA. The mildness of the effects of mutating PCNA’s charged residues on its sliding speed along DNA compared with the corresponding effect on sliding by transcription factors (13,31,33) is expected to be linked to the unique toroidal topology of PCNA and the involvement of both repulsive and attractive electrostatic forces. The repulsive electrostatic forces are more extensive than the attractive interactions however the former are more long-range because the negative charges are mostly on the outer surface while the positive charges are mostly at the inner ring. These two opposite and dominant forces cancel out, resulting in a small net effect, and thus in very weak salt dependence. Support for the notion that the weak ionic strength dependence of the PCNA–DNA interaction is related to PCNA’s toroidal topology and its electrostatic properties is obtained from the quantification of the electrostatic binding free energy, which is weakly dependent on salt (Figure 9). The Sap1 transcription factor, however, exhibits a strong salt effect on binding energy, which, as expected, decreases as salt concentration increases (Figure 9).

Figure 9.

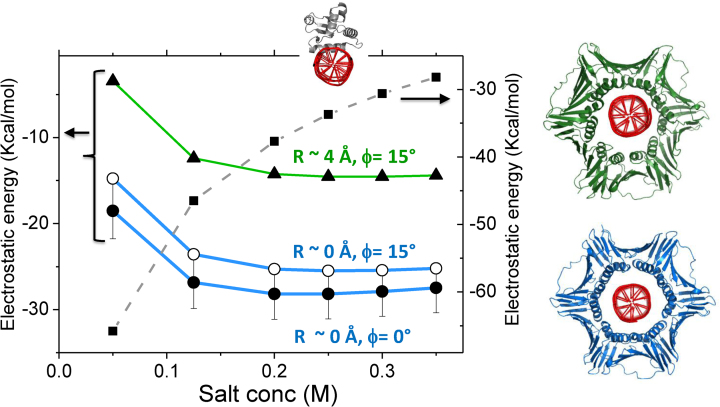
The electrostatic free energy for interactions of human PCNA with nonspecific DNA. The electrostatic binding free energies were calculated using APBS (34) for three different PCNA–DNA complexes that differ by tilt angle ϕ and the distance R. The binding energy was estimated for different salt concentrations. The complex with R ∼ 4 Å and tilt of 15° (green line) was modeled using pdb ID 5L7C (19) where a direct interface PCNA–DNA is formed via specific salt-bridges. The green and blue curves correspond to complexes with R distance 4 or 0 Å, respectively, and the PCNA in the models (right) was colored accordingly. For comparison, the electrostatic binding free energy was similarly estimated for Sap1 transcription factor (PDB 1bc8). In all cases, a DNA of 30 bp was used for the energy calculations.

The ionic-strength dependency of the linear diffusion coefficient of PCNA translocating along nonspecific DNA is much weaker than found computationally and experimentally for globular transcription factors. Experimental measurements also find that salt has a weak effect on the D₁ of PCNA, with findings of a 2.2-fold change in D₁ across a 13-fold change in ionic strength. The relationship between D₁ and salt concentration, the observation that the DNA is centered in the inner ring, and that uncharged PCNA can also diffuse along DNA suggest that the electrostatic PCNA–DNA interface is weak. The weaker electrostatic interface that PCNA forms with nonspecific DNA in comparison with the interfaces formed by other DBPs is supported by a recently reported K_D for PCNA–DNA of 0.7 mM (19) while the corresponding value for other proteins is a few μM (44). The dynamic PCNA–DNA interface is also supported by the high B-factors of the DNA in its crystalized complex with PCNA (19). It was recently suggested that PCNA simultaneously forms direct salt-bridges that are arranged geometrically to support its rotation along the DNA (19). However, the strength of the formed salt-bridges at the PCNA–DNA interface is estimated from the measured K_D to be ∼0.86 Kcal/mol, which is a lower value than the 1–5 kcal/mol value estimated for salt-bridges in biomolecules (45,46). To examine the interaction between PCNA and DNA, we used APBS (34) to estimate the electrostatic binding free energy in complexes in which the DNA directly interact with PCNA via specific salt bridges (pdb ID 5L7C; Figure 9 green line) or in which it is located in the center of the inner ring (Figure 9, blue lines). Figure 9 shows that, for tilt angles of 0° or 15°, the latter is more stable.

During linear diffusion, the DNA tends to remain close to the central axis of the inner PCNA cavity, as indicated by the small values of R (0–4 Å) (Figure 5). This is reasonable given the symmetrical distribution of positive charge around the surface of the inner ring of symmetrical toroidal proteins (i.e. PCNA, β-clamp and gp45). The only scenario which led to a close interaction of the DNA with a given subunit of PCNA was when the symmetric electrostatic potential of the inner ring was broken by modifying the charged residues of one or two of the subunits. The shift of the DNA from the central axis of the cavity also resulted in slower diffusion. The heterotrimeric 9-1-1 protein, where the distribution of charge on the inner ring is asymmetric, also exhibits slower diffusion. One may hypothesize that modifying some Lys residues of PCNA (e.g. acetylation (47) or ubiquitination (48)) may break the electrostatic symmetry and therefore modify its linear diffusion along DNA.

Linear diffusion of the toroidal proteins along DNA is often performed when the protein ring is tilted relative to the DNA axes. We found that the tilt angle, ϕ, for the four studied proteins is ∼10 ± 5°. The tilt angle depends on the geometry of the inner ring, its electrostatic potential, as well as the electrostatics of the outer ring and therefore it varies to some extent for the different proteins. Modifying electrostatic potential by mutations may change the tilt angle. A smaller tilt angle (∼5°) was found for the PCNA variant that is purely negatively charged and for the variant with a neutralized inner ring. By contrast, a larger tilt angle (∼20°) was measured for variants that are purely positively charged.

Changes in tilt angle are linked to changes in the D₁ values. The tilt angle of PCNA increases for higher salt concentrations, suggesting again that decreasing the repulsive electrostatic interactions between PCNA and DNA can affect the tilt angle. The value of the tilt angle found for the four studied ring-shaped proteins is ∼10°, which is smaller than the ∼22° tilt angle found in the crystal structure of β-clamp with 10 bp dsDNA (49). The crystal structure of PCNA shows a smaller tilt angle of 16° (50,51), however a tilt angle of ∼40° was measured in a different crystal structure (52). Two earlier molecular dynamics simulations using atomistic representation reported a larger tilt angle of 20° (16) or 30° (14,19). The tilt angle reported using the coarse-grained simulations is smaller but increases with salt concentration. The deviation between the coarse-grained and atomistic simulations may stem from the low resolution model of the former, mostly because side-chains are not explicitly represented, or from the short timescale simulations of the latter. Alternatively, the different measured tilt angle may indicate its inherent flexibility, which is supported by the distributions of tilt angle with a variance of about 10°, as presented in the current study. Regardless of the uncertainty in the size of the angle, all these studies agree that PCNA clamps diffuse along dsDNA while tilted relative to the DNA axis. This tilt angle relative to DNA is found also in higher clamp-protein complexes (53,54).

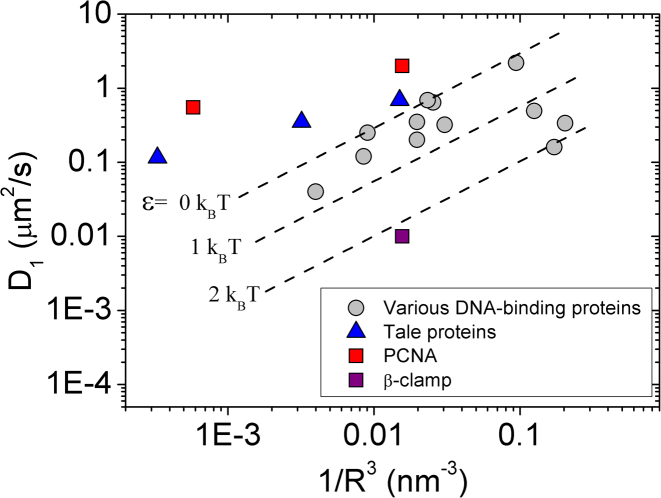
The PCNA diffusion mechanism that emerges from the current study involves the PCNA ring engaging in a combination of rotation and translation along the DNA, consistently with the two reported diffusion modes from single-molecule experiments (17). The rotation of PCNA along DNA may result in a smaller linear diffusion coefficient regardless of the degree of coupling between the rotation and translation of the ring along DNA. Accordingly, our results suggest that the indirect evidence for coupled rotation-translation (17) should be reconsidered. The dependence of D₁ on the dimension of the protein, R, for PCNA is very similar to that of the TALE protein that was shown to follow uncoupled rotation-translation diffusion on DNA (43) (Figure 10). Our observation that the DNA is localized in the center of the inner ring does not contradict the formation of transient salt-bridges at the PCNA–DNA interface, as the system is quite dynamic and the centers of mass of the DNA and PCNA fluctuate. Fluctuations in the localization of the DNA within the inner ring may originate from the extensive electrostatic forces that are applied isotropically between the DNA cylinder and the inner ring of PCNA. The PCNA–DNA interface therefore is frustrated by the electrostatic forces between the ring and the cylindrical DNA. Given the impossibility of satisfying all the potential electrostatic interactions simultaneously, the lowest energy is achieved when the DNA is located at the center of the ring (Figure 9). It is possible that this electrostatic frustration and the imperfect geometrical fit of the DNA within the inner ring of the PCNA results in fast linear diffusion that shows only weak coupling between rotation and translocation.

Figure 10.

Linear diffusion coefficient (D₁) versus radius (R) plot of DNA-binding proteins. DNA-binding proteins that follow rotation-coupled transition diffusion are shown in gray. These proteins may have slower diffusion due to energetic ruggedness (dashed lines for ϵ > 0). The experimental D₁ values of PCNA (taken from (17)) exhibit similar behavior to that of the TALE protein that was shown to follow rotation-uncoupled translation dynamics (43). The D₁ values for PCNA and β-clamp were taken from refs. (17) and (18). This plot was inspired by plots in (43,56).

This study serves as another example of how the molecular features of the DBPs can affect the details of their diffusion along DNA. We show that the toroidal structures may dictate different mechanisms of linear diffusion than those that were reported for non-toroidal DBPs. Nonetheless, our observation that PCNA and similar ring-shaped DBPs do not slide along DNA but rather mostly perform hopping dynamics when they linearly diffuse along DNA are not necessarily exclusive to toroidal proteins. Uncoupled rotation–translation was previously reported for other proteins, such as p53 (55) and the TALE protein (43).

FUNDING

Federal German Ministry for Education and Research. Israel Science Foundation grant number 1583/17. Funding for open access charge: Internal funding.

Conflict of interest statement. None declared.