Statistical methods to detect novel genetic variants using publicly available GWAS summary data

We propose statistical methods to detect novel genetic variants just using genome-wide association studies (GWAS) summary data without access to raw genotype and phenotype data. With more and more summary data being posted for public access in the post GWAS era, the proposed methods are practically very useful to identify additional interesting genetic variants and shed lights on the underlying disease mechanism. We illustrate the utility of our proposed methods with application to GWAS meta-analysis results of fasting glucose from the international MAGIC consortium. We found several novel genome-wide significant loci that are worth further study.

1 Introduction

In the past decade, the genome-wide association studies (GWAS) have been very successful in identifying thousands of common genetic variants that are associated with various traits and diseases (Visscher et al., 2017). These GWAS are primarily based on the paradigm of single variant single trait association tests, and have typically made publicly available the association test summary statistics, which include, e.g., the minor allele frequency (MAF), the estimated effect sizes with their standard errors, and significance p-values for each single nucleotide polymorphism (SNP) analyzed in a GWAS. Since it is generally much harder to access the individual-level GWAS phenotype and genotype data due to privacy concerns and various logistical considerations, it has motivated tremendous interest in developing new methods for further analyzing GWAS association test summary data (Pasaniuc and Price, 2017). For example, for the single variant based association test, the GWAS meta-analysis (Evangelou and Ioannidis, 2013) is typically conducted based on the association test summary statistics, which can be as efficient as analyzing individual-level data across all studies (Lin and Zeng, 2010). Similar methods have been developed for meta-analysis of the rare variant set association across studies (Hu et al., 2013; Lee et al., 2014). Specifically Hu et al. (2013) showed that the score statistics across variants approximately followed the same correlation as the rare variant genotype scores, and developed a novel Wald chi-square test for the rare variant set association just using single rare variant association score statistics. For joint association test of a single variant with multiple correlated traits, Stephens (2013) and Zhu et al. (2015) proposed methods using only individual GWAS summary statistics and GWAS meta-analysis summary results. The key insight of these approaches is that for a single variant, the association test Z-statistics across different traits share the same correlation as the traits (Stephens, 2013). Most identified common variants have small effect sizes and contribute a small proportion to the overall heritability (Manolio et al., 2009), it often helps to aggregate signals across multiple variants to boost the detection power (Wu et al., 2010). In this work, we study methods for genome-wide variant set association test at the gene level using only GWAS summary data. We provide a transparent derivation showing that the correlation of GWAS (meta-analysis) association test Z-statistics across variants can be computed based on the variant linkage disequilibrium (LD) matrix. Hence we can leverage LD information from a population reference panel to estimate the correlation of Z-statistics and conduct variant set association test. We further develop and post publicly available R programs that can very efficiently and accurately compute p-values for the summary data based association tests. The proposed methods are practically very useful to further mine the vast amount of public GWAS summary data to identify additional interesting genetic variants. We illustrate the utility of our proposed methods with application to GWAS meta-analysis results of fasting glucose from the international MAGIC consortium.

2 Materials and Methods

Consider the single variant association test for a continuous trait Y based on the following linear regression model $Y=X{\alpha }_j+G_j{\beta }_j+{\in }_j$ for the variant G_j, j = 1,…,M. Here X is a vector of p covariates to be adjusted (including the intercept, age, and gender, e.g.), and α_j and β_j are the regression coefficients. 𝜖_j is assumed to follow a normal distribution N(0,σ_j²). The random error 𝜖_j has been indexed depending on each variant, since in principle 𝜖_j consists of two parts: variation due to random measurement error and polygenic contributions. The random measurement error can be assumed identical across all variants. But the polygenic contribution could be different since part of it will be captured by G_jβ_j for those risk variants. Therefore null variants will have identical errors with the same variance, while the variances are potentially different for risk variants and those nearby variants in linkage disequilibrium (LD) with the risk variants.

Given the observations of n unrelated individuals, denote X as the n×p design matrix, Y the n-vector of outcomes, G_j the n-vector of genotypes for the j-th variant. Denote projection matrix P = I_n − X(X^T X)⁻¹X^T , where I_n is a n-th order identity matrix. We can check that

$$\widehat{{\beta }_j}=\frac{Y^{T}P{G}_j}{G_j^{T}P{G}_j},\upsilon \text{ar}\left({\widehat{\beta }}_j\right)=\frac{{\sigma }_{{}^j}^2}{G_j^{T}P{G}_j}.$$

The GWAS summary Z-statistics are computed as the standardized genetic regression coefficients by their estimated standard errors where the unknown variance ${\sigma }_j^2$ is replaced by their estimate ${\widehat{\sigma }}_j^2$

$$z_j=\frac{\widehat{{\beta }_j}}{\sqrt{\widehat{\upsilon ar}\left(\widehat{{\beta }_j}\right)}}=\frac{Y^T\stackrel{\sim }{G_j}}{{\widehat{\sigma }}_j},\stackrel{\sim }{G_j}=\frac{P{G}_j}{\sqrt{G_j^{T}P{G}_j}}.$$

Here $\stackrel{\sim }{G_j}$ is essentially the vector of standardized genotypes adjusting for other covariates. We can check that asymptotically $Var\left(z_j\right)=1,Co\upsilon \left(z_j,z_l\right)={\rho }_{jl},$ where ${\rho }_{jl}=\frac{G_j^{T}P{G}_l}{\sqrt{(G_j^{T}P{G}_j)(G_l^{T}P{G}_l)}}$(see appendix for details). When the adjusted covariates are all independent of tested variants (e.g., age and gender), we can unbiasedly estimate the covariance between the summary Z-statistics using cor(G_j,G_l), i.e., the LD correlation matrix (see appendix for details). Therefore we can compute the null covariance matrix of summary Z-statistics by leveraging the LD information from a population reference panel, e.g., the 1000 Genomes Project (Abecasis et al., 2012), or some existing GWAS data of similar ancestry. As argued by Hu et al. (2013), for weakly informative covariates, the LD can still provide a very good approximation to the correlation of score statistics, which is proportional to the Z-statistics. Therefore in general we expect the LD correlation matrix provides a good estimate of the Z-statistic correlations. The previous results also hold for GWAS meta-analysis summary results (see appendix for details).

For simplicity of notation, consider a set of m variants in a gene region, denote their summary Z-statistics as (z₁,…,z_m), and R = (r_ij) the estimated null correlation matrix computed based on the variant LD. We consider the following three SNP-set association tests: (1) sum test (ST), $B={\displaystyle {\sum }_{j=1}^m{z}_j}$, which is a type of burden test statistic (Madsen and Browning, 2009); (2) squared sum test (S2T), $Q={\displaystyle {\sum }_{j=1}^m{z}_{{}_j}^2}$, which is a type of SKAT statistic (Wu et al., 2010); and (3) adaptive test (AT), based on the minimum p-value T = min_ρ∈[0,1] P(Q_ρ), where Q_ρ = (1 − ρ)Q + ρB² and P(Q_ρ) denotes its p-value. The AT is in the same vein as the SKAT-O statistic (Lee et al., 2012). We can readily check that $B^2/\left({\sum }_{i,j}{r}_i{}_j\right)$ asymptotically follows the $x_1^2$ distribution; and Q is asymptotically distributed as the weighted sum of independent $x_1^2$ random variables with weights being the eigenvalues of R. We follow the approach of Wu et al. (2016) to efficiently and accurately compute the p-value for the AT based on an one-dimensional numerical integration. In practice we search over $\rho \in (0,{0.1}^2,{0.2}^2,{0.3}^2,{0.4}^2,{0.5}^2,0.5,1)$for the minimum p-value. The ST has good performance when all variants have effects of same direction and approximately equal size, but is sensitive to the direction of variant effects. The S2T has better performance than the ST under a mix of protective and deleterious variants. The AT could adapt to the data and generally has more consistent and robust performance with good detection power across a wide range of scenarios.

3 Results

3.1 Simulation study

We first conduct a simulation study to assess the type I errors of the three tests. We simulate 10⁸ random vectors from N(0,R) to estimate their type I errors at significance levels $\alpha ={10}^{-4},{10}^{-5}$, and 2.5 × 10⁻⁶. We consider a set of 20 SNPs in the NPHS2 gene and take their LD matrix as R. Table 1 summarizes the results. Overall we can see that all three tests have well-controlled type I errors.

Table 1:

Ratio of empirical type I errors divided by the significance level α estimated over 10⁸ simulations: listed within parentheses are the standard errors. S2T is based on the sum of squared Z-statistics; ST is the sum of Z-statistics, and AT is the adaptive test.

	10−4	10−5	2.5 × 10−6
S2T	1.01 (0.01)	0.99 (0.03)	0.98 (0.06)
ST	1.00 (0.01)	0.99 (0.03)	1.02 (0.06)
AT	0.99 (0.01)	0.88 (0.03)	0.81 (0.06)

3.2 Application to fasting glucose GWAS meta-analysis summary results

We analyze the summary data from the GWAS meta-analysis of fasting glucose conducted by the international MAGIC consortium (Dupuis et al., 2010). The association results are based on 21 GWAS with around 46,186 non-diabetic participants of European descent who are informative for fasting glucose. The summary data is publicly available at ftp://ftp.sanger.ac.uk/pub/magic/MAGIC_FastingGlucose.txt. The summary data consists of the MAF, effect size estimate and its associated standard error, and p-value for 2,470,476 SNPs. For illustration, we first remove 290 genome-wide significant SNPs with p-value less than 5 × 10⁻⁸ and then filter out those SNPs with MAF < 0.05. We download the list of genes and their coordinates (transcription start and end positions based on the hg19/GRChB37 reference genome) from the UCSC genome browser (Kent et al., 2002). We take all SNPs that are located in or near a gene as a set to be analyzed for joint association. Specifically following Wu et al. (2010), we group all SNPs from 20 kb upstream of a gene to 20 kb downstream of a gene. For each SNP set corresponding to a gene, we also perform LD pruning: we remove those SNPs that have pairwise LD r² > 0.8 with other SNPs. Using these criteria, we obtain 18,725 SNP sets that have at least two SNPs. We set our genome-wide SNP set significance level as 2.67 × 10⁻⁶, which is the Bonferroni corrected significance level for the total number of tested SNP sets.

We note that the MAGIC consortium has performed a followup replication study using a Metabochip consisting of a small panel of promising SNPs and a much larger sample size from 66 fasting glucose GWAS with around 133,010 non-diabetic participants (Scott et al., 2012). The summary data contains the results for 64,493 pre-selected SNPs, and is available at ftp://ftp.sanger.ac.uk/pub/magic/MAGIC_Metabochip_Public_data_release_25Jan.zip. We use them as partial validation for our analysis of Dupuis et al. (2010) summary data.

When applying the three SNP-set tests to the summary data of Dupuis et al. (2010), the ST identified 12 significant genes, S2T identified 20 genes, and AT identified 22 significant genes. The adaptive test AT captures the majority of significant genes identified by ST and S2T. An interesting case is the significant gene FADS1 identified only by the adaptive test AT with a significance p-value of 2.39 × 10⁻⁶, and ST and S2T reported p-values of 1.40 × 10⁻⁵ and 4.41 × 10⁻⁶, respectively. This gene harbored genome-wide significant SNPs in the study of Dupuis et al. (2010) and the followup study of Scott et al. (2012). Figure 1 shows the Venn diagram comparing the number of significant genes identified by the proposed tests. Among all 25 significant genes identified by the three SNP-set tests, 10 are novel genes which didn’t harbor any significant SNPs in the study of Dupuis et al. (2010). These novel genes contain promising SNPs (often with small or modest effect sizes) worth further study. And among these 10 novel genes, 6 genes have been found to contain genome-wide significant SNPs in the followup study of Scott et al. (2012). Table 2 lists the test p-values for some novel genes together with the minimum p-values across all SNPs in the gene in the two studies. The complete results are available at the supplementary materials.

Figure 1:

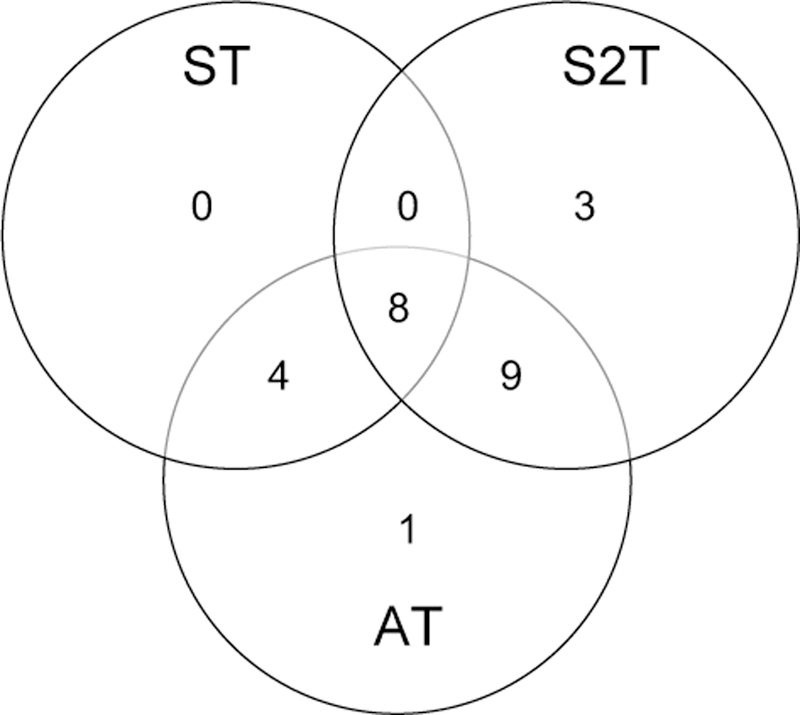
Venn diagram of number of significant genes identified by three summary data based SNP-set tests.

Table 2:

Some novel genes found by the proposed SNP-set tests: we listed the test p-values for S2T, ST and AT and the minimum p-value across all SNPs in the gene for Dupuis et al. (2010) study (denoted as minP-2010) and Scott et al. (2012) study (denoted as minP-2012).

Gene	S2T	ST	AT	minP-2010	minP-2012
ZNF512	2.09e-06	5.49e-01	3.82e-06	1.40e-06	9.68e-20
GPN1	2.51e-06	5.38e-01	4.62e-06	2.96e-06	9.68e-20
SLC4A1AP	1.22e-06	6.06e-01	1.55e-06	2.96e-06	3.21e-17
PROX1	1.39e-06	8.17e-06	1.61e-06	7.08e-08	3.22e-12
SUPT7L	1.76e-06	4.16e-01	2.30e-06	2.96e-06	6.59e-12
C2CD4B	6.31e-07	5.64e-02	6.31e-07	5.89e-07	2.05e-08

For illustration, we also performed SNP-set tests using all SNPs and obtained similar conclusions. The complete results are available at the supplementary materials.

4 Discussion

In summary, we have proposed SNP-set tests using the GWAS summary data. The proposed methods are efficient and scalable to analyze summary data for millions of genome-wide SNPs. As more and more summary data are now being posted for public access in the post GWAS era, these methods will be practically very useful to identify more genetic variants associated with various diseases.

Our previous discussions have implicitly assumed equal weights for variants. We note that we can readily incorporate variant weights into the proposed tests as follows. Denote the associated variant weights as W = (w₁,…,w_m), which can be determined by the variant MAFs (p₁,…,p_m). We then consider weighted summary statistics (w₁z₁,…,w_mz_m), and their associated covariance matrix is then diag(W)Rdiag(W). Note that the Z-statistics are inherently standardized: the Z-statistic is roughly proportional to the score statistic scaled by the genotype standard error. So setting the constant weight corresponds to using weight $w_j=1/\sqrt{p_j\left(1-p_j\right)}$ following the approach of Wu et al. (2010) and Madsen and Browning (2009). There have been some recent research that leverages additional functional annotation information and public GWAS summary data to further identify novel genetic variants (Gusev et al., 2016; Mancuso et al., 2017), which can be approached as incorporating variant weights W under the proposed framework. We are currently exploring this approach and will report the results in the future.

We want to remark that it is more productive to treat the proposed SNP-set tests as a complementary instead of competing approach to the traditional single variant based association test. Therefore we recommend applying the proposed tests to genes that do not harbor genome-wide significant SNPs to further identify more novel variants. We have implemented the proposed methods in an R package available at http://www.github.com/baolinwu/mkatr. We provide sample R codes to install and use the package at the supplementary materials.

highlights.txt.

1. 1. propose useful and efficient GWAS summary data based SNP-set association test methods to identify more novel variants

2. 2. provide efficient implementation of the proposed methods in a publicly available R package

3. 3. demonstrate the utility of proposed methods via application to analysis of fasting glucose GWAS meta-analysis results, and find several novel loci worth further study

Appendix

GWAS summary Z-statistics

Denote Y as the continuous outcome observed for a cohort of n unrelated individuals. Denote the n×p covariate matrix as X, which includes the intercept and other commonly adjusted covariates (e.g., age and gender). Here p denotes the total number of covariates.Under the marginal working regression model for variant j, Y = Xα_j+G_jβ_j+𝜖_j, where ${\in }_j\sim \mathcal{N}(0.{\sigma }_j^2{I}_n),$ we have ${\widehat{\beta }}_j=G_j^{T}PY/\left\{G_j^{T}P{G}_j\right\}$, where $P=In-X{(X^{T}X)}^{-1}{X}^T$ is the projection matrix. Hence$\left(\widehat{{\beta }_j},\widehat{{\beta }_l}\right)=cor(G_j^{T}PY,G_l^{T}PY)=r_{jl},$ where $r_{jl}=\frac{G_j^{T}P{G}_j}{\sqrt{(G_j^{T}P{G}_j)}\sqrt{(G_l^{T}P{G}_l)}}.$When the covariates X do not contain ancestry covariates (e.g., for the homogeneous European population), G_j is independent of X: hence r_jl equals to the LD correlation between the two variants, cor(G_j,G_l). Let z_j denote the standardized $\widehat{{\beta }_j}$ (i.e., the summary Z-statistic)

$z_j=\frac{\widehat{{\beta }_j}}{\sqrt{\widehat{Var}\left(\widehat{{\beta }_j}\right)}}=\frac{Y^T\stackrel{\sim }{G_j}}{{\widehat{\sigma }}_j},\stackrel{\sim }{G_j}=\frac{P{G}_j}{\sqrt{G_j^{T}P{G}_j}},$where ${\widehat{\sigma }}_j^2=\left|\right|PY-\stackrel{\sim }{G_j}\widehat{{\beta }_j}|{|}^2/\left(n-p-1\right).$ Note that generally the estimated variance ${\widehat{\sigma }}_j^2$ are slightly different across SNPs. For null variants not associated with the outcome, ${\widehat{\sigma }}_j^2$ are all unbiased estimates of the same outcome variance. Therefore for null variants, asymptotically $Var(z_j)=1$ and $Co\upsilon (z_j,z_l)=r_{jl}$For a variant associated with the outcome, if it explains only a very small proportion of the total trait variation, which is true for most variants under polygenic model, the previous equations approximately hold.Denote the (raw or after adjusting for top ancestry PCs) LD correlation matrix R =(r_jl). For relatively homogeneous population (e.g., of European descent), we can use the LD matrix computed from public population samples.

Consider K separate GWAS each with n_k individuals, k = 1,2,…,K. For the k-th GWAS, denote Y_k as the outcome, P_k the covariate projection matrix, G_kj the genotype scores for SNP j, and β^ˆ_kj the regression parameter estimates for the j-th SNP. With homogeneous population and no ancestry covariates, P_kG_kj amounts to centering the genotypes. Without loss of generality, assume the genotype scores have been centered. We have P_kG_kj = G_kj, and hence ${\widehat{\beta }}_{kj}=G_{kj}^T{Y}_k/\left\{G_{kj}^T{G}_{kj}\right\}.$ Denote $Var(Y_k)={\sigma }^2{I}_{n_k}.$Let θ_j denote the variance of genotype scores for SNP j. For null variants, we have asymptotically V ar(${\widehat{\beta }}_{kj}$) = σ²/(n_kθ_j), and Cov$Co\upsilon \left({\widehat{\beta }}_{kj,}{\widehat{\beta }}_{kl}\right)=r_{jl}{\sigma }^2/(n_k\sqrt{{\theta }_j{\theta }_l}.$ They also approximately hold for those variants with small effects. The meta-analysis estimate is typically based on the weighted average, denoted as $\widehat{{\beta }_j}={\displaystyle {\sum }_{k=1}^K{a}_k}\widehat{{\beta }_{kl}}.$ Here the weight a_k is typically determined by the GWAS sample size. For example, one common choice is$a_k=n_k/({\displaystyle {\sum }_{k=1}^K{n}_k}).$ Another popular choice is based on the inverse variance weighting, which amounts to setting $a_k=Var{(\widehat{{\beta }_{kj}})}^{-1}\left[{\displaystyle {\sum }_{k=1}^{K}Var{(\widehat{{\beta }_{kj}})}^{-1}}\right],$ which asymptotically equals to$n_k/({\displaystyle {\sum }_{k=1}^K{n}_k}).$ Hence for null variants we have asymptotically , $Var(\widehat{{\beta }_j})=\left({\displaystyle {\sum }_{k=1}^K{a}_k^2/n_k}\right){\sigma }^2/{\theta }_j,andCo\upsilon (\widehat{{\beta }_j},\widehat{{\beta }_l})=\left({\displaystyle {\sum }_{k=1}^K{a}_k^2/n_k}\right)r_{jl}{\sigma }^2/\sqrt{{\theta }_j{\theta }_l}.$ Therefore for the GWAS meta-analysis Z-statistics, we also have asymptotically Cov(z_j,z_l) = r_jl. We note that with $a_k=n_k/({\displaystyle {\sum }_{k=1}^K{n}_k}).$, we have $Var(\widehat{{\beta }_j})={\sigma }^2/{\theta }_j/\left({\displaystyle {\sum }_{k=1}^K{n}_k}\right).$ Therefore the meta-analysis approach has the same asymptotic efficiency as the mega-analysis, which pools all GWAS individual samples for analysis. This agrees with the theoretical results of Lin and Zeng (2010).