Skip to main content
PMC home page
Karger Author's Choice logoLink to Karger Author's Choice
. 2018 Apr 11;75(3):219–244. doi: 10.1159/000484938

Sound Symbolic Patterns in Pokémon Names

Shigeto Kawahara a,*, Atsushi Noto b, Gakuji Kumagai c
PMCID: PMC6159826  PMID: 29649803

Abstract

This paper presents a case study of sound symbolism, cases in which certain sounds tend to be associated with particular meanings. We used the corpus of all Japanese Pokémon names available as of October 2016. We tested the effects of voiced obstruents, mora counts, and vowel quality on Pokémon characters' size, weight, strength parameters, and evolution levels. We found that the number of voiced obstruents in Pokémon names correlates positively with size, weight, evolution levels, and general strength parameters, except for speed. We argue that this result is compatible with the frequency code hypothesis of Ohala. The number of moras in Pokémon names correlates positively with size, weight, evolution levels, and all strength parameters. Vowel height is also shown to have an influence on size and weight - Pokémon characters with initial high vowels tend to be smaller and lighter, although the effect size is not very large. Not only does this paper offer a new case study of sound symbolism, it provides evidence that sound symbolism is at work when naming proper nouns.

1 Introduction

This paper offers a new case study of sound symbolic patterns, in which particular sounds tend to be associated with particular meanings or images (e.g., Blasi et al., 2016; Dingemanse et al., 2015; Hamano, 1986; Hinton et al., 1994, 2006; Lockwood and Dingemanse, 2015; Perniss et al., 2010; Sapir, 1929; Sidhu and Pexman, 2017). Although language is a system which can in principle combine any phonotactically permissible sound sequences to any meanings (the thesis of arbitrariness; Hockett, 1959; Saussure, 1916), there are some systematic exceptions. The claim that there can be connections between sounds and meanings goes back to Socrates, who argues in the dialogue Cratylus that Greek ρ (= “r”) is used in many words that express movement, that α (= “a”) means “large,” and that o means “round,” etc. (Plato, Cratylus, 423B, 426–427). Modern research on sound symbolism was inspired by experimental work by Sapir (1929), who showed that English speakers feel /a/ to be larger than /i/. Since then, research has revealed many sound-meaning connections, which demonstrably hold across many languages (Blasi et al., 2016). For example, voiced obstruents (/b/,/d/, /g/, /z/) are often associated with “heaviness” and “largeness,” and these associations have been shown to hold for English speakers (Newman, 1933) as well as for Japanese speakers (Hamano, 1986; Kawahara and Shinohara, 2012; Shinohara and Kawahara, 2016; Sidhu and Pexman, 2015) and for Chinese speakers (Shinohara and Kawahara, 2016).

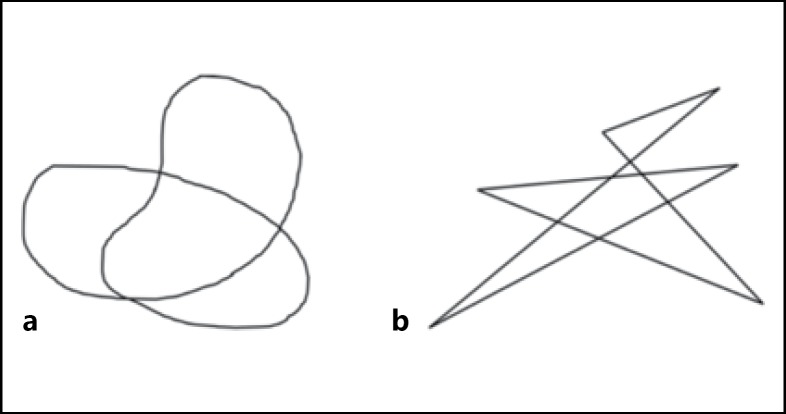
It has also been demonstrated that sound symbolism can affect naming patterns (Berlin, 2006; Kawahara and Shinohara, 2012; Köhler, 1947; Perfors, 2004; Ramachandran and Hubbard, 2001; Sapir, 1929; Shinohara and Kawahara, 2013; Shinohara et al., 2016). For example, Köhler's classic study (1947) shows that, given a pair of a round object and an angular object, as in Figure 1, people tend to associate maluma with the former and takete with the latter (see Hollard and Wertheimer, 1964; Kawahara et al., 2015; Koppensteiner et al., 2016; Lindauer, 1990; Nielsen and Rendall, 2013; Shinohara et al., 2016, for follow-up studies of this effect). It seems to be the case that in general, sonorants tend to be associated with round objects, whereas obstruents tend to be associated with angular objects (Shinohara et al., 2016). In a similar situation, a round object is more likely to be associated with bouba than with kiki (D'Onofrio, 2014; Fort et al., 2015; Maurer et al., 2006; Ramachandran and Hubbard, 2001; Sidhu and Pexman, 2015).

Fig. 1.

Fig. 1

Open in a new tab

Schematic illustration of maluma (a) and takete (b) figures. A pair of a round object and an angular object; the former is more likely to be named maluma/bouba, and the latter is more likely to be named takete/kiki. The figures are taken from Kawahara and Shinohara (2012), itself inspired by Köhler (1947).

Likewise, Berlin (2006) argues that sound symbolism is operative when naming animals and insects in many languages – for example, animals that move slowly tend to be named with sounds with low frequency energy, such as labial consonants and nasal consonants. For example, Berlin (2006) compares names of 2 kinds of birds – rail and tinamou, the latter of which moves more slowly – in 17 different languages. He found that both nasals and labials are more likely to be used for slow-moving tinamou (e.g. mami in Cuiba and aawaa in Bora) than for rail. To provide another example, the experiment reported in Perfors (2004) reveals that English male names with stressed front vowels are judged to be more attractive than those with back vowels, but English female names with stressed back vowels are judged to be more attractive than those with front vowels. A number of studies show that female and male names in English are (stochastically) distinguished by many phonological features (Brown and Ford, 1961; Cassidy et al., 1999; Cutler et al., 1990; Slater and Feinman, 1985; Wright and Hay, 2002; Wright et al., 2005), some of which are grounded in sound symbolic principles; for example, female names are more likely to contain sonorants than male names, an observation that may be related to why the round figure in Figure 1 is more likely to be called maluma than takete. All of these studies indicate that the choice of sounds in naming patterns is not entirely random, but rather governed, at least partially, by some sound symbolic principles. In addition, a growing body of work has also examined the impact of sound symbolism in brand names, and has shown that sound symbolism may affect the attractiveness of the products as well as the perception of their priciness (Abel and Glinert, 2008; Bolts et al., 2016; Coulter and Coulter, 2010; Klink, 2000; Peterson and Ross, 1972; Yorkston and Menon, 2004).

Building on this research tradition, we ask whether there are any sound symbolic effects in Japanese Pokémon names (see Miura et al., 2012, and Ohyama, 2016, for previous linguistic analyses of Pokémon names). Japanese has a large class of mimetic words, which are sound symbolic (Hamano, 1986), and some Pokémon names are based on such mimetic words. For example, gaburi represents an action of a “big bite,” and there is a Pokémon character named gaburiasu; likewise, goron is a mimetic word representing rolling movement, and a rock-like Pokémon character is named goroon. Therefore, Japanese offers an interesting test case to address whether Pokémon names show sound symbolic patterns (although we do not want to imply at this point that studying Pokémon names in other languages is uninteresting, which is contrary to what we hope; see the conclusion section).

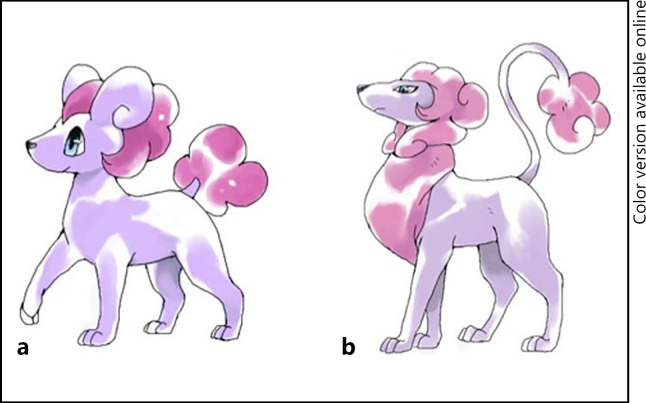
Pokémon, whose name is etymologically a truncated compound of poketto “pocket” and monsutaa “monster,” started as a video game in 1995 by Nintendo and has been very popular in Japan and many other countries (see Tobin, 2004, and the Wikipedia article1 for details). Pokémon features fictional creatures, themselves called “Pokémon,” who trainers can collect, train, and battle. One feature of the Pokémon game is that Pokémon characters evolve into different, related forms with new names. Although for copyright reasons, we are unable to reproduce actual Pokémon pictures in this paper, Figure 2 presents a pre- and post-evolution pair of (non-official) Pokémon characters, drawn by a digital artist.2 (These pictures were judged by many Pokémon players to look authentic, and have been used for an experiment related to this study; Kawahara and Kumagai, in press.) Each Pokémon character officially has size, height, and strength parameters, the last of which includes HP (for “hit point” = stamina), attack, defense, special attack, special defense, and speed.

Fig. 2.

Fig. 2

Open in a new tab

A sample of a pre- (a) and post-evolution (b) pair of Pokémon. Drawn by a digital artist, toto-mame.

As of 2016, there are more than 700 Pokémon characters in total, which is the target of the current study. The current corpus-based study suggests that there are indeed some systematic patterns in Pokémon characters' names, which can be considered to be sound symbolic. More specifically, we show that the number of voiced obstruents in Pokémon names positively correlates with a Pokémon character's size, weight, evolution levels, and general strength parameters, except for speed. The number of moras in Pokémon names positively correlates with size, weight, evolution levels, and all strength parameters. Finally, Pokémon characters with high vowels in the initial syllables tend to be smaller and lighter, although its effect size is small; no apparent effects of vowel quality on evolution levels or strength parameters are observed.

There are several reasons for using the corpus of Pokémon characters in order to explore sound symbolic patterns in naming patterns of proper names. First, there are more than 700 Pokémon characters, as of October 2016, guaranteeing enough data points for a quantitative analysis. Although there is an impressionistic observation in Japanese phonology that voiced obstruents are associated with heavy images (Hamano, 1986; Kawahara, 2015; Kubozono, 1999b), for example, there has been no quantitative study on the sound symbolic pattern using a natural corpus.3 Second, each Pokémon character has many numeric parameters, such as size, weight, and various strength parameters, which allow us to examine which parameters correlate with which sound properties.

This paper targets the effects of voiced obstruents, mora lengths, and vowel quality in initial syllables, but we by no means claim that these are the only sound symbolic patterns lurking behind the Pokémon naming systems in Japanese – interested researchers are welcome to follow up on our case study.

One final important caveat is in order. Pokémon names do sometimes include real, existing words in Japanese. For example, hushigidane consists of hushigi “mysterious” and tane “seed” (the first consonant of the second word becomes voiced by a morphophonological process called rendaku; Vance, 2015; Vance and Irwin, 2016). Since real words do not often follow sound symbolic relationships (the thesis of arbitrariness; Hockett, 1959; Saussure, 1916), we expected that the effects of sound symbolism would not be perfect. Nevertheless, as with other cases of sound symbolism, there could be stochastic tendencies. Principles of sound symbolism may even possibly affect the choice of real words in Pokémon naming in such a way that their names represent their characteristics, although this influence too would be stochastic, if present at all. To illustrate this point, let us take an actual Pokémon pre- and post-evolution pair, goosuto and gengaa, the second of which is the evolved version of the first. The first name is based on the English word ghost, and the second name is based on the German word Gänger. Why was it that gengaa, rather than goosuto, was chosen as the name for the more evolved version of the character? One answer is that since gengaa contains more voiced obstruents than goosuto, it was chosen as a more suitable name for the evolved version of the Pokémon character. In this way, a sound symbolic principle may affect the choice of real words, but this principle too would be stochastic. For this reason, in order to examine sound symbolic patterns in Pokémon names, we take a statistical approach using the large corpus.

2 Method

2.1 Hypotheses Tested

This paper analyzes three types of sound symbolic effects: those of voiced obstruents, prosodic (mora) length, and vowel quality. Voiced obstruents include a set of sounds (/b/, /d/, /g/, /z/), which are produced with strong constriction or complete closure in the oral cavity – strong enough to result in aperiodic noise, frication or burst – accompanied with vocal fold vibration (see Kawahara, 2006, for a detailed acoustic description of voiced obstruents in Japanese). Moras are basic prosodic units in Japanese (much like syllables in English), which include a vowel (optionally preceded by a consonant), a coda nasal, and the first half of a geminate (Ito, 1989; Kawahara, 2016; Kubozono, 1999a; Labrune, 2012; Vance, 1987). For example, [to-o-kyo-o] “Tokyo” contains 4 moras, [ho-n-da] “Honda” contains 3 moras, and [po-k-ki-i] “Pocky” contains 4 moras (here and throughout, “-” represents a mora boundary). Moras, rather than segments or syllables, are used in the current analysis, as moras are psycholinguistically prominent prosodic units for Japanese speakers (Inagaki et al., 2000; Kureta et al., 2006; Otake et al., 1993; though see Cutler and Otake, 2002; Kawahara, 2016). Most importantly in this context, moras are units that are used by adult Japanese speakers when counting the number of sounds.

One reason to study the effects of voiced obstruents is that sound symbolic meanings of voiced obstruents are prevalent in Japanese (Hamano, 1986; Kawahara, 2015; Kawahara et al., 2008; Kubozono, 1999b; Shinohara and Kawahara, 2016). For example, there is a minimal pair in Japanese mimetic (or ideophonic) words, goro-goro and koro-koro – both of these words represent the state of a rock rolling; however, the former implies that the rolling rock is big and heavy (Hamano, 1986). Likewise, Kawahara (2015) observes that gandamu, a giant robot (about 15 m and 7,500 kg) in a science fiction series anime, would sound very funny if we turn the voiced obstruents into voiceless obstruents, i.e. kantamu. In fact, kantamu is used as a name for a parody character in the anime Kureyon Shinchan, which looks very light. These examples illustrate that there is a clear sense in which voiced obstruents are associated with large and heavy images in Japanese.

These associations may have a phonetic basis, which makes sense under the frequency code hypothesis, proposed and developed by Bauer (1987) and Ohala (1984, 1994) (see also Berlin, 2006, Gussenhoven, 2004, 2016, and others, who extended this hypothesis). In this theory, sounds with high fundamental frequency (f0) imply small objects, whereas those with low f0 imply large objects, reflecting physical laws of sound vibration. Acoustically, voiced obstruents are characterized by low frequency during their constriction (Lisker, 1978, 1986; Raphael, 1981; Stevens and Blumstein, 1981), as well as in their surrounding vowels, especially in their low f0 and low F1 (Diehl and Molis, 1995; Kingston and Diehl, 1994, 1995; Lisker, 1986). The low frequency components of voiced obstruents would lead to large images, according to the frequency code hypothesis, and everything else being equal, heavy ones.4

The effects of mora length came out during our data-mining stage. We noticed that those Pokémon characters with higher mora counts tend to have strong parameters, heavy and large. For example, go-o-su-to (4 moras) is stronger than go-o-su (3 moras); likewise, nyo-ro-bo-n (4 moras) is stronger than nyo-ro-zo (3 moras). Also, the pair, pi-chu-u and pi-ka-chu-u, is very telling. In the first generation, there existed only pikachuu; in the second generation, pichuu was added as a preevolved state of pikachuu. In this pair, the “weakness” of the pre-evolution state was expressed by the truncation of the second mora, ka. Therefore, there seems to be a “longer-is-stronger” principle in Pokémon naming conventions. In order to test this hypothesis more rigorously, we statistically examined the effects of mora counts in the corpus of Pokémon names. As far as we know, no previous studies have proposed sound symbolic relationships between word length on the one hand, and notions such as size and weight on the other (although see some examples of “quantitative iconicity” in natural languages discussed in section 3.2). Therefore, this is a new and interesting hypothesis to test in a quantitative fashion.

The final target of the analysis was vowel quality. The effects of vowel quality are arguably the best-studied topic in the studies of sound symbolism. Sapir (1929), who inspired much of modern research on sound symbolism, showed that English speakers feel mal to be larger than mil. Jespersen (1922) discussed the sound symbolic nature of the vowel /i/, pointing out, among others, that it can imply images that are “small, slight, insignificant, or weak” (p. 557). An extensive body of work has revealed that cross-linguistically, high vowels tend to be judged to be smaller than nonhigh vowels, and front vowels smaller than back vowels (e.g., Berlin, 2006; Coulter and Coulter, 2010; Jakobson, 1978; Jespersen, 1922; Newman, 1933; Sapir, 1929; Shinohara and Kawahara, 2016; Ultan, 1978, among many others). It may be that degrees of oral aperture and the size of the oral cavity in front of the constriction are projected onto the images of size. We thus explored the effects of vowel quality in Pokémon names. Since different Pokémon characters have different numbers of vowels, we analyzed the initial vowels, which are prominent psycholinguistically (Browman, 1978; Brown and MacNeill, 1966; Cole, 1973; Marslen-Wilson, 1975; Mattys and Samuel, 2000; Nooteboom, 1981).

2.2 Analyses

For our analysis, we started with the corpus of the names of all the Pokémon characters available as of October 2016.5 To be conservative, we excluded those Pokémon names that are prefixed with mega “mega.” These Pokémon characters tend to be larger and heavier, and this prefix contains a voiced obstruent. Some Pokémon characters are distinguished only in terms of having a suffix mesu “female” or osu “male,” and these are also excluded to avoid counting the same characters twice. There is one Pokémon character with 4 voiced obstruents (jiguzaguma), which was excluded. This is because we cannot get a reliable estimate for this condition with just a single item. After excluding these characters, 715 Pokémon names remained for the following analysis.

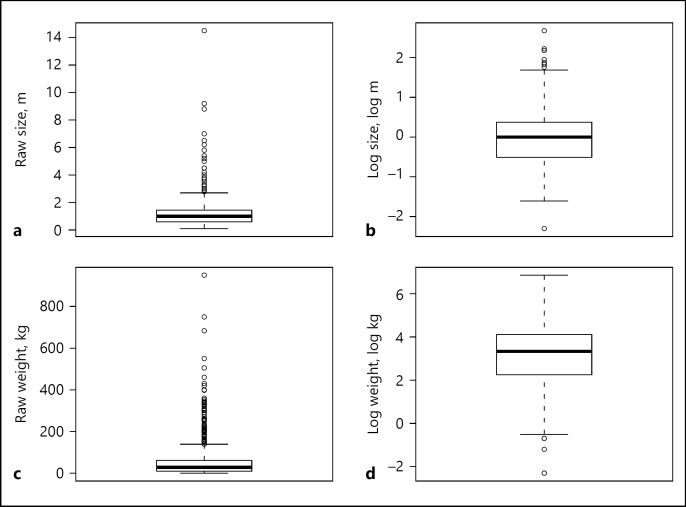
Each Pokémon character has its size (m) and weight (kg) specified. However, some Pokémon characters are outstandingly large and/or heavy. For example, guraadon is 3.5 m and 950 kg, while pikachuu is only 0.4 m and 6 kg. Since the distributions of these measures are heavily right-skewed, we took the natural logarithm of these measures, which made the distributions less skewed, as illustrated in Figure 3.

Fig. 3.

Fig. 3

Open in a new tab

Boxplots illustrating the distribution of size (a, b) and weight (c, d) values. Raw values are shown in a and c; log-transformed values are shown in b and d. The distributions are less skewed and have fewer outliers after log transformation.

Most Pokémon characters undergo “evolution” (see Fig. 2), and when they do, they are called by a different name. For example, nyoromo becomes nyorozo and then nyorobon. We coded these evolution levels as 0, 1, 2, respectively. Pokémon came out in different series in different years, and 16 Pokémon characters were introduced as “pre-evolution” versions of an already existing character – they are referred to as “baby Pokémon.” For example, pichuu was added as the baby Pokémon of pikachuu, whose evolved version is raichuu. In such cases, their evolution levels are coded as −1, 0, 1, where the baby Pokémon is coded as −1. Some Pokémon characters do not undergo any evolution, in which case they are coded as 0. Finally, each Pokémon is specified for its strength parameters, including HP, attack, defense, special attack, special defense, and speed. These measures were also used as dependent variables.

To summarize, in our analysis, the independent variables are (1) the number of voiced obstruents, (2) the number of moras, and (3) the vowel quality (in initial syllables) in each Pokémon's name. The dependent variables are (1) size and weight, (2) evolution levels, and (3) their strength parameters. Unless otherwise stated, since the number of voiced obstruents and the number of moras are non-continuous variables, we use non-parametric Spearman rank-sum correlation analyses (ρ) to examine the potential correlations between the dependent variables and the independent variables. When necessary, post hoc comparisons are made using non-parametric Wilcoxon signed-rank tests. Since vowel quality is a categorical variable, its effects were assessed via regression analyses and ANOVA. All statistical calculations were computed using R (R Development Core Team, 1993).

3 Results and Discussion

3.1 Voiced Obstruents

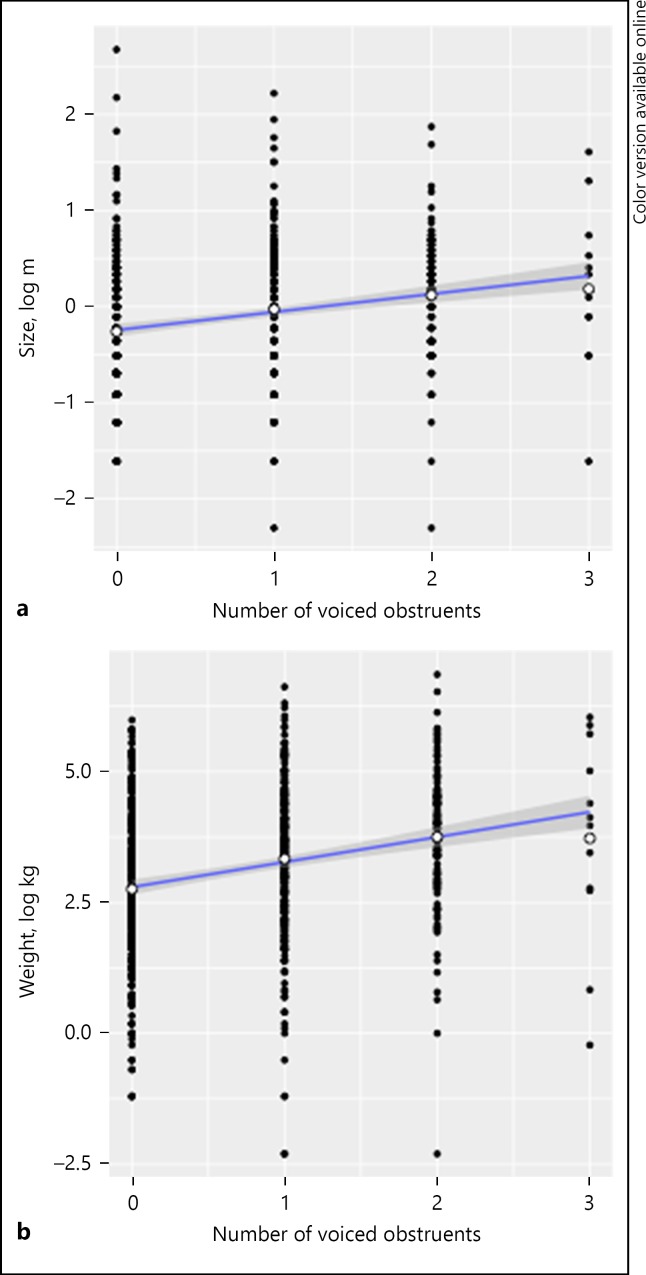
Figure 4 illustrates the effects of voiced obstruents on (log-transformed) size and weight values. The linear regression lines show that the correlations are positive. The positive correlations are significant for both size and weight, as revealed by non-parametric Spearman correlation analyses (ρ = 0.25, p < 0.001 and ρ = 0.28, p < 0.001). These results support the hypothesis that in Japanese Pokémon names, voiced obstruents imply largeness and heaviness. This conclusion is consistent with previous studies of the images of voiced obstruents in Japanese (Hamano, 1986; Kawahara and Shinohara, 2012; Shinohara and Kawahara, 2016; Shinohara et al., 2016), but offer the very first quantitative support for this intuition using a large natural corpus of existing names. The results are also consistent with the frequency code hypothesis (Ohala, 1984, 1994), in which sounds with low frequency should be perceived as large: since voiced obstruents are characterized by low frequencies in Japanese – closure voicing, low f0 and F1 (Kawahara, 2006) – they should invoke “large” images.6

Fig. 4.

Fig. 4

Open in a new tab

The effects of voiced obstruents on size (a) and weight (b). The size and weight values are log-transformed (the base = e). The linear regression line is superimposed, with the shaded area representing the 95% confidence intervals. The means in each condition are shown as white dots. The strengths and significance of the linear correlation are tested by a non-parametric Spearman rank-based correlation test.

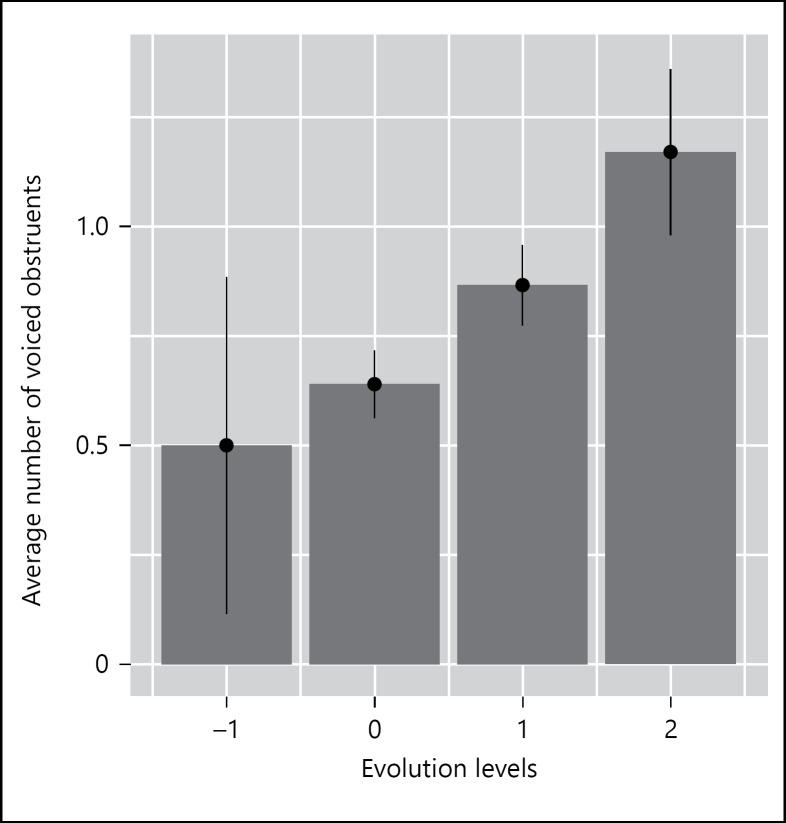
Figure 5 illustrates the average number of voiced obstruents in Pokémon names for each evolution level, with the error bars representing 95% confidence intervals. We observe that the more evolved a Pokémon character is, the more voiced obstruents its name contains on average. The Spearman correlation coefficient between the evolution level and the number of voiced obstruents is 0.22, which is significant at the p < 0.01 level. Post hoc comparisons using a non-parametric Wilcoxon signed-rank test show that all the differences between the adjacent evolution levels are significant at the p < 0.001 level as well. Indeed then, the more voiced obstruents a Pokémon name contains, the more likely it is used for a more evolved Pokémon.

Fig. 5.

Fig. 5

Open in a new tab

The average numbers of voiced obstruents contained in Pokémon names for each evolution level. The error bars represent 95% confidence intervals. Numbers = 16, 368, 251, 81. The number is small for the “–1” category, because it represents baby Pokémon characters, which are not very common.

We further explored the effects of voiced obstruents on evolution by comparing each Pokémon character pair before and after its evolution, e.g. goosu (evolution level = 0) versus goosuto (evolution level = 1) and goosuto (evolution level = 1) versus gengaa (evolution level = 2). For each pair, we coded whether the number of voiced obstruents increased, decreased, or stayed constant after the evolution. The observed distributions were compared to a null hypothesis in which the 3 changes occur with equal probability (= 33.3%) using a χ2 test, followed by residual analyses. The results appear in Table 1.

Table 1.

Comparison between pairs of pre- and post-evolution Poké;mon characters

Numbers Skew
Increase 120 (35%) ns
Decrease 48 (14%) ↓ (p < 0.001)
Constant 177 (51%) ↑ (p < 0.001)
Total 345
Open in a new tab

An illustrative example for each category: “increase”: karakara (0) → garagara (2); “decrease”: kibago (2) → onondo (1); “constant”: riguree (1) → oobemu (1).

The number of voiced obstruents stayed constant about half of the time. More importantly, we observed that decreasing the number of voiced obstruents between pre- and post-evolution Pokémon pairs is less likely than expected by chance. This analysis provides further support to the conclusion that voiced obstruents tend to be associated with Pokémon characters with a higher evolution level.

Table 2 shows a correlation vector between the number of voiced obstruents on the one hand and various strength parameters on the other. It demonstrates that the number of voiced obstruents exhibits a significant correlation with HP, attack, defense, special attack, special defense, but not with speed. The lack of significant correlation with speed is particularly interesting – in the actual world, objects that are large and heavy tend to move slowly, and therefore voiced obstruents in names may represent something that moves slowly (see also Saji et al., 2013, for a related observation in Japanese); this effect may have cancelled out the general effects of voiced obstruents indicating strengths, as observed in the other parameters. This lack of correlation between the number of voiced obstruents and speed indicates that the sound symbolic patterns which we are observing in Pokémon names is not random, but something that makes sense given the natural observation that those animals that are large and heavy generally do not move fast. Except for speed, however, the presence (and its number) of voiced obstruents makes Pokémon characters generally stronger.

Table 2.

A correlation vector between the number of voiced obstruents and various strength parameters

HP Attack Defense Special attack Special defense Speed
ρ 0.12 0.21 0.15 0.10 0.11 0.05
p value < 0.01 < 0.001 < 0.001 < 0.01 < 0.01 0.18
Open in a new tab

The first row represents Spearman rank-based coefficients ρ. The second row shows their p values. HP, hit point.

3.2 Mora Counts

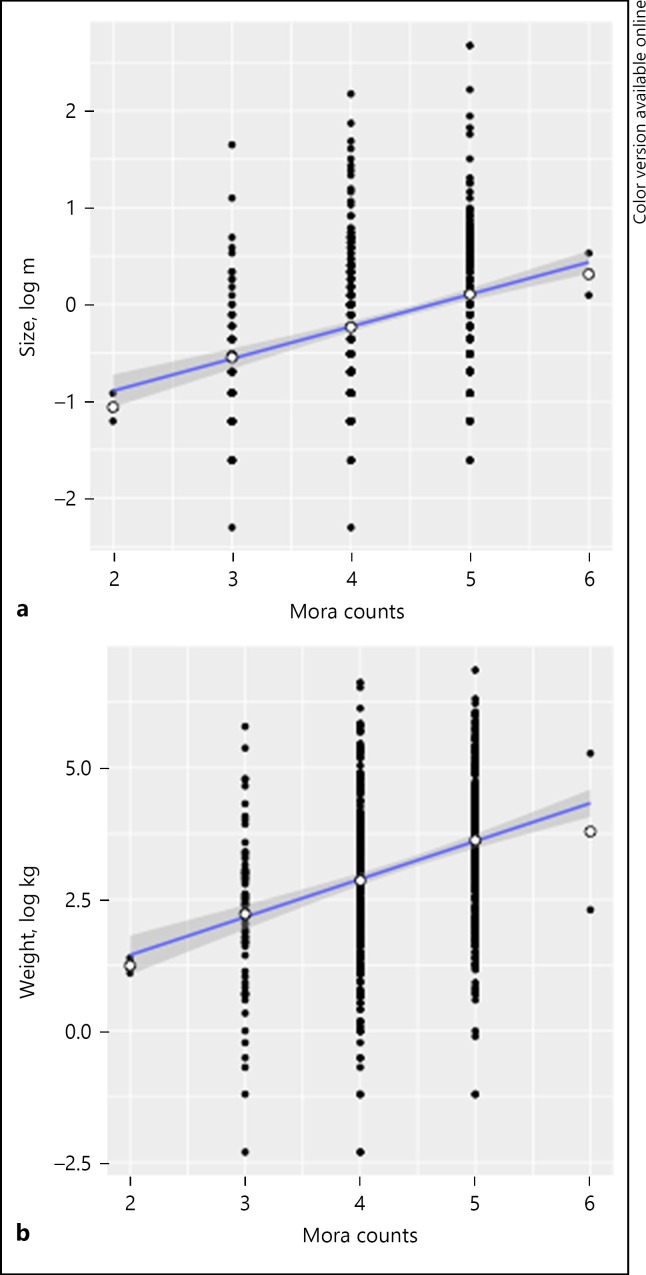
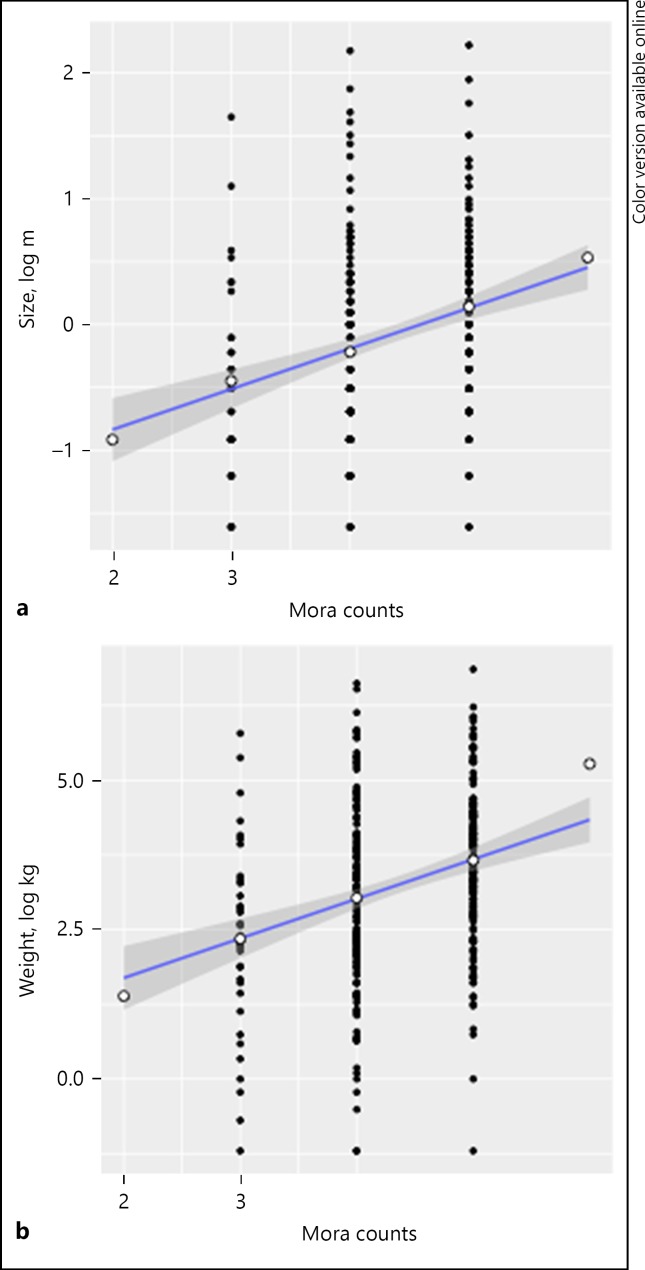
Figure 6 shows the correlation between the mora counts on the one hand, and size and weight values on the other. It demonstrates that the higher the mora counts (i.e., the longer the name), the larger and heavier the Pokémon character is. The positive correlations are both significant (ρ = 0.36, p < 0.001 and ρ = 0.34, p < 0.001). There are only 2 data points for 2 moras and 6-mora conditions; even excluding these 2 conditions, the correlations remain significant (ρ = 0.35, p < 0.001 and ρ = 0.34, p < 0.001). These results confirm our impressionistic observation during the data-mining stage that Pokémon characters with longer names are heavier and larger.

Fig. 6.

Fig. 6

Open in a new tab

The effects of mora counts on the size (a) and weight (b) values. The white dots represent the means in each condition. The positive correlations are significant at the p < 0.001 level, even excluding the 2-mora and 6-mora conditions.

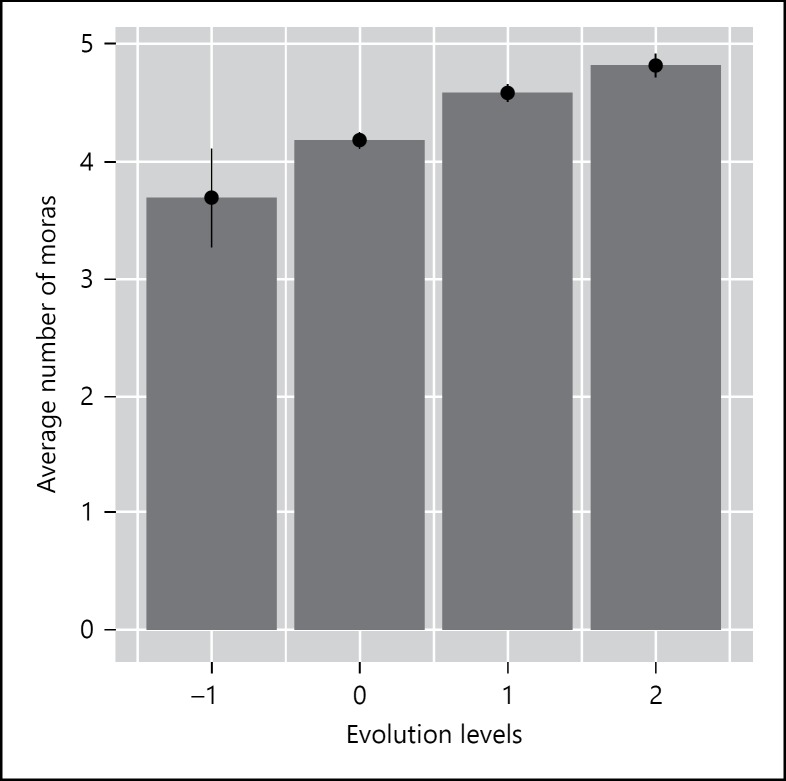
Figure 7 illustrates the average number of moras in the Pokémon names for each evolution level. We observed that the more evolved a Pokémon character is, the more moras its name contains. The Spearman correlation coefficient is 0.38, which is significant at the p < 0.001 level. Post hoc comparisons with the non-parametric Wilcoxon test show that all adjacent evolution levels are significantly different in terms of their mora counts at the p < 0.001 level.

Fig. 7.

Fig. 7

Open in a new tab

The average number of mora counts for each evolution level. Pairs that are potentially related by (quasi-)morphological derivation are eliminated. The total number is 322.

Table 3 shows a within-Pokémon comparison before and after evolution in terms of mora counts. Just like voiced obstruents, the probability of decreasing mora counts after evolution is lower than expected by chance. We observe that about half of the time, the mora counts increase after evolution. The likelihood of the mora counts staying constant is also higher than chance level. These are due to the fact that “the decrease category” is significantly underrepresented.

Table 3.

A within-Pokémon comparison between pre- and postevolution Pokémon in terms of mora counts

Numbers Skew
Increase 166 (48%) ↑ (p < 0.001)
Decrease 20 (6%) ↓ (p < 0.001)
Constant 159 (46%) ↑ (p < 0.001)
Total 345
Open in a new tab

An illustrative example for each category: “increase”: hi-m-ba-su (4) → mi-ru-ka-ro-su (5); “decrease”: ku-nu-gi-da-ma (5) → fo-re-to-su (4); “constant”: ra-ru-to-su (4) → ki-ru-ri-a (4).

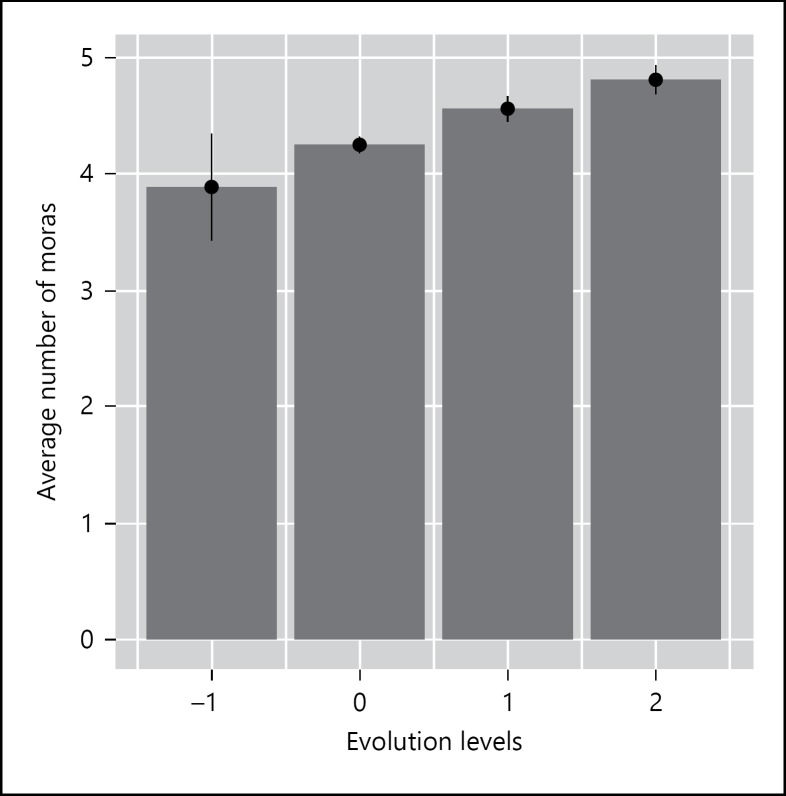
Overall, the analyses so far have shown that evolved Pokémon names are generally longer. One objection that may be raised against this conclusion is that this result may not have to do with phonological length, but instead with morphological complexity. In some Pokémon pairs, the postevolution characters are expressed via quasi-affixation: ri-za-a-do → ri-za-a-do-n, in which the final /n/ could be considered as a Pokémon-specific suffix (it is not an existing suffix in Japanese). In order to address this morphological complexity hypothesis, we eliminated all pairs that could be considered as morphologically related, even when the observed “affixes” do not actually exist in Japanese. The results appear in Figure 9 – the pattern remained the same, the more evolved Pokémon characters tend to have longer names, although the Spearman correlation coefficient became slightly lower in this analysis (ρ = 0.32, p < 0.001).7

Fig. 9.

Fig. 9

Open in a new tab

The average number of mora counts for each evolution level. Pairs that are potentially related by (quasi-)morphological derivation are eliminated. The total number is 322.

Another reason to consider that phonological length, rather than – or at least, in addition to – morphological complexity, plays a role in influencing naming of pre- and post-evolution Pokémon names comes from a nonce word experiment reported in Kawahara and Kumagai (in press). In that study, within each trial, the participants were presented with a pair of Pokémon characters (like the one in Fig. 2) and were provided with 2 unrelated nonce words like he-na-ro-ho (4 moras) and no-shi-yo-ho-ya (5 moras). The results showed that the participants were more likely to associate the longer nonce word names with the post-evolution Pokémon characters. Since the stimuli were all nonce words and the stimulus pairs were not related by morphological derivation in any sense, this result cannot be explained in terms of morphological complexity.

Turning to the relationship between mora counts and strength, Table 4 shows the correlation vector between the number of moras on the one hand and the strength parameters on the other. It shows that all the correlations are significant at the p < 0.001 level. The results show that the longer the name, the stronger the Pokémon character is in every parameter.

Table 4.

A correlation vector between the number of moras and strength parameters

HP Attack Defense Special attack Special defense Speed
ρ 0.26 0.27 0.29 0.20 0.25 0.15
p value < 0.001 < 0.001 < 0.001 < 0.001 < 0.001 < 0.001
Open in a new tab

HP, hit point.

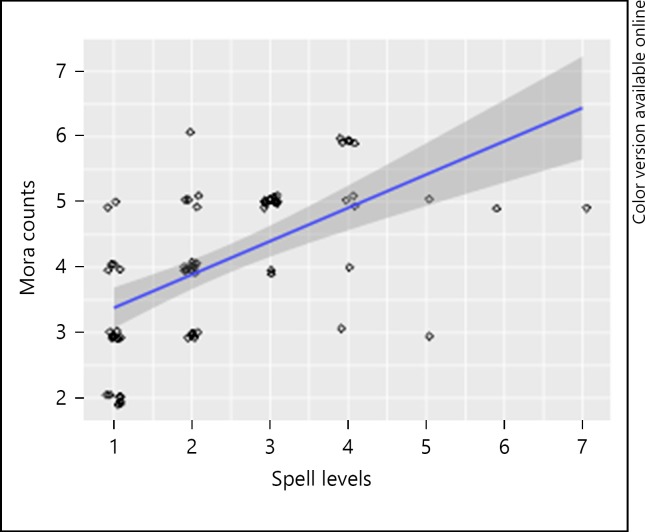
One remaining question is how general this sound symbolic8 “longer-is-stronger” relationship is – is it specific to Pokémon names, or specific to proper names, or more generally operative in natural languages? One relevant observation comes from the spell names in the Dragon Quest series – a nationally renowned role playing game9 – which follow the same “longer-is-stronger” principle as the Pokémon naming: in a series of 4 spells related to fire, me-ra (2 moras) is the weakest, me-ra-mi (3 moras) next, me-ra-zo-o-ma (5 moras) next, and me-ra-ga-i-ya-a (6 moras) is the strongest; similarly, gi-ra (2 moras) becomes be-gi-ra-ma (4 moras) when it gets stronger, and then be-gi-ra-go-n (5 moras), and then gi-ra-gu-re-i-do (6 moras) when it is strongest. The same can be said for i-o (2 moras), i-o-ra (3 moras), i-o-na-zu-n (5 moras) and i-o-gu-ra-n-de (6 moras), although there are exceptions to this “longer-is-stronger” principle, too; e.g. be-ho-ma (3 moras) is stronger than be-ho-i-mi (4 moras), and ma-hya-do (3 moras) is stronger than hya-da-i-n (4 moras). Kawahara (2017) systematically studied this correlation between the levels of each spell and the length of their names in the Dragon Quest series, and found a positive correlation (ρ = 0.67, p < 0.001), as shown in Figure 10.10

Fig. 10.

Fig. 10

Open in a new tab

The relationship between the levels of the spells and the mora counts of their names in the Dragon Quest series. Based on Kawahara (2017).

An anonymous reviewer pointed out that this “longer-is-stronger” principle may be a specific case of what is more generally known as “iconicity of quantity” in the literature on the role of iconicity in grammar (Haiman, 1980, 1985). An example of quantitative iconicity includes comparatives and superlatives in Latin (e.g., long(-us) “long” < long-ior “long-er” < long-issim(-us) “long-est”). More generally, Haiman (1980, p. 528) suggests that “generally speaking, the positive, comparative, and superlative degrees of adjectives show a gradual increase in the number of phonemes.” Many languages, including Japanese, express plurality, repetition, and intensification using reduplication (a Japanese example: yama “mountain” and yama-yama “mountains”), which would also be an example of quantitative iconicity (Haiman, 1980). Dingemanse et al. (2015) cite an example from Japanese and Siwu in which vowel lengthening expresses “long-ness.” In short, there may be some cases in natural languages in which the “longer-is-stronger” principle is at work. Exploring the relationship between the current finding in Pokémon naming and the general quantitative iconicity patterns in natural languages offers an interesting line for future research.

3.3 Multiple Regression Analyses

Having established the effects of voiced obstruents and those of mora counts, we need to address an important question. Given that the effects of both voiced obstruents and mora counts are present, could it be the case that we obtained significant results of both factors, because a longer word is more likely to contain voiced obstruents? In other words, are the effects of voiced obstruents and mora counts independent of one another? In order to address this question, multiple regression analyses were run. The independent variables were log-transformed weight, log-transformed size, evolution level, and total strength (the sum of all strength parameters except for speed). The dependent variables were the number of voiced obstruents and mora counts, and their interaction. Table 5 summarizes the results.

Table 5.

The results of multiple regression analyses

df F p value
Weight
Voiced obstruents 1, 712 53.2 < 0.001
Mora counts 1, 712 71.7 < 0.001
Interaction 1, 712 < 1 0.82
Size
Voiced obstruents 1, 712 36.7 < 0.001
Mora counts 1, 712 75.1 < 0.001
Interaction 1, 712 < 1 0.69
Evolution
Voiced obstruents 1, 712 42.3 < 0.001
Mora counts 1, 712 99.3 < 0.001
Interaction 1, 712 2.7 0.10
Strength
Voiced obstruents 1, 712 23.7 < 0.001
Mora counts 1, 712 69.9 < 0.001
Interaction 1, 712 1.9 0.16
Open in a new tab

The effects of voiced obstruents and mora counts are significant, but their interaction terms are not.

In all the regression models, the effects of voiced obstruents and those of mora counts are highly significant, but none of the interaction effects are. These results show that the effects of voiced obstruents and those of mora counts independently hold. In other words, the effects of voiced obstruents are present, regardless of the number of moras that a particular Pokémon name contains.

3.4 Vowel Quality

We now turn to the analysis of vowels. Since Pokémon names differ substantially in their length (recall section 3.2), we analyzed the effects of vowels in initial syllables. We know from the previous psycholinguistic research that initial segments and/or syllables play an important role in speech perception and processing (Browman, 1978; Brown and MacNeill, 1966; Cole, 1973; Marslen-Wilson, 1975; Mattys and Samuel, 2000; Nooteboom, 1981), and that psycholinguistic prominence may play a significant role in shaping the phonology of human languages (Becker et al., 2012; Beckman, 1998; Hawkins and Cutler, 1988; Smith, 2002).

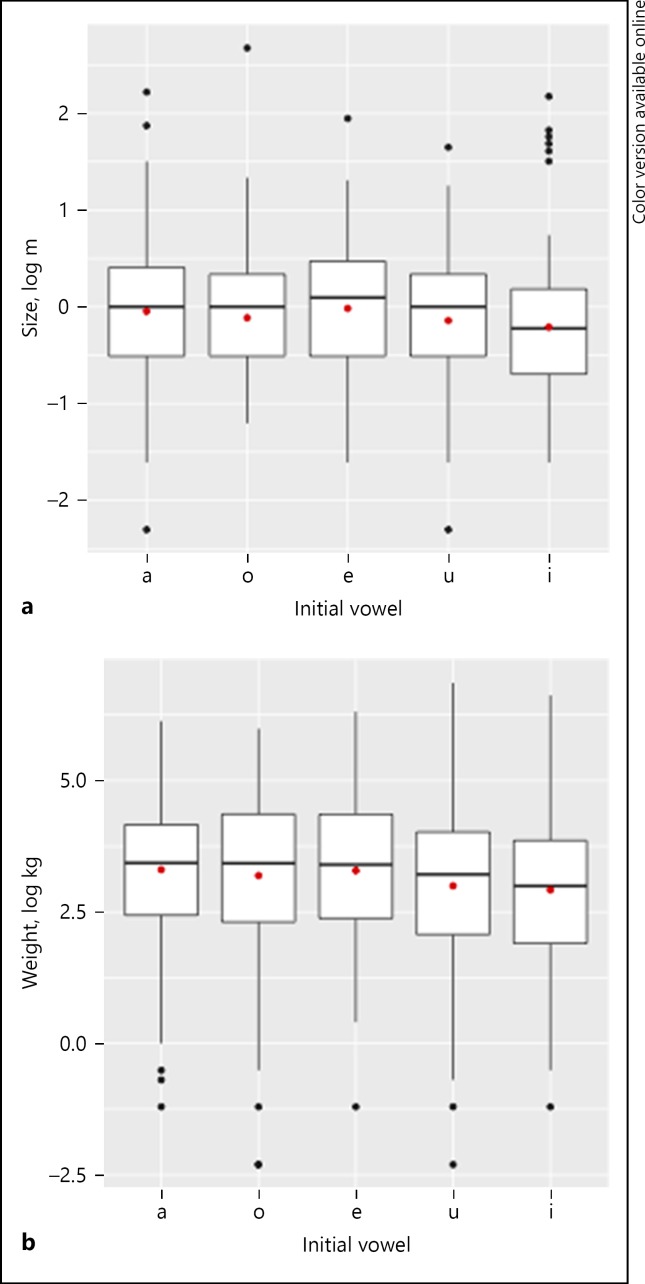
Figure 11a and b presents the distribution of log-transformed size and weight, broken down by initial vowels.11 We observe in Figure 11a that there are no large differences among the 5 vowels (the means: /a/ = −0.05; /o/ = −0.11; /e/ = −0.02; /u/ = −0.14; /i/ = −0.21), although 2 high vowels (/u/ and /i/) show the 2 smallest values. To assess the significance of height and backness on size, since vowel quality is not a numerical variable, a regression analysis was run with log-transformed size as the dependent variable and height (high vs. nonhigh) and backness (back vs. front), as well as their interaction, as independent variables. The results were that height was significant (t(713) = −2.06, p < 0.05), but not backness (t(712) = −0.74, ns) or the interaction (t(711) = 1.07, ns).

Fig. 11.

Fig. 11

Open in a new tab

The distribution of size (a) and weight (b) (log-transformed), broken down by initial vowels. Red dots represent the means.

A similar tendency is observed in terms of weight (Fig. 11b). The differences are not substantial, but high vowels tend to be associated with smaller weights (the means: /a/ = 3.31; /o/ = 3.19; /e/ = 3.29; /u/ = 3.00; /i/ = 2.92). A regression analysis shows that height was nearly significant (t(713) = −1.80, p = 0.07), but not backness (t(712) = −0.17, ns) or the interaction (t(711) = 0.43, ns). A model without the interaction term shows a significant effect of height (t(713) = −2.49, p < 0.05), which shows that some variability of height was soaked up by the interaction term.12 All in all, it seems justified to conclude that vowel height has a sound symbolic effect in such a way that high vowels represent something smaller and lighter, although its effect size is not very substantial in the Pokémon naming patterns.

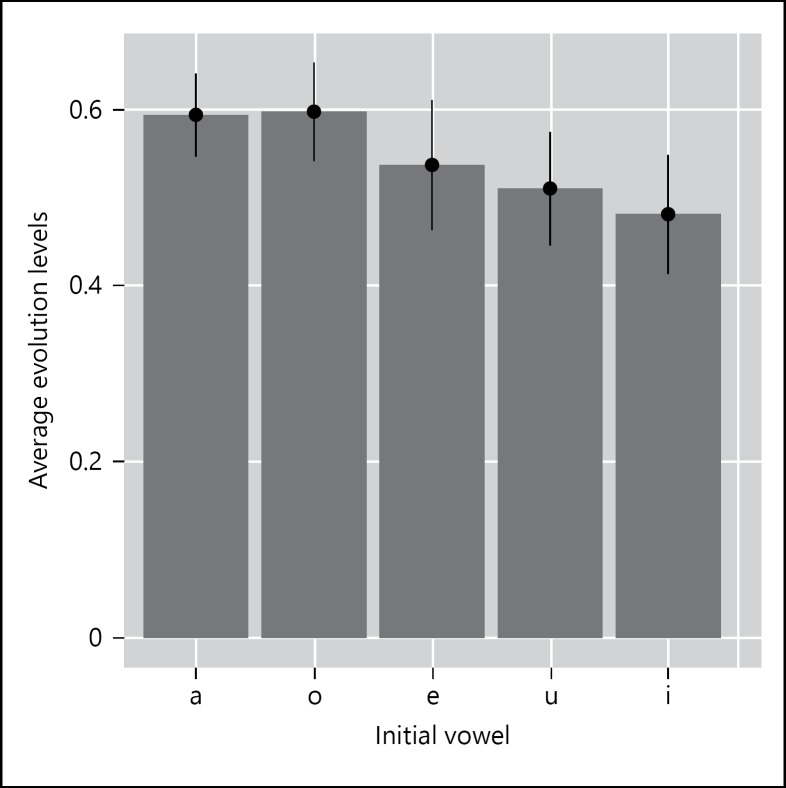
Figure 12 shows the average evolution levels for each type of initial vowel. It shows the /a/ and /o/ tend to represent more evolved characters, whereas /u/ and /i/ – particularly /i/ – represent less evolved characters, and /e/ represents those inbetween. However, the effect sizes are very small (note that the y-axis scale ranges from 0 to 0.6), and indeed no significant differences were found in terms of height (t(713) = −0.55, ns), backness (t(712) = 0.72, ns), or their interaction (t(711) = −0.24, ns).

Fig. 12.

Fig. 12

Open in a new tab

The average evolution levels for each vowel quality in initial syllables.

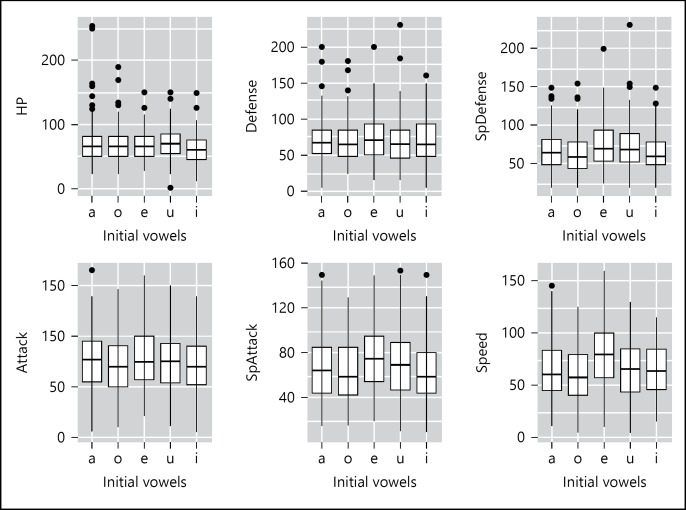
Finally, Figure 13 shows the effects of initial vowels on each strength parameter. No consistent patterns seem to exist, except that /e/-initial names show slightly high values in special attack, special defense, and speed. /u/ shows values that are higher than /a/, /o/, and /i/ in terms of special defense. One-way ANOVA was run with strength parameters as independent variables and vowel type as dependent variables; HP: F(4, 711) = 1.72, ns; attack: F(4, 711) = 1.75, ns; defense: F(4, 711) = 0.47, ns; special attack: F(4, 711) = 4.38, p < 0.01; special defense: F(4, 711) = 5.30, p < 0.001; speed: F(4, 711) = 6.64, p < 0.001. A post hoc test with /a/ as the baseline shows that /e/ is higher than /a/ in terms of special attack (t(711) = 2.78, p < 0.01), special defense (t(711) = 2.28, p < 0.05), and speed (t(711) = 4.15, p < 0.001). /u/ is higher than /a/ in terms of special defense (t(711) = 2.13, p < 0.05). We unfortunately do not have a clear explanation of these complicated patterns.

Fig. 13.

Fig. 13

Open in a new tab

The effects of initial vowels on each strength parameter (points). HP, hit point.

4 Conclusion

In natural languages, sound symbolic relationships hold between sounds and meanings, although these relationships are only stochastic and not deterministic (i.e., the sound-meaning relationships can be arbitrary; Hockett, 1959; Saussure, 1916). Previous studies have shown that sound symbolic patterns are operative in naming patterns of proper names as well (Berlin, 2006; Kawahara and Shinohara, 2012; Köhler, 1947; Perfors, 2004; Ramachandran and Hubbard, 2001; Shinohara and Kawahara, 2013; Shinohara et al., 2016; Sidhu and Pexman, 2015; Wright and Hay, 2002; Wright et al., 2005). The current study adds to this body of the literature on the existence of sound symbolic relationships in proper names, using a new corpus of data.

One advantage of the analysis presented in this paper is the fact that we were able to conduct statistical and quantitative analyses of sound symbolic patterns, using Pokémon names as a natural corpus. Japanese speakers do have an impressionistic intuition that “voiced obstruents are heavy,” for example, and this intuition has been reported in some linguistic work (Hamano, 1986; Kawahara, 2015; Kubozono, 1999b). However, we believe that we are the first to quantitatively test this sound symbolic connection using a natural corpus.

This study on the sound symbolic nature of Pokémon names did not cover all aspects of Pokémon; for example, all Pokémon characters belong to some “class” (e.g., water, grass, poison, fire, etc.). Some Pokémon characters are also specified for their gender (either male or female). Whether the classes and/or gender are expressed via particular sound symbolic patterns is an interesting topic for future investigation in the analysis of Pokémon names. Nor has the current study tested all possible sound symbolic relationships that may be lurking behind Pokémon naming conventions. For example, place of articulation is something to look at, given a recent observation that Japanese speakers very often use labial consonants for names of baby diapers (Kumagai and Kawahara, 2017). Our hope is that future research will uncover other sound symbolic patterns in Pokémon names.

Another dimension in which this project can be extended is the analysis of Pokémon names in languages other than Japanese. Since Pokémon names are translated into many languages, including Chinese, English, French, and Russian, the sound symbolic study of Pokémon names provides a forum for cross-linguistic comparisons. We thus invite interested readers to follow-up on the current study.

Another task is to address whether the patterns identified in this paper are merely facts about the “Pokémon lexicon,” or whether these patterns are internalized by native speakers of Japanese. Testing this issue requires experimentation using new Pokémon characters (see Kawahara and Kumagai, in press, for the initial attempt). This experiment has shown that when given a pair of complete nonce words and a pair of pre- and post-evolution versions of Pokémon as in Figure 2, Japanese speakers tend to associate those names with voiced obstruents and those names that are longer with the post-evolution Pokémon. We also invite other researchers to test the same issue with speakers with different language backgrounds.

Disclosure Statement

The authors have no conflicts of interest to declare.

Fig. 8.

Fig. 8

Open in a new tab

The correlations between mora counts and size (a) and weight (b). Pairs that are potentially related by (quasi-)morphological derivation are eliminated.

Acknowledgments

This paper grew out of a seminar that the first author gave at Tokyo Metropolitan University in September 2016. We thank the students who participated in that seminar. Some of the analyses in this paper were used in introductory phonetics classes at International Christian University, Keio University, Kwansei Gakuin University, Otsuma University, and Tokyo Metropolitan University; this paper was also presented as invited lectures at Keio University, Meio University, Seoul International Phonology Conference, and Tokyo Institute for Advanced Studies of Language, where we received interesting feedback. We thank 2 anonymous Phonetica reviewers, who provided detailed comments on a previous version of this paper, as well as Sharon Inkelas, Darya Kavitskaya, Yasuyo Minagawa, Stephanie Shih, and Alan Yu who provided helpful comments on this general project. We are grateful to Donna Erickson for proofreading the manuscript. The remaining errors are ours.

Appendix

Long Vowels and Geminates

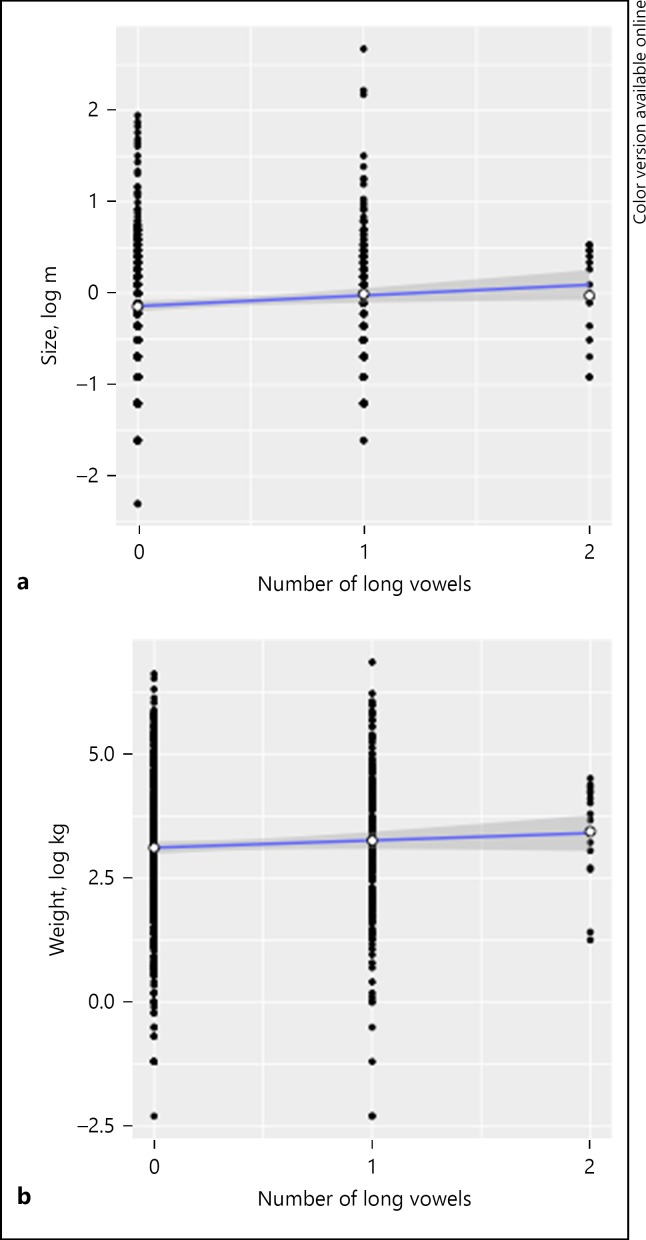
It has been asked multiple times whether long vowels and long consonants (a.k.a. geminates) would affect size and weight of Pokémon characters. Figure 14 represents the effects of long vowels on size and weight. There is a slight positive correlation between the number of long vowels and size (top, ρ = 0.09, p < 0.05), but not between the number of long vowels and weight (bottom, ρ = 0.05, ns).

Fig. 14.

Fig. 14

Open in a new tab

The effects of long vowels on size (a) and weight (b).

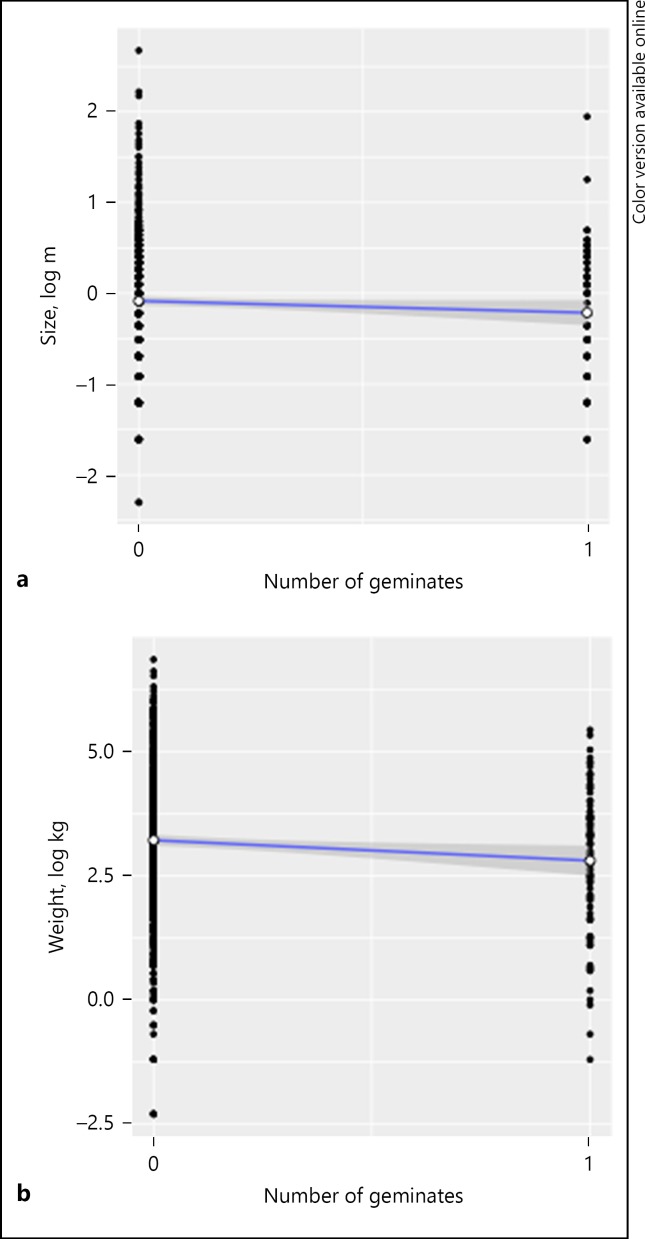
Figure 15 illustrates the effects of the presence of geminates on size and weight (there were no names in which there is more than 1 geminate). Both in terms of size and weight, the correlation is negative, and the correlation between the presence of geminates and weight is significant (ρ = −0.06, ns for size; ρ = −0.09, p < 0.05 for weight). We do not have a clear explanation of why the presence of geminates would lead to lower weight.

Fig. 15.

Fig. 15

Open in a new tab

The effects of geminates on size (a) and weight (b).

References

  1. Abel GA, Glinert L. Chemotherapy as language: sound symbolism in cancer medication names. Soc Sci Med. (2008);66:1863–1869. doi: 10.1016/j.socscimed.2007.12.016. [DOI] [PubMed] [Google Scholar]
  2. Bauer HR. Frequency code: orofacial correlates of fundamental frequency. Phonetica. (1987);44:173–191. doi: 10.1159/000261793. [DOI] [PubMed] [Google Scholar]
  3. Becker M, Nevins A, Levine J. Asymmetries in generalizing alternations to and from initial syllables. Language. (2012);88:231–268. [Google Scholar]
  4. Beckman J. Positional Faithfulness; doctoral dissertation, University of Massachusetts, Amherst. (1998) [Google Scholar]
  5. Berlin B. The first congress of ethnozoological nomenclature. J R Anthropol Inst. (2006);12:23–44. [Google Scholar]
  6. Blasi D, Wichman S, Hammarström H, Stadler PF, Christianson MH. Sound-meaning association biases evidenced across thousands of languages. PNAS. (2016);113:10818–10823. doi: 10.1073/pnas.1605782113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bolts GM, Mangigian GM, Allen BM. Phonetic symbolism and memory for advertisement. Appl Cogn Psychol. (2016);30:1088–1092. [Google Scholar]
  8. Browman C. Tip of the tongue and slip of the ear: implications for language processing. UCLA Work Pap Phonet 42. (1978) [Google Scholar]
  9. Brown R, Ford M. Address in American English. J Abnorm Soc Psychol. (1961);62:375–385. [Google Scholar]
  10. Brown R, MacNeill D. The “tip of the tongue” phenomenon. J Verbal Learn Verbal Behav. (1966);5:325–337. [Google Scholar]
  11. Cassidy KW, Kelly MH, Sharoni LJ. Inferring gender from name phonology. J Exp Psychol Gen. (1999);128:362–381. [Google Scholar]
  12. Cole R. Listening for mispronunciations: a measure of what we hear during speech. Percept Psychophys. (1973);13:153–156. [Google Scholar]
  13. Coulter K, Coulter RA. Small sounds, big deals: phonetic symbolism effects in pricing. J Consumer Res. (2010);37:315–328. [Google Scholar]
  14. Cutler A, McQueen J, Robinson K. Elizabeth and John: sound patterns of men's and women's names. J Ling. (1990);26:471–482. [Google Scholar]
  15. Cutler A, Otake T. Rhythmic categories in spoken-word recognition. J Mem Lang. (2002);46:296–322. [Google Scholar]
  16. Diehl R, Molis M. Effects of fundamental frequency on medial [voice] judgments. Phonetica. (1995);52:188–195. doi: 10.1159/000262170. [DOI] [PubMed] [Google Scholar]
  17. Dingemanse M, Blasi DE, Lupyan G, Christiansen MH, Monaghan P. Arbitrariness, iconicity and systematicity in language. Trends Cogn Sci. (2015);19:603–615. doi: 10.1016/j.tics.2015.07.013. [DOI] [PubMed] [Google Scholar]
  18. D'Onofrio A. Phonetic detail and dimensionality in sound-shape correspondences: refining the bouba-kiki paradigm. Lang Speech. (2014);57:367–393. [Google Scholar]
  19. Fort M, Martin A, Peperkamp S. Consonants are more important than vowels in the bouba-kiki effect. Lang Speech. (2015);58:247–266. doi: 10.1177/0023830914534951. [DOI] [PubMed] [Google Scholar]
  20. Gussenhoven C. Cambridge: Cambridge University Press; (2004). The Phonology of Tone and Intonation. [Google Scholar]
  21. Gussenhoven C. Foundations of intonational meaning: anatomical and physiological factors. Topics Cogn Sci. (2016);8:425–434. doi: 10.1111/tops.12197. [DOI] [PubMed] [Google Scholar]
  22. Haiman J. The iconicity of grammar: isomorphism and motivation. Language. (1980);56:515–540. [Google Scholar]
  23. Haiman J. Amsterdam, Benjamins. (1985). Iconicity in Syntax. [Google Scholar]
  24. Hamano S. The Sound-Symbolic System of Japanese; doctoral dissertation, University of Florida. (1986) [Google Scholar]
  25. Hawkins J, Cutler A, Psycholinguistic factors in morphological asymmetry . Explaining Language Universals. In: Hawkins JA, editor. Oxford: Blackwell; (1988). pp. pp 280–317. [Google Scholar]
  26. Hinton L, Nichols J, Ohala J. Cambridge: Cambridge University Press; (1994). Sound Symbolism. [Google Scholar]
  27. Hinton L, Nichols J, Ohala J. ed 2. Cambridge: Cambridge University Press; (2006). Sound Symbolism. [Google Scholar]
  28. Hockett C. Animal “languages” and human language. Hum Biol. (1959);31:32–39. [PubMed] [Google Scholar]
  29. Hollard M, Wertheimer M. Some physiognomic aspects of naming, or maluma and takete revisited. Percept Motor Skills. (1964);19:111–117. doi: 10.2466/pms.1964.19.1.111. [DOI] [PubMed] [Google Scholar]
  30. Inagaki K, Hatano G, Otake T. The effect of kana literacy acquisition on the speech segmentation unit used by Japanese young children. J Exp Child Psychol. (2000);75:70–91. doi: 10.1006/jecp.1999.2523. [DOI] [PubMed] [Google Scholar]
  31. Ito J. A prosodic theory of epenthesis. Nat Lang Ling Theory. (1989);7:217–259. [Google Scholar]
  32. Jakobson R. Cambridge: MIT Press; (1978). Six Lectures on Sound and Meaning. [Google Scholar]
  33. Jespersen· Symbolic value of the vowel i. Phonologica. (1922);1:283–303. [Google Scholar]
  34. Kawahara S. A faithfulness ranking projected from a perceptibility scale: the case of [+voice] in Japanese. Language. (2006);82:536–574. [Google Scholar]
  35. Kawahara S. Oto-to Kotoba-no Hushigi-na Sekai. Tokyo, Iwanami. (2015) [Google Scholar]
  36. Kawahara S. Japanese has syllables: a reply to Labrune (2012) Phonology. (2016);33:169–194. [Google Scholar]
  37. Kawahara S. Sound symbolism in spell names in Dragon Quest series. J Phon Soc Japan. (2017);21:38–42. [Google Scholar]
  38. Kawahara S, Kumagai G, (in press) Expressing evolution in Pokémon names: experimental explorations. J Jpn Ling.
  39. Kawahara S, Shinohara K, (2012) A tripartite trans-modal relationship between sounds, shapes and emotions: a case of abrupt modulation. Procedings of CogSci. 2012:pp 569–574. Sapporo. [Google Scholar]
  40. Kawahara S, Shinohara K, Grady J, Iconic inferences about personality: from sounds and shapes . Iconicity: East Meets West. In: Hiraga M, Herlofsky W, Shinohara K, Akita K, editors. Amsterdam: Benjamins; (2015). pp. pp 57–69. [Google Scholar]
  41. Kawahara S, Shinohara K, Uchimoto Y. A positional effect in sound symbolism: an experimental study. Proceedings of the Japan Cognitive Linguistics Association 8, Tokyo. (2008):pp 417–427. [Google Scholar]
  42. Kingston J, Diehl R. Phonetic knowledge. Language. (1994);70:419–454. [Google Scholar]
  43. Kingston J, Diehl R, Intermediate properties in the perception of distinctive feature values . Papers in Laboratory Phonology IV: Phonology and Phonetic Evidence. In: Connell B, Arvaniti A, editors. Cambridge: Cambridge University Press; (1995). pp. pp 7–27. [Google Scholar]
  44. Klink RR. Creating brand names with meaning: the use of sound symbolism. Marketing Lett. (2000);11:5–20. [Google Scholar]
  45. Köhler W. New York: Liveright; (1947). Gestalt Psychology: An Introduction to New Concepts in Modern Psychology. [Google Scholar]
  46. Koppensteiner M, Stephan P, Jäschke JPM. Shaking takete and flowing maluma. Non-sense words are associated with motion patterns. PLoS One. (2016) doi: 10.1371/journal.pone.0150610. DOI: 10.1371/journal.pone.0150610. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Kubozono H, Mora and syllable . The Handbook of Japanese Linguistics. In: Tsujimura N, editor. Oxford: Blackwell; (1999a). pp. pp 31–61. [Google Scholar]
  48. Kubozono H. Tokyo: Iwanami; (1999b). Nihongo-no Onsei: Gendai Gengogaku Nyuumon 2 (Japanese Phonetics: An Introduction to Modern Linguistics 2) [Google Scholar]
  49. Kumagai G, Kawahara S. How abstract is sound symbolism? Labiality in Japanese diaper names (in Japanese). Proceedings of the 31st Meeting of the Phonetic Society of Japan. Tokyo. (2017):pp 49–54. [Google Scholar]
  50. Kureta Y, Fushimi T, Tatsumi I. The functional unit of phonological encoding: evidence for moraic representation in native Japanese speakers. J Exp Psychol Learn Mem Cogn. (2006);32:1102–1119. doi: 10.1037/0278-7393.32.5.1102. [DOI] [PubMed] [Google Scholar]
  51. Labrune L. Oxford: Oxford University Press; (2012). The Phonology of Japanese. [Google Scholar]
  52. Lindauer SM. The meanings of the physiognomic stimuli taketa and maluma. Bull Psychonom Soc. (1990);28:47–50. [Google Scholar]
  53. Lisker L. On buzzing the English /b/ Haskins Lab Status Rep Speech Res. (1978):251–259. SR-55/56. [Google Scholar]
  54. Lisker L. “Voicing” in English: a catalog of acoustic features signaling /b/ versus /p/ in trochees. Lang Speech. (1986);29:3–11. doi: 10.1177/002383098602900102. [DOI] [PubMed] [Google Scholar]
  55. Lockwood G, Dingemanse M. Iconicity in the lab: a review of behavioral, developmental, and neuroimaging research into sound-symbolism. Front Psychol. (2015) doi: 10.3389/fpsyg.2015.01246. DOI: 10.3389/fpsyg.2015.01246. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Marslen-Wilson W. Sentence perception as an interactive parallel process. Science. (1975);189:226–228. doi: 10.1126/science.189.4198.226. [DOI] [PubMed] [Google Scholar]
  57. Mattys S, Samuel A. Implications of stress-pattern differences in spoken-word recognition. J Mem Lang. (2000);42:571–596. [Google Scholar]
  58. Maurer D, Pathman T, Mondloch CJ. The shape of boubas: sound-shape correspondences in toddlers and adults. Dev Sci. (2006);9:316–322. doi: 10.1111/j.1467-7687.2006.00495.x. [DOI] [PubMed] [Google Scholar]
  59. Miura S, Murata M, Hoda S, Miyabe M, Aramaki E. Onshoochoo-no kikaigakushuu-niyoru saigen: saikyoono pokemon-no seisei. Gengoshori Gakkai Happyou Ronbunshuu. (2012);18:65–68. [Google Scholar]
  60. Newman S. Further experiments on phonetic symbolism. Am J Psychol. (1933);45:53–75. [Google Scholar]
  61. Nielsen AKS, Rendall D. Parsing the role of consonants versus vowels in the classic Takete-Maluma phenomenon. Can J Exp Psychol. (2013);67:153–163. doi: 10.1037/a0030553. [DOI] [PubMed] [Google Scholar]
  62. Nooteboom S. Lexical retrieval from fragments of spoken words: beginnings vs endings. J Phon. (1981);9:407–424. [Google Scholar]
  63. Ohala JJ, The origin of sound patterns in vocal tract constraints . The Production of Speech. In: MacNeilage P, editor. New York: Springer; (1983). pp. pp 189–216. [Google Scholar]
  64. Ohala JJ. An ethological perspective on common cross-language utilization of F0 of voice. Phonetica. (1984);41:1–16. doi: 10.1159/000261706. [DOI] [PubMed] [Google Scholar]
  65. Ohala JJ. The frequency code underlies the sound symbolic use of voice pitch. In: Hinton L, Nichols J, Ohala JJ, Sound Symbolism, editors. Cambridge: Cambridge University Press; (1994). pp. pp 325–347. [Google Scholar]
  66. Ohyama Y. What Can Pokémon Names Tell Us about Japanese and English Morphology and Phonology; master's thesis, University College London. (2016) [Google Scholar]
  67. Otake T, Hatano G, Cutler A, Mehler J. Mora or syllable? Speech segmentation in Japanese. J Mem Lang. (1993);32:258–278. [Google Scholar]
  68. Perfors A. What's in a name? The effect of sound symbolism on perception of facial attractiveness. In: Forbus K, Gentner D, Regier T, 26th Annual Conference of the Cognitive Science Society, editors. Chicago: Psychology Press; (2004). [Google Scholar]
  69. Perniss P, Thompson RL, Vigiliocco G. Iconicity as a general property of language: evidence from spoken and signed languages. Front Psychol. (2010) doi: 10.3389/fpsyg.2010.00227. DOI: 10.3389/fpsyg.2010.00227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Peterson RA, Ross I. How to name new brand names. J Advertising Res. (1972);12:29–34. [Google Scholar]
  71. Proctor MI, Shadle CH, Iskarous K. Pharyngeal articulation differences in voiced and voiceless fricatives. J Acoust Soc Am. (2010);127:1507–1518. doi: 10.1121/1.3299199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. R Development Core Team R: a language and environment for statistical computing. Vienna, R Foundation for Statistical Computing. (1993) [Google Scholar]
  73. Ramachandran V, Hubbard EM. Synesthesia - a window into perception, thought, and language. J Conscious Stud. (2001);8:3–34. [Google Scholar]
  74. Raphael L. Duration and contexts as cues to word-final cognate opposition in English. Phonetica. (1981);38:126–147. [Google Scholar]
  75. Saji N, Akita K, Imai M, Kantartzis K, Kita S, (2013) Cross-linguistically shared and language-specific sound symbolism for motion: an exploratory data mining approach. Procedings of CogSci. 2013:pp 1253–1258. Berlin. [Google Scholar]
  76. Sapir E. A study in phonetic symbolism. J Exp Psychol. (1929);12:225–239. [Google Scholar]
  77. Saussure F. Paris: Payot; (1916). Cours de linguistique générale. [Google Scholar]
  78. Shinohara K, Kawahara S. The sound symbolic nature of Japanese maid names. Proceedings of the 13th Annual Meeting of the Japanese Cognitive Linguistics Association, Tokyo. (2013);vol 13:pp 183–193. [Google Scholar]
  79. Shinohara K, Kawahara S. A cross-linguistic study of sound symbolism: the images of size. Proceedings of the Thirty-Sixth Annual Meeting of the Berkeley Linguistics Society, Berkeley. (2016):pp 396–410. [Google Scholar]
  80. Shinohara K, Yamauchi N, Kawahara S, Tanaka H. Takete and maluma in action: a cross-modal relationship between gestures and sounds. PLoS One. (2016) doi: 10.1371/journal.pone.0163525. DOI: 10.1371/journal.pone.0163525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Sidhu D, Pexman PM. What's in a name? Sound symbolism and gender in first names. PLoS One. (2015) doi: 10.1371/journal.pone.0126809. DOI: 10.1371/journal.pone.0126809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  82. Sidhu D, Pexman PM. Five mechanisms of sound symbolic association. Psychonom Bull Rev, Epub ahead of print. (2017) doi: 10.3758/s13423-017-1361-1. [DOI] [PubMed] [Google Scholar]
  83. Slater AS, Feinman S. Gender and the phonology of North American first names. Sex Roles. (1985);13:429–440. [Google Scholar]
  84. Smith J. Phonological Augmentation in Prominent Positions; doctoral dissertation, University of Massachusetts, Amherst. (2002) [Google Scholar]
  85. Stevens K, Blumstein S, The search for invariant acoustic correlates of phonetic features . Perspectives on the Study of Speech. In: Eimas P, Miller JD, editors. Mahwah: Earlbaum; (1981). pp. pp 1–38. [Google Scholar]
  86. Tobin J. Durham: Duke University Press; (2004). Pikachu's Global Adventure: The Rise and Fall of Pokémon. [Google Scholar]
  87. Ultan R, Size-sound symbolism . Universals of Human Language II: Phonology. In: Greenberg J, editor. Stanford: Stanford University Press; (1978). pp. pp 525–568. [Google Scholar]
  88. Vance T. New York: SUNY Press; (1987). An Introduction to Japanese Phonology. [Google Scholar]
  89. Vance T, Rendaku . The Handbook of Japanese Language and Linguistics: Phonetics and Phonology. In: Kubozono H, editor. Berlin: Mouton de Gruyter; (2015). pp. pp 397–441. [Google Scholar]
  90. Vance T, Irwin M. Amsterdam: Benjamins; (2016). Sequential Voicing in Japanese Compounds: Papers from the NINJAL Rendaku Project. [Google Scholar]
  91. Wright S, Hay J, Fred and Trema: a phonological conspiracy . Gendered Practices in Language. In: Benor S, Rose M, Sharma D, Sweetland J, Zhang Q, editors. Stanford: CSLI Publications; (2002). pp. pp 175–191. [Google Scholar]
  92. Wright S, Hay J, Tessa B. Ladies first? Phonology, frequency, and the naming conspiracy. Linguistics. (2005);43:531–561. [Google Scholar]
  93. Yorkston E, Menon G. A sound idea: phonetic effects of brand names on consumer judgments. Journal of Consumer Research. (2004);31:43–51. [Google Scholar]
  94. Yorkston E, Menon G. A sound idea: phonetic effects of brand names on consumer judgments. Journal of Consumer Research. (2004);31:43–51. [Google Scholar]

Articles from Phonetica are provided here courtesy of Karger Publishers

RESOURCES