Abstract
Confinement of hydrocarbons in nanoscale pockets and pores provides tunable capability for controlling molecules in catalysts, sorbents, and membranes for reaction and separation applications. While computation of the enthalpic interactions of hydrocarbons in confined spaces has improved, understanding and predicting the entropy of confined molecules remains a challenge. Here we show, using a set of nine aluminosilicate zeolite frameworks with broad variation in pore and cavity structure, that the entropy of adsorption can be predicted as a linear combination of rotational and translational entropy. The extent of entropy lost upon adsorption is predicted using only a single material descriptor, the occupiable volume (Vocc). Predictive capability of confined molecular entropy permits an understanding of the relation with adsorption enthalpy, the ability to computationally screen microporous materials, and an understanding of the role of confinement on the kinetics of molecules in confined spaces.
Short abstract
Entropy of adsorption is quantitatively predicted using a single material descriptor; less rotational entropy is retained in more confining environments, while translational entropy is unaffected.
Introduction
The adsorption of hydrocarbons into cavities and pores within nanomaterials is at the heart of profound chemical technology advancements in heterogeneous catalysis, carbon capture, chemical separations, and pollution control. The ability of molecules to move, rotate, and vibrate inside a confined space determines their ability to bond with the surface. For this reason, applications utilize an array of materials from zeolites to nanotubes and metal–organic frameworks (MOFs) with nanoporous spaces, each of which is designed to manipulate the motion of molecules. The efficacy of any adsorption-based technology is determined by the capability of the engineered pore to discriminate between molecules and control molecular behavior on the surface.
Adsorption is driven by enthalpy and entropy, with entropy dominating at elevated temperatures. Advances have been made in the understanding and quantification of the enthalpy of adsorption of chemical species on solid surfaces.1−5 However, despite contributing substantially to the energetics of adsorption, the entropy of adsorption for any molecule/surface combination remains difficult to predict. Recently, Campbell and Sellers6 showed that the entropy of adsorption of a molecule onto a flat surface can be described by a simple equation
| 1 |
that estimates the entropy of molecular adsorption using only the entropy of a molecule in the gas phase, a readily available quantity. The relationship was found to hold for alkanes, alcohols, and permanent gases adsorbing onto MgO(100), TiO2(110), ZnO(0001), PdO(101), Pt(111), and C(0001) single crystal surfaces. Given the power and ease of use of this approach, it has found application in surface science,7 heterogeneous catalysis,8−10 and computational modeling.11
Prediction of the entropy of hydrocarbons for any realistic application based on gas-phase entropy requires a description of the role of confinement on restricting molecular motion. In materials such as zeolites or metal–organic frameworks where the pore diameter of only a few angstroms approaches the size of the adsorbing hydrocarbon, the effect of confinement dominates molecular motion. Molecules that are free to rotate on a flat surface become hindered from rotating within a pore. Therefore, predictions of entropy such as eq 1 by Campbell and Sellers, developed on single crystal surfaces free of confinement, must be expanded to account for entropy losses due to confinement in real materials which possess a porous structure where adsorption occurs.
Here we evaluate the adsorption of a broad range of hydrocarbons and permanent gases in nine well-defined zeolite frameworks of varying nanoporosity to develop a global predictive equation of adsorption entropy for molecules in confined porous spaces. The impact of confinement on translational and rotational motion is quantified, and a single structural descriptor of nanoporous materials that allows for global prediction of adsorption entropy is identified. A simple yet fundamental correlation is developed that captures the effects on confinement on translational and rotational motion, accurately matching experimentally measured adsorption entropies. We further derive an exchange correlation between the enthalpy and entropy of adsorption, based solely on gas-phase values independent of adsorption measurements. This allows for the estimation of the free energy change of adsorption a priori. Entropic losses are further related to the kinetics of desorption, where the rate of desorption scales exponentially with entropy lost due to confinement.
Results and Discussion
To investigate the effect of confinement on adsorption, we collected numerous experimentally measured entropies of adsorption on aluminosilicate zeolites (Table S1). Nine different zeolite frameworks of varying extents of confinement were considered including: MFI,12−15 CHA,16,17 TON,18,19 FER,19 KFI,19 LTL,20 BEA,14 MOR,14,21 and FAU.14,21,22 To minimize adsorbate–adsorbate interactions, selected adsorption entropies were limited to those of low coverage measurements. Characteristic of aluminosilicate materials are Brønsted acidic bridging hydroxyls; generated through the tetrahedral incorporation of aluminum into the silica framework, molecules can adsorb onto these sites from the bulk fluid phase. Here we specifically consider the adsorption of linear alkanes, branched alkanes, and permanent gases onto Brønsted acidic bridging hydroxyls. Experimental entropies of adsorption were measured through a variety of methods including FT-IR, a combination of gravimetry and calorimetry, volumetric uptake, and inverse gas chromatography.
Entropies of adsorption are relatively insensitive to temperature,13,14 which can be rationalized by considering the difference between the heat capacity of a molecule in the gas phase and its adsorbed state on the surface (Cp,gas – Cp,adsorbate). If the entropy of adsorption was to vary with temperature, the heat capacity of the adsorbate on the surface would need to be significantly different from that in the gas phase. Previous discussions estimate this relative difference in heat capacity to be ∼5 J mol–1 K–1 for alkane adsorption on Brønsted acidic zeolites, which results in a less than 5% change in the entropy of adsorption over a temperature range of 450 K.13 We therefore assume that the entropy of adsorption is not a function of temperature and employ a standard state for adsorption of 298 K and 1.0 bar. Entropy measurements were also collected over a variety of Si/Al ratios, which alters the Brønsted acid site density and their spatial distribution.23 Consistent with previous reports, the entropy of adsorption is relatively insensitive to the Si/Al ratio12 (Supporting Information, Figure S1).
Considering the associative adsorption of a molecule onto a flat surface, akin to that of a rectangular slab (Figure 1), the free energy of adsorption is defined by the corresponding enthalpy and entropy of adsorption
| 2 |
where a molecule typically gains energy through enthalpic contributions due to stabilizing interactions with the surface (ΔHads0). In contrast, a molecule will lose entropy upon adsorption (ΔSslab0) due to its restricted motion on the surface relative to the gas phase. To maintain thermodynamic consistency, the loss in entropy due to adsorption cannot exceed what is available in the gas phase (ΔSads0 ≤ Sgas0). Under conditions typical of associative adsorption, the adsorption–desorption process is reversible and nonactivated.6 This leads to a transition state of adsorption (TS) positioned at a particular distance from the surface such that it loses approximately one degree of translational freedom relative to the gas phase (ΔSTS0 = S1D,trans).24−26
Figure 1.
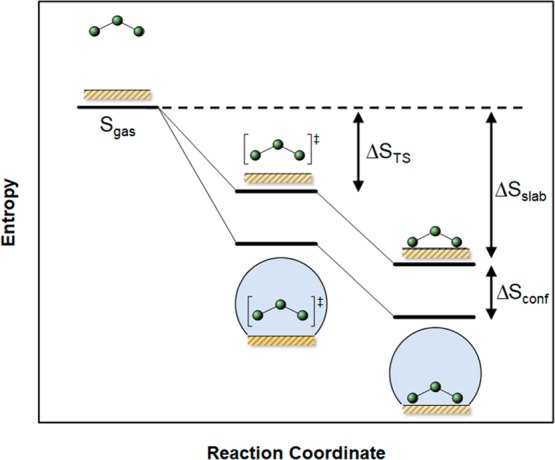
Entropy loss upon adsorption on surfaces and confined spaces.
As the adsorbing surface becomes curved akin to a pore, the motion of an adsorbed molecule is further restricted due to confinement, yielding an additional loss in entropy (Figure 1, ΔSconf).22,27 While this leads to a less favorable entropy of adsorption, this can also lead to an additionally favorable enthalpic stabilization through Van der Waals interactions with the pore wall.27,28 While these enthalpic confinement effects are documented for multiple surface chemistries,13,29−31 adsorption included,32−34 a quantitative prediction of entropy lost to confinement is not yet available.
We therefore propose a simple hypothesis that the entropy of adsorption of a given molecule, for any degree of confinement, can be described as a linear combination
| 3 |
where ΔSslab and ΔSconf are the entropic losses associated with the adsorption of a molecule on a flat unconfined surface such as a slab and that associated with confinement, respectively. While Campbell et al. have established ΔSslab,6 the relationship between molecular shape and confinement in nanoporous structures described within ΔSconf remains to be determined.
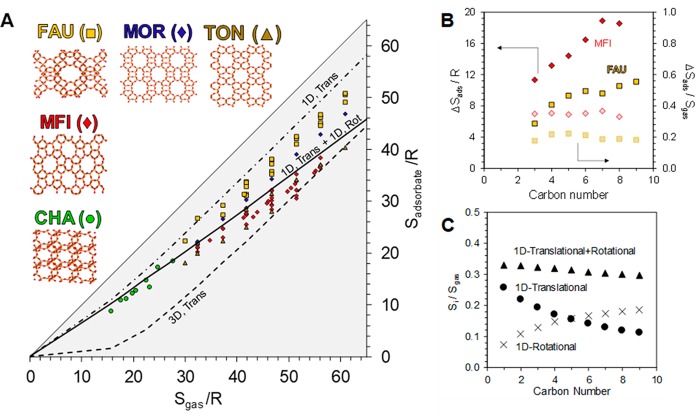
To define ΔSconf, we begin by comparing the adsorption of alkanes in five different zeolite structures: MFI, CHA, TON, FAU, and MOR. Depicted in Figure 2A is the relationship between the entropy of an adsorbed molecule (alkanes and permanent gases) and its gas-phase entropy, where the molecular entropy on the surface never exceeds that in the gas phase. While a significant loss in entropy occurs in all five zeolites, the absolute loss in entropy is distinct for each framework. Adsorbates in TON exhibit the largest loss in entropy upon adsorption, while FAU results in the smallest entropic losses. If the molecules were to behave as immobile adsorbates on the surface, the entropy lost upon adsorption (ΔSads) can be approximated to be equal to three degrees of translational freedom,3,35,36 which can be calculated from statistical mechanics using the Sackur–Tetrode equation37
| 4 |
where SAr,298K0 is the entropy of Ar in the gas phase at 298 K and 1.0 bar, 154.8 J mol–1 K–1; R is the universal gas constant, m the molecular weight of the molecule of interest, mAr that for Argon, and T the temperature at which the entropy is calculated. Alternatively, for the case of a mobile adsorbate, the entropy of adsorption can be approximated to be equal to one degree of translational freedom (Strans/3, eq 4).38,39 A loss of one degree of translational freedom overestimates the entropy of the adsorbate on the surface, while three degrees of translation result in an underestimation (Sadsorbate, Figure 2A).
Figure 2.
(A) Comparison of adsorbate and gas-phase entropy in MFI, CHA, TON, FAU, and MOR. The gray triangle indicates the entropy region that is thermodynamically accessible; the entropy of the adsorbate cannot exceed what is available in the gas phase. (B) Entropy of adsorption of linear alkanes on MFI and FAU. Absolute values of the entropy of adsorption and those normalized by gas-phase entropy are indicated by filled and open symbols, respectively. (C) Entropy associated with one degree of translational and rotational movement, as well as the sum of the two modes as a fraction of the total gas-phase entropy for linear alkanes.
Another approximation, in addition to translational losses, is to consider the loss in rotational entropy upon adsorption.14 While an adsorbed molecule may rotate freely parallel to the surface (i.e., helicopter rotations) and about its own axis, rotations perpendicular to the surface (i.e., cartwheel rotations) may become severely hindered. Combining this approximation with the case of the mobile adsorbate, which underestimates the entropy of adsorption, we define the loss in entropy due to adsorption as
| 5 |
| 6 |
where S1D,trans0 and S1D,rot0 are the entropies associated with one degree of translational (Strans/3, eq 4) and rotational (Srot/3, eq 6) freedom. IA, IB, and IC are the principle moments of inertia. σ is the external symmetry number, and kB and h are the Boltzmann and Planck constants, respectively. While this approximation does not perfectly capture the entropies of adsorption, it does begin to more accurately capture trends in MFI, CHA, and TON structures (Figure 2A, solid line). Restrictions in molecular motion upon adsorption therefore appear to include rotational motion as well. However, none of these models, which are commonly applied in the literature, describe the entropies of all adsorbates in all of the porous materials considered.
The trends in adsorption entropies can be understood by considering each particular zeolite framework individually. Depicted in Figure 2B is the entropy of adsorption for linear alkanes (C3–C9) in MFI and FAU zeolites. While the absolute loss in entropy (ΔSads) increases linearly with carbon number, the fraction of entropy available in the gas phase lost upon adsorption appears to be a fixed value (ΔSads/Sgas) for each framework type. This is consistent with the observations of Campbell and Sellers, where the entropy lost upon adsorption for alkanes and other adsorbates on flat single crystal surfaces was found to be approximately one-third of the gas-phase entropy.6 In the case of a confined system, the fraction of gas-phase entropy lost upon adsorption is a function of the framework type (i.e., the degree of confinement). Linear alkanes lose approximately 38% of their gas-phase entropy upon adsorption in MFI, a medium pore zeolite, while experiencing a smaller loss of 20% in the larger pore FAU framework.
The loss of a fixed fraction of entropy upon adsorption is rationalized by comparing translational and rotational components of the gas-phase entropy of a molecule to that lost upon adsorption. Considering again the case of the mobile adsorbate, where one degree of translational entropy is lost upon adsorption (Figure 2C), a decrease in the fraction of gas-phase entropy lost upon adsorption with increasing carbon number of the adsorbate (e.g., C3 propane, C4 butane) is expected. A similar situation will arise in the case of the immobile adsorbate; the fraction of entropy lost is three times larger but will also decrease with carbon number. This is contrary to the experimental results of Figure 2B where the fraction of gas-phase entropy lost is relatively fixed. Alternatively, a combination of the entropy of one degree of translational and rotational freedom (eq 5) provides a relatively flat trend with carbon number (Figure 2C), consistent with experimental observations (Figure 2B).
Adsorption can therefore be best described by considering entropic losses due to both translational and rotational motions, where different extents of each are lost depending on the structural framework. To evaluate this hypothesis, eq 5 can be expanded to account for adsorption in different sized cavities
| 7 |
where Ftrans and Frot are the fractional losses (0 ≤ Fj ≤ 1) in translational and rotational entropy upon adsorption in different zeolite frameworks, corresponding to zero-to-three degrees of freedom. Here, i and j indicate the identity of the molecular adsorbate and adsorbing framework, respectively. Ftrans and Frot are fitted simultaneously to the experimentally measured entropies of adsorption for each zeolite framework, the results of which are illustrated in Figure 3A. Details of the fitting results are provided in the Supporting Information (Table S3).
Figure 3.
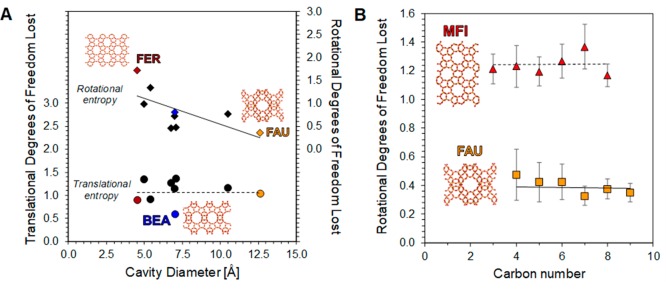
(A) Degrees of translational (●) and rotational (⧫) freedom lost upon adsorption on various zeolites of varying cavity diameter. (B) Rotational degrees of freedom lost in MFI (red ▲) and FAU (yellow ■) zeolites for varying hydrocarbon size. Error bars indicate 95% confidence intervals.
Across nine different zeolite frameworks with significant variation in cavity diameter, the lost degrees of translational freedom (Ftrans) remained constant at approximately one degree of freedom (Figure 3A). Conversely the lost degrees of rotational freedom (Frot) varied with zeolite framework, where Frot decreased with increasing cavity diameter. This result is consistent with recent computations by Marin et al.;14 they assumed the loss of rotational entropy in a medium pore zeolite such as MFI to be equal to two degrees of freedom, while only one degree of rotational freedom was lost in larger pore zeolites such as FAU or BEA. The loss in translational entropy was also limited to one degree of freedom in the different zeolite structures. This is further illustrated in Figure 3B, where despite losing similar degrees of translational freedom, alkanes adsorbed in MFI experience a 3-fold larger loss in rotational degrees of freedom than in the larger pore FAU. Similarly, for Ne, Ar, Kr, and Xe, which possess only translational entropy, one degree of translational freedom was lost upon adsorption in CHA (Supporting Information, Figure S2). One physical interpretation is that confined adsorbates continue to travel throughout the porous network (along but not through the porous surface), thus preserving two degrees of translational freedom. However, rotational motion becomes more restricted in a pore, where molecular rotation about the central atom (i.e., helicopter rotations) will become obstructed by shrinking pore walls creating a confining space.
Based on the results in Figure 3A, Ftrans was set equal to one degree of freedom. Equation 7 then becomes
| 8 |
where one degree of translation freedom will be lost upon adsorption regardless of the adsorbing zeolite framework (S1D,trans,i0). In contrast, the rotational freedom lost (Frot) is a strong function of zeolite framework and the degree to which a molecule is confined in its adsorbed state. Fitting eq 8 to the various frameworks and adsorbates presented in Table S1, the degrees of rotational freedom lost upon adsorption in different zeolite frameworks are determined (Table 1). From the tabulated data, a trend exists between the degrees of rotational freedom lost, the size of the adsorbing pore, and the measured molecular entropy of adsorption. For example, the loss in entropy upon the adsorption of propane increases with the lost degrees of rotational freedom. Also, more rotational entropy was lost in smaller pore zeolites (FER ∼ 4.3 Å) when compared to larger pore zeolites (FAU ∼ 13 Å); in this case, the average cavity diameter is a descriptor for zeolite framework and indicates the extent of confinement. These observations are physically consistent; as the zeolite pore becomes smaller, the adsorbate is more confined and loses more entropy due to its increasingly restricted motion.
Table 1. Physical Characteristics of Zeolite Frameworks.
| framework | –ΔSads,propanea (J mol–1 K–1) | rotational degrees of freedom lostb | cavity diameter (Å) | Voccc (Å3) |
|---|---|---|---|---|
| FER | 102.6 | 1.62 ± 0.15 | 4.3 | 198.8 |
| TON | 103.8 | 1.28 ± 0.12 | 5.0 | 175.3 |
| MFI | 95.0 | 1.28 ± 0.05 | 5.5 | 177.4 |
| LTL | 88.0 | 1.11 ± 0.36 | 9.0 | 243.4 |
| CHA | 87.7 | 1.00 ± 0.27 | 7.4 | 276.6 |
| KFI | 85.0 | 0.95 ± 0.13 | 10.7 | 292.0 |
| MOR | 85.0 | 0.67 ± 0.06 | 7.0 | 223.0 |
| BEA | 71.3d | 0.51 ± 0.07 | 7.5 | 290.1 |
| FAU | 47.7 | 0.39 ± 0.06 | 12.6 | 370.0 |
Broad characterization of rotational entropy of adsorption requires a physical descriptor valid across the different classes of porous materials. While the use of cavity diameter as a predictor of confinement effects is intuitive, its selection can be ambiguous; some zeolite frameworks do not possess a single cavity size. This is further exacerbated by the definition of a cavity diameter which assumes a spherical cage, despite zeolite cages not necessarily being perfectly spherical or cylindrical in nature. An alternative descriptor of size was proposed by Treacy et al., where they address this issue of geometric mismatch with the idea of an occupiable volume (Vocc). Defined as the number of spheres with a diameter of 2.8 Å that can be packed into zeolite framework, the occupiable volume has been calculated through computational methods for 176 different zeolite frameworks.40 When the occupiable volume is smaller, the degree of confinement is greater. From Table 1, we observe that a trend exists between the loss in rotational entropy and the occupiable volume. A zeolite with a smaller occupiable volume results in a larger loss of rotational degrees of freedom for an adsorbate. This relationship is further illustrated in Figure 4, where the entropy of a molecular adsorbate on the surface increases with increasing occupiable volume. The trend is independent of the hydrocarbon adsorbate chain length, since the loss in entropy per unit occupiable volume (i.e., the slope) is approximately constant for C3–C9 linear alkanes. By this comparison, the occupiable volume of a material qualitatively predicts the average effect of various confining adsorption sites on the entropy of adsorption and can serve as a descriptor of porous materials.
Figure 4.
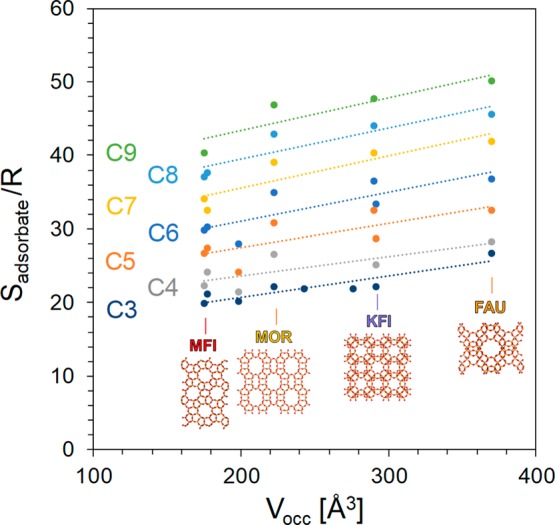
Relationship between adsorbate entropy (Sadsorbate) and the occupiable volume of the adsorbing zeolite framework (Vocc) for C3–C9 linear alkanes.
To utilize occupiable volume as a quantitative descriptor of confinement in zeolites, the loss in rotational degrees of freedom must be defined as a function of occupiable volume. Analogous to eq 3 where entropy losses are treated as a linear combination of adsorption on a flat surface and confinement effects, we define losses in rotational freedom as
| 9 |
| 10 |
where the loss in rotational freedom upon adsorption is the linear combination of rotational degrees of freedom lost on a flat slab (Frot,slab) and the additional loss due to confinement (Frot,conf). Frot,slab is a fixed value, while Frot,conf is a function of the zeolite’s occupiable volume. The rotational function, f, is limited by two conditions. As the occupiable volume approaches larger values associated with less confinement, Frot,conf approaches a value of zero. This is physically consistent as confinement must become negligible in larger pores where the molecule no longer feels its surrounding environment. Additionally, as the occupiable volume decreases, the effect of confinement will rapidly increase as it approaches a critical volume (Vcritical). Previously, Derouane considered the effect of confinement on the enthalpy of adsorption, describing confinement through geometric consideration of the pore.32,41 Based on a Van der Waals model, a scaling relationship was proposed to describe confinement as a function of the adsorbate size relative to that of the pore. Here we apply an analogous relationship, modified to use occupiable volume as a descriptor of the porous material
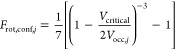 |
11 |
where a critical volume (Vcritical) describes the point at which all degrees of rotational freedom are lost. As the occupiable volume increases; the material ultimately becomes more like a flat surface, and the effect of confinement is completely lost. A combination of eqs 8–11 provides a quantitative framework by which to describe the entropy of adsorption with any degree of confinement.
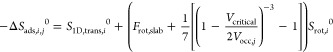 |
12 |
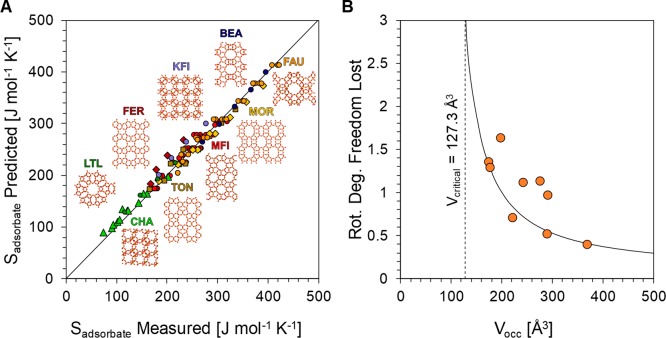
By applying eq 12 to all of the adsorbates in the nine zeolite frameworks (fitting of 112 data points from Table S1), the relationship between the measured entropy of adsorption and the predicted entropy of adsorption collapses to a single line (Figure 5A) indicating quantitative prediction of the entropy of adsorption for all adsorbate/framework combinations. The optimal fit is provided by an Frot,slab of 0.03 and a critical volume (Vcritical) of 127.3 Å3. With these parameters, entropies of adsorption calculated by eq 12 result in an average absolute error and standard deviation of 4.4% and 2.3%, respectively. An Frot,slab close to zero suggests that adsorbates experience negligible loss in rotational entropy in the case of an unconfined system. Additionally, when the occupiable volume approaches the critical value, 127.3 Å3, a confined adsorbate will experience a complete loss of rotational entropy (Figure 5B). A physical rationalization is that the maximum included spherical diameter associated with the critical volume (4.6 Å) is similar to the kinetic diameter of alkanes (4–5 Å),32 such that an adsorbate is no longer able to rotate as its confining space approaches its kinetic diameter. The impacts of the size of the confining environment (Vocc) and the size of the adsorbate (Vcritical) on total loss in entropy upon adsorption thus relate by the ratio of Vcritical/Vocc, as it appears in eq 12.
Figure 5.
(A) Comparison of predicted and experimentally measured entropies of adsorption for alkanes and permanent gases. (B) Rotational degrees of freedom lost upon adsorption on various zeolites of varying occupiable volume (Vocc).
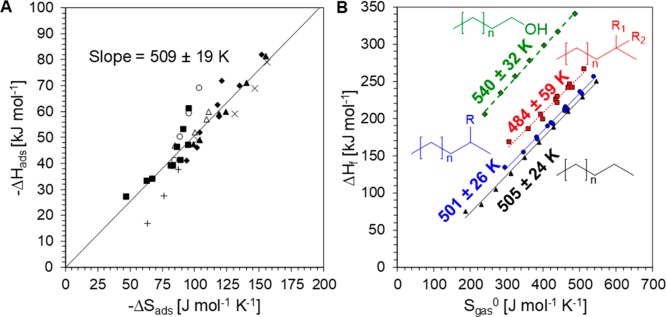
While separate in their effect on the overall free energy of adsorption, the enthalpy and entropy of adsorption are frequently reported to be correlated through what is commonly referred to as compensation. As the enthalpy of adsorption becomes more exothermic leading to a more favorable adsorption, the entropy decreases and counters the enthalpic stabilization. With two opposing effects, enthalpy and entropy, it is difficult to establish a priori whether confinement will energetically favor adsorption. Previous measurements of compensation have reported a dependence on framework identity, where the gain in enthalpy for every unit of entropy lost changes from one zeolite framework to another.14,22,42 Illustrated in Figure 6A is the comparison of enthalpies and entropies of adsorption measured across seven zeolite frameworks. Selected data was limited to that where the enthalpy of adsorption was measured independently using microcalorimetry as opposed to experimental measurements used to extract enthalpy and entropy simultaneously (Table S4). Considering the various frameworks independently, it may appear that each framework possesses a different exchange rate between the enthalpy and entropy of adsorption. However, consideration of all frameworks and measurements by various authors simultaneously results in a single correlation, with a characteristic slope of 509 ± 19 K. For every J mol–1 K–1 of entropy lost upon adsorption, 509 J mol–1 of enthalpy is gained; this exchange rate is the same within error for all seven frameworks (Figure S3, Supporting Information).
Figure 6.
(A) Relationship between enthalpy and entropy of adsorption for alkanes in FER (×), TON (▲), FAU (■), MFI (◆), KFI (Δ), MOR (○), and CHA (+). (B) Relationship between the enthalpy of formation and gas-phase entropy of linear (black ▲), singly branched (blue ●), twice branched (red ■), and alcohols (green ◆).
The origin of the exchange rate between the enthalpy and entropy of adsorbed species on aluminosilicates presented in Figure 6A has been previously attributed to van der Waals interactions.27 However, a quantitative description of the exchange rate independent of adsorption measurements is unavailable. One comparison with the adsorption compensation exchange rate is the relationship between the heat of formation (ΔHf) and the entropy of hydrocarbons in the gas phase (Sgas0), as shown in Figure 6B. Linear alkanes, singly branched alkanes, and doubly branched alkanes exhibit a gas-phase enthalpy–entropy exchange rate of 505 ± 24, 501 ± 26, and 484 ± 59 K, respectively, which is same as the adsorption compensation exchange rate of Figure 6A within error. It is noted that other classes of species such as primary alcohols exhibit a higher gas-phase exchange rate of 540 ± 32 K. While it is possible to consider the hypothesis that the adsorption compensation exchange rate derives solely from adsorbate identity, thereby resulting in the same entropy–enthalpy exchange rate both on the surface and in the gas phase, there exists insufficient experimental adsorption data with other classes of molecules (e.g., alcohols, amines) to support this conclusion.
While confinement can have a profound effect on the thermodynamics of adsorption, the kinetics of adsorption/desorption are also impacted by the size and shape of porous materials. When considering an Arrhenius description of desorption, the pre-exponential factor (vdes) for a molecular adsorbate from a surface can be defined as6
| 13 |
where ΔSTS,des is the entropy change associated with the molecular adsorbate approaching the transition state of desorption as it desorbs from the surface. Applying eq 8 from this work, we now define the pre-exponential factor for desorption as
| 14 |
The pre-exponential factor
for desorption is therefore a function
of confinement, dictated by the loss of rotational entropy (Frot,jSrot,i) which appears in the exponential. Details
of the derivation are provided in the Supporting Information (eqs S1–S9). As the adsorbate becomes more
confined and loses additional degrees of rotational freedom, vdes increases exponentially (Figure S4). For example, propane desorbing from FAU and MFI
frameworks possesses desorption pre-exponential factors of 1015 and 1020 s–1, respectively.
We note that these values are orders of magnitude larger than the
typically applied value of 1013 s–1 for
desorption and many other surface chemistries.43 Interestingly, in the case of an unconfined system (Frot ∼ 0), the desorption pre-exponential
factor will be approximately the standard value of 1013 s–1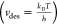 . Additionally, the pre-exponential
factor
for desorption in an unconfined system is weakly dependent on molecular
size. Conversely in a confined system, the desorption pre-exponential
factor depends on the rotational entropy (Srot) and thus varies with molecular size.
. Additionally, the pre-exponential
factor
for desorption in an unconfined system is weakly dependent on molecular
size. Conversely in a confined system, the desorption pre-exponential
factor depends on the rotational entropy (Srot) and thus varies with molecular size.
Conclusions
Confinement of hydrocarbons adsorbed in nanoporous aluminosilicates significantly restricts molecular motion. Adsorbates lose one degree of translational motion (translation perpendicular to the surface), while rotational motion decreases in increasingly smaller and more confining pores. The surface entropy was described by a linear combination of the entropy lost on a flat surface plus the entropy loss resulting from confinement. By evaluating saturated hydrocarbons and permanent gases in nine different zeolite frameworks, the surface entropy of adsorbates was predicted using only a single descriptor of nanoporous materials, the occupiable volume, to determine the extent of lost rotational motion. This equation provides a simple method to predict the entropy of adsorption, where only the occupiable volume of a material and critical volume of the adsorbate need to be determined. The entropy lost to adsorption is compensated by a single exchange rate between enthalpy and entropy, regardless of the degree of confinement; this exchange rate is the same as the gas-phase analog, which relates the enthalpy of formation and gas-phase entropy of a saturated hydrocarbon. Finally, confinement influences the kinetics of desorption, where the pre-exponential factor of the desorption rate coefficient is predicted to increase orders of magnitude depending on the extent of molecular confinement.
Acknowledgments
We acknowledge financial support of the Catalysis Center for Energy Innovation, a U.S. Department of Energy—Energy Frontier Research Center under Grant DE-SC0001004.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00419.
Tabulated values of adsorption entropies, rotational and translational entropy of adsorbates, and derivations of kinetic expressions (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Auroux A. Microcalorimetry methods to study the acidity and reactivity of zeolites, pillared clays and mesoporous materials. Top. Catal. 2002, 19 (3), 205–213. 10.1023/A:1015367708955. [DOI] [Google Scholar]
- Campbell C. T.; Sellers J. R. V. Enthalpies and entropies of adsorption on well-defined oxide surfaces: Experimental measurements. Chem. Rev. 2013, 113 (6), 4106–4135. 10.1021/cr300329s. [DOI] [PubMed] [Google Scholar]
- Cardona-Martinez N.; Dumesic J. A. In Advances in catalysis; Eley D. D., Pines H., Weisz P. B., Eds.; Academic Press: Cambridge, MA, 1992; Vol. 38, pp 149–244. [Google Scholar]
- Andersen P. J.; Kung H. H. In Catalysis; Spivey J. J., Agarwal S. K., Eds.; The Royal Society of Chemistry: Cambridge, UK, 1994; Vol. 11, pp 441–466. [Google Scholar]
- Parrillo D. J.; Gorte R. J. Characterization of stoichiometric adsorption complexes in h-zsm-5 using microcalorimetry. Catal. Lett. 1992, 16 (1), 17–25. 10.1007/BF00764350. [DOI] [Google Scholar]
- Campbell C. T.; Sellers J. R. V. The entropies of adsorbed molecules. J. Am. Chem. Soc. 2012, 134 (43), 18109–18115. 10.1021/ja3080117. [DOI] [PubMed] [Google Scholar]
- Zhao W.; Carey S. J.; Mao Z.; Campbell C. T. Adsorbed hydroxyl and water on ni(111): Heats of formation by calorimetry. ACS Catal. 2018, 8 (2), 1485–1489. 10.1021/acscatal.7b04041. [DOI] [Google Scholar]
- Abdelrahman O. A.; Heyden A.; Bond J. Q. Microkinetic analysis of c3–c5 ketone hydrogenation over supported ru catalysts. J. Catal. 2017, 348, 59–74. 10.1016/j.jcat.2017.01.022. [DOI] [Google Scholar]
- Heard C. J.; Hu C.; Skoglundh M.; Creaser D.; Grönbeck H. Kinetic regimes in ethylene hydrogenation over transition-metal surfaces. ACS Catal. 2016, 6 (5), 3277–3286. 10.1021/acscatal.5b02708. [DOI] [Google Scholar]
- Sarazen M. L.; Iglesia E. Stability of bound species during alkene reactions on solid acids. Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (20), E3900–E3908. 10.1073/pnas.1619557114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H.; Paolucci C.; Schneider W. F. Zeolite adsorption free energies from ab initio potentials of mean force. J. Chem. Theory Comput. 2018, 14 (2), 929–938. 10.1021/acs.jctc.7b00716. [DOI] [PubMed] [Google Scholar]
- Li H.; Kadam S. A.; Vimont A.; Wormsbecher R. F.; Travert A. Monomolecular cracking rates of light alkanes over zeolites determined by ir operando spectroscopy. ACS Catal. 2016, 6 (7), 4536–4548. 10.1021/acscatal.6b01025. [DOI] [Google Scholar]
- Bhan A.; Gounder R.; Macht J.; Iglesia E. Entropy considerations in monomolecular cracking of alkanes on acidic zeolites. J. Catal. 2008, 253 (1), 221–224. 10.1016/j.jcat.2007.11.003. [DOI] [Google Scholar]
- De Moor B. A.; Reyniers M.-F.; Gobin O. C.; Lercher J. A.; Marin G. B. Adsorption of c2–c8 n-alkanes in zeolites. J. Phys. Chem. C 2011, 115 (4), 1204–1219. 10.1021/jp106536m. [DOI] [Google Scholar]
- Denayer J. F.; Souverijns W.; Jacobs P. A.; Martens J. A.; Baron G. V. High-temperature low-pressure adsorption of branched c5–c8 alkanes on zeolite beta, zsm-5, zsm-22, zeolite y, and mordenite. J. Phys. Chem. B 1998, 102 (23), 4588–4597. 10.1021/jp980674k. [DOI] [Google Scholar]
- Piccini G.; Alessio M.; Sauer J.; Zhi Y.; Liu Y.; Kolvenbach R.; Jentys A.; Lercher J. A. Accurate adsorption thermodynamics of small alkanes in zeolites. Ab initio theory and experiment for h-chabazite. J. Phys. Chem. C 2015, 119 (11), 6128–6137. 10.1021/acs.jpcc.5b01739. [DOI] [Google Scholar]
- Barrer R. M.; Davies J. A. Sorption in decationated zeolites. I. Gases in hydrogen-chabazite. Proc. R. Soc. London, Ser. A 1970, 320 (1542), 289–308. 10.1098/rspa.1970.0210. [DOI] [Google Scholar]
- Denayer J. F.; Baron G. V.; Martens J. A.; Jacobs P. A. Chromatographic study of adsorption of n-alkanes on zeolites at high temperatures. J. Phys. Chem. B 1998, 102 (17), 3077–3081. 10.1021/jp972328t. [DOI] [Google Scholar]
- Eder F.; Lercher J. A. On the role of the pore size and tortuosity for sorption of alkanes in molecular sieves. J. Phys. Chem. B 1997, 101 (8), 1273–1278. 10.1021/jp961816i. [DOI] [Google Scholar]
- Barrer R. M.; Davies J. A. Sorption in decationated zeolites ii. Simple paraffins in h-forms of chabazite and zeolite l. Proc. R. Soc. London, Ser. A 1971, 322 (1548), 1–19. 10.1098/rspa.1971.0050. [DOI] [Google Scholar]
- Eder F.; Stockenhuber M.; Lercher J. A. Brønsted acid site and pore controlled siting of alkane sorption in acidic molecular sieves. J. Phys. Chem. B 1997, 101 (27), 5414–5419. 10.1021/jp9706487. [DOI] [Google Scholar]
- Eder F.; Lercher J. A. Alkane sorption in molecular sieves: The contribution of ordering, intermolecular interactions, and sorption on brønsted acid sites. Zeolites 1997, 18 (1), 75–81. 10.1016/S0144-2449(96)00127-3. [DOI] [Google Scholar]
- Knott B. C.; Nimlos C. T.; Robichaud D. J.; Nimlos M. R.; Kim S.; Gounder R. Consideration of the aluminum distribution in zeolites in theoretical and experimental catalysis research. ACS Catal. 2018, 8 (2), 770–784. 10.1021/acscatal.7b03676. [DOI] [Google Scholar]
- Tait S. L.; Dohnálek Z.; Campbell C. T.; Kay B. D. N-alkanes on mgo(100). Ii. Chain length dependence of kinetic desorption parameters for small n-alkanes. J. Chem. Phys. 2005, 122 (16), 164708. 10.1063/1.1883630. [DOI] [PubMed] [Google Scholar]
- Fichthorn K. A.; Miron R. A. Thermal desorption of large molecules from solid surfaces. Phys. Rev. Lett. 2002, 89 (19), 196103. 10.1103/PhysRevLett.89.196103. [DOI] [PubMed] [Google Scholar]
- Weaver J. F. Entropies of adsorbed molecules exceed expectations. Science 2013, 339 (6115), 39–40. 10.1126/science.1231552. [DOI] [PubMed] [Google Scholar]
- Gounder R.; Iglesia E. The catalytic diversity of zeolites: Confinement and solvation effects within voids of molecular dimensions. Chem. Commun. 2013, 49 (34), 3491–3509. 10.1039/c3cc40731d. [DOI] [PubMed] [Google Scholar]
- Yang L.; Trafford K.; Kresnawahjuesa O.; Šepa J.; Gorte R. J.; White D. An examination of confinement effects in high-silica zeolites. J. Phys. Chem. B 2001, 105 (10), 1935–1942. 10.1021/jp002964i. [DOI] [Google Scholar]
- Maestri M.; Iglesia E. First-principles theoretical assessment of catalysis by confinement: No-o2 reactions within voids of molecular dimensions in siliceous crystalline frameworks. Phys. Chem. Chem. Phys. 2018, 20 (23), 15725–15735. 10.1039/C8CP01615A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santiso E. E.; George A. M.; Turner C. H.; Kostov M. K.; Gubbins K. E.; Buongiorno-Nardelli M.; Sliwinska-Bartkowiak M. Adsorption and catalysis: The effect of confinement on chemical reactions. Appl. Surf. Sci. 2005, 252 (3), 766–777. 10.1016/j.apsusc.2005.02.101. [DOI] [Google Scholar]
- Gounder R.; Iglesia E. The roles of entropy and enthalpy in stabilizing ion-pairs at transition states in zeolite acid catalysis. Acc. Chem. Res. 2012, 45 (2), 229–238. 10.1021/ar200138n. [DOI] [PubMed] [Google Scholar]
- Derouane E. G.; Andre J.-M.; Lucas A. A. Surface curvature effects in physisorption and catalysis by microporous solids and molecular sieves. J. Catal. 1988, 110 (1), 58–73. 10.1016/0021-9517(88)90297-7. [DOI] [Google Scholar]
- Lucas A. A.; Derycke I.; Lambin P.; Vigneron J. P.; Leherte L.; Elanany M.; André J. M.; Larin A. V.; Vercauteren D. P. Confinement in molecular sieves: The pioneering physical concepts. J. Mol. Catal. A: Chem. 2009, 305 (1), 16–23. 10.1016/j.molcata.2009.02.040. [DOI] [Google Scholar]
- Sastre G.; Corma A. The confinement effect in zeolites. J. Mol. Catal. A: Chem. 2009, 305 (1), 3–7. 10.1016/j.molcata.2008.10.042. [DOI] [Google Scholar]
- Martens G. G.; Marin G. B.; Martens J. A.; Jacobs P. A.; Baron G. V. A fundamental kinetic model for hydrocracking of c8 to c12 alkanes on pt/us–y zeolites. J. Catal. 2000, 195 (2), 253–267. 10.1006/jcat.2000.2993. [DOI] [Google Scholar]
- Bond J. Q.; Jungong C. S.; Chatzidimitriou A. Microkinetic analysis of ring opening and decarboxylation of γ-valerolactone over silica alumina. J. Catal. 2016, 344, 640–656. 10.1016/j.jcat.2016.10.021. [DOI] [Google Scholar]
- D.A M.Statistical mechanics; University Science Books: Sausalito, CA, p 86. [Google Scholar]
- De Moor B. A.; Reyniers M.-F.; Marin G. B. Physisorption and chemisorption of alkanes and alkenes in h-fau: A combined ab initio-statistical thermodynamics study. Phys. Chem. Chem. Phys. 2009, 11 (16), 2939–2958. 10.1039/b819435c. [DOI] [PubMed] [Google Scholar]
- Wise H. Energy exchange between gases and solids. J. Phys. Chem. Solids 1963, 24 (11), 1291–1296. 10.1016/0022-3697(63)90172-0. [DOI] [Google Scholar]
- Treacy M. M. J.; Foster M. D. Packing sticky hard spheres into rigid zeolite frameworks. Microporous Mesoporous Mater. 2009, 118 (1), 106–114. 10.1016/j.micromeso.2008.08.039. [DOI] [Google Scholar]
- Derouane E. G.; André J.-M.; Lucas A. A. A simple van der waals model for molecule-curved surface interactions in molecular-sized microporous solids. Chem. Phys. Lett. 1987, 137 (4), 336–340. 10.1016/0009-2614(87)80895-3. [DOI] [Google Scholar]
- Eder F.; He Y.; Nivarthy G.; Lercher J. A. Sorption of alkanes on novel pillared zeolites; comparison between mcm-22 and mcm-36. Recueil des Travaux Chimiques des Pays-Bas 1996, 115 (11–12), 531–535. 10.1002/recl.19961151114. [DOI] [Google Scholar]
- Chorkendorff I.; Niemantsverdriet J. W.. Concepts of modern catalysis and kinetics; John Wiley & Sons: Weinheim, 2006, p 125. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.