Abstract
The concept of the Anthropocene is based on the idea that human impacts are now the primary drivers of changes in the earth’s systems, including ecological systems. In many cases, the behavior that causes ecosystem change is itself triggered by ecological factors. Yet most ecological models still treat human impacts as given, and frequently as constant. This undermines our ability to understand the feedbacks between human behavior and ecosystem change. Focusing on the problem of species dispersal, we evaluate the effect of dispersal on biodiversity in a system subject to predation by humans. People are assumed to obtain benefits from (a) the direct consumption of species (provisioning services), (b) the non-consumptive use of species (cultural services), and (c) the buffering effects of the mix of species (regulating services). We find that the effects of dispersal on biodiversity depend jointly on the competitive interactions among species, and on human preferences over species and the services they provide. We find that while biodiversity may be greatest at intermediate levels of dispersal, this depends on structure of preferences across the metacommunity.
Keywords: Bioeconomics, Biodiversity, Dispersal, Non-consumptive benefits, Spatial insurance
1. Introduction
In the age of the Anthropocene, humans have impacted almost all of the world’s ecosystems (Crutzen and Stoermer, 2000; Lewis and Maslin, 2015; Steffen et al., 2007). Among the most important anthropogenic drivers of ecosystem change is globalization, or the closer integration of the world economy (Perrings, 2014). Trade and travel have connected ecosystems far beyond the natural dispersal of species (Costello et al., 2007; Hulme, 2009; Lenzen et al., 2012; Mack et al., 2000). At the same time, the way people have exploited ecosystems has fundamentally altered their vulnerability to introduced species (Dalmazzone, 2000; Hanspach et al., 2008; Pyšek et al., 2010; Vila and Pujadas, 2001). Yet most ecological models abstract from human impacts, treating them as given, constant, or ignoring them completely. There is a need for a "new ecology" that treats people’s actions as part of the system (Schmitz, 2016). In this article we revisit the theory of species dispersal in metacommunities to take into account the feedbacks between dispersal, biodiversity, and human exploitation in model systems. In particular, we revisit the theoretical link between dispersal and species diversity in metacommunities subject to human exploitation.
A central result in the theory of species dispersal is that very low or very high rates of dispersal tend to reduce diversity, whereas intermediate rates of dispersal tend to increase diversity (Amarasekare and Nisbet, 2001; Loreau and Mouquet, 1999; Loreau et al., 2003; Mouquet and Loreau, 2003). Intermediate dispersal provides source-sink and rescue effects that replenish locally threatened populations, so maintaining species diversity without leading to the competitive exclusion that drives down diversity when dispersal rates are extreme (Brown and Kodric-Brown, 1977; Holt, 1985; Pulliam, 1988). There are some exceptions to this. For example, Haegeman and Loreau (2014) identify conditions in which resource and consumer dispersal can exhibit strictly increasing relationships with diversity.
Results from experimental and field research are not decisive. Some experimental studies have found support for the intermediate dispersal hypothesis (Howeth and Leibold, 2010; Kneitel and Miller, 2003; Venail et al., 2008), but others conclude that the relationship between diversity and dispersal depends on the type of organism and spatial scale of the study (Cadotte, 2006; Cadotte and Fukami, 2005; Cadotte et al., 2006). For example, in a meta-analysis of experimental studies of the impact of dispersal on species diversity, Cadotte (2006) argues that the "hump" shaped relationship between dispersal and diversity is specific to the animal kingdom. Other research supports a strictly increasing relationship between dispersal and diversity, such as in microcosm communities (Gilbert et al., 1998; Gonzalez and Chaneton, 2002; Gonzalez et al., 1998; Holyoak, 2000; Thompson and Shurin, 2012; Warren, 1996). In contrast, field studies often find that dispersal has only negative effects on species diversity. Invasion biologists, for example, routinely document cases where the effect of dispersal is strongly negative, even at large spatial scales (Chisholm, 2012; Ehrenfeld, 2010; McKinney and Lockwood, 1999; Rhymer and Simberloff, 1996a; Vilà et al., 2011).
An important omission in the understanding of species dispersal is the role of human intervention. Seemingly natural systems are subject to a range of interventions that alter their responses to dispersal. Crops are promoted while crop competitors, predators, and pathogens are suppressed. Charismatic mega-fauna are often protected while inconspicuous plants or insects are ignored. People indirectly select for or against species as in, for example, the consequences of nutrient deposition from agriculture into aquatic ecosystems or the accidental introduction of invasive species (Chisholm, 2012). The observed mix of species in actual ecosystems reflects the joint effects of human control and natural ecological dynamics (Horan et al., 2011; Liu et al., 2007).
We consider interactions between dispersal, competition, predation, and species diversity in the presence of human preferences for particular ecological states. We take metacommunities that are subject to anthropogenic predation (e.g. harvest) and ask how dispersal affects species diversity when humans alter relative abundances by promoting or suppressing species. We build on the metacommunity models of Loreau et al. (2003) and Gonzalez et al. (2009) to investigate the relationship between biodiversity and dispersal when people derive consumptive benefits from harvesting individual species and non-consumptive benefits from species abundance and richness (mix of species) (Barbier, 2007; Bertram and Quaas, 2016). Non-consumptive benefits from species abundance refer to benefits arising directly from species’ biomass, such as carbon sequestration or aesthetic and spiritual values. Non-consumptive benefits from richness or the mix of species refer to benefits such as the regulation of water quality or soil erosion.
We hypothesize that the relationship between diversity and dispersal depends not only on the competitive interactions between species, but also on patterns of harvest/control that reflect human preferences for species and the benefits that they provide. We expect harvest/control to alter the ecological dynamics of the system, resulting in a different diversity-dispersal relationship than occurs in an ecological model that ignores (or assumes fixed) human behaviors. Human harvest alters species abundances, and this can change the source-sink dynamics created by species dispersal between patches. If people value one species over another, we expect harvest/control to promote more preferred species while suppressing less preferred species. Similarly, if people derive non-consumptive benefits from species we expect harvest/control to increase the biomass of preferred species in the patch or maintain even abundances. We find that while the intermediate dispersal hypothesis holds in some cases, diversity can be monotonically increasing in dispersal depending on ecological competition parameters and human preferences across species.
2. The ecological model
We adapt the model developed by Loreau et al. (2003) and Gonzalez et al. (2009) which has a metacommunity comprising three communities, each initially made up of three species. Within each ecological community, all species compete for a single limiting resource. Species consume a deterministically variable quantity of resource depending on environmental conditions and time. Communities are coupled together through dispersal.
Changes in species biomass N and resource biomass R in the jth community are described by the equations:
| (1) |
| (2) |
for species i = 1, 2, 3 and communities j = 1, 2, 3 at time t. Species are assumed to consume resources at rate cij(t), convert resources to new biomass with efficiency e, and die at rate m. The limiting resource is assumed to increase in all communities by a fixed amount, I, and be lost at a constant rate l. The system assumes a Holling type I predator response, where all species have the same conversion efficiency but differ in their consumption (predation) rates. Species disperse among communities at a constant proportion or rate a.
Species consumption of the resource is a non-linear function of species-specific competitive ability and environmental variation fluctuating over time for each species in each community such that:
| (3) |
| (4) |
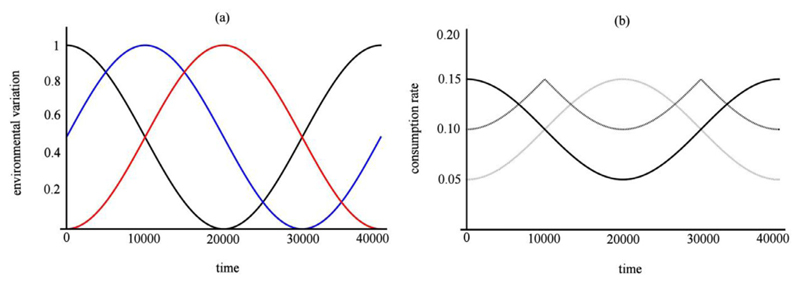
Consumption rates are constrained to lie within the range [0.05, 0.15]. Hi is a dimensionless, species-dependent competition parameter such that H1 = 1, H2 = 1/2, and H3 = 0. It is assumed that environmental conditions, Fj, fluctuate over time as a sinusoidal function. A phase parameter (x1 = π/2, x2 = 0, x3 = –π/2) shifts the environmental variation along its horizontal axis (Fig. 1). The period of environmental variation and hence consumption rates is given by TF. Depending on the length of each phase TF, in the absence of human intervention or dispersal a single species will exclude all others in a given community. If TF is sufficiently large, this will be the set of species that possess the highest initial consumption rate, cij(t). If TF is small, this will be the set of species whose consumption rates are closest to the average across all communities (a "generalist" species). In our model, having consumption rates close to the average across communities is equivalent to the characteristics of generalist species in ecology - the ability to occupy a broad range of environments (Futuyma and Moreno, 1988; Poisot et al., 2012; Schluter, 2000).1
Fig. 1.
Community environmental variation (a) and species consumption (b) curves over time. In (a), color denotes community number: black (community 1, x1 = π/2), blue (community 2, x2 = 0), red (community 3, x3 = −π/2). The phase parameter, xj, shifts environmental variation along its x-axis. In (b), species consumption rates are for community 1 and species is indicated by color: black (H1 = 1), charcoal (H2 = 1/2), and light gray (H3 = 0). Consumption rate is determined by the interaction between the species competition parameter and environmental variation. Reproduced from Shanafelt et al. (2015). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The ecological model depends on several assumptions. First, it is assumed that communities initially contain the same set of species and differ only in their environmental variation over time as defined by the phase parameter xj. Second, species differ only in their consumption rates, which vary by community as a function of Hi and xj. This implies that species are more or less similar in their ecological function and exist within a single trophic level. Third, species compete for a single limiting resource whose natural influx and loss rates are constant and independent across time and communities. Fourth, species competition arises solely from resource consumption. There is no direct interaction between individuals within and across patches (e.g. local competition for light or nutrients in plant systems). Finally, we assume that dispersal is density-independent and occurs at a constant rate of dispersal. These assumptions, while restrictive, simplify the analysis while providing a structure for analyzing competition over a range of environmental conditions, and the effect of harvest on species composition. These assumptions, and how they relate to the economic model, are discussed in more detail in Supplementary Appendix A. For a detailed analysis and extension of the Loreau spatial insurance model, see Loreau et al. (2003), Gonzalez et al. (2009), Urban (2006), Shanafelt et al. (2015), Thompson and Gonzalez (2016) and Thompson and Gonzalez (2017).
3. The bioeconomic model
Consider a managed ecosystem of three communities, where each patch can be thought of as an independent management area containing three species. We assume that people obtain benefits from the direct consumption of species (harvest), from non-consumptive benefits arising from species abundance (stocks), and from biodiversity (the composition of those stocks). The benefits from consumption include the provisioning services of the ecosystem (e.g. the production of foods, fuels, fibers etc). The non-consumptive stock benefits of species abundance include, for example, cultural and regulating services such as the value of biomass for carbon sequestration, and the aesthetic, totemic or spiritual values of species. The non-consumptive stock benefits of diversity include the stabilizing effects of biodiversity on ecosystem functioning and the subsequent flow of ecosystem services (regulating services) (Millennium Ecosystem Assessment, 2005). We assume that all species are positively valued in consumption, and so do not consider cases where species are a direct source of disutility (e.g. pests or pathogens).
We may rewrite (1) and (2) to reflect the impact of harvest, equal to qEij(t)Nij(t), on the abundance of species and the resource:
| (5) |
| (6) |
where effort in harvesting speciesion patch j is given byEij (0 ≤ Eij ≤ Emax) and q is the constant efficiency of effort. This is a Schaefer harvest function, common in economics and fisheries science (Schaefer, 1957). We arbitrarily set the maximum harvest effort such that it is possible to maintain species biomass at any chosen level.2
We further assume that in each community a resource manager harvests species in that community in order to maximize an index of net social benefits, ignoring the actions of managers in other communities connected by species dispersal. That is, managers act independently, and do not condition their decisions on the harvest decisions of others. Formally, we define the jth manager’s problem as:
| (7) |
where pij is the unit price of each species harvested (a measure of the marginal social benefit of harvest of species i) and w is the marginal cost of harvest effort. The marginal non-consumptive benefits of species abundance are given by the parameter αij. The total social non-consumptive benefit of species biomass is taken to be a non-saturating, linear function which - as is the case for an ecosystem service such as carbon sequestration - scales with the biomass of species i on patch j. The parameter βj is a measure of the non-consumptive benefits of biodiversity. It represents the value of ecosystem functioning and regulating services that increase with biodiversity. For simplicity βj is taken to be a weighted Simpson’s index of diversity (Simpson, 1949).3 Total benefits from biodiversity are maximized when there is an even number of species abundances. N(t) measures the biomass of all species in the community. δ is the discount rate, and τ is the time horizon over which harvest is determined. In addition, at the terminal time, the transversality condition requires that the social (shadow) value of an extra unit of each species and the resource are constrained to zero.
The full optimal solution to the system (5)–(7) is set of feedback responses that approach the optimal harvest at the most rapid rate possible (Clark, 2010; Conrad and Clark, 1987). This approach path is optimal because the system is linear in the control variables and there exists a separate control for each state variable. We may formally write the complete solution of the optimal choice of harvest as a feedback rule dependent on the stock of each species:
| (8) |
If the marginal net benefit of harvest effort is positive for a species, then harvest effort is set to its maximum level, Emax. If the marginal net benefit of harvest effort for a species is negative, then harvest effort is set to zero. If the marginal net benefit of harvest effort is zero, then harvest effort is equal the ‘singular solution’ - the optimal level of harvest effort at equilibrium,
At the singular solution, harvest balances the marginal benefits and costs of a change in stock size (Clark, 2010; Conrad and Clark, 1987):
| (9) |
Eq. (9) implies that if the optimal solution is jointly optimal for all species, then there are separate optimal harvest policies for each species and patch in each moment of time (Fenichel and Horan, 2007a; Fenichel et al., 2011). The first term in the square brackets is the present value of marginal benefits from preserving the resource to be consumed by species in the future (Melstrom and Horan, 2013). The second term represents the marginal user cost of harvest: the forgone future growth in the abundance of all species as a result of harvesting now. The final two terms are the marginal non-consumptive benefits of species abundance and biodiversity, respectively. See Supplementary Appendices B–D for its derivation and more detailed discussions of the economic model.4
It is worth re-emphasizing that the decision-maker in each social-ecological community focuses only on conditions in that social-ecological community. They do not take into account the harvest of species in other patches, nor is there trade of harvested resources among social-ecological systems. Decision-makers also take the dispersal of species between communities as given and at a constant proportion. Thus the harvest regime in a particular community is optimal only with respect to conditions in that community. Any impacts that local decisions have on other communities are ‘external effects’ of those decisions. This is in contrast to the aggregate social-planner problem in which an overarching decision-maker coordinates local decisions and selects harvest rates of species across all communities to maximize aggregate system-level social welfare (Clark, 2010; Conrad and Clark, 1987). However, solving the social-planner problem requires restructuring the maximization problem in Eq. (7) and is left for future work.
We consider three preference structures: 1) people derive utility from the direct consumption of species only (provisioning services secured by harvest), 2) people derive utility from the direct consumption of species and from the non-consumptive use of aggregate biomass (provisioning services from harvest plus regulating services from standing biomass), and 3) people derive utility from the direct consumption of species and from the non-consumptive benefits of the composition of species (provisioning services from harvest plus cultural and/or regulating services from biodiversity).
We solve the general version of the maximization problem numerically in (7) using the forward-backward sweep method of Lenhart and Workman (2007). This method exploits the fact that the optimal control problem is constrained to a set of initial conditions for the state variables, and a set of terminal conditions for the co-state variables (transversality conditions)—variables accounting for the value of an extra unit of each species and the resource. Given initial conditions for species and resource biomass and an initial guess as to the harvest trajectory, the state variables are solved forward to the terminal time. Using the transversality conditions and the values of the state and control variables, the co-state variables are solved backwards to the origin. Harvest is updated, and the procedure repeated until the solution converges.5 We adopted a time horizon of 100 time steps. We allowed environmental variation to cycle with a period of 25 time steps. For a full list of parameter values, see Table 1.
Table 1. Ecological and economic model parameters.
| Ecological parameters | ||
|---|---|---|
| Variable | Value | Interpretation |
| S | 3 | Total number of species |
| M | 3 | Total number of patches (communities) |
| cij(t) | Variable [0, 0.15] | Species consumption rate of resource biomass |
| E | 0.2 | Resource to species biomass conversion efficiency |
| M | 0.2 | Natural mortality rate |
| I | 165 | Patch resource influx |
| l | 10 | Rate of resource loss |
| a | Variable [0, 1] | Species dispersal rate |
| Hi | Variable 1, 1/2, 0 | Species competition parameter |
| xj | Variable 1, 0, −1 | Environmental phase parameter |
| TF | 25 | Period of environmental variation |
| Economic parameters | ||
| Variable | Value | Interpretation |
| pij | Variable 14, 15, 16 25, 5, 1 | Price per unit species harvested |
| q | 0.2 | Efficiency of harvest effort |
| w | Variable 45, 65 | Cost per unit of species harvest |
| αij | Variable [0, 1.5] | Marginal social benefits of species abundance |
| βj | Variable [0, 50] | Social benefits of biodiversity |
| Δ | 0.01 | Discount rate |
| T | 100 | Terminal time |
Note that “ij” indicates species i on patch j where i = 1, 2, 3 and j = 1, 2, 3.
4. Results
We present our findings as a progression–reporting the results of models of increasing complexity. We begin by describing the behavior of the system without people. This most closely tracks the case discussed by Loreau et al. (2003) and Gonzalez et al. (2009). We then present the results of the bioeconomic model, starting with the case in which all species respond to environmental conditions in the same way, and concluding with the case in which all species are different. Our results are summarized in Table 2.
Table 2. Summary of results.
| Species | Benefits | Dispersal | Prices between patches | Result |
|---|---|---|---|---|
| Same Hi = 1/2 | Harvest | No | – | • Harvest of all species. • Suppression of lesser valued species. |
| Harvest abundance | No | – | • Harvest declines with benefits from abundance. • If benefits from abundance greatly exceed benefits from harvest, then harvest ceases. |
|
| Harvest biodiversity | No | – | • As benefits from biodiversity increase, species are harvested to maintain more even abundances. • Levels of biomass depend on the set of relative prices. |
|
| Harvest | Yes | Same | • Quantity and evenness of species harvested increases with dispersal. • Diversity increases with dispersal. |
|
| Harvest | Yes | Different | • Harvest rates for each species converge at intermediate dispersal, then diverge at high dispersal. • Quantity of species harvested increases with dispersal. • Diversity maximized at intermediate dispersal. |
|
| Different Hi = 1, 1/2, 0 | Harvest | Yes | Same | • At low (high) dispersal, the generalist (least valuable) species dominates. • Diversity maximized at intermediate dispersal. |
| Harvest | Yes | Different | • At low dispersal, the generalist species dominates. • Initial suppression of species increase with dispersal, leading to greater coexistence but lower biomass. • Diversity increases with dispersal. |
4.1. Dispersal in the absence of human predation
Our baseline is a system without humans. The main finding of Loreau et al. (2003) and Gonzalez et al. (2009) is that intermediate rates of species dispersal between communities maximize community-level (local) and metacommunity-level (global) biodiversity, productivity, and stability. At low dispersal rates, each community functions as a separate closed system, and the species with the highest initial consumption rate competitively excludes all others. At high dispersal rates, the system functions as a single community and the species with the highest average consumption rate dominates. At intermediate dispersal rates immigration maintains local biodiversity while preserving global biodiversity and maximizing ecological productivity and stability of productivity.
We assume the same structure of three communities in the coupled system, each composed of three species. The species with the greatest average consumption rate in each community and across all three communities (the "generalist" species) competitively excluded other species in the system regardless of the natural dispersal rate. This is because populations of the generalist species were never driven down enough in adverse environmental conditions to prevent them from suppressing other species under favorable environmental conditions.
4.2. No dispersal—harvest of functionally identical species for consumptive and non-consumptive benefits in isolated communities
We next considered the impact of anthropogenic predation or harvest in each community without dispersal. All species within each patch were assumed to be functionally identical. All species experienced the same response to environmental conditions and possessed the same resource consumption rate curves. We present results for Hi = 1/2 for i = 1, 2, 3. See Supplementary Appendix E for the outcomes under other species competition parameters and environmental conditions. We take three cases.
4.2.1. Case 1: harvest for consumptive benefits
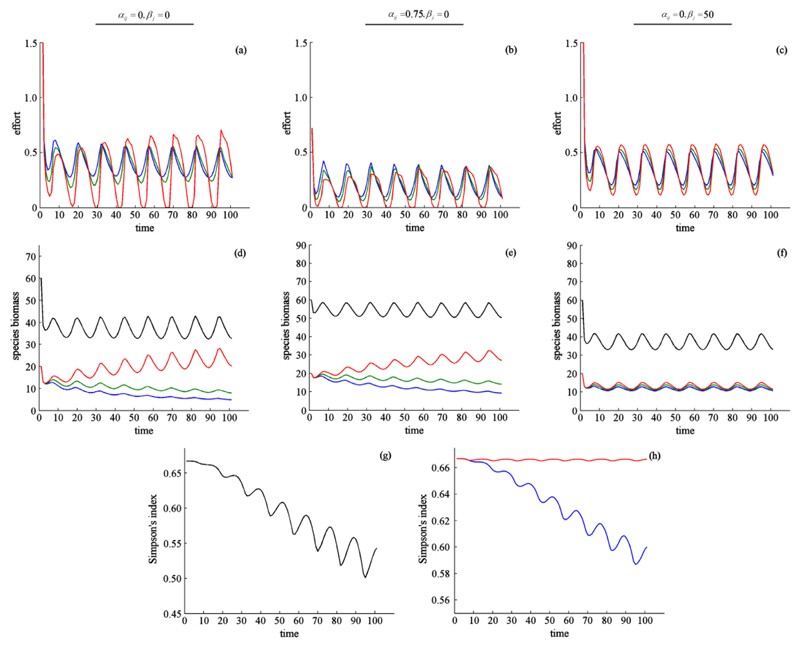
When benefits were obtained solely through species harvest (pij > 0; αij, βj = 0), managers initially drove the stock to its equilibrium value by setting harvest effort to the maximum. Managers then maintained the equilibrium stock via harvest effort at the singular solution, which fluctuated over time by species and patch. In our case the equilibrium was a stationary cycle that oscillated deterministically according to a sine function. As in other studies of stochastic (Clark, 1976; Parma, 1990; Reed, 1979) and fluctuating (Carson et al., 2009; Costello et al., 1998; Costello et al., 2001) growth rates, we found that species harvest rates fluctuated with species consumption rates, with more valuable species being extracted at higher rates than less valuable species (Fig. 2a; Supplementary Appendix G).
Fig. 2.
Effect of harvest price when benefits are obtained from harvest only (a, d), harvest and abundance (b, e), and harvest and the mix of species (c, f). Harvest effort (a–c), species biomass (d-f), and biodiversity (g, h). In (a–f) color indicates harvest effort and species biomass for species 1 (red, highest harvest price), species 2 (green), and species 3 (blue, lowest harvest price). Black shows aggregate species biomass. In (g, h) color indicates the types of benefits: harvest only (black), harvest and abundance (blue), harvest and the mix of species (red). Note the difference in the y-axes in (g) and (h). The dynamics when benefits are derived solely from harvest take longer to reach equilibrium than when benefits are also derived from abundance and the mix of species, or when the system is coupled via dispersal. For the sake of comparison we present results for a 100 step time horizon here (a, d, g). We present results for a longer timescale in Supplementary Appendix G. The dynamics follow the same trajectory as here, saturating and settling into a persistent, fluctuating equilibrium. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
In choosing the level of harvest, managers balanced current net benefits of harvest against the benefits of future harvests. Since species compete for resources within the ecological community, managers suppressed less valuable species in order to relieve competitive pressure on more valuable species. This effect involved a high initial pulse of harvest that drove down the biomass of all species, but particularly the biomass of the least valued species. The result was that abundance of the least valued species was reduced, and abundance of the more valued species was increased (Fig. 2d; Supplementary Appendix G). The lower the price of a species, the greater its initial suppression. See Supplementary Appendix F for examples when the price is low or negative (a pest species).
While suppression of the less valued species increased growth of the most profitable species, it also reduced biodiversity (Fig. 2g; Supplementary Appendix G). Biodiversity, as measured by a Simpson’s index, declined and became more variable over time. As less profitable species were suppressed, fluctuations in the proportion of species biomasses reside increasingly in the single, most profitable species.
4.2.2. Case 2: harvest for consumptive and non-consumptive benefits (abundance)
If people derived benefits from both harvest (a flow benefit) and abundance (a stock benefit) (pij, αij > 0; βj = 0), managers harvested less at lower rates and more evenly across species (Fig. 2b, e; Supplementary Appendix G), and biodiversity increased (Fig. 2h). As stock benefits exceeded market prices, species became more valuable if left in the "wild" than for consumption. Holding harvest price constant and increasing αij resulted in the aggregate benefit of all species approaching the same value. Managers maximized net benefits by balancing the marginal net benefits of harvesting and abundance - which depends on the ratio of pij to αij. A given species was harvested only if harvest benefits exceeded abundance benefits, and harvest decreased when a species was valued for other, non-consumptive benefits (Hartman, 1976). If a desirable species was threatened by competitive exclusion, and the benefits from suppressing the competing species exceeded benefits from its abundance, then the competing species would be suppressed.
4.2.3. Case 3: harvest for consumptive and non-consumptive benefits (biodiversity)
When people derived benefits both from harvest and from the mix of species (pij, βj > 0; αij = 0), we found that harvest effort resulted in an even distribution of species abundances (Fig. 2c, f; Supplementary Appendix G). The Simpson’s biodiversity index increased with the benefits from biodiversity, though differences were found to be negligible at high values of βj (Fig. 2h; Supplementary Appendix G). While the most desirable species stock was maintained at a higher level than other species, we did not observe suppression of less valuable species.
4.3. Dispersal—harvest of functionally identical species for consumptive benefits
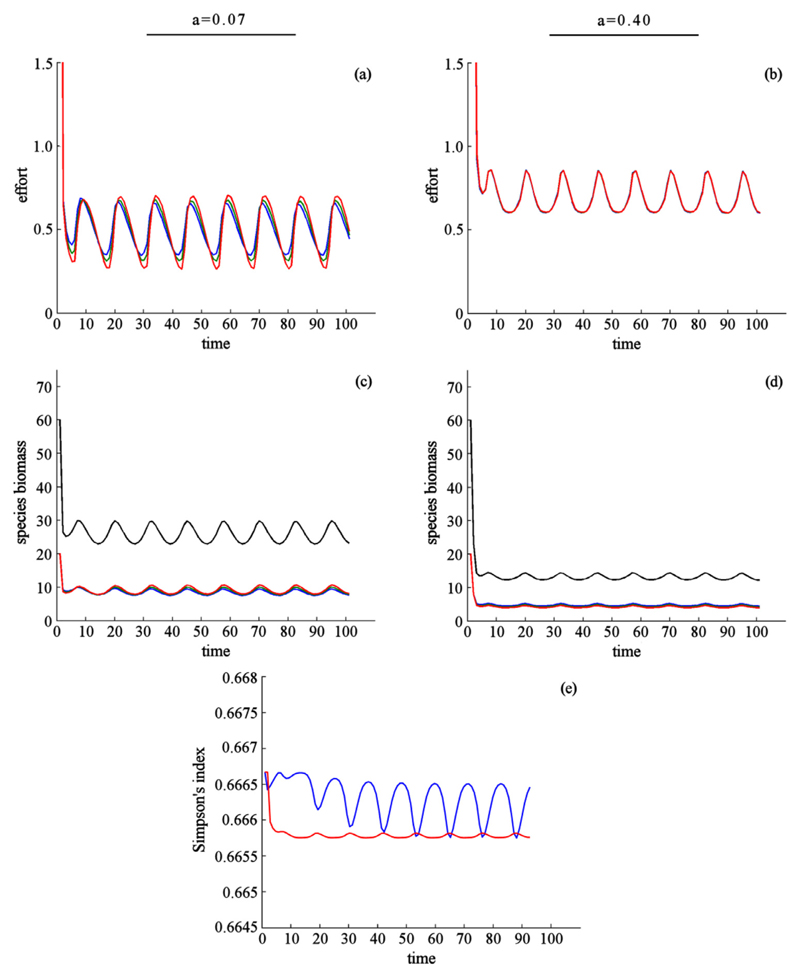
Beyond the baseline we considered two additional scenarios. In the first we assumed species in the different communities to be functionally identical, and explored the implications of uniform and non-uniform preferences over species. If preferences are uniform, the value of each species is identical across communities (pi,1 = pi,2 = pi,3 for all i). This means that in the absence of dispersal, each community would harvest species in the same fashion. Differing environmental conditions affect fluctuations in species biomass but not harvest decisions (Supplementary Appendix E). In the presence of dispersal, optimal harvest patterns change. As dispersal rates increase we observed a shift in harvest away from the suppression of less valuable species and towards identical harvest rates for all species (Fig. 3a, b). As a consequence, species populations converged to similar levels of biomass (Fig. 3c, d). As expected the Simpson’s index also increased with dispersal (Fig. 3e). The increase in harvest with dispersal is due to the fact that the marginal benefits of conserving species falls with the inflow of species—which is taken as exogenous in the harvest regime. Since managers fail to internalize the effects that their harvest decisions have on other communities, harvest drives down the size of breeding stocks retained in each community limiting local growth in each community.
Fig. 3.
Effect of dispersal when species have identical ecological parameters, benefits are obtained through harvest only, and preferences for species are identical across patches. Environmental conditions differ between patches. Harvest effort (a, b), species biomass (c, d), and biodiversity (e). In (a–d) dispersal rate is indicated by column: a = 0.07(a, c), and a = 0.40(b, d). Color indicates harvest effort and species biomass for species 1 (red, highest harvest price), species 2 (green), and species 3 (blue, lowest harvest price). Black shows aggregate species biomass. In (e) color indicates the dispersal rate: intermediate (blue, a = 0.07), high (red, a = 0.40). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
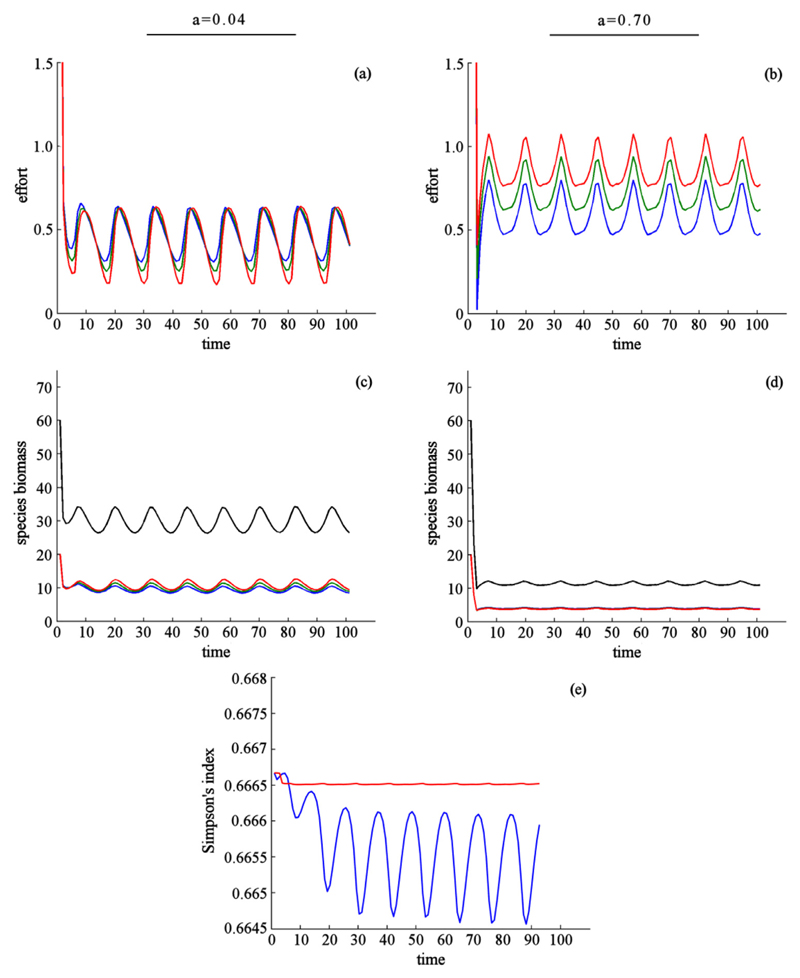
If preferences are not uniform, species are valued differently in each community. That is, the set of relative prices for each unit of species harvested varied between communities (pi, 1 ≠ pi, 2 ≠ pi, 3 for all i). The most highly valued species in one community was taken to be the least valued in another. Harvest regimes, and by extension the abundance of species, differed between communities. At low and intermediate dispersal rates, we found the same harvest strategies as when preferences for species were the same between patches (Fig. 4a, c). However, at high dispersal rates, we found a strong effect on harvest. The greater the rate of dispersal between communities, the stronger the source-sink effect—the rate at which depleted populations were replenished. This additional biomass was harvested depending on its relative value: the highest valued species being harvested the most, the lowest valued being harvested the least (Fig. 4b, d). The Simpson’s index was maximized at an intermediate dispersal rate, although the difference in the index "over the hump" was found to be negligible (Fig. 4e).
Fig. 4.
Effect of dispersal when species have identical ecological parameters, benefits are obtained through harvest only, and preferences for species differ across patches. Environmental conditions differ between patches. Harvest effort (a, b), species biomass (c, d), and biodiversity (e). In (a-d) dispersal rate is indicated by column: a = 0.04(a, c), and a = 0.70(b, d). Color indicates harvest effort and species biomass for species 1 (red, highest harvest price), species 2 (green), and species 3 (blue, lowest harvest price). Black shows aggregate species biomass. In (e) color indicates the dispersal rate: intermediate (blue, a = 0.04), high (red, a = 0.70). Results are presented for patch 1. Other patches are symmetric with respect to the preferences for each species. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4.4. Dispersal—harvest of functionally different species for consumptive benefits
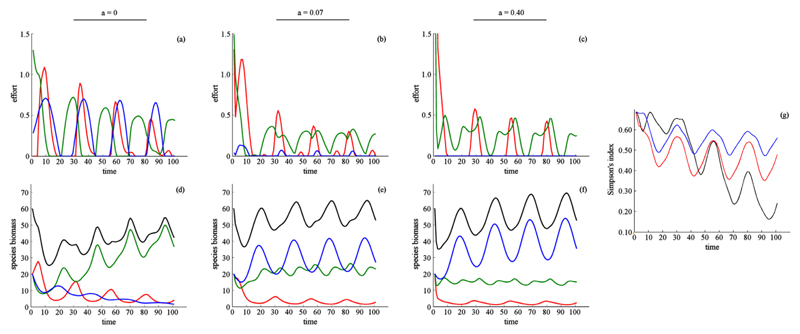
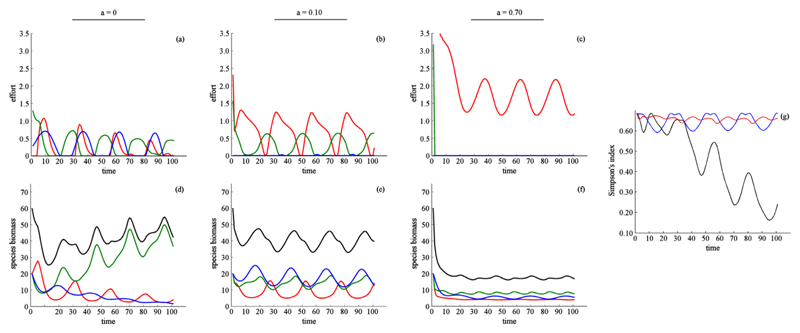
In our second scenario we assumed all species within each community to be functionally unique and to respond to environmental conditions differently (H1 = 1; H2 = 1/2;H3 = 0, Fig. 1). We further assumed all species to be positively valued (pij > 0) for their consumptive benefits only, and again explored the implications of uniform and non-uniform preferences over species. Recall that in the absence of harvest the generalist species, or the species with the highest average consumption rate, dominates the system. At low rates of dispersal, we found that the combination of harvest and competition allowed the generalist species to dominate the system even if it was the least valued (Figs. 5d and 6d).
Fig. 5.
Effect of dispersal when species have different ecological parameters, benefits are obtained through harvest only, and preferences for species are identical between patches. Environmental conditions are the same across patches. Harvest effort (a–c), species biomass (d–f), and biodiversity (g). In (a–f) dispersal rate is indicated by column: a = 0(a, d), a = 0.07(b, e), and a = 0.40(c, f). Color indicates harvest effort and species biomass for species 1 (red, highest harvest price), species 2 (green), and species 3 (blue, lowest harvest price). Black shows aggregate species biomass. In (g) color indicates the dispersal rate: low (black, a = 0), intermediate (blue, a = 0.07), high (red, a = 0.40). For visualization we present results with a 100 step time horizon. At longer timescales the dynamics follow the same trends and trajectories (Supplementary Appendix G). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 6.
Effect of dispersal when species have different ecological parameters, benefits are obtained through harvest only, and preferences for species differ between patches. Environmental conditions differ across patches. Harvest effort (a–c), species biomass (d–f), and biodiversity (g). In (a–f) dispersal rate is indicated by column: a = 0(a, d), a = 0.10(b, e), and a = 0.70(c, f). Color indicates harvest effort and species biomass for species 1 (red, highest harvest price), species 2 (green), and species 3 (blue, lowest harvest price). Black shows aggregate species biomass. In (g) color indicates the dispersal rate: low (black, a = 0), intermediate (blue, a = 0.10), high (red, a = 0.70). Results are presented for patch 1. Other patches are symmetric with respect to the preferences for each species. For visualization we present results with a 100 step time horizon. At longer timescales the dynamics follow the same trends and trajectories (Supplementary Appendix G). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
As before, we first considered the case where preferences for species were the same across communities (pi,1 = pi,2 = pi,3 for all i). In this case, increasing dispersal rates caused harvest to decline, particularly for the least valued species (Fig. 5a–c). The most valued species were heavily harvested, while the generalist species were partially suppressed. What is particularly interesting is that at intermediate dispersal rates harvest relieved competitive pressure on the least valued species, allowing for a more even distribution of species abundances. However, at high dispersal rates the least valuable species was able to dominate the system (Fig. 5d–f).
Harvest and abundance were jointly determined by harvest price and species growth. These in turn depended on resource consumption, harvest and dispersal (mortality is held constant). When multiple species are considered, competitive pressure from the generalist species plays a large role in determining abundances. The effect of harvest is twofold. Harvest can suppress highly competitive species but can also place additional pressure on species biomass. In our case, the least valuable species was not valuable enough to be harvested, nor are the benefits great enough to justify suppression. In contrast, the generalist species was harvested for its benefits and, particularly at high dispersal rates, suppression.
Biodiversity measured by a Simpson’s index first rose and then fell due to two shifts in the ratio of species abundances (Fig. 5g). At low dispersal rates generalist species dominated. At intermediate dispersal rates the least valuable species and the generalist species coexisted. At high dispersal rates the least valuable species dominated.
We finally considered the case where preferences for species were different between patches. In particular, species 1 was assumed to be the highest valued species in patch 1, species 2 the highest valued species in patch 2, and species 3 the highest valued species in patch 3. We found that as dispersal rates increased, harvest increased in the most valuable species. For the less valuable species, we observed two simultaneous shifts in harvest. Specifically, we observed declining rates of pulsed (on-off) harvest, and increasing rates of initial suppression. After the initial suppression, competition and dispersal maintained a more even ratio of species abundances (Fig. 6a–f), implying that biodiversity, as measured by the Simpson’s index, increased with dispersal (Fig. 6g). However, aggregate species biomass declined as the metacommunity became more connected (Figs. 6d–f).
5. Discussion
In ecological systems without people, the spatial insurance hypothesis predicts a non-monotonic relationship between biodiversity and dispersal (Gonzalez et al., 2009; Loreau et al., 2003; Mouquet and Loreau, 2003). However, in a social-ecological system the effect of dispersal on biodiversity depends only partly on the competitive interactions between species. Just as important is the structure of human preferences for species within and across locations. Since the structure of preferences determines the rate at which each species is harvested, it also determines relative abundances. The consequence is that background species dispersal plays a different role than it does in a pure ecological model. Specifically, we found that biodiversity increased monotonically with dispersal either if species possessed the same ecological competition parameters and preferences were identical across communities, or if species possessed different ecological competition parameters and preferences were different across communities. Biodiversity was maximized at intermediate dispersal rates only if ecological competition parameters and preferences were different between communities.
The difference between our findings and those that bound the system in a way that excludes humans is due to the non-random pressure harvest places on particular species. Indeed, what determines the relative abundances of species in a social-ecological system are the interactions between competition, dispersal, and harvest. If people elect to specialize in the consumption of a single highly-valued species, then dispersal of competitors is undesirable. Indeed, this is often the case in agriculture where people select for particular crops in monocultures and competitors (weeds) are controlled. The rate at which any one species is harvested depends on the relative value of the benefits it offers. If only the direct benefits from consumption are considered, we frequently observe the suppression of less valuable species—a specialization effect of the sort identified by Brock and Xepapadeus (2002). Other joint-harvest models have found that extirpation of the least valuable species may be privately optimal (Clark, 1973; Hilborn, 1976; Mesterton-Gibbons, 1996), particularly if the manger can sufficiently target the low or negatively valued species (Fenichel and Horan, 2007b; Fenichel and Horan, 2016). In contrast, considering benefits other than direct consumption leads to the preservation of species (Bertram and Quaas, 2016).
If people’s preferences are for services supported by aggregate biomass, such as carbon sequestration, or for services supported by the diversity of species in the system (e.g. the regulation of soil erosion or water quality), then the degree of connectivity that leads to the greatest biodiversity is less clear. In practice, species deliver a mix of benefits depending of their traits and abundances. These characteristics determine the degree to which different species are complements or substitutes in the provision of ecosystem services. System management in such cases reflects the ecological interactions between species, and species dispersal from other locations can either be beneficial or harmful. In cases where a species might not naturally persist, dispersal can either accelerate or slow the process. Whether dispersal is beneficial or not then depends on the value attached to the various services that such a species provides.
One of the stylized facts reflected in this paper is that resource managers in each community do not consider the effects of dispersal to other communities. The impacts of their decisions on other communities are ’external effects’ of those decisions (Bird, 1987; Brock and Xepapadeus, 2010; Fenichel et al., 2014; Shogren and Crocker, 1991; Smith et al., 2009). By changing the abundance of species in each community, resource managers determine the rate at which those species disperse to other communities, but ignore the consequences of this. This allows us to explore the unanticipated effects of dispersal. These effects may be positive or negative. Mass and rescue effects (Brown and Kodric-Brown, 1977; Shmida and Wilson, 1985) can prevent extinction of at-risk species, and source-sink effects can maintain spatially distinct populations of species (Holt, 1985; Pulliam, 1988), but these effects are only a benefit if the target populations are positively valued. There are certainly empirical examples of dispersal replenishing depleted but valuable stocks (Brown and Roughgarden, 1997; Sanchirico and Wilen, 1999), and the relation between harvest and the dispersal of harvested species is one of the main motivations for establishing marine protected areas (Gell and Roberts, 2003; Lubchenco et al., 2003) or wildlife management areas (Johannesen and Skonhoft, 2005; Schulz and Skonhoft, 1996). There are also empirical examples of dispersal causing changes in species composition and/or ecosystem dynamics (Chisholm, 2012; Ehrenfeld, 2010; McKinney and Lockwood, 1999; Rhymer and Simberloff, 1996b). The dispersal of non-native species, for example, is argued to be among the greatest threats to local biodiversity (Gurevitch and Padilla, 2004; Sax and Gaines, 2008). From an economic perspective it could be a form of "biological pollution" with potentially harmful species damaging valued species through either predation or competition (Horan et al., 2002). Whether dispersal has positive or negative effects for the social system therefore depends on the social value attaching to the species impacted by it.
If resource managers in each community take no account of the effects of their decisions on others, their actions may harm the metacommunity as a whole. In such cases there notionally exists an aggregate social-planner problem in which an overarching decision-maker, possessing perfect information about the states of the world, coordinates local decision-makers and selects harvest rates of species across all communities to maximize aggregate system-level social welfare (Clark, 2010; Conrad and Clark, 1987). The role of the ecological analysis is then to identify the cross-community consequences of dispersal, and hence provide the scientific basis for developing corrective measures to protect the public interest.
There are many possible extensions to the model including solving the aggregate social-planner problem or allowing decision-makers to take account of the states of other patches. Decision-makers could also form coalitions, cooperating to jointly maximize the benefits of their group. By eliminating the externality of species dispersal a social planner will provide the highest social welfare. Increasing coordination between decision-makers or information on the states of other patches will increase welfare compared to our baseline case, though it will be second best to the social planner. Further, while we only considered benefits from harvest with species dispersal, there are many extensions regarding the types and distribution of preferences across the metacommunity.
The relationship between dispersal and the pattern of species diversity in a social-ecological system depends both on the competitive interactions between species, and the preferences that determine human interventions in the system. In many real systems, the central driver of anthropogenic biodiversity change is the production of foods, fuels, and fibers from a limited set of plants and domesticated animals. This has led to a reduction in species diversity, and with it the capacity of the system to accommodate changing environmental conditions. In the language of the Millennium Ecosystem Assessment, it has led to a reduction in the buffering or regulating services (Millennium Ecosystem Assessment, 2005; Perrings, 2014). In this paper, we see the same effect when the resource-manager values only the consumptive benefits of individual species. As in real systems, the effect is the result of feedbacks between the values that determine harvest, and the dynamic interactions between harvested species. The scientific challenge is to bring feedbacks of this kind into the analysis of ecosystem dynamics in a routine way. We have focused on dispersal as one of the main drivers of ecological change, but the point applies to all anthropogenic stressors equally. Our results, for example, imply that accounting for only ecological and environmental conditions is insufficient to accurately predict community assemblages in response to climate change. Modeling ecological dynamics in the Anthropocene requires that human behavior be integrated into the analysis of species interactions more generally.
Supplementary Material
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.jtbi.2018.08.041.
Acknowledgements
Authors acknowledge financial support from NSF grant 1414374 as part of the joint NSF-NIH-USDA Ecology and Evolution of Infectious Diseases program, and the United Kingdom Biotechnology and Biological Sciences Research Council grant BB/M008894/1. DWS and ML were supported by the BIOSTASES Advanced Grant, funded by the European Research Council under the European Union’s Horizon 2020 Research and Innovation Programme (grant agreement number 666971). DWS, JC, and ML were supported by the TULIP Laboratory of Excellence (ANR-10-LABX-41).
Footnotes
We would expect our results to hold in a time-invariant environment, e.g. in the absence of temporal variability in environmental conditions. Loreau et al. (2003) and Gonzalez et al. (2009) use temporal variability in species biomass as a mechanism for local species coexistence, sensu the paradox of the plankton (Hutchinson, 1961). However, other models of the intermediate dispersal hypothesis find non-monotonic relationships between biodiversity and dispersal in systems where species growth rates are held constant (Haegeman and Loreau, 2014; Haegeman and Loreau, 2015; Wang and Loreau, 2016).
Our choice of harvest function assumes perfect targeting of species - a standard assumption in the literature (Clark, 2010; Conrad and Clark, 1987). In reality managers face problems with imperfect selection. For example, in fisheries different types of fishing practices - hook lines, nets, or trawling - result in different rates of by-catch (the capture of non-target species) (Davies et al., 2009; Hall et al., 2000). This means that the effect of harvest between species need not always be independent, e.g. the harvest of one species may directly affect the abundance of another species. In general this idea is treated implicitly. For example, in a fisheries context Abbott and Wilen (2009) utilize a separate function to account for by-catch in setting stock quotas. Mesteron-Gibbons (1988), Fenichel and Horan (2007), and Fenichel et al. (2010) explicitly take into account the indirect effects of harvesting one or more interacting species in predator-prey, host-pathogen, and invasive species contexts. Traditional optimal control problems in economics generally assume the existence of control variables for each state variable and that each control variable perfectly controls a different state variable at every moment in time (Conrad and Clark, 1987; Clark, 2010). Violating this assumption results in an ‘imperfect control’, which has been shown to lead to complex feedback rules for efficient management (Fenichel et al., 2010; Fenichel et al., 2011; Fenichel and Horan, 2007; Horan and Wolf, 2005). Indeed, in our context relaxing this assumption will result in a complex interplay between ecological, economic, and spatial dynamics to determine the relationship between biodiversity and dispersal. We leave this for future work.
The Simpson’s index can be interpreted as the probability that two individuals selected at random with replacement from a population will not belong to the same type. A number of indices exist to measure biodiversity, many of which are strongly correlated (Bandeira et al. 2013). See Humphries et al. (1995) for a review of diversity metrics used in conservation ecology. In using a Simpson’s index, as opposed to species richness, we assert that people value species abundances as well as species presence or absence.
Note that the singular solution in [9] is a simplification. Due to the complex nature of the problem, we assume a global interior solution of the state variables. We evaluate the validity of this assumption in Appendices C and D.
The system of equations was solved numerically using a 4th order Runge-Kutta ODE estimator with an adjustable step size. It should be noted that this estimator allows for infinitely small population sizes. A species population will never reach zero and be extirpated from the patch or system. Further, a species cannot be eradicated by harvest because of the nature of the Schaefer harvest function.
References
- Abbott JK, Wilen JE. Regulation of fisheries bycatch with common-pool output quotas. J Environ Econ Manage. 2009;57:195–204. [Google Scholar]
- Amarasekare P, Nisbet RM. Spatial heterogeneity, source-sink dynamics, and the local coexistence of competing species. Am Nat. 2001;158:572–584. doi: 10.1086/323586. [DOI] [PubMed] [Google Scholar]
- Bandeira B, Jamet JL, Jamet D, Ginoux JM. Mathematical converges of biodiversity indices. Ecol Indic. 2013;29:522–528. [Google Scholar]
- Barbier EB. Valuing ecosystem services as productive inputs. Econ Policy. 2007;22:179–229. [Google Scholar]
- Bertram C, Quaas MF. Biodiversity and optimal multi-species ecosystem management. Environ Resour Econ. 2016 Online First. [Google Scholar]
- Bird PJWN. The transferability and depletability of externalities. J Environ Econ Manage. 1987;14:54–57. [Google Scholar]
- Brock W, Xepapadeus A. Optimal ecosystem management when species compete for limiting resources. J Environ Econ Manage. 2002;44:189–220. [Google Scholar]
- Brock W, Xepapadeus A. Pattern formation, spatial externalities and regulation in coupled economic-ecological systems. J Environ Econ Manage. 2010;59:149–164. [Google Scholar]
- Brown G, Roughgarden J. A metapopulation model with private property and a common pool. Ecol Econ. 1997;22:65–71. [Google Scholar]
- Brown JH, Kodric-Brown A. Turnover rates in insular biogeography: effect of immigration on extinction. Ecology. 1977;58:445–449. [Google Scholar]
- Cadotte MW. Dispersal and species diversity: a meta-analysis. Am Nat. 2006;167:913–924. doi: 10.1086/504850. [DOI] [PubMed] [Google Scholar]
- Cadotte MW, Fukami T. Dispersal, spatial scale, and species diversity in a hierarchically structured experimental landscape. Ecol Lett. 2005;8:548–557. doi: 10.1111/j.1461-0248.2005.00750.x. [DOI] [PubMed] [Google Scholar]
- Cadotte MW, Fortner AM, Fukami T. The effects of resource enrichment, dispersal, and predation on local and metacommunity structure. Oecologia. 2006;149:150–157. doi: 10.1007/s00442-006-0426-z. [DOI] [PubMed] [Google Scholar]
- Carson RT, Granger CWJ, Jackson JBC, Schlenker W. Fisheries management under cyclical population dynamics. Environ Resour Econ. 2009;42:379–410. [Google Scholar]
- Chisholm R. The ecology, economics, and management of alien invasive species. In: Levin S, editor. Princeton Guide to Ecology. Princeton University Press; Princeton, New Jersey: 2012. [Google Scholar]
- Clark CW. The economics of overexploitation. Science. 1973;181:630–634. doi: 10.1126/science.181.4100.630. [DOI] [PubMed] [Google Scholar]
- Clark CW. A delayed-recruitment model of population dynamics, with an application to baleen whale populations. J Math Biol. 1976;3:381–391. doi: 10.1007/BF00275067. [DOI] [PubMed] [Google Scholar]
- Clark CW. Mathematical Bioeconomics: The Mathematics of Conservation. John Wiley & Sons, Inc; Hoboken, New Jersey: 2010. [Google Scholar]
- Conrad JM, Clark CW. Natural Resource Economics: Notes and Problems. Cambridge University Press; 1987. [Google Scholar]
- Costello C, Adams RM, Polasky S. The value of El Nino forecasts in the management of salmon: a stochastic dynamic assessment. Am J Agricult Econ. 1998;80:765–777. [Google Scholar]
- Costello C, Polasky S, Solow A. Renewable resource management with environmental prediction. Can J Econ. 2001;1:196–211. [Google Scholar]
- Costello C, Springborn M, McAusland C, Solow A. Unintended biological invasions: does risk vary by trading partner? J Environ Econ Manage. 2007;54:262–276. [Google Scholar]
- Crutzen PJ, Stoermer EF. The "Anthropocene". Int Geosphere-Biosphere Programme Newslett. 2000;41:17–18. [Google Scholar]
- Dalmazzone S. Economic factors affecting vulnerability to biological invasions. In: Perrings C, editor. The Economics of Biological Invasions. Edward Elgar; Cheltenham, United Kingdom: 2000. pp. 17–30. [Google Scholar]
- Davies RWD, Cripps SJ, Nickson A, Porter G. Defining and estimating global marine fisheries bycatch. Mar Policy. 2009;33:661–672. [Google Scholar]
- Ehrenfeld JG. Ecosystem consequences of biological invasions. Annu Rev Ecol Evol Syst. 2010;41:59–80. [Google Scholar]
- Fenichel EP, Horan RD. Jointly-determined ecological thresholds and economic trade-offs in wildlife disease management. Nat Resour Model. 2007a;20:511–547. [Google Scholar]
- Fenichel EP, Horan RD. Gender-based harvesting in wildlife disease management. Am J Agricult Econ. 2007b;89:904–920. [Google Scholar]
- Fenichel EP, Horan RD. Tinbergen and tipping points: could some thresholds be policy-induced? J Econ Behav Organ. 2016;132:137–152. [Google Scholar]
- Fenichel EP, Horan RD, Bence JR. Indirect management of invasive species with biocontrol: a bioeconomic model of salmon and alewife in Lake Michigan. Resour Energy Econ. 2010;32:500–518. [Google Scholar]
- Fenichel EP, Richards TJ, Shanafelt DW. The control of invasive species on private property with neighbor-to-neighbor spillovers. Environ Resour Econ. 2014;59:231–255. doi: 10.1007/s10640-013-9726-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenichel EP, Castillo-Chavez C, Ceddia MG, Chowell G, Gonzalez Parra PA, Hickling GJ, Holloway G, Horan R, Morin B, Perrings C, Springborn M, et al. Adaptive human behavior in epidemiological models. Proc Natl Acad Sci. 2011;108:6306–6311. doi: 10.1073/pnas.1011250108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Futuyma DJ, Moreno G. The evolution of ecological specialization. Annu Rev Ecol Evol Syst. 1988;19:207–233. [Google Scholar]
- Gell FB, Roberts CM. Benefits beyond boundaries: the fishery effects of marine reserves. Trends Ecol Evol. 2003;18:448–455. [Google Scholar]
- Gilbert F, Gonzalez A, Evans-Freke I. Corridors maintain species richness in the fragmented landscapes of a microecosystem. Proc R Soc Lond Ser B Biol Sci. 1998;265:577–582. [Google Scholar]
- Gonzalez A, Chaneton EJ. Heterotroph species extinction, abundance and biomass dynamics in an experimentally fragmented microecosystem. J Anim Ecol. 2002;71:594–602. [Google Scholar]
- Gonzalez A, Mouquet N, Loreau M. Biodiversity as spatial insurance: The effects of habitat fragmentation and dispersal on ecosystem functioning. In: Naeem S, editor. Biodiversity, Ecosystem Functioning, and Human Wellbeing et a. Oxford University Press; 2009. [Google Scholar]
- Gonzalez A, Lawton JH, Gilbert FS, Blackburn TM, Evans-Freke I. Metapopulation dynamics, abundance, and distribution in a microecosystem. Science. 1998;281:2045–2047. doi: 10.1126/science.281.5385.2045. [DOI] [PubMed] [Google Scholar]
- Gurevitch J, Padilla DK. Are invasive species a major cause of extinctions? Trends Ecol Evol. 2004;19:470–474. doi: 10.1016/j.tree.2004.07.005. [DOI] [PubMed] [Google Scholar]
- Haegeman B, Loreau M. General relationships between consumer dispersal, resource dispersal and metacommunity diversity. Ecol Lett. 2014;17:175–184. doi: 10.1111/ele.12214. [DOI] [PubMed] [Google Scholar]
- Haegeman B, Loreau M. A graphical-mechanistic approach to spatial resource competition. Am Nat. 2015;185:E1–E13. doi: 10.1086/679066. [DOI] [PubMed] [Google Scholar]
- Hall MA, Alverson DL, Metuzals KI. By-catch: problems and solutions. Mar Pollut Bull. 2000;41:204–219. [Google Scholar]
- Hanspach J, Kuhn I, Pysek P, Boos E, Klotz S. Correlates of naturalization and occupancy of introduced ornamentals in Germany. Persp Plant Ecol Evol Syst. 2008;10:241–250. [Google Scholar]
- Hartman R. The harvest decision when a standing forest has value. Econ Inq. 1976;14:52–58. [Google Scholar]
- Hilborn R. Optimal exploitation of multiple stocks by a common fishery: a new methodology. J Fish Res Board Can. 1976;33:1–5. [Google Scholar]
- Holt RD. Population dynamics in two-patch environments: some anomalous consequences of an optimal habitat distribution. Theor Popul Biol. 1985;28:181–208. [Google Scholar]
- Holyoak M. Habitat subdivision causes changes in food web structure. Ecol Lett. 2000;3:509–515. [Google Scholar]
- Horan RD, Wolf CA. The economics of managing infectious wildlife disease. Am J Agricult Econ. 2005;87:537–551. [Google Scholar]
- Horan RD, Perrings C, Lupi F, Bulte EH. Biological pollution prevention strategies under ignorance: the case of invasive species. Am J Agricult Econ. 2002;84:1303–1310. [Google Scholar]
- Horan RD, Fenichel EP, Drury KLS, Lodge DM. Managing ecological thresholds in coupled environmental-human systems. Proc Natl Acad Sci. 2011;108:7333–7338. doi: 10.1073/pnas.1005431108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howeth JG, Leibold MA. Species dispersal rates alter diversity and ecosystem stability in pond metacommunities. Ecology. 2010;91:2727–2741. doi: 10.1890/09-1004.1. [DOI] [PubMed] [Google Scholar]
- Hulme PE. Trade, transport and trouble: managing invasive species pathways in an era of globalization. J Appl Ecol. 2009;46:10–18. [Google Scholar]
- Hutchinson GE. The paradox of the plankton. Am Nat. 1961;95:137–145. [Google Scholar]
- Johannesen AB, Skonhoft A. Tourism, poaching and wildlife conservation: what can integrated conservation and development projects accomplish? Res Energy Econ. 2005;27:208–226. [Google Scholar]
- Kneitel JM, Miller TE. Dispersal rates affect species composition in meta-communities of Sarracenia purpurea inquilines. Am Nat. 2003;162:165–171. doi: 10.1086/376585. [DOI] [PubMed] [Google Scholar]
- Lenhart S, Workman JT. Optimal Control Applied to Biological Models. Chapman and Hall; 2007. [Google Scholar]
- Lenzen M, Moran D, Kanemoto K, Foran B, Lobefaro L, Geschke A. International trade drives biodiversity threats in developing nations. Nature. 2012;486:109–112. doi: 10.1038/nature11145. [DOI] [PubMed] [Google Scholar]
- Lewis SL, Maslin MA. Defining the anthropocene. Nature. 2015;519:171–180. doi: 10.1038/nature14258. [DOI] [PubMed] [Google Scholar]
- Liu J, Dietz T, Carpenter SR, Alberti M, Folke C, Moran E, Pell AN, Dadman D, Kratz T, Lubchenco J, Ostrom E, et al. Complexity of coupled human and natural systems. Science. 2007;317:1513–1516. doi: 10.1126/science.1144004. [DOI] [PubMed] [Google Scholar]
- Loreau M, Mouquet N. Immigration and the maintenance of local species diversity. Am Nat. 1999;154:427–440. doi: 10.1086/303252. [DOI] [PubMed] [Google Scholar]
- Loreau M, Mouquet N, Gonzalez A. Biodiversity as spatial insurance in heterogeneous landscapes. Proc Natl Acad Sci. 2003;100:12765–12770. doi: 10.1073/pnas.2235465100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lubchenco J, Palumbi SR, Gaines SD, Andelman S. Plugging a hole in the ocean: the emerging science of marine reserves. Ecol Appl. 2003;13:S3–S7. [Google Scholar]
- Mack RN, Simberloff D, Lonsdale WM, Evans H, Clout M, Bazzaz FA. Biotic invasions: causes, epidemiology, global consequences, and control. Ecol Appl. 2000;10:689–710. [Google Scholar]
- McKinney ML, Lockwood JL. Biotic homogenization: a few winners replacing many losers in the next mass extinction. Trends Ecol Evol. 1999;14:450–453. doi: 10.1016/s0169-5347(99)01679-1. [DOI] [PubMed] [Google Scholar]
- Melstrom RT, Horan RD. Managing excessive predation in a predator-en-dangered prey setting. Ecol Econ. 2013;90:85–93. [Google Scholar]
- Mesterton-Gibbons M. On the optimal policy for combining harvesting of predator and prey. Nat Resour Model. 1988;3:63–90. [Google Scholar]
- Mesterton-Gibbons M. A technique for finding optimal two-species harvesting policies. Ecol Modell. 1996;92:235–244. [Google Scholar]
- Millennium Ecosystem Assessment. Ecosystems and Human Well-Being: Biodiversity Synthesis. World Resources Institute; Washington, D.C.: 2005. [Google Scholar]
- Mouquet N, Loreau M. Community patterns in source-sink metacommunities. Am Nat. 2003;162:544–557. doi: 10.1086/378857. [DOI] [PubMed] [Google Scholar]
- Parma AM. Optimal harvesting in fish populations with non-stationary stock-recruitment relationships. Nat Resour Model. 1990;4:39–76. [Google Scholar]
- Perrings C. Our Uncommon Heritage: Biodiversity, Ecosystem Services and Human Wellbeing. Cambridge University Press; Cambridge: 2014. [Google Scholar]
- Poisot T, Canard E, Mouquet N, Hochberg ME. A comparative study of ecological specialization estimators. Methods Ecol Evol. 2012;3:537–544. [Google Scholar]
- Pulliam HR. Sources, sinks, and population regulation. Am Nat. 1988;132:652–661. [Google Scholar]
- Pyšek P, Jarošík V, Hulme PE, Kühn I, Wild J, Arianoutsou M, Bacher S, Chiron F, Didžiulis V, Essl F, Genovesi P, et al. Disentangling the role of environmental and human pressures on biological invasions across Europe. Proc Natl Acad Sci. 2010;107:12157–12162. doi: 10.1073/pnas.1002314107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed WJ. Optimal escapement levels in stochastic and deterministic harvesting models. J Environ Econ Manage. 1979;6:350–363. [Google Scholar]
- Rhymer JM, Simberloff D. Extinction by hybridization and introgression. Annu Rev Ecol Syst. 1996a;27:83–109. [Google Scholar]
- Rhymer JM, Simberloff D. Extinction by hybridization and introgression. Annu Rev Ecol Evol Syst. 1996b;27:83–109. [Google Scholar]
- Sanchirico JN, Wilen J. Bioeconomics of spatial exploitation in a patchy environment. J Environ Econ Manage. 1999;37:129–150. [Google Scholar]
- Sax DF, Gaines SD. Species invasions and extinction: the future of native biodiversity on islands. Proc Natl Acad Sci. 2008;105:11490–11497. doi: 10.1073/pnas.0802290105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaefer MB. Some considerations of population dynamics and economics in relation to the management of the commercial marine fisheries. J Fish Res Board Can. 1957;14:669–681. [Google Scholar]
- Schluter D. The Ecology of Adaptive Radiation. Oxford University Press; New York: 2000. [Google Scholar]
- Schmitz OJ. The New Ecology: Rethinking a science for the Anthropocene. Princeton University Press; Princeton, New Jersey: 2016. [Google Scholar]
- Schulz C-E, Skonhoft A. Wildlife management, land-use and conflicts. Environ Dev Econ. 1996;1:265–280. [Google Scholar]
- Shanafelt DW, Dieckmann U, Jonas M, Franklin O, Loreau M, Perrings C. Biodiversity, productivity, and the spatial insurance hypothesis revisited. J Theor Biol. 2015;380:426–435. doi: 10.1016/j.jtbi.2015.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmida A, Wilson MV. Biological determinants of species diversity. J Biogeogr. 1985;12:1–20. [Google Scholar]
- Shogren JF, Crocker TD. Cooperative and noncooperative protection against transferable and filterable externalities. Environ Resour Econ. 1991;1:195–214. [Google Scholar]
- Simpson EH. Measurement of diversity. Nature. 1949;163:688. [Google Scholar]
- Smith MD, Sanchirico JN, Wilen JE. The economics of spatial-dynamic processes: applications to renewable resources. J Environ Econ Manage. 2009;57:104–121. [Google Scholar]
- Steffen W, Crutzen PJ, McNeill JR. The Anthropocene: are humans now overwhelming the great forces of nature? Ambio. 2007;36:614–621. doi: 10.1579/0044-7447(2007)36[614:taahno]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Thompson PL, Rayfield B, Gonzalez A. Loss of habitat and connectivity erodes species diversity, ecosystem functioning, and stability in metacommunity networks. Ecography. 2017;40:98–108. [Google Scholar]
- Thompson PL, Shurin JB. Regional zooplankton biodiversity provides limited buffering of pond ecosystems against climate change. J Anim Ecol. 2012;81:251–259. doi: 10.1111/j.1365-2656.2011.01908.x. [DOI] [PubMed] [Google Scholar]
- Thompson PL, Gonzalez A. Ecosystem multifunctionality in metacommunities. Ecology. 2016;97:2867–2879. doi: 10.1002/ecy.1502. [DOI] [PubMed] [Google Scholar]
- Urban MC. Maladaptation and mass effects in a metacommunity: consequences for species coexistence. Am Nat. 2006;168:28–40. doi: 10.1086/505159. [DOI] [PubMed] [Google Scholar]
- Venail P, MacLean R, Bouvier T, Brockhurst M, Hochberg M, Mouquet N. Diversity and productivity peak at intermediate dispersal rate in evolving metacommunities. Nature. 2008;452:210–214. doi: 10.1038/nature06554. [DOI] [PubMed] [Google Scholar]
- Vila M, Pujadas J. Land-use and socio-economic correlates of plant invasions in European and North African countries. Biol Conserv. 2001;100:397–401. [Google Scholar]
- Vilà M, Espinar JL, Hejda M, Hulme PE, Jarošík V, Maron JL, Pergl J, Schaffner U, Sun Y, Pyšek P. Ecological impacts of invasive alien plants: a meta-analysis of their effects on species, communities and ecosystems. Ecol Lett. 2011;14:702–708. doi: 10.1111/j.1461-0248.2011.01628.x. [DOI] [PubMed] [Google Scholar]
- Wang S, Loreau M. Biodiversity and ecosystem stability across scales in metacommunities. Ecol Lett. 2016;19:510–518. doi: 10.1111/ele.12582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren PH. The effects of between-habitat dispersal rate on protist communities and metacommunities. Oecologia. 1996;105:132–140. doi: 10.1007/BF00328801. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.