Abstract
The objective of the present study was to quantify the relationship between udder skin surface temperature (USST) and somatic cell count (SCC) in lactating dairy cows. Data were recorded on the same 14 Holstein-Friesian cows, at evening (15:00 to 16:00) milking every day over a 2-mo period. Surface temperature measurements of all udders were extracted from thermal images. After imaging, milk was extracted from each quarter and analyzed for SCC. Environmental and cow-related factors (i.e., ambient temperature, humidity, rainfall, wind speed, distance walked to the parlor, number of days since the udder was shaved, parity, and stage of lactation) were recorded on each day of the experiment. A large array of descriptive temperature parameters (DTP) were extracted from every udder image including temperature-based (e.g., maximum, average and minimum USST), pixel count-based, and textural-based DTPs. Several different analytical methods were tested in an attempt to relate any given DTP to SCC; this included investigating the relationship between USST and the log transform of SCC (i.e., somatic cell score; SCS). The temperature range within each udder was also compared with the natural log of the range in SCC of the respective quarters. In a separate analysis, the temperature difference between each DTP and its respective daily baseline (i.e., average of the 5 lowest values of that DTP across the herd) was compared with SCS. Finally, the association between environmental and cow-related factors with each DTP was investigated to create prediction models for each DTP, the residuals of which were compared with SCC. Results from the present study indicate that the correlation between any DTP and SCS was weak (range of −0.16 to 0.19) and so could not be used to identify quarters with high SCC. Although some alternative measures had a significant relationship with SCS, again, the correlation was too weak for practical use on its own. Maximum and average USST could be predicted with a root mean square error of 0.23 and 0.35 °C, respectively, although the residuals from the prediction model could not be used to identify animals with high SCC. This suggests that infrared thermography alone could not be used as a real-time automated tool to detect high SCC for dairy cows in a pasture-based system.
Keywords: dairy cows, infrared thermography, somatic cell count
INTRODUCTION
An elevation in somatic cell count (SCC) in the milk of a cow is a common method of detecting infection in the mammary gland (Harmon, 1994). Mammary gland infections and high SCC can reduce farm profitability due to loss in milk sales, greater veterinary treatment, and greater involuntary culling (Geary et al., 2011). Previous studies have shown the prevalence of mastitis to vary from 31% to 48% (Wilson et al., 1997; Pitkälä et al., 2004) with culling rates in Ireland due to mastitis ranging from 3% to 13% (Geary et al., 2013). At present, only parlors that use separate milk lines for each teat cup (e.g., automatic milking systems) have the capability to automatically measure the SCC of each quarter on a daily basis. When a single milk line is used for all 4 teat cups, obtaining a measure of SCC for each quarter can be subjective and labor intensive; therefore, alternative, noninvasive methods are required.
Infrared thermography (IRT) is a noninvasive technology that can estimate the temperature of an object based on the radiating energy (Speakman and Ward, 1998). Previous research indicated that IRT has the ability to approximate the SCC of lactating cows by measuring the udder skin surface temperature (USST) (Colak et al., 2008; Polat et al., 2010), but both of these studies were conducted on a single day and in a controlled environment. In Ireland, the majority of milk is produced from cows grazing in situ; therefore, environmental and cow-related factors must be considered (Berry et al., 2003).
The objective of the present study was to investigate the feasibility of using udder IRT to predict SCC in dairy cows on a daily basis. This study aims to investigate the relationship between SCC and a plethora of descriptive temperature parameters (DTPs) and ultimately create a prediction model for USST, the residuals of which may be used to predict SCC. Results from this study could aid in the implementation of a real-time automated tool to detect high SCC.
MATERIALS AND METHODS
The study was conducted over a 2-mo period on the Moorepark Research Farm, Teagasc, Fermoy, Co. Cork, Ireland (52.16175 latitude, −8.25344 longitude) commencing in September 2016. All procedures were conducted under approval from the Teagasc Animal Ethics Committee on experimental animal use (TAEC127-2016) in accordance with the Cruelty to Animals Act 1876 and the European Communities Regulations, 1994.
To quantify the relationship between USST and SCC over time, data were recorded on the same 14 Holstein-Friesian cows at evening (15:00 to 16:00) milking every day over a 2-mo period. Cows enrolled in the study were chosen to have a highly variable SCC in the months preceding the experiment. All udders were shaven before (21 September 2016) and halfway through (1 November 2016) the 2-mo experimental period. Animals were allocated to a new grass paddock each day and received a small quantity of concentrate during each morning and evening milking. The animals walked from the paddock to the parlor at their own pace each day and were allowed a 10-min acclimatization period in the parlor prior to imaging. Three replicate thermal images were taken of each udder each day prior to the evening milking as per Byrne et al. (2017). All thermal images were captured using a calibrated FLIR T430sc thermal camera (FLIR SYSTEMS Inc., Stockholm, Sweden). The spectral range of the camera was between 7.5 and 13 µm. The camera resolution was 320 × 240, the thermal sensitivity was <0.03 °C, and the accuracy was ±2 °C. All images were captured by the same operator each day in a 30-stand herringbone unit. The operator stood directly behind the animal in the pit of the milking parlor to capture the ventral face of each udder at a distance of 0.8 m.
After the thermal images were captured and the first 10 mL of milk from each quarter discarded, milk samples, of 35 mL each (1% of total yield), were then taken from each quarter to be analyzed individually for SCC (Somacount 300, Bentley Instruments, Inc., Chaska, MN). A California Mastitis Test was also performed on all quarter samples by the same operator (Godden et al., 2017).
Additional information was also recorded during the experimental period including the distance the animals walked to the parlor every day using Google maps (87 to 967 m; Google Inc., Mountain View, CA), whether each animal was laying or standing in the paddock before evening milking, and the number of days since the animal’s udder was shaved. Ambient temperature and humidity of the parlor were recorded every minute using a Lascar EL-USB-2 data logger (Lascar Electronics, Whiteparish, UK). External environment-related variables were recorded on an hourly basis from a weather station located on the Teagasc research farm, and these included ambient temperature, relative humidity, rainfall, and wind speed. The data for each external environment-related factor were retained 1 and 2 h before imaging each day, and the maximum and average values for each variable were used in the analysis. Parity and stage of lactation (i.e., days in milk) were also available for each cow.
Image Analysis
Image analysis and temperature extraction were undertaken using the Thermovision LabVIEW toolkit 3.3 (FLIR Systems Inc., Stockholm, Sweden) based on the procedures outlined previously (Byrne et al., 2017). All image parameters (i.e., emissivity, ambient temperature, humidity, object distance, and reflected temperature) were adjusted in each image before analysis. Emissivity in all images was set to 0.98; ambient temperature and humidity data varied between images, and the respective values were taken from the Lascar EL-USB-2 data logger (Lascar Electronics).
For every udder image, a border was drawn by freehand around the ventral face of each quarter, and all calculations were made using only the enclosed pixels (Fig. 1). Teats and any background information (e.g., legs, underbelly) were not included within the borders.
Figure 1.
A thermal image of an udder is shown on the left, and the image on the right shows how this image was cropped. A freehand border (shown in black) was drawn around the ventral face of each quarter, and all descriptive temperature parameters were extracted from these regions.
Descriptive Temperature Parameters
Initial DTPs that were extracted from each image consisted of the maximum, minimum, and average temperature. As the Thermovision LabVIEW toolkit 3.3 allows manipulation of every pixel in an image, more complex DTPs were also created (Table 1). Because the extracted maximum temperature is derived from a single pixel in the image, it can be prone to noise; therefore, a DTP called Mxavg was created, whereby the average temperature of the 3 × 3 pixel region with its center lying on the hottest pixel in an udder quarter was calculated. In addition, to remove the influence of dirt or hair on the udder, a threshold of 32 °C was applied to each quarter whereby any pixel with a temperature less than 32 °C was removed from the analysis; the average temperature was then calculated using the remaining pixels, thus creating a threshold average above 32 °C (Tavg32). A threshold average above 35 °C (Tavg35) was also created using the same approach. For 2 additional DTPs, a threshold relative to the maximum temperature of each quarter was chosen; the weighted maximum at 0.5 °C (Wmax0.5) was created by retaining only the pixels within 0.5 °C of the maximum temperature of each udder quarter and calculating an average temperature using the retained pixels. The weighted maximum at 2 °C (Wmax2.0) was also calculated in the same way, but the threshold was set to within 2 °C of the maximum temperature of each udder quarter.
Table 1.
The abbreviation and description of all descriptive temperature parameters (DTPs) calculated in the present study
| DTP abbreviation | DTP description |
|---|---|
| Avg | The average temperature of an udder quarter |
| AASM1 | |
| ACT1 | |
| AC1 | |
| ASOS1 | |
| AIDM1 | |
| AE1 | |
| Max | The maximum temperature of an udder quarter |
| Min | The minimum temperature of an udder quarter |
| Mxavg | The average of the 3 × 3 pixel region with its center lies on the hottest pixel in an udder quarter |
| PA32 | The percentage of pixels above 32 °C in an udder quarter |
| PA35 | The percentage of pixels above 35 °C in an udder quarter |
| PAM-2.0 | The percentage of pixels above 2.0 °C less than the maximum temperature |
| PAM-0.5 | The percentage of pixels above 0.5 °C less than the maximum temperature |
| Tavg32 | The average temperature of all pixels above 32 °C |
| Tavg35 | The average temperature of all pixels above 35 °C |
| Wmax2.0 | The average temperature of all pixels above 2 °C less than the maximum temperature |
| Wmax0.5 | The average temperature of all pixels above 0.5 °C less than the maximum temperature |
1 P(i, j) is the (i, j)th entry in a matrix of temperature measurements, Ng is the number of distinct temperature measurements in the quantized matrix, was the sum of all rows, was the sum of all columns, was the mean of Px, was the mean of Py, is the mean value of P, was the SD of Px, and was the SD of Py.
A series of new DTPs were also created based on the pixel count percentages. A threshold was set at 32 °C, and the number of pixels above this threshold was divided by the total number of pixels in the udder quarter to calculate the percentage of pixels above 32 °C (PA32). A similar method was applied but using a threshold at 35 °C to calculate the percentage of pixels above 35 °C (PA35). The percentage of pixels within 0.5 °C of the maximum temperature (PAM-0.5) was calculated as the number of pixels within 0.5 °C of the maximum temperature divided by the total number of pixels in the udder quarter. A similar procedure was used to calculate the percentage of pixels within 2 °C of the maximum temperature of each udder quarter (PAM-2.0).
Textural patterns on the surface of the udder were also investigated using gray-level co-occurrence matrices (GCLMs) (Haralick and Shanmugam, 1973), which were adapted for thermal imaging for use in the present study. Although the aforementioned DTPs quantify temperature- and pixel count-based attributes of the udder, the GCLMs allow the thermal pattern on the udder to be compared with infection status, similar to Milosevic et al. (2014) who used GCLMs of thermal images to detect breast cancer in humans. Each cell (i, j) in the GCLM denotes the number of times 2 pixels with gray levels i and j lie a distance D apart at a given angle ϴ in the image of interest, irrespective of location. Both D and ϴ were defined before the GCLMs were constructed. Generally, the dimensions of the square GCLM is defined by the number of gray levels in an image, but in the present study, the dimensions of the GCLM was defined as the number of distinct temperature levels in a given image. To facilitate the definition of the dimensions of the GCLM, every temperature in each thermal image was rounded to 1 decimal place. For the present study, a distance of 1 pixel and 4 different angles 0°, 45°, 90°, and 135° were considered for all GCLMs. Therefore, 4 different GCLMs were constructed for each udder quarter, and 6 different textural values (Milosevic et al., 2014) were calculated for each GCLM. The mean value for each textural feature was taken across all 4 angles for each udder quarter; all the textural features were unitless. The calculated textural features were as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where P(i, j) is the (i, j)th entry in a matrix of temperature measurements, Ng is the number of distinct temperature measurements in the quantized matrix, was the sum of all rows, was the sum of all columns, was the mean of Px, was the mean of Py, is the mean value of P, was the SD of Px, and was the SD of Py.
Statistical Analyses
To investigate the association between the DTPs (described in Table 1) and SCC, as well as the association between each environmental factor and DTP, a series of analyses was undertaken as shown below.
Linear regression.
By examining 62 cows on a single day, Polat et al. (2010) demonstrated a linear relationship between the natural log of SCC [also known as somatic cell score (SCS)] and USST; to test the validity of this, the Pearson correlation coefficient between every DTP in the present study and SCS across the entire dataset was calculated (PROC CORR; SAS Institute, 2010).
Association of the range of a DTP and SCC within udder.
To investigate whether an animal can be used as its own control to facilitate the prediction of milk SCC from a DTP, a selection of additional DTP and SCC variables were created. The range in each DTP within each udder was calculated as the difference in temperature between the quarter with the highest DTP value and the quarter with the lowest DTP value. The natural logarithm of the difference in SCC between the respective quarters was also calculated. A linear regression was performed using PROC REG (SAS Institute, 2010) for each of the 18 DTPs individually where the dependent variable was the log of the difference in SCC and the calculated DTP range was the independent variable. Fit statistics, the regression coefficient, and the Pearson correlation coefficient (PROC CORR; SAS Institute, 2010) were calculated.
Association of SCS and the divergence of a DTP from a daily baseline.
The difference in a DTP from a quarter of a given cow relative to the average of the 5 coldest quarters on that day (i.e., baseline value), which could have come from between 2 and 5 different cows each day, was calculated to quantify its usefulness as a predictor of milk SCS (natural log of SCC). A linear regression was performed using PROC REG (SAS Institute, 2010) for each of the 18 DTPs individually where SCS was the dependent variable and the difference between a DTP value and the respective baseline DTP value was the independent variable. Fit statistics, the regression coefficient, and the Pearson correlation coefficient (PROC CORR; SAS Institute, 2010) were calculated.
Association between environmental factors and DTPs.
To create prediction models for each DTP, the residuals of which could be compared with SCC, the association between each DTP and a range of environmental-level (i.e., external ambient temperature, external relative humidity, ambient temperature at the site of imaging, relative humidity at the site of imaging, rainfall, and wind speed) and cow-level factors [i.e., parity (1, 2, 3, 4, and ≥5) and stage of lactation (classified in 20-d intervals)] was first quantified. A stepwise selection using a multiple regression model in PROC REG (SAS Institute, 2010) was performed whereby each DTP was included separately as the dependent variable and all environmental and cow-related factors were considered as covariates. The significance threshold for entry and exit of the terms into/from the model was set at 0.1% before testing for collinearity between the factors. Normality checks were performed on all model residuals.
Prediction of each DTP using a single environmental factor.
To investigate the usefulness of a single environmental factor in predicting a DTP on a per quarter basis, the most influential environmental factor (MIF) [calculated from previous analysis (section on Association between environmental factors and DTPs)] for each DTP was used to predict a DTP on a single day (day 0) for each cow. A predefined number of training days (day −2, day −5, and day −10) prior to each prediction day (day 0) were used, whereas all other recorded DTPs were temporarily discarded. Each DTP was then estimated for every day using a linear mixed model with a random intercept term in PROC MIXED (SAS Institute, 2010), where quarter nested within cow was used as a random effect (Eq. 7):
| (7) |
where µp is the population intercept, aj is the individual cow intercept, µi is the individual quarter intercept, and bp is the population regression coefficient of the MIF. To measure the fit of the model, the estimated DTP and actual recorded DTP were used to calculate root mean square error (RMSE) and R2. The 5th and 95th percentiles of the residual values were also calculated. To investigate whether the residuals from a linear mixed model with a random intercept could be used to predict health status of an animal, the residuals (calculated from Eq. 7) and actual DTPs were compared with animal health status. The udder quarter health status of the animals was determined based on SCC; a healthy quarter was defined as a quarter with an SCC < 400,000 cells/mL, and if the SCC was between 400,000 and 1,000,000 cells/mL but did not increase by 300,000 cells/mL from the previous day, it was also considered healthy; all other quarters were classified as nonhealthy. To investigate the association between the USST of healthy and nonhealthy animals, and the residuals from the mixed model analysis, a linear model in PROC GLM (SAS Institute, 2010) was used where the mixed model residuals were the dependent variable and animal health status (categorized by SCC) was the independent variable.
RESULTS
Ambient temperature during the experimental period ranged from 2.6 to 16.2 °C, whereas the relative humidity ranged from 58% to 95%; the average daily USST ranged from 31.1 to 35.5 °C. Somatic cell count ranged from 1,000 to 10,000,000 cells/mL. The mean (SD in parenthesis) days in milk of all cows at the start of the experiment was 218 (72) d. Two cows were treated for mastitis during the experiment, but only a temporary reduction in SCC was observed in both cases.
Linear Regression
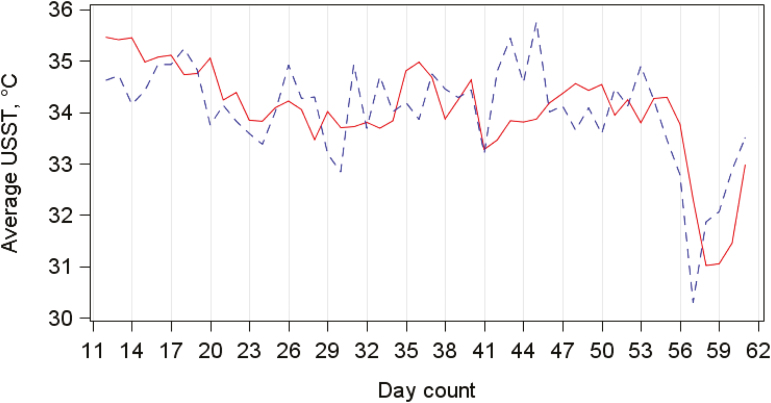
The Pearson correlation coefficient between recorded maximum USST and SCS was −0.01. Similarly, the Pearson correlation coefficient between recorded average USST and SCS was 0.01. The average USST recorded in the present study and USST calculated by Polat et al. (2010) are shown in Fig. 2, where a clear disparity between the results of both studies can be seen. All textural-based DTPs had a significant relationship with SCS with the Pearson correlation coefficient ranging from −0.16 [average entropy (Eq. 6)] to 0.19 [average inverse difference moment (Eq. 5)]. The only other DTP that had a significant relationship (P < 0.05) with SCS was PAM-0.5, where a Pearson correlation coefficient of 0.07 was observed.
Figure 2.
The recorded (○) and expected (—) average udder skin surface temperature (Avg USST) (Polat et al., 2010) for (a) the expected logarithmic relationship between SCC and USST and (b) the expected linear relationship between somatic cell score (SCS) and USST.
Association of the Range of a DTP and SCC Within Udder
The range of PAM-2.0 (2% to 66%) within each udder was the only DTP to be associated (P < 0.05) with the log of the difference in SCC. The R2 for PAM-2.0 was 0.02, and the regression coefficient (SE in parenthesis) was 18 (5).
Association of SCS and the Divergence of a DTP From a Daily Baseline
When the difference between a DTP value and its respective daily baseline was regressed onto SCS, all DTPs were associated (P < 0.05) with SCS, with the exception of PAM-2.0. The regression coefficients of all DTPs were positive, with the exception of average entropy (Eq. 6), average contrast (Eq. 2), and PAM-0.5. The regression coefficients for temperature-based DTPs ranged from 0.07 (minimum USST) to 0.44 (Tavg35). The regression coefficients (SE in parenthesis) for average entropy (Eq. 6), average contrast (Eq. 2), and PAM-0.5 were −1.59 (0.13), −0.31 (0.03), and −8.63 (2.92), respectively. The proportion of variation (i.e., R2) in SCS, which was explained by the DTPs, ranged from 0.00 (PAM-0.5) to 0.05 [average entropy (Eq. 6)] (Table 2).
Table 2.
The R2, regression coefficient (b), and the corresponding SE for the association between somatic cell score and the difference between a DTP value and the baseline (i.e., average of the 5 lowest values of that DTP) for the respective day
| DTP1 | R 2 | b | SE |
|---|---|---|---|
| AE | 0.05 | −1.59 | 0.13 |
| AIDM | 0.05 | 4.88 | 0.41 |
| ACT | 0.04 | −0.31 | 0.03 |
| Avg | 0.03 | 0.30 | 0.03 |
| Max | 0.02 | 0.36 | 0.05 |
| Wmax0.5 | 0.02 | 0.36 | 0.05 |
| PA32 | 0.02 | 1.42 | 0.18 |
| AASM | 0.02 | 91.77 | 12.18 |
| ASOS | 0.02 | 0.00 | 0.00 |
| Wmax2.0 | 0.02 | 0.32 | 0.04 |
| Min | 0.02 | 0.07 | 0.01 |
| Tavg32 | 0.02 | 0.30 | 0.05 |
| Tavg35 | 0.01 | 0.44 | 0.08 |
| AC | 0.01 | 0.00 | 0.00 |
| Mxavg | 0.01 | 0.15 | 0.03 |
| PA35 | 0.01 | 0.49 | 0.12 |
| PAM-0.5 | 0.00 | −8.63 | 2.92 |
1Avg = average temperature of an udder quarter; AASM = average angular second moment; ACT = average contrast; AC = average correlation; ASOS = average sum of squares; AIDM = average inverse difference moment; AE = average entropy; Max = maximum temperature of an udder quarter; Min = minimum temperature of an udder quarter; Mxavg = average of the 3 × 3 pixel region with its center lies on the hottest pixel in an udder quarter, PA32 = percentage of pixels above 32 °C in an udder quarter; PA35 = percentage of pixels above 35 °C in an udder quarter; PAM-0.5 = percentage of pixels within 0.5 °C of the maximum temperature; Tavg32 = average temperature of all pixels above 32 °C; Tavg35 = average temperature of all pixels above 35 °C; Wmax2.0 = average temperature of all pixels within 2 °C of the maximum temperature; Wmax0.5 = average temperature of all pixels within 0.5 °C of the maximum temperature.
Association Between Environmental Factors and DTPs
When the association between the environmental factors and DTPs were investigated, the environmental factors accounted for between 6% [average correlation (Eq. 3)] and 53% (average USST) of the variation in the investigated DTPs. Irrespective of DTP, the number of environmental factors that were associated (P < 0.01) with each DTP ranged from 4 [average correlation (Eq. 3)] to 7 (average USST), albeit much of the variation was accounted for by a single factor (R2 = 3% to 36%), which differed by the DTP under investigation (Table 3). The number of days since the udder was shaved accounted for between 10% and 23% of the variation in most textural-based DTPs (i.e., average angular second moment, average contrast, average inverse difference moment, and average entropy). For the average correlation (Eq. 3), ambient temperature at the time of imaging accounted for 3% of the variation, whereas the maximum ambient temperature observed 2 h before imaging accounted for 13% of the variation in the average sum of squares DTP (Eq. 1). For all temperature- and pixel count-based DTPs, except PAM-0.5, the maximum ambient temperature observed 2 h before imaging accounted for the largest proportion of variation (R2 = 9% to 36%). Other influential factors that accounted for some of the variation in the DTPs included parity (R2 = 2% to 12%), stage of lactation (R2 = 0% to 4%), and the total amount of precipitate that fell 2 h before imaging (R2 = 0% to 4%). Humidity- and wind-related factors accounted for a small proportion of the variation in any DTPs (0% to 3%). The distance animals walked to the parlor was not associated with any of the DTPs investigated in the present study. The DTPs with the greatest proportion of total variation accounted for by multiple environmental factors were average USST (53%), PA32 (51%), and maximum USST (50%) (Table 3). The DTPs with the greatest proportion of total variation accounted for by a single environmental factor, which in all cases was the maximum ambient temperature observed 2 h before to imaging, were average USST (36%), PA32 (35%), and Wmax0.5 (31%) (Table 3).
Table 3.
The number of significant environmental factors (no. of factors), associated R2, the most influential environmental factor (MIF), and the R2 when only the MIF is included in the model (R2 with MIF) for each descriptive temperature parameters (DTP)
| DTP1 | R 2 | No. of factors | MIF2 | R 2 with MIF |
|---|---|---|---|---|
| Avg | 0.53 | 7 | Amb2hmax | 0.36 |
| PA32 | 0.51 | 6 | Amb2hmax | 0.35 |
| Max | 0.50 | 5 | Amb2hmax | 0.30 |
| Wmax0.5 | 0.49 | 5 | Amb2hmax | 0.31 |
| Tavg32 | 0.48 | 7 | Amb2hmax | 0.29 |
| Wmax2.0 | 0.48 | 5 | Amb2hmax | 0.30 |
| AIDM | 0.45 | 7 | Days unshaven | 0.23 |
| PA35 | 0.41 | 7 | Amb2hmax | 0.23 |
| Tavg35 | 0.40 | 5 | Amb2hmax | 0.25 |
| ACT | 0.39 | 6 | Days unshaven | 0.18 |
| AE | 0.37 | 6 | Days unshaven | 0.12 |
| Min | 0.36 | 7 | Amb2hmax | 0.23 |
| Mxavg | 0.34 | 5 | Amb2hmax | 0.21 |
| AASM | 0.29 | 7 | Days unshaven | 0.10 |
| ASOS | 0.27 | 5 | Amb2hmax | 0.11 |
| PAM-2.0 | 0.23 | 6 | Amb2hmax | 0.09 |
| PAM-0.5 | 0.07 | 5 | Amb1h | 0.03 |
| AC | 0.06 | 4 | Amb1h | 0.03 |
1Avg = average temperature of an udder quarter; AASM = average angular second moment; ACT = average contrast; AC = average correlation; ASOS = average sum of squares; AIDM = average inverse difference moment; AE = average entropy; Max = maximum temperature of an udder quarter; Min = minimum temperature of an udder quarter; Mxavg = average of the 3 × 3 pixel region with its center lies on the hottest pixel in an udder quarter; PA32 = percentage of pixels above 32 °C in an udder quarter; PA35 = percentage of pixels above 35 °C in an udder quarter, PAM-2.0 = percentage of pixels within 2.0 °C of the maximum temperature; PAM-0.5 = percentage of pixels within 0.5 °C of the maximum temperature; Tavg32 = average temperature of all pixels above 32 °C; Tavg35 = average temperature of all pixels above 35 °C; Wmax2.0 = average temperature of all pixels within 2 °C of the maximum temperature; Wmax0.5 = average temperature of all pixels within 0.5 °C of the maximum temperature.
2Amb2hmax = the maximum ambient temperature observed 2 h before imaging; Days unshaven = the number of days since the udder was shaven; Amb1h = the ambient temperature at the time of imaging.
Prediction of Each DTP
The R2 for the prediction of maximum USST on a single day (day 0) for each cow, increased from 67% to 76% when the number of training days increased from 2 to 10; for average USST, the R2 increased from 65% to 74% for the same increase in training days. The RMSE decreased as the number of training days increased, decreasing from 0.27 to 0.23 °C for maximum USST and from 0.38 to 0.35 °C for average USST when 2 and 10 training days were used, respectively. The difference between the 5th and 95th percentile of the maximum USST model residuals (discrepancy between predicted and actual maximum USST) decreased from 4.78 to 1.84 °C when the number of training days was increased from 2 to 10; a similar trend was observed for all other DTPs.
When a linear mixed model with a random intercept was used, a single environmental factor accounted for between 48% (PAM-0.5) and 79% [average entropy (Eq. 3)] of the variation in the DTPs using a 10-d training period (Table 4). The temperature-based DTP with the greatest R2 (77%) was Wmax2.0; an RMSE of 0.23 °C was achieved, and the 5th and 95th percentiles of the model residuals were −0.99 and 0.92 °C, respectively (Table 4). Results for maximum USST were very similar to Wmax2.0; an illustration of the relationship between recorded and predicted maximum USST is shown in Fig. 3. The pixel count-based DTP with the greatest R2 (71%) was PA35; an RMSE of 10% was achieved, and the 5th and 95th percentiles of the model residuals were −39% and 40%, respectively (Table 4).
Table 4.
The R2, the root mean squared error (RMSE), and the 5th (5th Perc) and 95th (95th Perc) percentiles of the model residuals when linear mixed model with a random intercept was used to estimate each descriptive temperature parameter (DTP) with 10 d of training data
| DTP | R 2 | RMSE | 5th Perc | 95th Perc |
|---|---|---|---|---|
| AE | 0.79 | 0.09 | −0.34 | 0.35 |
| AIDM | 0.78 | 7.81 | −0.11 | 0.11 |
| Wmax2.0 | 0.77 | 0.23 | −0.99 | 0.92 |
| Max | 0.77 | 0.23 | −0.96 | 0.88 |
| Wmax0.5 | 0.76 | 0.24 | −0.97 | 0.88 |
| AASM | 0.75 | 0.04 | 0.00 | 0.00 |
| ACT | 0.75 | 0.37 | −1.26 | 1.61 |
| ASOS | 0.75 | 6,366.35 | −151.47 | 179.28 |
| Avg | 0.74 | 0.35 | −1.58 | 1.44 |
| Tavg35 | 0.74 | 0.14 | −0.56 | 0.54 |
| PA35 | 0.71 | 0.10 | −0.39 | 0.40 |
| Tavg32 | 0.71 | 0.23 | −1.15 | 1.10 |
| PA32 | 0.67 | 0.08 | −0.21 | 0.16 |
| AC | 0.66 | 152,951.53 | −422,726.25 | 457,744.04 |
| PAM2.0 | 0.64 | 0.10 | −0.27 | 0.31 |
| Mxavg | 0.59 | 0.61 | −1.06 | 1.05 |
| Min | 0.54 | 1.68 | −5.35 | 4.27 |
| PAM0.5 | 0.48 | 0.01 | −0.01 | 0.02 |
1Avg = average temperature of an udder quarter; AASM = average angular second moment; ACT = average contrast; AC = average correlation; ASOS = average sum of squares; AIDM = average inverse difference moment; AE = average entropy; Max = maximum temperature of an udder quarter; Min = minimum temperature of an udder quarter; Mxavg = average of the 3 × 3 pixel region with its center lies on the hottest pixel in an udder quarter; PA32 = percentage of pixels above 32 °C in an udder quarter; PA35 = percentage of pixels above 35 °C in an udder quarter; PAM-2.0 = percentage of pixels within 2.0 °C of the maximum temperature; PAM-0.5 = percentage of pixels within 0.5 °C of the maximum temperature; Tavg32 = average temperature of all pixels above 32 °C; Tavg35 = average temperature of all pixels above 35 °C; Wmax2.0 = average temperature of all pixels within 2 °C of the maximum temperature; Wmax0.5 = average temperature of all pixels within 0.5 °C of the maximum temperature.
Figure 3.
The recorded (− −) and estimated (―) maximum udder skin surface temperature across the experimental period of the right hind quarter of a single cow using linear mixed model with a random intercept and 10 d of training data.
A total of 459 records (18%) were categorized as nonhealthy using the observed SCC. Based on the residuals calculated from the mixed model, 4 DTPs [PA35, Tavg32, PAM-2.0, and average correlation (Eq. 3)] had the ability to differentiate healthy from nonhealthy animals (Table 5). When Tavg32 was considered, the SD of residuals for healthy and nonhealthy animals was 0.74 and 0.73 °C, respectively, whereas the mean (SE in parenthesis) of the residuals for healthy and nonhealthy animals was 0.01 (0.01) and 0.10 (0.03) °C, respectively. The residual mean of PA35 and PAM-2.0 for healthy and nonhealthy animals was similar across both DTPs, but the SD of the model residuals for PA35 (25%) was larger in comparison to PAM-2.0 (19%). The mean residual (SE) for healthy and nonhealthy animals was 35,449.61 (11,949) and 24,314.25 (25,859.34) (unit less), respectively, implying that healthy and nonhealthy animals were indistinguishable.
Table 5.
The mean (SE in parenthesis) and SD of the residuals from the significant (P < 0.05) descriptive temperature parameter (DTP) models for healthy and nonhealthy animals
| DTP1 | Healthy mean | Healthy SD | Nonhealthy mean | Nonhealthy SD |
|---|---|---|---|---|
| PA35 | 0.00 (0.01) | 0.25 | 0.03 (0.01) | 0.25 |
| Tavg32 | 0.01 (0.01) | 0.74 | 0.10 (0.03) | 0.73 |
| PAM-2.0 | 0.00 (0.00) | 0.19 | 0.02 (0.01) | 0.19 |
| AC | 35,449.61 (11,949) | 591,881.81 | −24,314.25 (25,859.34) | 572,590.55 |
1AC = average correlation; ASOS = average sum of squares; PA35 = percentage of pixels above 35 °C in an udder quarter; PAM-2.0 = percentage of pixels within 2.0 °C of the maximum temperature; Tavg32 = average temperature of all pixels above 32 °C.
DISCUSSION
Elevated SCC can be due to an infection in the mammary gland and, as such, can negatively impact farm profitability. Most milking parlors cannot easily measure SCC at an individual quarter level; therefore, a new approach is required to generate such data. The objective of the present study was to investigate the feasibility of using IRT of the udder to predict the SCC of grazing Holstein-Friesian cows on farm. The relationship between SCC and a multitude of different DTPs was tested using various analytical techniques. Results indicate that SCC could not be readily predicted using IRT. Although the maximum and average USST could be predicted with an RMSE of 0.23 and 0.35 °C, respectively, deviations in recorded USST from an expectation could not differentiate healthy and nonhealthy animals.
Integrity in Experimental Procedure
To ensure reliability of the results in any experiment, the data must be collected and analyzed thoroughly; the 2 main sources of data in this experiment were USST measured using IRT and SCC of milk, both of which require certain procedures to reduce erroneous measurements. A temperature measurement taken from an animal using IRT can be affected by a range of factors, including the environment, stress on the animal, activity, circadian rhythm, hair on the region of interest, the precision of the camera, and the consistency of the operator (Berry et al., 2003; Church et al., 2014; Byrne et al., 2017). To ensure all of these factors do not cause erroneous measurements, each must be recorded or mitigated through certain procedures. First, environmental factors were recorded throughout the experiment both on farm and at the site of imaging so the impact of each factor could be quantified through analysis. In the present study, ambient temperature accounted for most of the explainable variation in temperature- and pixel count-based DTPs (range of 9% to 36%). Second, stress experienced by the animal was minimized as all animals were allowed to walk from the field into the milking parlor at their own pace in the same manner as they would for milking. The distance animals walked to the parlor was recorded every day as an estimate of exercise. This distance did not have a significant relationship with any of the DTPs, indicating that the 10-min acclimatization period was sufficient to reduce the effect of exercise on USST. A change in USST due to the circadian rhythm was mitigated against as animals were imaged at the same time each day; 15:00 to 16:00 was chosen because variation of USST due to the circadian rhythm is minimized during this time period (Berry et al., 2003). The number of days since the udder was shaved was recorded as an estimate for the amount of hair on the udder, but only had a significant association with textural-based DTPs and average USST, which indicates that some temperature-based DTPs, such as maximum USST, were robust to variations in udder hair. As the animals were allowed out to pasture each day, none had large amounts of dirt on the udder. Byrne et al. (2017) recommended that 3 thermal image replicates should be taken of every udder, and the same operator should capture every image within a study to increase the precision of IRT; the present study followed this protocol. Finally, to further increase the integrity of the experimental procedure, a calibrated camera was used and no udder was handled prior to imaging, as this can cause a change in USST (Paulrud et al., 2005).
When extracting milk samples for the measurement of SCC, similar methods were used to those described by Polat et al. (2010), whereby the first 10 mL of milk was discarded before 35 mL of milk was collected from each quarter on a daily basis. Alternative methods of milk collection involve taking samples of milk throughout the entire milking. Nielsen et al. (2005) demonstrated that although SCC can increase slightly during milking, the difference in SCC between healthy and nonhealthy quarters remains consistent throughout milking. Thermal images and milk samples in the present study were taken at evening milking (15:00 to 16:00). Consequently, animals in the present study only had a 7-h period since last milking; this may have resulted in slightly higher SCC, although this does not offset the difference in SCC between healthy and nonhealthy animals (Nielsen et al., 2005). Both SCS and the California mastitis test results were assessed as part of the present study and found to have a high concordance (r = 0.85).
Experimental Outputs
Polat et al. (2010) demonstrated a linear relationship between SCS and USST with an R2 of 72%. Results from the present study showed a large discrepancy between expected (Polat et al., 2010) and recorded USST (Fig. 2). One of the main factors that possibly contributed to the differences between both studies was the ambient temperature, which may affect an animal’s thermoregulatory response to infection; Polat et al. (2010) kept the animals in a room that was at an animal’s thermal neutral zone (18 to 23 °C) before imaging, whereas the present study allowed animals to stand in a parlor with temperatures ranging from 3.5 to 16.2 °C, which is typical of grazing-based systems in Ireland. Dissimilarities were not resolved when data from the single hottest day in the present study were compared with the results from Polat et al. (2010). Additional distinctions between the methodology of the present study and that of Polat et al. (2010) include animal breed [Holstein-Friesian (present study) vs. Brown Swiss (Polat et al., 2010)], acclimatization period (30 vs. 10 min), number of nonhealthy records (459 vs. 154), and udder thermal image view (lateral and caudal view vs. ventral view).
Previous studies have traditionally used the average temperature of the udder (Berry et al., 2003; Hovinen et al., 2008; Polat et al., 2010; Pampariene et al., 2016) to determine the effect of exercise, ambient temperature, and infection status on USST. Although Metzner et al. (2014) also compared maximum and minimum USST to infection status, no agricultural study investigated how alternative DTPs from udder thermal images relate to SCS. In the present study, the correlation observed between any of the DTPs and SCS (−0.16 to 0.19) was too weak for practical use, as any predictions would contain a large number of false positives and false negatives. Therefore, alternative methodologies were tested. Previous studies have successfully related the temperature difference between 2 regions on the hoof to hoof lesions (Nikkhah et al., 2005; Alsaaod and Büscher, 2012), in effect using the animal as her own control. Paulrud and Rasmussen (2004) also suggested detecting mastitis using contralateral teat temperature differences. Similarly, in the present study, the temperature range within each udder was compared with the respective natural log of the range in SCC, essentially also using the animal as her own control in an attempt to mitigate factors such as ambient temperature and the amount of hair on the udder. This technique would not be useful on farm as many of these measures did not have a significant relationship with the log of the range in SCC. In a separate analysis, the temperature difference between a DTP and its daily baseline (i.e., average of the 5 lowest values of that DTP) was compared with SCS, thereby using the daily baseline as a control in an attempt to mitigate environmental factors, which the entire herd would be subjected to (e.g., ambient temperature). The proportion of variation in SCS (0% to 5%), which was accounted for by the difference between a DTP and its daily baseline, was too weak for practical use.
Although using the animal as its own control did not help to predict SCS, the next step was to quantify the association between various environmental and cow-related factors with each DTP. Berry et al. (2003) showed that ambient temperature, exercise, and circadian rhythm were associated with average USST, but no study investigated how alternative udder DTPs are associated with various environmental or cow-related factors. Temperature-based DTPs (maximum USST, average USST, minimum USST, Wmax0.5, Wmax2.0, Tavg32, Tavg35, and Mxavg) had the greatest association with ambient temperature [R2 ranged from 21% (Mxavg) to 36% (average USST)], which is consistent with previous literature for the average USST of dairy cattle (Berry et al., 2003). Parity had the second greatest association with temperature-based DTPs [R2 ranged from 2% (Tavg35) to 12% (maximum USST)], with all temperature-based DTPs decreasing as parity increased; Nikkhah et al. (2005) showed a similar association between parity and the hoof temperature of cattle but not with USST. Other factors such as days since the udder was shaved had a minor association with average USST (R2 = 3%), yet it was not related to maximum USST. As maximum USST is derived from the single hottest pixel it was taken from the skin rather than the hair, unlike average USST that is calculated using every element of the udder. Although some studies have used shaven (Metzner et al., 2014) or unshaven udders (Berry et al., 2003), no study investigated the association between hair on the udder of a dairy cow and various DTPs. Only a small proportion of the total variation (6% to 45%) in textural-based DTPs could be accounted for by environmental factors, indicating that the textural-based DTPs may be more prone to noise in comparison to other DTPs.
When linear mixed models were used to predict each DTP, a single factor could account for between 3% and 36% of the variation in the DTPs. When linear mixed models with a random intercept term were used, a single factor could account for between 48% and 79% of the variation because each udder quarter was modeled individually. A linear mixed model with a random regression coefficient was also tested, but RMSE and R2 values were not improved. Berry et al. (2003) used a linear regression model with lag to predict average USST and achieved slightly better RMSE and R2 in comparison to the present study. Gloster et al. (2011) suggested that colder conditions cause a greater variability in the temperatures of some anatomical regions, which may account for the difference in results between the present study and the study by Berry et al. (2003).
Ultimately, the present study aimed to differentiate healthy and nonhealthy animals (defined by SCC) using USST. Gloster et al. (2011) suggested that mathematical models could be used to predict the temperature of an anatomical area and any deviations from the prediction (the model residuals) could be related to infection. Therefore, a prediction model for USST was developed. The natural deviation due to infection must be greater than the distribution of the prediction model residuals as any deviation due to infection less than the distribution of the residuals can only be attributed to model inaccuracy rather than infection. The 5th and 95th percentiles of maximum USST with a 10-d training period (−0.96 and 0.88 °C Table 4) were less than the difference between healthy and nonhealthy animals reported by previous studies, which ranged from 0.9 to 2.4 °C (Colak et al., 2008; Polat et al., 2010). However, in the present study, the magnitude of the maximum USST residuals did not differ between healthy and nonhealthy animals. Although the residuals of Tavg32 differed (0.9 °C; P < 0.05) between healthy and nonhealthy animals, a large number of animals from both data sets could not be differentiated. The expected difference between actual and predicted USST is due to a change in blood flow to the site of infection due to the inflammatory response (Martins et al., 2013). Hovinen et al. (2008) and Pezeshki et al. (2011) inoculated udders with Escherichia coli and suggested that this change in blood flow may only last a number of hours and hence images taken daily may not be sufficient to detect infection in the udder. Although these studies (Hovinen et al., 2008; Pezeshki et al., 2011) have investigated the change in USST due to E. coli, no study exists that investigated the USST differences between various udder pathogens.
CONCLUSION
The present study attempted to relate USST and SCC by using simple linear regression, a cow as her own control, a daily baseline, and a linear mixed model with a random intercept; none of these proved to be sufficiently accurate to differentiate healthy and nonhealthy animals. Future studies may attempt to repeat the work of the present study in warmer/more controlled environments and to gather more frequent measurements (i.e., greater than once a day) in conjunction with an automatic milking machine or water trough; the effect of the circadian rhythm on the animals USST must be accounted for in these scenarios. Finally, the analytical methods and additional DTPs developed as part of this study could be tested on various anatomical regions for measuring alternative phenotypes, for example, feed efficiency or infection in the hoof.
Footnotes
Funding from the Department of Agriculture, Food and Marine Research Stimulus Fund (RSF 11/S/133) is gratefully acknowledged.
LITERATURE CITED
- Alsaaod M., and Büscher W.. 2012. Detection of hoof lesions using digital infrared thermography in dairy cows. J. Dairy Sci. 95:735–742. doi: 10.3168/jds.2011-4762 [DOI] [PubMed] [Google Scholar]
- Berry R., Kennedy A., Scott S., Kyle B., and Schaefer A.. 2003. Daily variation in the udder surface temperature of dairy cows measured by infrared thermography: Potential for mastitis detection. Can. J. Anim. Sci. 83:687–693. [Google Scholar]
- Byrne D. T., Berry D. P., Esmonde H., and McHugh N.. 2017. Temporal, spatial, inter-, and intra-cow repeatability of thermal imaging. J. Anim. Sci. 95:970–979. doi: 10.2527/jas.2016.1005 [DOI] [PubMed] [Google Scholar]
- Church J. S., Hegadoren P. R., Paetkau M. J., Miller C. C., Regev-Shoshani G., Schaefer A. L., and Schwartzkopf-Genswein K. S.. 2014. Influence of environmental factors on infrared eye temperature measurements in cattle. Res. Vet. Sci. 96:220–226. doi: 10.1016/j.rvsc.2013.11.006 [DOI] [PubMed] [Google Scholar]
- Colak A., B. Polat Z. Okumus M. Kaya L. E. Yanmaz, and Hayirli A.. 2008. Short communication: Early detection of mastitis using infrared thermography in dairy cows. J. Dairy Sci. 91:4244–4248. doi: 10.3168/jds.2008-1258 [DOI] [PubMed] [Google Scholar]
- Geary U., Begley N., McCoy F., O’Brien B., O’Grady L., and Shalloo L.. 2011. Estimating the impact of mastitis on the profitability of Irish dairy farms. In: Hogeveen, H., and Lam, T. J. G. M., editors. Udder health and communication. Wageningen, The Netherlands: Springer; p. 221–228. [Google Scholar]
- Geary U., Lopez-Villalobos N., O’Brien B., Garrick D., and Shalloo L.. 2013. Examining the impact of mastitis on the profitability of the Irish dairy industry. Irish J. Agr. Food Res. 95:135–149. doi: 10.3168/jds.2011-4863 [DOI] [Google Scholar]
- Gloster J., Ebert K., Gubbins S., Bashiruddin J., and Paton D. J.. 2011. Normal variation in thermal radiated temperature in cattle: Implications for foot-and-mouth disease detection. BMC Vet. Res. 7:73. doi: 10.1186/1746-6148-7-73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godden S. M., Royster E., Timmerman J., Rapnicki P., and Green H.. 2017. Evaluation of an automated milk leukocyte differential test and the California mastitis test for detecting intramammary infection in early- and late-lactation quarters and cows. J. Dairy Sci. 100:6527–6544. doi: 10.3168/jds.2017-12548 [DOI] [PubMed] [Google Scholar]
- Haralick R. M., and Shanmugam K.. 1973. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 3:610–621. doi 10.1109/TSMC.1973.4309314 [Google Scholar]
- Harmon R. J. 1994. Physiology of mastitis and factors affecting somatic cell counts. J. Dairy Sci. 77:2103–2112. doi: 10.3168/jds.S0022-0302(94)77153-8 [DOI] [PubMed] [Google Scholar]
- Hovinen M., Siivonen J., Taponen S., Hänninen L., Pastell M., Aisla A. M., and Pyörälä S.. 2008. Detection of clinical mastitis with the help of a thermal camera. J. Dairy Sci. 91:4592–4598. doi: 10.3168/jds.2008-1218 [DOI] [PubMed] [Google Scholar]
- Martins R. F., do Prado Paim T., de Abreu Cardoso C., Stéfano Lima Dallago B., de Melo C. B., Louvandini H., and McManus C.. 2013. Mastitis detection in sheep by infrared thermography. Res. Vet. Sci. 94:722–724. doi: 10.1016/j.rvsc.2012.10.021 [DOI] [PubMed] [Google Scholar]
- Metzner M., Sauter-Louis C., Seemueller A., Petzl W., and Klee W.. 2014. Infrared thermography of the udder surface of dairy cattle: Characteristics, methods, and correlation with rectal temperature. Vet. J. 199:57–62. doi: 10.1016/j.tvjl.2013.10.030 [DOI] [PubMed] [Google Scholar]
- Milosevic M., Jankovic D., and Peulic A.. 2014. Thermography based breast cancer detection using texture features and minimum variance quantization. EXCLI J. 13:1204–1215. [PMC free article] [PubMed] [Google Scholar]
- Nielsen N. I., Larsen T., Bjerring M., and Ingvartsen K. L.. 2005. Quarter health, milking interval, and sampling time during milking affect the concentration of milk constituents. J. Dairy Sci. 88:3186–3200. doi: 10.3168/jds.S0022-0302(05)73002-2 [DOI] [PubMed] [Google Scholar]
- Nikkhah A., Plaizier J. C., Einarson M. S., Berry R. J., Scott S. L., and Kennedy A. D.. 2005. Short communication: Infrared thermography and visual examination of hooves of dairy cows in two stages of lactation. J. Dairy Sci. 88:2749–2753. doi: 10.3168/jds.S0022-0302(05)72954-4 [DOI] [PubMed] [Google Scholar]
- Pampariene I., Veikutis V., Oberauskas V., Zymantiene J., Zelvyte R., Stankevicius A., Marciulionyte D., and Palevicius P.. 2016. Thermography based inflammation monitoring of udder state in dairy cows: Sensitivity and diagnostic priorities comparing with routine California mastitis test. J. Vibroeng. 18:511–521. [Google Scholar]
- Paulrud C. O., Clausen S., Andersen P. E., and Rasmussen M. D.. 2005. Infrared thermography and ultrasonography to indirectly monitor the influence of liner type and overmilking on teat tissue recovery. Acta Vet. Scand. 46:137–147. doi:10.1186/1751-0147-46-137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulrud C. O., and Rasmussen M. D. 2004. Teat thermography, hot or not. Proc. NMC 43rd Annu. Meeting, Charlotte, NC p. 159–168. [Google Scholar]
- Pezeshki A., P., Stordeur H., Wallemacq F., Schynts M., Stevens P., Boutet L. J., Peelman B., De Spiegeleer L., Duchateau F., Bureau, et al. 2011. Variation of inflammatory dynamics and mediators in primiparous cows after intramammary challenge with Escherichia coli. Vet. Res. 42:15. doi: 10.1186/1297-9716-42-15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitkälä A., M. Haveri S. Pyörälä V. Myllys, and Honkanen-Buzalski T.. 2004. Bovine mastitis in Finland 2001 – Prevalence, distribution of bacteria, and antimicrobial resistance. J. Dairy Sci. 87:2433–2441. doi: 10.3168/jds.S0022-0302(04)73366-4 [DOI] [PubMed] [Google Scholar]
- Polat B., Colak A., Cengiz M., Yanmaz L. E., Oral H., Bastan A., Kaya S., and Hayirli A.. 2010. Sensitivity and specificity of infrared thermography in detection of subclinical mastitis in dairy cows. J. Dairy Sci. 93:3525–3532. doi: 10.3168/jds.2009-2807 [DOI] [PubMed] [Google Scholar]
- SAS Institute 2010. SAS/STAT Software, Release 9.3. SAS Institute Inc, Cary, NC. [Google Scholar]
- Speakman J., and Ward S.. 1998. Infrared thermography: Principles and applications. Zool. Anal. Complex Syst. 101:224–232. [Google Scholar]
- Wilson D. J., Gonzalez R. N., and Das H. H.. 1997. Bovine mastitis pathogens in New York and Pennsylvania: Prevalence and effects on somatic cell count and milk production. J. Dairy Sci. 80:2592–2598. doi: 10.3168/jds.S0022-0302(97)76215-5 [DOI] [PubMed] [Google Scholar]