Conceptual framework for investigating causal effects from observational data in livestock

Abstract

Understanding causal mechanisms among variables is critical to efficient management of complex biological systems such as animal agriculture production. The increasing availability of data from commercial livestock operations offers unique opportunities for attaining causal insight, despite the inherently observational nature of these data. Causal claims based on observational data are substantiated by recent theoretical and methodological developments in the rapidly evolving field of causal inference. Thus, the objectives of this review are as follows: 1) to introduce a unifying conceptual framework for investigating causal effects from observational data in livestock, 2) to illustrate its implementation in the context of the animal sciences, and 3) to discuss opportunities and challenges associated with this framework. Foundational to the proposed conceptual framework are graphical objects known as directed acyclic graphs (DAGs). As mathematical constructs and practical tools, DAGs encode putative structural mechanisms underlying causal models together with their probabilistic implications. The process of DAG elicitation and causal identification is central to any causal claims based on observational data. We further discuss necessary causal assumptions and associated limitations to causal inference. Last, we provide practical recommendations to facilitate implementation of causal inference from observational data in the context of the animal sciences.

INTRODUCTION

Obtaining insight into causal effects (i.e., going beyond nondirectional associations suggested by correlations) is crucial to untangle functional links among the multiple and often interdependent parts of a biological system. Causal understanding can further enable prediction of how the parts of a system can be expected to behave in response to targeted interventions. Specific to animal agriculture, understanding the cause-and-effect mechanisms that underlie interrelationships among environmental factors, management practices, animal physiology, and performance outcomes is arguably a prerequisite for effective and efficient decision making in the context of an integrated production system.

The study of causal effects has been traditionally conducted in the realm of randomized experiments, whereby units of study (e.g., subjects, animals, cells, or pens) are randomly allocated to the putative causes of interest (e.g., treatments) following a preplanned experimental design. By contrast, observational studies exploit data recorded during a course of events without direct intervention from the researcher. Observational data of this nature are becoming increasingly prevalent in the animal sciences, particularly those originated from routine operations of commercial livestock farms and processing facilities along the supply chains of animal agriculture (Wolfert et al., 2017). Operational data are further aligned with a growing interest on precision livestock management that relies heavily on automated real-time monitoring through sensors and image analysis (Berckmans, 2017).

In data analysis, relationships or associations between variables are often expressed as correlations, covariances, or even regression coefficients, none of which necessarily convey information about causal effects. As the popular adage goes, in the absence of a randomization process, “correlation does not imply causation.” For example, in a simple case, a correlation between 2 variables, say V₁ and V₂, could be explained by an effect of V₁ on V₂ (i.e., V₁ → V₂), as a causal effect is expected to give rise to observable associations; in such case, “causation does imply correlation.” However, a correlation between V₁ and V₂ could also be explained by an effect of V₂ on V₁ (i.e., V₁ ← V₂), or by a confounding effect of a third variable, say V₃, on both V₁ and V₂ (i.e., V₁ ← V₃ → V₂), among other possibilities. If the focus of interest were a potential causal effect of V₁ on V₂, either of the latter 2 mechanisms would yield a spurious result that is not informative of the targeted effect of V₁ on V₂. Herein lies the inevitable ambiguity of exploring targeted causal effects from correlation patterns observed in data. Indeed, distinguishing specific causal effects of interest from spurious relationships is the central challenge in learning causality from data, particularly from observational data.

The objectives of this review are as follows: 1) to introduce a unifying conceptual framework for investigating causal effects from observational data in livestock, 2) to illustrate its implementation in the context of the animal sciences, and 3) to discuss opportunities and challenges associated with this framework. This review article builds upon previous work by Rosa and Valente (2013) to formalize the thought process underlying causality from observational data. We further articulate key theoretical concepts, associated nuances, and the inherent limitations of inferring causal effects from observational data; we also provide suggestions and practical considerations for analytical implementation. Foundational to the proposed conceptual framework are graphical objects known as directed acyclic graphs (DAGs) (Pearl, 2000, 2009), which constitute both formal mathematical constructs and practical tools with which causality can be communicated in an intuitive, yet rigorous manner. The proposed conceptual framework can be understood by biological scientists because it relies on graphical rules, as opposed to probabilistic or algebraic derivations. By explicit elicitation of assumptions and conditions, DAGs can be used to dissect what can and what cannot be learned from observational data in a given context, thereby helping us to clarify misunderstandings and debunk fallacies in the process of learning causality.

Our focus is on the process of eliciting DAGs to assess causality from observational data in a way that it is relevant to the animal sciences. Proper DAG elicitation is a critical pre-requisite for identification of causal effects and for subsequent specification of statistical models and implementation of data analysis strategies. To emphasize this point, we illustrate the proposed conceptual framework using graphical representations of selected examples, but we purposely forgo any specific dataset and do not conduct any explicit statistical inference. All graphics and functions associated with DAG elicitation are implemented in the web-based application DAGitty through an R-CRAN software interphase (Textor et al., 2016). Relevant R code is available in Supplementary Material to this article.

THE ROLE OF RANDOMIZATION

First posited by Sir Ronald Fisher (1926), the experimental principle of randomization provides a strategy to resolve the directional ambiguity of observable associations and can be a powerful aid in distinguishing between causal effects and noncausal associations. Specifically, random allocation of units to treatments or exposure groups is expected to average out any potential effect of extraneous factors and prevent systematic differences between groups, thus mitigating the effect of confounder variables (e.g., V₃ in V₁ ← V₃ → V₂) (Kuehl, 2000; Mead et al., 2012). Confounders such as V₃ may be observed or not and, more importantly, may be known or unknown. Particularly for this reason, the randomized experiment continues to be widely regarded as the scientific gold standard to assess whether a causal effect exists, and if so, to estimate its magnitude (Kuehl, 2000; Mead et al., 2012). In fact, randomization is a core principle of experimental design, an important arm of the statistical sciences dating back to the early 20th century (Fisher, 1935). Modern randomization schemes can be highly sophisticated and accommodate intricate treatment structures and multiple sources of variability embedded in animal agriculture (Kuehl, 2000; Milliken and Johnson, 2009).

Yet, randomization sometimes does not work or it may not be feasible. Ethical and financial considerations, as well as matters of scale and logistics, often limit random treatment assignment. Even when randomization is feasible, the sample size and amount of biological replication at the intended level of inference may be inadequate (Bello et al., 2016). At times in the animal sciences, randomized experiments are only possible under highly controlled conditions that are not representative of real-world commercial operations. For example, estimation of nutritional requirements or feed efficiency in dairy cattle requires intensive and individualized measurement of intake and performance, as well as personalized animal management that, while doable in an experimental station, is often hard to implement in commercial farms in which animals are housed and managed in cohorts. An often overlooked consideration is that, even when feasible and realistic, randomization only works on average and is only relevant to assess causal effects of a selected combination of factors (e.g., treatments, breed, or parity groups) on one or a few individual outcomes of interest considered one at a time. Furthermore, randomization does not necessarily provide a coherent insight into mechanistic interconnections among the many variables involved in the cascade of events ensued by treatment application. This is particularly relevant for the study of phenotypic networks (Rosa et al., 2011), in which physiological traits may exert causal effects on each other, with some acting as physiological mediators that are not necessarily amenable to direct manipulation. For example, enhanced liver blood flow and metabolism associated with increased feed intake in high producing dairy cows can affect circulating concentrations of critical innate reproductive hormones such as estradiol and progesterone, which in turn can affect their reproductive performance (Wiltbank et al., 2006); none of these physiological conditions are amenable to direct manipulation through randomization. Last but not least, the ever shrinking availability of research funding poses growing constraints to the economic viability of randomized experiments, which can be considerably costly to conduct. Taken together, the combination of ethical, logistical, and economical considerations poses practical constraints to randomized experiments. Thus, alternative methods for the study of complex systems in the evolving landscape of animal agriculture are required. Fortunately, as stated by Holland (1986)“the [randomized] experiment is not the only proper setting for discussing causality.”

OBSERVATIONAL DATA AND CAUSAL INFERENCE

Animal scientists have been increasingly taking advantage of the wealth of operational data regularly recorded by commercial farms or processing facilities (Rosa and Valente, 2013). Operational data are collected for the main purpose of internal management and decision making. By the time the researcher accesses such records, there is often no possibility of implementing an experimental design or a randomization scheme, so most operational data are observational in nature. As a result, confounder-driven systematic differences are not only plausible, but highly likely, thereby substantiating concerns about making causal claims from such data. Yet, there are compelling advantages to observational data, such as a realistic representation of commercial operations in the agricultural industry, larger sample sizes, and broader scopes of inference than those drawn from designed experiments, as well as alleviating concerns about experimental use of animals and associated ethical considerations. Moreover, these data are often easily accessible to researchers through farms or regional record databases (e.g., Dairy Herd Improvement companies).

In addition, operational data pose unique opportunities, as made evident by standard research practices in the field of veterinary epidemiology (Dohoo et al., 2009). More specifically, operational data are likely to contain relevant information about the inner causal mechanisms of the production system that generated it. Recent theoretical developments in the field of causal inference have enabled new opportunities to investigate causality from observational data (Spirtes et al., 1993, 2001; Pearl, 2000, 2009). Causal inference is an evolving research field of multidisciplinary reach and relevance, with meaningful contributions in theory, methods and implementation from scientific domains as diverse as computer science (Pearl, 2000, 2009), philosophy (Spirtes et al., 1993, 2001), statistics (Rubin, 2006), quantitative genetics (Wright, 1921; Gianola and Sorensen, 2004), biology (Shipley, 2000), sociology (Morgan and Winship, 2014), econometrics (Angrist and Pischke, 2009), and public health (Vanderweele, 2015).

Learning causality from observational data is a powerful proposition, though not without pitfalls, and thus requires careful consideration. Such limitations, however, should not curtail extracting whatever information is available and ascertaining what can be learned along the continuum between complete certainty and complete ignorance. As argued by Rosa and Valente (2013), there is “much to be learned from observational data.” Indeed, it is possible to make causal claims based on observational data provided that some important assumptions are met. It is in this inherently ambiguous context that one needs to be especially mindful of blind spots as “what you do not know can [and often will] hurt you.” To this end, it is absolutely critical that the conditions and assumptions framing causal inference are explicitly specified, thus ensuring a clear understanding of what can go wrong and enabling informed decision making in a specific context.

One may then legitimately ask what specifically can be learned from observational data. The theory of causal inference supports making causal claims from observational data under specified conditions (Pearl, 2000, 2009), so the answer to the causality-acolyte is straightforward. For the lingering skeptic, secondary justifications are no less compelling and can be quite practical in nature, as will become apparent throughout this manuscript. In short, causal claims from observational data may be used to refine a research hypothesis before proceeding to empirical validation with a targeted randomized experiment. Alternatively, causal inference can be used to evaluate a laboratory-tested causal theory under a broader array of conditions that better represents real world farm conditions. In addition, the conceptual framework of causal inference can help with study design, by elucidating what set of variables should be measured (and which others might be redundant) for legitimate identification of causal effects. Taken together, causal inference from observational data can, at the very least, help maximize efficiency in the allocation and use of research funding. It must be kept in mind that no study, be it experimental or observational, can warrantee answers with 100% certainty. Science evolves with the accumulation of evidence generated by a series of many studies, including both experimental and observational data.

DIRECTED ACYCLIC GRAPHS

The pioneering work of the geneticist Sewall Wright proposed a graphical representation of causal mechanisms in the form of path diagrams (Wright, 1921). Yet, it was not until the 1980s that directed graphs received a rigorous mathematical treatment, thus enabling formal connections between causality and probability theory (Verma and Pearl, 1988). In this article, we focus on a special type of graph known as DAG, insofar as they encode causal models. By their graphical nature, DAGs are highly intuitive and have quickly become popular across many scientific domains, including the animal sciences (Valente et al., 2010).

DAG Components

A DAG is a graphical object that encodes qualitative causal mechanisms between variables in the form of a joint probability distribution that describes their mutual associations and independencies. As such, a DAG can be used as a causal model to describe an underlying true data generation process or to describe beliefs about how a process works (Pearl, 2000, 2009; Greenland, 2010). By definition, DAGs do not contain cycles and thus assume no feedback loops between variables.

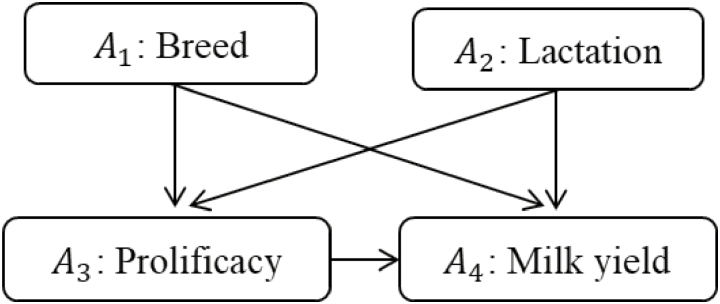
The basic components of a DAG consist of nodes, arrows, and missing arrows (Pearl, 2000, 2009). For illustration, consider the DAG in Figure 1 illustrating a hypothesized causal network connecting breed, parity, and prolificacy, with milk yield of dairy sheep, as adapted from Ferreira et al. (2017). This DAG consists of nodes A₁, A₂, A₃, and A₄, each of which represents a variable. Variables may be observed or unobserved. If observed, the measurement scale of the variable may be continuous or discrete. For example, node A₁ may indicate breed in a binary scale (e.g., East Friesian/Lacaune), whereas node A₄ indicates milk yield using a continuous scale (e.g., liters). Nodes are connected to each other by directed edges, or arrows; each of these arrows represents a direct causal effect from the variable at the arrow tail (i.e., cause) to the variable at the arrow head (i.e., effect). For example, in Figure 1, the arrow from A₃ pointing to A₄ indicates a direct effect of prolificacy on milk yield. Importantly, the causal directionality conveyed by arrows does not presume any specific functional form; that is, the effect of A₃ on A₄ may be linear or nonlinear (e.g., quadratic, sigmoidal, stepwise, threshold, or other) and either positive or negative in sign and varying in magnitude. Notably, arrows also indicate temporal order of the nodes, thus eliciting the sequence of events such that A₁ preceded A₃, which in turn preceded A₄. It is also common to interpret arrows as “kinship” relationships following the direction of the arrows. For example, A₁ is a parent to child node A₃, which in turn is a parent to child node A₄. Meanwhile, node A₁ is a common ancestor to nodes A₃ and A₄ (both directly and through A₃), whereas A₄ designates a common descendent to all other nodes in Figure 1 (Supplementary Material for implementation details).

Figure 1.

Hypothetical network illustrating connections between breed, parity, and prolificacy, and their combined effects on milk yield of dairy sheep, as adapted from Ferreira et al. (2017).

By their very presence, nodes and arrows define a DAG and explicitly indicate the causal relationships that do exist, or are believed to exist, between variables. These relationships are usually the focus of interest for the subject-matter scientist. Yet, for the purpose of studying causality, it is the arrows that are absent from a DAG that yield the most important information. A missing arrow indicates absence of any causal direct effect between a pair of variables and thus represents independence constraints between variables in a multivariate joint distribution (Pearl, 2010). For this reason, missing arrows are essential to extract causal information from observational data. Note, however, that scientists are often more focused on what relationship is or could exist, as opposed to what does not.

By convention, DAGs seldom display the so-called “idiosyncratic causes,” which typically represent exogenous causes assumed to affect each variable independently. Examples of idiosyncratic causes are independent error terms defined for each variable, such as e₁ → A₁ or e₄ → A₄ (Pearl, 2010). Although statistically relevant to explaining the behavior of each node, such idiosyncratic causes provide no assistance for identification of causal effects and thus are not displayed in DAGs.

Paths: Flow of Association

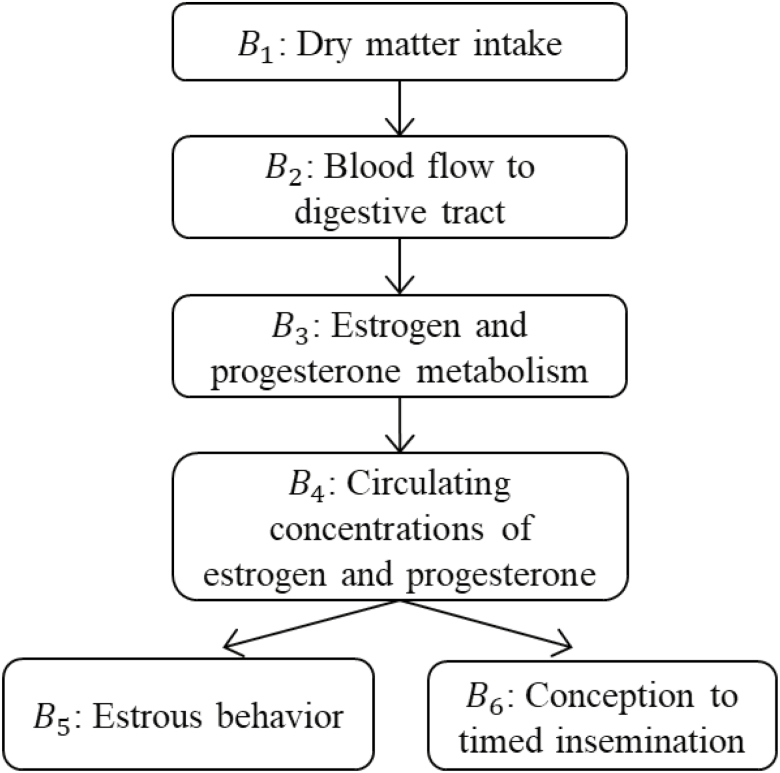
Having defined nodes and arrows as the granular components of a DAG, consider now their combination to define paths. Any sequence of consecutive edges connecting 2 nodes is defined as a path. Importantly, a path can pass through a given node only once (i.e., a path is, by definition, nonintersecting). Paths play a critical role in DAGs because all associations between nodes travel along paths (Pearl, 2010). Notably, the direction of the edges is irrelevant to the definition of a path. All edges on a path may be oriented in the same direction, in which case the path is considered causal. If at least one of the arrows on a path points against the flow, the path is considered noncausal. Causal paths allow associations to flow between nodes and thus induce observable associations in data. Noncausal paths may or may not, depending on their configuration, allow for flow of associations. Any observable association transmitted along a noncausal path is considered spurious. For example, consider the hypothetical causal network in Figure 2 illustrating the effects of dry matter intake on reproductive outcomes of dairy cattle, as adapted from Wiltbank et al. (2006). The sequences B₁ → B₂ → B₃ → B₄ and B₅ ← B₄ → B₆ both constitute paths and transmit associations between the corresponding end nodes. The first path illustrates a causal effect of B₁ (i.e., dry matter intake) on B₄ (i.e., circulating hormonal concentrations) mediated by B₂ (i.e., blood flow to the digestive tract) and by B₃ (i.e., liver metabolism of reproductive hormones); the second path describes a noncausal, thus spurious, relationship between B₅ (i.e., estrous behavior) and B₆ (i.e., conception to timed insemination) that is mediated by the common cause B₄. In a given DAG, it may be possible to isolate multiple paths connecting a pair of nodes; this process can be easily streamlined using software (Supplementary Material).

Figure 2.

Hypothetical network illustrating the effect of dry matter intake on reproductive performance of dairy cattle, as adapted from Wiltbank et al. (2006).

As mentioned above, all associations, be they causal or spurious, travel along paths. However, not all paths transmit associations: only open paths do, whereas blocked paths do not (Pearl, 2000, 2009). A path is considered open unless it contains a special type of node known as a collider. A collider is a node on a path with 2 arrows pointing into it. Consider, for example, the hypothetical causal network in Figure 1. In this case, A₃ (i.e., prolificacy) serves as a collider on the path A₁ → A₃ ← A₂ connecting breed (A₁) and lactation (A₂). The presence of collider A₃ effectively closes the path, thus blocking the flow of association between A₁ and A₂. In fact, all paths connecting A₁ and A₂ in Figure 1 contain a collider and are thus blocked, thereby rendering A₁ and A₂ marginally independent of each other. Colliders are notably path-specific, meaning that a given node, say A₃ can be a collider in one path (such as the one described above), but not in another (e.g., A₁ → A₃ → A₄).

Conditioning as a Tool to Control the Flow of Association

The information-transmitting status of a path can be modified. That is, an open path can be blocked whereas a naturally closed path can be unblocked, thereby stopping or reopening transmission of information, respectively. One of the most common strategies used to modify the flow of association along a path is conditioning. Broadly, conditioning involves incorporating information on the realized values of variables and taking this information into consideration when assessing dependencies between variables, as well as causal effects of interest (Elwert and Winship, 2014). In the animal sciences, conditioning often takes the form of regression control through the practice of covariate adjustment whereby realized values of explanatory variables are included in the linear predictor of a statistical model (Dohoo et al., 2009), producing a regression function $E\left(Y|X=x\right)$ (i.e., mean value of Y given realized value x of random variable X). In this way, any effect of a covariate can be “adjusted for” or “controlled for” before focusing on the behavior of a response variable as a function of a treatment or exposure of interest (Milliken and Johnson, 2001).

Other forms of conditioning may not be so obvious (Dohoo et al., 2009). Examples include data stratification, as illustrated by clustered data structures (e.g., animals managed in pens) or by the common practice of blocking by parity in dairy cattle experiments. Group-specific analysis is another way of implicit conditioning, for instance, in the context of a multiherd study for which data analyses may be conducted separately for each herd. Also, selective data collection poses an implicit conditioning mechanism through the specification of an inclusion criterion. For example, a study carried out in multiparous cows implies a construed fertility-based selection criterion, as only cows that got pregnant and calved in a timely manner during their first lactation can be recruited. Based on any of these practices, a causal effect of interest may be inadvertently, though effectively, conditioned on a stratum (i.e., parity), a specific group (i.e., herd), or a selection criteria (i.e., previous fertility). An additional flavor of conditioning is that of nonresponse (Dohoo et al., 2009), such as censoring or attrition, as illustrated by culling practices. Any analysis restricted to those animals not culled inherently implies conditioning on the reason for culling. If such reason were associated with the causal effect of interest, the implicit conditioning could be relevant.

TYPES OF ASSOCIATIONS AND CORRESPONDING BIASES

Using paths as functional units amenable to control by conditioning, it is possible to characterize, and at times even manipulate, the flow of associations between nodes in a network in order to dissect the causal mechanisms that underlie observable associations. For this purpose, associations are traced back to 3 basic path configurations, namely, chains, forks, and inverted forks (Pearl, 2000, 2009), as described in detail below. Conveniently, each of these path configurations can, in turn, be aligned with a type of bias induced by conditioning strategies that either disrupt causal effects or incorrectly transmit noncausal associations, as summarized in Table 1.

Table 1.

Basic types of path configurations found in a directed acyclic graph (DAG), corresponding types of associations implied by paths, and sources of biases due to conditioning practices

Basic path configuration in a DAG	Type of association implied by the path	Type of bias for estimation of causal effects	Bias resolution
Chain B1 → B2 → B3 → B4 → B5	Causal effect, from B1 to B5	Overcontrol bias induced by conditioning on at least one of the mediators B2, B3 or B4, thus blocking the path from B1 to B5 B1→ B2 → B3 → B → B5 B1 → B2 → B3 → B4 → B5 B1→ B2 → B3 → B4 →B5	Do not condition on any of the mediators B2, B3 or B4
Fork B5 ← B4 → B6	Noncausal association between B5 and B6 due to the common-cause variable B4	Confounding bias due to the naturally open path through common cause B4	Condition on the common-cause variable to block the non-causal path: B5 ← B4 → B6
Inverted fork D1 → D3 ← D2	No association (i.e., marginal independence) between D1 and D2. Path is naturally blocked by collider D3	Endogenous selection bias or common-outcome bias induced by conditioning on collider D3: D1 → D3 ← D2	Do not condition on the collider D3 to avoid reopening a naturally blocked noncausal path

Conditioning is depicted in the table by boxing the variable that is being conditioned on. DAGs in Figures 2 and 4 are used for illustration.

Chains and Overcontrol Bias

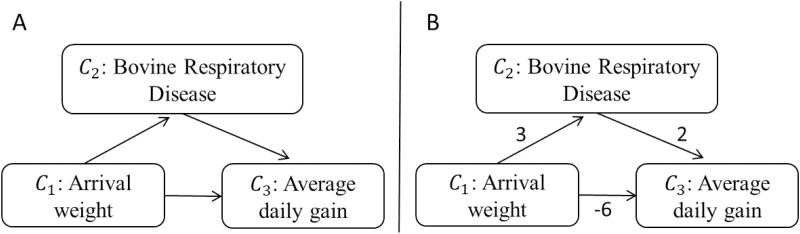
First, consider the path configuration of chains, as in the path B₁ → B₂ → B₃ → B₄ → B₅ in Figure 2. A chain conveys a directed causal effect between the end nodes, specifically from a node in the upstream path position (i.e., B₁) to another node downstream in the path (i.e., B₅). This effect is reflected in marginal pairwise associations between the nodes. Chains can convey causal effects either directly or indirectly through an intermediate mediator. Figure 3 illustrates 2 chain paths transmitting the effect of arrival weight (i.e., C₁) on beef cattle performance (i.e., C₃) in a simplified feedlot production system (adapted from Cha et al., 2017). One of the paths shows a direct effect (i.e., C₁ → C₃), whereas the other one indicates an indirect effect (i.e., C₁ → C₂ → C₃) mediated by the health indicator C₂. Conditioning on the mediator C₂ effectively intercepts the health-mediated indirect effect, thus disrupting the corresponding total causal effect of arrival weight on average daily gain. A conditioning action that intercepts a causal effect along a chain is said to induce overcontrol bias (Table 1). The total causal effect may be partially disrupted by overcontrol bias or it may be completely nullified. In the context of Figure 2, for instance, conditioning on any of nodes B₂, B₃, or B₄ would intercept the causal effect of B₁ on B₅ and render dry matter intake and estrous behavior conditionally independent of each other.

Figure 3.

Hypothetical causal network illustrating direct and indirect effects between weight performance and health indicators (A) in a beef feedlot production system, as adapted from Cha et al. (2017). (B) extends the graph in (A) to illustrate a hypothetical situation of lack of faithfulness due to cancelation of direct and indirect effects. Units of each direct causal effect are suppressed for simplicity.

Forks and Confounding Bias

A second path configuration involves forks. Forks occur when 2 nodes share a common cause, as is the case in Figure 2 with path B₅ ← B₄ → B₆, connecting behavioral estrus (B₅) and conception to timed insemination (B₆). The node at the vertex of the fork, namely, circulating hormonal concentrations (B₄), constitutes a shared source to both B₅ and B₆, thus rendering the latter nodes marginally associated with each other, though spuriously so (i.e., not causally). Unless controlled away by conditioning on the common-cause B₄, one may erroneously conclude that there is a causal effect of B₅ on B₆ (or vice versa).

Consider now Figure 1, whereby prolificacy has a direct effect on milk yield (i.e., A₃ → A₄), though these 2 variables are also connected by the common causes A₁ and A₂ through the forks (A₃ ← A₁ → A₄) and (A₃ ← A₂ → A₄), respectively. Unless these common causes are conditioned on to block transmission of associations along the corresponding forks, any assessment of the actual causal effect A₃ → A₄ will be biased in magnitude. Failing to condition on common-cause nodes along a fork introduces the so-called confounding bias (or common-cause bias).

Inverted Forks and Endogenous Selection Bias

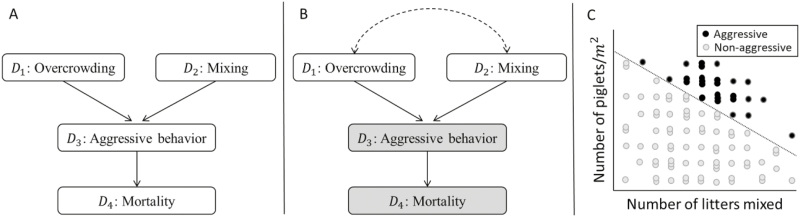
A third and last type of path configuration is that of inverted-forks. There, the path between 2 nodes goes through a collider (or common-outcome variable). For illustration, consider the hypothetical network in Figure 4A describing aggressive behavior in pig (i.e., D₃) caused by management practices, namely, overcrowding (i.e., D₁) and group mixing (i.e., D₂). In this DAG, nodes D₁ and D₂ are connected only through the path D₁ → D₃ ← D₂ containing the common outcome D₃, which acts as a collider that naturally blocks the flow of association between D₁ and D₂, rendering them marginally independent, as apparent from the scatterplot in Figure 4C. Indeed, for this example, we consider these management practices to be independent of each other, as one does not cause the other, neither do they share a common cause. However, if one were to focus on the groups of pigs for which aggressive behavior was apparent (i.e., black circles in Figure 4C), the actual null association between D₁ and D₂ gives way to a spurious negative relationship whereby aggressive groups of pigs with greater mixing rates tend to also have lower crowding density, and vice versa. That is, knowledge of low animal density in aggressive groups suggests that a mixing event was likely the culprit. The practice of focusing on aggressive groups of pigs may be considered akin to data-subsetting, group-specific analysis, imposing of a selection criterion or even covariate control for aggressiveness. In any case, focusing on aggressive groups effectively amounts to conditioning on the collider D₃. Doing so unblocks the flow of association along the inverted fork and induces a noncausal spurious association between the end nodes D₁ and D₂; this is called common-outcome bias or endogenous selection bias (Pearl, 2000, 2009; Elwert and Winship, 2014) and is depicted in Figure 4B. by a dashed line connecting the affected nodes D₁ and D₂.

Figure 4.

(A) Hypothetical network illustrating an inverted fork type of path configuration in the context of piglet behavior (Merk Manual Veterinary Manual Online at http://www.merckvetmanual.com/behavior/normal-social-behavior-and-behavioral-problems-of-domestic-animals/behavioral-problems-of-swine). (B) The same network is depicted where conditioning (represented in gray) on either aggressive behavior (D₃) or mortality (D₄) creates a spurious association between overcrowding (D₁) and mixing (D₂), represented by the double-headed dashed arrow line. (C) Scatterplot of groups of pigs that either showed aggressive behavior (•) or did not (°), characterized by animal density (expressed as number of piglets/m²) and level of mixing (expressed as number of litters mixed).

To beware, the descendent of a collider can serve as a troublesome proxy of the collider due to the information overlap inherent to the kinship between the two. In the context of Figure 4B, conditioning on the descendent node D₄ is akin to conditioning on the collider D₃ itself and is likely to have similar consequences for the perceived relationship between D₁ and D₂. In fact, the better a proxy the descendent variable is, the more pronounced the spurious association between the parent nodes resulting from conditioning on it (Elwert and Winship, 2014).

Spurious associations due to endogeneous selection bias seem to be quite prevalent, mostly because they can be inadvertently introduced through ubiquitous practices, as illustrated above, and this is often unintentional and not always obvious (Dohoo et al., 2009; Elwert and Winship, 2014; Valente et al., 2015). Despite any sound subject-matter justification for conditioning on a collider, and even if such conditioning is not explicit, the harmful biasing effects of this practice are not diminished.

Recap

In summary, the type of path configuration connecting nodes in a network and conditioning practices (or lack thereof) along such paths determines the types of associations between nodes. Some transmitted associations are causal in nature, others are not. Noncausal associations that are either not properly blocked or artificially induced can bias causal associations. Such biases can be interpreted as analytic mistakes, either of omission (i.e., by failing to condition, as with confounding bias) or of commission (i.e., by inappropriate conditioning, as in overcontrol bias or endogeneous selection bias).

DIRECTED SEPARATION

In complex causal networks, two nodes of interest may be connected by multiple paths that jointly transmit combinations of causal effects and noncausal associations, which are eventually reflected in associational patterns in data. In these situations, reconciling causality with observable associations is challenging. Verma and Pearl (1988) proposed the concept of directed separation, or d-separation for short, to enable translation between the language of causality, as implied by DAGs, and the probabilistic density functions onto which statistical inference from data is founded. More specifically, d-separation is a graphical criterion that determines which paths (and under what conditions) transmit associations, and which ones do not. The primary theoretical developments state that “if all paths between two variables A and B are blocked (i.e. d-separated), then A and B are statistically independent, […whereas…] if at least one path between variables A and B is open (i.e. d-connected), the two variables are statistically dependent (i.e. associated)” (Verma and Pearl, 1988). For example, consider the 4 paths connecting breed (A₁) and lactation (A₂) in Figure 1, namely, A₁ → A₃ ← A₂, A₁ → A₃ → A₄ ← A₂, A₁ → A₄ ← A₂, and A₁ → A₄ ← A₃ ← A₂. All 4 paths are naturally blocked by colliders A₃ or A₄, thus rendering breed and lactation mutually independent of each other, as might be expected. Furthermore, d-separation contemplates changes in the natural information-transmitting status of a path through conditioning.

From a practical standpoint, d-separation enables direct reading of all implied pairwise dependencies and independencies, both marginal and conditional, out of a DAG. Such association patterns can be expected to show in data and thus constitute the so-called testable implications of the causal assumptions embedded in a DAG (Pearl, 2000, 2009); these can be readily obtained from software (Supplementary Material). Testable implications can be used to crosscheck the proposed causal model with actual data for consistency, or even to learn about structural aspects of the DAG (Spirtes et al., 1993, 2001; Valente et al., 2010). Successful examples of doing so span a growing spectrum of applications in the animal sciences (Valente et al., 2011; Bouwman et al., 2014; Inoue et al., 2016).

EQUIVALENCE CLASSES

The causal mechanisms outlined in a DAG elicit a completely resolved pattern of correlations that is unambiguously defined through d-separation and that, sampling error notwithstanding, can be recovered from observed data, provided that the condition of faithfulness (to be discussed later) is met. However, the opposite is not necessarily true. That is, a pattern of testable implications and subsequent correlations in observed data may not be unique to a single DAG (Pearl, 2000, 2009). Herein lays the fundamental ambiguity of making causal claims from observational data, as more than one DAG may encode the same joint probability distribution and, thus, yield the same set of marginal and conditional independencies in data. As such, causally distinct models (i.e., different DAGs) with identical testable implications for patterns of conditional independence are said to be observationally equivalent (Pearl, 2000, 2009). Observationally equivalent DAGs are characterized by the same nodes and a shared skeleton of partially directed edges, the direction of which cannot be fully determined based solely on correlational data patterns; rather, substantive knowledge is required.

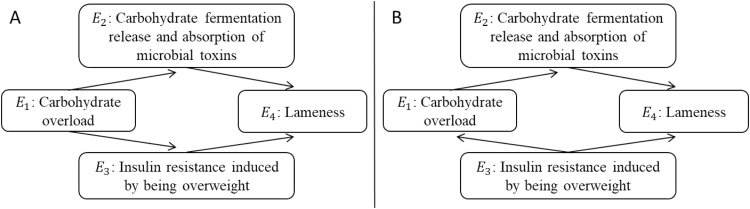
As such, observational data can be used to distinguish between DAGs from different equivalence classes, but it is not possible to make distinctions within a class. Equivalence classes are discriminated based on the pattern of so-called v-structures, defined by colliders whose parents are not directly connected by an arrow, also known as unshielded colliders (Pearl, 2000, 2009). V-structures determine a conspicuous pattern of conditional independencies in the joint probability distribution of data. For illustration, consider Figure 5 depicting 2 observationally equivalent causal models explaining nutritionally induced mechanisms for lameness in obese horses. Both of these causal models have the same v-structure (i.e., E₂ → E₄ ← E₃) and thus belong to the same equivalence class. The remaining edges connecting E₁ and E₂, as well as E₁ and E₃, could take any of the following directions within the equivalence class, namely, E₂ ← E₁ → E₃ as in Figure 5A, E₂ ← E₁ ← E₃ as in Figure 5B, or E₂ → E₁ → E₃. Any of the causal models so specified can be expected to yield data with the same correlation patterns, thus making it impossible to uniquely identify the true underlying causal mechanism; this illustrates the limits of inferring causality from data alone. That is, it would not be possible to use observational data to ascertain whether carbohydrate overload causes insulin resistance (i.e., E₁ → E₃) or whether the latter triggers the former (i.e., E₁ ← E₃). Subject-matter knowledge of the system of interest, such as physiological insight or temporal order, would be imperative to make any such distinctions.

Figure 5.

Hypothetical networks illustrating observationally equivalent mechanisms of nutritional induced lameness in obese horses, adapted from Kienzle and Fritz (2013).

IDENTIFICATION OF CAUSAL EFFECTS

Causal identification refers to the possibility of effectively purging any spurious components from observed associations, thereby enabling extraction of causal relationships between variables in a network. More formally, causal identification is the condition under which 2 nodes of interest in a DAG are d-separated along all noncausal paths, while remaining d-connected along all causal paths (Pearl, 2000, 2009).

In experimental studies, causal identification is a natural byproduct of randomization. As above mentioned, randomization is intended to remove any systematic common-cause confounding that might affect both the cause and the effect. Graphically, randomization can be reflected in a DAG by removal of any arrows pointing towards the presumed causal node (i.e., treatment), thereby dismantling any potential fork paths connecting it to the outcome of interest and preventing ensuing common-cause confounding.

With observational data inherently lacking randomization, we are forced to consider other strategies to reasonably ascertain causal identification. A number of graphical identification criteria have been developed, among which the so-called adjustment criterion (Shpitser et al., 2010) stands out for its practicality. Refined from Pearl’s back-door criterion (Pearl, 1993), the adjustment criterion relies heavily on conditioning by covariate adjustment. The key idea behind the adjustment criterion is to identify a subset of nodes in the DAG that must be conditioned on to enable blocking of all noncausal paths between the node pair of interest, without disrupting any causal paths between them. So implemented, the adjustment criterion enables dissection of causal effects from an observed association that may be cloaked with ambiguity due to noncausal components. A subset of variables fulfilling the adjustment criterion is called an adjustment set and is not necessarily unique; that is, multiple different subsets may achieve the same goal (Shpitser et al., 2010), thereby conferring considerable flexibility to this approach.

We illustrate how to implement causal identification by adjustment in the context of the DAG in Figure 1 and start by revisiting our previous discussion about assessing the causal effect of prolificacy (i.e., A₃) on milk yield (i.e., A₄). Accompanying software code is provided in Supplementary Material. The first step in eliciting an adjustment set to identify a causal effect of interest within the context of a DAG requires a comprehensive listing of all paths connecting the corresponding pair of nodes and distinguishing the causal paths from noncausal ones. For our example, we list 1 causal chain direct effect (i.e., A₃ → A₄) and 2 noncausal fork paths with common causes A₁ and A₂, namely, A₃ ← A₁ → A₄ and A₃ ← A₂ → A₄, respectively. Next, we consider if and how the noncausal paths may be blocked; in our case, doing so calls for conditioning on the fork vertexes, namely, A₁ and A₂. One should also take special care to avoid inadvertently opening any naturally blocked noncausal paths by conditioning on a collider; this does not seem to be a concern for our example as none of the listed paths include a collider. As a final check, we ensure that all causal paths remain open and untouched; again, this is not a concern in our case as the causal effect of interest is a direct effect (i.e., A₃ → A₄) and thus not amenable to adjustment by conditioning. Any subset of nodes that fulfills these conditions defines an adjustment set. If there were more than one causal path connecting the nodes of interest, the total causal effect would be identified as the sum of all connecting causal paths. Taken together, we notice that the subset consisting of both A₁ and A₂ fulfills the necessary conditions of the adjustment criterion and thus defines an adjustment set for causally identifying the effect of A₃ on A₄.

Also from Figure 1, consider now causal identification for the total effect of breed (i.e., A₁) on milk yield (A₄) of dairy sheep, as well as that for only the direct effect between them. A total of 3 paths connect A₁ and A₄, namely, 2 causal chains consisting of a direct effect A₁ → A₄ and an indirect causal effect A₁ → A₃ → A₄, as well as a noncausal path A₁ → A₃ ← A₂ → A₄ containing the collider A₃. The causal paths are naturally open, whereas the noncausal path is naturally blocked by a collider, so causal identification for the total causal effect of A₁ and A₄ is straightforward: the adjustment set is empty and no specific conditioning action is required. An alternative adjustment set containing only A₂ would also be viable for identification of the total effect, as conditioning on A₂ does not change the information-transmitting status of any of the paths connecting A₁ on A₄. That is, conditioning on A₂ is unnecessary but not harmful, though it could be useful if it accounted for noise, thus increasing precision. Note, however, that adjusting for A₃ biases the total effect of A₁ on A₄ in 2 ways, by blocking the indirect causal effect A₁ → A₃ → A₄ (i.e., overcontrol bias) and by unblocking the noncausal path A₁ → A₃ ← A₂ → A₄ (i.e., endogenous selection bias). Thus, conditioning on A₃ is harmful to identification of the total causal effect of A₁ on A₄ and should be avoided.

Consider now a related, though strikingly different situation: that of causal identification for only the direct effect of A₁ on A₄ (i.e., A₁ → A₄). In this case, conditioning on A₃ is required in order to block the indirect causal effect A₁ → A₃ → A₄. However, as noticed in the previous paragraph, conditioning on A₃ also unblocks the noncausal path A₁ → A₃ ← A₂ → A₄. It is then necessary to also condition on A₂ in order to ensure that the noncausal path remains blocked. Therefore, identification of the direct causal effect of A₁ on A₄ requires that both A₂ on A₃ be adjusted for.

Taken together, the cases discussed above illustrate that elicitation of an appropriate adjustment set depends on the specific causal effect of interest within a DAG (Greenland et al., 1999). Moreover, any conclusions about causal identification are conditional on the validity of the causal model stated in the DAG (Pearl, 1995; Greenland et al., 1999).

To note, causal identification as discussed in this section, is a distinct concept and should not be confused with the concepts of estimation, parameter identifiability, and goodness of fit, which have a purely statistical connotation related to model complexity and sample size (Wu et al., 2010). In fact, when causal claims are the ultimate goal, causal identification is advocated as a pre-requisite to model fitting, parameter estimation, and statistical inference (Elwert, 2013). In other words, without causal identification, statistical identifiability is but a moot point. Instead, if the goal is prediction of new observations, causal knowledge may be helpful but it is not necessarily required (Valente et al., 2015).

CAUSAL ASSUMPTIONS: NONTRIVIAL, YET UNAVOIDABLE

Any modeling exercise inherently requires simplification of a much more complex reality so that the main driving features of the process of interest are captured in the mathematical expression of a model. As a consequence, modeling inevitably implies simplifying assumptions. Graphical causal models such as DAGs are no exception.

Similarly, causal identification necessarily requires assumptions, specifically causal assumptions (Pearl, 2000, 2009) that are qualitative in nature and cannot be tested directly on data. As such, untangling of causal effects from observational data relies heavily on substantive theoretical knowledge of the mechanisms that presumably underlie the data generation process. More specifically, any causal claims from observational data are based on the following 3 critical assumptions:

• 1) The first fundamental condition invoked by causality is that of causal sufficiency, which essentially states that the DAG captures all the causal structure relevant to the process of interest. In other words, any confounder is known and either has been measured or can be accounted for by other measured variables. Causal sufficiency is the fundamental condition for claiming causality from observational data and poses a serious limitation (Robins, 1999). In fact, it is the very “Achilles heel” of the causality endeavor, as it cannot be guaranteed to hold in an observational setting and cannot be tested on data. Although the assumption may seem reasonable in a specific context, there is always the possibility of additional unknown players in the system.

• 2) On a more technical note, causality from observational data invokes the Markov condition, the local version of which states that, given complete information on its parents, a node is conditionally independent of all nondescendent variables in the network. Relatedly, in its global version, the Markov condition states that, given its Markov Blanket (defined by its parents, children and spouses), a node is conditionally independent of any other variables in the network (Pearl, 2000, 2009).

• 3) Finally, the assumption of faithfulness or stability guarantees that total causal effects are not effectively canceled out by competing causal paths of opposite signs. For numerical illustration, Figure 3B shows a hypothetical situation of lack of faithfulness, with units removed for simplicity. Here, the direct and indirect effects of arrival weight (C₁) on average daily gain (C₃) have the exact same absolute magnitude but opposite signs (i.e., direct effect = (−6); indirect effect = 3*2 = 6). As a result, the effects of both paths cancel each other out, yielding a deceptively null total effect that fails to reflect the underlying causal mechanisms.

Understandably, these assumptions can make scientists uncomfortable, particularly given that, except for the Markov condition, they are not testable from data. Yet, making assumption-free causal claims from observational data is essentially impossible. One may then argue that it is not about the existence of assumptions per se but rather about the quality of such assumptions. Substantive knowledge within a scientific domain, such as the animal sciences, lays at the core of credible causal assumptions; DAGs help articulate such knowledge and corresponding assumptions in an inherently transparent and concise manner.

Causal assumptions are fundamentally different from, and take precedence over, statistical assumptions (Pearl, 2000, 2009), including those often made in the context of linear models commonly used in the animal sciences, namely, independence, distributional behavior, and functional forms. Normal linear approximations, as implemented by linear models, have turned out to be surprisingly robust (or at least adaptable) to departures from basic statistical assumptions, due in no small part to the auspice of the Central Limit Theorem and to the fact that linear models often provide reasonable local approximations to a problem. Indeed, reasonably hardy inference can often be observed even under conditions of outright violations of statistical assumptions (Larrabee et al., 2014). It is then perhaps not surprising that oftentimes statistical assumptions receive little attention or are overlooked during a modeling exercise, despite at-times-serious detrimental consequences. Special care should be exercised to avoid this attitude from permeating the causality framework, whereby qualitative causal assumptions are in direct trade-off with the theoretical and methodological sophistication that empower causal inference from observational data.

Also worth noticing is that the underlying causal assumptions are not necessarily overcome by large sample sizes. In fact, large sample sizes do not mitigate structural biases and can, in some cases, make matters worse by inducing a false sense of security based on yielding highly precise, though biased, estimates (Lazer et al., 2014; Hemani et al., 2017). This has direct implications for making causal claims from “big” observational datasets, including operational data from livestock production systems.

PRACTICAL CONSIDERATIONS FOR EXPLORING CAUSALITY FROM OBSERVATIONAL DATA

Causal learning from observational data using DAGs is already making inroads in the animal sciences, particularly through the parametric expression of DAGs as structural equation models, which encode a multivariate system of linear regression equations. Applications in the field range from quantitative genetics (Gianola and Sorensen, 2004) to molecular genetics (Penagaricano et al., 2015a), to physiology (Penagaricano et al., 2015b) and management (Theil et al., 2014), among others.

Of special interest to modern animal scientists is the increasing availability of “big” operational data and the unprecedented opportunity they offer to learn about interconnections among animal physiology, management practices, and environmental conditions in the context of livestock production systems. Further insight will likely require an open-minded approach that is rigorous and methodical to carefully specify the causal question of interest, followed by use of graphical tools to visualize the structure of the system and assess causal identification, along with explicit elicitation of conditions and assumptions. Only then, if granted, may one implement specialized statistical tools for estimation and inference from data.

Recall, though, that causal insight from observational data is subject to restrictions and may be limited, even unsatisfactory. Ultimately, the evidence to support causal claims from observational data may not be as strong or clean as that from experimental data. Yet, in the absence of randomization, the mainstream alternative to causal inference remains complete ignorance. This is hardly acceptable given the undeniably opportunities to improve the knowledge basis, as posed by the causal revolution instigated by Pearl and colleagues. In the words of Pearl (2000, 2009), “…although [it may not be possible] to distinguish genuine causation from spurious covariation in every conceivable case, in many cases it is.” To the inevitable follow-up question on how safe this task really is, his “[the] answer is: not absolutely safe, but good enough to tell a tree from a house and good enough to make useful inferences without having to touch every physical object that we see.” To this end, we discuss practical considerations and cautionary notes to facilitate causal learning from observational data.

The Importance of Substantive Knowledge

First and foremost, substantive knowledge about the system of study is absolutely critical to make any causal claims from observational data. As mentioned previously, DAGs can serve as invaluable tools to explicitly articulate this knowledge and its limitations in meaningful ways. Specifically, DAGs can help visualize the structure of a system and clarify what effects can be causally identified (and which ones cannot).

By contrast to substantive knowledge, the practice of blind mining of correlational data patterns for potential causal effects should be avoided, especially as scientists recognize the all-too-common fallacy of just-so storytelling or Justifying After Results are Known (i.e., JARKing) (Nuzzo, 2015). Some aspects of a DAG can be learnt from data (Spirtes et al., 1993, 2001; Valente et al., 2010), but a comprehensive DAG specification is not a process amenable to automation; a keen understanding of the subject matter is imperative.

Considerations on the Complexity of DAGs

In practice, substantive knowledge about a system is reflected, for example, on the density of arrows in a DAG. Density of arrows determines the number of paths connecting any 2 nodes of interest and thus is of direct relevance to causal identification. Arrows should be dictated by substantive knowledge and thus are not necessarily amenable for negotiation. Yet, a kin awareness of the implications associated with density can be helpful during practical implementation.

With many nodes in a densely interconnected network, causal identification may be difficult and DAGs can easily become unmanageable. Recall that presence of an arrow represents a plausible causal effect, or at least an unwillingness to exclude the possibility of such effect (Pearl, 2010). In fact, if in doubt, the standard recommendation calls for keeping the arrow in a DAG so as to recognize the corresponding uncertainty (Pearl, 2010). In turn, a missing arrow between a pair of nodes makes the much stronger and more informative statement of no direct causal effect between them, with the corresponding signature of conditional independence in the joint probability distribution. It is thus not surprising that sparser, more parsimonious DAGs are easier to handle and can facilitate extraction of causal information, provided their proper substantiation by subject-matter knowledge.

Even when a densely connected DAG allows for causal identification, there is the additional challenge of parameter identifiability for statistical estimation (Wu et al., 2010). For illustration, consider a DAG composed of 10 nodes, the densest version of which consists of 45 (= 10*(10–1)/2) directed edges corresponding to 45 covariance parameters. By contrast, a sparser DAG would entail a more parsimonious causal model (Rosa et al., 2016), often a desirable statistical feature particularly in multivariate modeling.

For contrast, consider incorporating new nodes into a DAG. Doing so can introduce new information into the system and thus be of assistance for causal identification (Pearl, 2000, 2009). Perhaps the most simplified case entails a research question targeting the causal effect between 2 variables. Observational data available on just these 2 variables is rarely enough to assess potential causality; additional variables relevant to the system will be required to control for biases and enable causal identification. As DAGs incorporate more data through new nodes, computational burden should also be taken into consideration.

Biases as Preventable Analytical Errors

Biases, particularly those unknown or unforeseen, pose constant threats when working with observational data and can be inadvertently introduced through analytical errors of omission or commission brought about by misguided conditioning practices, as previously explained. Therefore, it is critical that the thought process of specification of causal models in the form of DAGs, along with causal identification of effects of interest, precedes the exercise of statistical modeling, parameter estimation, and inference. In particular, special care should be taken to avoid collapsing the process of eliciting the conceptual causal framework with code writing and implementation of statistical software.

Such cautionary note may be considered the observational-data-equivalent to proper planning and design of randomized experiments. In his well-known quote “To consult the statistician after an experiment is finished is often merely to ask him to conduct a post mortem examination. He can perhaps say what the experiment died of,” Sir Ronald A. Fisher (1890–1962) emphasized the importance of scientific thought early on in the experimental process, certainly prior to data collection and analysis. In the animal sciences, large operational datasets are often readily available to the researcher without the possibility of any a priori thought. Such instantaneous availability can at times give the false impression of circumventing careful thought. Much to the contrary, when dealing with observational data, it is paramount that deliberate attention is placed on specifying whether, and if so how, an effect of interest can be causally identified from the information available, thus preventing the structural problems posed by biases. Meaningful statistical estimation and inference can proceed only if that is indeed the case.

Asymmetry of Causal Models vs. Reversible Assignment of Statistical Models

In the animal sciences, standard linear models such as regression, analysis of variance, and mixed models arguably constitute the workhorse of statistical practice. Yet, statistical models are not the same as causal models, as encoded in DAGs (Pearl, 2000, 2009); this distinction is particularly relevant for the analysis of observational data. In a DAG, the arrow in V₁ → V₂ implies a directed, inherently asymmetrical, causal effect from V₁ to V₂. Meanwhile, the equal sign “=” in a regression-type linear model such as V₂= f₁ (V₁) represents a mere assignment mechanism that is reversible and thus, innately unconnected to any specific causal claim. Indeed, a regression equation can be easily turned around such that V₁= f₂ (V₂); this is called reverse regression (Pearl, 2013) and is often used for validation of new measurement instruments, for calibration against known standards and even for predictive purposes. Regardless of orientation of the regression assignment, the causal effect V₁ → V₂ implies that V₂ will respond to changes in V₁, whereas V₁ will remain impervious to changes in V₂.

Differing Goals: Prediction and Causality

Since causal identification can be obtained by adjustment, it seems to be a common misconception that “adjusting for more variables is better.” Unprincipled covariate adjustment or selection of explanatory variables into a model based purely on associational criteria cannot only fail to remove existing biases, but even introduce new ones (Elwert and Winship, 2014; Valente et al., 2015). In other words, for causal insight, the practice of throwing the “kitchen sink” of available explanatory covariates into a regression is not only a nonviable solution, but it may actually make matters worse and lead the analyst astray.

Rather, the specific criterion for selecting variables for adjustment should be determined based on the ultimate goal of a modeling task, whether prediction of new observations or inference on a causal mechanism (Valente et al., 2015). For predictive purposes, the minimal subset of explanatory variables needed for conditioning is determined by the Markov Blanket (Pearl, 1988). As previously indicated, a Markov Blanket consists of the parents and the children of the variable to be predicted, as well as all other nodes that share a child with it (i.e., spouses), and is thus readily apparent from a DAG. Importantly, conditional on its Markov Blanket, a variable is independent of all other variables in the DAG. This concept has been successfully exploited for predictive purposes in agriculture (Scutari et al., 2013; Felipe et al., 2015). For illustration, consider making predictions on node E₂ in Figure 5. In either panel, such prediction would entail joint adjustment for E₁ (i.e., parent), E₄ (i.e., child), and E₃ (i.e., spouse) (Table 2). If additional network variables outside of the Markov Blanket were available, their inclusion for adjustment would be neither necessary nor harmful for prediction, though it may pose computational and statistical challenges due to unnecessary model complexity.

Table 2.

Subsets of explanatory variables to be conditioned on for the purpose of prediction and causal inference

Purpose of the modeling task	Conditioning variables in the model	True causal mechanism
		Figure 5A	Figure 5B
Prediction of E2	Necessary	E1, E3, E4	E1, E3, E4
	Harmful	None	None
Inferring the causal effect of E3 on E2	Necessary	E1a	Nonea
	Harmful	E4	E1, E4

Refer to Figure 5 for the corresponding causal mechanisms.

^aBy construct, E₃ is the presumed causal node and thus should be included in the linear predictor, along with any conditioning variables, if applicable.

For causality purposes, however, the selection of variables for adjustment is not so permissive and needs to be specifically catered to causal identification of the targeted effect within the mechanistic structure described in the DAG. In this case, the adjustment criterion is critical to decide which variables should and which others should not be controlled for to effectively separate causal effects from noncausal spurious associations without introducing new biases. For example, reconsider the DAGs in Figure 5 for inferring upon the (actually null) causal effect of E₃ on E₂. Specification of the appropriate adjustment set in each case would depend on substantive knowledge of the mechanisms connecting E₃ and E₂, either those in Figure 5A or Figure 5B. In Figure 5A, nodes E₃ and E₂ are connected through 2 paths, namely, a fork (i.e., E₃ ← E₁ → E₂) and an inverted fork (i.e., E₃ → E₄ ← E₂), both of which are noncausal in nature and thus should not be allowed to transmit associations. This is straightforward to accomplish by conditioning on the vertex E₁, while realizing that the inverted fork path is naturally blocked by the collider E₄ and does not require any action. Therefore, an appropriate adjustment set for assessing the causal effect of E₃ on E₂ based on the DAG shown in Figure 5A should include E₁ but not E₄ (Table 2).

In contrast, in Figure 5B, nodes E₃ and E₂ are connected by a chain path through E₁ (i.e., E₃ → E₁ → E₂) and also by an inverted fork (i.e., E₃ → E₄ ← E₂). The first path is causal and should not be disrupted; the second path, while noncausal, is naturally closed by collider E₄. Thus, it is imperative that neither E₁ nor E₄ be conditioned on, lest overconditioning bias blocks the transmission of causal information or conditioning on a collider introduces endogenous selection bias, respectively (Table 2).

With larger DAGs, it is possible that more than one set of variables satisfies the adjustment criterion for identification of a causal effect. In this case, the specific choice of variables to condition on may depend on practical issues, such as ease and expense of variable measurement. Also, more parsimonious adjustment sets (i.e., those containing fewer variables) are likely to be preferred.

Regardless of whether the modeling task is geared towards prediction or causality, DAGs provide a unified assessment strategy to decide on what variables to condition on and can also serve as tools to understand situations in which either conditioning or failure to condition on a variable may bias an empirical analysis.

A Few Shortcuts to Identification by Adjustment

When inferring causality, conditioning on a collider should be avoided whenever possible, thereby ensuring that naturally blocked paths remain blocked. Most often, colliders occur after the putative causal node and either before or after the putative downstream outcome (Dohoo et al., 2009; Pearl, 2013). For this reason, descendants of a putative causal node are often considered collider suspects, unnecessary at best, harmful at worst, and one should be wary about adjusting for them (Pearl, 2013; Elwert and Winship, 2014). This is consistent with the standard analysis of covariance recommendation that discourages the use of post-treatment variables as explanatory covariates (Milliken and Johnson, 2001).

Instead, consider conditioning on variables that are upstream from the putative causal node along the DAG, ideally its parent nodes, especially if such parent nodes act as common-cause confounders. In practice, though, one should be aware that this can have detrimental implications for model fitting and parameter estimation because adjusting for the parents of the putative cause will control its variability. This is known to impair stability and precision of parameter estimates in linear regression (Milliken and Johnson, 2001). Furthermore, one should refrain from conditioning on all parents of the putative downstream effect node and focus on those along noncausal paths connected to the putative cause, lest a causal path be inadvertently blocked. Be suspicious of nodes that, while upstream of the putative causal node, do not seem to have a credible causal mechanism on the affected node. These are often colliders in disguise and conditioning on them can cause trouble for causal identification (Elwert, 2013).

Analytic practices such as attrition, censoring, and data subsetting based on the affected node itself should be carefully reconsidered, as these effectively amount to conditioning on a collider, thereby potentially inducing endogenous selection bias (Elwert and Winship, 2014). Finally, if a node acts both as a collider and as a confounder along separate paths connecting variables of interest, such node should probably be conditioned on, though adjustment for additional variables will likely be required to ensure that any inappropriately reopened paths remain blocked.

Beyond Causal Identification by Adjustment

One of the main appeals of the adjustment criterion for causal identification is that it can be easily implemented in statistical linear methods, as the adjustment set defines what explanatory variables should be included in the linear predictor. Yet, causal identification by adjustment may not be possible in every scenario. When it is not, as cleverly illustrated in a sociological setting (Lalonde, 1986), standard regression-type estimators applied to observational data can perform quite poorly in estimating causal effects relative to randomized experiments. When identification by adjustment fails, standard linear models are not appropriate analytic tools for causal inference based on observational data and other, more advanced statistical methods must be considered.

Although beyond the scope of this review, the statistical toolbox available for causal inference is substantial, sophisticated, and in on-going development. Specific examples include instrumental variables (Angrist and Krueger, 2001), propensity scores (Rosenbaum and Rubin, 1983), matching (Rubin, 2006), and structural equation models (Gianola and Sorensen, 2004), among others. Importantly, though, none of these statistical methods can, by themselves, guarantee causality. Rather, it is the conceptual framework of causal models that provide the context and conditions under which causal claims from observational data may be admissible. As such, causal inference emphasizes the subject-matter core of the animal sciences while opening opportunities for targeted training in advanced quantitative methods as well as for collaborative research efforts across disciplines.

CONCLUSIONS

Understanding of causal effects is essential for efficient decision making that encompasses complex systems, such as animal agriculture enterprises. In this review article, we discuss a conceptual graphical framework based on DAGs and argue for their enabling capability for making causal claims from observational data under specified conditions. Despite inevitable ambiguities and inherent limitations, the growing field of causal inference indicates that there is indeed much to be learnt from observational data. We believe that the time to explore such opportunities is ripe, particularly within the animal sciences given the wealth of operational data increasingly available from commercial livestock operations. Thus, our goal in this review is to empower animal scientists to properly utilize such “big data” to enhance our causal understanding of livestock production systems beyond just mere nondirectional associations. We aim to educate animal scientists and make them aware of the difficulties and limitations associated with inferring causality from observational data. In a nutshell, it is not as simple as fitting a regression model and claiming a causal effect.

We emphasize the importance of the thought process underlying specification of causal models in the form of DAGs and that of causal identification of an effect of interest as requisite conditions for any data analyses that may follow. Deliberate elicitation of this conceptual framework is critical as no statistical methods or software tools can, by themselves, guarantee causality based solely on data. We further argue that biases due to spurious associations can be interpreted as analytic mistakes due to misguided conditioning practices and are thus preventable through a careful thought process based on substantive knowledge of the system under study. We provide practical recommendations to facilitate causal identification and inference, mostly by implementation of the adjustment criterion.

Recognizing that science advances on the accumulation of evidence, both experimental data and observational data, have arguably important roles to play as building blocks in the current research landscape. Beyond substantiating circumspect causal claims from observational data, causal inference can help better target experimental studies and aid in their design, thus ensuring efficient use of ever-shrinking research funds. Moreover, causal inference can enable broader evaluation of the validity of theories across diverse realistic conditions beyond the highly controlled research setting. As summarized by Judea Pearl in his parting message at a 1996 academic lecture on “The Art and Science of Causal Effects,” “Data is all over the place. The insight is yours. And now, an abacus is at your disposal.” We join him in the “hope that the combination amplifies each of these components” to the betterment of science, especially in our field of animal agricultural sciences.

SUPPLEMENTARY DATA

Supplementary data are available at Journal of Animal Science online.