Environmental effects on water intake and water intake prediction in growing beef cattle

Abstract

Water is an essential nutrient, but there are few recent studies that evaluate how much water individual beef cattle consume and how environmental factors affect an individual’s water intake (WI). Most studies have focused on WI of whole pens rather than WI of individual animals. Thus, the objective of this study was to evaluate the impact of environmental parameters on individual-animal WI across different seasons and develop prediction equations to estimate WI, including within different environments and management protocols. Individual daily feed intake and WI records were collected on 579 crossbred steers for a 70-d period following a 21-d acclimation period for feed and water bunk training. Steers were fed in 5 separate groups over a 3-yr period from May 2014 to March 2017. Individual weights were collected every 14 d and weather data were retrieved from the Oklahoma Mesonet’s Stillwater station. Differences in WI as a percent of body weight (WI%) were analyzed accounting for average temperature (TAVG), relative humidity (HAVG), solar radiation (SRAD), and wind speed (WSPD). Seasonal (summer vs. winter) and management differences (ad libitum vs. slick bunk) were examined. Regression analysis was utilized to generate 5 WI prediction equations (overall, summer, winter, slick, and ad libitum). There were significant (P < 0.05) differences in WI between all groups when no environmental parameters were included in the model. Although performance was more similar after accounting for all differences in weather variables, significant (P < 0.05) seasonal and feed management differences were still observed for WI%, but were less than 0.75% of steer body weight. The best linear predictors of daily WI (DWI) were dry mater intake (DMI), metabolic body weights (MWTS), TAVG, SRAD, HAVG, and WSPD. Slight differences in the coefficient of determinations for the various models were observed for the summer (0.34), winter (0.39), ad libitum (0.385), slick bunk (0.41), and overall models (0.40). Based on the moderate R² values for the WI prediction equations, individual DWI can be predicted with reasonable accuracy based on the environmental conditions that are present, MWTS, and DMI consumed, but substantial variation exists in individual animal WI that is not accounted for by these models.

INTRODUCTION

Water is a key nutrient that aids in temperature regulation, growth, digestion, metabolism, and excretion (NRC, 2000). More knowledge about how animals respond to environmental changes, especially how climate change might affect water intake (WI), would be useful (Mader, 2003). Understanding how weather changes affect cattle WI will allow producers to better manage water resources. This can be particularly important in the summer, when cattle exposed to high heat loads can have their thermal equilibrium disrupted, due to the key role of water in maintaining thermal equilibrium (Arias and Mader, 2011). The Livestock Weather Safety Index (LWSI; LCI 1970) has established benchmark levels for heat stress and use the temperature–humidity index (THI) to quantify environmental conditions. The THI equation used by LWSI only contains temperature and humidity as reported by Thom (1959) and NOAA (1976). However, later work by Mader et al. (2006) showed that temperature and humidity were not the only factors that affect heat stress. Mader et al. (2006) suggested that solar radiation (SRAD) and wind speed (WSPD) were also important factors contributing to heat stress in cattle.

Having the ability to accurately predict daily WI (DWI) could allow producers to better manage water resources and ensure adequate water availability. Winchester and Morris (1956) developed a method to predict WI by using ratios of WI to dry mater intake (DMI) at specific temperature thresholds. To build upon Winchester and Morris’s (1956) prediction equation, Arias and Mader (2011) examined how temperature differences during the summer and winter affected DWI for cattle managed in a commercial feedlot setting and used these data to develop WI prediction equations for summer, winter, and an overall model that includes average temperature (TAVG), SRAD, DMI, WSPD, average humidity (HAVG), and precipitation. Sexson et al. (2012) developed an equation to predict DWI in feedlot cattle using low, high, and average relative humidity; low and high temperature; low, high, and average sea level pressure; WSPD; body weight; previous day high temperature; and metabolic body weight (MWTS). Parker et al. (2000), Arias and Mader (2011), and Sexson et al. (2012) utilized pen WIs, and to the best of our knowledge, no contemporary studies have developed WI prediction equations utilizing individual animal daily feed and WI. The objective of this study was to characterize the impact of environmental conditions on DWI for individual animals and develop prediction equations for DWI utilizing both season and bunk management protocols.

MATERIALS AND METHODS

Study Design

All animal procedures were approved by the Institutional Animal Care and Use Committee at Oklahoma State University (protocol AG13-18) in accordance with Federation of Animal Science Societies (FASS, 2010) guidelines.

Over a 3-yr period, 38,543 daily feed and WI records for individual steers (n = 579) were collected using an Insentec system (Hokofarm Group, The Netherlands) in Stillwater, Oklahoma. Steers (n = 579) were crossbred or commercial Angus and fed in 5 separate feeding groups. This facility is located at latitude 36^o11ʹ N and longitude 97^o6ʹ W, with a mean elevation of 273.34 m above sea level and is classified as Cfa by the Koppen–Geiger Climate Classification (Kottek et al. 2006). Data were collected on each group using a 21-d acclimation period followed by a 70-d feed and gain intake test (BIF, 2016). The timing of trials allowed collection of data across different seasons: group 1 (n = 117) from May 2014 to August 2014, group 2 (n = 116) from November 2014 to January 2015, group 3 (n = 118) from May 2015 to July 2015, group 4 (n = 105) from June 2016 to August 2016, and group 5 (n = 123) from January 2017 to March 2017. Groups 2 and 5 were considered winter groups and the remainder was considered summer groups.

The facility contained 4 separate pens that comprise both shaded (103.0 m²) and unshaded (255.9 m²) areas. The barn is open on the south, has an automated curtain on the north side, and roll-up doors on the east and west side. The doors and curtain were opened during the summer to add ventilation and were closed during the winter.

All groups were fed the same growing diet that was approximately 4,524.6 cal/g gross energy on a dry matter basis (Allwardt et al., 2017). The percent dry matter was 74.02%, 73.70%, 73.11%, 73.24%, and 70.04% for groups 1, 2, 3, 4, and 5, respectively. Steers fed in groups 1 to 3 were managed using a slick bunk feed call procedure and steers fed during groups 4 and 5 had ad libitum access to feed. Regardless of the feed management protocol, all steers had ad libitum access to water. To ensure data quality, feed and WI records were filtered as outlined by Allwardt et al. (2017). Briefly, data were filtered for start and end weights, bunk visit duration, equipment malfunction, and weigh days to ensure that all records were reasonable and ad libitum conditions were achieved, wherever necessary. Because of the requirement for ad libitum feed intake (FI) in groups 4 and 5, FIs were also treated as missing in these groups on days that ad libitum intake was not achieved. Ad libitum feed was considered unfulfilled on days that the bunks were slick in between feed deliveries.

Individual body weights were collected every 14 d. The average daily gain (ADG) for each animal was obtained by regressing body weight over time to account for differences in fill. Individual daily weights (dWT) were calculated as follows:

$${\text{dWT}}_{\text{id}}=\text{Intercept}+\widehat{ADG}{\text{*day}}_{\text{d}}+{\text{e}}_{\text{id}},$$

where intercept is the weight of the individual animal when day is equal to zero, $\widehat{ADG}$ is the estimated average daily gain, dWT_id is the individual daily weights for the ith individual on the dth day, day_d is the dth day weights taken, and e_id is the random residual error.

Each DWI measure was converted to WI as a percent of body weight (WI%) by dividing DWI by dWT. Reporting WI as a percent of body weight for each individual daily measure roughly accounts for the difference in size of individuals.

Environmental Data

Weather data were obtained from the Stillwater station of the Oklahoma Mesonet (Brock et al., 1995) for the study dates. The Oklahoma Mesonet is a network of environmental monitoring stations covering Oklahoma and is maintained by scientists at the University of Oklahoma and Oklahoma State University. Data downloaded from Mesonet were daily maximum, minimum, and average temperature, relative humidity, average daily WSPD, and total daily SRAD (daily accumulation of SRAD), which were generated from measurements taken every 5 min throughout the day. Mesonet measures air temperature and relative humidity at 1.5 m above ground using a thermistor-sortion probe (Campbell Scientific, Inc., Logan, Utah; Brock et al., 1995). SRAD is measured using a silicon photodiode-type pyranometer (LI-COR, Lincoln, NE) that is mounted on a separate tripod at 1.75 m (Brock et al., 1995). WSPD and direction were measured using an R. M. Young m5103 model probe (Young, Traverse City, Michigan) that was mounted 10 m high (Brock et al., 1995). Daily minimums and maximums were determined for each 24-h period starting at 12:00 a.m. and ending at 11:59 p.m. THI was calculated using the equation reported by Mader et al. (2006).

Statistical Analysis

Selection of variables.

Analyses in this study were based on consumed water only; water from feed was not included. To determine which variables had the greatest impact on predicting WI, several variables and combinations of variables were tested to maximize the fit of a regression model (R²). This was performed using the selection option within the regression procedure of SAS version 9.4 (SAS Institute Inc., Cary, NC, USA). The general model fit was as follows:

$$\text{DWI}={\text{b}}_0+{\text{b}}_1\text{Variable}+\dots +{\text{b}}_{\text{n}}\text{Variable}+\text{e,}$$

where b₀ is the intercept value, b_n is the coefficient for a specific weather variable, and variable is a general term to denote the variables that were tested for the prediction model which included DMI, MWTS, minimum temperature, maximum temperature, TAVG, temperature difference (maximum temperature minus minimum temperature within each day), previous day maximum temperature, previous day minimum temperature, minimum relative humidity, maximum relative humidity, HAVG, minimum dew point, maximum dew point, and average dew point SRAD, WSPD, and THI. Minimum, maximum, and average daily dew point were included in the model selection as a to determine whether measures of dew point do a better job predicting WI than relative humidity due to the fact that for HAVG, the temperature at which the humidity was measured is not known (Walter et al., 2000). There is a very strong relationship between temerature and humidity and it is much worse to be hot and humid than just humid or hot, which is not well described by HAVG (Walter et al., 2000). Average daily dew point is a measure of the temperature at which the air becomes saturated with water vapor. Temperature difference was added to the model at the same time as TAVG to account for variability in daily temperature. The variables used in subsequent predictions were determined by the model that had the largest coefficient of determination with the smallest number of factors included. For an additional factor to be added to the analysis, a larger coefficient of determination was needed (defined as an increase in R² of 0.01) in order to keep the final models as simple and user-friendly as possible. Bayesian information criterion (BIC) can be utilized rather than coefficient of determination (Appuhamy et al., 2016); however, in this study, using BIC selected the same model as using R² values. WI was used to develop prediction equations instead of WI% because MWTS were included in the model.

Effect of environmental conditions on WI.

Cattle drink different amounts of water during different seasons, which reflects differences in magnitude of weather variables (Arias and Mader, 2011). A better understanding of WI requirements for cattle at different time points during the year and how intake is affected by changes in different weather variables is needed. The weather variables determined to be the best predictors of WI from the regression analysis above were used to determine the extent to which each factor affects WI as a percent of body weight (WI%). Summary statistics for the weather conditions in each group were calculated using the means procedure in SAS 9.4 (SAS Institute Inc., Cary, NC, USA). Pair-wise comparisons between TAVG, HAVG, SRAD, and WSPD were made between all groups using the general linear model procedure in SAS 9.4 (SAS Institute Inc., Cary, NC, USA) to establish where significant differences in environmental parameters occurred between each feeding period.

Steers were fed during different seasons and years, so environmental factors varied for each group. A baseline model that did not include any weather data was used to quantify the differences in raw intakes between groups and was constructed as follows:

$${\text{WI\%}}_{\text{ijk}}={\text{group}}_{\text{i}}+\text{group}{(\text{pen})}_{\text{i}(\text{j})}+{\text{Animal}}_{\text{k}}+{\text{e}}_{\text{ijk}},$$

where WI%_ijk is the DWI as a percent of body weight for the kth individual from ith group and the jth pen, group_i is the fixed effect for the ith group where I = 1–5, group(pen)_i(j) is the fixed effect for the jth pen nested within the ith group, animal is the random effect of the kth individual, and e_ijk is the normally distributed random residual.

Significance of each individual factor was first ascertained by adding each individual weather variable identified by the model selection procedure to the baseline model in 5 separate univariate repeated measures analyses, and each was fitted using a first-order auto-regressive covariance structure with pen by day as the subject (because temperatures are not different for each animal within a given day) using PROC GLIMMIX in SAS 9.4. (SAS Institute Inc., Cary, NC, USA). Then, to examine environmental differences between the feeding groups, the first variable was added to the baseline model as a covariate. Subsequently, every additional weather factor was included in the model, in a step-wise fashion, until all variables were included (last column in Table 1). By adding the 4 weather variables to the baseline model in a stepwise fashion, a total of 5 different models were utilized: baseline, baseline plus variable 1, baseline plus variables 1 and 2, baseline plus variables 1–3, and baseline plus all variables. The order for addition of weather variables was determined based on the size of the F statistic of each univariate model, where the variable with the highest F value was added to the model first. For each model, contrasts were constructed to determine the effect of feed management (slick bunk in groups 1–3 vs. ad libitum in groups 4 and 5), season (summer for groups 1, 3, and 4 vs. winter in groups 2 and 5), and bunk management and season jointly (summer slick bunk in groups 1 and 3 vs. summer ad libitum in group 4 and winter slick bunk for group 2 vs. winter ad libitum in group 5). Differences between groups, seasons, and bunk management were considered significant at the P ≤ 0.05 level.

Table 1.

Effect of environmental variables on LSMeans water intake as a percent of mid-test body weight for cattle fed in different groups, seasons, and under different bunk management protocols

Groupa	Season	Baseline	+Solar Radiation, MJ/m2	+Temperature, oC	+Humidity, %	+Wind speed, km/h
1	Summer	10.72b	10.30b	9.74b	9.85b	9.84b
2	Winter	6.90c	7.69c	8.74c	8.58c	8.60c
3	Summer	8.63d	8.28d	7.84d	8.00d	8.00d
4	Summer	10.80b	10.25b	9.44e	9.54e	9.51e
5	Winter	8.44e	8.85e	9.47e	9.26f	9.28f
SP vs. WP		2.34***	1.34***	−0.09	0.21*	0.18*
Slk vs. AL		−0.87***	−0.79***	−0.68***	−0.59***	−0.58***
SP Slk vs. AL		−1.13***	−0.96***	−0.65***	−0.61***	−0.59***
WP Slk vs. AL		−0.77***	−0.58***	−0.37***	−0.34***	−0.34***

The baseline model with no environmental variables included was augmented with each additional weather variable in the table until all 4 variables were fitted in the model.

^aSP includes intakes collected during the summer, WP includes intakes collected during the winter, Slk are groups under slick bunk management, and AL are groups with ab libtium access to feed.

^b–fDifferences in superscripts within each column indicate significant differences between groups (P < 0.05).

*Significant difference between contrasts for each analysis (0.0001***, 0.01**, and 0.05*).

Cross-validation.

A 5-fold cross-validation was performed to determine whether there were systematic differences between groups that would limit our ability to combine data across groups for the generation of prediction models. For the cross-validation, a prediction equation was developed (using the variables selected in the model selection procedure described previously) within 4 of the 5 groups and used to predict the intakes for steers in the fifth group. Thus, predictions in the fifth group were generated independently of the training population. Correlations between predicted and actual intakes were computed to determine how similar the predicted DWIs were to the observed DWIs.

WI prediction equation.

After variable selection and cross-validation, the prediction equation was derived using simple linear regression analysis from the regression procedure in SAS 9.4 (SAS Institute Inc., Cary, NC, USA). The general model fit was as follows:

$$\text{DWI}={\text{b}}_0+{\text{b}}_1\text{Variable}+\dots {\text{b}}_{\text{n}}\text{Variable}+\text{e,}$$

where b₀ is the intercept value, b₁ to bn is the coefficient for a specific weather variable, and variable was a general term to denote the individual regression analyses fitted for DMI, dMWTS, TAVG, HAVG, SRAD, and WSPD, and e was the random error.

These univariate analyses were conducted for each set of data available (all, summer, winter, slick bunk, and ad libitum).

Finally, WI prediction equations were developed using the weather variables identified previously in the model selection procedure for all of the data, only slick bunk management, only ad libitum feed availability, only winter, and only summer. To validate the overall prediction equation, the equation was utilized to predict DWI in an independent group of animals not utilized in the development of the equation (group 6). Group 6 cattle were fed the same diet (mean dry matter % = 70.04) and managed similarly to the previous 5 groups. They were allowed ad libitum access to feed and water and were fed from September 2017 to November 2017. Predictions from the equations developed in this study were also compared with values calculated from prediction equations developed by Winchester and Morris (1956) and Arias and Mader (2011). Predictions from the current study were not compared with DWI predictions by Sexson et al. (2012) because daily high sea level pressure was not available.

RESULTS AND DISCUSSION

Environmental Variables

The simplest linear prediction model with the best fit included the following: DMI, MWTS, TAVG, HAVG, SRAD, and WSPD. A summary of environmental conditions for each group is presented in Table 2 and summary statitics for DWI, DMI, and start weight are presented in Table 3. Significant differences in average daily ambient temperature were detected across the summer groups (groups 1 and 3, P = 0.04); groups 1 and 4, P < 0.01; and groups 3 and 4, P < 0.0001). Unsurprisingly, there were significant average daily temperature (P < 0.0001) differences between summer and winter groups. Group 4 experienced the highest average daily ambient temperature (28.1 °C) and group 2 experienced the lowest average daily ambient temperature (4.0 °C). Even though the 3 summer groups were fed at roughly the same time of year, there were still significant differences in HAVG detected between groups 1 and 3 (P = 0.04) and groups 3 and 4 (P < 0.01). However, there were no differences in HAVG observed between groups 1 and 4 (P = 0.21). Group 3 cattle experienced the highest HAVG (75.71%) and group 5 experienced the lowest HAVG (63.00%). For the summer groups (1, 3, and 4), there were no significant differences in SRAD except between groups 3 and 4 (P = 0.01). Differences in SRAD were observed between the winter groups (P < 0.0001). Similar to TAVG, group 4 cattle experienced the highest SRAD (24.08 MJ/m²) and group 2 steers experienced the lowest (7.89 MJ/m²). Fewer differences between groups were noted for WSPD. The only significant differences observed were between summer and winter groups: 1 and 5 (P = 0.03), 2 and 4 (P = 0.04), 3 and 5 (P = 0.02), and 4 and 5 (P < 0.0001). Cattle fed during group 5 experienced the highest WSPD (12.72 km/h) and group 4 cattle experienced the lowest (10.18 km/h).

Table 2.

Means, standard deviations (Std), minimums (Min), maximums (Max), and CV% for environmental variables observed during the feeding period for each group

Variables	Group	Mean	Standard deviation	Minimum	Maximum	CV%
Temperature, °C	1	25.03a	3.13	17.33	30.85	12.5
	2	4.03b	6.05	−7.10	17.86	150.1
	3	23.35c	4.67	13.07	29.94	20.0
	4	28.06d	2.52	21.63	31.93	9.0
	5	9.66e	6.27	−1.35	25.25	64.9
Relative humidity, %	1	71.33a	10.05	47.52	95.84	14.1
	2	70.98a,b	16.44	42.65	98.76	23.2
	3	75.71c	10.91	52.98	96.52	14.4
	4	68.60a,b,d	8.41	52.26	89.53	12.3
	5	63.00e	16.25	23.51	99.92	25.8
Wind speed, km/h	1	11.33a	3.45	4.75	20.48	30.5
	2	11.50a,b	4.61	3.11	22.10	40.1
	3	11.22a,b,c	3.14	5.57	20.15	68.1
	4	10.18a,c,d	2.90	3.51	17.64	28.5
	5	12.72d,e	4.70	5.31	27.70	36.9
Solar radiation, MJ/m2	1	22.33a	6.73	3.36	31.03	30.1
	2	7.89b	4.55	1.58	15.40	57.7
	3	21.39a,c	8.51	3.88	30.29	17.9
	4	24.08a,d	5.24	6.35	31.01	21.8
	5	12.86e	5.90	1.39	22.33	45.9

^a–eDifferences in superscripts within each column and variable indicate significant differences between groups (P < 0.05).

Table 3.

Means, standard deviations (Std), minimums (Min), maximums (Max), and CV% for daily water intake (DWI), dry matter intake (DMI), and starting weight within each group

Variables	Group	Mean	Standard deviation	Minimum	Maximum	CV%
DWI, kg	1	40.50	8.01	21.20	65.80	19.8
	2	28.23	5.63	15.60	44.70	19.9
	3	36.37	6.75	24.10	61.40	18.6
	4	49.46	13.07	32.00	101.40	26.4
	5	34.92	4.84	25.50	50.90	13.9
DMI, kg	1	10.12	1.39	6.36	13.69	13.7
	2	10.23	1.62	6.04	14.07	15.8
	3	10.24	1.52	7.16	14.76	14.8
	4	10.53	0.92	7.76	12.74	8.7
	5	11.67	1.23	8.96	16.17	10.5
Start weight, kg	1	327.81	24.75	253.64	388.18	7.6
	2	331.75	37.10	200.45	438.18	11.2
	3	366.93	29.02	283.64	445.45	7.9
	4	403.34	27.10	33.93	470.98	6.7
	5	341.30	37.27	262.73	434.55	10.2

Effect of Environmental Variables on WI

Different seasons have varying TAVG, HAVG, SRAD, and WSPD which affects the WI% that an animal consumes. Single-factor models for each weather variable were analyzed to determine the order of importance for each variable. All weather variables identified during model selection (TAVG, HAVG, SRAD, and WSPD) had a significant (P < 0.0001) effect on WI% when analyzed as single factors. P-values could not be detected as different because all were P < 0.0001, so the F-statistic was used to determine relative importance of each variable. Surprisingly, SRAD (F-value = 2040.01) had the highest F-statistic, even though cattle had access to shade. Average daily ambient temperature (F-value = 1225.75) was determined to have the second most significant effect on WI%, followed by relative humidity (F-value = 1016.70) and WSPD (F-value = 41.28).

Baseline model.

Differences in WI% are shown in Table 1. WI% was significantly different (P < 0.05) between all groups, except for groups 1 and 4, when no environmental factors are included in the model. Differences in WI% among the groups could be attributed to animals attempting to regulate body temperture by reducing heat load (Beede and Collier, 1986). Increases in WI could be attributed to the animals relying on peripheral vasodilation and water evaporation to regulate body temperature (Berman et al., 1985).

Seasonal effects were observed, and steers fed during the summer months had significantly (P < 0.0001) higher WI% than steers fed during the winter, with summer steers drinking, on average, about 2.34% of their body weight more than steers in the winter. Understanding how WI% differs between seasons can be benificial to producers, allowing them to provide ample water for cattle to maximize performance and minimize heat stress. This would be especially beneficial at times when there might be a shortage in the quality or quantity of water (e.g., during a drought), thus allowing for better management of water resources. Bunk management also had an impact on WI%. Steers that had access to ad libitum feed drank significantly more water (0.87% of body weight; P < 0.0001) than steers managed under a slick bunk protocol. This result is different from Mader and Davis (2004), which reported no difference in WI between ad libitum (39.35 kg/d) and slick bunk mangagement (41.18 kg/d) using pen WIs allocated to individual animals over an 82-d feeding period. Differences in WI% were also found when examining the interaction between bunk management and season. Cattle that were on a slick bunk management protocol and fed during the summer drank significantly less (1.13% of body weight; P < 0.0001) than ad libitum steers fed during the summer. The same trend followed for cattle fed during the winter that were on the slick bunk management protocol, who drank significantly less (0.77% of body weight; P < 0.0001) than their ad libitum counterparts. Differences between slick and ad libitum FI in the winter groups were significant, but of a smaller magnitude than in the summer (0.77% of body weight vs. 1.13% of body weight), which was expected given that intakes in the summer are generally higher. Significant differences were noted among seasons, feed management, and their interaction, and ranged from 0.77% to 2.34% of body weight. These differences indicate that specific predictions equations for seasons and management protocols may be advantageous when trying to predict WI.

Solar radiation.

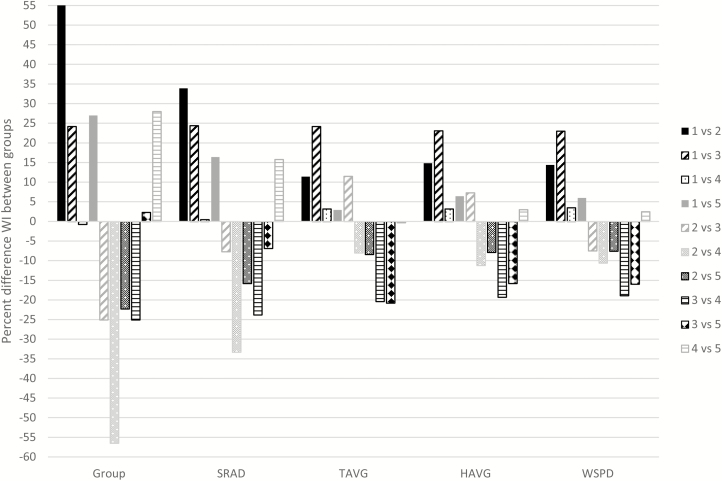
SRAD was added to baseline model and results are reported in column 4 of Table 1. Significant differenences in WI% were detected between all of the groups (P < 0.0001), except between groups 1 and 4 (P = 0.56), but the magnitude of the differences was generally smaller and intakes were more similar across groups after accounting for SRAD (Figure 1). The amount of exposure to SRAD can affect the temperature of surfaces where animals come into contact with as well as directly affect body temperature, particularly in dark-hided cattle (Mader et al., 2006). Cattle of different hide colors also absorb SRAD at different rates, with black-hided cattle absorbing the most and white-hided cattle absorbing the least (Silanikove, 2000). Arp et al. (1983) reported that, due to relative absorptivity and emissivity differences between black-haired and white-haired cattle, surface body temperature of black-haired cattle can be up to 21 °C greater than white-haried cattle. Group 5 steers were all black-hided compared with the other groups which contained a mixture of black and nonblack hided animals. Even with differences in exposure to SRAD between seasons and potential differences in use of shade, SRAD is clearly an important predictor of WI% in this study. The impact of SRAD also reinforces the impact of shade as an important mitigator of heat stress in beef cattle (Mader et al., 1999). However, previous research has shown that providing shade for cattle does not always improve performance (Brown-Brandl et al., 2005). The ability of cattle to acclimate and compensate for short-term losses in FI and gain caused by heat stress may be why increases in performances are not always seen in cattle with access to shade (Mader et al., 1999). Shade may not have been shown to consistently improve cattle performance, but access to shade has been shown to lower core body temperature and respiration rate (Valtorta et al., 1997; Mitlōehner et al., 2001).

Figure 1.

Percent increase or decrease in WI% between each group with the step-wise addition of weather variables to the model. Group = Baseline model which consisted of $WI{\text{\%}}_{ijk}=grou{p}_i+group{(pen)}_{i(j)}+e_{ijk}$; SRAD = the addition of average daily solar radiation as MJ/m² to baseline model $WI{\text{\%}}_{ijk}=grou{p}_i+group{(pen)}_{i(j)}+SRAD+e_{ijk}$; TAVG = The addition of average daily temperature in Celsius to the model$WI{\text{\%}}_{ijk}=grou{p}_i+group{(pen)}_{i(j)}+SRAD+TAVG+e_{ijk}$; HAVG = the addition of average daily relative humidity as a percentage to the model $WI{\text{\%}}_{ijk}=grou{p}_i+group{(pen)}_{i(j)}+SRAD+TAVG+HAVG+e_{ijk}$; WSPD = the addition of average daily wind speed in kilometers per hour to the model $WI{\text{\%}}_{ijk}=grou{p}_i+group{(pen)}_{i(j)}+SRAD+TAVG+HAVG+WSPD+e_{ijk}$

Seasonal differences were observed, with summer groups having higher WI% (1.34% of body weight; P < 0.0001) than cattle fed during the winter. However, the magnitude of the difference in WI% between summer and winter shrank by almost half when accounting for SRAD. Cattle that were managed with the slick buck protocol drank less (0.79% of body weight; P < 0.0001) than steers that had access to ad libitum feed. During the summer months, cattle that were managed with a slick bunk protocol consumed less (0.96% of body weight; P < 0.0001) water as a unit of body weight than cattle that had access to ad libitum feed. A similar result was also found for cattle fed during the winter when comparing slick and ad libitum management (0.58% of body weight; P < 0.0001), although the magnitude of the difference shrinks in the winter when compared with the summer.

Average daily temperature.

Both SRAD and TAVG were added to the baseline model and results are reported in column 5 of Table 1. Significant differences were detected in WI% between all groups (P < 0.05), except between groups 4 and 5 (P = 0.83). When accounting for TAVG, cattle fed during the winter tended to drink more than cattle fed during the summer, but intakes were not significantly different between seasons (P = 0.26). However, significant differences remain for feed management (P < 0.0001). The magnitude of the difference in WI% between different bunk management protocols decreased with the addition of TAVG (0.68% vs. 0.79% of body weight). The slick bunk managed cattle consumed less WI% than cattle that had access to ad libitum feed. The interactions between feed management and season for the summer (P < 0.0001) and winter (P < 0.0001) groups were still significant. Cattle that had access to ad libitum feed drank more water than slick bunk cattle whether they were fed during the summer or winter. WI as a percent of body weight for slick bunk cattle fed during the summer was 0.65% of body weight lower than ad libitum steers (P < 0.0001). A slighlty smaller difference was seen for cattle fed during the winter months (0.37% of body weight; P < 0.0001), with slick bunk managed steers consuming less than ad libitum steers. Steers that had access to ad libitum feed had higher WI%; however, the addition of TAVG reduced the difference between slick bunk managed cattle and ad libitum fed cattle, regardless of season.

Average daily relative humidity.

When the model described previously was augmented with the addition of HAVG, there were still significant differences (P < 0.05) in WI% between all groups (Table 1, column 6). As shown in Figure 1, differences between groups decreased after the addition of HAVG. SRAD, TAVG, and HAVG are major contributing factors to heat stress (Mader et al., 2006), and heat stress can increase consumption of water. By accounting for differences in these 3 variables between groups, smaller differences in WI% would be expected. Although relative humidity had less impact on WI% than temperature in this study, it still contributed to the heat load experienced by cattle. When humidity and ambient temperature rise, evaporative cooling effects decline as humidity reduces respiratory and surface evaporation, potentially resulting in cattle consuming more water to regulate body temperature during times of high heat load (Silanikove, 2000).

Seasonal differences were still significant after the addition of HAVG to the model, with summer cattle having a higher WI% than winter cattle (0.21% of body weight; P = 0.01). Cattle that had access to ad libitum feed consumed more water (0.59% of body weight; P < 0.0001) than cattle managed with a slick bunk protocol. This trend is also true for the interaction between management protocol and season (summer P < 0.0001 and winter P < 0.0001). The magintude of differences among management, season, and management by season was all less than 0.62% of body weight.

Average daily WSPD.

WSPD was the final weather factor added to the model, and there were significant (P < 0.05) differences between WI% in all the groups (Table 1, column 7) when accounting for WSPD. Figure 1 shows additional reductions in differences between groups when all weather variables were added to the model. The impact of WSPD on WI% may not have been as significant in this study, as access to the barn limited the amount of wind exposure for the cattle. Minor differences in the amount of convection cooling that was possible in each group would be expected. Convection cooling is when cooler air comes in contact with a warmer body; thus, the body dissipates heat which is carried away with air movement (Silanikove, 2000). Cattle use evaporative cooling to dissipate heat load (Morrison, 1983); however, evaporative colling increases the need for cattle to consume water to maintain homeostasis (Arias and Mader, 2011). Evaporative cooling can also contribute to cold stress in the winter (Mader, 2003).

Seasonal differences were still significant with the addition of WSPD to the model with summer cattle having a higher WI% than winter cattle (0.18% of body weight; P = 0.03). Even though there were significant differences between these groups, this study included more than 38,000 records, which resulted in even small differences being detected as significant. This small difference suggests that after accounting for differences in weather, cattle fed during the summer and winter have similar levels of WI%. Differences that remain are likely due to individual animal gentic variation (including breed composition) or prior environmental effects that have not been accounted for in these models. Cattle that had access to ad libitum feed consumed more water (0.58% of body weight; P < 0.0001) than cattle managed with a slick bunk protocol. This trend is also true for the interaction between management protocol and season (summer P < 0.0001 and winter P < 0.0001). The magintude of differences among management, season, and management by season was all less than 0.58% of body weight after accounting for all 4 environmental variables.

WI Prediction

Cross-validation.

A 5-fold cross-validation was performed to determine whether it was appropriate to combine data across different groups to create a joint prediction model for WI. Correlations between the observed WI and predicted WI (generated using the model developed with the other 4 groups) were 0.53, 0.38, 0.61, 0.44, and 0.64 for groups 1, 2, 3, 4, and 5 respectively. Even though group 5, which was also a winter group, was included in the training set when predicting group 2, temperatures during group 5 were significantly warmer than group 2 (Table 2). Thus, correlations were likely lower when predicting group 2 because intakes were being predicted at temperatures that were not reflected in the training set. Lower correlations for group 4 were likely due to differences in body weight. Group 4 steers were the heaviest, having an initial average start weight of 412 kg, compared with 321, 333, 367, and 341 kg for groups 1, 2, 3, and 5, respectively. Therefore, predictions were being made in this group on sizes of animals that were not well represented in the training. These differences likely mean that including groups 2 and 4 would increase the robustness of the prediction. The other groups had relatively high correlations between predicted and observed values given that breed composition environmental factors, body size, breed composition differences, and genetic differences were not accounted for in this analysis. Based on these results, data were combined across groups for further analysis and development of an overall prediction equation for WI.

Overall prediction.

Results from univariate analyses predicting DWI are shown in Table 4. When using data from all groups, DMI was positively (P < 0.0001) related to DWI. As steers consumed more feed, they also tended to consume more water. The current study, as well as Winchester and Morris (1956), Arias and Mader (2011), and Sexson et al. (2012), all showed a positive relationship between DWI and DMI in their prediction equations. However, the current study suggests a higher slope estimate (2.17) than Arias and Mader (1.03; 2011) and Sexson et al. (0.349; 2012). The prediction equation from Winchester and Morris (1956) is based on DMI at different temperature levels. Depending on the season, the relationship between DWI and DMI is known to differ. DWI generally increases and DMI generally decreases during the summer and the opposite occurs during the winter (Sexson et al., 2012). When differing relationships exist between DMI and DWI depending on the season, prediction of DWI from DMI can be inconsistent (Sexson et al., 2012). However, this relationship was not observed in the current study, as both DWI and DMI have a positive relationship during both the summer and winter. Also, DWI was related to MWTS (P < 0.0001). Larger steers tended to consume more water, which is supported by Meyer et al. (2004), who found a similar result in a population of dairy cows.

Table 4.

Univariate regression analysis of each variable used for predicting water consumption (kg/d) of crossbred steers

Variable	Slope estimate	SE	R 2	P-value
All data
DMI, kg	2.17	0.029	0.12	<0.0001
MWTS, kg	0.61	0.008	0.13	<0.0001
Average temperature, oC	0.65	0.006	0.21	<0.0001
Relative humidity, %	-0.18	0.005	0.03	<0.0001
Solar radiation, MJ/m2	0.72	0.008	0.19	<0.0001
Wind speed, km/h	-0.08	0.018	0.0005	<0.0001
Summer
DMI, kg	2.74	0.042	0.16	<0.0001
MWTS, kg	0.59	0.011	0.10	<0.0001
Average temperature, oC	1.74	0.023	0.20	<0.0001
Relative humidity, %	-0.52	0.010	0.12	<0.0001
Solar radiation, MJ/m2	0.67	0.014	0.09	<0.0001
Wind speed, km/h	-0.04	0.032	0.0001	<0.0001
Winter
DMI, kg	2.25	0.028	0.29	<0.0001
MWTS, kg	0.53	0.009	0.20	<0.0001
Average temperature, oC	0.39	0.013	0.06	<0.0001
Relative humidity, %	-0.52	0.010	0.12	<0.0001
Solar radiation, MJ/m2	0.67	0.014	0.09	<0.0001
Wind speed, km/h	-0.04	0.032	0.0001	0.2120
Ad libitum
DMI, kg	1.62	0.058	0.05	<0.0001
MWTS, kg	0.66	0.014	0.14	<0.0001
Average temperature, oC	0.76	0.010	0.26	<0.0001
Relative humidity, %	-0.06	0.009	0.003	<0.0001
Solar radiation, MJ/m2	0.89	0.014	0.22	<0.0001
Wind speed, km/h	-0.18	0.028	0.003	<0.0001
Slick bunk
DMI, kg	2.15	0.033	0.15	<0.0001
MWTS, kg	0.48	0.011	0.08	<0.0001
Average temperature, oC	0.58	0.008	0.19	<0.0001
Relative humidity, %	-0.18	0.007	0.03	<0.0001
Solar radiation, MJ/m2	0.64	0.008	0.19	<0.0001
Wind speed, km/h	0.02	0.023	0.00	0.5097

^aDMI = Dry mater intake, MWTS = mid metabolic body weight.

Temperature was positively associated with DWI (P < 0.0001), as expected. As temperature increases past 25 °C (as it did for 37, 0, 31, 61, and 1 d in groups 1, 2, 3, 4, and 5, respectively), cattle begin to experience heat stress (NRC, 2000). Water can play a key role in regulating body temperature (Berman et al., 1985); thus, as cattle experience higher temperatures, they would be expected to consume more water. The result in this study is consistent with both Arias and Mader (2011) and Sexson et al. (2012), which showed that increases in temperature were associated with increases in DWI. In our study, for every 1 °C increase in temperature, there is an increase in DWI consumption of 0.65 kg, which is intermediate to previous literature estimates. Arias and Mader (2011) used maximum temperature (TMAX) in their prediction equation instead of TAVG, but reported that as TMAX increases by 1 °C, DWI increased by 0.45 kg. Sexson et al. (2012) reported that an increase of 1 °C in TAVG produces a 1.034-kg increase in DWI.

Cattle experiencing increases in HAVG during the feeding period had decreased (P < 0.0001) DWI. One way that cattle lose water is through respiration (Sexson et al., 2012). However, respiratory air is highly saturated with water; thus, water losses through respiration are greater when humidity is low (Sexson et al., 2012). The amount of humidity in the air can also effect the rate of evaporative cooling processes (Morrison, 1983). Thus, cattle exposed to high HAVG would be expected to have a more difficult time dissipating heat through evaporative cooling. Arias and Mader (2011) found that HAVG did not contribute to differences in DWI over all seasons. However, Sexson et al. (2012) found that as HAVG increases, DWI decreases.

As outlined in Table 4, an increase in DWI consumption of 0.72 kg was estimated due to an increase of 1 MJ/m² in SRAD. Exposure to SRAD can increase body temperature, which can lead to increases in DWI to help regulate body temperature (Arias and Mader, 2011). Providing shade to cattle has been shown to reduce heat load up to 30% (Mader et al., 1999). Beede and Collier (1986) suggested that providing cattle with protection from SRAD is one of the most immediate and cost-effective ways to increase productivity in ruminants.

Increases in WSPD decreased (P < 0.0001) DWI, possibly because of increased air flow leading to evaporative cooling. Evaporative cooling is one of the most practical means to cool livestock in times of heat stress (Morrison, 1983). Mader et al. (1999) also suggested that increased WSPD leads to enhanced convection and evaporative cooling due to the increased air flow. WSPD is more effective when HAVG is low, because as HAVG increases, evaporative cooling is limited (Mader et al., 2006).

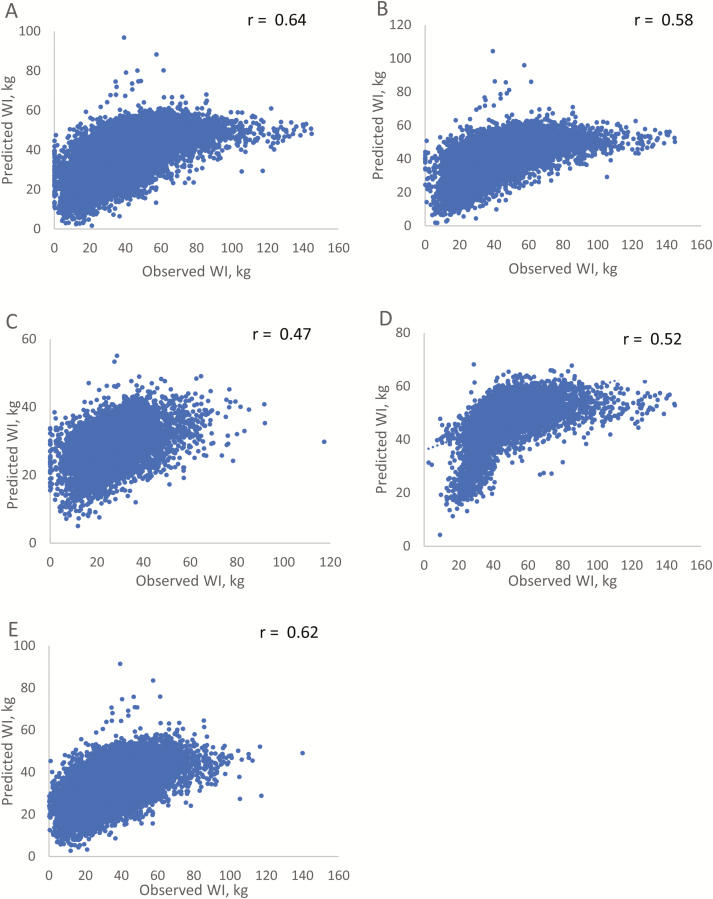
Results from the multiple regression analyses predicting DWI are shown in Table 5. It is also important to analyze weather variables cumulatively in a single model to predict DWI, as there are interrelationships between the weather variables and their effects on DWI. The overall model explained 40% of the variation in DWI when including DMI, MWTS, TAVG, HAVG, SRAD, and WSPD and can be visualized in Figure 2A. This is not comparable to Arias and Mader (2011), who explained 65% of the variation with their overall model, but is slightly higher than Sexson et al. (2012), who explained 32% of the variation in DWI. Although the number of experimental units in Arias and Mader (2011) was smaller than the current study (n = 142 vs. n=579), the use of pen intakes may improve model fit due to the fact that the data structure may mask individual differences between animals, which would contribute to greater overall variability in our dataset.

Table 5.

Partial regression coefficients for daily water intake prediction models including environmental factors, DMI, and metabolic body weights.

	Overall		Summer		Winter		Slick bunk		Ad libitum
Variablea	Estimate	Partial R2	Estimate	Partial R2	Estimate	Partial R2	Estimate	Partial R2	Estimate	Partial R2
Intercept	−4.18		−9.74		−4.24		−2.25		0.71
DMI, kg	2.00	0.124	2.32	0.155	1.76	0.290	1.86	0.15	2.63	0.05
MWTS, kg	0.22	0.057	0.11	0.040	0.22	0.032	0.20	0.01	−0.009	0.11
TAVG, oC	0.57	0.194	1.31	0.137	0.26	0.033	0.45	0.19	0.76	0.23
HAVG, %	−0.15	0.025	−0.17	0.006	−0.09	0.032	−0.14	0.03	−0.06	0.01
WSPD, km/h	−0.16	0.001	−0.27	0.003	−0.06	0.0006	−0.08	0.004	−0.11	0.01
SRAD, MJ/m2	0.14	0.003	−0.03	0.000001	0.13	0.003	0.18	0.001	0.23	0.001
R 2		0.40		0.34		0.39		0.39		0.41

^aDMI = Dry mater intake; MWTS = mid metabolic body weight; TAVG = average daily temperature; HAVG = average daily relative humidity; WSPD = average daily wind speed; SRAD = average daily solar radiation.

Figure 2.

Plots of observed versus predicted daily water intakes (WIs) using various models developed in this study. (A) Overall model. (B) Summer model. (C) Winter model. (D) Ad libitum model. (E) Slick bunk model.

Average temperature and DMI were the most important predictors of DWI and explained 19.4% and 12.4% of the variation, respectively. The overall model developed by Arias and Mader (2011) included 3 variables (DMI, SRAD, and TMIN), with minimum temperature (partial R² = 0.56) as the most key variable and DMI (partial R² = 0.02) as the least important variable. This result may be due to the fact that they utilized pen water and FIs extrapolated out to individual animals, which might have minimized the importance of DMI by masking individual differences among animals. DMI measurements on individual animals assist in predicting DWI in this study where intakes are not averaged across a pen, leading to the increased importance of DMI in this model. Minimum temperature was established by Mader (2003) and Amundson et al. (2006) as an important measure of energy balance, primarily due to dissipation of heat during the night. The ability of animals to reduce heat load during the night may influence the amount of water cattle consume to help regulate body temperature. In the current study, TAVG was determined to be a better predictor of DWI than TMIN, and the addition of TMIN did not substantially improve the model fit. Minimum temperature may not have been as useful in predicting DWI in the current study because TMIN may not have been low enough, especially during the summer feeding groups, to dissipate heat during the night. Arias and Mader (2011) reported that if TMIN does not reach below 12 °C, that heat loss through convection and conduction methods may not be as successful. In the current study, the night temperature reached below 12 °C in the summer groups 1, 3, and 4 for only 0, 5, and 0 d, respectively. It is also possible that TMIN did not reach low enough temperatures for a long enough period of time to have an effect on DWI.

To better explore differences in models published in the scientific literature and the one developed in this study, observed DWI from an independent group of animals (winter, ad libitum) was used to compare the overall model from this study with predicted DWI from models developed by Arias and Mader (2011) and Winchester and Morris (1956). The correlation between intakes predicted with the model developed in this study and observed DWI in the validation group was 0.49 when using individual intakes. To test whether the prediction would be more effective when utilizing pen intakes, WI was pooled within each pen and averaged, and the correlation was reevaluated. The correlation between intakes predicted with the model developed in this study and DWI averaged across animals within a pen in the validation group was 0.68, indicating that utilizing the pen intakes does mask individual animal differences. The correlation between DWI predicted using the equation in Arias and Mader (2011) and observed DWI was similar at 0.51 when utilizing individual intakes. When the pen intakes calculated in our study were utilized, the correlation increased to 0.63. The correlation of predicted intakes from Winchester and Morris (1956), which were based on individual-animal data, and the observed individual intakes in this study was also 0.49. The model from Arias and Mader (2011) likely has a slight numeric advantage over the Winchester and Morris (1956) model because it accounts for other weather variables in addition to temperature. However, the current study includes more weather variables and still did not perform as well as Arias and Mader (2011) when individual intakes were used. However, when pen, intakes from the current study were used, including more weather variables in the prediction equation did improve the prediction of DWI. Arias and Mader (2011) utilized 1,275 animals in 142 pens to develop their DWI prediction equations where Winchester and Morris (1956) utilized approximately 50 head. Using more records to develop prediction equations should create more robust equations that can predict over a wider range of intakes and weather variables. In addition, using a large number of animals fed in pens may be an advantage in this process, since predictions are generally focused on the average animal. Winchester and Morris (1956) collected individual WI over 1- to 2-wk intervals, recording temperature and FI as well. Results from Ahlberg et al. (2017) indicate that a 1- to 2-wk collection period for DWI is too short to accurately collect DWI using automated collection systems. Despite these factors, based on this validation, all models performed similarly (R² = 0.49–0.51) and the best equation could only explain 51% of the variation between predicted and actual DWI. This result suggests that weather variables, body size, and DMI are not the only factors that contribute to variation in DWI. Differences in genetic merit for DWI and individual-animal variation in response to thermal stresses could be one reason why the correlations were not higher.

Overall prediction models are beneficial during times that do not easily fit into a specific time period like summer or winter. However, these models are only as robust as the data on which they were trained. Thus, if predicting DWI on animals of different size, body composition, or in different environmental conditions to the training data, the prediction of DWI will not be as reliable. Robustness can also suffer if sudden weather events take place that expose animals to weather variables that are extreme. As an example, prediction of DWI during extremely cold subzero temperatures might result in very low to even negative estimates of DWI if temperature is heavily weighted in a model. Some of these issues may be alleviated by using seasonal models when they are available. In any case, overall or seasonal prediction models should be augmented with new data as it is collected (particularly on different classes of animals and in different locations that might have more extreme weather conditions) to improve WI predictions; all models should be compared utilizing independent data sets to determine the optimum prediction. Augmenting the current study’s analysis with additional DWI records collected on different classes of animals and in other locations will make sure that the DWI prediction equation is robust enough to accurately predict DWI broadly over a variety of production scenarios.

Seasonal models.

Results from univariate analysis predicting DWI in summer and winter are shown in Table 4. The summer and winter univariate analyses follow the same trends as the overall data, but there are some differences in the magnitude of the effects on DWI. For the summer and winter data, DWI increases by 2.74 and 2.25 kg for every 1-kg increase in DMI, respectively. Interestingly, these values are greater than those observed when using all available data jointly. For the summer data, TAVG (R² = 0.20) explained more variation than in the winter data (R² = 0.06). Unsurprisingly, TAVG is more important to predicting DWI during the summer, likely due to the impact that TAVG can have on heat load and the relative lack of cold stress in this particular environment. Cattle fed during the summer time tend to experience higher TAVG and greater heat load than cattle fed during the winter. However, for the winter data, DMI (partial R² = 0.29) and MWTS (partial R² = 0.20) explained more variation than DMI (partial R² = 0.16) and MWTS (partial R² = 0.10) for summer groups. The variation explained by HAVG, SRAD, and WSPD was similar between the summer and winter data.

Results from the summer and winter multiple regression are shown in Table 5. The summer model, developed using data from groups 1, 3 and 4, only explained 34% of the variation in DWI and can be visualized in Figure 2B. Of the 6 variables that were included in the model, DMI (partial R² = 0.155) and TAVG (partial R² = 0.137) explained more than 29.2% of the variability. Arias and Mader (2011) predicted DWI during the summer months using DMI, SRAD, and minimum temperature (TMIN) and explained 23% of the variation in DWI. Dry mater intake and a measure of temperature (TAVG vs. TMIN) were key factors for predicting intakes during the summer in both studies. In this study, SRAD explains very little of the variation in the summer model (partial R² = 0.000001), whereas it was the major contributor that explained the most variation in the summer model developed by Arias and Mader (2011; partial R² = 0.14). This may be because the steers in Arias and Mader (2011) did not have access to shade, whereas steers in this study had access to shade, and, anecdotally, the cattle appeared to spend considerable time in the shade during the summer months, which limited their exposure to SRAD. The inclusion of SRAD in a seasonal prediction equation when shade has been provided may not be as useful for predicting WI as it is for cattle that do not have access to shade. Sexson et al. (2012) also predicted DWI in yearling steers fed during the summer and developed a model that explained 32% of the variation in DWI, which is similar to this study. The model in Sexson et al. (2012) included 14 variables instead of the 3 and 6 variables included in the model for Arias and Mader (2011) and this study, respectively. Not only was the current daily maximum temperature included, but Sexson et al. (2012) also accounted for the previous daily maximum temperature as well as a quadratic effect of temperature. Previous day maximum temperature had a smaller impact than the current day maximum temperature (Sexson et al., 2012), possibly because steers had the ability to dissipate heat during the night. Sexson et al. (2012) also included high and average sea pressure in their prediction equation, although it had minimal impact (partial R² from 0.056 to 0.01). Increases in barometric pressure can reduce water vaporization in the lungs, which reduces water loss through respiration causing cattle to consume less water (IOM, 2005), but that effect did not appear to be a large contributor to variation in DWI in Sexson et al. (2012). The Sexson et al. (2012) model also differed from Arias and Mader (2011) and the current study’s summer model because it did not include DMI.

The winter model explained slightly more variation than the summer model (39%), which may be because DWI is more variable in the summer and can be visualized in Figure 2C. This can be seen by the larger standard deviations of DWI observed during the summer groups (8.1, 6.6, and 13.8 kg for groups 1, 3, and 4, respectively) vs. winter groups (5.4 and 4.8 kg for groups 2 and 5, respectively). Of the 6 factors included in the model, DMI (R² = 0.291) explains the overwhelming majority of the variation. Steers fed during the winter experienced only 1 d of heat stress and 25 d of cold stress (where temperature was below 0 °C; Young, 1981) between both groups. Winchester and Morris (1956), Murphy et al. (1983) and Hicks et al. (1988) showed that DMI is a strong predictor of DWI. Bond et al. (1976) suggested that the ability to predict DWI from DMI is associated with the percent roughage in the diet, with DWI being more easily predicted from DMI when roughage content in the diet is higher. This could not be tested in this study as the same diet was used for all groups. Arias and Mader (2011) included 6 variables in their winter model (R² = 0.23), including DMI, SRAD, maximum temperature (TMAX), WSPD, HAVG, and precipitation. Maximum temperature (partial R² = 0.05), WSPD (partial R² = 0.04), HAVG (partial R² = 0.07), and precipitation (partial R² = 0.05) are the 4 variables that explain the majority of the variation in the Arias and Mader (2011) winter model. In our study, the environmental factors explained far less variation in DWI (~7%), with most of the emphasis placed on DMI. However, the Arias and Mader (2011) study was conducted when average temperatures were much colder (−2.0 °C vs. 17.3 °C), and more humid (74.4% relative humidity vs. 67.4%). Bedding was provided for some of the feed groups during the winter time in Arias and Mader (2011), but no bedding was provided for the current study.

Ad libitum vs. slick bunk management.

Results from ad libitum and slick bunk univariate analyses are shown in Table 4. For the ad libitum data, MWTS, TAVG, and SRAD are the variables that drive DWI. However, for the slick bunk data, DMI, TAVG, and SRAD are the variables that explain the most variation in DWI. Although 2 of those factors are common between the management techniques, the estimates and coefficients of determination vary substantially.

Temperature and SRAD both play key roles in predicting DWI for both feed management prediction equations, likely because cattle fed during the summer that were managed under both ad libitum and slick bunk were exposed to heat stress (THI exceeding 74) for 38, 32, and 62 d for groups 1, 3, and 4, respectively. High temperatures paired with high SRAD increase body temperature, which could result in cattle consuming more water to help regulate their body temperature (Berman et al., 1985). Dry mater intake is an important factor to predict DWI for cattle managed under a slick bunk protocol, and it has the highest coefficient of determination other than temperature. Under a slick bunk protocol, some animals may have limited DMI, which could alter the relationship between DMI and DWI. On the other hand, MWTS are a more important factor for the ad libitum group, and the variation explained by DMI is much lower. Similarly to the winter model, WSPD is not significant (P = 0.51) in the slick bunk univariate analysis (Table 1), although it has a small, but significant effect in the ad libitum data.

Results from ad libitum and slick bunk multiple regressions predicting DWI are shown in Table 5. The ad libitum model explained 41% of the variation in DWI and the slick bunk slightly less, at 39% and can be visualized in Figure 2D and E. Of the 6 variables included in the ad libitum model, MWTS (partial R² = 0.11) and TAVG (partial R² = 0.23) explained about 34% of the variability in DWI. Unlike the seasonal models, using just 2 variables explained the majority of the variation observed, with TAVG alone explaining 23% of the variation. The slick bunk model explained 39% of the variation in DWI and of the 6 variables that were included in the model, DMI (partial R² = 0.15) and TAVG (partial R² = 0.19) explained 34% of the variability. The slick bunk management model follows the same trend as the overall and summer models, with DMI and TAVG being the most important factors in predicting DWI. Relative humidity, SRAD, and WSPD each explained approximately 3%, 0.4%, and 0.1% of the variation, respectively, in the slick bunk model.

Temperature explains the most variation in both the ad libitum and slick bunk models, which is consistent with the importance of temperature in predicting DWI in the other models described in this study. In the ad libitum model, there was a slight negative estimate for MWTS; however, for the slick bunk model, the estimate is positive and substantially larger even though it contributes less to explaining variation in the data. Sexson et al. (2012) showed a positive association between DWI and body weight for animals 500 kg or less and a negative association with body weight when weight is greater than 500 kg. For the current study, many of the ad libitum fed steers started at a higher weight than the slick bunk steers, and likely spent more of the feeding period over the 500-kg threshold. The change in association between body weight and DWI is likely a result of the changes in composition of gain as cattle approach slaughter weights (Sexson et al., 2012). For the slick bunk model, DMI is an important driver of DWI, and DMI has the second highest coefficient of determination. On the other hand, MWTS explain more variation for the ad libitum fed group, and partial R² for DMI is much lower. Unlike the summer or winter prediction models, MWTS is the second most important factor when predicting DWI in the ad libitum model. DMI only explained 5% of the variation in the ad libitum prediction model, but explains 15.5% of variation in the summer model, 29% in the winter, and 15% in the slick bunk model. This result suggests that limiting the amount of dry matter available for consumption alters the relationship between DMI and DWI in some of the steers, leading to DMI and temperature driving the prediction of DWI in slick bunk steers. Conversely, the ad libitum fed steers do not have this restriction, and thus, DWI is instead driven by size of the animal and temperature.

There are no DWI prediction equations for different feed management protocols previously published in the literature, so no direct comparisons between models can be made. Cattle utilized in the Sexson et al. (2012) prediction had access to ad libitum feed and the cattle utilized for the Arias and Mader (2011) study were a mixture of slick bunk managed and ad libitum managed cattle. Although Arias and Mader (2011) had cattle managed with 2 different feed protocols, they did not develop separate equations for the different feed management strategies. Cattle fed in a feedlot setting are often managed with a slick bunk protocol. However, grazing breeding stock often have ad libitum access to forage, unless they are experiencing a shortage in feed resources due to drought or limit feeding hay and supplement during the winter. Having prediction equations that are specific to the type of feed management being practised could allow producers to more accurately predict the water resources needed for their livestock.

CONCLUSION

Differences in WI% were observed between each group, which likely stem from a combination of environment, management, genetic background, and individual animal variation. The magnitude of the differences between groups decreased as different environmental factors were adjusted for in the data. After accounting for all environmental parameters (SRAD, TAVG, HAVG, and WSPD), significant differences were still observed across groups, with WI% ranging from 8.00% to 9.84% of body weight. Seasonal differences in WI% were also detected between cattle fed in the winter and summer (0.18% of body weight). Even though the seasonal differences detected were significant, a difference of 0.18% of body weight is reasonably small. Because of the large number of observations in the data set, small differences can be detected as significant that may not accurately represent the magnitude of differences in the underlying biology. Differences in feed management affected WI%, but the differences between steers that had access to ad libitum feed or steers managed with a slick bunk protocol were less than 1% of body weight when all environmental factors were accounted for in the model.

WI prediction equations were developed that included variables of DMI, MWTS, TAVG, HAVG, SRAD, and WSPD. The amount of variation explained by different models ranged from 0.34 to 0.41, with the summer model as the least predictive and ad libitum model as the most predictive. Slick bunk management makes DWI more difficult to predict and the relative importance of variables in these 2 models shifted depending on the feed management protocol. The prediction of DWI for steers that had access to ad libitum feed was the only prediction equation where MWTS was 1 of the 2 most important factors in predicting DWI. Weather variables have a significant effect on DWI and play a vital role in predicting DWI along with DMI and body size; however, individual animal variation in WI is an important factor that contributes to variation in WI that cannot be explained by current models.