Evaluation of nonadditive effects in yearling weight of tropical beef cattle

Abstract

Nonadditive effects may contribute to genetic variation of complex traits. Their inclusion in genetic evaluation models may therefore improve breeding value estimates and lead to more accurate selection decisions. In this study, we evaluated a systematic series of models accounting for additive, dominance and first-order epistatic interaction (additive by additive, GxG; additive by dominance, GxD; and dominance by dominance, DxD) on body yearling weight (YWT) of 2,550 Tropical Composite (TC) and 2,111 Brahman (BB) cattle in Australia. For both breeds, similar estimates of additive and phenotypic variances and narrow and broad-sense heritability values were obtained across the evaluated models except when GxG effect was considered. In this case, additive variance was slightly lower than that obtained in the models which do not consider this effect. The estimated dominance and epistatic variances from additive and dominance effects (AD) and additive, dominance and epistatic effects models (ADE) were greater than that ADH and ADEH models (as described above plus heterozygosity as a covariate). However, all genetic parameter estimates were associated with a large standard deviation. Averaged across ADH and ADHE models, the magnitude of dominance variance compared to the phenotypic variance of YWT was 14% (BB) and 10% (TC). The magnitude of epistasis compared to the phenotypic variance for BB and TC was 17% and 29%, respectively for GxG; 0.7% and 0% for GxD; and 0% and 0% for DxD. The inclusion of nonadditive effects slightly improves the predictive accuracy of breeding values from 0.28 for A to 0.33 for ADHE_GxG and from 0.18 for A to 0.23 ADE_GxD in BB and TC cattle. Models that included heterozygosity (ADH and ADHE) must be used to estimate nonadditive genetic variance components. A 1 Mb sliding window analysis identified a region on BTA 14 explaining 10.08% and 1.21% of total genetic variance (additive + dominance) of YWT in BB and TC, respectively. Our results suggest that dominance, epistasis, and heterozygosity should be included in models for genetic parameters estimation. To identify the animals with the highest additive genetic value in selection decisions, only the additive effect should be used in evaluation models.

INTRODUCTION

The total genetic value of an individual is the sum of additive (i.e., breeding value) and nonadditive effects. Nonadditive genetic effects result from allelic interactions, being the intralocus interaction known as dominance, and interlocus interactions known as epistasis (Lynch and Walsh, 1998). When nonadditive genetic effects are an important source of variation, an optimal genomic selection strategy might improve the expected response (Toro and Varona, 2010). The contribution of nonadditive effects on mating selection has been confirmed in dairy cattle (Ertl et al., 2014; Aliloo et al., 2017). Thus, how much genetic variation is explained by nonadditive effects in traits of interest for beef cattle remains largely unknown. Genomic additive relationship matrix, in contrast to pedigrees, directly measure Mendelian sampling (Heffner et al., 2009). Further, it can measure relationships even in diverse, nominally unrelated samples, expanding the potential for studying inheritance in breeding populations (Lorenz et al., 2011). Matrices of dominant and epistatic genomic relationships across individuals have also been proposed (Vitezica et al., 2013, 2017). Through these genomic matrices, genomic evaluation models implicitly fit breeding values, dominance and epistatic deviations. In linkage and Hardy-Weinberg equilibrium, the genetic value decomposition in these terms is orthogonal. This means, for instance, that going from an additive to an additive plus dominant model should not change much neither the estimates of variance components, nor the estimates of breeding values and dominant deviations. In the present study, we use high-density single nucleotide polymorphism (SNP) genotypes to estimate additive and nonadditive (dominance and epistasis) variance components for body yearling weight (YWT) in 2,111 Brahman (BB) and 2,550 Tropical Composite (TC) cattle.

MATERIAL AND METHODS

Animal Care and Use Committee approval was not obtained for this study because historical data was used and no animals were handled as part of the study. Analysis was performed on phenotypic data and DNA samples that had been collected previously as part of the Australian Cooperative Research Centre for Beef Genetic Technologies (Beef CRC; http://www.beefcrc.com/).

Animals, Phenotypes, and Genotypes

Animals, phenotypes, and genotypes used in this study were a subset of those recently described in Raidan et al. (2018). In brief, we used the data of 2,111 BB and 2,550 TC cows and bulls genotyped using either the BovineSNP50 (Matukumalli et al., 2009) or the BovineHD (Illumina Inc., San Diego, CA). Animals that were genotyped with the lower density array had their genotypes imputed to higher density as described previously by Bolormaa et al. (2014). The average, minimum and maximum of YWT (kg) were 227.7, 115, and 353 kg for BB, and 247.07, 120.5, and 394.5 kg for TC. Moreover, the average, minimum and maximum of age at YWT was 360, 302, and 416 d for BB, and 361, 319, and 403 d for TC.

Additive, Dominance, and Epistatic Genomic Relationship Matrices

A marker-based additive genomic relationship matrix (GRM), G was constructed following the method described by VanRaden (2008):

$$\mathit{G}=\frac{{\mathit{Z}}_a{\mathit{Z}}_a^{\text{'}}}{2{{\displaystyle \sum }}_{k=1}^m{p}_k{q}_k},$$

where matrix ${\mathit{Z}}_a$ has dimensions of the number of individuals (n) by the number of loci (m), with elements that are equal to $2-2p_k$ and $-2p_k$ for opposite homozygous (A₁A₁ and A₂A₂ respectively) and $1-2p_k$ for heterozygous genotypes, $p_k$ is the frequency of allele A₁ of locus k, and $q_k=1-p_k$.

A marker-based dominance GRM (D) was constructed following the method described by Vitezica et al. (2013):

$$\mathit{D}=\frac{{\mathit{Z}}_d{\mathit{Z}}_d^{\text{'}}}{4{{\displaystyle \sum }}_{k=1}^m{p}_k^2{q}_k^2},$$

where matrix ${\mathit{Z}}_d$ has dimensions of the number of individuals (n) by the number of loci (m), with elements that are equal to $-2q_k^2$ for genotype A₁A₁, $2p_k{q}_k$for genotype A₁A₂ and $-2p_k^2$ for genotype A₂A₂.

A marker-based epistatic GRM due to first degree epistatic terms (E) were computed using Hadamard products (i.e., cell-by-cell product denoted as #) with a standardization based on the trace of the GRM (Vitezica et al., 2017):

• (i) additive-by-additive relationships: ${\mathit{E}}_{GxG}=\frac{\mathit{G}\#\mathit{G}}{tr(\mathit{G}\#\mathit{G})/n}$;

• (ii) dominance-by-dominance relationships: ${\mathit{E}}_{DxD}=\frac{\mathit{D}\#\mathit{D}}{tr(\mathit{D}\#\mathit{D})/n}$;

• (iii) additive-by-dominance relationships: ${\mathit{E}}_{GxD}=\frac{\mathit{G}\#\mathit{D}}{tr(\mathit{G}\#\mathit{D})/n}$.

Statistical Analyses

All analyses were carried out with the software AIRemlf90 (Misztal et al., 2002). Estimates of variance components were obtained by using 6 models ranging from a simple additive model to a full model including additive, dominance and first-order epistatic effects. The first model included additive effects only (A). The second (AH) and third (AD) models include heterozygosity as a covariate and dominance deviation as a random effect, respectively. The fourth (ADH) model included additive, dominance and heterozygosity effects. The fifth (ADE_x) models included additive, dominance deviation and epistatic deviation as random effects (x = additive by additive, GxG or additive by dominance, GxD or dominance by dominance epistatic effect, DxD). Finally, the sixth (ADEH_x) model included additive, dominance deviation and epistatic deviation as random effects and heterozygosity as a covariate. This full model (ADEH_x) is described below:

$$\mathit{y}=1\mu +b\left(Het-\overline{\text{Het}}\right)+\mathit{Wu}+\mathit{Wv}+\mathit{W}{\mathit{t}}_x+\mathit{es}\text{;}$$

where y is the vector of phenotypes for each trait; $\mu$ is the population mean; b is the linear regression coefficient of phenotype on average heterozygosity (Het) computed for each individual based on SNPs; W is the incidence matrix relating observations to genetic effects; u is the vector of breeding values; v is the vector of dominance deviations; t is the vector of epistatic deviations and e is the vector of random residual terms. The subscript x in t corresponds to additive by additive (GxG), or additive by dominance (GxD) or dominance by dominance epistatic effect (DxD).

The goodness of fit of models was compared on the basis of a likelihood ratio test (i.e., each model was compared with the null model; e.g., model AD vs. model A). Predictive ability as given by accuracy (ACC) was measured by the correlation between genomic estimated breeding value (GEBV) and adjusted phenotypes in a 5-way cross-validation scheme each subset with 20% of randomly assigned missing data (as a validation set) and the remaining 80% (calibration set) used to train the model. The ACC values and all genetic parameter estimates were then averaged across the 5 cross-validation subsets.

We estimated SNP additive (substitution effect) and dominance effects after back-solving from GEBV and predictions of dominance deviation. The procedure followed the S1 scenario described in Wang et al. (2012), with GEBV computed once and weights of SNP effects refined through 3 iterations, as follows:

$$\hat{\alpha }={\mathit{Z}}_a\text{'}{\mathit{G}}^{-1}\hat{\mathit{u}}\frac{1}{{{\displaystyle \sum }}^{\text{}}2pq}$$

$$\hat{\mathit{d}}={\mathit{Z}}_d\text{'}{\mathit{D}}^{-1}\hat{\mathit{v}}\frac{1}{{{\displaystyle \sum }}^{\text{}}{\left(2pq\right)}^2}$$

in which, $\alpha$ is the substitution effect and $d$ is the dominant effect of a SNP.

Finally, we investigated chromosomal regions where SNP effects were blocked into adjacent windows of 1 Mb. Genetic variances contributed by the SNP were explained per window and estimated through PostGSf90 (http://nce.ads.uga.edu/) software by calculating the variance explained by the n-th Mb window of adjacent SNPs (segments) with their respective effects as input. This was used to identify potential candidate genes that may affect YWT as additive and dominance effects. The individual variance of SNP effect was estimated following the approximation proposed by Zhang et al. (2010) as

$$\widehat{{\sigma }_{{\alpha }_i}^2}={\widehat{{\alpha }_i}}^{2}2p_i(1-p_i)\widehat{{\sigma }_{d_i}^2}={\widehat{d_i}}^{2}2p_i(1-p_i)$$

in which, $p_i$ is the observed allele frequency for the second allele of the ith marker in the current population.

RESULTS

Of the total of 689,818 SNP (TC) and 651,253 SNP (BB), respectively, only 646 SNP (0.10%) and 193 SNP (0.03%) were not in Hardy-Weinberg equilibrium (HWE; P > 0.05). Distribution of density and correlations of off-diagonal elements of each GRM showed that the mean of off-diagonals elements of each matrix was equal to 0 (Supplementary Figure S1), which further confirms that these populations were in HWE.

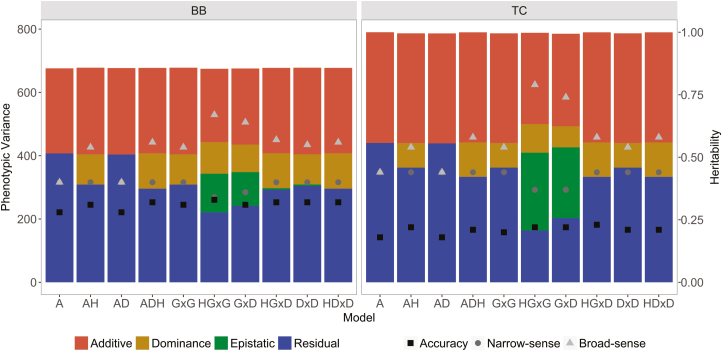
For both breeds, estimated additive genetic and phenotypic variances and broad (H²) and narrow-sense heritability (h²) values were similar across all of the evaluated models, regardless of whether nonadditive effects were included in the model, except when additive by additive epistatic effect was considered. In this case, smallest values of additive genetic variance and narrow-sense h² and higher values for H² were obtained in the models ADE_GxG and ADHE_GxG (Fig. 1), however those means are related to large standard deviations.

Figure 1.

Brahman (BB, left) and Tropical Composite cattle (TC, right) estimated additive, dominance, epistatic, residual, and phenotypic variances (bars, left y-axis), narrow-sense heritability (gray triangles, right y-axis) and broad-sense heritability estimates (gray dots, right y-axis) and accuracy (black squares, right y-axis) for yearling weight using 6 models.

In all the models, epistatic variance estimates had large standard deviations. These results point out the difficulties in obtaining a good estimate of epistatic variances also from genomic information even when these are only first-order interactions and the additive by additive epistatic variance explain up to 25% and 39% of total genetic variance of YWT in BB and TC, respectively. Therefore, further research is needed.

The magnitude of dominance variance relative to phenotypic variance was up to 13% and 10% in BB and TC, respectively. Estimates of the dominance variance as a proportion of additive genetic variance averaged across the models were 26% and 19%, respectively for BB and TC. Thus, dominance variance represents a significant proportion of the total phenotypic and additive genetic variances for YWT in both breeds.

The inclusion of heterozygosity reduced the estimates of dominance and epistatic variances for YWT in both breeds (Fig. 1), however, those means were associated with a large standard deviation (Supplementary Table 1) and no significant differences were observed among them. In BB, the dominance variance with AD and ADH models were 111.72 ± 66.05 kg² and 95.58 ± 66.49 kg², respectively; and the dominance variance with ADE and ADHE were respectively 99.65 ± 66.13 kg² and 86.81 ± 66.52 kg² for GxG, 110.3 ± 35.04 kg² and 95.2 ± 31.71 kg² for GxD and 111.72 ± 65.89 kg² and 95.56 ± 66.35 kg² for DxD. In TC cattle, the same values for AD and ADH were 108.8 ± 55.48 kg² and 77.78 ± 56.01 kg², and the values for ADE and ADHE were 90.19 ± 55.72 kg² and 66.47 ± 55.92 kg² for GxG, 108.86 ± 55.36 kg² and 77.78 ± 55.80 kg² for GxD and 108.86 ± 55.37 kg² and 77.78 ± 55.80 kg² for DxD.

The ACC of GEBV were slightly higher with models that included nonadditive effects. The values ranged from 0.28 for A to 0.33 for ADHE_GxG in BB cattle, and from 0.18 for A to 0.23 for ADE_GxD in TC cattle (Fig. 1).

The goodness of fit varied modestly for the best models, with no clear advantage of one model relative to the others. The lowest values of −2logL (i.e., the highest likelihood) were 19,269.16 and 23,505.41 for ADHE_GxG models in BB and TC, respectively (Supplementary Table 1).

As expected, the sizes of additive SNP effects were consistent across all models, however the sizes of nonadditive SNP effects were slightly smaller for the models in which heterozygosity effects were included (ADH and ADHE) when compared to SNP effects from models AD and ADE. Despite differences in the magnitude of dominant SNP effects, the Pearson correlation among SNP dominance effects from all evaluated models were higher than 0.99 (results not shown), indicating that all marker effects were shrunk to the same degree.

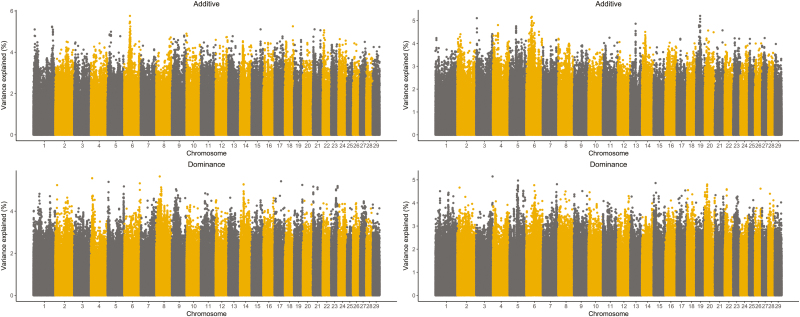
For the additive effect, SNP windows with a 1 Mb length (Fig. 2) were built across the genome with an average SNP density of 122 and 120 SNPs per window in BB and TC, respectively. In BB (TC), a total of 5 (4) SNP windows explaining more than 1% (0.5%) of the total genetic variance were identified (Fig. 2). Together, they explained 8.00% (2.79%) of the total genetic variance (Supplementary Tables S2 and S3). These windows of additive effect were used to locate candidate genes affecting YWT on BTA 14 for BB and on BTA 4, 5, and 14 for TC. The SNP window (n = 240 SNPs and n = 260 SNPs) with the highest proportion of total genetic variance explaining approximately 2.25% and 0.86%, was located on BTA 14 and 5 for BB and TC, respectively. For dominance, 1 and 2 windows explained more than 2.09% and 1.27% of the total genetic variance and the density per window was 331 and 328 SNPs in BB and TC, respectively.

Figure 2.

Proportion of additive (top panels) and dominant (bottom panels) variance explained by single nucleotide polymorphism (SNP) windows for yearling weight of Brahman (left) and Tropical Composite (right).

DISCUSSION

Partitioning genetic variance into its additive and nonadditive “statistical” components does not allow an understanding of the genetic architecture of a trait (Huang and Mackay, 2016); however, it is useful for maximizing genetic gain by designing mating schemes (Aliloo et al., 2017). Pedigree information can be used to estimate dominance variance (Misztal et al., 1998), however, partitioning genetic variance components is notoriously difficult, requiring specialized breeding designs (e.g., diallel crosses) and pedigree information (Lynch and Walsh, 1998), often limiting the genetic diversity that can be sampled in any one given study. In contrast, genome-wide molecular marker data now offer tools to quantify dominance and epistatic variances (Vitezica et al., 2013, 2017) more accurately. The present study provided estimates of additive and nonadditive variance components in beef cattle.

Our results show that additive genetic variance was well estimated even when dominance variance was included in the model. However, when additive by additive epistatic effects were included, the variance explained by the additive component decreased. These results showed that there is dependency between variance component estimations and thus, the partition of additive and nonadditive effects is not empirically orthogonal. The linkage disequilibrium might explain the confounding nature of additive and nonadditive effects (Hill et al., 2008). Bayesian regression models allow the fitting of a priori dependencies between additive and nonadditive effects. However, the treatment of dependencies between breeding values and dominance or epistatic deviation is rather complex (Wellmann and Bennewitz, 2012). It is worth highlighting that linkage equilibrium and unlinked markers are required by Hadamard matrix multiplication (Schnell, 1963). However, SNP markers are linked, thus some bias could be included in epistatic variance estimates.

Furthermore, the significant proportion of nonadditive effects on the total phenotypic and/or genetic variance of YWT could be explained by factors such as large environmental variance and low relationships among recorded animals, factors which have shown to apply to the dataset studied here (Bolormaa et al., 2014). In addition, datasets with repeated measurements appear to allow better decomposition of phenotypic variance into additive and nonadditive, because the permanent environmental effects capture a large proportion of the nonadditive effects if the model does not explicitly account for it (Aliloo et al., 2017).

By construction, models AD and ADE imply that the mean of nonadditive effects is equal to zero, which is not true when directional dominance exists. Thus, the dominance variance could be overestimated if the mean heterozygosity (or inbreeding) is not included in the models (Xiang et al., 2016; Aliloo et al., 2017). Even if these results were not confirmed in this study, ADH and ADHE models must be used to estimate nonadditive variance components.

Inclusion of nonadditive effects resulted in a slight increase in accuracy. These results were in agreement with other authors. With the exception of Aliloo et al. (2016) (for fat yield in Holstein), in most of studies, the inclusion of dominance in GBLUP model did not improve predictive ability of the model (Su et al., 2012; Ertl et al., 2014; Xiang et al, 2016; Esfandyari et al., 2016; Moghaddar and van der Werf, 2017).

In accordance with our additive effects estimates, previous results presented and discussed by Porto-Neto et al. (2014), identified a major quantitative trait locus (QTL) located at ~25 Mbp on bovine chromosome (BTA) 14 explaining a significant proportion of phenotypic variance of YWT. This QTL has been attributed to 2 potential functional variants, PLAG1 and CHCHD7 affecting weight (Karim et al., 2011; Fink et al., 2017). Also, a relevant additive contribution of QTL located at ~47 Mbp on BTA 5 was identified in TC, with the closest annotated candidate gene being HELB (Fortes et al., 2013; Porto-Neto et al., 2014).

Similarly to Aliloo et al. (2017), in our results different sets of SNP were responsible for additive “statistical” effects suggesting that some markers could be potential candidates for studying the “biological” effects of the genes involved in YWT. For instance, a dominant QTL located at ~27 Mbp on BTA 14 was identified in BB and some genes in this region act on growth and development of tissues throughout the body. One of these genes is the aspartate beta-hydroxylase (ASPH) protein coding gene which plays an important role in calcium homeostasis and muscle metabolism (Porto-Neto et al., 2014). Moreover, the chromodomain helicase DNA binding protein 7 (CHD7) protein belongs to a family of proteins that are thought to play a role in the organization of chromatin and is active in a bundle of nerve cells that is critical for the perception of odors (Feng et al., 2017). In TC, dominant QTLs were located in different regions, for example at ~60 Mbp on BTA 5 and ~81 Mbp on BTA 6.

In conclusion, the better goodness of fit and ACC improvement of models ADH and ADHE suggest that, dominance, epistasis, and heterozygosity should be included in models for estimation of genetic parameters and breeding values. However, for selection decisions, the additive genetic effect on its own (in evaluation models) is able to identify the most productive animals.

SUPPLEMENTARY DATA

Supplementary data are available at Journal of Animal Science online.

Conflict of interest statement. None declared.