Abstract
EMAN2 is an extensible software suite with complete workflows for performing high-resolution single particle analysis, 2-D and 3-D heterogeneity analysis, and subtomogram averaging, among other tasks. Participation in the recent CryoEM Map Challenge sponsored by the EMDatabank led to a number of significant improvements to the single particle analysis process in EMAN2. A new convolutional neural network particle picker was developed, which dramatically improves particle picking accuracy for difficult data sets. A new particle quality metric capable of accurately identifying “bad” particles with a high degree of accuracy, no human input, and a negligible amount of additional computation, has been introduced, and this now serves as a replacement for earlier human-biased methods. The way 3-D single particle reconstructions are filtered has been altered to be more comparable to the filter applied in several other popular software packages, dramatically improving the appearance of sidechains in high-resolution structures. Finally, an option has been added to perform local resolution-based iterative filtration, resulting in local resolution improvements in many maps.
Keywords: CryoEM, single particle analysis, image processing, 3-D reconstruction, structural biology, EMDatabank map challenge
Introduction:
EMAN2 (Tang et al., 2007) was released in 2007 as a modular and expandable version of the EMAN (Ludtke et al., 1999) software suite for quantitative image analysis, with a focus on biological TEM. EMAN2 is widely used for single particle analysis (SPA), subtomogram averaging and other workflows, as well as providing a wide range of utility functions able to interact with virtually every file format used in this community. Its predecessor, EMAN, was written purely in C++, whereas EMAN2 adopted Python for all end-user programs with a C++ library providing image processing/math support, making the software easily adaptable to user needs and new innovations in the field. The EMAN2 suite has continued to be updated 2-3 times a year to add new features and adapt to new developments in the CryoEM field (Murray et al., 2014).
The 2015-2016 CryoEM Map Challenge hosted by the Electron Microscopy Data Bank (EMDatabank) presented EMAN2 developers with an excellent opportunity to critically evaluate our approach to SPA and compare to other available solutions. As a result, our team has made several significant improvements, which dramatically reduce human bias on maps, and produce better structures with more visible sidechains at high-resolution. First, we introduce two new filtration strategies: one is similar to the standard methodology applied in post-processing in Relion (Scheres, 2012), and the other is a local filtration approach useful when maps have varying levels of motion in different structural domains. Second, we introduce a new semi-automatic particle selection algorithm using convolutional neural networks (CNNs), which has demonstrated better accuracy than reference-based pickers and is comparable to a human even on challenging data sets. Finally, we introduce a new metric for assessing the quality of individual particles in the context of a SPA and eliminating bad particles without human input. We demonstrate quantitatively that eliminating “bad” particles can improve both internal map resolution as well as agreement with the “ground truth”.
Local and Global Filtration of 3D Maps
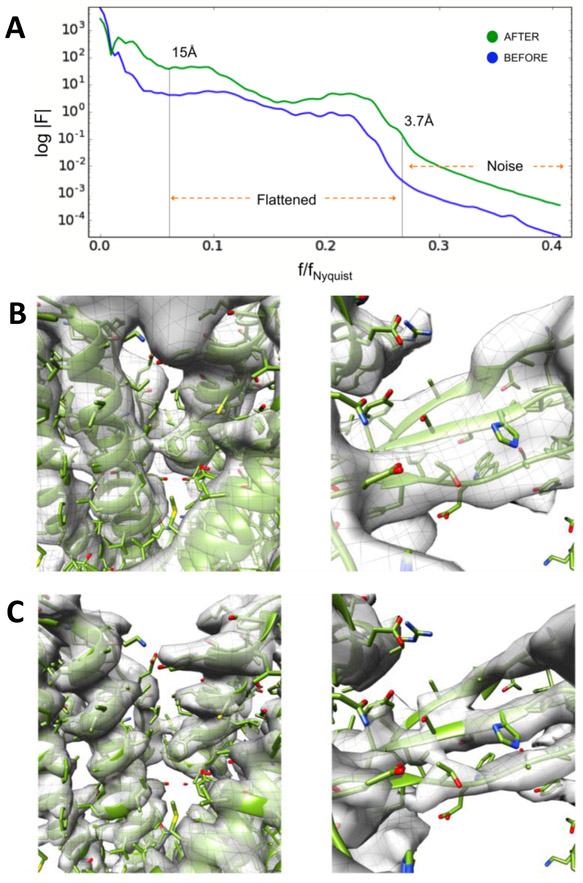
Prior to the CryoEM Map challenge, users observed that, even when the measured resolution was identical, near atomic resolution structures solved with Relion (Scheres, 2012) would often appear to have more detail than the same structures solved with EMAN2. Since both Relion and EMAN2 use CTF amplitude correction combined with a Wiener filter during reconstruction, the cause of this discrepancy remained a mystery for some time. During the challenge, we realized that the Relion post-processing script was replacing the Wiener filter with a tophat (sharp-cutoff) low pass filter, which has the effect of visually intensifying features near the resolution cutoff at the expense of adding weak ringing artifacts to the structure, under the justification that effectively the same strategy is used in X-ray crystallography. In response, we added the option for a final tophat filter with B-factor sharpening (Rosenthal and Henderson, 2003) to EMAN2.2 (Figure 1A). This eliminated this perceptual difference, so when the resolution was equivalent, the visual level of detail would also match (Figure 1B, 1C).
Figure 1: B-factor Sharpening.
A. Guinier plot of the spherically averaged Fourier amplitude calculated using the canonical EMAN2 “structure factor” approach (blue) and our latest “flattening” correction (green). B. TRPV1 (EMPIAR-5778) reconstruction obtained using “structure factor” amplitude correction. C. TRPV1 reconstruction after iterative, “flattening” amplitude correction with a tophat filter.
However, this equivalence really applies only to rigid structures with no significant conformational variability at the resolution in question. For structures with significant local variability, we observe that different software packages tend to produce somewhat different results, even in cases where the overall resolution matches. It is impossible to define a single correct structure in cases where the data is conformationally variable. When comparing EMAN2, which uses a hybrid of real and Fourier space methods, to packages like Relion or Frealign which operate almost entirely in Fourier space, we often observe that the Fourier based algorithms provide somewhat better resolvability in the most self-consistent regions of the structure, at the cost of more severe motion averaging in the regions undergoing motion. EMAN2 on the other hand seems to produce more consistent density across the structure, including variable regions, at the cost of resolvability in the best regions. These differences appear only when structurally variable data is forced to combine in a single map, or when “bad” data is included in a reconstruction.
EMAN2 has a number of different tools designed to take such populations and produce multiple structures, thus reducing the variability issue (Ludtke, 2016). However, this does not answer the related question of how to produce a single structure with optimal resolution in the self-consistent domains, and appropriate resolution in variable domains. To address this, EMAN2.21 implements a local resolution measurement tool, based on FSC calculations between the independent even/odd maps. In addition to assessing local resolution, this tool also provides a locally filtered volume based on the local resolution estimate. Rather than simply being applied as a post-processing filter, this method can be invoked as part of the iterative alignment process, producing demonstrably improved resolution in the stable domains of the structure. Flexible domains are also filtered to the corresponding resolution, making features resolvable only to the extent that they are self-consistent. At 2-4 Å resolution, sidechains are seen to visibly improve in stable regions in the map using this approach. This apparent improvement is logical from both a real-space perspective, where fine alignments will be dominated by regions with finer features, as well as Fourier space, where the high-resolution contributions of the variable domains in the map have been removed by a low-pass filter, and only the rigid domains contribute to the alignment reference. Iteratively, this focuses the fine alignments on the most self-consistent domains, further strengthening their contributions to subsequent alignments.
The approach for computing local resolution is a straightforward FSC under a moving Gaussian window, similar to other tools of this type (Cardone et al., 2013). While other local resolution estimators exist, ResMap being the most widely used (Kucukelbir et al., 2014), we believe that our simple and fast method meshes well with the existing refinement strategy and is sufficient to achieve the desired result. The size of the moving window and the extent to which windows overlap is adjustable by the user, though the built-in heuristics will produce acceptable results. While the heuristics are complicated, and subject to change, in general the minimum moving window size is 16 pixels with a target size of 32 Å, with a Gaussian Full Width Half Max (FWHM) of 1/3 the box size for the FSC. While the relatively small number of pixels in the local FSC curves means there is some uncertainty in the resulting resolution numbers, they are at least useful in judging relative levels of motion across the structure. The default overlap typically produces one resolution sample for every 2-4 pixel spacings. A tophat lowpass filter is applied within each sampling cube, then a weighted average of the overlapping filtered subvolumes is computed, with the Gaussian weight smoothing out edge effects.
The local resolution method and tophat filter described above must be explicitly invoked to be used iteratively for SPA. B-factor sharpening is the default for structures at resolutions beyond 7 Å, whereas EMAN’s original structure factor approach (Yu et al., 2005) is used by default at lower resolutions. The defaults can be overridden by the user, and any of the new methods can be optionally used at any resolution. Each of these features are available when running refinements in EMAN2 from the GUI (e2projectmanager.py) or command line via e2refine_easy.py.
Convolutional Neural Network (CNN) Based Particle Picking
The problem of accurately identifying individual particles within a micrograph is as old as the field of CryoEM, and there are literally dozens of algorithms, (Liu and Sigworth, 2014; Scheres, 2015; Woolford et al., 2007; Zhu et al., 2004) to name a few, which have been developed to tackle this problem. These include some neural network-based methods (Ogura and Sato, 2001; Wang et al., 2016). Nearly any of these algorithms will work with near perfect accuracy on easy specimens, such as icosahedral viruses with a uniform distribution in the ice. However, the vast majority of single particles do not fall in this category, and the results of automatic particle selection can vary widely. In addition to problems of low contrast, and picking accuracy variation with defocus, frequent false positives can also be caused by ice and other contamination. There can also be difficulties with partially denatured particles, partially assembled complexes, and aggregates, which may or may not be appropriate targets for particle selection depending on the goals of the experiment. In one famous example from the particle picking challenge in 2004 (Zhu et al., 2004) participants were challenged to use the particle picker of their choice on a standardized data set consisting of high contrast proteasome images. Two of the most widely varying results were the manual picks by two different participants. One decided to avoid any particles with overlaps or contact with other particles, and the other opted to include anything which could plausibly be considered a particle. This demonstrates the difficulty in establishing the ground truth for particle picking. In the end, the final arbiter of picking quality is the quality of the 3-D reconstruction produced from the selected particles, but the expense of the reconstruction process often makes this a difficult metric to use in practice.
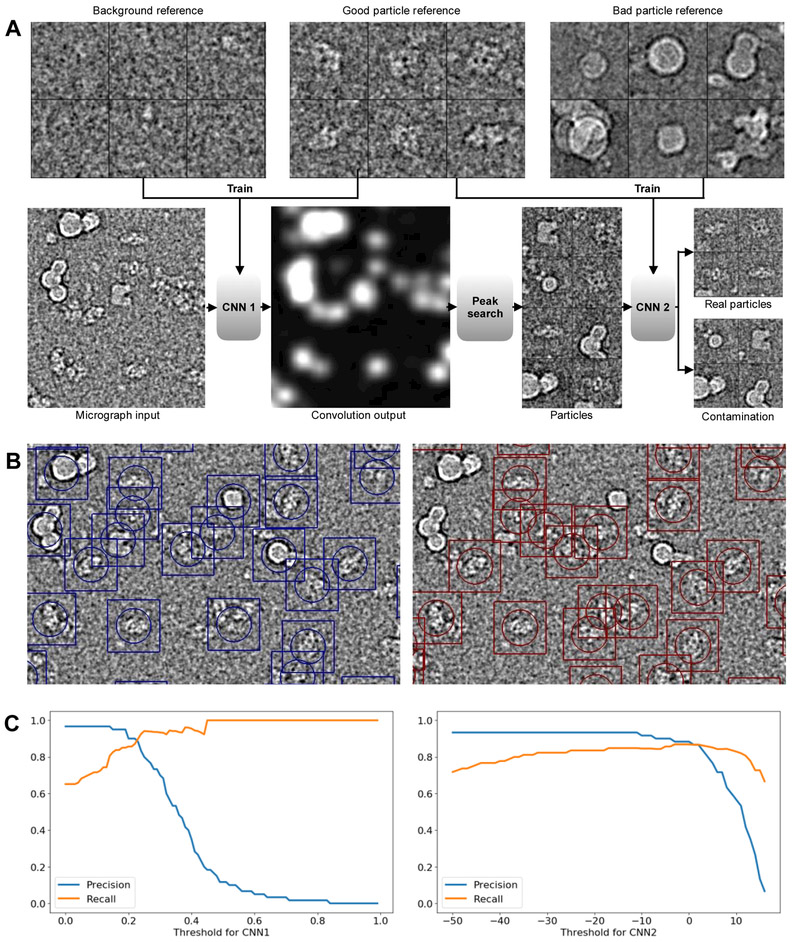
With the success of the CNN tomogram segmentation tool in EMAN2.2 (Chen et al., 2017) we decided to adapt this method to particle picking, which is now available within e2boxer.py (Figure 2). The general structure of the CNN is similar to that used for tomogram segmentation, with two primary changes: first, the number of neurons is reduced from 40 to 20 per layer. Second, in tomogram annotation, the training target is a map identifying which pixels contain the feature of interest. In particle picking, the training target is a single Gaussian centered in the box whenever a centered particle is present in the input image, and zero when a particle is not present. That is, the output of the final CNN will be pixel values related to the probability that each pixel is at the center of a particle.
Figure 2. Particle Picking.
A. Workflow of CNN based particle picking. Top: examples of background, good and bad particle references. Bottom: Input test micrograph and output of the trained CNNs. B. A comparison of template matching to the CNN picker. Left: Template matching based particle picking, using 24 class averages as references. Right: Results of CNN based particle picking, with 20 manually selected raw references of each type (good, background and bad). C. Left: Precision-recall curves of CNN1 on a test set, with the threshold of CNN2 fixed at −5. Right: Precision- recall curves of CNN2 with the threshold of CNN1 fixed at 0.2
The overall process has also been modified to include two stages, each with a separate CNN. The first stage CNN is trained to discriminate between particles and background noise. The second stage CNN is designed to assess whether putative particles are particles or ice contamination. In short, the first network is designed to distinguish between low contrast background noise, and particle shaped/sized objects, and the second stage is designed to identify and eliminate identified high-contrast objects which are actually contamination.
To train the two CNNs, the user must provide 3 sets of reference boxes, each requiring only ~20 representative images. The first set includes manually selected, centered and isolated individual particles drawn from images at a range of defocuses in a range of different particle orientations. The second set includes regions of background noise, again, drawn from a variety of different micrographs. Finally, the third set contains high contrast micrograph regions containing ice contamination or other non-particles. Sets 1 and 2 are used to train the first stage CNN and sets 1 and 3 are used to train the second stage CNN. While ~20 images in each set is generally sufficient, the user may opt to provide more training data if they prefer. We have found that gains in CNN performance diminish for most specimens beyond ~20 references, as long as the 20 are carefully selected. If the micrographs contain a particularly wide range of defocuses, or if the particles have widely varying appearance in different orientations, a larger number of examples may be required for good results. The thresholds for the CNNs can be adjusted interactively, so users can select values based on the performance on a few micrographs before applying the CNNs to all images. The default values, which are used in the example are 0.2 for CNN1 and −5.0 for CNN2. The rationale for this choice is that, for single particle analysis, having false positives or bad particles can damage the reconstruction results, while missing a small fraction of particles in micrographs is generally not a serious problem (Figure 2C).
This methodology performed extremely well on all of the challenge data sets, including the beta galactosidase data set, which includes significant levels of ice contamination with similar dimensions to real particles. We also tested this on our published (Fan et al., 2015) and unpublished IP3R data sets, which were sufficiently difficult targets that, for publication, 200,000+ particles had been manually selected. Even this challenging set was picked accurately using the CNN strategy. While picking accuracy is difficult to quantify on a particle-by-particle basis due to the lack of a reliable ground-truth, we performed 3-D reconstructions using particles selected by the CNN picker, and results were as good or better than those produced by manual selection.
We believe this particle picker may offer a practical and near-universal solution for selecting isolated particles in ice. Filamentous objects can also be approached using similar methods, but for this case, the tomogram annotation tool might be more appropriate. An adaptation designed specifically to extract particles for Iterative Helical Real Space Reconstruction (IHRSR) (Egelman, 2010) does not exist but could be readily adapted from existing code.
Automated CTF correction
EMAN (Ludtke et al., 1999) and SPIDER (Penczek et al., 1997) were the first software packages to support CTF correction for general purpose SPA with full amplitude correction. Not only does the historical EMAN approach determine CTF directly from particles, but it also uses a novel masking strategy to estimate particle spectral signal to noise ratio directly from the particle data. In addition to being used in the correction process, this provides an immediate measure of whether the particles in a particular image have sufficient signal for a reliable 3-D reconstruction.
While this method has served EMAN well over the years, it has become clear that more accurate defocus estimates can be made using the entire micrograph, particularly when astigmatism correction is required. The whole micrograph approach also has disadvantages, as some image features, such as the thick carbon film at the edge of holes or ice contamination on the surface, may have a different mean defocus than the target particles.
In response to this, EMAN2.2 has now adopted a two-stage approach. First, the defocus, and optionally astigmatism and phase shift, are determined from the micrographs as they are imported into the project. These can be determined using EMAN’s automatic process, which is quite fast, or metadata can be imported from other packages, such as CTFFIND (Rohou and Grigorieff, 2015). In the second stage defocus can be fine-tuned, and SSNR is estimated, along with the 1-D structure factor, from the particle images themselves.
Unlike earlier versions of EMAN2, which required several manual steps, CTF processing is fully automated whether running e2ctf-auto.py from the command line or the project manager. The primary failure mode, in which the first zero is inaccurately placed coincident with the second zero or a strong structure factor oscillation, is rare, and can be readily detected and corrected. A quick check of the closest and furthest from focus images after automatic processing is generally sufficient to detect any outliers, and in most projects, there are none.
In addition to determining CTF and other image parameters, CTF auto-processing also generates filtered and down-sampled particles in addition to CTF phase-flipped particles at full resolution. These down-sampled particle stacks are provided as a convenience for speed in the initial stages of processing where full resolution data is not required. Use of the down-sampled stacks is entirely at the user’s discretion. Decisions about the amount of down-sampling and filtration is based on the user’s specification of whether they plan to target low, intermediate or high-resolution. Only the final high-resolution refinement is normally performed with the unfiltered data at full sampling. While such filtered, masked and resampled particles could be generated on-the-fly from the raw data, the down-sampled data sets significantly decrease disk I/O during processing, and the filtration/masking processes are sufficiently computationally intensive preprocessing is sensible.
The current version also includes initial support for automatic or manual fitting of Volta-style phase-plate data with variable phase shift. Mathematically, phase shift and amplitude contrast (within the weak-phase approximation) are equivalent parameters. Phase shift can be represented either as a −180 to 180 degree range, or it can be represented as amplitude contrast in which case it is nonlinearly transformed to a −200% to +200% range, matching the conventional %AC definition for small shifts. While the amplitude contrast ranges make little intuitive sense when used in this way, this approach avoids adding a redundant parameter, such as the approach used in CTFFIND4 (Rohou and Grigorieff, 2015).
Identifying and Removing “Bad” Particles
The core assumption at the heart of the entire SPA process is that each of the particles used for the reconstruction represents a 2-D projection of the same 3-D volume in some random orientation. There are numerous ways in which this assumption may be violated, any of which will have an adverse effect on the final 3-D reconstruction. First, the 3-D particles may have localized compositional or conformational variability, second, the particles may be partially denatured, third, some of the identified particles may not be particles at all but may rather be some form of contamination. If our goal is a single self-consistent reconstruction representing some state of the actual 3-D molecule, then eliminating particles in any of these 3 classes would be the appropriate response. However, if our aim is to understand the complete behavior of the particle in solution, then particles in the first class should be retained, and used to characterize not just a single structure, but also the local variability. Particles in the other two classes, however, should always be eliminated if they can be accurately identified.
There have been a range of different methods attempted over the years to robustly identify and eliminate “bad” particles (Bharat et al., 2015; Borgnia et al., 2004; Fotin et al., 2006; Guo and Jiang, 2014; Schur et al., 2013; Wu et al., 2017). The early approaches, also supported in EMAN, largely rely on assessing the similarity of individual particles to a preliminary 3-D structure or to a single class-average. The risk in this approach is producing a self-fulfilling prophecy, particularly if some sort of external reference is used to exclude bad particles. Still, such approaches may be reasonable for excluding significant outliers, which will generally consist of ice contamination or other incorrectly identified particles.
Another approach, commonly used in Relion, involves classifying the particles into several different populations via multi-model 3-D classification, then manually identifying which of the 3-D structures are “good” and which are “bad”, keeping only the particles associated with the “good” maps (Scheres, 2010). While particles which are highly self-consistent should group together, there is no reason to expect that particles which are “bad” in random ways would also group with each other. It is logical that such particles would be randomly distributed, and a significant fraction would also still associate (randomly) with the “good” models, so this approach will clearly only be able to eliminate a fraction of the “bad” particles. This process also introduces significant human bias into the reconstruction process, raising questions of reliability and reproducibility. Nonetheless, as long as one states that the goal is to produce one single map with the best possible resolution which is self-consistent with some portion of the data, this approach may be reasonable. If the goal is to fully characterize the particle population in solution, then clearly any excluded subsets must also be carefully analyzed to identify whether the exclusion is due to compositional or conformational variability or due to actual image quality issues. One problem with current approaches using absolute model vs. particle similarity metrics is that, due to the imaging properties of the microscope, particles far from focus have improved low-resolution contrast, making them easier to orient, but generally at the cost of high-resolution contrast. Therefore, absolute similarity metrics will tend to consider far-from-focus particles better absolute matches to the reference than the closer to focus particles which have the all-important high-resolution information we wish to recover. Such metrics do eliminate truly bad particles, but when used aggressively they also tend to eliminate the particles with the highest resolution data. The simplest correction, allowing the bad particle threshold to vary with defocus, is marginally better, but still tends to prioritize particles with high contrast at low-resolution over particles with good high-resolution contrast.
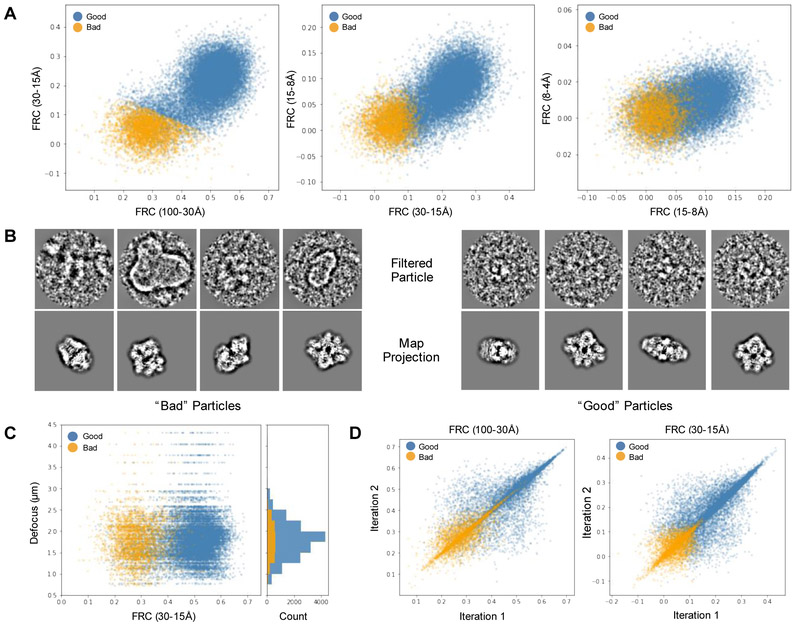
We now propose a composite metric that demonstrably identifies “bad” particles with a high level of accuracy for most data sets, without being subject to defocus dependencies (Figure 3). We define a “bad” particle to be non-particle images incorrectly picked, actual particles with contrast too low to align reliably, and, possibly, partially denatured or otherwise distorted particles (Figure 3B). First, we compute the integrated Fourier Ring Correlation (FRC) between each aligned particle and its corresponding best projection reference over four different resolution bands (100-30 Å, 30-15 Å, 15-8 Å and 8-4 Å, Figure 3A). These are computed twice: once for the final iteration in a single iterative refinement run, and again for the second-to-final iteration to assess self-consistency. While the 8-4 Å FRC remains almost pure noise even for the best contrast high-resolution datasets, the first two bands remain strong measures for all but the worst data sets. This is not to say that the particles are not contributing to the structure at 8-4 Å resolution or beyond, simply that the FRC from a single particle in this band has too much uncertainty to use as a selection metric.
Figure 3: Bad Particle Classification.
A. Particle/projection FRCs integrated over 4 bands and clustered via K-means algorithm with K=4. The cluster with the lowest sum of integrated FRC values are marked as “bad” while particles in the remaining 3 are labeled “good.” B. Example beta-galactosidase particles (EMPIAR 10012 and 10013) and projections from bad (left) and good (right) clusters. C. Defocus vs. low-resolution integrated FRC. D. Left. Iteration-to-iteration comparison of integrated particle/projection FRC values at low (left) and intermediate (right) spatial frequencies.
For all but the furthest from focus images, the lowest resolution band is primarily a measure of overall particle contrast and is strongly impacted by defocus. The second band is integrated over a broad enough range that defocus has a limited impact (Figure 3C). If two particles have roughly the same envelope function, then we would expect the second FRC band to increase fairly monotonically, if not linearly, with the lowest resolution FRC. If, however, a particular particle has weak signal at very high-resolution, this will also have some influence on the intermediate resolution band where the FRC values are less noisy. Indeed, we have found that, after testing on a dozen completely different data sets, there tends to be a characteristic relationship among the first two or, for high-resolution data, three FRC bands. Particles that deviate from this relationship are much more likely to be bad. Furthermore, if we look at these FRC values from the final iteration vs. the same value in the second to last iteration, an additional pattern emerges, with some particles clearly having significant random variations between iterations, and others which are largely self-consistent from one iteration to the next (Figure 3D).
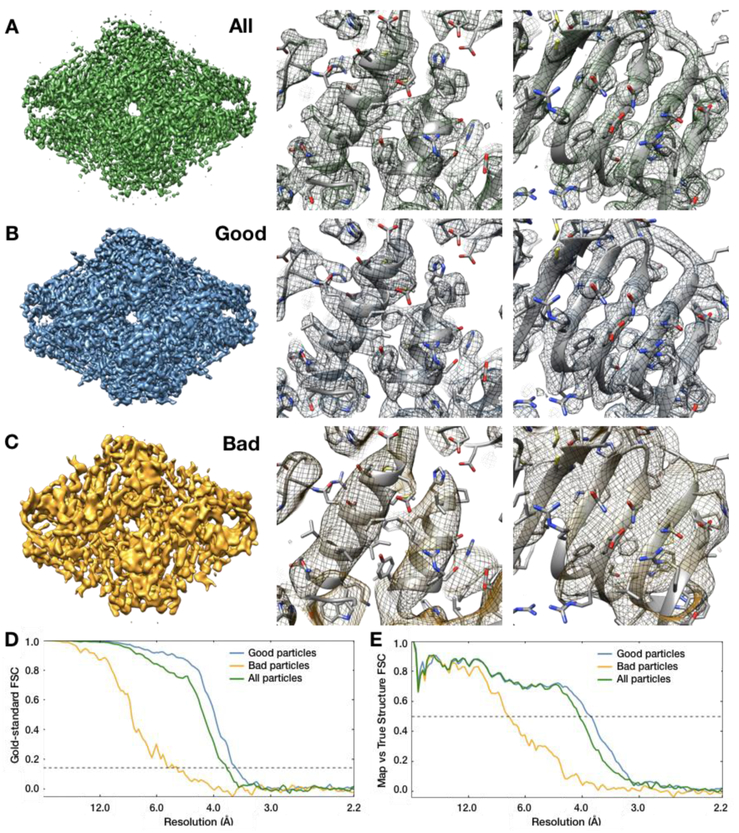
This approach is available both from the project manager GUI as well as the e2evalrefine.py command. After computing the metric described above for the full particle population, k-means segmentation is used to separate the particle set into 4 classes, only the worst of which is excluded from the new particle set, meaning that each time this method is applied up to ~1/4 of particles may be excluded. The actual excluded fraction will depend on how well the particular data set clusters, and with what distribution. In extensive testing using “good” and “bad” particle populations in various data sets, refinements from the “good” population have consistently achieved better or at least equivalent resolution to the refinement performed with all of the data, generally with improved feature quality in the map (Figure 4). Refinement using the “bad” particles will often still produce a low-resolution structure of the correct shape, but the quality and resolution is uniformly worse than either the original refinement or the refinement from the “good” population (Figure 4C). The fact that this method produces improved resolution despite decreasing the particle count is a strong argument for its performance.
Figure 4: Resolution enhancements obtained from bad particle removal.
A. Beta galactosidase map refined using all 19,829 particles, B. using only the “good” particle subset (15,211), and C. using only the “bad” particle subset (4,618). D. Gold standard FSC curves for each of the three maps in A-C. E. FSC between the maps in A-C and a 2.2Å PDB model (5A1A) of beta galactosidase. Note that the “good” particle subset has a better resolution both by “gold standard” FSC and by comparison to the ground-truth, indicating that the removed particles had been actively degrading the map quality.
Conclusions
In this time of rapid expansion in the CryoEM field, and the concomitant ease with which extremely large data sets can be produced, it is important to remember the need to critically analyze all of the resulting data and exclude data only when quantitative analysis indicates low data quality. There is still considerable room for the development of new tools for enhancing the rigor and reproducibility of CryoEM SPA results. Community validation efforts such as the EMDatabank map challenge are important steps in ensuring that the results of our image analysis are a function only of the data, and not of the analysis techniques applied to it, or at least that when differences exist, the causes are understood.
In addition to the algorithm improvements described above, EMAN2.2 has transitioned to use a new Anaconda-based distribution and packaging system which provides consistent cross-platform installation tools, and properly supports 64-bit Windows computers. As part of ongoing efforts to stabilize and modernize the platform we are beginning the process of migrating from C++03 to C++14/17, Python 2 to Python 3, and Qt4 to Qt5. We have also enabled and improved the existing unit-testing infrastructure, integrated with GitHub, to ensure that code changes do not introduce erroneous image processing results.
EMAN2 remains under active development. While the features and improvements discussed in this manuscript are available in the 2.21 release, using the most up-to-date version will provide access to the latest features and improvements.
Highlights:
Release of EMAN2.21, with changes inspired by the Map Challenge
High-resolution SPR maps are now filtered to enhance sidechain visibility
A new neural network-based particle picker provides accurate picking even on challenging data
Per-particle CTF correction routine now fully automated
Development of a new algorithm for identifying “bad” particles
Acknowledgements
This work was supported by the NIH (R01GM080139, P41GM103832). The 2016 EMDatabank Map Challenge, which motivated this work was funded by R01GM079429. Beta Galactosidase micrograph and particle data was obtained from EMPIAR 10012 and 10013. We also used beta-galactosidase model PDB-5A1A (Milne and Subramaniam, 2015). TRPV1 data was obtained from EMPIAR-10005.
Abbreviations:
- CryoEM
Electron cryomicroscopy
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Present/permanent address: Baylor College of Medicine; 1 Baylor Plaza; Houston, TX 77030
References
- Bell JM, Chen M, Baldwin PR, Ludtke SJ, 2016. High resolution single particle refinement in EMAN2.1. Methods 100, 25–34. 10.1016/j.ymeth.2016.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bharat TAM, Russo CJ, Löwe J, Passmore LA, Scheres SHW, 2015. Advances in Single-Particle Electron Cryomicroscopy Structure Determination applied to Sub-tomogram Averaging. Structure 23, 1743–1753. 10.1016/j.str.2015.06.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borgnia M, Shi D, Zhang P, Milne J, 2004. Visualization of alpha-helical features in a density map constructed using 9 molecular images of the 1.8 MDa icosahedral core of pyruvate dehydrogenase. J. Struct. Biol 147, 136–145. 10.1016/j.jsb.2004.02.007 [DOI] [PubMed] [Google Scholar]
- Cardone G, Heymann JB, Steven AC, 2013. One number does not fit all: Mapping local variations in resolution in cryo-EM reconstructions. J. Struct. Biol 184, 226–236. 10.1016/j.jsb.2013.08.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M, Dai W, Sun SY, Jonasch D, He CY, Schmid MF, Chiu W, Ludtke SJ, 2017. Convolutional neural networks for automated annotation of cellular cryo-electron tomograms. Nat. Methods 14, 983–985. 10.1038/nmeth.4405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egelman EH, 2010. Reconstruction of helical filaments and tubes. Methods Enzymol. 482, 167–183. 10.1016/S0076-6879(10)82006-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan G, Baker ML, Wang Z, Baker MR, Sinyagovskiy PA, Chiu W, Ludtke SJ, Serysheva II, 2015. Gating machinery of InsP3R channels revealed by electron cryomicroscopy. Nature 527, 336–341. 10.1038/nature15249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fotin A, Kirchhausen T, Grigorieff N, Harrison SC, Walz T, Cheng Y, 2006. Structure determination of clathrin coats to subnanometer resolution by single particle cryo-electron microscopy. J. Struct. Biol 156, 453–460. 10.1007/s10439-011-0452-9.Engineering [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo F, Jiang W, 2014. Single Particle Cryo-electron Microscopy and 3-D Reconstruction of Viruses. 10.1007/978-1-62703-776-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucukelbir A, Sigworth FJ, Tagare HD, 2014. Quantifying the local resolution of cryo-EM density maps. Nat. Methods 11, 63–5. 10.1038/nmeth.2727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Sigworth FJ, 2014. Automatic cryo-EM particle selection for membrane proteins in spherical liposomes. J. Struct. Biol 185, 295–302. 10.1016/j.jsb.2014.01.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludtke SJ, 2016. Single-Particle Refinement and Variability Analysis in EMAN2.1. Methods Enzymol. 579, 159–189. 10.1016/bs.mie.2016.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludtke SJ, Baldwin PR, Chiu W, 1999. EMAN: Semiautomated software for high-resolution single-particle reconstructions. J. Struct. Biol 128, 82–97. 10.1006/jsbi.1999.4174 [DOI] [PubMed] [Google Scholar]
- Milne JLS, Subramaniam S, 2015. 2.2 Å resolution cryo-EM structure of β-galactosidase in complex with a cell-permeant inhibitor 348, 1147–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray S, Galaz-Montoya J, Tang G, Flanagan J, Ludtke S, 2014. EMAN2.1 - A New Generation of Software for Validated Single Particle Analysis and Single Particle Tomography. Microsc. Microanal 20, 832–833. 10.1017/S143192761400588124806975 [DOI] [Google Scholar]
- Ogura T, Sato C, 2001. An automatic particle pickup method using a neural network applicable to low-contrast electron micrographs. J. Struct. Biol 136, 227–238. 10.1006/jsbi.2002.4442 [DOI] [PubMed] [Google Scholar]
- Penczek P, Zhu J, Schröder R, Frank J, 1997. Three Dimensional Reconstruction with Contrast Transfer Compensation from Defocus Series. Scanning Microsc. 11, 147–154. 10.1016/0304-3991(92)90011-8 [DOI] [Google Scholar]
- Rohou A, Grigorieff N, 2015. CTFFIND4: Fast and accurate defocus estimation from electron micrographs. J. Struct. Biol 192, 216–221. 10.1016/j.jsb.2015.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenthal PB, Henderson R, 2003. Optimal determination of particle orientation, absolute hand, and contrast loss in single-particle electron cryomicroscopy. J. Mol. Biol 333, 721–745. 10.1016/j.jmb.2003.07.013 [DOI] [PubMed] [Google Scholar]
- Scheres SHW, 2015. Semi-automated selection of cryo-EM particles in RELION-1.3. J. Struct. Biol 189, 114–122. 10.1016/J.JSB.2014.11.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheres SHW, 2012. RELION: Implementation of a Bayesian approach to cryo-EM structure determination. J. Struct. Biol 180, 519–530. 10.1016/j.jsb.2012.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheres SHW, 2010. Maximum-likelihood methods in cryo-EM. PartII: application to experimantal data. Methods Enzym. 6879, 295–320. 10.1016/S0076-6879(10)82012-9.Maximum-likelihood [DOI] [Google Scholar]
- Schur FKM, Hagen WJH, De Marco A, Briggs JAG, 2013. Determination of protein structure at 8.5Aresolution using cryo-electron tomography and sub-tomogram averaging. J. Struct. Biol 184, 394–400. 10.1016/j.jsb.2013.10.015 [DOI] [PubMed] [Google Scholar]
- Tang G, Peng L, Baldwin PR, Mann DS, Jiang W, Rees I, Ludtke SJ, 2007. EMAN2: An extensible image processing suite for electron microscopy. J. Struct. Biol 157, 38–46. 10.1016/j.jsb.2006.05.009 [DOI] [PubMed] [Google Scholar]
- Wang F, Gong H, Liu G, Li M, Yan C, Xia T, Li X, Zeng J, 2016. DeepPicker: A deep learning approach for fully automated particle picking in cryo-EM. J. Struct. Biol 195, 325–336. 10.1016/j.jsb.2016.07.006 [DOI] [PubMed] [Google Scholar]
- Woolford D, Ericksson G, Rothnagel R, Muller D, Landsberg MJ, Pantelic RS, McDowall A, Pailthorpe B, Young PR, Hankamer B, Banks J, 2007. SwarmPS: Rapid, semi-automated single particle selection software. J. Struct. Biol 157, 174–188. 10.1016/j.jsb.2006.04.006 [DOI] [PubMed] [Google Scholar]
- Wu J, Ma Y, Congdon C, Brett B, Chen S, Xu Y, Ouyang Q, Mao Y, 2017. Massively parallel unsupervised single- particle cryo-EM data clustering via statistical manifold learning 1–25. 10.1371/journal.pone.0182130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu X, Acehan D, Ménétret JF, Booth CR, Ludtke SJ, Riedl SJ, Shi Y, Wang X, Akey CW, 2005. A structure of the human apoptosome at 12.8 A resolution provides insights into this cell death platform. Structure 13, 1725–1735. 10.1016/j.str.2005.09.006 [DOI] [PubMed] [Google Scholar]
- Zhu Y, Carragher B, Glaeser RM, Fellmann D, Bajaj C, Bern M, Mouche F, De Haas F, Hall RJ, Kriegman DJ, Ludtke SJ, Mallick SP, Penczek PA, Roseman AM, Sigworth FJ, Volkmann N, Potter CS, 2004. Automatic particle selection: Results of a comparative study. J. Struct. Biol 145, 3–14. 10.1016/j.jsb.2003.09.033 [DOI] [PubMed] [Google Scholar]