Determining Synchrony Between Behavioral Time Series: An Application of Surrogate Data Generation for Establishing Falsifiable Null-Hypotheses

Abstract

Synchrony between interacting systems is an important area of nonlinear dynamics in physical systems. Recently psychological researchers from multiple areas of psychology have become interested in nonverbal synchrony (i.e., coordinated motion between two individuals engaged in dyadic information exchange such as communication or dance) as a predictor and outcome of psychological processes. An important step in studying nonverbal synchrony is systematically and validly differentiating synchronous systems from non-synchronous systems. However, many current methods of testing and quantifying nonverbal synchrony will show some level of observed synchrony even when research participants have not interacted with one another. In this article we demonstrate the use of surrogate data generation methodology as a means of testing new null-hypotheses for synchrony between bivariate time series such as those derived from modern motion tracking methods. Hypotheses generated by surrogate data generation methods are more nuanced and meaningful than hypotheses from standard null-hypothesis testing. We review four surrogate data generation methods for testing for significant nonverbal synchrony within a windowed cross-correlation (WCC) framework. We also interpret the null-hypotheses generated by these surrogate data generation methods with respect to nonverbal synchrony as a specific use of surrogate data generation, which can then be generalized for hypothesis testing other repeated observation psychological data.

Nonverbal communication is a vital component of the way individuals take in and express information with one another. This communication takes on many forms, from changes in eye gaze and facial expression to modulations in body language and posture (Ekman, 2004; Ekman & Friesen, 1969). There are many theories regarding the functions of these communication methods in dyadic information exchange (e.g., Argyle & Dean, 1965; Cappella, 1981; Cappella & Greene, 1982). Developmentally, nonverbal communication appears to be a key component in information transfer and bonding between parents and their infants (Dickson, Walker, & Fogel, 1997; Feldman, Magori-Cohen, Galili, Singer, & Louzoun, 2011). Nonverbal communication later in life influences close relationship formation, relationship maintenance, and rapport building between individuals (Noller, 1980; Tickle-Degnen & Rosenthal, 1990). Ramseyer and Tschacher (2011) have shown a positive association between nonverbal behavior and psychotherapeutic outcomes such that greater synchrony between patient and therapist is related to better patient outcomes.

Defining and efficiently measuring such synchrony is vital to making claims in regard to synchronous systems. Currently, many methods for assessing synchrony rely on standard null-hypothesis testing. However, in behavioral time series, standard null-hypothesis testing methods tend to show significant synchrony between two individuals even when there is in reality no synchrony to be found (Ramseyer & Tschacher, 2010). In the current article, we discuss the use of surrogate data generation as an alternative to standard null-hypothesis tests for the presence of nonverbal synchrony in behavioral time series. We show how four surrogate data generation methods for four data types establish new null-hypotheses regarding nonverbal synchrony. We also demonstrate the ability of these methods to distinguish artifactual pseudosynchrony from synchrony due to interdependence given targeted null-hypothesis generated by these surrogate methods.

Measuring Nonverbal Synchrony

The concept of nonverbal synchrony can be considered to be a form of behavioral matching between two individuals. Such matching behavior need not occur at the exact same time nor must it involve the same kinds of motion, but it should exhibit some sort of coordinated back and forth play between individuals (Ramseyer & Tschacher, 2006). For example, an individual shaking his/her head while another individual waves his/her hand would exhibit some level of nonverbal synchrony even if these individuals were not perfectly in time with each other. There are also bounds on interpersonal interpretations of different amounts of nonverbal synchrony. While perfect nonverbal synchrony between two individuals can be defined as mimicry, the lack of synchrony between two individuals may seem insincere and uncomfortable (Ramseyer & Tschacher, 2006, 2011). Optimal nonverbal synchrony must then exist between these two extremes. Boker and Rotondo (2002) proposed a theory that involves building and breaking of conversation symmetry as a regulator of the amount of nonverbal synchrony between two individuals. Argyle and Dean (1965) and Cappella (1981) noted the trend of individuals to reach a comfortable point of equilibrium in their nonverbal synchrony. Researchers have linked such optimal levels of nonverbal synchrony to feelings of closeness and affiliation between individuals and general feelings of personal affect (Hove & Risen, 2009; Tschacher, Rees, & Ramseyer, 2014). Feldman et al. (2011) found that mothers and infants obtain nonverbal synchrony, and thus feelings of closeness, through synchronizing their heart beats with one another during repeated physical contact.

As objective definitions of nonverbal synchrony vary by researcher, so do the data collection methods used by these researchers. Some have used peer ratings of video recorded conversations by trained observers to measure synchrony between two individuals (Bernieri, Reznick, & Rosenthal, 1988; Bernieri & Rosenthal, 1991; Geerts, Titus, Johan, & Netty, 2006). Others have used more technical methods such as video analysis software or motion tracking to collect bivariate time series data from participants (Boker et al., 2009; Kwon, Ogawa, Ono, & Miyake, 2015; Ramseyer & Tschacher, 2011). These researchers then use some method of measuring similarity between the resulting dyadic time series data to obtain estimates of synchrony between participants. However, measurement errors and recursive qualities in human movement cause many of these methods to show some level of synchrony even when participants have not interacted with one another (Ramseyer & Tschacher, 2010). This is in part due to problems in standard null-hypothesis testing in which a value and some measure of uncertainty about that value is tested against zero, which is an impossible value for many nonverbal synchrony quantification methods. This is a well known problem with null-hypothesis testing (Anderson, Burnham, & Thompson, 2000). Thus, using standard null-hypothesis testing methods, a researcher would find significant nonverbal synchrony even in situations where no synchrony is present.

Additionally, common practices by many researchers increase the chance of finding effects where none exist. The Slutzky-Yule Effect is an example of this where applying a moving average can create correlations in data with originally no oscillatory behavior (Loynes, 2005). A similar phenomenon occurs when a time series is generated from average effects (Working, 1960). Working (1960) found that serial correlations can occur between differenced data even when no real correlations exist in the original data set. It is the goal of this article to describe a method of creating new null-hypotheses that are both falsifiable and informative for researchers seeking to establish the existence of nonverbal synchrony in their own data.

Synchrony vs. Pseudosynchrony

A specific challenge researchers face while analyzing time series obtained from nonverbal synchrony studies is the problem of distinguishing observed synchrony from pseudosynchrony (Bernieri et al., 1988; Ramseyer & Tschacher, 2010). Pseudosynchrony can be seen as the amount of apparent and spurious synchrony between two individuals not engaged in information exchange with one another. Pseudosynchrony occurs because humans tend to be in a constant state of motion. From breathing during sleep to preforming extreme sports, people constantly move. These motions keep to certain patterns depending on what situation an individual finds him or herself. Ashenfelter, Boker, Waddell, and Vitanov (2009) found that motion between individuals in conversation exhibits a fractal-like structure (i.e., motions of individuals engaged in conversation have qualities which are self-similar with respect to time). There is then some level of commonality and recursiveness in the structure of information transfer between individuals during conversation due simply to the act of being in conversation. Thus it is likely that some level of observed nonverbal synchrony will be obtained from any of the methods previously mentioned in this article, even when two individuals were never actually interacting. Additionally, common statistical practices leading to such phenomena as the Slutzky-Yule and Working effects can cause pseudosynchrony-like patterns in data sets. The problem of pseudosynchrony makes the alpha inflation of standard null-hypothesis testing so great as to make it worthless to researchers since there will always be some level of observed synchrony greater than zero obtained through any of these methods.

Thus, the hypothesis of "no synchrony exists between two individuals" is theoretically impossible and can easily be falsely rejected by standard null-hypothesis testing methods. This problem of testing impossible null-hypotheses is a common critique of standard null-hypothesis significance testing as it promotes the occurrence of type-I error (Cohen, 1994; Murphy, 1990; Szucs & Ioannidis, 2017). Indeed, standard null-hypothesis testing methods have been recognized as having multiple problems, from misunderstandings of p-values to what some researchers see as an over-reliance on this method for progressing scientific theory; see Harlow, Mulaik, and Steiger (2016) for an overview of these problems and counterarguments. In order for researchers to test for significant nonverbal synchrony above and beyond random chance, as opposed to simply above and beyond no synchrony, either standard null-hypothesis testing methods need to be modified in order to account for a range of possible pseudosynchrony values, or researchers need to apply an entirely separate method.

Surrogate Data Generation and Analysis

Surrogate analysis is a way around many of the limitations of standard null-hypothesis significance testing (Theiler, Eubank, Longtin, Galdrikian, & Farmer, 1992; Theiler & Prichard, 1996). In a surrogate analysis framework one identifies some theoretical quality of interest which one’s data may or may not contain (e.g., synchrony). Then some specific method is used to modify this data set in such a way that destroys this quality of interest (if this quality exists to begin with) while keeping all other qualities intact. A researcher then compares a chosen statistic of their original data set to a distribution of the same statistic from many surrogate data sets where the null-hypothesis is guaranteed to be true, thus finding how unlikely a statistic of the real data is given a hypothesis that the null is true. What is most important to know when using surrogate analysis methods is exactly what quality is being destroyed in a given data set and if this destruction ensures that the null-hypothesis of interest is true.

Theiler et al. (1992) originally conceptualized surrogate generation as a method for testing non-linearity within a time series. Theiler et al. (1992) accomplished this by scaling a given time series to be Gaussian and then converting this scaled time series to the frequency domain through Fourier transformation. This Fourier series is then used to generate surrogate time series with similar frequency which are then rescaled to match the amplitudes of the original time series. The methods employed by Theiler et al. (1992) preserve the linear qualities of a time series but destroy any non-linear qualities. Thus a test for non-linearity can be made by comparing statistics derived from these surrogate time series to those from an original time series.

Surrogate generation has since been used in areas such as physics, analysis of chaos, and statistical mechanics to test a multitude of phenomenon in regards to time series analysis (Schreiber & Schmitz, 2000). Schreiber and Schmitz (1996) expanded surrogate data generation to allow for less destructive methods which generate surrogates with similar autocorrelation and distributional properties compared to a time series of interest. Lucio, Valdés, and Rodríguez (2012) further expanded on this method to allow for nonstationary surrogates. Borgnat and Flandrin (2009) used surrogate data generation methodology to develop a test specifically for stationarity. It is our goal to further expand surrogate data generation to test for synchrony between two behavioral time series by destroying synchronous behavior between two time series of interest while keeping the distributional properties of these time series intact. These surrogate generation methods have few assumptions, are non-parametric, and hold so long as data points can be meaningfully exchanged with one another.

Conceptualizing Surrogate Data Generation

To illustrate utility of the destructive processes occurring during surrogate data generation, consider a randomization/permutation test (see Edgington & Onghena, 2007; Kutner, Nachtsheim, Neter, & Li, 2005). Surrogate data generation methods can then be seen as a more general form of randomization/permutation tests which can be applied to both cross-sectional and time series data. Assume we collect 50 data points each from two groups, group A and group B. We would end up with two data vectors A_i and B_i, i ∈ {1,…,50}. A standard method for null-hypothesis testing of such a data structure would be a Student’s t-test (assuming all appropriate statistical assumptions are met) testing a null-hypothesis that the population mean difference between the two groups is equal to 0. If we reject this null-hypothesis then it follows that the population mean of one of these groups is different than the population mean of the other group. Notice what is important in this stream of logic is the structure of A_i and B_i. If indeed the groups differ on their means and the grouping of observations i was improperly structured, say some element of group A were accidentally placed in group B, then we would expect that our mean difference would also be affected. If all elements of group A were less than group B, then this accidental data shuffling would make it seem like the means of these groups were closer together than reality. In a surrogate analysis framework we can take advantage of this property. We can obtain a single statistic, G, from our observed groupings such that G = mean(A_i) − mean(B_i). We can then combine A_i and B_i into a single data vector and then randomly sample this new data vector without replacement into two new surrogate data vectors, $A_i^s$ and $B_i^s$, each of size 50. We can then obtain a single statistic, S, from this surrogate data set such that $S=\mathit{\text{mean}}(A_i^s)-\mathit{\text{mean}}(B_i^s)$. Repeating this process M-many times will produce a distribution of S. This distribution of surrogate statistics, S, from data which has been disordered in such a way as to destroy any existing group-based ordering of that data. We can then test if G fell outside of some percentile of this distribution. Assuming an α of .05, we can test if G fell outside of 97.5% of the data points in our surrogate distribution on either side. This process tests a null-hypothesis that "The difference in means of this data in this particular organization is the same as if these data points were randomly grouped together". If this null-hypothesis is rejected then one could say that there is something important about the specific grouping structure of our data which is influencing observed mean differences above and beyond chance. Compared to a Student’s t-test which tests a hypothesis about values and assumes a distribution, the surrogate hypothesis is concerned with order and structure. Order and structure caused by the original grouping was destroyed and then the test was whether the original grouping showed more order than expected by chance. This surrogate data generates hypotheses which are more nuanced than standard null-hypothesis testing methods and do not rely on parametric assumptions.

The remainder of the current article is as follows. Four common data types are described and a general analysis framework for measuring similarity between two times series, windowed cross-correlations, is discussed. Then four methods of generating surrogates which destroy synchrony, if any exists, between time series are proposed and the new null hypotheses created by these methods are discussed.

Method

Data Types

Data from four sources were examined which yield data structures similar to those common in behavioral sciences:

1. Simulated waveforms;

2. Motion capture data;

3. A motion energy analysis of a dyadic interaction; and

4. Random noise.

Simulated waveforms were sampled from pairs of time-lagged 0.9 Hz sine waves sampled at 10Hz for 5-minutes. Researchers may choose to use models of such waveforms when examining periodicity of a behavioral time series. By studying the behaviors of these time-lagged sine waves within the context of surrogate generation one may inspect how each surrogate generation method affects each waveform. For this study, sine waves act as an ideally synchronous system. Thus, each surrogate generation method should show some obvious visual effect on the structure of these sine waves. The motion capture data comes from a study of individuals engaged in dyadic conversation over video and consists of head angular velocity sampled at 83Hz for 5-minutes. This angular velocity data serves as a more variable and pragmatic data set than time-lagged sine waves. Studies using motion capture are becoming common in psychological research researchers develop more advanced collection methods. The third data set used in this study comes from a motion energy analysis (MEA) of a female-female dyad engaged in a cooperation task sampled at 10Hz for 5-minutes and smoothed with a moving average function of 0.4s. MEA data were included because they are a measure of magnitude and have a lower bound of 0 as a possible value. Much like motion capture data, MEA measures some quality of movement but is a less fine-grained motion assessment than motion capture. The fourth data set was two sets of random normal noise sampled at 10Hz for 5-minutes. In comparison to synchronized sine waves, this random noise has an expectation of no synchrony and thus acts as a counter example to synchronous behavior. Any method which claims to measure synchrony for any null-hypothesis of no synchrony should cause researchers to fail to reject the null for this random noise pair. These four data types then show a gradient from perfectly synchronous and clean, to pure white noise. There is little probability that these data show pseudosynchrony given that the generated data were not aggregated prior to analysis and the raw data samples used employed a very fine resolution of data in time and the data were not differenced prior to analysis.

Obtaining Synchrony from Bivariate Time Series: Windowed Cross-Correlations

Time series data such as those generated by video analysis software and motion tracking equipment contain a large amount of information and may exhibit many complicated qualities such as phase offsets, nonstationarity, and changing frequency and amplitudes. Additionally, these data points are discrete observations which may not be fully informative of a given underlying continuous process if the data are not properly sampled (Shannon, 1949). Given this complicated underlying structure, what qualities of two time series are required in order for two time series data to be considered synchronized? Researchers have attacked this problem in different ways and have developed multiple measures of similarity between bivariate time series, each looking at different qualities. Some methods rely on the total amount of mutual information between two time series based on their Shannon entropy (Quiroga, Kraskov, Kreuz, & Grassberger, 2002; Steuer, Kurths, Daub, Weise, & Selbig, 2002). Other analysis methods mark specific events in pairs of time series and compare qualities of these events through temporal relation and causality estimation (Chen, Rangarajan, Feng, & Ding, 2004; Quiroga, Kreuz, & Grassberger, 2002). Still other methods transform time series through Fourier methods to inspect similarity in the frequency domain (Pereda, Quiroga, & Bhattacharya, 2005; Quiroga, Kraskov, et al., 2002).

The methods of obtaining synchrony examined in this article rely on a windowed time-lagged extension of cross-correlation, called windowed cross-correlation (WCC). Boker, Xu, Rotondo, and King (2002) developed WCC as a method of obtaining cross-correlations between two time series when these time series are nonstationary. Psychological time series can rarely be assumed to be stationary and typical methods of correlating time series (e.g., cross-correlation) are not adequate estimates of similarity when time series are nonstationary (Hendry & Juselius, 2000, 2001; Jebb, Tay, Wang, & Huang, 2015). In a WCC context, a pair of time series are first broken into a number of short paired windows. These short windows are more likely to behave as a stationary process than a full-length time series. Windows are cross-correlated at differing lags by lagging one window positively or negatively in time. In this way WCC accounts for time delays between time series. The output of WCC is then a matrix r of correlations at different lags and windows defined as

$$r(\mathit{\text{Wx}},\mathit{\text{Wy}})=\frac{1}{T_w}\sum _{t=1}^{T_w}\frac{({\mathit{\text{Wx}}}_t-\overline{W}x)({\mathit{\text{Wy}}}_t-\overline{W}y)}{\mathit{\text{sd}}(\mathit{\text{Wx}})\mathit{\text{sd}}(\mathit{\text{Wy}})},$$ (1)

where T_w is the number of observations in each window, Wx_t and Wy_t are elements of two time series for t ∈ {1…T_w}, X and Y within the windows Wx and Wy, W̄x and W̄y are the mean values of each window, and sd(Wx) and sd(Wy) are the standard deviations of each window.

Researchers need to choose four parameters in order to fully specify a WCC analysis: window size, maximum lag, window increment, and lag increment. The first parameter, window size, determines the number of data points in each window. If a window is too short, WCC will not be able to capture sufficient information to adequately describe the relationship between time series of interest. If a window is too long, shifting leads and lags between the two time series may cancel one another, leading to artificially low correlations. However there is no one-size-fits-all rule for window size selection as separate researchers interested in studying synchronous processes occurring at differing time scales may need to choose different window sizes. For instance, a researcher interested in short bursts of synchrony may want a short window to account for these bursts, while a researcher interested in longer periods of synchrony may want to use longer window sizes. Previous research suggests using window sizes ranging from 2-seconds to 30-seconds for motion sampled from participants in conversation (Boker et al., 2002; Ramseyer & Tschacher, 2010). In the current study window sizes between these values were used for each data set in the analysis. The next parameter, maximum lag, determines how far each window may be shifted either forward or backward in time before being correlated. If a researcher chooses a lag that is too long then WCC may be correlating events which happen far from each other, thus correlating things which are unlikely to be part of a synchronous feedback loop between participants. A lag that is too short will not allow WCC to account for the necessary time delay for individuals to respond to one another. Finally, window increment and lag increment determine the step size of shifts in observations from one window to the next and lag shift respectively. These parameters may be seen as resolution parameters with lag increment giving lag resolution and window increment giving resolution in elapsed time. Lower values of both will give a more smooth change between points in a WCC correlation matrix but increase computational time.

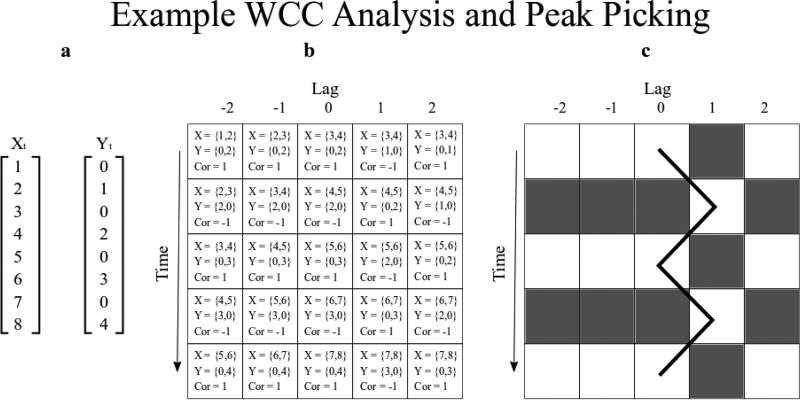
As an example of WCC, consider Figure 1. Figure 1 uses WCC parameters window size = 2, maximum lag = 2, window increment = 1, and lag increment = 1. In building r(Wx,Wy), the first element of the first row would be the correlation value between X_t = {1, 2} and Y_t = {0, 2}, or the correlation between two points (window size) in Y_t and two points in X_t from two time points in the past (maximum lag). For the next element in this row of r(Wx,Wy), X_t would be shifted one time point into the future (lag increment) such that X_t = {2, 3}. This process is repeated as shown in Figure 1 until a WCC matrix is completed.

Figure 1.

Sub-figures are (a) two time series to be window cross-correlated, (b) sections of (a) used to make each cell of the WCC matrix with window size = 2, window increment = 1, max lag = 2, and lag increment = 1, (c) shaded version of (b) with example peak picking algorithm following the peak positive correlation from lag 0. Notice how the black line follows the peak positive correlation value over time. By recording the correlation values of the elements of this matrix traced by this line, and the lag associated with each peak correlation value, one can determine 4 synchrony measures: mean peak correlation, sd peak correlation, mean lag, and sd lag.

Synchrony Quantification

The remainder of this article will focus on the global measure of synchrony, mean absolute Fisher’s z, and each of the four synchrony measures obtained from peak picking as estimates of synchrony between two behavioral time series for a total of five synchrony measures. These synchrony values are explained below.

Fisher’s z

In order to derive a measure of nonverbal synchrony from WCC matrices, two methods were used. The first method, described by Ramseyer and Tschacher (2006), is a global measure of synchrony between two time series. This value was obtained by applying Fisher’s z transformation to each WCC matrix r from each time series pair i

$$z=\frac{1}{2}\mathit{\text{ln}}\frac{(1+r)}{(1-r)}$$ (2)

$$z={\mathit{\text{tanh}}}^{-1}(r),$$ (3)

where z is a matrix of Fisher’s z transformed values of the matrix r. Fisher’s z transformation changes the geometric structure of these correlations from a linear correlation space to a hyperbolic correlation space, which normalizes values within a correlation matrix and has a well defined standard error under this normalization(Bond & Richardson, 2004; Winterbottom, 1979). The mean absolute value of all elements in the matrix z yields a single measure of global synchrony between two time series. This transformation is used to normalize the correlation values in a WCC matrix such that the mean absolute value of the Fisher’s Z transformed correlation matrix is a good single measure of the average correlation magnitude between two time series at all lags of interest. Thus, this value defines synchrony as the average magnitude of the hyperbolic correlation between two time series at all time-lags of interest. In order to satisfy the above equation, a small amount (SD = 0.001) of random normal noise was added to one of our sine waves of interest to keep correlations within windows from being exactly 1 as a correlation value of r=1 would be undefined in solving for z.

Peak picking

The method of peak picking proposed by Boker et al. (2002) was employed as a second measure of nonverbal synchrony obtained from each of our WCC matrices, Figure 1 (c). The peak picking algorithm starts at the center column (lag 0) of the first row of a WCC matrix. It then simultaneously searches from this center point in both positive and negative lag directions until it reaches the maximum correlation value at a lag closest to 0. This value and its associated lag are then recorded. Peak picking then steps to the next row in a WCC matrix and repeats this process from the column with the associated lag value obtained in the first row of said WCC matrix. In this way, the peak picking algorithm steps through each row of a WCC matrix, recording peak correlation value and its associated lag along the way. The end result of the peak picking algorithm is vector of peak correlation values $P_i^C$, and a vector of lag values associated with each of these peak correlation values $P_i^L$, i ∈ {1…M}.

Two measures of synchrony can be obtained from each of these vectors. From $P_i^C$, a mean peak correlation value and the standard deviation of these correlations can obtained. Mean peak correlation value defines synchrony as the average correlation between two windowed time series at time-lags which maximize this correlation. Standard deviation of correlation values defines synchrony as the amount of variation between correlations in two windowed time series at time-lags which maximize correlation. Researchers may be interested in mean peak correlation values when assessing strength of synchrony and standard deviation of these values when assessing stability of synchrony. From $P_i^L$, a mean peak time-lag value and the standard deviation of these time-lag can obtained. Mean peak time-lag defines synchrony as the average time-lag between two windowed time series at time-lags which maximize the correlation between said windowed time series. Standard deviation of time-lags defines synchrony as the amount of variation between time-lag in two windowed time series at time-lags which maximize correlation between said windowed time series. Researchers may be interested in mean peak time-lag values when assessing which time series tends to lead and which time series tends to follow in a given context, and standard deviation of these time-lag values when assessing switching between leading and following behaviors between two time series.

Surrogate Generation

Multiple methods for synchrony surrogate generation were examined. Each of these methods destroy some synchronous quality or set of synchronous qualities between two time series. As presented, each method is arranged from most to least data manipulative.

Data shuffling

The first method, data shuffling, is the most destructive of the methods we examined. Data shuffling can be seen as a time series equivalent of a randomization/permutation test. For each pair of time series (X, Y) each data point, X_i, is randomly shuffled to create a new time series, X^s, with points $X_j^s$ until no single data point existed at its original time point $X_i\ne X_j^s$. We then ran this new time series through a WCC analysis along with the unshuffled time series Y. By shuffling data this way X^s retains the same mean, variance, and distribution as X, but all time dependent properties of this series are now destroyed. As a result, any relation between X^s and Y due to time dependency between successive points of measurement is also destroyed. The null-hypothesis of no time dependency is thus ensured to be true for each surrogate generated in this way. Both peak picking vectors and mean absolute Fisher’s Z were obtained for this WCC matrix giving five synchrony measures for each surrogate pair. The process was repeated 1000 times in order to obtain a distribution of surrogate synchrony values for each synchrony measure. Observed synchrony scores were then compared to the 95^th percentile of these distributions. If an observed synchrony score falls outside of this range then a significant finding (α=.05, 1-tailed) was obtained.

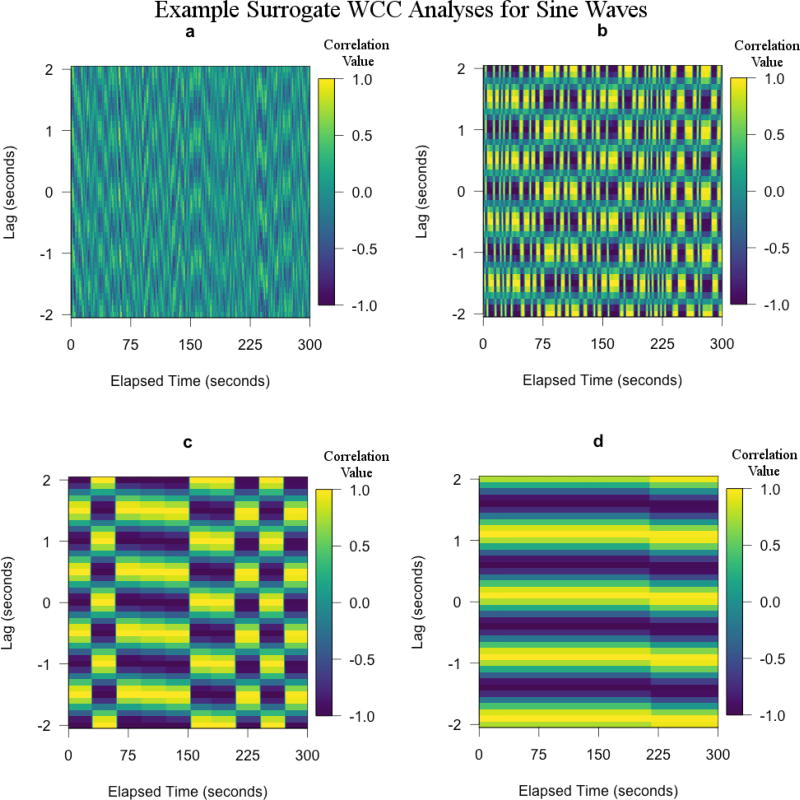
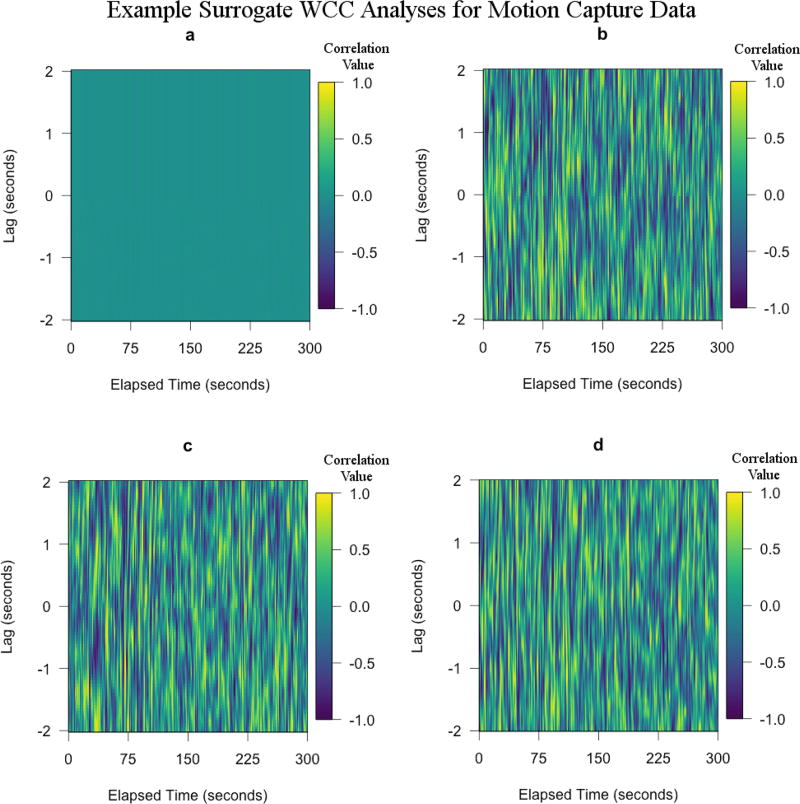
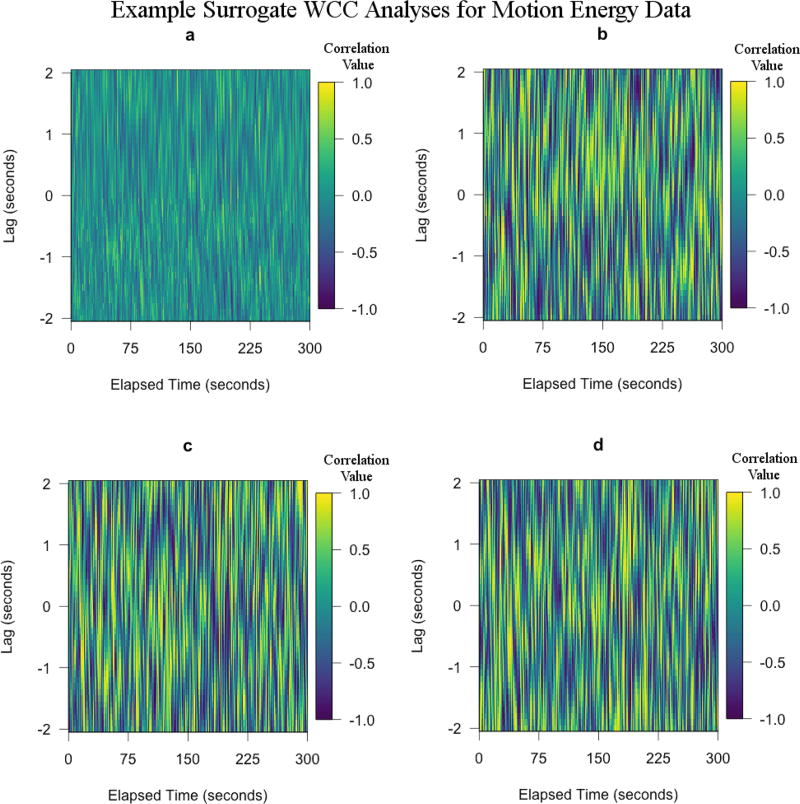
To intuitively understand how destructive data shuffling is, we can plot the WCC matrices generated by this method (Fig 4 [a], Fig 5 [a],Fig 6 [a]). Since the synchrony statistics can be seen as an attempt to quantify the amount and strength of order in a given WCC matrix, our new null-hypotheses generated by a given surrogate data method (i.e., a method which seeks to destroy order in a WCC matrix) should then show some visual difference from the ordered values. The destructive nature of data shuffling can be seen when comparing figures 2 (b) with figures 4 (a) –6 (a). The clean horizontal lines observed in the WCC matrices for sine waves have been greatly distorted by data shuffling and the average strength of correlations appear to be closer to 0. The same effect is observed for both our motion capture and MEA data sets, albeit not as starkly.

Figure 4.

Example surrogate WCC analyses for sine waves with window size = 2 seconds and max time-lag = 2 seconds. (a) Data Shuffling, (b) 2-second Segment Shuffling, (c) 30-second Segment Shuffling, (d) Data Sliding. Notice that (a) preserves much less order in the WCC matrix compared to all other methods. (b) and (c) both cause distortion in the WCC matrix, but (b) has obviously a stronger impact on order within the WCC matrix than (c). (d) has the smallest distortion effect on the WCC matrix and thus shows much of the same behavior as the original WCC matrix of Figure 1 (a).

Figure 5.

Example surrogate WCC analyses for motion capture data with window size = 2 seconds and max time-lag = 2 seconds. (a) Data Shuffling, (b) 2-second Segment Shuffling, (c) 30-second Segment Shuffling, (d) Data Sliding. As with most other data types studied in the current article, (a) shows the most difference in the behavior of the WCC matrix with no discernible patterns at all. However, (b), (c), and (d) all look very similar. This is because, in most cases, the motion capture data did not yield significant synchrony values.

Figure 6.

Example surrogate WCC analyses for motion energy data with window size = 2 seconds and max time-lag = 2 seconds. (a) Data Shuffling, (b) 2-second Segment Shuffling, (c) 30-second Segment Shuffling, (d) Data Sliding. As with most other data types studied in the current article, (a) shows the most difference in the behavior of the WCC matrix with very little structure. (b), (c), and (d) all retain some structure, however this structure is weaker than that of Figure 2 (d).

Figure 2.

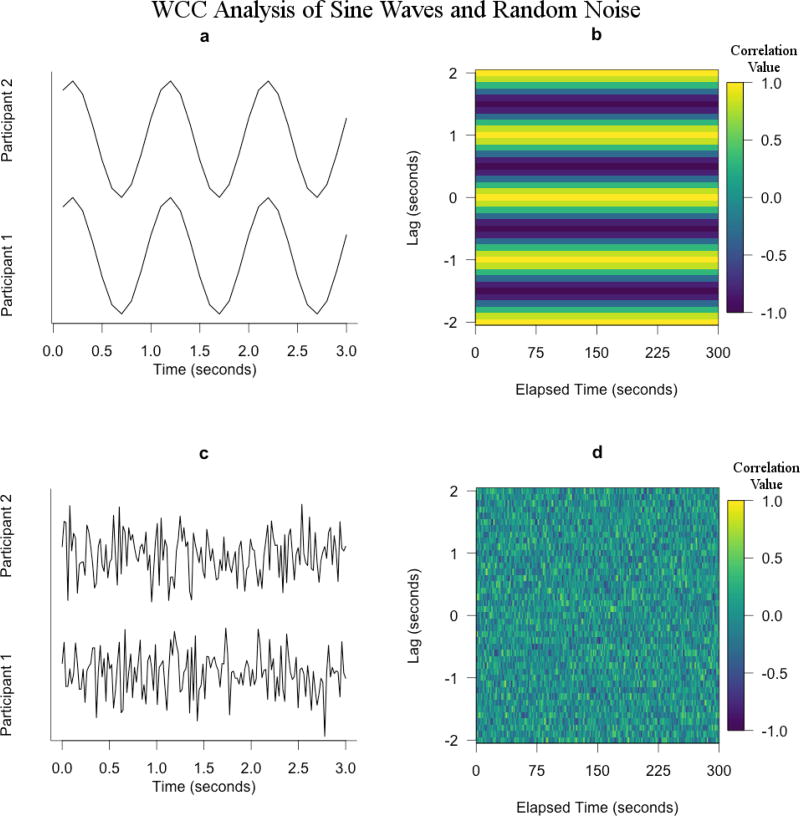
Sub-figures are (a) 3-second section of 5-minute 0.9Hz sine waves sampled at 10Hz, (b) Windowed cross-correlation of (a) with window size of 2-seconds and maximum lag of 2-seconds, (c) 3-second section of 5-minutes of random noise sampled at 10Hz, and (d) Windowed cross-correlation of (c) with window size of 2-seconds and maximum lag of 2-seconds. (a) represents perfect synchrony and exhibits strong and symmetric sections of positive correlation in (b). (c) represents a complete lack of synchrony and its corresponding windowed cross-correlation analysis (d) shows no distinguishable patterns. The more a windowed cross-correlation shows structures similar to (b), the higher the synchrony between those two series.

The use of data shuffling for surrogate generation has an important implication for understanding the new null-hypothesis tested with this method. As measures of synchrony rely on time dependence both within and across time series, surrogate synchrony scores obtained through data shuffling should be weak relative to observed synchrony since data shuffling destroys time dependency between successive data points. The null-hypothesis generated from data shuffling is then "there is no time dependency at all between these two time series". If a researcher cannot show that some quality of interest (e.g., observed synchrony scores) differs from surrogate data generated in this manner then no claims about time-based dynamics, such as synchrony, can be made between the time series of interest. Statistical significance in this regard does not imply synchrony, only that time independence between two time series is unlikely. When applied to motion capture data, any time series X^s obtained through data shuffling almost assuredly has multiple points which would be biologically impossible motions and thus would create a null-hypothesis test between a constrained biological system and a distribution of values from biologically impossible systems. For example, assume a researcher collects head horizontal position data X_t sampled h times per-second. Each successive data point X_t+1 would not only be highly correlated with the previous data point, but we would also expect X_t+1 to have a distribution of possible differences from X_t as a function of h due to biological limitations in horizontal velocity. Velocities and accelerations obtained outside of this distribution would indicate either measurement error or would be physically damaging to a participant. Data shuffled time series X^s would contain many such points. Thus testing real data against this null-hypothesis may show significance simply because this null-hypothesis is not biologically possible.

Segment shuffling

We used segment shuffling as a second surrogate generation method (Ramseyer & Tschacher, 2010). This method requires researchers to cut a time series X into shorter sections of size m which are randomly appended to one another to create a new time series X^s until no section is in its original position. Surrogate time series are run through a WCC analysis along with the unshuffled Y time series. Peak picking and mean absolute Fisher’s Z are used on the resulting WCC matrix to obtain five synchrony measures for each surrogate pair. The process was repeated 1000 times, each time changing the order by which the size m shorter sections are appended into X^s such that no section in X^s is in its original location. One surrogate distribution is thereby created per synchrony measure. Again, if the observed synchrony score is outside of 95% of these surrogate data, it indicates a significant finding. As opposed to other methods presented in the current article which can be used with little a priori theory, the choice of m is dependent on theorized lengths of synchrony. If m is too small, synchronous behaviors between two time series will be broken into pieces similar to that of data shuffling, creating a similarly easy to reject null-hypothesis. If m is too large, little synchronous information between time series of interest will be destroyed, resulting in a overly difficult to reject null-hypothesis. In the current article, we chose m = 2 seconds and m = 30 seconds to illustrate hypotheses of both short-term and long-term synchronous processes.

Comparing the visual structure of WCC matrices for section sliding (Fig. 4 (b) –6 (b) with observed synchrony WCC matrices (Fig. 2–3 [b]) it can be seen how this surrogate generation method affects order within WCC matrices. WCC matrices obtained from sine waves show the most apparent changes as there are now vertical sections of abrupt change leading to a checkered pattern most apparent in figure 4 (b). This visual distinction becomes less apparent for the motion capture and MEA data sets.

Figure 3.

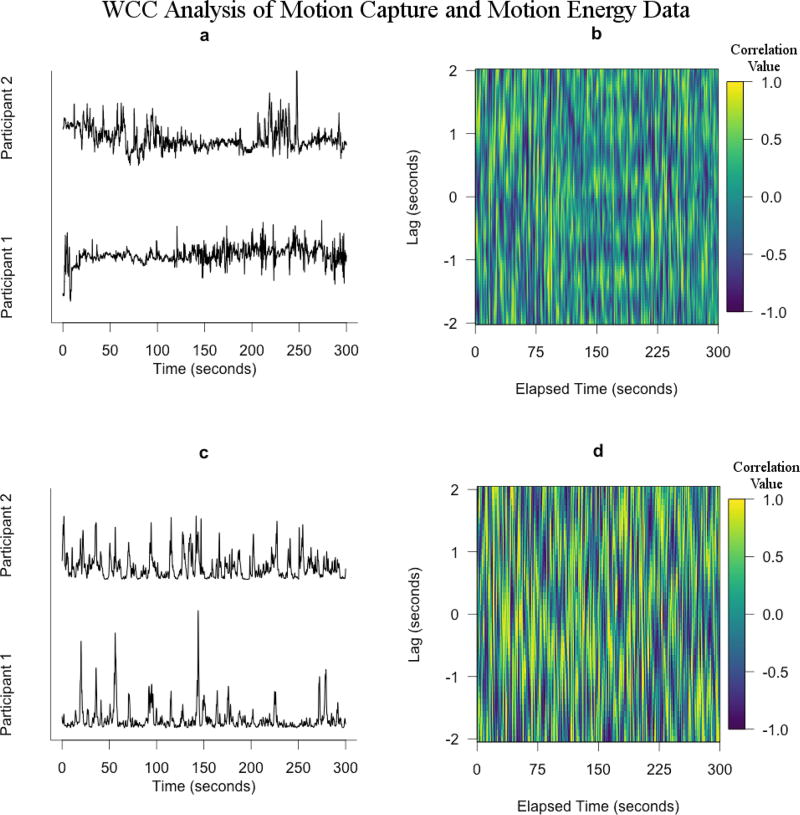
Sub-figures are (a) 5-minutes of motion capture data between two individuals in conversation, (b) Windowed cross-correlation of (a) with window size of 2-seconds and maximum lag of 2-seconds, (c) 5-minutes of motion energy analysis data between two individuals in conversation, and (d) Windowed cross-correlation of (c) with window size of 2-seconds and maximum lag of 2-seconds. Comparing (b) to (d), there is noticeably more order (striped patterns and strength of correlations) in (d) than in (b). This is because most synchrony measures obtained from (d) were higher than that of (b). However both of these time series show more order than Figure 1 (d), but less order than Figure 1 (b).

Segment shuffling conserves more time dependent structure within a given time series than data shuffling. While data shuffling entirely destroys the time dependency between points in a time series, segment shuffling conserves all time dependence within each section. Each successive point X_j+1 conserves time dependence with point X_j within each section, but then is unrelated to successive points from an appended section. Additionally, any periodic behavior longer than the time interval comprising each section is also affected by segment shuffling. The null-hypothesis generated from segment shuffling is then "synchrony does not exist between sections of size m in these two time series". As opposed to data shuffling in which every successive point X_j+1 has a chance of having a biologically impossible relationship to previous point X_j, segment shuffling has only m − 1 of these points (i.e., one per boundary between sections). Surrogate data sets generated by window shuffling would have then higher pseudosynchrony values when compared to data shuffling, but should still not be as high as observed synchrony assuming a bivariate time series shows observed synchrony.

Data sliding

Data sliding was used as a third surrogate generation method (Ashenfelter et al., 2009). Whereas researchers implement segment shuffling by appending multiple sections of a time series X to itself to create X^s, researchers wishing to implement data sliding create a single cut at some point relatively late in X. Data past this point is first removed from the end of X and then appended to the beginning of X to create surrogate time series X^s. It is important that the placement of this cut be further along in a time series than the window size parameter selected for the WCC matrix but not near the very end of a time series. Placing a cut too early or too late in a time series would not shift the time series enough so as to correlate far off events. We suggest selecting a point in the middle 60% of a time series. This new time series was run through a WCC analysis along with the unshuffled Y time series. Again, peak picking and mean absolute Fisher’s Z were used to obtain five synchrony measures for this surrogate pair. This process was repeated 1000 times, randomly placing the point at which X was cut. This resulted in one surrogate distribution per synchrony measure. If the observed synchrony score is outside of 95% of these surrogate statistics, a significant finding is indicated.

WCC matrices generated by data sliding are visually similar to WCC matrices generated by an original bivariate time series. Due to this strong similarity between original and surrogate WCC matrices, synchrony statistics measuring order within these matrices would be likely to also be similar (Fig. 2–3 [b] and Fig. 4–6 [d]).

Data sliding conserves most time dependent structure within a given time series. As there is only one cut, there is only one point in the entire series which could be biologically impossible. Data sliding also conserves most periodic behavior within a time series. The null-hypothesis generated from data sliding is then "long lags between these two time series do not influence synchrony". Assuming the alternative is true we would say that long lags do influence observed synchrony, indicating that the specific time related order of time series of interest is what is influencing observed synchrony values. Surrogate data sets generated by data sliding should have higher pseudosynchrony values when compared to data shuffling or segment shuffling, but should still not be as high as observed synchrony.

Participant shuffling

The final method of surrogate generation, participant shuffling, works by pairing time series X from participant interaction (X,Y) with a time series X′ from a second set of participant interactions (X′,Y′), forming a surrogate interaction (X,X′) between two individuals who did not converse with one another (Bernieri et al., 1988). Each surrogate time series pair was submitted to a WCC analysis. Again, peak picking and mean absolute Fisher’s Z were used on the resulting WCC matrix to obtain five synchrony measures for each surrogate pair. The process was repeated for each possible pseudo-interaction pair in the data set, resulting in one surrogate distribution per synchrony measure. Again, if an observed synchrony statistic is outside of 95% of the surrogate statistics then a significant finding is indicated.

Participant shuffling is unique to the methods described in this article since all qualities of a given time series in this method are biologically possible. The null-hypothesis generated from participant shuffling is "the amount of observed synchrony between participants engaged in conversation with one another is no different than participants not in conversation with one another". Participant shuffling is only applicable then when a researcher has sufficient dyadic interactions to create pseudo-interactions. We suggest using this method when researchers have data from at least 50 additional participants’ data for which to correlate with a specific participant’s time series. Too few and the resulting surrogate distribution will not be adequate to test the null-hypothesis. Additionally, if all dyadic interactions share a similar prompt, talking point, or behavior, the pseudosynchrony scores obtained from this surrogate generation method may be inflated due to patterned behavior associated with these topics (e.g., asking participants to do a specific dance or sing a specific song together). In such a case, the null-hypothesis generated by this method will be difficult to reject due to behavioral similarities across participants.

Results

Presented in Table 1 are the results of testing for synchrony using standard null-hypothesis testing methods for both genuine time series and surrogate data. All measures of synchrony show significant synchrony even when participants have not interacted with one another. To overcome this problem, two goals were established for this simulation and data analysis. The first goal was to examine the destructive effects of each of the four surrogate data generation methods (data shuffling, window shuffling, data sliding, and participant shuffling) on synchrony between different types of time series (sine waves, motion capture, motion energy, and random noise) in order to define the specific null-hypotheses generated by these methods. The second goal was to determine the viability of each surrogate data generation method for testing different levels of synchrony obtained from five common metrics of synchrony (mean peak correlation, sd peak correlation, mean peak lag, sd peak lag, and mean absolute Fisher’s Z). Again, significant synchrony between two time seres was defined as obtaining an observed synchrony value which fell outside 95% of a given surrogate data distribution. These goals were achieved by both examining how WCC matrices of a surrogate time series pair differ from a WCC matrix of a genuine time series, and by comparing each of the five common synchrony metrics obtained from these observed time series to those obtained from multiple surrogate time series.

Table 1.

Significance of Synchrony Values Obtained When Using Standard Null-Hypothesis Testing

Participant	Conversation	Mean Absolute Fisher’s Z	Mean Peak Correlation	SD Peak Correlation	Mean Peak Time-Lag	SD Peak Time-Lag
1	1	0.40* (0.12*)	0.42* (0.13*)	0.33* (0.04*)	3.82* (0.89*)	41.56* (15.77*)
2	1
59	30	0.31* (0.07*)	0.33* (0.08*)	0.28* (0.05*)	−1.66* (−1.22*)	27.93* (13.33*)
64	32
52	26	0.35* (0.08*)	0.35* (0.09*)	0.29* (0.04*)	0.71* (0.51*)	31.12* (12.78*)
85	43
13	7	0.32* (0.08*)	0.34* (0.10*)	0.26* (0.04*)	1.24* (1.01*)	36.51* (12.56*)
6	3
5	3	0.30* (0.08*)	0.32* (0.09*)	0.26* (0.05*)	−2.62* (−1.34*)	30.29* (11.92*)
16	8

^*p < 0.05

Note. Synchrony values and significance for an interacting pair and four noninteracting pairs for motion capture data. Values in parentheses are values obtained form a surrogate analysis of the same dyad. Only participants 1 and 2 ever had any interaction with one another within this data. Effect sizes in parentheses. All other pairs are drawn at random and run through a WCC analysis. Even when individuals had not interacted with one another, a significant observed synchrony value is obtained. This pattern holds true for all other pseudo-interactions and synchrony quantifications used in this study and for all surrogate data generation methods.

Observed Synchrony

We created WCC matrices with window size and maximum lag parameters of either 2-seconds and 2-seconds or 30-seconds and 5-seconds respectively for each data type; sine waves, motion capture, MEA, and random noise. These parameters were chosen since resulting WCC matrices show fairly different visual behaviors and because these parameters values have been justified by previous researchers interested in nonverbal synchrony. Table 2 contains observed synchrony values from these analyses. As expected, sine waves exhibit the most ideal estimates of synchrony across all measures due to the purely periodic nature of these waveforms (Fig. 2 [a & b]). MEA data shows the next highest level of synchrony of the four data types (Fig. 3 [c & d]). Although the WCC matrices of the MEA data do not show as strongly apparent synchrony as sine waves, there is still order in these WCC matrices greater than that of random noise. WCC matrices for motion capture data displayed the lowest levels of observed synchrony of the time series which were expected to contain synchrony (Fig. 3 [a & b]). As expected, random noise shows the lowest amount of observed synchrony across all synchrony indices (Fig. 2 [c & d]).

Table 2.

Five Observed Synchrony Values for Four Common Data Types

Data Types	Mean Peak Correlation	SD Peak Correlation	Mean Peak Time-Lag	SD Peak Time-Lag	Mean Absolute Fisher’s Z
WSize=2sec, τMax=2sec
Sine Waves	0.91*	< 0.001	0	0	1.16
Motion Capture	0.42	0.33	3.82	41.56	0.40
Motion Energy Analysis	0.75	0.30	0.42	7.33	0.66
Random Noise	0.02	0.01	−1.65	22.55	0.06
WSize=30sec, τMax=5sec
Sine Waves	0.25*	< 0.001	0	0	1.90
Motion Capture	0.18	0.18	43.41	98.88	0.14
Motion Energy Analysis	0.47	0.20	−1.23	8.99	0.22
Random Noise	0.03	0.02	0.78	7.48	0.05

^*Values less than 1 due to loess smoothing in peak picking function

Note. WSize is the size of the windows used in a windowed cross-correlation of these data sources and τMax is the maximum time-lag value for the same windowed cross-correlation.

Surrogate Methods

In order to determine if observed synchrony values obtained from WCC analyses represent observed synchrony as opposed to pseudosynchrony, surrogate distributions of size 1000 were created for each proposed surrogate method for each of our data types which we were able given our data. observed synchrony values were then compared to the 95^th percentile of the surrogate data. A finding was considered significant (i.e., a finding strong enough that a researcher would reject the null-hypothesis for a given surrogate generation method) if our observed synchrony values fall outside of this range. An effect size was computed as

$$\text{Effect Size}=G-\mathit{\text{mean}}(S)$$ (4)

where G is a synchrony value obtained from an original data set and S is a vector of surrogate data points from a given surrogate analysis method. Although this effect size is fairly easy to obtain, it does assume values of a given surrogate data vector follow a symmetric distribution, which lends itself to its mean being a good estimation of the center of said distribution (e.g., normal distribution). For example, if a surrogate distribution is highly skewed then mean(S) will not be an adequate measure of the center of this distribution and thus the above equation will not be an adequate measure of distance from the center of a surrogate distribution. As such, a researcher interested in quantifying effect sizes for determining synchrony should inspect their surrogate distributions before performing an effect size calculation. This effect size is presented as a reference for the difficulty of rejecting the new null-hypotheses generated by each of the surrogate data generation methods and not for determining significance. Table 3 summarizes findings for each surrogate method.

Table 3.

Size 1000 Surrogate Data Distribution Means and Effect Sizes

Data Types	Mean Peak Correlation	SD Peak Correlation	Mean Peak Time-Lag	SD Peak Time-Lag	Mean Absolute Fisher’s Z
	Data Shuffling
WSize=2sec, τMax=2sec
Sine Waves	0.28* (0.63)	0.13* (−0.13)	−0.11 (0.11)	4.08* (−4.08)	0.19* (0.97)
Motion Capture	0.07* (0.35)	0.07* (0.26)	0.14 (3.68)	30.03* (11.53)	0.06* (0.34)
Motion Energy Analysis	0.29* (0.46)	0.16* (0.14)	−0.39* (0.81)	6.15* (1.18)	0.19* (0.47)
Random Noise	0.02 (−0.001)	0.08 (0.07)	0.04 (−1.61)	4.73 (17.82)	0.02 (0.04)
WSize=30sec, τMax=5sec
Sine Waves	0.002* (0.25)	0.01* (−0.01)	−0.24 (0.24)	4.51* (−4.51)	0.05* (1.85)
Motion Capture	0.01* (0.17)	0.01* (0.17)	1.53 (2.88)	58.94* (39.94)	0.02* (0.12)
Motion Energy Analysis	0.06* (0.41)	0.05* (0.15)	−0.40 (−0.83)	11.97 (−2.98)	0.05* (0.17)
Random Noise	0.02 (0.01)	0.01 (0.01)	0.18 (0.60)	7.61 (−0.13)	0.05 (−0.001)
	2-Second segment shuffling
WSize=2sec, τMax=2sec
Sine Waves	0.90* (0.01)	0.01* (−0.01)	−0.001 (0.001)	0.09* (−0.09)	1.20* (−0.04)
Motion Capture	0.39 (0.03)	0.32 (0.01)	0.79 (3.03)	41.47 (0.09)	0.39 (0.01)
Motion Energy Analysis	0.64* (0.11)	0.32 (−0.02)	−0.07 (0.49)	6.89 (0.65)	0.57* (0.09)
Random Noise	0.02 (−0.001)	0.08 (−0.07)	−0.01 (−1.64)	6.10 (16.45)	0.02 (0.04)
WSize=30sec, τMax=5sec
Sine Waves	0.06* (0.19)	0.03* (−0.03)	0.01 (−0.01)	4.44* (−4.44)	1.13* (0.77)
Motion Capture	0.12 (0.06)	0.12 (0.06)	−8.18 (51.59)	79.11 (19.77)	0.11* (0.03)
Motion Energy Analysis	0.18* (0.29)	0.18 (0.02)	0.51 (−1.74)	14.42 (−5.43)	0.14* (0.08)
Random Noise	0.02 (0.01)	0.01 (0.01)	0.20 (0.58)	7.41 (0.07)	0.05 (−0.001)
	30-Second segment shuffling
WSize=2sec, τMax=2sec
Sine Waves	0.89* (0.02)	0.01* (−0.01)	−0.003 (0.003)	0.09 (−0.09)	1.23 (−0.07)
Motion Capture	0.41 (0.01)	0.33 (0.001)	0.24 (3.58)	40.10 (1.46)	0.39 (0.01)
Motion Energy Analysis	0.69* (0.06)	0.33* (−0.03)	0.38 (3.46)	7.03 (34.53)	0.63* (0.03)
Random Noise	0.01 (0.01)	0.08 (−0.07)	−0.02 (−1.63)	2.97 (19.58)	0.02 (0.04)
WSize=30sec, τMax=5sec
Sine Waves	0.19* (0.06)	0.04* (−0.04)	0.70 (−0.70)	4.12* (−4.12)	1.03* (0.87)
Motion Capture	0.15 (0.03)	0.13 (0.05)	30.31 (13.10)	95.88 (3.00)	0.14 (0.001)
Motion Energy Analysis	0.20* (0.27)	0.22 (−0.02)	−0.60 (−0.63)	13.61 (−4.62)	0.18* (0.04)
Random Noise	0.02 (0.01)	0.02 (0.001)	1.09 (−0.31)	7.10 (0.38)	0.05 (−0.001)
	Data Sliding
WSize=2sec, τMax=2sec
Sine Waves	0.87 (0.04)	0.005 (−0.005)	−0.25 (0.25)	2.28 (−2.28)	1.10 (0.06)
Motion Capture	0.40 (0.02)	0.34 (−0.01)	1.07 (2.75)	43.21 (−1.64)	0.42 (−0.02)
Motion Energy Analysis	0.49 (0.26)	0.35* (−0.05)	0.12 (0.30)	7.04 (0.29)	0.65 (0.01)
Random Noise	0.02 (−0.001)	0.07 (−0.06)	0.00 (−1.65)	6.19 (16.36)	0.02 (0.04)
WSize=30sec, τMax=5sec
Sine Waves	0.23 (0.02)	0.01 (−0.01)	0.60 (−0.60)	1.08 (−1.08)	1.06* (0.84)
Motion Capture	0.11* (0.07)	0.08* (0.10)	0.33 (43.08)	81.85 (17.03)	0.09* (0.05)
Motion Energy Analysis	0.23* (0.24)	0.22 (−0.02)	−0.47 (−0.76)	14.28 (−5.29)	0.17* (0.05)
Random Noise	0.02 (0.01)	0.01 (0.01)	0.16 (0.62)	7.41 (0.07)	0.05 (0.001)
	Participant Shuffling
WSize=2sec, τMax=2sec
Sine Waves	0.45 (0.46)	0.04 (−0.04)	0.93 (−0.93)	3.77* (−3.77)	0.35* (0.81)
Motion Capture†	0.34* (0.08)	0.23* (0.10)	−0.01* (3.83)	3.32* (38.24)	0.32* (0.08)
Random Noise	0.01 (0.01)	0.08 (−0.07)	0.07 (−1.72)	2.18 (20.37)	0.02 (0.04)
WSize=30sec, τMax=5sec
Sine Waves	0.23 (0.02)	0.01 (−0.01)	0.60 (−0.60)	1.11 (−1.11)	1.14* (0.76)
Motion Capture†	0.61* (−0.43)	0.20 (−0.02)	−0.001* (43.41)	0.07* (98.81)	0.28 (−0.14)
Random Noise	0.01 (0.02)	0.01 (0.01)	0.78 (−0.001)	19.27 (−11.79)	0.04 (0.01)

^*observed synchrony scores outside of 95% of surrogate data distribution

^†due to data limitations, only 155 surrogate data points were used to created these values

Note. WSize is the size of the windows used in a windowed cross-correlation of these data sources and τMax is the maximum lag value for the same windowed cross-correlation. Effect sizes appear in parentheses and are calculated as (observed synchrony value - surrogate distribution mean). Participant shuffling for motion capture data uses fewer surrogate data points due to the data set only containing 155 interacting pairs.

Data shuffling

All data types except for random noise yielded statistics which allowed for researchers to reject the null-hypothesis generated by utilizing data shuffling for synchrony statistics: mean peak correlation, sd peak correlation, and mean absolute Fisher’s Z for both window sizes. The data shuffling null hypothesis was not rejected for random noise. This indicates that all data types but random noise showed some level of time dependence between paired data sets greater than expected for random chance as measured by these statistics. The null-hypothesis generated by this method was not rejected for mean peak time-lag for any data set except for i) MEA data analyzed with WCC parameters window size of 2-seconds and maximum lag of 2-seconds, and ii) sd peak time-lag for our MEA data WCC matrix with window size of 30-seconds and maximum lag of 5-seconds.

Segment shuffling

The null-hypothesis generated by utilizing segment shuffling (i.e., synchrony does not exist between sections of size m in these two time series) proved to be a more difficult hypothesis for researchers to reject in all of data sets. For the shorter segment shuffling surrogate method (2-second sections) sine waves yielded statistics which allowed the rejection of this null-hypothesis for mean peak correlation, sd peak correlation, sd peak time-lag, and mean absolute Fisher’s Z for both WCC parameter settings. Motion capture data yielded statistics which did not allow the rejection of this null-hypothesis for any synchrony index except for mean absolute Fisher’s Z for WCC matrices with window size of 30-seconds and maximum lag of 5-seconds. MEA data rejected this null-hypothesis only for mean peak correlations and mean absolute Fisher’s Z for both WCC parameter settings. No data set yielded statistics which allowed the rejection of this null-hypothesis for mean peak time-lag. This null-hypothesis was not rejected for any synchrony statistic given random noise.

For the larger segment shuffling surrogate method (30-second sections) sine waves yielded synchrony statistics large enough for researchers to reject this null-hypothesis for mean peak correlation and sd peak correlation across both WCC parameter settings. However, sine waves did not yield synchrony statistics large enough for researchers to reject this null-hypothesis for sd peak time-lag and mean absolute Fisher’s Z for WCC analyses with parameters window size of 2-seconds and maximum lag of 2-seconds but did yield synchrony statistics large enough for researchers to reject this null-hypothesis for these synchrony indices using WCC analyses with parameters window size of 30-seconds and maximum lag of 5-seconds. Motion capture data did not yield synchrony statistics large enough for researchers to reject this null-hypothesis for any synchrony index at these WCC parameters. MEA data yield synchrony statistics large enough for researchers to reject this null-hypothesis for mean peak correlations and mean absolute Fisher’s Z for both WCC analysis parameter values. MEA data also yield synchrony statistics large enough for researchers to reject this null-hypothesis for sd peak correlation using WCC analyses with parameters window size of 2-seconds and maximum lag of 2-seconds. Again, this null-hypothesis was not rejected for any synchrony statistic for random noise. No data set yielded synchrony statistics large enough for researchers to reject this null-hypothesis for mean peak time-lag.

Data sliding

The null-hypothesis generated by data sliding (i.e., long lags between these two time series do not influence synchrony) proved to be the most difficult hypothesis for researchers to reject. Sine waves only yielded synchrony statistics large enough for researchers to reject this null-hypothesis for mean absolute Fisher’s Z using WCC analyses parameter settings with window size of 30-seconds and maximum lag of 5-seconds. Motion capture data yielded synchrony statistics large enough for researchers to reject this null-hypothesis for mean peak correlation, sd peak correlation, mean absolute Fisher’s Z using WCC analyses parameter settings with window size of 30-seconds and maximum lag of 5-seconds. MEA data yielded synchrony statistics large enough for researchers to reject this null-hypothesis for i) sd peak correlation using WCC analyses parameter settings with window size of 2-seconds and maximum lag of 2-seconds, and ii) mean peak correlation and mean absolute Fisher’s Z using WCC analyses parameter settings with window size of 30-seconds and maximum lag of 5-seconds. This null-hypothesis was not rejected for any synchrony statistic for random noise.

Participant shuffling

The null-hypothesis generated by participant shuffling (i.e., the amount of synchrony between participants engaged in conversation with one another is no different than participants not in conversation with one another) was tested with only motion capture data, sine waves, and random noise since there were insufficient pairs of MEA data. For sine waves, this null-hypothesis was rejected for sd peak time-lag and mean absolute Fisher’s Z using WCC analyses parameter settings with window size of 2-seconds and maximum lag of 2-seconds. This null-hypothesis was only rejected for sine waves for mean absolute Fisher’s Z using WCC analyses parameter settings with window size of 30-seconds and maximum lag of 5-seconds. For motion capture data this null-hypothesis was rejected for mean peak correlation, mean peak time-lag, and sd peak time-lag for both window sizes. This null-hypothesis was rejected by motion capture data for synchrony statistics sd peak correlation and mean absolute Fisher’s Z using WCC analyses parameter settings with window size of 2-seconds and maximum lag of 2-seconds. This null-hypothesis was not rejected for any synchrony statistic for random noise.

Discussion

More and more, researchers interested in synchronous behaviors are collecting intensively measured multivariate time series. We examined the use of surrogate data as a means of testing for observed synchrony (i.e., observed synchrony above and beyond pseudosynchrony) between pairs of variables in such data. We also proposed specific null-hypotheses generated by each surrogate data method and examined how these null-hypothesis generating methods quantitatively and visually affected results from windowed cross-correlation analyses.

The first surrogate method examined was the method of data shuffling. Utilization of data shuffling created a null-hypothesis for which most of our observed synchrony indices were able to yield synchrony statistics large enough for researchers to reject this null-hypothesis (Table 2). This makes sense since data shuffling destroys all time relatedness between observations in synchronous time series. If any of the proposed measures of synchrony indeed measure mutual time dependence, then this should be a fairly simple hypothesis to reject. However, one of the proposed measures of nonverbal synchrony values we examined, mean peak time-lag, only yielded synchrony statistics large enough for researchers to reject this null-hypothesis in one instance. As such, while mean peak time-lag may be an important descriptive piece of information it may be a poor indicator of nonverbal synchrony. When beginning to assess nonverbal synchrony researchers are suggested to start with the proposed data shuffling surrogate data generation method since this method generates the null hypothesis which is the last difficult to reject:, "There is no time dependency at all between these two time series". It is important to note that each WCC generated by data shuffling still showed some level of observed synchrony and order in a WCC matrix greater than what was presented by random noise in Figure 2.

Researchers interested in bursts of synchrony of some amount of time should consider section sliding for generating testable null-hypotheses. As this method tests the null-hypothesis that "synchrony does not exist between sections of size m in these two time series", time series cut into shorter sections reject this null-hypothesis more often than time series cut into larger sections but larger section sizes account allow for larger sections of possible synchronous behavior. Only sine waves were able to reject this null-hypothesis in all synchrony measures except mean peak correlation using 30-second windows from a 2-second lagged WCC analysis (Table 2). Motion capture data did not reject this hypothesis using 2-second lagged WCC analysis but did reject this hypothesis for both global synchrony and sd peak correlation values. These differences in findings exemplify the importance of choice of the parameters of both the WCC analysis and segment shuffling surrogate generation method. For some research interests, shorter bursts of synchrony may be all that is necessary to argue the existence of certain synchrony related phenomenon (e.g., symmetry building and breaking in a conversation), for other topics (e.g., synchrony in psychiatric counseling sessions) longer bursts of synchrony may be key to understanding a phenomena. Researchers are suggested to make an a priori estimate of the length of nonverbal synchrony that they expect would be present with regards to their phenomena of interest and test nonverbal synchrony using that window size. Most synchrony statistics could not distinguish order within the original WCC matrices from order within these matrices. Indeed we were unable to distinguish order in the WCC matrices for motion capture data from 30-second segment shuffling WCC matrices at all. This finding (or lack there of) is an important quality of surrogate generation methodology as this demonstrates that, unlike when comparing synchrony indices to 0, researchers can fail to reject a null-hypothesis generated by surrogate data methods.

If a researcher is more interested in global synchrony of a behavior than in short bursts we suggest the use of data sliding as a surrogate generation method. This method tests the hypothesis that "long lags between these two time series do not influence synchrony" and is fairly difficult to reject as nearly all other qualities of a given time series are preserved using this method. The synchrony statistics for sine waves were similar in observed WCC matrices and WCC matrices generated by this surrogate method (Fig. 2 [b] vs. Fig. 4 [d]).

Finally, if a researcher wanted to test for nonverbal synchrony due to specific interactions then we suggest considering participant shuffling. The null-hypothesis generated by this method "the amount of synchrony between participants engaged in conversation with one another is no different than participants not in conversation with one another", is rejected more often than data sliding in the real data. This surrogate data generation method appears to test a null-hypothesis that intuitively reflects synchrony as a phenomena between individuals engaged in conversation with one another. This method requires sufficient interactions to build a surrogate distribution to test against. Results obtained from this method will differ strongly depending on the quality and types of interactions generating each time series. In Table 3 we found that motion capture data actually displayed less than the expected amount of synchrony obtained by this hypothesis. Thus in some context, significant desynchronization may be observed.

It is important to note that the surrogate data generation methods described in the current article are not solely useful for detecting synchrony within a WCC context. Each surrogate data generation method destroys synchrony between two time series and are manipulations of the data only. Although this article used WCC as a framework for assessing synchrony, these surrogate data methods should be applicable for other synchrony detection measures.

Limitations and Future Directions

Although surrogate data generation appears to be a tempting alternative to standard null-hypothesis testing, it is not without flaws. It is difficult to know the full extent of what is being destroyed by a given surrogate data generation method due to the inherent complexities of nonlinear time series (Kugiumtzis, 1999). Indeed some effects, such as the previous mentioned "Working’s effect", may not be destroyed by such methods and could influence the results of a surrogate analysis. For this study, although we can be fairly sure that the surrogate data generation methods suggested here do indeed destroy synchrony between two time series, we can not be sure that some other quality between said time series is not also destroyed. Thus, when testing observed synchrony against a surrogate data distribution, researchers can not always be sure that differences found between observed synchrony and surrogate data distributions is due to synchrony alone. It is also difficult to determine what new null-hypothesis a given surrogate generation method tests without rigorous examination and data simulation (Schreiber & Schmitz, 2000). Specifically for this current article, limitations exist in the general applicability of the methods suggested here. These methods require many data points (we suggest at least 500) to be applicable. In addition the time series of interest must be sampled at the same sapling rate and must be of the same size. Additionally the data sets described in the current article do not represent the whole of the many types of nonlinear behaviors one might expect when dealing with psychological time series (Jebb et al., 2015). This limits the applicability of the proposed methods when applied to time series exhibiting drastically different behaviors than those presented. Researchers may also want to consider controlling for spurious or noise-like spiking behaviors within a given time series by utilizing methods such as winsorization (Working, 1960). Researchers utilizing data created from an aggregate may also need to seek additional control methods.

However, given that a researcher understands his/her system well enough, surrogate data generation and testing allows for much more control and precision for hypothesis testing than standard null-hypothesis testing methods. Researchers using surrogate data generation can specify nuanced hypotheses based around order and structure, as opposed to simply testing against a null value. Additionally, modern data collection methods for multivariate time series may generate hundreds of observations a minute, easily meeting data requirements for many possible surrogate data generation methods.

For future work regarding surrogate data generations, recently methods have been developed to assess synchrony between multiple time series (e.g., Richardson, Garcia, Frank, Gergor, & Marsh, 2012). Although promising, these methods may also exhibit the same alpha inflation observed when measuring synchrony between two time series. As such, methods of surrogate data generation for testing synchrony between more than two time series are needed. Additionally, although surrogate data generation greatly reduces the alpha inflation brought upon by standard synchrony measurements, little is known about the power of these methods. Thus a power simulation study for each of these methods is warranted.

Surrogate Data in Practice

We suggest researchers consider the surrogate data generation methods presented in this article when testing for nonverbal synchrony between behavioral time series. We have attempted to demonstrate that:

1. Some level of observed synchrony grater than 0 will be present in an analysis using WCC as a method, rendering standard null-hypothesis testing techniques inadequate, see table 1.

2. Surrogate data methods provide a way to generate new and appropriately testable null-hypotheses.

3. Different surrogate methods generate different theoretically interesting hypotheses which can be more or less difficult for a specific pair of synchronous time series to reject depending on properties within and between those time series. That is, each surrogate method may be used to test different hypothesis regarding synchrony between two time series.

Thus researchers need to consider which surrogate method is most appropriate for their specific research hypothesis. Researchers also need to consider the number of surrogate tests to run. In this article we chose 1000 but could have generated more. Larger surrogate data generation runs would increase the power of a given surrogate test but also increase computation time.

Surrogate data generation methods are a viable and nuanced means for testing for significant synchrony between individual pairs of time series. Identifying the new null-hypotheses generated by each of the surrogate data generation methods reviewed in this article gives researchers a theoretical framework, outside of standard null hypothesis testing methods, for testing for different levels of synchronous behavior between two time series. In practice, researchers wanting to simply test for time dependence should consider a surrogate data generation method which yields a hypothesis similar to that of data shuffling. Researchers concerned with more robust synchronous behavior should consider a surrogate method that generates a more difficult to reject null-hypothesis such as data sliding, or test multiple surrogate generation methods.

Nonverbal synchrony impacts many aspects of dyadic interaction and is a rich area with many possible research trajectories, both theoretical and applied. Valid measures of nonverbal synchrony are key to understanding how this phenomena influences human affect, behavior, and cognition. Although standard null-hypothesis testing may not be adequate for nonverbal synchrony within a given interaction, surrogate data generation and analysis provides a way for researchers to create their own testable hypotheses appropriate for their data and theory. These tests of order and structure, as opposed to differences in values, allow researchers a much more flexible paradigm for asking scientific question. The surrogate generation methods reviewed in this article are not the only surrogate methods possible for establishing forms of nonverbal synchrony and researchers are encouraged to consider other methods tailored to the specifics of their data and theories. Surrogate generation is a broad class of methodology and can be applied to testing more psychological phenomena than just nonverbal synchrony. Each surrogate data method generates its own null-hypothesis and these null-hypotheses can be tuned to test specific hypotheses. Having a framework to properly test for nonverbal synchrony is vital to drawing valid conclusions from studies involving nonverbal synchrony and we believe the surrogate data generation methods suggested in this article help establish surrogate data generation as part of this framework.