Abstract
Lipid membranes play key roles in cells, such as in trafficking, division, infection, remodeling of organelles, etc. The key step in all these processes is creating membrane curvature, typically under the control of many anchored, adhered or included proteins. However, it has become clear that the membrane itself can mediate the interactions among proteins to produce highly ordered assemblies. Computer simulations are ideally suited to investigate protein organization and the dynamics of membrane remodeling at near-micron scales, something that is extremely challenging to tackle experimentally. We review recent computational efforts in modeling protein-caused membrane deformation mechanisms, specifically focusing on coarse-grained simulations. We highlight work that exposed the membrane-mediated ordering of proteins into lines, meshwork, spirals and other assemblies, in what seems to be a very generic mechanism driven by a combination of short and long-ranged forces. Modulating the mechanical properties of membranes is an underexplored signaling mechanism in various processes deserving of more attention in the near future.
Keywords: Coarse-grained simulations, BAR proteins, Multiscale simulations, Membrane curvature, Self-assembly, Lipids, Membrane proteins, Computational modeling
Dynamics of cell membranes at multiple scales: The need for coarse-grained computer simulations
The cell membrane is the first stop en route into the cell. While integral membrane proteins, such as signaling receptors, often control the trafficking of cargo in and out of the cell, lipid membranes play significant roles in this process. The most common way of entering the cell is via endocytosis, in which a small portion of the membrane curves and eventually breaks off, handing over the engulfed cargo down the path of intracellular trafficking. Membrane curvature is essential for many other aspects of cell’s survival [1]. For instance, highly curved protrusions called filopodia are formed at the leading edge of a motile cell to allow migration and cell-to-cell contact. Curvature is also a structural feature of many organelles, such as the endoplasmic reticulum, which comprises a system of interconnected tubules and vesicles. In recent years, it has become apparent that membrane curvature can provide signaling downstream of protein binding, through a finely balanced interaction between curvature sensing and curvature induction by proteins [2]. Many questions about this interaction still remain unsolved, such as understanding how proteins correctly and rapidly assemble at the right place and the right time and precisely how the cell modulates the activity of curvature proteins.
Over the past five decades, the elastic description of cell membranes has been successful in elucidating a number of membrane-remodeling mechanisms and it has provided a powerful framework for understanding experimental data. However, the long-wavelength dynamics of membranes is deeply connected to their molecular structure. In other words, molecular diffusion and the interactions at the lipid-protein interface will have a strong impact on the collective organization of proteins and the overall membrane shape. Considering such strong molecular-mesoscopic coupling, it is important to understand the protein-membrane remodeling from molecular as well as continuum viewpoints.
Computer simulations allow a microscopic and dynamical view into membrane remodeling, something that is too challenging for any experimental imaging technique. In particular, coarse-grained (CG) models bridge the gap between high-resolution static imaging and optical microscopy at the micron-scale [3]. Here, we review recent insights learned from simulating membrane-curving proteins and particles at near-micron scales and highlight new paradigms in protein self-assembly that emerged from combined simulations and experimental measurements.
General mechanisms of membrane bending by BAR domains and other proteins
Many proteins regulate membrane curvature in the cell. The basis of their interactions typically involves inducing a local asymmetry in the lipid bilayer either by virtue of their shape, local clustering, inclusion into the bilayer, active force, or by a combination of multiple effects [1]. Many proteins bind peripherally to interact with a membrane’s shape. Typically they are themselves intrinsically curved or they form curved multi-protein assemblies when bound to the surface. Examples include Bin/amphiphysin/Rvs (BAR) proteins, clathrin, and dynamin [1]. Often, they form large-scale 3D assemblies and act as scaffolds that mold the underlying membrane into a vesicle or a tubule [1,2]. Another mechanism of bending membranes is by shallow insertion of amphipathic helices into the bilayer [4]. Many proteins contain amphipathic helices, especially those involved in endoctytosis and trafficking, such as epsins and BAR proteins [1].
The most highly studied group of membrane remodelers are BAR domain proteins [5]. The group comprises dozens of members whose roles have been linked to a number of cellular compartments and membrane-bending phenomena [2]. Based on the shape of their BAR domain, one divides them into (1) BAR/N-BAR, (2) F-BAR, both positively curving and (3) I-BAR, inducing negative curvature [5]. Even within each group, the BAR domain still varies in size, surface charge, curvature, and the presence of amphipathic helices; thus, further contributing to the diversity of their interactions. An additional complication is that their activity depends on protein density, surface tension, and membrane shape [2]. For instance, it was experimentally shown that two regimes can be distinguished: at low protein surface densities, they essentially act as curvature sensors whereas at high density they globally bend membranes [6,7], likely by forming a scaffold [8]; in between, there is a cross-over regime where they have both actions simultaneously. Under the scaffolding regime, they can even induce scission of tubular membranes [9], adding to their remarkable arsenal of activity.
Bending membranes by proteins: insights from CG simulations
Many CG lipid and protein models with varying degree of coarseness have been designed in the recent years to study membrane bending by proteins (Figure 1A,B). The higher-resolution CG models, such as MARTINI [10], retain much of the sub-molecular information and are therefore well suited for questions where the chemical specificity of components is important (Figure 1A). For instance, MARTINI MD simulations have shown how the embedded voltage sensor Kv [11] or small peptides [12] couple with the local membrane deformations. Simulations of a lattice composed of α-synuclein molecules showed how their binding strength, helix length, and the depth of insertion correlates with membrane bending, suggestive of tubule formation [13,14].
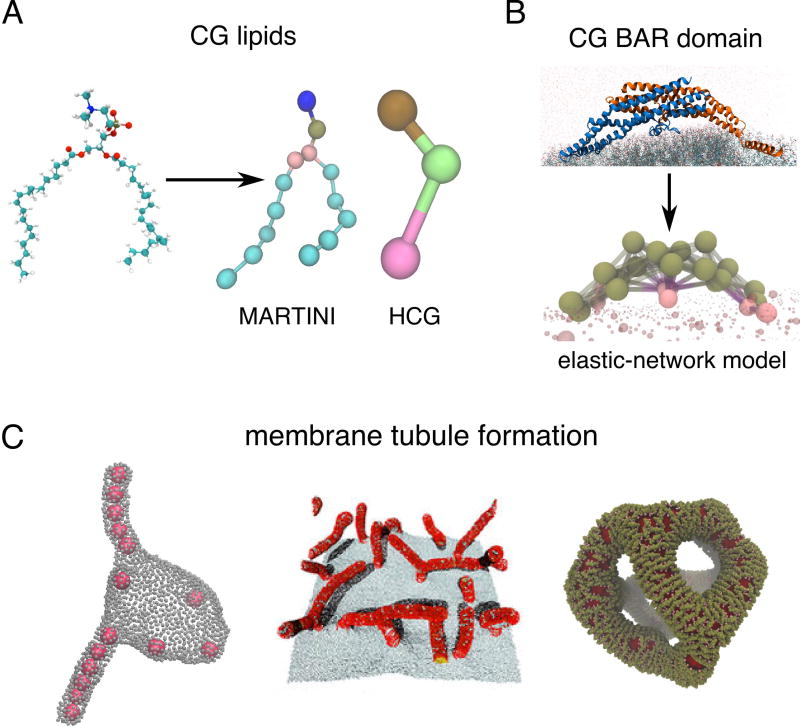
Figure 1.
CG modeling to simulate membrane-curving phenomena. (A) Comparing the atomic picture of a lipid with CG lipid models of different resolution, MARTINI and the three-site HCG model. (B) Elastic-network CG modeling of the N-BAR domain. (C) Different mechanisms of creating membrane tubules from flat membranes and vesicles. From left to right: co-operative invagination of adhered nanoparticles (courtesy of A. Saric [20]), emanation of tubules toward embedded curved rods (reprinted from [34]), reticulation of a vesicle into a network of tubules induced by densely adhered N-BARs (based on [35]).
Lower resolution CG lipids, in which a lipid molecule is represented with three or fewer sites such as the hybrid CG (HCG) model (Figure 1A) [15], together with various continuum or phenomenological CG models [16] have been developed to investigate membrane dynamics at micron-scales. Important progress has been made in understanding the role of adhesive forces and local membrane deformation in the engulfment of nanoparticles by membranes [17]. For instance, the efficiency of engulfment was linked to particle shape [18] which can possibly be tuned to inhibit their uptake [19]. Simulations of multiple nanoparticles showed an unexpected cooperative interaction among particles, which drives tubulation into the membrane vesicle [20,21] (Figure 1C, left). These simulations may help to shed light on the mechanism of passive entry into the cell by large particles, such as viruses, and potentially aid in designing efficient drug carriers.
Endocytosis is not a passive transport of material into the cell. Quite the contrary, it is finely orchestrated by its many different components, often coupling with an active, energy-driven process. Simulating single components interacting with the membrane helps in understanding their individual roles. In the best known endocytic pathway, clathrin molecules polymerize into a basket-shaped structure that molds the membrane into a vesicle [22]. CG simulations employing a patchy-particle model of clathrin have been used to identify some of the key interactions that drive clathrin assembly, fleshing out new intermediates in the budding pathway [23,24]. The last step of clathrin-mediated endocytosis is the GTP-driven constriction of polymerized dynamin followed by membrane scission [25]. Recent efforts using a semi-quantitative CG model, that mimics some aspects of dynamin structure, predicted that scission requires dynamin units to induce local positive curvature to properly drive scission, perhaps by shallow insertion of amphipathic moieties, thus complementing the classical picture of membrane constriction by scaffolding [26].
BAR proteins are found in almost all pathways of endocytosis, where they function in curvature sensing, bilayer bending and even scission [2] (see Figure 1B for a structure of an N-BAR domain). Atomic MD simulations of N-BAR, F-BAR and, more recently, I-BAR domains adhered to a small membrane patch have shown that single BAR domain molecules have a bending capacity through interactions between positively charged residues and negatively charged lipid head groups [27–30]. The same approach has identified the details of how amphipathic helices wedge into the bilayer, demonstrating that without the BAR domain backbone, helices alone would need to cover the membrane at a much larger surface fraction to impose as much curvature [31]. All-atom studies of N-BAR domains started to delineate the role of individual subdomains in their interactions with membrane curvature at the molecular level.
More recent CG and continuum approaches simulated many BAR proteins attached to the membrane, revealing different modes of large-scale membrane remodeling. Simulations using various CG models, in which the rigidity and spontaneous curvature can be externally tuned, have shown that bent rods or nematogenic particles embedded in the membrane can induce continuous tubulation of the membrane surface, as seen in cells with overexpressed BAR domains [32–34] (Figure 1C, center). Interestingly, these studies demonstrated that the local shape of the deformation—isotropic vs. anisotropic—will greatly affect how embedded rods interact with one another. A different mechanism was revealed by combined CG and continuum simulations of large (~500 nm) vesicles with electron microscopy (EM). At very high surface coverage, N-BAR proteins create a nematic stress field, causing the bilayer to break topology and fold into a network of tubules (Figure 1C, right) [35,36], matching very well with structures seen with EM [35]. While the radius distribution of tubules in the experiments with N-BARs was relatively uniform, MARTINI-like simulations of freestanding membrane patches decorated by BAR lattices showed that the tubule radius can also be affected by how individual proteins are arranged in the lattice [28,37], but this radius also depends critically on the strength of water-screened interactions between the BAR domain and the lipid headgroups – an effect that must be carefully treated in any CG model [38]. However, the tubular transformation of membrane vesicles is likely not relevant for understanding endocytosis, as BAR proteins presumably do not get so densely bound, but it is potentially important for understanding mitochondrial or T-tubule reticulation [2].
At the onset of endocytosis, proteins, especially BARs and epsins, must likely aggregate from low concentrations to the remodeling sites. Recently, initiation of membrane curvature by these proteins was studied with CG models, which were based on their actual atomic structures. These simulations have shed light on how local curvature imposed by single BAR domains couples with bud formation whose radius of curvature is much larger than the size of the protein. A key feature is the anisotropic interaction with the lipid bilayer likely coming from the elongated shape of the BAR domain [39] and probably amplified by enhanced adhesion due to amphipathic helices [40]. Somewhat similar in spirit, a cooperative action among multiple epsin N-terminal homology domains, which stabilize large-scale membrane curvature, were seen in simulations of a few MARTINI proteins on a membrane patch [41]. This cooperativity and coupling with membrane curvature seems to be a common theme in initial protein assembly, with important implications in how complex membrane remodeling phenomena may be controlled and fine tuned.
Membranes mediate the formation of highly ordered protein assemblies
Simulations summarized in the previous section demonstrated that protein-bilayer interactions can give rise to local and global membrane deformations. However, the reverse process—the effect of membrane curvature on protein interactions—is equally important in understanding membrane-remodeling phenomena. It is especially important in the context of BAR proteins, which, according to experimental measurements, do not induce global curvature when sparsely bound to the membrane; rather, they most likely form higher-order assemblies [6–8].
A number of analytical studies over the years have predicted that membranes can mediate both the attractive and the repulsive interactions among bound particles [16,42]; however recent works have captured the dynamics of these interactions and how they play into the organization of many components. For instance, CG simulations of nanoparticles on vesicles have demonstrated that the membrane mediates attractions between adhered particles that induce local curvature [43–45] and experiments visualized their interactions [46]. Intriguingly, it has been seen with both nanoparticles and N-BAR proteins that they undergo a very specific assembly mechanism when bound to membranes, characterized by rapid formation of long linear aggregates (Figure 2A) [39,44]. Given the absence of explicit attractions between particles in the CG model, these effective interactions must be membrane driven. Based on simulations of N-BARs, it seems that the anisotropic curvature interactions activate very long-ranged interactions among proteins—much larger than its length—attracting others into the 1D cluster [39]. While spherical particles themselves interact isotropically, their pairing may be seen as the asymmetric unit. Interestingly, linear and circular assemblies of inclusion in membranes were first predicted using an analytical potential that modeled anisotropic inclusions in the membrane [47].
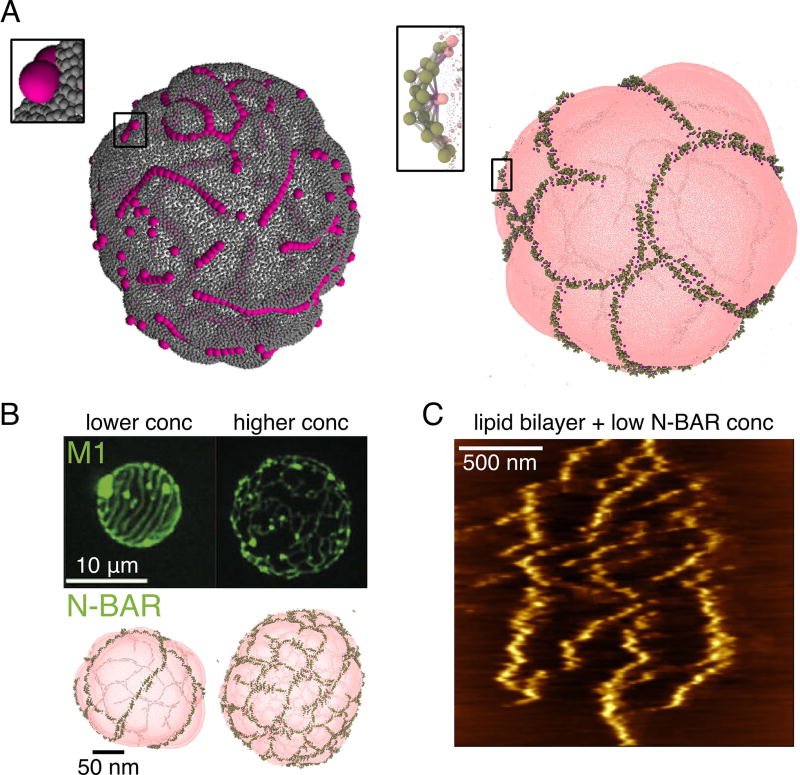
Figure 2.
Membrane-mediated assembly of curvature-generating proteins. (A) Linear aggregation of nanoparticles (left) and N-BAR proteins (right) on lipid vesicles. Left modeled with a triangular-mesh model and adhesive spherical particles (courtesy of A. Saric [44]), right modeled with the HCG lipid model and elastic-network model N-BAR domain (based on [39]). (B) Comparing the assembly of M1 and N-BAR proteins on lipid vesicles. Top row confocal images reprinted from [50], bottom row CG simulations based on [39]. (C) Atomic force microgram of N-BAR proteins assembled on a supported lipid bilayer (reprinted from [51]).
After the initial computational discovery, experimental evidence for the protein linear aggregates has also emerged. First, very long filaments of F-BAR proteins were seen with EM [48]; however, considering that F-BARs are known to interact in solution as well, the role of the membrane in this case is less clear. Single-molecule imaging of a BAR domain in yeast has shown that it forms very long filaments, albeit much denser than seen in simulations. However, this has shown that the protein exchange only happens at the edges, suggesting a very stably held filament [49], as measured in CG simulations [45]. Interestingly, a membrane curving protein matrix M1 from the influenza virus, unrelated to the BAR family, was also seen with confocal microscopy to form microns-long lines, orderly spaced on lipid vesicles (Figure 2B) [50]. The resemblance to simulations of N-BARs on vesicles is striking (Figure 2B), even recapitulating crosslinking and quasi-meshing seen with increased protein density. The difference, however, is in the length scale, which could be internally set by the spontaneous curvature induced by the protein and other parameters. These observations suggested (1), that the mechanism of linear protein aggregation on membranes is likely a general assembly phenomenon and (2), that membranes can drive not only local or intermediate-range protein interactions, but potentially control high-order assemblies, by mediating filament interactions. Indeed, recently it has been observed with atomic force microscopy and supported by free energy calculations that membranes not only mediate the formation of N-BAR protein lines, but they also give rise to strong repulsions between protein filaments over long distances, creating a striped pattern on the near-micron scale (Figure 2C) [51]. The combination of short-range attractions and the long-range repulsions thus drives the formation of complex higher order structures, such as a meshwork on lipid vesicles [39], and spirals as part of a protein scaffold bound to a tubular membrane [8].
Protein assembly can also be modified by tuning the physical properties of the membrane. Increased surface tension or bending rigidity decreases the propensity of linear aggregation and introduces a higher variability in assembly, such as side-by-side interactions vs. tip-to-tip for BARs [45], but also much more generally for cylindrically bound particles [52]. The cell could potentially complement the intrinsic differences in the way individual proteins affect membrane shape, and use membrane’s physical properties to fine-tune their organization and delivery to membrane-remodeling sites.
Future Outlook
We expect CG simulation to tackle several more complex questions in the near future. First, every membrane-remodeling phenomenon involves multiple types of proteins and their correct and timely assembly. It will be interesting to use CG models to simulate multiple BAR proteins, and BAR proteins interacting with other types of proteins, such as epsins and clathrin, in the same system. These simulations will help in resolving the controversial issue of the temporal order of recruitment and activity of individual proteins in endocytosis. Simulating multiple BAR proteins on the membrane will also help in understanding their differential recruitment during endosomal sorting. Second, membrane scission by dynamin or facilitated by motor proteins is challenging to simulate as it contains an energy-driven component. Future challenges in CG modeling will be how to account for active processes and conformational changes of proteins during simulations. Third, continuum modeling can access essentially arbitrary length scales, always at a cost of resolution. We anticipate that effort will be made to create better statistical-mechanical connections between models of different resolutions and, perhaps, even modeling membrane-remodeling processes using mixed-resolution models, so to capture global membrane changes with continuum mechanics, while keeping the essential molecular understanding of these processes, with connections to CG modeling.
The computational efforts that we reviewed here have only opened a window into the understanding the dynamics of protein interactions on membranes. CG simulations will surely bring many more insights into membrane remodeling and cellular trafficking in the coming years, and they will become increasingly utilized to interpret experimental studies and to even make key predictions that will be subsequently confirmed.
Acknowledgments
M.S. and G.A.V acknowledge their research reported in this publication as being supported by the National Institute of General Medical Sciences of the National Institutes of Health under award number R01-GM063796. The P.B. group belongs to the CNRS consortium CellTiss; to Labex CelTisPhyBio (ANR-11-LABX0038) and to Paris Sciences et Lettres (ANR-10-IDEX-0001-02). M.S. is a Junior Fellow of the Simons Society of Fellows.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.McMahon HT, Gallop JL. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature. 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 2.Simunovic M, Voth GA, Callan-Jones A, Bassereau P. When Physics Takes Over: BAR Proteins and Membrane Curvature. Trends Cell Biol. 2015;25:780–792. doi: 10.1016/j.tcb.2015.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Saunders MG, Voth GA. Coarse-graining methods for computational biology. Annu Rev Biophys. 2013;42:73–93. doi: 10.1146/annurev-biophys-083012-130348. [DOI] [PubMed] [Google Scholar]
- 4.Campelo F, McMahon HT, Kzozlov MM. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys J. 2008;95:2325–2339. doi: 10.1529/biophysj.108.133173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Qualmann B, Koch D, Kessels MM. Let's go bananas: revisiting the endocytic BAR code. EMBO J. 2011;30:3501–3515. doi: 10.1038/emboj.2011.266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6*.Sorre B, Callan-Jones A, Manzi J, Goud B, Prost J, Bassereau P, Roux A. Nature of curvature coupling of amphiphysin with membranes depends on its bound density. Proc Natl Acad Sci U S A. 2012;109:173–178. doi: 10.1073/pnas.1103594108. This work was crucial in experimentally determining that the way BAR proteins interact with the membrane is dependent on their bound density. Namely, at low protein densities they primarily act as curvature sensors, while at high densities they deform the membrane to spontaneously form long tubules. At high densities, they form stable scaffolds around tubular membranes. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7*.Shi Z, Baumgart T. Membrane tension and peripheral protein density mediate membrane shape transitions. Nat Commun. 2015;6:5974. doi: 10.1038/ncomms6974. In this work, it was experimentally shown that in addition to surface density, the action of BAR proteins is dependent on membrane tension. The higher the tension, the higher threshold density is required to deform the membrane. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Simunovic M, Evergren E, Golushko I, Prevost C, Renard HF, Johannes L, McMahon HT, Lorman V, Voth GA, Bassereau P. How curvature-generating proteins build scaffolds on membrane nanotubes. Proc Natl Acad Sci U S A. 2016;113:11226–11231. doi: 10.1073/pnas.1606943113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Simunovic M, Manneville JB, Renard HF, Evergren E, Raghunathan K, Bhatia D, Kenworthy AK, Voth GA, Prost J, McMahon HT, et al. Friction Mediates Scission of Tubular Membranes Scaffolded by BAR Proteins. Cell. 2017;170:172–184 e111. doi: 10.1016/j.cell.2017.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Marrink SJ, Tieleman DP. Perspective on the Martini model. Chem Soc Rev. 2013;42:6801–6822. doi: 10.1039/c3cs60093a. [DOI] [PubMed] [Google Scholar]
- 11.Bond PJ, Sansom MS. Bilayer deformation by the Kv channel voltage sensor domain revealed by self-assembly simulations. Proc Natl Acad Sci U S A. 2007;104:2631–2636. doi: 10.1073/pnas.0606822104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fuhrmans M, Marrink SJ. Molecular view of the role of fusion peptides in promoting positive membrane curvature. J Am Chem Soc. 2012;134:1543–1552. doi: 10.1021/ja207290b. [DOI] [PubMed] [Google Scholar]
- 13.Braun AR, Lacy MM, Ducas VC, Rhoades E, Sachs JN. alpha-Synuclein's Uniquely Long Amphipathic Helix Enhances its Membrane Binding and Remodeling Capacity. J Membr Biol. 2017;250:183–193. doi: 10.1007/s00232-017-9946-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14*.Braun AR, Lacy MM, Ducas VC, Rhoades E, Sachs JN. alpha-Synuclein-Induced Membrane Remodeling Is Driven by Binding Affinity, Partition Depth, and Interleaflet Order Asymmetry. J Am Chem Soc. 2014;136:9962–9972. doi: 10.1021/ja5016958. Here, the MARTINI CG MD simulations were used to simulate several α-synuclein amphipathic helices on a membrane patch. Together with experimental measurements, it was shown that membrane remodeling is dependent on several physical parameters, such as binding strength and partition depth. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Srivastava A, Voth GA. A Hybrid Approach for Highly Coarse-grained Lipid Bilayer Models. J Chem Theory Comput. 2013;9:750–765. doi: 10.1021/ct300751h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Saric A, Cacciuto A. Self-assembly of nanoparticles adsorbed on fluid and elastic membranes. Soft Matter. 2013;9:6677–6695. [Google Scholar]
- 17.Reynwar BJ, Deserno M. Membrane-mediated interactions between circular particles in the strongly curved regime. Soft Matter. 2011;7:8567–8575. [Google Scholar]
- 18**.Vacha R, Martinez-Veracoechea FJ, Frenkel D. Receptor-Mediated Endocytosis of Nanoparticles of Various Shapes. Nano Letters. 2011;11:5391–5395. doi: 10.1021/nl2030213. This work employs MD simulations of nanoparticles adhered to a membrane to study their passive transport through the membrane. By exploring different particle shapes and membrane-adhesion strengths, they expose the spherocylindrical shape as more efficient in being endocytosed compared to a sphere, which could be important for improved drug design. [DOI] [PubMed] [Google Scholar]
- 19.Schubertova V, Martinez-Veracoechea FJ, Vacha R. Design of Multivalent Inhibitors for Preventing Cellular Uptake. Sci Rep. 2017;7:11689. doi: 10.1038/s41598-017-11735-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20*.Saric A, Cacciuto A. Mechanism of membrane tube formation induced by adhesive nanocomponents. Phys Rev Lett. 2012;109:188101. doi: 10.1103/PhysRevLett.109.188101. This work, together with Ref-21, shows that large adhered nanoparticles can form large tubular invaginations in the membrane, in a cooperative manner. [DOI] [PubMed] [Google Scholar]
- 21*.Bahrami AH, Lipowsky R, Weikl TR. Tubulation and aggregation of spherical nanoparticles adsorbed on vesicles. Phys Rev Lett. 2012;109:188102. doi: 10.1103/PhysRevLett.109.188102. See description for Ref-20. [DOI] [PubMed] [Google Scholar]
- 22.Fotin A, Cheng Y, Sliz P, Grigorieff N, Harrison SC, Kirchhausen T, Walz T. Molecular model for a complete clathrin lattice from electron cryomicroscopy. Nature. 2004;432:573–579. doi: 10.1038/nature03079. [DOI] [PubMed] [Google Scholar]
- 23.Matthews R, Likos CN. Structures and pathways for clathrin self-assembly in the bulk and on membranes. Soft Matter. 2013;9:5794–5806. [Google Scholar]
- 24.Giani M, den Otter WK, Briels WJ. Early stages of clathrin aggregation at a membrane in coarse-grained simulations. Journal of Chemical Physics. 2017;146 doi: 10.1063/1.4979985. [DOI] [PubMed] [Google Scholar]
- 25.McMahon HT, Boucrot E. Molecular mechanism and physiological functions of clathrin-mediated endocytosis. Nat Rev Mol Cell Biol. 2011;12:517–533. doi: 10.1038/nrm3151. [DOI] [PubMed] [Google Scholar]
- 26.Fuhrmans M, Muller M. Coarse-grained simulation of dynamin-mediated fission. Soft Matter. 2015;11:1464–1480. doi: 10.1039/c4sm02533d. [DOI] [PubMed] [Google Scholar]
- 27.Arkhipov A, Yin Y, Schulten K. Four-scale description of membrane sculpting by BAR domains. Biophys J. 2008;95:2806–2821. doi: 10.1529/biophysj.108.132563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yu H, Schulten K. Membrane sculpting by F-BAR domains studied by molecular dynamics simulations. PLoS Comput Biol. 2013;9:e1002892. doi: 10.1371/journal.pcbi.1002892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Takemura K, Hanawa-Suetsugu K, Suetsugu S, Kitao A. Salt Bridge Formation between the I-BAR Domain and Lipids Increases Lipid Density and Membrane Curvature. Scientific Reports. 2017;7 doi: 10.1038/s41598-017-06334-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ayton GS, Lyman E, Voth GA. Hierarchical coarse-graining strategy for protein-membrane systems to access mesoscopic scales. Faraday Discuss. 2010;144:347–357. doi: 10.1039/b901996k. discussion 445-381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Blood PD, Swenson RD, Voth GA. Factors influencing local membrane curvature induction by N-BAR domains as revealed by molecular dynamics simulations. Biophys J. 2008;95:1866–1876. doi: 10.1529/biophysj.107.121160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32**.Ramakrishnan N, Sunil Kumar PB, Ipsen JH. Membrane-mediated aggregation of curvature-inducing nematogens and membrane tubulation. Biophys J. 2013;104:1018–1028. doi: 10.1016/j.bpj.2012.12.045. A numerical membrane model was used to simulate the clustering and membrane deformations by elongated nematic inclusions with anisotropic spontaneous curvature. It was shown that even at 10% surface coverage, the inclusions aggregate and can locally deform the membrane. Higher densities can induce the formation of tubules and discs. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Noguchi H. Acceleration and suppression of banana-shaped-protein-induced tubulation by addition of small membrane inclusions of isotropic spontaneous curvatures. Soft Matter. 2017;13:7771–7779. doi: 10.1039/c7sm01375b. [DOI] [PubMed] [Google Scholar]
- 34*.Noguchi H. Membrane tubule formation by banana-shaped proteins with or without transient network structure. Scientific Reports. 2016;6 doi: 10.1038/srep20935. By simulating rigid curved rods embedded in a CG membrane, this work shows that a spontaneous curvature in the direction perpendicular to the rod can have significant influence on the way it deforms the membrane. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Simunovic M, Mim C, Marlovits TC, Resch G, Unger VM, Voth GA. Protein-mediated transformation of lipid vesicles into tubular networks. Biophys J. 2013;105:711–719. doi: 10.1016/j.bpj.2013.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Davtyan A, Simunovic M, Voth GA. The mesoscopic membrane with proteins (MesM-P) model. J Chem Phys. 2017;147:044101. doi: 10.1063/1.4993514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yin Y, Arkhipov A, Schulten K. Simulations of membrane tubulation by lattices of amphiphysin N-BAR domains. Structure. 2009;17:882–892. doi: 10.1016/j.str.2009.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lyman E, Cui H, Voth GA. Water under the BAR. Biophys J. 2010;99:1783–1790. doi: 10.1016/j.bpj.2010.06.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39**.Simunovic M, Srivastava A, Voth GA. Linear aggregation of proteins on the membrane as a prelude to membrane remodeling. Proc Natl Acad Sci U S A. 2013;110:20396–20401. doi: 10.1073/pnas.1309819110. This work and Ref-44 demonstrate by using CG simulations that BAR proteins and, more generally, nanoparticles (Ref-44) can form long filamentous aggregates when bound to lipid membranes. The interactions among proteins (or particles) are driven by local membrane curvature induced by their adhesive interactions with the bilayer. These works showed that proteins can get recruited from very long distances despite lacking explicit attractions with one another and form highly ordered assemblies. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chen Z, Zhu C, Kuo CJ, Robustelli J, Baumgart T. The N-Terminal Amphipathic Helix of Endophilin Does Not Contribute to Its Molecular Curvature Generation Capacity. J Am Chem Soc. 2016;138:14616–14622. doi: 10.1021/jacs.6b06820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bradley RP, Radhakrishnan R. Curvature-undulation coupling as a basis for curvature sensing and generation in bilayer membranes. Proceedings of the National Academy of Sciences of the United States of America. 2016;113:E5117–E5124. doi: 10.1073/pnas.1605259113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Goulian M. Inclusions in membranes. Curr Opin Colloid In. 1996;1:358–361. [Google Scholar]
- 43.Vahid A, Saric A, Idema T. Curvature variation controls particle aggregation on fluid vesicles. Soft Matter. 2017;13:4924–4930. doi: 10.1039/c7sm00433h. [DOI] [PubMed] [Google Scholar]
- 44**.Saric A, Cacciuto A. Fluid membranes can drive linear aggregation of adsorbed spherical nanoparticles. Phys Rev Lett. 2012;108:118101. doi: 10.1103/PhysRevLett.108.118101. See description for Ref.-39. [DOI] [PubMed] [Google Scholar]
- 45.Simunovic M, Voth GA. Membrane tension controls the assembly of curvature-generating proteins. Nat Commun. 2015;6:7219. doi: 10.1038/ncomms8219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.van der Wel C, Vahid A, Saric A, Idema T, Heinrich D, Kraft DJ. Lipid membrane-mediated attraction between curvature inducing objects. Scientific Reports. 2016;6 doi: 10.1038/srep32825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Dommersnes PG, Fournier JB. N-body study of anisotropic membrane inclusions: Membrane mediated interactions and ordered aggregation. Eur Phys J B. 1999;12:9–12. [Google Scholar]
- 48.McDonald NA, Vander Kooi CW, Ohi MD, Gould KL. Oligomerization but Not Membrane Bending Underlies the Function of Certain F-BAR Proteins in Cell Motility and Cytokinesis. Dev Cell. 2015;35:725–736. doi: 10.1016/j.devcel.2015.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lacy MM, Baddeley D, Berro J. Single-molecule imaging of the BAR-domain protein Pil1p reveals filament-end dynamics. Mol Biol Cell. 2017;28:2251–2259. doi: 10.1091/mbc.E17-04-0238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Saletti D, Radzimanowski J, Effantin G, Midtvedt D, Mangenot S, Weissenhorn W, Bassereau P, Bally M. The Matrix protein M1 from influenza C virus induces tubular membrane invaginations in an in vitro cell membrane model. Sci Rep. 2017;7:40801. doi: 10.1038/srep40801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51*.Simunovic M, Šarić A, Henderson JM, Lee KYC, Voth GA. Long-Range Organization of Membrane-Curving Proteins. ACS Central Science. 2017;3:1246–1253. doi: 10.1021/acscentsci.7b00392. By using a combination of AFM imaging and CG MD simulations, this work experimentally visualizes for the first time the linear aggregates of N-BAR proteins on flat membranes. It demonstrates that protein filaments on membranes have intrinsic repulsions, acting at very large distances, that help determine the hierarchical assembly on the membrane. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ghosh SK, Cherstvy AG, Petrov EP, Metzler R. Interactions of rod-like particles on responsive elastic sheets. Soft Matter. 2016;12:7908–7919. doi: 10.1039/c6sm01522k. [DOI] [PubMed] [Google Scholar]