Band-Like Charge Transport in Cs₂AgBiBr₆ and Mixed Antimony–Bismuth Cs₂AgBi_1–xSb_xBr₆ Halide Double Perovskites

Abstract

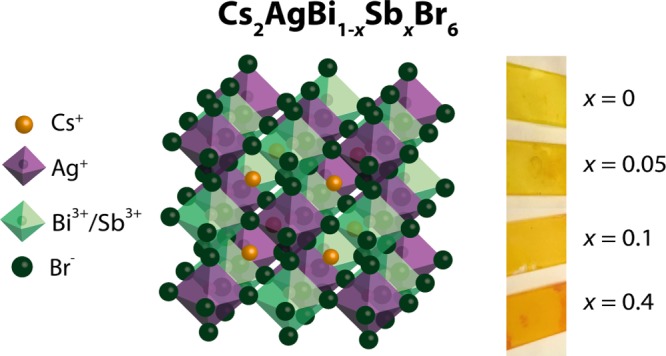
Recently, halide double perovskites (HDPs), such as Cs₂AgBiBr₆, have been reported as promising nontoxic alternatives to lead halide perovskites. However, it remains unclear whether the charge-transport properties of these materials are as favorable as for lead-based perovskites. In this work, we study the mobilities of charges in Cs₂AgBiBr₆ and in mixed antimony–bismuth Cs₂AgBi_1–xSb_xBr₆, in which the band gap is tunable from 2.0 to 1.6 eV. Using temperature-dependent time-resolved microwave conductivity techniques, we find that the mobility is proportional to T^–p (with p ≈ 1.5). Importantly, this indicates that phonon scattering is the dominant scattering mechanism determining the charge carrier mobility in these HDPs similar to the state-of-the-art lead-based perovskites. Finally, we show that wet chemical processing of Cs₂AgBi_1–xSb_xBr₆ powders is a successful route to prepare thin films of these materials, which paves the way toward photovoltaic devices based on nontoxic HDPs with tunable band gaps.

1. Introduction

Halide double perovskites (HDPs) such as Cs₂AgBiBr₆ have recently emerged as a nontoxic alternative to lead-based perovskites¹⁻⁵ and were successfully applied as radiation absorbers both in sensitive X-ray detectors and in photovoltaic devices.⁶⁻⁸ Still, the power conversion efficiencies of Cs₂AgBiBr₆-based solar cells are relatively low,^7,8 which can be partially understood from its poor visible light absorption because of its indirect band gap of 2.19 eV.² It was recently shown that alloying Tl³⁺ or Sb³⁺, both thought to substitute for Bi³⁺, can be used as a strategy to decrease the band gap of Cs₂AgBiBr₆ toward values more relevant for single-junction solar cells.^9,10 However, to date, there have been no reports presenting synthesis routes to prepare thin films of alloyed HDPs, which is a crucial step toward devices of these materials. Furthermore, although HDPs of various compositions have been designed,⁹⁻¹³ it remains unclear whether the transport properties of these HDPs are as favorable as for their lead-based analogues.

In this work, we study the optoelectronic properties of Cs₂AgBiBr₆ and mixed antimony–bismuth HDPs with the general formula Cs₂AgBi_1–xSb_xBr₆, which show an absorption red shift with increasing x, reaching ∼1.6 eV upon replacing 40% of the Bi³⁺ with Sb³⁺ (i.e. x = 0.4).¹⁰ We use pulse-radiolysis time-resolved microwave conductivity (PR-TRMC) measurements to gain insight in the mobility of free charges as a function of x and temperature.¹⁴⁻¹⁶ Interestingly, we find that the charge carrier mobility decreases only marginally on increasing x. Furthermore, we observe that, independent of the antimony content, the mobility decreases with increasing temperature in between 140 and 420 K. Importantly, the dependence of the mobility on temperature (T^–p, with p ≈ 1.5) indicates band-like transport of charges in both Cs₂AgBiBr₆ and mixed antimony–bismuth analogues, in which the mobility is limited by phonon scattering. The observation that the charge-transport mechanism in these HDPs is very similar to lead-based perovskites,¹⁷⁻¹⁹ highlights their potential as nontoxic alternatives. Finally, we find that dissolving the mixed antimony–bismuth HDP powders, synthesized using solid-state reactions, is a successful route to spin-coat thin Cs₂AgBi_1–xSb_xBr₆ films. The preparation of thin HDP films with mixed trivalent metals paves the way toward photovoltaic devices based on HDPs with tunable band gaps.

2. Results and Discussion

2.1. Powders of Cs₂AgBi_1–xSb_xBr₆

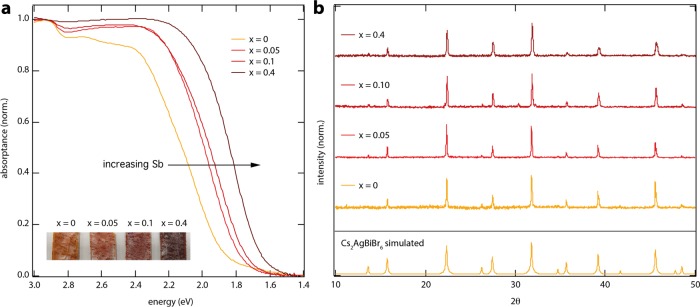
Powders of Cs₂AgBi_1–xSb_xBr₆, with x values ranging from 0 to 0.4, were prepared from stoichiometric mixtures of the precursors CsBr, AgBr, BiBr₃, and SbBr₃, following previously reported solid-state reaction procedures.¹⁰ Here, x represents the amount of SbBr₃ added to the reaction mixture, and the formulas are written assuming full substitution at the Bi site. The content of Sb in each sample was estimated using X-ray photoelectron spectroscopy (XPS). Although some variation across the sample is observed, we find that the Sb-to-Bi ratio increases monotonically with increasing Sb content in the precursors (see Supporting Information Table S1). Figure 1a shows the absorption spectra, measured using an integrating sphere, of Cs₂AgBi_1–xSb_xBr₆ powders with x = 0, 0.05, 0.1, and 0.4, attached to quartz substrates using optically clear adhesive. Consistent with the previous reports,^10,11 these spectra show that increasing the Sb content gradually reduces the band gap, resulting in absorption onset values close to 1.6 eV for x = 0.4. Furthermore, all of the samples show X-ray reflections characteristic of the double perovskite structure, see Figure 1b, which monotonically shifts to larger angles on increasing x (see also Supporting Information Figure S1), supporting the replacement of Bi³⁺ with the smaller Sb³⁺.

Figure 1.

(a) Absorptance spectra normalized to unity to account for different surface coverages and (b) powder X-ray diffraction (XRD) patterns (Cu Kα radiation, λ = 1.54 Å) of mixed antimony–bismuth HDP powders with the general formula Cs₂AgBi_1–xSb_xBr₆. Inset shows images of the powders with different Sb content.

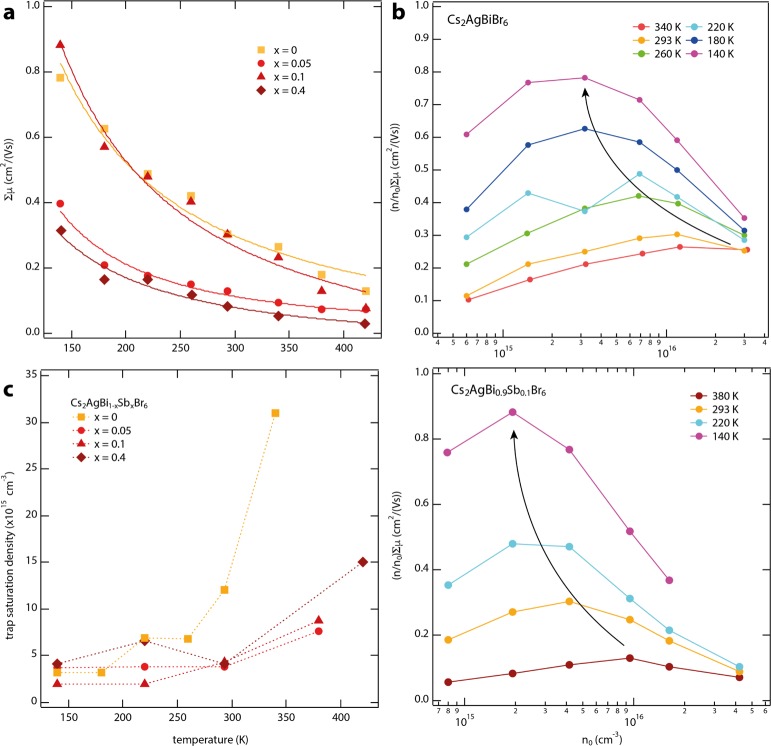
To investigate the suitability of Cs₂AgBiBr₆ and mixed antimony–bismuth HDPs for photovoltaic applications, we studied the transport of free charges in powders of these materials using the PR-TRMC technique.^14,15 With the PR-TRMC technique, free charges are homogeneously generated throughout the sample by irradiation with a high-energy electron pulse. These primary electrons are not injected but lose a part of their energy by ionizing the sample, resulting in a uniform distribution of electrons and holes. The density of charges initially generated by each high-energy electron from the pulse can be calculated using previously reported procedures (see Experimental Methods). The total density of free charges n₀ created by the electron pulse can be varied by changing its duration. A microwave probe is then used to measure the change in conductivity on the generation of free charges, which scales with the number and mobility (μ) of charge carriers.^14,16 Importantly, because the initial density of free charges can be tuned independently of the exciton binding energy, the PR-TRMC technique is very suitable to determine the temperature-dependent mobility. Similar to the more widely used laser-induced TRMC,^20,21 the end-of-pulse charge density n can however still be affected by fast trapping or recombination of mobile charges within the instrumental response time of 1 ns. Therefore, we choose a pulse length at which losses are minimized so that n/n₀ is closest to unity. Figure 2a shows the sum of electron and hole mobility ∑μ for Cs₂AgBi_1–xSb_xBr₆ with x = 0, 0.05, 0.1, and 0.4 at temperatures ranging from 140 to 420 K. From here, we find that at room temperature, ∑μ is at least 0.3 cm²/(V s) for Cs₂AgBiBr₆ (x = 0) powders, which is only about four times lower than the mobility observed in CsPbBr₃ crystals using the same technique.^15,20

Figure 2.

(a) Dots: mobility ∑μ as function of temperature for x = 0 (squares), x = 0.05 (spheres), x = 0.1 (triangles), and x = 0.4 (diamonds), determined using the PR-TRMC technique. On fitting these mobilities to μ(T) ∝ T^–p, added as solid lines, we obtained p-values of 1.15 (x = 0), 1.62 (x = 0.05), 1.19 (x = 0.1), and 1.34 (x = 0.4). (b) (n/n₀)∑μ as function of n₀ and temperature for x = 0 (top) and x = 0.1 (bottom). (c) Trap saturation density as a function of temperature for x = 0 (squares), x = 0.05 (spheres), x = 0.1 (triangles), and x = 0.4 (diamonds), obtained from the maximum n/n₀.

The lower mobilities observed in Cs₂AgBiBr₆ are consistent with the effective masses of electrons and holes being somewhat larger than those for its lead-based analogue (i.e., CsPbBr₃).^4,22 In addition, the scattering times may be shorter because of enhanced scattering with phonons or defects. On partially replacing the Bi³⁺ with Sb³⁺, slightly reduced mobilities are observed, although at each temperature, the absolute values stay within the same order of magnitude. Furthermore, independent of x, the mobility decreases with rising temperatures in between 140 and 420 K. On further analysis of the data, we find that ∑μ scales with T^–1.15 for x = 0, T^–1.62 (x = 0.05), T^–1.19 (x = 0.1), and T^–1.34 (x = 0.4). Importantly, these negative powers indicate that phonon scattering (i.e., μ ∝ T^–1.5) is the dominant scattering mechanism determining the charge carrier mobility in these HDPs. These powers are within the same range as the state-of-the-art lead-based perovskites, for which values in between −1.2 and −1.6 have been reported.^17,19,23,24 Additionally, the observation that these negative powers are very similar for different x values suggests that the charge-transport mechanism is not substantially disturbed on mixing bismuth with antimony. This means that independent of the Sb³⁺ content in the Cs₂AgBiBr₆ lattice, there is band-like transport of charges with no indication of substantial defect scattering.

As mentioned above, charge carrier losses within the instrumental response time lead to a reduction of n/n₀. Therefore, to get insight into sub-nanosecond recombination processes, we can plot (n/n₀)∑μ as a function of n₀ (cm^–3). This is shown in Figure 2b for Cs₂AgBiBr₆ (upper panel) and Cs₂AgBi_0.9Sb_0.1Br₆ (lower panel) for temperatures ranging from 140 to 420 K. At each temperature, (n/n₀)∑μ initially rises on increasing the charge carrier densities. We attribute this to sub-nanosecond charge carrier trapping, leading to low yields if the trap density is higher than the charge carrier density.^25,26 Gradual saturation of these traps then results in increased n values for higher n₀, and thus an enhancement of n/n₀. On further increasing n₀, n/n₀ decreases again, which is typically observed if higher order recombination starts to dominate.^27,28 Therefore, the charge carrier concentration at which (n/n₀)∑μ reaches maximum values represents the regime in which band-to-band recombination is in competition with trap-assisted recombination and can thus be used as an indication of the trap saturation density (cm^–3).

Figure 2c displays the densities at which the traps are saturated as a function of temperature for the sample with (x > 0) and without (x = 0) antimony. For Cs₂AgBiBr₆, this shows a clear increase from 3 × 10¹⁵ cm^–3 at 140 K to more than 3 × 10¹⁶ cm^–3 for T > 340 K. The room-temperature value of 1.2 × 10¹⁶ cm^–3 is close to the previously suggested upper limit of 10¹⁶ cm^–3 for a Cs₂AgBiBr₆ single crystal.²⁹ Interestingly, the temperature dependence of (n/n₀)_max suggests that the trap density is enhanced with increasing temperatures, which could be because the origin of the traps is related to vacancies or interstitials, resulting from thermal displacement of ions. Alternatively, it might be that trap states originate from thermal ionization of defects, which also results in an increased number of available traps at higher temperatures. For the Sb-containing HDPs, the trap saturation densities at 140 K are 2–4 × 10¹⁵ cm^–3 and thus close to the antimony-free Cs₂AgBiBr₆. Also here, an enhancement is observed as the temperature rises, with (n/n₀) reaching a maximum just below 10¹⁶ cm^–3 at 380 K for Cs₂AgBi_0.9Sb_0.1Br₆ (see bottom panel in Figure 2b) and the other mixed antimony–bismuth HDP powders (see also Supporting Information Figure S2). Most importantly, at and above room temperature, the trap-saturation densities for x > 0 are about a factor three lower than that for x = 0, see Figure 2c. If indeed the trap states in Cs₂AgBiBr₆ are related to thermal ionic motion or defect ionization, these results suggest that this can be partially suppressed by Sb³⁺ substitution.

2.2. Thin Films of Cs₂AgBi_1–xSb_xBr₆

The preparation of thin films of alloyed HDPs is a crucial step toward devices employing HDPs with tunable band gaps and also important to further investigate their optoelectronic properties using spectroscopic techniques.³⁰ Although it was recently shown that Cs₂AgBiBr₆ films can be spin-coated from a solution of its precursors in dimethyl sulfoxide (DMSO),⁷ there have been no reports on mixed trivalent metal HDP films. Here, we used the products of the solid-state synthesis to prepare thin films of Cs₂AgBi_1–xSb_xBr₆, see also Experimental Methods. These powders were dissolved in DMSO at 0.5 M, yielding clear solutions with yellow to orange color (depending on x). The solutions, preheated to 75 °C, were then spin-coated on quartz substrates, followed by annealing at 200 °C (x = 0)⁷ or 90 °C (for x > 0). Note that we used lower annealing temperatures for the Sb-containing films, as we noticed the formation of undesired side phases (such as Cs₃Sb₂Br₉) on using high annealing temperatures (see Supporting Information Figure S4).

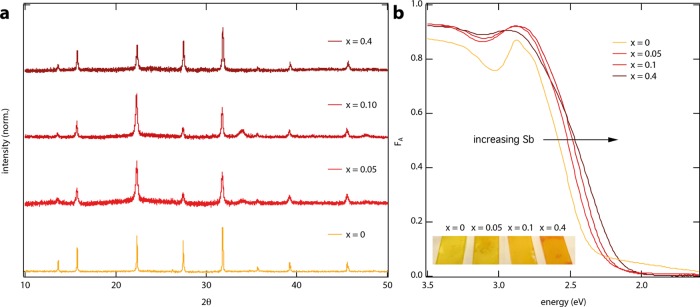
Figure 3a shows the XRD patterns of the resulting films with x = 0, 0.05, 0.1, and 0.4, showing all of the reflections characteristic of the HDP crystal structure. The shift to higher angles (see also Supporting Information Figure S5) shows that the lattice parameters are reduced on addition of Sb, consistent with Sb³⁺ replacing the larger Bi³⁺ in these HDP thin films. In addition, we observe that the reflections are broader for x > 0 than that for x = 0, suggesting that the crystalline domains are larger for the latter. Note that the different relative intensities of the reflections compared to the corresponding powders (Figure 2c) most likely result from preferential orientations of the crystalline domains with respect to the substrate. XPS analysis (Supporting Information Figure S6 and Table S2) of the thin films indicates higher Sb fractions for increasing x, which we find to be homogeneously distributed according to the scanning electron microscopy–energy dispersive X-ray spectroscopy analysis (Supporting Information Figure S7).

Figure 3.

(a) XRD patterns and (b) absorptance spectra of thin Cs₂AgBi_1–xSb_xBr₆ films, spin-coated from solutions of the powders (0.5 M) in DMSO.

Figure 3b shows the absorptance (i.e., attenuation) spectra of the thin films. Although we expect the absorption coefficients to be identical, the absorption onsets for the sub-micron thick films and for the corresponding millimeter-sized powders are very different. This can be attributed to the low absorption coefficients close to the (indirect) band gap of these materials, which makes the onset of the absorptance very sensitive for the sample thickness (see Supporting Information Figure S8 for the absorption coefficients of Cs₂AgBi_1–xSb_xBr₆ for x = 0 and x = 0.4).^1,10 However, consistent with the Cs₂AgBi_1–xSb_xBr₆ powders, the absorption onset of the films is red-shifted on increasing x, indicating that alloying Bi³⁺ and Sb³⁺ is an effective strategy to manipulate the band gap in thin HDP films. Altogether, the above results indicate that the Sb substitution in antimony–bismuth alloyed thin films increases when using higher values of x, although we note that the absolute stoichiometry in the films might deviate from the powders, as indicated by nonmonotonic shifts in the XRD patterns (see Supporting Information Figure S5).

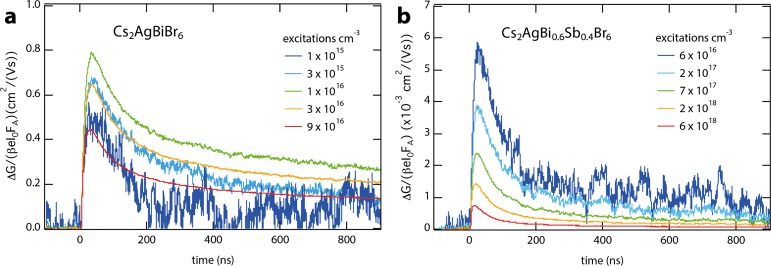
To investigate to what extent the PR-TRMC results of the antimony–bismuth alloyed HDP powders (Figure 2) are representative for light-generated charges in the thin Cs₂AgBi_1–xSb_xBr₆ films, we recorded the photoconductance using laser-induced TRMC measurements.^20,21Figure 4 shows the photoconductance as a function of time for the Cs₂AgBiBr₆ (Figure 4a) and Cs₂AgBi_0.6Sb_0.4Br₆ (Figure 4b) films, using an excitation energy of 2.8 eV. Here, the maximum signal height represents the yield-mobility product φ∑μ, in which the yield φ represents the ratio between free charges and absorbed photons.²¹ For Cs₂AgBiBr₆ (Figure 4a), consistent with the PR-TRMC measurements, we initially observe an enhancement of the maximum signal height (i.e., φ∑μ), followed by a decrease on further increasing the excitation density in Cs₂AgBiBr₆ (Figure 4a). Interestingly, the maximum φ∑μ is found at a charge density 1 × 10¹⁶ cm^–3, meaning that the density at which the traps are saturated in these thin films is nearly identical to that of the corresponding powders (i.e., 1.2 × 10¹⁶ cm^–3 at room temperature, recall Figure 2c).

Figure 4.

Photoconductance as a function of time after excitation at 2.8 eV for Cs₂AgBiBr₆ (a) and Cs₂AgBi_0.6Sb_0.4Br₆ (b).

We can further conclude from the maximum φ∑μ that the sum of the electron and hole mobilities amounts to at least 0.8 cm²/(V s) for the nonalloyed HDP (Figure 4a, x = 0), similar to previously reported values for a Cs₂AgBiBr₆ thin film.²⁹ This relatively low mobility value compared to lead-based perovskites is in agreement with the larger effective masses of both electrons and holes.⁴ The photoconductance signals decay at time scales on the order of a microsecond, which suggests that the microsecond lifetime recently observed using transient absorption spectroscopy on similar samples originates at least partially from mobile charges.³⁰ We note that this observation is in contrast with our previous TRMC results, which showed that all mobile charges recombined within several nanoseconds after exciting a Cs₂AgBiBr₆ film synthesized under ambient conditions.²⁹ We suspect that the longer recombination lifetimes in the films of the current work are due to the fact that all of these samples were synthesized under inert conditions and not exposed to air at any time before or during the measurements. The microsecond lifetimes in Cs₂AgBiBr₆ films synthesized under inert conditions (Figure 4a) suggest that at least one of the charges remains free, and that the decay represents the recombination between a free charge and its trapped counter-charge. On the basis of the mobility and half lifetime, we estimate that the diffusion length of the free charge carrier in Cs₂AgBiBr₆ thin film amounts to 0.6 μm (see Supporting Information Table S3). Although this is relatively short compared to fully optimized state-of-the-art lead-based perovskites,^15,27 this value suggests that Cs₂AgBiBr₆ is a potential nontoxic alternatives to lead-based perovskites.

For the Cs₂AgBi_0.6Sb_0.4Br₆ (Figure 4b) thin film, the φ∑μ decreases on increasing the charge density from 6 × 10¹⁶ to 6 × 10¹⁸ cm^–3, indicating that higher order recombination processes dominate in this regime.²⁸ Additionally, the maximum φ∑μ is 2 orders of magnitude smaller than for the antimony-free HDP film (Figure 4a). On measuring the corresponding powders with laser-induced TRMC, we also obtained lower photoconductance signals for the Sb-containing HDPs (Supporting Information Figure S9), although here the difference in φ∑μ is 1 order of magnitude. This can at least partially be explained considering that the charge carrier lifetimes for Cs₂AgBi_1–xSb_xBr₆ with x = 0.4 as observed by PR-TRMC traces, shown in Figure S3, are very short: less than 10 ns. Because the light-induced TRMC measurements make use of a cavity with a response time close to 18 ns, we can thus expect a severe reduction in φ∑μ. For thin films, however, the lower φ∑μ on Sb substitution (Figure 4b) might also be because of a decreased ∑μ resulting from its smaller crystalline domain sizes.³¹ In addition, the trap density might be higher in thin films, for instance, because of oxidation of a small fraction of Sb³⁺, which we are currently investigating. However, in view of the well-preserved charge-transport properties for the Sb-substituted Cs₂AgBiBr₆ powders (Figure 2), it seems likely that further optimizing the synthesis procedure and annealing conditions will improve the sample quality and hence increase both mobilities and lifetimes in thin films of Sb-containing HDPs. Finally, we want to highlight that the introduction of Sb results in a band gap narrowing instead of the formation of intra band gap defect states. On excitation of Cs₂AgBi_1–xSb_xBr₆ (x = 0.4) powder at 1.7 eV, which is below the onset of Cs₂AgBiBr₆, the maximum TRMC signal heights and thus φ∑μ are similar to those obtained at 2.8 eV, as shown in Figure S9. Similar results are obtained for the films.

3. Conclusions

To summarize, we have investigated the optoelectronic properties of the double-perovskite Cs₂AgBiBr₆ and mixed antimony-bismuth HDPs with the general formula Cs₂AgBi_1–xSb_xBr₆, in which the band gap can be tuned from 2.0 to 1.6 eV by increasing the antimony content. With PR-TRMC measurements on Cs₂AgBi_1–xSb_xBr₆ powders, we observe that for all x values, the charge carrier mobility increases on decreasing the temperature. The power law dependence of the mobilities on temperature show that phonon scattering (i.e., μ ∝ T^–1.5) is the dominant scattering mechanism determining the charge-carrier mobility in these HDPs. Importantly, these results show that for both Cs₂AgBiBr₆ and mixed trivalent metal Cs₂AgBi_1–xSb_xBr₆, the charge-transport mechanism is similar to the state-of-the-art lead-based perovskites. The combination of band-like transport and band gap tunability in Cs₂AgBi_1–xSb_xBr₆ highlights the potential of these materials as nontoxic alternatives to lead-based perovskites. Finally, we demonstrate the preparation of thin films of Cs₂AgBi_1–xSb_xBr₆, showing that the incorporation of Sb can red shift the absorption onset up to a few 100 meV in thin Cs₂AgBiBr₆ films. Altogether, these results represent a crucial step toward lead-free perovskite devices implementing antimony–bismuth-alloyed HDPs.

4. Experimental Methods

4.1. Cs₂AgBi_1–xSb_xBr₆ Powders

CsBr (1 mmol), 0.5 mmol AgBr, (1 – x)0.5 mmol BiBr₃, and 0.5x mmol SbBr₃ were ground until fine powders were obtained. The mixtures were sealed in glass tubes under vacuum and heated in a box furnace to 320 °C (heating rate of 3 °C/min) and kept at this temperature for 3 h.¹⁰ After cooling down to room temperature (cooling rate of 3 °C/min), the closed tubes containing the products were transferred to a nitrogen-filled glovebox. For this work, x was varied between 0 and 0.4; attempts to prepare higher concentrations of x failed.

4.2. Cs₂AgBi_1–xSb_xBr₆ Thin Films

Cs₂AgBi_1–xSb_xBr₆ (0.5 mmol) was dissolved in 1 mL of DMSO at 75 °C under magnetic stirring in a nitrogen-filled glovebox.⁷ Quartz substrates were cleaned with isopropanol and treated with an ozone plasma for 30 min. The Cs₂AgBi_1–xSb_xBr₆/DMSO solutions were filtered and kept at 75 °C. Then, 100 μL of the filtered solution was spin-coated on a quartz substrate using a two-step procedure starting at 500 rpm for 30 s (ramping speed of 100 rpm/s), followed by 60 s at 5000 rpm (ramping speed of 5000 rpm/s). The Cs₂AgBiBr₆ (x = 0) films were annealed at 200 °C for 3 min, and the Sb-containing films were annealed at 90 °C for 3 min.

4.3. X-ray Diffraction

XRD patterns were obtained with a Bruker D8 diffractometer in a Bragg–Brentano configuration, using Cu Kα (λ = 1.54 Å) radiation.

4.4. X-ray Photoelectron Spectroscopy

XPS measurements were performed with a Thermo Scientific K-alpha instrument, equipped with an Al Kα X-ray source and a flood gun to avoid charging of the sample. For the high-resolution scans of C 1s, O 1s, Ag 3d, Bi 4f, Br 3d, Sb 3d, and Cs 3d signals, the following parameters were used: spot size of 400 μm, pass energy of 50 eV, energy step size of 0.1 eV, dwell time of 50 ms, and 10 scans. XPS spectra were corrected using the atmospheric carbon C peak position (284.8 eV). Elemental quantification was performed using the Avantage software. High-resolution scans of each element were fit with a mixture of Gaussian and Lorentzian functions; the area under each peak was used to determine the concentration of each element.

4.5. Optical Characterization

Absorption and transmission spectra were recorded with a PerkinElmer Lambda 1050 spectrophotometer equipped with an integrated sphere. The thin Cs₂AgBi_1–xSb_xBr₆ films were placed in front of the sphere to measure the fraction of the transmitted light (F_T) and under an angle of 10° inside the sphere to detect the total fraction of reflected and transmitted photons (F_R+T). From here, we calculated the fraction of absorbed light (absorptance; F_A)

The fraction of reflected light (F_R) was determined from

The absorption coefficient α is often calculated from the transmission spectrum using

where I_L/I₀ equals F_T for a sample of thickness L with a negligible reflection. However, since thin perovskite films are highly reflective, α was obtained from

The Cs₂AgBi_1–xSb_xBr₆ powders were attached to quartz substrates using optically clear adhesive tape (Thorlabs), and the fraction of absorbed light was determined from the experimental F_R+T, as described above.

4.6. PR-TRMC Measurements

About 30 mg of each Cs₂AgBi_1–xSb_xBr₆ powder was put in a sample holder and covered with polymethyl methacrylate (PMMA), drop-casted from a 10 mg/mL PMMA/chlorobenzene solution, to protect from moisture and air. PR-TRMC measurements involve the generation of charge carriers through irradiation by a short pulse of high-energy electrons (3 MeV) and the monitoring of the changes in conductivity because of mobile charge carriers using high-frequency microwaves (28–38 GHz).^14,16 The change in conductivity is proportional to the absorbed microwave power via a sensitivity factor A

The experimental frequency dependence of ΔP/P can be fitted with an analytical expression to determine the dielectric constant, ε, and change in conductivity, Δσ.¹⁴

The mobility is then calculated by

where n₀ is the initial concentration of charge carriers at the end of the pulse and μ is the sum of the mobilities for electrons and holes. n₀ is a function of the mass of material (m), volume of the sample holder (V_sh), irradiation energy deposited in the sample (D), and the radiation-ionization energy required for the generation of an electron–hole pair (E_p)

D is proportional to the electron density of the material, and perovskites has been determined to be ∼1 J/kg/nC.¹⁵ The latter is derived from previous radiation dosimetry experiments. E_p has been determined according to Klein’s theoretical model³² and Alig’s equation³³ for semiconductor materials, which relates it to the band gap of the material, phonon losses, and the residual kinetic energy

In the PR-TRMC setup, the cell is contained in a cryostat in which the temperature can be varied between 123 and 473 K. The temperature was maintained for ∼15 min before doing the actual measurement to assure the equilibrium of the system. The overall time response of the setup is limited by the rise time of the detector diode and the length of the excitation pulse (∼1 ns).

4.7. Laser-Induced TRMC Measurements

The thin films on quartz substrates were placed in an airtight microwave cell inside a N₂-filled glovebox. The TRMC technique was used to measure the change in microwave (8.5 GHz) power after pulsed excitation (repetition rate 10 Hz) of the samples at various excitation wavelengths. Neutral density filters were used to vary the intensity of the incident light. The illuminated sample area is ∼2.5 cm². The time-resolved change in conductance ΔG(t) was obtained from the photoexcitation-induced change in microwave power ΔP(t), which are related by a sensitivity factor K(21)

The rise of ΔG is limited by the width of the laser pulse (3.5 ns full width at half maximum) and the response time of our microwave system (18 ns). The slow repetition rate of the laser of 10 Hz ensures full relaxation of all photoinduced charges to the ground state before the next laser pulse hits the sample. Before and during the photoconductance measurements, the samples were not exposed to moisture and air to prevent degradation.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01705.

• Elemental analysis, XRD, and additional TRMC data (PDF)

The authors declare no competing financial interest.