Significance
Determining the state of an individual’s internal physiological clock has important implications for precision medicine, from diagnosing neurological disorders to optimizing drug delivery. To be useful, such a test must be accurate, minimally burdensome to the patient, and robust to differences in patient protocols, sample collection, and assay technologies. TimeSignature is a machine-learning approach to predict physiological time based on gene expression in human blood. A powerful feature is TimeSignature’s generalizability, enabling it to be applied to samples from disparate studies and yield highly accurate results despite systematic differences between the studies. This quality is unique among expression-based predictors and addresses a major challenge in the development of reliable and clinically useful biomarker tests.
Keywords: circadian rhythms, gene expression dynamics, machine learning, cross-platform prediction
Abstract
Circadian clocks play a key role in regulating a vast array of biological processes, with significant implications for human health. Accurate assessment of physiological time using transcriptional biomarkers found in human blood can significantly improve diagnosis of circadian disorders and optimize the delivery time of therapeutic treatments. To be useful, such a test must be accurate, minimally burdensome to the patient, and readily generalizable to new data. A major obstacle in development of gene expression biomarker tests is the diversity of measurement platforms and the inherent variability of the data, often resulting in predictors that perform well in the original datasets but cannot be universally applied to new samples collected in other settings. Here, we introduce TimeSignature, an algorithm that robustly infers circadian time from gene expression. We demonstrate its application in data from three independent studies using distinct microarrays and further validate it against a new set of samples profiled by RNA-sequencing. Our results show that TimeSignature is more accurate and efficient than competing methods, estimating circadian time to within 2 h for the majority of samples. Importantly, we demonstrate that once trained on data from a single study, the resulting predictor can be universally applied to yield highly accurate results in new data from other studies independent of differences in study population, patient protocol, or assay platform without renormalizing the data or retraining. This feature is unique among expression-based predictors and addresses a major challenge in the development of generalizable, clinically useful tests.
Circadian clocks drive a vast repertoire of periodic biochemical, physiological, and behavioral processes. At the cellular level, they are governed by a complex network of biochemical interactions that regulate circadian dynamics in virtually every organ. Genetic studies in the fruit fly, mouse, and humans have revealed an evolutionarily conserved mechanism driven by the oscillatory activation and repression of core clock genes (including Clock, Bmal1, Per1-3, and Cry1-3) (1, 2). In mammals, this system potentially regulates the expression of nearly half the genome (3) (in aggregate across tissues), transmitting temporal information to coordinate cellular processes. These hundreds of rhythmic genes exhibit diurnal expression peaks in many organs at various times, presumably reflecting time of day-specific functions in different tissues.
Abundant epidemiological evidence links circadian regulation to human health, with consequences for disease risk and drug efficacy (3–20). This body of evidence suggests that assessments of physiological time could be valuable for disease risk prediction, diagnostic assays, and refined treatment protocols and has motivated a growing interest in using measurements of circadian regulation in the clinic. Although a number of measures are currently used to assay human circadian clocks in clinical and research settings (melatonin, cortisol, core body temperature, actigraphy, and even core clock gene expression) (21), they suffer shortcomings that limit their utility. The major limitation of these techniques is the need for serial sampling over extended periods of several hours, which is both costly and burdensome to the patient.
The discovery that the clock gene program is present in almost all tissues, including peripheral blood mononuclear cells (PBMCs), suggests the existence of cell-autonomous clocks and offers an alternative approach for circadian assessment. These peripheral clocks are synchronized with the neural pacemaker in the hypothalamic suprachiasmatic nucleus (SCN) (22), which drives rhythmic expression of the pineal hormone melatonin and adrenal cortisol secretion, as well as body temperature and feeding rhythms. Changes in gene expression in PBMC correlates with habitual sleep-wake timing, consistent with the notion that PBMC rhythms are reset by the circadian pacemaker in the SCN, which also drives circadian sleep–wake changes (23). Peripheral clocks thus serve as a surrogate marker of the circadian state in the brain. The development of an assay from a small number of blood draws would represent a major step forward, facilitating assessments of circadian timing in a range of conditions.
A promising approach for such an assay would be to use transcriptional profiling of PBMC to detect circadian rhythms by using variations in gene expression as an indicator of circadian state. Identifying molecules whose expression varies periodically with the circadian cycle has been the focus of multiple studies (24, 25), with a number of methods proposed for this problem (26–30). Recently, the periodic structure of cycling transcripts has been exploited to identify molecular rhythms from unordered expression measurements (31). In general, however, the inverse problem of attempting to infer circadian time from a set of transcriptomic markers has received little attention. From an analytical standpoint, this challenge is a machine-learning problem: that of predicting the value of a periodic variable (time of day) from variations in a high-dimensional feature space (gene expression). To be clinically useful, such a predictor should ideally have three major capabilities. First, it must yield highly accurate predictions in human subjects (not simply in model organisms under strictly controlled conditions) with enough precision that a clinically relevant shift in an individual’s circadian rhythm could be reliably inferred from the difference in the predicted and true time of day. Second, it must be able to yield these predictions using a minimal number of samples from the tested individual (so as to minimize the invasiveness of the test) with a parsimonious set of markers (i.e., tens rather than thousands of genes) both to ensure feasibility and to reduce noise. Third, the predictor must be insensitive to differences in sample processing or assay technologies [e.g., different microarray platforms, RNA-sequencing (RNA-seq), RT-PCR, etc.], including platforms that differ from the training data, to ensure its generalizability.
No method proposed for this purpose to date has achieved all of the above capabilities. The Molecular Timetable method (32), which uses the peak expression times of a complement of 50 genes to assess circadian time, is highly inaccurate when applied to human data (33, 34). BioClock (35), a related approach that uses deep neural networks to learn the time from a complement of cycling genes, has also only been successfully applied to well-controlled mouse data. The machine-learning–based ZeitZeiger method (33, 36) improves upon the accuracy in human data but cannot be applied to a new sample without retraining the entire machine, thus sacrificing reproducibility and interpretability (since in effect each new subject will have a different predictor). A more recent method using partial least squares regression (PLSR) (34) also exhibits improved accuracy but requires assaying a complement of 26,000 transcripts to standardize the 100 genes ultimately used in the PLSR model.
Most critically, none of the algorithms proposed to date has established that a predictor trained in one set of human samples can accurately generalize to a completely new dataset, which may exhibit different characteristics from the training data that cannot be accounted for when fitting the model. In all cases (32–34, 36), when separate datasets were used, they were first combined and co-normalized (and, in some cases, constrained to follow the same protocol and platform) before being separated into training and testing subsets. Because the validation data in these studies did not comprise independent external samples, the generalizability and reproducibility of these methods remains an open question.
Demonstrating the ability of the predictor to generalize to external datasets is crucial in two ways. First, it ensures that the predictor is not sensitive to systematic differences between the training data and the dataset used in the prediction. When the disparate datasets are combined before being redivided into training and testing subsets, it creates an artificial expectation that the testing data will statistically resemble the training data in a manner that is unrealistic in practice (where new patients would comprise a distinct batch). Second, it ensures that the predictor remains relevant even as new assay technologies are developed; a model that was devised using microarray data, for example, should remain accurate when applied to RNA-seq data if the underlying signal is biologically relevant. The need for an accurate and generalizable predictor that is able to overcome differences in clinical and experimental protocols motivates this work.
Results
Here we present “TimeSignature,” a machine-learning approach that yields precise predictions of time of day from human blood transcriptomic data. The TimeSignature algorithm, described in detail below, uses a unique within-subject normalization procedure that is well-suited to circadian profiling and reduces the variability between studies without requiring common experimental platforms, batch correction, or retraining the machine to account for cross-study variability. The resulting predictor comprises only genes, which can be assayed using any quantitation method. As we demonstrate below, the predictor maintains high accuracy when applied to completely separate validation datasets, including those using different microarray platforms and RNA-seq. The result is a time-prediction algorithm that is efficient, accurate, and generalizable.
To demonstrate TimeSignature’s capabilities, we applied our predictor to public data from a microarray study quantifying the human blood transcriptome over the circadian cycle (37) and then validated it using three independent datasets: two other public microarray studies (38, 39) as well as new data from 11 additional healthy subjects profiled by RNA-seq. In all of the public studies and our new data, we were able to predict the time of day at which the sample was collected with a median error rate of under 2 h in human subjects. We compare our results to those obtained using state-of-the-art methods (34, 36) demonstrating that TimeSignature significantly outperforms competing methods in efficiency, accuracy, and generalizability.
As we show below, a key feature of the TimeSignature predictor is its consistent accuracy across study protocols, patient conditions, and transcriptomics platforms. Once trained on microarray data from a single public circadian expression profiling study, the predictor can be applied with high accuracy to data from other studies using different microarray platforms or RNA-seq without renormalizing the data or retraining the machine. This capability is exceptional in the context of omics analyses, where the systematic variation of “batch effects” often overwhelms the signal of interest. The robust detection of the TimeSignature signal, even across distinct studies and platforms, supports the notion that the pattern of circadian gene expression being detected by the algorithm is strong and highly reproducible. The generalizability of the predictor is also an extremely useful feature from a practical standpoint, making TimeSignature a promising diagnostic tool.
The TimeSignature Method
The basic framework consists of a rescaling/normalization step, fitting the predictor using the training data, and applying it to predict time of day in new samples from disparate studies.
Within-Subject Renormalization.
To ensure that the predictor can be applied to high-throughput gene expression profiling data independently of the measurement platform used, it is necessary to ensure that the data are expressed on a consistent and unitless scale. To this end, the gene expression measurements are first transformed (as is customary for transcriptomic data), such that a unit increase in gene expression values within each study considered represents a doubling in mRNA abundance. We will denote the () expression of gene in sample as , where sample corresponds to a measurement from subject taken at time . Next, for each subject in each study, the mean expression level of each gene is computed across all assayed timepoints for that subject over the circadian cycle, and the data for each gene are centered about its diurnal mean on a per-subject basis:
| [1] |
where is an indicator function that ensures that the normalization is performed within, rather than across, subjects. The resulting renormalized value thus represents the fold-change deviation of gene at time from its mean over time in subject . Equivalently, is the log of the ratio of the raw mRNA measurement to its geometric mean; it is therefore a unitless quantity and hence independent of the original assay platform.
It should be noted that for Eq. 1 to be meaningful, each subject must have expression data for at least two timepoints and that these should be spaced in time such that the second term of Eq. 1 represents a valid summary of the average expression of gene over the course of a day. In practice (see Application to Human Data), two measurements per subject separated in time by 10 h are sufficient without compromising prediction accuracy. Because we envision that the typical use case will have the minimal number of draws per subject, in what follows we will only be using two samples per subject for the normalization when making predictions.
Fitting the Periodic Elastic Net Predictor.
Having transformed the training data as described above, a multivariate regression model with elastic net regularization (40) is fit to predict sinusoidal functions of the time of day as a function of the transformed gene expression data. Specifically, we perform a bivariate regression of the cartesian coordinates corresponding to the angle of the hour hand on a 24-h clock,
| [2] |
where denotes the time of day for observation , is the (observations) × (genes) matrix of predictors after the transformation described in Eq. 1, and follows a bivariate normal distribution. (Note here that denotes the number of observations, not the number of subjects; that is, if there are subjects each with a time-series comprising blood draws, the total number of observations is .)
In our application, the number of possible predictors (genes) far outstrips the number of observations; more importantly, we expect that the vast majority of assayed genes will not be strongly predictive of time. To reduce overfitting and obtain a parsimonious model, we use elastic net regularization (40) for feature selection. That is, rather than computing a least squares fit to Eq. 2, we solve the penalized problem
| [3] |
where is a -dimensional column vector containing the full gene expression profile for sample , is the 2-dimensional vector of cosine and sine time terms derived from (the time at which the sample was taken), and correspond to the entries in the row of the matrix (representing the coefficient for gene modeling the cosine and sine time terms, respectively), and denotes the Frobenius (Euclidean) norm—that is, the square root of the sum of the squares of the matrix elements.
In Eq. 3, the first term corresponds to the usual total least squares fit, while the second term assigns a penalty, tuned by , that depends upon the norms of the regression coefficients. As shown in ref. 40, when , the penalty terms shrink the coefficients toward 0, ultimately removing predictors from the model if the improvement to the least squares fit produced by keeping them does not adequately compensate the penalty. The parameter governs the stiffness of the penalty and hence the degree of shrinkage; larger values of will produce more parsimonious models. In practice, both and (which governs the trade-off between the Frobenius and group norm penalty) are tuned by cross-validation, as described in ref. 40.
It can be seen from the second () penalty term in Eq. 3 that a group lasso penalty is applied to each pair of coefficients , implying that the gene’s influence on both the cosine and sine time terms are considered simultaneously. This has the appealing property of yielding sparsity in the overall model while limiting sparsity within the group; when , the group lasso penalty implies that a given gene will have nonzero s for either both the cosine and sine time functions or neither (41). This use of elastic net yields a more accurate predictor using fewer genes compared with other methods.
Predicting Time of Day and Assessing Accuracy.
Once the coefficients are fit, predictions for the time of day may be estimated from the above model using the four-quadrant inverse tangent as
| [4] |
where the modulo is used to ensure that the conversion from angle to time ranges on . We can then compare this to the true time of day for sample to assess the prediction accuracy. Crucially, however, we are only interested in the hours by which the prediction is off, modulo whole days. We thus compute
| [5] |
to assess the prediction error for a sample , where the function ensures that a 23-h difference is treated as a 1-h difference. This may be thought of as the angular error, in hours, of the predicted time of day.
It bears observing that the values predicted by Eq. 2 are not guaranteed to lie on the unit circle (where the true response data lie) and that in fitting Eq. 3 we seek to minimize the square of the total error. This is given in Cartesian coordinates as the first term of Eq. 3, and it is easy to see (by a simple coordinate transformation) that this will also minimize the combined angular and radial errors as the Frobenius norm is invariant under orthogonal transformation. In assessing the accuracy via Eqs. 4 and 5, however, we concern ourselves solely with the angular component, disregarding the radial error. While it is theoretically possible that allowing the radial error to become arbitrarily large may permit better angular accuracy at the expense of the overall fit, we choose to fit Eqs. 2 and 3, minimizing the total error for mathematical convenience (enabling the use of standard multivariate regression tools) and as a soft constraint keeping the prediction close to the unit circle (since, in this setting, it is not clear how to interpret the meaning of a large radial error).
Application to Human Data
To demonstrate the accuracy of the TimeSignature algorithm, we apply it to data from four distinct transcription profiling studies of human blood. The first three of these datasets comprise publicly available microarray data from published studies (37–39). The final dataset comprises RNA-seq profiling data from 11 new subjects recruited by our team as described in Materials and Methods (detailed clinical and experimental protocols can be found in SI Appendix).
Data for all four studies were restricted to the genes assayed in common across the various studies, a total of 7,768 genes. Recognizing that in most applications only two samples, rather than a full circadian time course, would be available to calculate the within-subject normalization (Eq. 1), we mimicked the two-timepoint case by selecting the timepoint of interest and a single other sample 12 h away to compute the means in Eq. 1 for the prediction tests. The TimeSignature method was applied as described above. By way of comparison, both ZeitZeiger (33, 36) and the PLSR method (34) were applied using the same datasets following the protocols described in the respective papers. We also explored how the spacing of the samples affects the TimeSignature results.
Training TimeSignature and Identifying Predictive Genes.
A random subset comprising half of the subjects from the Möller–Levet dataset were selected to train the TimeSignature predictor. Within this training set, 10-fold cross-validation was used to tune the penalty parameters and , yielding a parsimonious model that may then be applied to other data.
Of the 7,768 genes input, the model with the optimal choice of penalties comprises approximately 40 genes, achieving the desired feature selection. Because this fit is, to some degree, influenced by the random selection of training samples, we repeated this process several times to investigate the overlap of the chosen predictors. In 12 such runs, a set of 18 genes were chosen as predictors a majority of the time (Table 1). However, when we attempted to reduce the set of predictors to those genes alone, we observed greater out-of-bag and testing errors than we obtained from the 40-gene models, indicating that the additional genes account for a nonnegligible component of the time prediction. The variability in these “auxiliary predictors” is thought to be due to correlated expression among genes.
Table 1.
TimeSignature predictive genes
| Gene | Freq. | Gene | Freq. | Gene | Freq. |
| DDIT4 | 1.00 | GZMB | 0.58 | CAMKK1 | 0.17 |
| GHRL | 1.00 | CLEC10 A | 0.50 | DTYMK | 0.17 |
| PER1 | 1.00 | PDK1 | 0.50 | NPEPL1 | 0.08 |
| EPHX2 | 0.92 | GPCPD1 | 0.50 | MS4A3 | 0.08 |
| GNG2 | 0.83 | MUM1 | 0.33 | IL13RA1 | 0.08 |
| IL1B | 0.83 | STIP1 | 0.33 | ID3 | 0.08 |
| DHRS13 | 0.83 | CHSY1 | 0.25 | MEGF6 | 0.08 |
| NR1D1 | 0.75 | AK5 | 0.25 | TCN1 | 0.08 |
| ZNF438 | 0.75 | CYB561 | 0.25 | NSUN3 | 0.08 |
| NR1D2 | 0.75 | SLPI | 0.25 | POLH | 0.08 |
| CD38 | 0.75 | PARP2 | 0.25 | SYT11 | 0.08 |
| TIAM2 | 0.75 | PGPEP1 | 0.17 | SH2D1B | 0.08 |
| CD1C | 0.75 | C12orf75 | 0.17 | REM2 | 0.08 |
| LLGL2 | 0.58 | FKBP4 | 0.17 |
A set of 41 genes is sufficient for accurate TimeSignature prediction. As described in the text, the predictors may vary slightly depending on the training data; the frequency with which each gene was selected as a predictor across 12 repeated runs using different training samples is given. Eighteen are selected the majority of the time; the remaining “auxiliary” predictors vary from run to run. Genes are sorted in order of selection frequency.
Within-Study Accuracy.
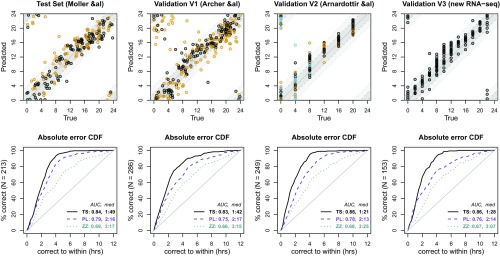
Having fit the model using the Möller–Levet training subset, we then applied the TimeSignature predictor to the remaining data (the Test Set) to obtain time of day predictions for each sample based on its renormalized gene expression data. (As mentioned previously, here only two samples per subject were used for the normalization step, Eq. 1.) A plot comparing predicted to true times for those samples is shown in the top row of the first column of Fig. 1. Below, a plot of the cumulative density of the absolute time error is shown; that is, for a given value on the axis, the axis indicates the proportion of samples with error (cf. Eq. 5). We observe a median error under 2 h in each dataset, with a median absolute error across all datasets of 1:37.
Fig. 1.
Accuracy of TimeSignature predictor applied to data from four distinct studies. Each column corresponds to the indicated dataset. The TimeSignature predictor was trained on a subset of subjects from the Möller–Levet study (37) and then applied to the remaining subjects (Test Set) along with three independent datasets: V1 (38), V2 (39), and V3. For each sample being predicted, two-point within-subject normalization was performed using that sample and a single other sample from the same subject 12 h away. In the top row, the predicted time of day vs. true time of day for each sample is shown. Dark and light gray bands indicate an error range of 2 and 4 about the true time. For the first three studies, color of the point indicates experimental condition: in the Test Set, control (black) vs. sleep restriction (orange); in V1, control (black) vs. forced desynchrony (orange); in V2, control days (black), sleep deprived day (orange), and recovery day (blue). In V3, all subjects () were in the control constant-routine condition (black). In the bottom row, we plot the fraction of correctly predicted samples for each study vs. the size of the error for the TimeSignature predictor (solid black), PLSR-based model (dashed purple), and ZeitZeiger (dotted cyan). Normalized area under the curves (nAUCs) (see Materials and Methods) and median absolute errors are listed for each. The TimeSignature median absolute error across all samples in all studies was 1:37.
In addition, we also compute the area under the error cumulative distribution function (CDF) curves in the Lower row. For completely random predictions, we expect that the error CDF should be a straight diagonal line, from 0% with error 0 at the lower left to 100% with error 12 h at upper right. (Recall that, per Eq. 5, 12 h is the maximum possible error.) To aid interpretability, we normalize the axes such that they range , forming a unit square, and compute the area under the normalized curve (nAUC). Under the null, where predictions are no better than chance, the error CDF would have nAUC 0.5; a perfect predictor would have nAUC 1. In the Test dataset, we obtain nAUC = 0.84, substantially better than chance.
Validation: Cross-Study and Cross-Platform Accuracy.
Ultimately, the utility of a predictor depends on how well it performs when applied to data collected in other settings, where the experimental protocols, sample preparation, and possibly even the expression profiling platform may differ from the data used in training. To validate the performance of our trained predictor, we applied it to data from three other independent studies: V1 (microarray data from ref. 38), V2 (microarray data from ref. 39), and V3 (new RNA-seq data).
Notably, not only were the experimental conditions (i.e., sleep protocols) different among the various studies (see refs. 37–39 and SI Appendix), the gene expression profiling platforms also differed: V1 used the same custom Agilent microarray platform used in the training data (38), while V2 used a different Rosetta/Merck Human RSTA Custom Affymetrix 2.0 microarray (39) and the new V3 samples were profiled by RNA-seq rather than microarray. As discussed previously, no between-study normalization or batch correction of any sort was performed; after the standard preprocessing of each dataset, TimeSignature was applied following Eqs. 1, 2, 4, and 5 without any additional manipulation of the data. In other words, at no point was the new data “recalibrated” with reference to the training data. The previously trained predictor was applied directly to each of these new datasets, without any retraining of the machine.
The results of these validation analyses are shown in the last three columns of Fig. 1. While it may be expected that systematic differences between the studies would result in diminished accuracy, we note that the performance in the validation sets are comparable to that of the Test Set, with median absolute errors ranging from 1:21 to 1:42. While V1 exhibited slightly greater errors, this was not statistically significant; indeed, none of the error distributions of the validation sets differed significantly from that of the within-study Test Set ( for V1, V2, and V3, respectively; Wilcoxon rank-sum test), nor was there any systematic variation in error across the four datasets (, Kruskal–Wallis). Likewise, the nAUCs obtained in those independent datasets were close to that of the Test Set, ranging from 0.83 to 0.86. We thus conclude that the accuracy of our predictor is stable across studies and transcription profiling platforms.
TimeSignature Is Accurate Across Sleep Protocols.
Each of the datasets used for testing TimeSignature used different sleep protocols for the subjects (see SI Appendix, Table S1). Additionally, the three public datasets to which we applied TimeSignature each came from studies investigating the transcriptional response to sleep-disrupting interventions: sleep restriction in the Test Set (37), forced desynchrony (FD) in V1 (38), and sleep deprivation in V2 (39). This large variety of distinct sleep protocols provides a natural means to examine how the accuracy of TimeSignature is affected by external conditions.
We find that TimeSignature remains accurate across all studies despite the differing protocols, including disruptive conditions such as sleep deprivation and FD. The results shown in the first three top panels of Fig. 1 are colored by the intervention status, with black corresponding to control and other colors indicating a disrupted condition. While the error is slightly greater in the disrupted conditions than in the controls within each study, the results are generally quite similar. The largest difference in accuracy was observed in the FD protocol used in study V1 (38) (median absolute error 2:05 for FD vs. 1:26 for controls), with the predicted times in the FD subjects lagging the true times by 2 h on average. These observations are consistent with what we would expect from a free-running clock in the FD condition; the subjects’ internal clocks, on which our predictions are based, will not align with the true time of day but will be systematically shifted in one direction due to the shifting sleep schedule. Nevertheless, we note that even in this extreme condition, the TimeSignature predictor maintains relatively high accuracy, suggesting that it is driven by biological rhythms rather than experimental conditions.
Optimal Sampling Interval.
A key step in the application of TimeSignature to make predictions is the within-subject renormalization described above, in which the expression level of each gene is expressed as a fold change from its mean over time in each subject (Eq. 1). As a result, every individual for whom we wish to make a prediction must have data from at least two blood draws so that the average can be computed.
All datasets used in our demonstration came from studies in which blood was collected every 2–4 h over a period of one or more days, resulting in a fairly large number of samples per subject (ranging from a low of 7 in dataset V1 to a high of 18 in dataset V2). From a practical standpoint, however, a high sampling resolution would be unfeasibly costly and burdensome to the patient. A more realistic application would involve the minimal number of blood draws (two) at different hours of the day, ideally far enough in time that their average represents the mean over the circadian cycle. As such, we have performed the predictions shown in Fig. 1 using two near-antipodal timepoints for the calibration rather than the full time course. In the majority of samples, the ideal spacing of 12 h could be achieved, with a handful (14 samples) having a pair only 8–10 h apart. This raises the question of how sensitive the accuracy is to the spacing of the two samples.
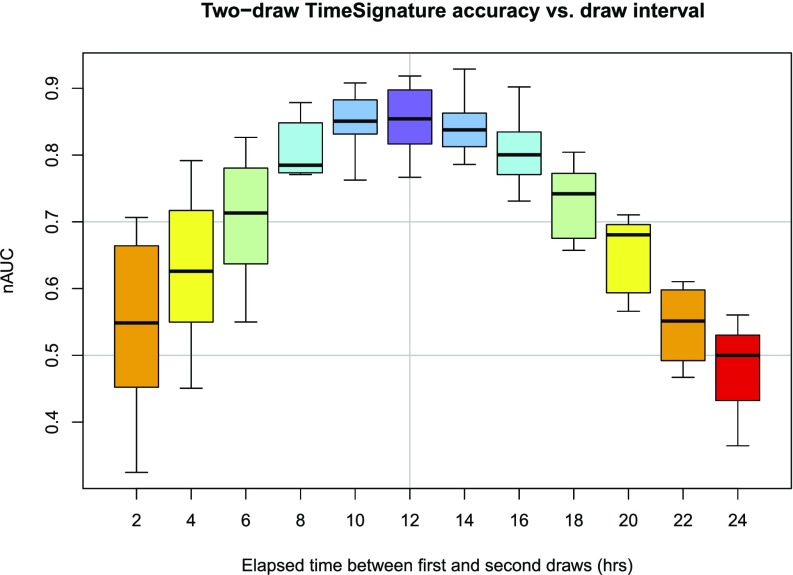
Using data from validation study V3, we explored how the spacing of the two samples affects the prediction accuracy. This was accomplished by subsetting the V3 data to two timepoints in the study (e.g., 8 AM and 4 PM), recomputing the renormalized data via Eq. 1 for each subject, and applying the previously trained TimeSignature predictor to the subsetted data. A systematic sweep of all time-point pairs at all possible distances in the V3 data demonstrated that TimeSignature’s accuracy depends on the distance between the draws (Fig. 2). We observe a trend toward higher nAUC as the interval approaches 12 h, which then decreases as the interval moves back toward 24 h. This is consistent with our assumption that the average of the two samples should be representative of the mean expression over the course of the day: For oscillating genes with a 24-h period, the average of two antipodal samples should yield an unbiased estimate of the diurnal mean, whereas the average of closely spaced timepoints will be biased toward the expression at a particular time of day, leading to worse predictions. It can be seen from Fig. 2 that intervals of 10–14 h perform best and that even intervals as narrow as 8 or 16 h yield median nAUC values . We also observe that the distributions are narrow for those intervals, indicating that the accuracy does not depend on the beginning or ending time of the interval (this is also apparent in Fig. 1, which shows that the accuracy is independent of the time being predicted, given that the pairs are well-spaced; further examples may be found in SI Appendix). Finally, we observe that the distributions from the 10-, 12-, and 14-h intervals closely overlap, indicating that precisely antipodal samples are not required for high-accuracy predictions and that spacings of as few as 8 h or as great as 16 h often achieve near-optimal accuracy.
Fig. 2.
Distribution of TimeSignature accuracy in the two-draw application as a function of elapsed time between the first and second draw (V3 data). Horizontal lines are given to guide the eye at nAUC = 0.5 (chance) and nAUC = 0.7 (generally considered good). Boxes are colored according to the absolute time-difference modulo full days (e.g., a 20-h interval corresponds to a 4-h difference in time of day, and thus both the 4-h and 20-h boxes are shaded yellow). A vertical line at 12 h indicates the axis of this symmetry.
Comparison with Competing Methods.
We compared TimeSignature against other methods for inferring circadian time from gene expression (33, 34, 36). Importantly, this serves not only as a comparison for the performance of TimeSignature but also the first attempt to apply these methods to datasets completely distinct from those on which they were trained, testing their generalizability.
Molecular Timetable.
Ueda and colleagues originally proposed a “Molecular Timetable” method for assessing circadian time in the mouse liver using a complement of rhythmic genes that exhibited unique peak times (32). By assessing the transcript levels of these “time-indicating genes” at a single time of day, they found that they could accurately ( SD) determine the time of day that the liver was taken from the mouse based on the relative expression levels of the time-indicating genes. Performance in human data were not evaluated in the original publication, as the method predated human circadian datasets; however, subsequent application to human data in refs. 33 and 34 indicated that it is strongly outperformed by more recent methods. (Accordingly, we omit further comparisons to Molecular Timetable and instead focus on the superior ZeitZeiger and PLSR-based methods.)
ZeitZeiger.
Recently, Hughey et al. (36) proposed “ZeitZeiger,” a supervised machine-learning method to predict time of day from high-dimensional observations. This method models each feature as a periodic spline with constant variance, generates a new set of observations by discretizing the spline fit, applies sparse principal component (SPC) projection of the new features to obtain a reduced set of predictors, and then uses a maximum likelihood estimator to predict the time of day. Parameters for the algorithm (including the number of spline knots, the number of discretization points, the penalty for the SPC regularization, and the number of SPC components) are chosen based on heuristics or tuned using cross-validation.
The authors originally applied ZeitZeiger to data from a large set of transcription profiling studies comprising a variety of mouse tissues, demonstrating much higher accuracy using a smaller number of genes than was obtained using the Molecular Timetable approach (36). A follow-up work applied ZeitZeiger to human data from three published studies (33). Data from the three studies were first combined, renormalized with respect to one another, and then batch-corrected using ComBat (42) to remove any systematic differences in the study platforms; this yielded a combined dataset of 498 samples from 60 unique individuals. ZeitZeiger’s performance was then assessed using subject-wise cross-validation (i.e., keeping all samples from the same subject in the same fold), yielding a median absolute error of 2.1 h for the best choice of parameter values among the cross-validation sets.
In contrast to ZeitZeiger, TimeSignature does not impose a periodic model upon the predictors. More importantly, TimeSignature does not necessitate that data from different studies be batch-corrected, as ZeitZeiger does, avoiding several drawbacks associated with this approach. In particular, application of ZeitZeiger to new data (such as that of a new patient) requires renormalizing and batch-correcting the new data with the training data and then retraining the machine. This process is both computationally intensive and results in a different predictive model every time ZeitZeiger is applied to new data, meaning that the model that predicts time from gene expression is not universal or comparable between runs. As a result, it would be difficult to compare results for a patient over time to monitor disease progression or treatment response. Moreover, the use of cross-validation (CV) can underestimate the error in the multibatch case, since some subjects from each batch will be included in the training data for every CV fold; no assessment was made in ref. 33 of how it might perform in a validation dataset comprising a distinct batch that does not contribute in any way to the training data.
PLSR and Differential PLSR.
Finally, a method based on PLSR was also recently proposed for application in human data (34). Like ZeitZeiger, the PLSR-based method also takes a machine-learning approach to generate a parsimonious predictor from the full set of gene expression measurements. Unlike ZeitZeiger, however, the PLSR-based method does not impose a periodic spline model on the genes and thus has fewer parameters that need to be set by the user (two parameters, the number of PLS components and the number of genes used in the model, are selected by cross-validation). The authors also considered a “differential PLSR” method, in which gene expression differences from two draws 12 h apart were used as the predictors rather than the gene expression values themselves.
To demonstrate the performance of the PLSR approach, the authors applied it to the combined data from two published studies (also used in ref. 33 and in the present work). Because these two datasets used the same microarray platform, little renormalization and no batch-correction were needed. The combined data were then split into training and testing subsets comprising 329 and 349 samples, respectively, with balanced amounts of data from each study in the training and testing sets. Parameters were tuned using cross-validation in the training set, and accuracy was assessed in the held-out testing samples. Performance using the same training/testing subsets was then compared with that of the Molecular Timetable and ZeitZeiger. The PLSR-based method exhibited a median absolute error of 1.9 h compared with 2.8 h for ZeitZeiger and 2.6 h for the Molecular Timetable. Using the differential PLSR approach, the authors were able to improve performance to a median absolute error of 1.1 h using a PLSR model using a set of 100 genes.
However, the performance of this approach in a distinct validation dataset remained unclear. While ref. 34 avoided the issues associated with batch correction, the fact that the studies being combined used identical microarray platforms eliminated considerable technical variability. Confining the method to use a specific microarray platform greatly limits the practical utility of the predictor, especially with rapidly evolving high-throughput technologies; on the other hand, performance with other platforms is unknown. Moreover, because the predictor was trained on a balanced mixture of the two datasets, it is not possible to tell how it would perform in a truly separate dataset. As in ZeitZeiger (33), training and testing on mixtures of datasets makes it impossible to assess the method’s sensitivity to systematic technical variations that are likely to occur when the method is used in practice (e.g., differences between platforms, sample handling, and laboratory protocols).
It must also be noted that even though the final PLSR predictor uses a selected set of 100 genes, an initial algorithmic step of -scoring each sample across all genes requires assaying all genes on the original array to obtain the scores for the predictive markers. As a result, any application of the predictor also requires assaying genes (the vast majority of which will not be used) to properly calibrate the scores for the 100 predictors. This cumbersome requirement may also limit the method’s translatability to practical application. In contrast, TimeSignature can be readily applied simply by assaying the 41 identified markers.
TimeSignature Outperforms ZeitZeiger and PLSR in Multiple Independent Datasets.
To compare TimeSignature’s performance to existing methods and to assess their generalizability and cross-platform accuracy, we performed a head-to-head comparison of TimeSignature to both ZeitZeiger (33, 36) and the PLSR-based approach (34). (Because both have been amply demonstrated to outperform the Molecular Timetable method in both mouse and human data, we omitted comparisons to the Molecular Timetable in our study.) To ensure consistency all methods were trained using the same samples that had been used to train TimeSignature and applied to the same testing and validation samples (SI Appendix, Table S1).
For ZeitZeiger, we used R packages provided by the author in ref. 43. Following ZeitZeiger’s published instructions (43), we first combined and batch-corrected the preprocessed gene expression data from all four studies (SI Appendix, Table S1) using the MetaPredict library (44). (We note here that this step, which is not required by TimeSignature, requires that each batch have multiple samples—that is, a batch cannot comprise data from a single new patient.) We then applied the ZeitZeiger method using the published code (43). As with TimeSignature, we report the accuracy in the testing and validation sets using a ZeitZeiger predictor that had been trained on the Möller–Levet training subset.
For the PLSR-based approach, we followed the protocol used in ref. 34 using the authors’ published code (45). The initial -scoring step was applied across all genes (as in refs. 34 and 45)—in this case, the 7,768 genes in common across all four datasets. Using the same subset of the Möller–Levet data used to train TimeSignature and ZeitZeiger, we performed leave-one-out cross-validation to select the optimal number of PLSR components (5) and genes with the highest weights (100) and then refitted the PLSR model against the complete training data as the final predictor. The trained model was then applied to the remaining 900 samples from the four studies, enabling direct comparison of TimeSignature, Zeitzeiger, and PLSR.
The bottom row of panels in Fig. 1 illustrates the accuracy obtained in human data using ZeitZeiger and PLSR compared with TimeSignature. For ZeitZeiger, median absolute errors exceeded 3 h in all datasets, with nAUCs ranging from 0.65 to 0.68; while these were better than random chance, they were significantly lower than the nAUCs obtained with TimeSignature. Consistent with prior findings (34), PLSR outperforms ZeitZeiger, with median absolute errors of 2.25 h and nAUCs between 0.75 and 0.79. TimeSignature consistently and significantly outperforms both ZeitZeiger and PLSR in all validation datasets with median absolute errors under 2 h and nAUCs exceeding 0.80. Moreover, TimeSignature achieves this accuracy using fewer predictors (41 TimeSignature genes versus 100 for PLSR).
A comparison of the computational efficiency of the various approaches is given in SI Appendix. Briefly, TimeSignature is faster to train and to apply than both ZeitZeiger and the PLSR method.
Discussion
Methods to accurately assess the state of an organism’s internal clock are necessary to understanding the role of circadian rhythms in biological processes, diagnosing circadian disruption, and targeting chronotherapeutics. To be practically useful, such a method must be robust enough to withstand variability among individuals and clinics and should minimize the burden on the patient. TimeSignature achieves these goals by training a supervised machine-learning algorithm to “learn” the time of day as a function of gene expression in blood. Once trained, the model may be applied to new gene expression data to yield predictions that reflect the internal state of the subjects’ biological clock. In our tests, we demonstrated that TimeSignature provides time predictions to within 2 h in human data, achieving considerably higher accuracy than competing methods using the same data. The high accuracy is achieved using a minimal number of markers (a panel comprising 40 genes), opening a promising avenue for the development of a simple and affordable diagnostic test.
A powerful feature of TimeSignature is that the resulting predictor is generalizable across patient populations, clinical protocols, and assay platforms. Above, we demonstrated that the TimeSignature predictor could be trained on a subset of microarray data from one public study and yield accurate predictions not only in the test subset of that study but also in three independent datasets that differed from the training dataset in systematic and fundamental ways. Notably, this cross-study compatibility was achieved without recalibrating the datasets with respect to one another or explicitly modeling/correcting batch effects, as is required by other methods, and without any retraining of the machine. This means that data from a new subject can be input directly into the trained predictor without restrictions on the assay technology and without requiring any recalibration. This feature is highly unusual among machine-learning algorithms for gene expression data, where systemic variations often limit generalizability and either expect specific microrarray platforms (as in ref. 34) or require batch correction of the data (as in ref. 36). The TimeSignature algorithm avoids both constraints, yielding a predictor that is more reliable, interpretable, and practical than competing methods.
TimeSignature is able to avoid the problems of cross-study renormalization by relying instead on within-subject renormalization. By centering the data for each subject about the daily mean for that gene in that subject, we remove not only batch effects but individual differences in baseline gene expression as well; in effect, we are removing any constitutive differential expression such that our model considers only the time-varying part. Since we expect that any systematic contribution to the gene expression will affect all timepoints equally, the fold changes from the mean should be independent of batch, platform, or any other external factors. Moreover, because this scheme removes not only batch effects but also any baseline subject-to-subject variation, we remove a source of noise in the prediction. We believe that this step is key to the exceptional accuracies yielded by TimeSignature.
We note that this scheme is effective because the signal relevant to inferring circadian time is the fluctuation about the mean of oscillating genes. In other contexts where the mean gene expression is the signal of interest (as is the case in most studies of differential gene expression), the within-subject renormalization presented here would remove the variable of interest. As such, the within-subject renormalization use by TimeSignature is designed for, and uniquely suited to, modeling cyclic behaviors such as circadian rhythms.
TimeSignature’s within-subject normalization is readily applied to new data, without manipulating the other data (including the training set) or the trained predictor in any way. While TimeSignature requires at least two samples (blood draws) from a given subject so that the diurnal mean can be estimated, the clinical burden of this requirement is mitigated by the fact that the draws may be flexibly scheduled; while spacing the samples 12 h apart is ideal, a spacing of 10, or even 8, yields highly accurate results. Moreover, the fact that TimeSignature is accurate independent of the sleep protocol and the time of day when the samples are taken permits great flexibility in scheduling patients for the two draws.
We also note that approaches that rely on cross-normalization (such as ZeitZeiger or the Molecular Timetable method) can only be applied to predict time of day from a single blood draw only when that sample was already part of the original dataset, since cross-normalization with the training data requires that there be at least two samples (and ideally many more) in the “batch” comprising the data from the new patient. As such, these approaches are likewise unable to overcome the need for multiple samples. Moreover, because batch correction ascribes any systematic differences between batches to a batch error, relevant biological differences will be lost. If a new batch of circadian data comes from only a limited range of phases (e.g., samples obtained at standard lab collection times), batch correction to a training set that spanned all circadian phases is likely to remove the circadian signal of interest. This is a significant limitation for methods that rely on batch correction.
In contrast, while the PLSR-based method is able to make single-draw predictions without batch correction, it achieves this by using genome-wide -scoring to calibrate the predictors, requiring thousands more genes to be assayed than are used in the model, and likewise exhibits improved performance when two samples with a 12-h separation are provided.* Additionally, the choice of elastic net over PLSR for feature selection in TimeSignature also likely contributes to its accuracy. It has been shown that PLSR tends to shrink the low-variance predictors but can also inflate the high-variance predictors, making it unstable and yielding a higher prediction error than penalized regression (46–48). In high dimensions, when the number of predictors is much greater than the sample size, elastic net has been shown to yield more accurate results than PLSR (48–50). TimeSignature’s ability to achieve high accuracy using only two samples from an individual with great flexibility in timing (8–12 h apart) using a complement of only 40 genes is a significant advance.
We suggest that it is this unique combination of two-sample normalization and the application of elastic net that enables TimeSignature to achieve its performance, as described above. Still, it may be of interest to investigate “hybrid” variations of TimeSignature and the other methods, which may further improve on TimeSignature performance or address its constraints (e.g., by eventually enabling the elastic net implementation to be applied to single samples).
Finally, we note that while we have successfully demonstrated TimeSignature’s ability to generalize across platforms and environmental conditions (such as sleep deprivation) when applied to healthy adults, to date no method (including ours) has been tested across a broad range of conditions and diseases, in particular those that are associated with circadian dysregulation. Additionally, while the predictor is robust to the short-term sleep disruption conditions probed in the various studies (37–39), it is not known how it will behave when such conditions are chronic. Both of these constitute an important avenue for future research. We also note that the predictor was designed using gene expression profiles in whole blood and so may require retraining to be applied in other tissues.
In total, TimeSignature represents a powerful new approach for assessing the internal state of the circadian clock, yielding high accuracies (within 2 h) even in “noisy” human data. Our results demonstrate that TimeSignature significantly outperforms competing approaches. The generalizability of the TimeSignature predictor is both exceptional and useful, enabling it to be applied in clinical settings without extensive recalibration or restrictions on experimental protocols. It requires only two blood samples from a subject, suitably but flexibly spaced in time, to achieve these results, making it much more feasible than 24-h serial sampling currently used in clinical settings. These results demonstrate TimeSignature’s clinical utility as a tool for the expression-based diagnosis of sleep disorders and targeted chronotherapies.
Materials and Methods
Public Data Sources.
We analyzed data from three independent studies comprising transcription profiling time courses in human blood. Data were obtained from the NCBI Gene Expression Omnibus (GEO) repository (51) and imported into R using GEO-query (52) under the following accession numbers: GSE39445 (37), GSE48113 (38), and GSE56931 (39). Details of the datasets may be found in SI Appendix, Table S1. Microarray preprocessing had been previously performed by the original authors (37–39) and was left unchanged for the purpose of the present study. The reference time was the clock time each sample was taken, as melatonin data are not universally available.
RNA-Seq Data.
Data from 11 new subjects comprise the final dataset, V3. Recruitment and inclusion/exclusion criteria are described in SI Appendix. Whole blood was collected every 2 h over a 28-h period (15 timepoints total) from each subject, yielding a total of 165 samples. Whole blood transcriptional profiling was carried out using RNA sequencing (see SI Appendix for details). Samples that did not meet the RNA quality thresholds were excluded from further analyses. RNA-seq data for the remaining 153 samples were processed as described in SI Appendix. For consistency with the other datasets, the reference time was the clock time each sample was taken.
Data Preparation.
Data were expressed on a scale appropriate to the platform ( normalized intensity for microarray data, for RNA-seq). Only data for genes in common to all four datasets (cf. SI Appendix, Table S1) were retained for analysis, resulting in a feature space of 7,768 genes. For TimeSignature, and TimeSignature only, the data were renormalized using two timepoints per subject: for a given sample taken at time , another selected as close to h as possible for that subject, and Eq. 1 would be applied to normalize those samples with respect to their mean.
TimeSignature Training and Feature Selection.
A random subset of 24 time courses from the GSE39445 dataset (37) was used to train the TimeSignature machine following Eq. 3. The selected time courses came from both the sleep restriction and the sleep extension (control) arms of the original study (37). Within this 24-time course training set, 10-fold CV was used to tune and , selecting values that best minimized the out-of-bag residuals. To obtain the “core” TimeSignature genes, we repeated this process 12 times using different subsets of GSE39445 for the training data. In all cases, the optimal models retained 40 genes, of which 18 appeared in at least 6 runs. Prediction accuracy was independent of the identity of the remaining auxiliary predictors, and thus, a single representative run was chosen as the trained TimeSignature model.
Timestamp Testing and Validation.
The trained model was then applied to the remaining 24 time courses from GSE39445 (37) that had not been chosen to form the training set, providing a truly independent test of the model accuracy. In addition, it was also applied to three independent validation datasets: GSE48113 (38), GSE56931 (39), and the new RNA-seq data. For each sample, a single other sample 12 h from the same subject was selected, and we applied Eq. 1 to those two samples to mimic the normalization when only two timepoints are available. We then applied the predictor to each of the samples following the 2-point within-subject normalization.
Application of ZeitZeiger.
Application of ZeitZeiger (36) followed the protocol described in the ZeitZeiger package vignette (43). The same 24 time courses used for the TimeSignature training were used to train ZeitZeiger, using the original normalized intensity data. We then applied it to data from each of the four studies separately. In each case, the original data for the test/validation set were combined with the training data and batch-corrected with ComBat (42) via the MetaPredict (44) R package, as dictated by the ZeitZeiger protocol. ZeitZeiger was then retrained and applied to the new data.
Application of PLSR.
Application of the PLSR method (34) followed the protocol implemented in code provided by the authors in ref. 45. Expression values were mean centered and normalized to unit variance across all 7,768 genes within each sample. Leave-one-out cross-validation was used to select the optimal number of PLSR components and high-weighted genes in the training data; these values were then used to train the PLSR model using all training samples, and the resulting model was applied to the test and validation data.
Statistical Analyses.
Nonparametric Wilcoxon and Kruskal–Wallis tests were used to compare distributions of errors between studies and between conditions. Empirical CDFs were computed for the error distributions, after dividing them by 12 to normalize them onto the range . The AUC was reported as the nAUC, where nAUC = 0.5 for a predictor that is no better than chance and nAUC = 1 for a perfect predictor. To compute statistical significance of the nAUCs, a bootstrap was used. For each study, we randomly generated time of day predictions by sampling from a uniform distribution on and computed the corresponding nAUC. This process was repeated times to obtain a reference distribution to which the true nAUCs were compared. In all cases (Timestamp, ZeitZeiger, and PLSR), the true nAUCs were strongly significant with , indicating that all methods perform better than chance. All statistical analyses were carried out in R (53).
Availability of Methods and Data.
R scripts to carry out the TimeSignature analysis are available from github.com/braunr/TimeSignatR. New RNA-seq data are publicly available from GEO under accession number GSE113883, https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE113883.
Supplementary Material
Acknowledgments
R.B. and M.I. were supported by Complex Systems Scholar Award 220020394 from the James S. McDonnell Foundation. All authors were supported by Defense Advanced Research Projects Agency (DARPA) Grant D15AP00027. Additional funding was provided by the Northwestern Center for Circadian and Sleep Medicine. This effort was in part sponsored by DARPA; the content of the information does not necessarily reflect the position or the policy of the government, and no official endorsement should be inferred.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: Raw and processed RNA-sequencing data used in this article are available from Gene Expression Omnibus (GEO), https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE113883 (accession no. GSE113883). R scripts to carry out the TimeSignature analysis (TimeSignature code) are available from github.com/braunr/TimeSignatR.
*It should be noted that the two-sample differential PLSR method (34) uses the known time separation in making the prediction, those yielding predictions that are necessarily 12 h apart, while TimeSignature makes the predictions independently (and is thus not directly comparable to the differential PLSR method). This constraint may make the differential PLSR method undesirable in cases where one wishes to detect asymmetries in the circadian rhythm.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1800314115/-/DCSupplemental.
References
- 1.Ko CH, Takahashi JS. Molecular components of the mammalian circadian clock. Hum Mol Genet. 2006;15:R271–R277. doi: 10.1093/hmg/ddl207. [DOI] [PubMed] [Google Scholar]
- 2.Boivin DB, et al. Circadian clock genes oscillate in human peripheral blood mononuclear cells. Blood. 2003;102:4143–4145. doi: 10.1182/blood-2003-03-0779. [DOI] [PubMed] [Google Scholar]
- 3.Zhang R, Lahens NF, Ballance HI, Hughes ME, Hogenesch JB. A circadian gene expression atlas in mammals: Implications for biology and medicine. Proc Natl Acad Sci USA. 2014;111:16219–16224. doi: 10.1073/pnas.1408886111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Eastman C, Gazda C, Burgess H, Crowley S, Fogg L. Advancing circadian rhythms before eastward flight: A strategy to prevent or reduce jet lag. Sleep. 2005;28:33–44. doi: 10.1093/sleep/28.1.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Barion A, Zee PC. A clinical approach to circadian rhythm sleep disorders. Sleep Med. 2007;8:566–577. doi: 10.1016/j.sleep.2006.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shields M. Shift work and health. Health Rep. 2002;13:11–33. [PubMed] [Google Scholar]
- 7.Roenneberg T, et al. Epidemiology of the human circadian clock. Sleep Med Rev. 2007;11:429–438. doi: 10.1016/j.smrv.2007.07.005. [DOI] [PubMed] [Google Scholar]
- 8.Puttonen S, Harma M, Hublin C. Shift work and cardiovascular disease - Pathways from circadian stress to morbidity. Scand J Work Environ Health. 2010;36:96–108. doi: 10.5271/sjweh.2894. [DOI] [PubMed] [Google Scholar]
- 9.Lemmer B. Clinical chronopharmacology of the cardiovascular system: Hypertension and coronary heart disease. Clin Ter. 2006;157:41–52. [PubMed] [Google Scholar]
- 10.Roenneberg T, Wirz-Justice A, Merrow M. Life between clocks: Daily temporal patterns of human chronotypes. J Biol Rhythms. 2003;18:80–90. doi: 10.1177/0748730402239679. [DOI] [PubMed] [Google Scholar]
- 11.Jones CR, et al. Familial advanced sleep-phase syndrome: A short-period circadian rhythm variant in humans. Nat Med. 1999;5:1062–1065. doi: 10.1038/12502. [DOI] [PubMed] [Google Scholar]
- 12.Chang AM, Reid KJ, Gourineni R, Zee PC. Sleep timing and circadian phase in delayed sleep phase syndrome. J Biol Rhythms. 2009;24:313–321. doi: 10.1177/0748730409339611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Toh KL, et al. An hPer2 phosphorylation site mutation in familial advanced sleep phase syndrome. Science. 2001;291:1040–1043. doi: 10.1126/science.1057499. [DOI] [PubMed] [Google Scholar]
- 14.Xu Y, et al. Functional consequences of a CKI mutation causing familial advanced sleep phase syndrome. Nature. 2005;434:640–644. doi: 10.1038/nature03453. [DOI] [PubMed] [Google Scholar]
- 15.Doherty CJ, Kay SA. Circadian control of global gene expression patterns. Annu Rev Genet. 2010;44:419–444. doi: 10.1146/annurev-genet-102209-163432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Patke A, et al. Mutation of the human circadian clock gene CRY1 in familial delayed sleep phase disorder. Cell. 2017;169:203–215. doi: 10.1016/j.cell.2017.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Levi F, Schibler U. Circadian rhythms: Mechanisms and therapeutic implications. Annu Rev Pharmacol Toxicol. 2007;47:593–628. doi: 10.1146/annurev.pharmtox.47.120505.105208. [DOI] [PubMed] [Google Scholar]
- 18.Videnovic A, et al. Circadian melatonin rhythm and excessive daytime sleepiness in Parkinson disease. JAMA Neurol. 2014;7:463–469. doi: 10.1001/jamaneurol.2013.6239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Su AI, et al. A gene atlas of the mouse and human protein-encoding transcriptomes. Proc Natl Acad Sci USA. 2004;101:6062–6067. doi: 10.1073/pnas.0400782101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kathale ND, Liu AC. Prevalence of cycling genes and drug targets calls for prospective chronotherapeutics. Proc Natl Acad Sci USA. 2014;111:15869–15870. doi: 10.1073/pnas.1418570111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Benloucif S, et al. Stability of melatonin and temperature as circadian phase markers and their relation to sleep times in humans. J Biol Rhythms. 2005;20:178–188. doi: 10.1177/0748730404273983. [DOI] [PubMed] [Google Scholar]
- 22.Stratmann M, Schibler U. Properties, entrainment, and physiological functions of mammalian peripheral oscillators. J Biol Rhythms. 2006;2:494–506. doi: 10.1177/0748730406293889. [DOI] [PubMed] [Google Scholar]
- 23.Archer SN, Viola AU, Kyriakopoulou V, von Schantz M, Dijk DJ. Inter-individual differences in habitual sleep timing and entrained phase of endogenous circadian rhythms of BMAL1, PER2 and PER3 mRNA in human leukocytes. Sleep. 2008;31:608–617. doi: 10.1093/sleep/31.5.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Patel VR, Eckel-Mahan K, Sassone-Corsi P, Baldi P. CircadiOmics: Integrating circadian genomics, transcriptomics, proteomics and metabolomics. Nat Meth. 2012;9:772–773. doi: 10.1038/nmeth.2111. [DOI] [PubMed] [Google Scholar]
- 25.Patel VR, et al. The pervasiveness and plasticity of circadian oscillations: The coupled circadian-oscillators framework. Bioinformatics. 2015;31:3181–3188. doi: 10.1093/bioinformatics/btv353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ruf T. The Lomb-Scargle periodogram in biological rhythm research: Analysis of incomplete and unequally spaced time-series. Biol Rhythm Res. 1999;30:178–201. [Google Scholar]
- 27.Hughes ME, Hogenesch JB, Kornacker K. JTK_CYCLE: An efficient nonparametric algorithm for detecting rhythmic components in genome-scale data sets. J Biol Rhythms. 2010;25:372–380. doi: 10.1177/0748730410379711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hutchison AL, et al. Improved statistical methods enable greater sensitivity in rhythm detection for genome-wide data. PLoS Comput Biol. 2015;11:e1004094. doi: 10.1371/journal.pcbi.1004094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Thaben PF, Westermark PO. Detecting rhythms in time series with RAIN. J Biol Rhythms. 2014;29:391–400. doi: 10.1177/0748730414553029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Perea JA, Deckard A, Haase SB, Harer J. Sw1PerS: Sliding windows and 1-persistence scoring; discovering periodicity in gene expression time series data. BMC Bioinform. 2015;1:257. doi: 10.1186/s12859-015-0645-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Anafi RC, Francey LJ, Hogenesch JB, Kim J. CYCLOPS reveals human transcriptional rhythms in health and disease. Proc Natl Acad Sci USA. 2017;114:5312–5317. doi: 10.1073/pnas.1619320114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ueda HR, et al. Molecular-timetable methods for detection of body time and rhythm disorders from single-time-point genome-wide expression profiles. Proc Natl Acad Sci USA. 2004;101:11227–11232. doi: 10.1073/pnas.0401882101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hughey JJ. Machine learning identifies a compact gene set for monitoring the circadian clock in human blood. Genome Med. 2017;9:19. doi: 10.1186/s13073-017-0406-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Laing EE, et al. Blood transcriptome based biomarkers for human circadian phase. eLife. 2017;6:e20214. doi: 10.7554/eLife.20214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Agostinelli F, Ceglia N, Shahbaba B, Sassone-Corsi P, Baldi P. What time is it? Deep learning approaches for circadian rhythms. Bioinformatics. 2016;32:i8–i17. doi: 10.1093/bioinformatics/btw243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hughey JJ, Hastie T, Butte AJ. ZeitZeiger: Supervised learning for high-dimensional data from an oscillatory system. Nucleic Acids Res. 2016;44:e80. doi: 10.1093/nar/gkw030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Moller-Levet CS, et al. Effects of insufficient sleep on circadian rhythmicity and expression amplitude of the human blood transcriptome. Proc Natl Acad Sci USA. 2013;110:E1132–E1141. doi: 10.1073/pnas.1217154110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Archer SN, et al. Mistimed sleep disrupts circadian regulation of the human transcriptome. Proc Natl Acad Sci USA. 2014;111:E682–E691. doi: 10.1073/pnas.1316335111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Arnardottir ES, et al. Blood-gene expression reveals reduced circadian rhythmicity in individuals resistant to sleep deprivation. Sleep. 2014;37:1589–1600. doi: 10.5665/sleep.4064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Ser B Stat. Meth. 2005;67:301–320. [Google Scholar]
- 41.Friedman J, Hastie T, Tibshirani R. 2010. A note on the group lasso and a sparse group lasso. arXiv:1001.0736. Preprint, posted January 5, 2010.
- 42.Johnson WE, Li C, Rabinovic A. Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics. 2007;8:118–127. doi: 10.1093/biostatistics/kxj037. [DOI] [PubMed] [Google Scholar]
- 43.Hughey JJ. 2016 ZeitZeiger package vignette, v.0.0.0.9021. Available at https://github.com/jakejh/zeitzeiger. Accessed August 9, 2016.
- 44.Hughey JJ. 2016 MetaPredict package vignette. v.0.0.0.9005. Available at https://github.com/jakejh/metapredict. Accessed August 9, 2016.
- 45.Laing EE, et al. 2017 Source code and data for “Blood transcriptome based biomarkers for human circadian phase.” Sleep Research @ University of Surrey. sleep-sysbio.fhms.surrey.ac.uk/PLSR_16/
- 46.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. 2nd Ed Springer Series in Statistics; New York: 2013. [Google Scholar]
- 47.Frank LE, Friedman JH. A statistical view of some chemometrics regression tools. Technometrics. 1993;35:109–135. [Google Scholar]
- 48.Chun H, Keleş S. Sparse partial least squares regression for simultaneous dimension reduction and variable selection. J R Stat Soc Ser B Stat Meth. 2010;72:3–25. doi: 10.1111/j.1467-9868.2009.00723.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Acharjee A, Finkers R, Visser RG, Maliepaard C. Comparison of regularized regression methods for omics data. Metabolomics. 2013;3:126. [Google Scholar]
- 50.Liu W, Li Q. An efficient elastic net with regression coefficients method for variable selection of spectrum data. PLoS One. 2017;12:e0171122. doi: 10.1371/journal.pone.0171122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wheeler D, et al. Database resources of the National Center for Biotechnology Information. Nucleic Acids Res. 2007;35:D5–12. doi: 10.1093/nar/gkl1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Davis S, Meltzer P. GEOquery: A bridge between the gene expression Omnibus (GEO) and BioConductor. Bioinformatics. 2007;14:1846–1847. doi: 10.1093/bioinformatics/btm254. [DOI] [PubMed] [Google Scholar]
- 53.R Core Team 2015. R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.