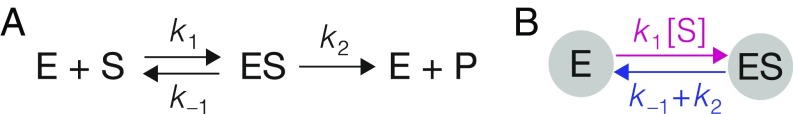Structural conditions on complex networks for the Michaelis–Menten input–output response

Significance

The Michaelis–Menten (MM) formula arose to explain simple enzyme behavior. It has since been found to describe input–output responses in several other biological contexts. Its ubiquity has been surprising and poorly understood. Here, we use the graph-based “linear framework” to show how the MM formula arises whenever appropriate structural conditions are satisfied, both at thermodynamic equilibrium and when energy is being dissipated. These conditions are based on separating the graph into two parts and constraining how and where the input variable appears. The conditions do not depend on parameter values and allow many of the details to be arbitrary. This explains the ubiquity of the MM formula and substantially generalizes previous results.

Abstract

The Michaelis–Menten (MM) fundamental formula describes how the rate of enzyme catalysis depends on substrate concentration. The familiar hyperbolic relationship was derived by timescale separation for a network of three reactions. The same formula has subsequently been found to describe steady-state input–output responses in many biological contexts, including single-molecule enzyme kinetics, gene regulation, transcription, translation, and force generation. Previous attempts to explain its ubiquity have been limited to networks with regular structure or simplifying parametric assumptions. Here, we exploit the graph-based linear framework for timescale separation to derive general structural conditions under which the MM formula arises. The conditions require a partition of the graph into two parts, akin to a “coarse graining” into the original MM graph, and constraints on where and how the input variable occurs. Other features of the graph, including the numerical values of parameters, can remain arbitrary, thereby explaining the formula’s ubiquity. For systems at thermodynamic equilibrium, we derive a necessary and sufficient condition. For systems away from thermodynamic equilibrium, especially those with irreversible reactions, distinct structural conditions arise and a general characterization remains open. Nevertheless, our results accommodate, in much greater generality, all examples known to us in the literature.

The Michaelis–Menten (MM) formula may be expressed as

$$f\left(x\right)=\frac{Ax}{B+x},$$ [1]

where $x$ is the input, $f\left(x\right)$ is the steady-state output, and $A,B$ are constants (i.e., they are independent of $x$) which are positive and depend on the system under study. Leonor Michaelis and Maud Menten introduced Eq. 1 in their foundational work on enzyme kinetics (1, 2). They derived the formula for a network of three reactions (Fig. 1A) in which an enzyme, $E$, catalyzes the conversion of substrate, $S$, to product, $P$. Their derivation relied on assuming a timescale separation in which the intermediate enzyme–substrate complex, $ES$, is a “fast” component, which reaches steady state rapidly in comparison with the “slow” components, $S$ and $P$. Irving Langmuir independently derived the same formula to describe adsorption onto a planar surface (3) and the right-hand side of Eq. 1 is sometimes referred to as the “Langmuir isotherm.”

Fig. 1.

MM network and graph. (A) Enzyme $E$ catalyzes formation of product $P$ from substrate $S$ through the intermediate enzyme–substrate complex $ES$, with the indicated rate constants for mass-action kinetics. (B) Corresponding linear framework graph. The vertices are the fast components in the timescale separation, $E$ and $ES$, with the slow component, $S$, appearing in the edge label. The colors refer to Fig. 2.

It has been appreciated gradually that Eq. 1 holds in far greater generality than the simple contexts considered by Michaelis and Menten and Langmuir. Table 1 summarizes the broad range of contexts known to us in which Eq. 1 has been found. These examples suggest a ubiquity in the MM formula, which transcends the variety of contexts, molecular components, and mechanisms under which it arises. It is this ubiquity which the present paper seeks to explain. Similar ubiquity has been explored for the empirical observation of sigmoidal input–output responses (4). Here, we seek answers in the architecture of the underlying molecular mechanisms, rather than the statistics of measurement and information. Our results encompass, in substantial generality, all of the examples in Table 1.

Table 1.

Contexts in which the MM formula or Langmuir isotherm (Eq. 1) arises

SI Appendix, Table S1 provides more details and explains which of our results applies to which reference.

^*The first reference for each entry uses the formula shown.

Several theoretical studies have attempted to identify appropriate regimes in which the MM formula appears (7–13, 30–36). Such studies have largely relied on simplifying assumptions, such as symmetric or regular networks (7, 11–13, 30, 35, 36) or restriction to networks in which the steady state is one of thermodynamic equilibrium (12, 13). Numerical studies have suggested that the MM formula generally does not arise away from equilibrium (37–40).

We approach the problem using the graph-based “linear framework” for timescale separation. The framework is described in refs. 41 and 42, applied to biological problems in refs. 43–46, and reviewed in ref. 47. We briefly describe its salient features here, with more details below.

In the linear framework, both macroscopic, deterministic systems, such as enzymes in well-mixed compartments, and microscopic, stochastic systems, such as individual molecular motors, can be described in the same way, by a graph (Fig. 1B). The vertices usually represent fast components or states, which are assumed to reach steady state under a timescale separation. The directed edges represent reactions between components or transitions between states. The influence of the slow components is incorporated into the edge labels, which specify the reaction rates.

Such a graph yields a linear differential equation for the concentrations or probabilities of the vertices. In the stochastic context, this is the master equation of the underlying Markov process. The linear dynamics gives the framework its name and is common to all applications but the slow components in the labels, which introduce nonlinearities, are dealt with in ways that depend on the context. Here, we assume that slow components are effectively constant over the timescale of the fast dynamics. Under this timescale separation, the dynamical equation reaches a steady state, which can be expressed algebraically in terms of the edge labels, without having to know in advance the numerical values of parameters or eigenvalues. This holds in generality for any graph (42) although we are concerned here with graphs for which the steady state is essentially unique (below). If the steady state is at thermodynamic equilibrium, the resulting expressions are equivalent to those of equilibrium statistical mechanics. Importantly, they remain valid away from equilibrium (48, 49), which permits a unified approach. The steady-state output response can be described in terms of these expressions as a rational function of the input variable (Eq. 2). The results below give conditions under which this rational function assumes the simple form in Eq. 1.

The conditions we find relate to whether the graph can be “split” into two subgraphs and where the input variable occurs with respect to this partition. They leave many other details unspecified, which explains the ubiquity of the MM formula and its independence from underlying mechanistic details.

Results

Linear Framework.

We introduce here some notation and terminology; for full details and more background, see SI Appendix, section S1 and refs. 41, 42, 44, and 45. We consider finite directed graphs with labeled edges and no self-loops (hereafter, “graphs”). As noted above, vertices typically represent fast components or states, edges represent reactions or transitions, and labels represent rates, with units of (time)⁻¹. The labels may include contributions from slow components that are not represented by vertices but interact with them (Fig. 1B). We assume that all graphs are connected, so that they cannot be decomposed into parts between which there are no edges. Vertices are denoted by indexes $1,\dots ,N$, and an edge from $i$ to $j$ by $i\to j$. To specify the label, we write $i\stackrel{a}{\to }j$ or $\ell \left(i\to j\right)=a$.

The graphs considered here are strongly connected. This means that, given any two distinct vertices, $i,j$, there is a path of edges directed from $i$ to $j$: $i=i_1\to i_2\to \cdots \to i_{p-1}\to i_p=j$. For a strongly connected graph, the linear dynamics described above has a unique steady state, up to a scalar multiple. If the steady-state concentration or probability of vertex $i$ is denoted by $u_i^{*}$, then the linear framework provides an expression for $u_i^{*}$ in terms of the edge labels. If $x$ denotes the concentration of the input variable ($x=\left[S\right]$ in Fig. 1B), then $u_i^{*}$ is a rational function of $x$, or a ratio of polynomials,

$$\frac{u_i^{*}}{u_{tot}}=\frac{a_0+a_{1}x+\cdots +a_k{x}^k}{b_0+b_{1}x+\cdots +b_n{x}^n}.$$ [2]

Here, $a_i,b_i$ are nonnegative coefficients which depend on the parameters other than $x$ in the edge labels, $k\le n$ and $u_{tot}$ is the total concentration of all vertices ($u_{tot}=1$ if $u^{*}$ denotes probability).

A steady state, $u^{*}$, is one of thermodynamic equilibrium when detailed balance is satisfied. This means that the graph is reversible, so that, if $i\to j$, then also $j\to i$, and each pair of reversible edges is independently in flux balance, so that $\ell \left(i\to j\right)u_i^{*}=\ell \left(j\to i\right)u_j^{*}$. In this case, the ratio of edge labels, denoted $\kappa \left(i\to j\right)=\ell \left(i\to j\right)/\ell \left(j\to i\right)$, becomes the salient parameter and can be interpreted in terms of the free energy difference between states $i$ and $j$. Eq. 2 is then seen to correspond to the prescription of equilibrium statistical mechanics, with the denominator being the partition function. As noted above, however, Eq. 2 continues to hold away from equilibrium, providing thereby a form of nonequilibrium statistical mechanics.

If a reversible graph forms a tree, with no proper cycles of reversible edges (i.e., cycles with at least three vertices), then it always satisfies detailed balance. Free energy may be dissipated in some reactions but there is no entropy production because that arises only from proper cycles (49).

For the results below, we consider the input–output response of a graph to be the steady-state concentration or probability of a specific vertex, $u_i^{*}$, as given by Eq. 2. In some applications the output is a property like an inverse mean first passage time of a Markov process, which can be identified with a steady-state output flux from an appropriate vertex, $k{u}_i^{*}$, with $k$ being some rate (50). The output may also be a sum of the form, ${\sum }_j{k}_j{u}_j^{*}$, over suitable vertices $j$. To show that this satisfies the MM formula, it is sufficient to show that each $u_j^{*}$ does so and that the denominator in Eq. 1 is the same for all $j$. This will emerge from the arguments below and we leave it to the reader to draw the appropriate conclusion for the particular context.

Partitions and Splitting.

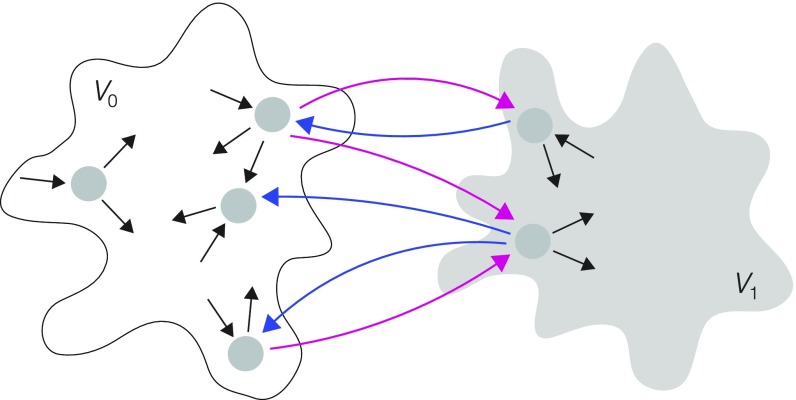
We introduce here the concepts needed for the main results. Given a graph $G$, with vertices forming the set $\nu \left(G\right)$, a partition of $G$ is a pair of subgraphs whose vertex subsets $V_0,\hspace{0.17em}{V}_1$ form a nontrivial disjoint partition of $\nu \left(G\right)$: $V_0,V_1\hspace{0.17em}\ne \hspace{0.17em}\varnothing$, $V_0\cup V_1=\nu \left(G\right)$, and $V_0\cap V_1=\varnothing$ (Fig. 2). An edge $i\to j$ is splitting for a partition if its source and target vertices lie in different subgraphs; it splits $V_0$ from $V_1$ if $i\in V_0$ and $j\in V_1$ and it splits $V_1$ from $V_0$ if $i\in V_1$ and $j\in V_0$. A partition is analogous to a “coarse graining” into the original MM graph in Fig. 1B, with $V_0$ and $V_1$ corresponding to vertices $E$ and $ES$, respectively.

Fig. 2.

Partitions and splitting. A partition is shown schematically, with a graph made up of two disjoint subgraphs, $V_0$ (white) and $V_1$ (gray), whose individual structures can be arbitrary, as suggested by the “cloud” outlines, with magenta edges splitting $V_0$ from $V_1$, blue edges splitting $V_1$ from $V_0$, and labels omitted for clarity.

In the examples summarized in Table 1, edge labels are usually simple expressions, such as $ax$ or $b$, where $a$ and $b$ are constants independent of $x$. However, more complicated expressions in $x$ can arise in the linear framework (43, 44, 51), so it may be helpful to allow for greater generality. A quantity, $\varphi$, such as an edge label or a ratio of edge labels, is said to be a monomial in $x$ if $\varphi =a{x}^d$, where $d\in R$ and $a$ does not depend on $x$. The degree of a monomial is the corresponding exponent of $x$: $\text{deg}\hspace{0.17em}\varphi =d$. Monomials often have integer degrees, $d\in Z$, but the added generality of $d\in R$ may also be useful. The product or ratio of monomials is also a monomial, with $\text{deg}\hspace{0.17em}\left({\varphi }_1{\varphi }_2\right)=\text{deg}\hspace{0.17em}\left({\varphi }_1\right)+\text{deg}\hspace{0.17em}\left({\varphi }_2\right)$ and $\text{deg}\hspace{0.17em}{\varphi }^{-1}=-\text{deg}\hspace{0.17em}\varphi$.

MM at Thermodynamic Equilibrium.

We first consider the case when a graph $G$ is at thermodynamic equilibrium, so that it is reversible. We say that $G$ has monomial ratios if $\kappa \left(i\to j\right)$ is a monomial in $x$ for all edges $i\to j$. This allows complexity in the individual labels, as long as it cancels out in the ratio: If $\ell \left(i\to j\right)=x^{p}f\left(x\right)$ and $\ell \left(j\to i\right)=x^{q}f\left(x\right)$, for any $f\left(x\right)$, then $i\to j$ has a monomial ratio and $\text{deg}\hspace{0.17em}\kappa \left(i\to j\right)=p-q$. We use the notation $X\backslash Y$ for the complement of $Y$ in $X$, or those elements of $X$ which are not in $Y$, $X\backslash Y=\left\{i\in X\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}i/\in Y\right\}$.

Proposition 1.

Let $G$ be a reversible graph with monomial ratios at thermodynamic equilibrium. If $G$ is partitioned by $V_0$ and $V_1$ so that $\text{deg}\hspace{0.17em}\kappa \left(i\to j\right)=1$ for all edges splitting $V_0$ from $V_1$ and $\text{deg}\hspace{0.17em}\kappa \left(i\to j\right)=0$ for all nonsplitting edges, then all vertices in $V_1$ satisfy the MM formula. Conversely, if some vertex satisfies the MM formula and $V_1\subseteq \nu \left(G\right)$ consists of all such vertices, then $V_0=\nu \left(G\right)\backslash V_1$ and $V_1$ form a partition of $G$ for which $\text{deg}\hspace{0.17em}\kappa \left(i\to j\right)$ has the same properties. In either direction, all vertices with the MM formula have the same denominator.

Proofs of Proposition 1 and other results below are in SI Appendix, sections S2–S6. The partition shown in Fig. 2 falls under Proposition 1 provided the graph is reversible and satisfies detailed balance and the only label ratios with $x$ are on the splitting edges, with the magenta edges having degree 1 and the blue edges correspondingly having degree −1. The coarse-graining analogy described above becomes closer here, with $x=\left[S\right]$ appearing only in the labels on edges from $V_0$ to $V_1$, just as in Fig. 1B.

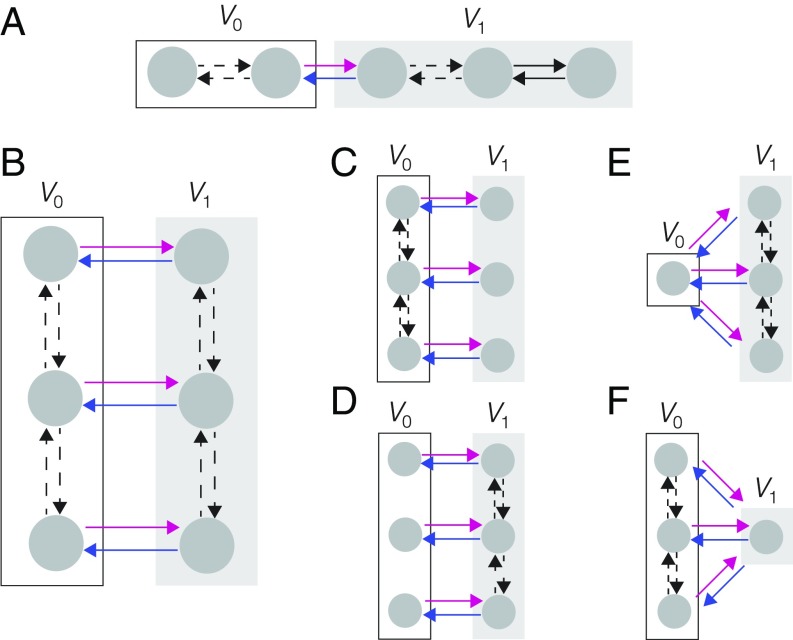
Sequence graphs, which consist of a series of vertices with nearest neighbors joined by reversible edges, as in Fig. 3A, have been used to model enzyme kinetics (5, 8–10, 52), gene regulation (16), and molecular motors (8, 25, 26). Since sequence graphs are trees, they satisfy detailed balance, as noted above, and can be considered to be at thermodynamic equilibrium. In the cited applications, the partitions break the sequence into two adjoining parts (Fig. 3A) and the requirements on the degrees of the label ratios conform to Proposition 1, from which the MM formula arises.

Fig. 3.

Graph structures for application examples, showing partitions into $V_0$ (white box) and $V_1$ (gray box), with the splitting edges in magenta and blue and labels omitted for clarity. In the applications cited in the text, the input variable occurs to degree 1 in the labels on magenta edges and nowhere else, although our results offer greater generality. Dashed edges indicate potential intervening vertices. (A) A sequence graph, as used in refs. 8, 16, and 52, to which Proposition 1 applies. (B) Parallel sequences provide a model of single-molecule enzyme kinetics, as explained in the text and used in refs. 7 and 11–14. If thermodynamic equilibrium is assumed, Proposition 1 applies. Away from equilibrium, additional parametric assumptions give rise to the graphs shown in C–F (SI Appendix, Table S1 and Fig. S2.) Proposition 2 applies to C and D, Proposition 3 applies to E, and Proposition 4 applies to F.

Several authors have independently shown that the MM formula arises for two sequence graphs connected in parallel (Fig. 3B), in the regime in which thermodynamic equilibrium holds (7, 11–13, 27). The application has mainly been to single-molecule enzyme kinetics, with the vertices along the sequences representing different enzyme and enzyme–substrate conformations (Fig. 1B). In this case, the input variable is found only on the magenta edges. Accordingly, these derivations of the MM formula at equilibrium follow from Proposition 1, with $V_0$ and $V_1$ being the two sequence subgraphs.

MM Away from Equilibrium, with Reversible Edges.

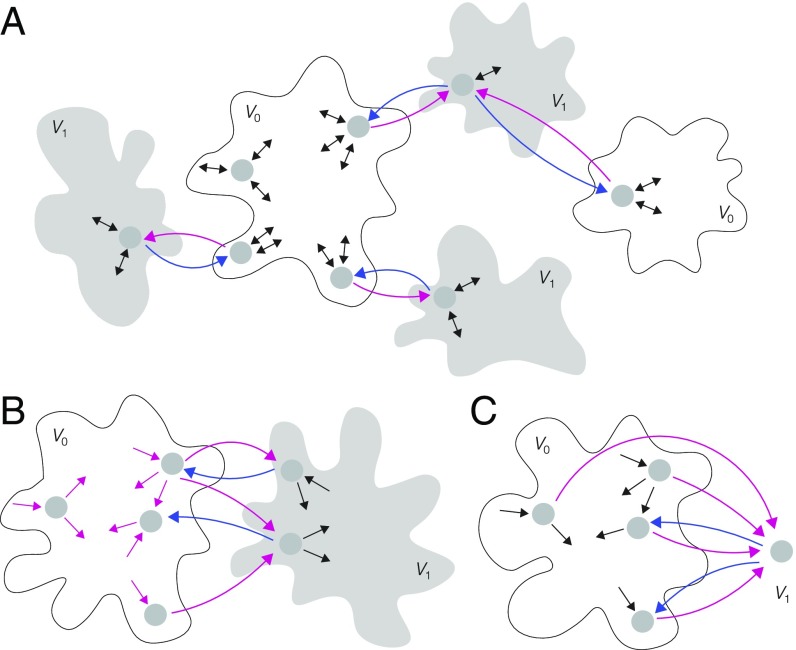
We now consider a reversible graph, $G$, which may not be at thermodynamic equilibrium. We say that $G$ has monomial labels if, for each edge $i\to j$, $\ell \left(i\to j\right)$ is a monomial in $x$. This is more restrictive than the monomial ratios required for Proposition 1. We say that $G$ is $x$-acyclic if no label in any proper cycle of edges depends on $x$, so that $\text{deg}\hspace{0.17em}\ell \left(i\to j\right)=0$ if $i\to j$ lies on a proper cycle. This constraint implies that if an edge on which $x$ occurs is removed, the graph becomes nonstrongly connected. This leads to the kind of structure depicted in Fig. 4A, in which the edges with $x$ in their labels (blue or magenta) link subgraphs through a subtree, with the subgraphs being arbitrarily complicated. As mentioned above, entropy production takes place on cycles, so being $x$-acyclic implies that the variable $x$ does not contribute to entropy production within the graph. With these restrictions, the MM formula arises under the same conditions as in Proposition 1.

Fig. 4.

Graphs and partitions illustrating the generality of Propositions 2–4. Reversibility is indicated by two-headed arrows and labels are omitted for clarity. (A) Reversible graph structure to which Proposition 2 applies. The input variable $x$ occurs only on the magenta or blue edges, which are splitting for the partition and which also lie on a subtree, so that removal of such an edge leads to loss of strong connectivity. (B) Graph structure to which Proposition 3 applies. Here, $x$ occurs only on the outgoing edges from vertices in $V_0$, which are colored magenta. (C) Graph structure to which Proposition 4 applies. The single vertex in $V_1$ is a sink and the labels on the edges to the sink (magenta) and from the sink (blue) are monomial labels, constrained as stated in Proposition 4, while the labels on all other edges (black) may be arbitrary algebraic expressions in $x$.

Proposition 2.

Let $G$ be a reversible graph with monomial labels that is $x$-acyclic. If $G$ is partitioned by $V_0$ and $V_1$ so that $\text{deg}\hspace{0.17em}\kappa \left(i\to j\right)=1$ for all edges splitting $V_0$ from $V_1$ and $\text{deg}\hspace{0.17em}\kappa \left(i\to j\right)=0$ for all nonsplitting edges, then all vertices in $V_1$ satisfy the MM formula. Conversely, if some vertex satisfies the MM formula and $V_1\subseteq \nu \left(G\right)$ consists of all such vertices, then $V_0=\nu \left(G\right)\backslash V_1$ and $V_1$ form a partition of $G$ for which $\text{deg}\hspace{0.17em}\kappa \left(i\to j\right)$ has the same properties. In either direction, all vertices with the MM formula have the same denominator.

As noted above, the parallel sequence graph in Fig. 3B has been used to model enzyme catalysis at the single-molecule level. If the graph is at thermodynamic equilibrium and the input variable occurs only on the magenta edges, then the graph satisfies the conditions of Proposition 1. When the graph is away from equilibrium, it cannot satisfy the conditions of Proposition 2 because it is not $x$-acyclic. However, parametric regimes have been identified in which the MM formula does emerge away from equilibrium (7, 11, 14). In these regimes, the bound, or the unbound, enzyme changes conformations very slowly, giving rise to the graphs in Fig. 3 C and D, respectively (SI Appendix, Table S1 and Fig. S2). These graphs are both $x$-acyclic and the emergence of the MM formula follows from Proposition 2.

MM Away from Equilibrium, with Irreversible Edges.

In many applications in which a system is away from thermodynamic equilibrium, certain reactions or transitions are treated as effectively irreversible. If the corresponding graph acquires an irreversible edge, it would not fall under the scope of either Proposition 1 or Proposition 2. The emergence of the MM formula now becomes much more delicate and, in contrast to the results above, we can identify only certain sufficient conditions. A restrictive case, which nonetheless applies to some examples (8, 15, 21, 29), is relegated to SI Appendix, Proposition S1.

Proposition 3.

Let $G$ be a strongly connected graph with monomial labels. If $G$ is partitioned into $V_0$ and $V_1$ so that $\text{deg}\hspace{0.17em}\ell \left(i\to j\right)=1$ for all edges with $i\in V_0$ and $\text{deg}\hspace{0.17em}\ell \left(i\to j\right)=0$ for all edges with $i\in V_1$, then all vertices in $V_1$ satisfy the MM formula with the same denominator.

Fig. 4B shows the kind of graph structure to which Proposition 3 applies, with the $x$-containing labels only on the magenta edges. In contrast to Proposition 2, the $x$-containing labels may be on proper cycles but are now required to be present on, and only on, the outgoing edges from any vertex in $V_0$.

In single-molecule enzyme studies, one of the nonequilibrium parametric regimes in which the MM formula emerges gives rise to a graph like that in Fig. 3E, which satisfies the conditions of Proposition 3 with $V_0$ being only a single vertex. In this application, the conformational fluctuations of the unbound enzyme are assumed to be extremely fast, so that there is effectively only a single conformation corresponding to the single vertex in $V_0$, and substrate binding induces slower conformational fluctuations (SI Appendix, Table S1 and Fig. S2) (7, 11, 14). Graphs satisfying the conditions of Proposition 3 have also arisen in four other applications. First, modified versions of the sequence graph in Fig. 3A have been used to model enzyme kinetics both macroscopically (6) and at the single-molecule level (8–10). Here, $V_0$ is a single vertex corresponding to the unbound enzyme and there are multiple bound enzyme conformations which change or fluctuate along a sequence, from which irreversible transitions can return to the single vertex in $V_0$. Second, they have been used in studies of the ribosome (17–19), in which the MM formula was found for the average ribosome velocity as a function of aminoacyl tRNA concentration. Here, $V_0$ is a single vertex corresponding to the bare ribosome conformation and tRNA binding gives irreversible outgoing edges from this vertex. Third, they have been used in studies of molecular motors, where the MM formula was found for the velocity of a molecular motor as a function of ATP concentration (20–24). Here, the vertices in $V_0$ correspond to motors with ATP hydrolysis giving outgoing edges from these vertices. Fourth, they have been used to study regulation in bacterial chemotaxis, where the MM formula was found for the phosphorylation rate of the histidine kinase CheA as a function of ATP concentration (28). Here, $V_0$ is a single vertex corresponding to the free kinase and ATP binding gives outgoing edges from this vertex. In all these studies, the emergence of the MM formula follows from Proposition 3, although none of them have exploited the generality it offers, as suggested in Fig. 4B.

Our final result requires one more concept: A vertex $j$ is a sink if there exists an incoming edge $i\to j$, from all other vertices $i$ in $G$.

Proposition 4.

Let $G$ be a strongly connected graph that is partitioned by $V_0$ and $V_1=\left\{j\right\}$, with $V_1$ containing only a single vertex, $j$, which is a sink. Suppose that all edges to and from $j$ have monomial labels for which $\text{deg}\hspace{0.17em}\ell \left(i\to j\right)=d$ and $\text{deg}\hspace{0.17em}\ell \left(j\to i\right)=d-1$ and that, furthermore, $\ell \left(i\to j\right)$ does not depend on $i$. Then $u_j^{*}$ satisfies the MM formula.

No restriction is placed on the labels of edges other than those to and from the sink vertex. Fig. 4C shows the kind of graph structure that satisfies Proposition 4. In studies of single-molecule enzyme kinetics, another parameter regime was identified in which the MM formula arises (7, 11, 14). Here, the conformational fluctuations of the bound enzyme are assumed to be extremely fast, so that there is effectively only a single conformation, and the on-rates for substrate binding are assumed to be independent of the unbound conformation, giving rise to the graph in Fig. 3F (SI Appendix, Table S1 and Fig. S2). These are exactly the assumptions required for Proposition 4, with the sink vertex being the unique bound conformation.

Discussion

The MM formula has been found to arise under timescale separation in a surprising variety of biological contexts (Table 1). Previous attempts to explain its ubiquity have largely focused on regular networks, such as the parallel sequence network in Fig. 3B, and identification of specific parameter regimes. In contrast, our approach considers general graphs and gives conditions in terms of graph structure and the location of the input variable (Propositions 1–4 and SI Appendix, Proposition S1). Most other details—the sizes and topologies of subgraphs, the arrangements of vertices and edges, and the numerical values of labels—prove to be irrelevant to the algebraic nature of the MM formula (Fig. 4). Instead, these details influence the quantities $A$ and $B$ in Eq. 1.

Our results provide a series of rules for determining whether or not the MM formula arises. If a graph is at thermodynamic equilibrium, then the MM formula holds, if, and only if, there is a partition of the graph for which the input variable, $x$, is found in the label ratios only on splitting edges in one direction and only to degree 1, as described in Proposition 1. This is analogous to a coarse graining into the original MM graph in Fig. 1B. If the graph is not at thermodynamic equilibrium but is still reversible, then it is important to check whether $x$ occurs in a label on any proper cycle. If not, then the MM formula holds if, and only if, the same coarse graining can be found as at equilibrium, as described in Proposition 2. If the graph is not $x$-acyclic or if it has irreversible edges, then the situation is more subtle. The MM formula holds if one of the special structural conditions in Proposition 3, Proposition 4, or SI Appendix, Proposition S1 is satisfied.

Eq. 2 offers a way to understand how the MM formula arises. Recall that the denominator of this rational function generalizes the partition function of equilibrium statistical mechanics. In Proposition 1 and SI Appendix, Proposition S1, the partition function takes the restricted form $b_0+b_{1}x$ while the numerator is $a_{1}x$ (SI Appendix, Proposition S1 and sections S2 and S6), from which MM formula follows easily. In Propositions 2 and 3, the partition function takes the form $b_{n-1}{x}^{n-1}+b_n{x}^n$, while the numerator is $a_n{x}^n$ (SI Appendix, sections S3 and S4). Here, $n$ is related to the structure of the graph. The MM formula follows by canceling $x^{n-1}$ in the ratio. In Proposition 4, the partition function factorizes as $p\left(x\right)\left(c+dx\right)$, with the numerator being $p\left(x\right)ax$, where $p\left(x\right)$ is a polynomial in $x$ (SI Appendix, section S5). The MM formula arises by canceling $p\left(x\right)$ in the ratio. The subtlety away from thermodynamic equilibrium is that the partition function can factorize in this way, which is particularly challenging to analyze; Proposition 4 is the most difficult of our results, despite the restrictive assumption of a single sink vertex. SI Appendix, section S7 and Fig. S1 gives further examples in which nontrivial factorizations of the partition function occur, which are not covered by Propositions 1–4 and SI Appendix, Proposition S1. It remains an interesting open problem to fully characterize those graphs which give rise to the MM formula.

Eq. 2 tells us that the input–output response of a graph-based system is a rational function of $x$. Propositions 1–4 and SI Appendix, Proposition S1 provide conditions under which this rational function takes its simplest form. Conditions can also be found which more broadly constrain the algebraic complexity of a response function (45, 46). A general advantage of the graph-based linear framework that we have exploited here is that it does not depend on numerical calculations or simulations, which require all details of the system to be specified and parameter values to be estimated. It focuses instead on the topological features of the graph, thereby rising above many of the mechanistic details. This capability is particularly well suited to analyzing biomolecular systems, in which many of the details may be obscure or unavailable, and it seems likely that more results of this kind remain to be uncovered.

Materials and Methods

Detailed proofs of Propositions 1–4 and SI Appendix, Proposition S1 and examples falling outside the scope of these results are given in SI Appendix, sections S2–S7 and Fig. S1.