Multi-level Supervision and Modification of Artificial Pancreas Control System

Abstract

Artificial pancreas (AP) systems provide automated regulation of blood glucose concentration (BGC) for people with type 1 diabetes (T1D). An AP includes three components: a continuous glucose monitoring (CGM) sensor, a controller calculating insulin infusion rate based on the CGM signal, and a pump delivering the insulin amount calculated by the controller to the patient. The performance of the AP system depends on successful operation of these three components.

Many APs use model predictive controllers that rely on models to predict BGC and to calculate the optimal insulin infusion rate. The performance of model-based controllers depends on the accuracy of the models that is affected by large dynamic changes in glucose-insulin metabolism or equipment performance that may move the operating conditions away from those used in developing the models and designing the control system. Sensor errors and missing signals will cause calculation of erroneous insulin infusion rates. And the performance of the controller may vary at each sampling step and each period (meal, exercise, and sleep), and from day to day.

Here we describe a multi-level supervision and controller modification (ML-SCM) module is developed to supervise the performance of the AP system and retune the controller. It supervises AP performance in 3 time windows: sample level, period level, and day level. At sample level, an online controller performance assessment sub-module will generate controller performance indexes to evaluate various components of the AP system and conservatively modify the controller. A sensor error detection and signal reconciliation module will detect sensor error and reconcile the CGM sensor signal at each sample. At period level, the controller performance is evaluated with information collected during a certain time period and the controller is tuned more aggressively. At the day level, the daily CGM ranges are further analyzed to determine the adjustable range of controller parameters used for sample level and period level.

Thirty subjects in the UVa/Padova metabolic simulator were used to evaluate the performance of the ML-SCM module and one clinical experiment is used to illustrate its performance in a clinical environment. The results indicate that the AP system with an ML-SCM module has a safer range of glucose concentration distribution and more appropriate insulin infusion rate suggestions than an AP system without the ML-SCM module.

Graphical abstract

1. INTRODUCTION

1.1 Overview of Artificial Pancreas and performance assessment

Artificial pancreas (AP) systems regulate blood glucose concentration (BGC) of people with type 1 diabetes (T1D) and those without a functional pancreatic beta cell population. An AP relies on a continuous glucose monitoring (CGM) sensor to provide BGC information at a high frequency (sampling time of 5 minutes), a controller to calculate the insulin infusion rate based on the CGM signal (BGC estimate) and an insulin pump that infuses the insulin calculated by the controller to a subcutaneous port on the body.

The performance of the AP relies on correct operation of all the three components, the CGM sensor, controller, and insulin pump. Various control strategies, ranging from proportional-integral-derivative (PID) control(Kovatchev et al., 2009; Renard et al., 2010; Ruiz et al., 2012; Sherr et al., 2013; G. Steil et al., 2006; G. M. Steil et al., 2011) to model-based techniques such as model predictive control(Harvey et al., 2014; Kovatchev et al., 2009; Luijf et al., 2013; Magni et al., 2007), generalized predictive control (GPC)(El-Khatib et al., 2014; Eren-Oruklu et al., 2009; Turksoy et al., 2014b), and knowledge-based systems with fuzzy logic(Atlas et al., 2010; Mauseth et al., 2010)have been used in developing the control algorithms for the AP. All strategies except the fuzzy logic approach use mathematical models that estimate BGC and insulin in formulating the control algorithms. The fuzzy logic controllers use rules derived from experiential knowledge and medical facts.

One of the challenges for AP systems is variation in BGC dynamics among different people with T1D and also from day to day, even minute to minute, for the same person. Factors such as meals and exercise will influence BGC dynamics. Various AP control systems have been proposed to address the effects of these factors and improve AP system.(Dassau et al., 2008; Perfect et al., 2012; Turksoy et al., 2015; Turksoy et al., 2014b; Turksoy et al., 2016) In a fully automated AP system, no announcement of meals or exercise is provided by patients as to meals or activities, and the controller needs to adapt to the dynamic changes in the human body by updating its model and/or insulin dose calculation algorithm. GPC uses a recursively updated data-driven model when a new CGM signal value is available.(El-Khatib et al., 2014; Eren-Oruklu et al., 2009; Turksoy et al., 2014b) Various modules that identify specific conditions such as meal detection module(Lee et al., 2009; Turksoy et al., 2016) and exercise module(Turksoy et al., 2015) provide additional information for making more accurate control decisions. However, the controller performance is often limited by the size of the database and richness of the historical information for training and tuning the controllers. For a new patient with different BGC dynamics (e.g., different insulin sensitivity), unexpected conditions (e.g., large meal, different types of exercise) or illness, the AP system may not able to regulate the BGC. Besides the challenges of the BGC dynamics, the performance of AP system also relies on the accuracy of CGM values reported. Sensor failures such as signal bias and outliers, and missing data will also affect insulin infusion rate calculation and may endanger the safety of the patient. (Baysal et al., 2014; Del Favero et al., 2014; Facchinetti et al., 2016) In this paper, we focus on the detection of controller performance deterioration caused by changes in glucose and insulin concentration dynamics and sensor failures, the diagnosis of the cause for the deterioration, and the retuning of the controller.

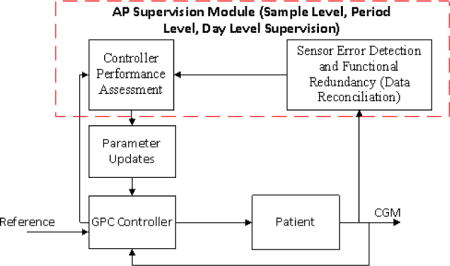
A multi-level supervision and modification (ML-SCM) module is developed to supervise the performance of the AP system and modify it to adapt to the patient’s current state and mitigate the impact of CGM sensor faults. The ML-SCM module contains three sub-modules based on different time scales: sample level supervision module (SLSM), period-level supervision module (PLSM) and 24-hour day level supervision module (DLSM). In previous work, an index based online controller performance assessment (CPA) module (Feng, Turksoy, & Cinar, 2016) and a hybrid CGM sensor error detection and functional reconciliation (SED&FR) module(Feng, Turksoy, Samadi, et al., 2016) based on outlier-robust Kalman filter (ORKF) and locally-weighted partial least square (LW-PLS) were developed for a GPC based AP(Turksoy et al., 2014a; Turksoy et al., 2014b). These two modules were capable of retuning the controller and reconciling the CGM signal values at each sampling time. In the ML-SCM module, the performance of the AP will not only be assessed at the sample level but also at period-level and day level. The CPA module is enhanced with more indexes to track different aspects of controller performance and combined with the SED&FR module to formulate the SLSM. The dynamic changes in the body triggered by meal or physical activity will last for many sampling times. Hence, the ML-SCM module should accommodate the effects of different situations over different time periods. The PLSM based on linear quadratic Gaussian (LQG) control-based tradeoff curve, and DLSM based on daily BG distribution analysis are developed to assess the AP performance in longer time scales.

1.2 Generalized predictive controller for the AP system

We have already developed an AP control system based on adaptive constrained weighted recursive identification methods and generalized predictive controller (GPC) (Figure 1), GPC model-based adaptive control.(Turksoy et al., 2014a) We have enhanced recursive time series modeling to assure the stability of every multi-input single-output model developed, used these models in our GPC, and introduced rules that improve its performance in presence of physical activity. (Turksoy et al., 2014a; Turksoy et al., 2014b; Turksoy et al., 2016) We also integrated a meal detection module to improve the performance against post-meal high glucose level for an AP without any meal announcement. (Turksoy et al., 2016)

Figure 1.

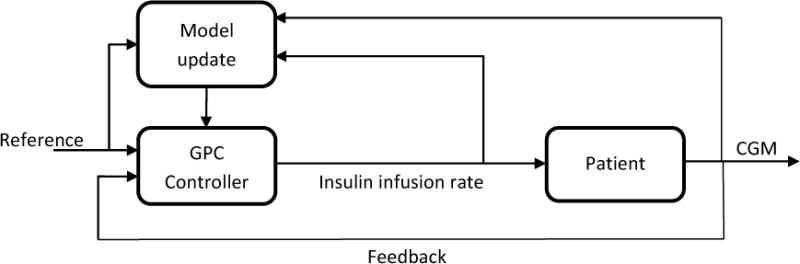
AP system with GPC algorithm

A single-variable version of this controller is used to conduct simulations with the UVa/Padova simulator. An autoregressive moving average model with exogenous inputs (ARMAX) is used to predict glucose concentration (GC) measured with a CGM.(Turksoy et al., 2014a) The insulin infusion rates computed in previous steps and past and current CGM readings are the inputs to the model. Model parameters are updated recursively at each sampling time and then the updated model provides GC predictions to the controller. The controller then computes the insulin dose to be infused.

In this paper, we outline the components of the controller that are relevant to the ML-SCM module and focus on the objective function for model estimation and the objective function of the GPC.

The optimum coefficients of the recursive ARMAX model are obtained by minimizing the objective function:

$$V\left(\hat{\mathrm{\theta }}\right)={\displaystyle {\sum }_{k=1}^N{\lambda }^{N-k}e{(k)}^2}$$ (1)

where $\hat{\mathrm{\theta }}$ is the vector of estimated model coefficients, N is the number of samples, λ is the forgetting factor, and e denotes the modeling error. The recursive model is updated by giving different weights to previous data based on part of the data that is more important to adjust the model. λ is the critical parameter that adjusts the relative importance of GC data collected and the effective size of the moving window for the input data.

Another important component of the controller is its objective function. The constrained controller signal I(k) is calculated by minimizing the objective function J (N₁,N₂,N_u w):

$$J(N_1,N_2,N_u,w)=\underset{I(k)}{\min }{\displaystyle \sum _{j=N_1}^{N_2}{\left[G{C}^{\mathit{\text{pred}}}\left(k+j|k\right)-r\left(k+j\right)\right]}^2}+{\displaystyle \sum _{j=1}^{N_u}{w}_j(k)\ast \mathrm{\Delta }I{\left(k+j-1\right)}^2}s.t.I_{\mathit{\text{Min}}}\le I\le I_{\mathit{\text{Max}}}$$ (2)

where N₁ and N₂ are the first and last time instants of the modeling horizon and N_u is the control horizon. I denotes the insulin infusion rate suggestions and only the first element I (k)of is implemented. GC^pred (k+j|k) is the predicted CGM reading at step k + j in the future based on the previous data at and before step k, r is the reference value, ΔI represents the changes of insulin infusion, and w_j is the jth diagonal element of weight matrix w(k) for ΔI. Insulin delivery is constrained by both the ability of the insulin pump and the maximum value calculated by the model to prevent hypoglycemia, and insulin value cannot be negative.

At step k, the equations for r (k+j) and w(k)are

$$r(k)=G(k)$$ (3)

$$r(k+j)=(1-\mu )r(k+j-1)+\mu r_0\mathrm{s}.\mathrm{t}.j=[1,2,\dots ,N_u]$$ (4)

$$\mathit{ISC}(k)=\mathit{G}{\mathit{C}}^{\mathit{\text{pred}}}./{[r(k+1),r(k+2),\dots ,r(k+N_u)]}^{\mathrm{T}}$$ (5)

$$\mathit{TDD}(k)=\mathit{ISC}(k).\ast \mathrm{BW}$$ (6)

$$\mathit{ISF}(k)=1800./\mathit{TDD}(k)$$ (7)

$$\mathit{w}(k)=\mathit{\text{diag}}(\mathit{ISF}(k))$$ (8)

where BW is the body weight and r₀ = 100 mg/dl is the constant “reference”, the desired GC trajectory(Turksoy et al., 2014a) and ./ denotes elementwise division. For Eq. 2 - 8, μ (between 0-1) is the parameter that determines the speed of approximation of the reference trajectory to r₀ such that as μ is reduced, the reference trajectory becomes smoother. The weight w_j in (2) is also influenced by μ and as μ is reduced, more weight is put on the insulin efficiency term. In other words, μ determines the aggressiveness of the controller in bringing the BGC closer to the reference r₀, μ is closer to 1 for more aggressive control action. A constant value is assigned to μ according to the age group and insulin resistance level of the subject (Table 2). (Turksoy et al., 2014a)

Table 2.

Value setting for μ

	Sensitive	Normal	Resistant
Adolescent	0.2	0.3	0.55
Adult	0.2	0.3	0.55
Child	0.45	0.7	0.9

This GPC-based AP is used to illustrate the performance of the ML-SCM. The detailed algorithm of failure detection and modification of AP system according to the ML-SCM is described in section 2. Simulations and results are reported in section 3. Discussion of the results is presented in section 4. Conclusions are provided in section 5.

2. METHOD

The ML-SCM includes three sub-level supervision modules: SLSM at sample level, PLSM at period level and DLSM at day (24-hour) level. The SLSM has an online CPA sub-module based on the computation and interpretation of several indexes, and a hybrid online sensor error detection and functional redundancy (SED&FR) sub-module. At each sampling time, the performance of the different components of the controller and the CGM sensor signal are evaluated and AP controller is modified conservatively. In PLSM, the controller performance during a specific time period is evaluated by the tradeoff curve method and the AP controller is modified more aggressively since more information has been collected and evaluated compared to SLSM. In DLSM, the BG variation within a 24-hour period is analyzed and the range of controller parameter retuning and insulin correction in SLSM and PLSM are modified.

2.1 Sample Level Supervision Module

The SLSM has two sub-modules, a CPA and a SED&FR. In previous work(Feng, Turksoy, & Cinar, 2016), an online CPA module with six indexes to track different aspects of a model-based controller was developed. The indexes used in the previous CPA module included model prediction error index (I_MPE), model error elimination speed index (I_MEES), dangerous change potential index (I_DCP), dangerous change index (I_DC), insulin constraints limitation index (I_ICL), and weight ratio index (I_WR). Three different types of controller failures, model prediction error, insulin constraints error, and weight ratio error, are detected and the controller is modified accordingly. The equations of these six indexes, controller failure detection and controller modification based on those indexes are described in the part I of appendix. Two additional indexes: idle index(Hägglund, 1999) (I_i) and performance watchdog(Rhinehart, 1995) (I_PW) are added to the CPA sub-module to detect sluggish control and offset from set-point (reference trajectory), respectively.

The I_i describes the relation between times of positive and negative correlation between the control signal (insulin infusion rate suggested) ΔI and the controlled variable (CGM signal) increments ΔG:

$$I_i(k)=\frac{t_{\mathit{\text{pos}}}(k)-t_{\mathit{\text{neg}}}(k)}{t_{\mathit{\text{pos}}}(k)+t_{\mathit{\text{neg}}}(k)}$$ (9)

$$t_{\mathit{\text{pos}}}(k)\{\begin{array}{cc}{t}_{\mathit{\text{pos}}}(k-1)(1-{\alpha }_i)+T_s{\alpha }_i& if\mathrm{\Delta }I(k)\ast \mathrm{\Delta }G(k)>0\\ t_{\mathit{\text{pos}}}(k-1)& if\mathrm{\Delta }I(k)\ast \mathrm{\Delta }G(k)\le 0\end{array}$$ (10)

$$t_{\mathit{\text{neg}}}(k)\{\begin{array}{cc}{t}_{\mathit{\text{neg}}}(k-1)\ast (1-{\alpha }_i)+T_s{\alpha }_i& if\mathrm{\Delta }I(k)\ast \mathrm{\Delta }G(k)>0\\ t_{\mathit{\text{neg}}}(k-1)& if\mathrm{\Delta }I(k)\ast \mathrm{\Delta }G(k)\ge 0\end{array}$$ (11)

where k indicates the time steps with 5-minutes sampling time, and ΔI(k) is the change between two consecutive samples (G (k) − G (k − 1)). The positive values of I_i (k) >0.4 indicate sluggish control.(Horch, 2000)

The performance watchdog index I_PW (k) represent the ratio of the controlled variable (CGM) variance, calculated in two different ways:

$$I_{pw}(k)=\frac{{\sigma }_{y_1}^2(k)}{{\sigma }_{y_2}^2(k)}$$ (12)

$${\sigma }_{y_1}^2(k)={\sigma }_{y_1}^2(k-1)\ast (1-{\alpha }_i)+{\alpha }_i\ast {(\frac{G(k)-r_0}{r_0})}^2$$ (13)

$${\sigma }_{y2}^2(k)={\sigma }_{y2}^2(k-1)\ast (1-{\alpha }_i)+{\alpha }_i\ast {(\frac{\mathrm{\Delta }G(k)}{\mathrm{\Delta }{G}^n})}^2$$ (14)

The variance ${\sigma }_{y1}^2(k)$ represents the normalized accumulated deviation of sample k from the reference value (r₀). Variance ${\sigma }_{y2}^2$ indicates the normalized distance between two consecutive samples. In this case, the averaged absolute consecutive samples difference is used for normalization $(\mathrm{\Delta }{G}^n={\displaystyle {\sum }_{j=1}^k\frac{\left|\mathrm{\Delta }G(j)\right|}{k}})$. The forgetting factor α_i is introduced in both I_i and I_PW to make them adaptive to the time-varying characteristics of the human body. I_PW >3 indicates that the CGM measurement is steady at a value which is far from the reference value (large offset).(Horch, 2000)

When I_i and I_PW indicate sluggish control or large offset, the parameter μ, which determines the aggressiveness of the controller, will be increased according to:

$$I_{\mathit{\text{slug}}}(k)=\{\begin{array}{cc}1& if{I}_i(k)>0.4\&GC(k)>r_0\\ 0& \mathit{\text{otherwise}}\end{array}$$ (15)

$$I_{\mathit{\text{offset}}}(k)=\{\begin{array}{cc}1& if{I}_{PW}(k)>3\&GC(k)>r_0\\ 0& \mathit{\text{otherwise}}\end{array}$$ (16)

$${\beta }_f=\max (\frac{1}{{\displaystyle {\sum }_{j=k-N_u}^k\left(I_{\mathit{\text{slug}}}(j)\right)}},\frac{1}{{\displaystyle {\sum }_{j=k-N_u}^k\left(I_{\mathit{\text{offset}}}(j)\right)}})$$ (17)

$$\mu (k)=\{\begin{array}{cc}{\beta }_f\ast \mu (k-1)+(1-{\beta }_f)\ast {\mu }_{\mathit{max}}& if\text{GC}(k)>r_0\&(I_{\mathit{\text{slug}}}(k)=1or{I}_{\mathit{\text{offset}}}(k)=1)\\ \mu (k-1)& \mathit{\text{otherwise}}\end{array}$$ (18)

Instead of a constant value related only to the insulin sensitivity and age group of the patient (Table 2), μ is updated at each sampling time based on the current conditions of the AP. The values listed in Table 2 now become the initial value of μ (μ(1)). μ is increased only when CGM is larger than reference value. When sluggish control or large offset was detected based on the accumulated time of error, μ is increased towards its upper bound (μ_max). When large offset is detected by I_PW, a correction insulin bolus (I_cor) needs to be delivered in order to bring the GC back to the reference value. I_cor is based on ISF:

$$I_{\mathit{\text{cor}}}(k)=\min (\frac{GC(k)-r_0}{\mathit{ISF}(k,1,1)},I_{\mathit{\text{cor}}}^{\mathit{max}})if{\displaystyle {\sum }_{j=k}^{k-1}\left(I_{\mathit{\text{cor}}}(k)\right)=0\&I_{\mathit{\text{offset}}}(k)=1}$$ (19)

where ISF (k,1,1) denotes the first element of(ISF(k)) More correction insulin need to wait until the effect of previous correction insulin bolus is cleared or it becomes clear that the previous correction is insufficient. A maximum constraint $\left(I_{\mathit{\text{cor}}}^{\mathit{max}}\right)$ was defined to prevent potential hypoglycemia that may be caused by the correction bolus. The clearance time (N_cor) changes according to the type of rapid-acting insulin. For this experiment, N_cor =24 to simulate 2-hour insulin clearance time.

If CGM< r₀ and may have potential towards hypoglycemia, then μ will be decreased towards the lower bound (μ_min). To include this change, Eq. 18 is modified as:

$${\beta }_{\mathit{\text{hypo}}}=\frac{r_0-\text{GC}(k)}{r_0}if\text{GC}(k)<r_0$$ (20)

$$\mu (k)=\{\begin{array}{cc}(1-{\beta }_{\mathit{\text{hypo}}})\mu (k-1)+({\beta }_{\mathit{\text{hypo}}}){\mu }_{\mathit{min}}\hfill & if\mathrm{GC}(k)<r_0\\ {\beta }_f\mu (k-1)+(1-{\beta }_f){\mu }_{max}\hfill & if\text{GC}(k)>r_0\&(I_{\mathit{\text{slug}}}(k)=1or{I}_{\mathit{\text{offset}}}(k)=1)\\ \mu (k-1)\hfill & \mathit{\text{otherwise}}\end{array}$$ (21)

In the CPA sub-module, μ is varied between μ_min to μ_max, in order to optimize the aggressiveness of the controller. The insulin infusion rate suggestion from the controller is modified when sluggish control or prediction error occurs (Eq. 19 and A.11), and these additional insulin doses are constrained by $I_{\mathit{\text{cor}}}^{\mathit{max}}$. The constraints μ_min, μ_max and $I_{\mathit{\text{cor}}}^{\mathit{max}}$ may also be changed as more information is collected from the operation of the AP, as described in Section 2.3 (PLSM).

The hybrid sensor error detection and functional redundancy (SED&FR) module of the SLSM detects and mitigates the effects of abnormal CGM sensor behavior (Figure 2).(Feng, Turksoy, Samadi, et al., 2016) All CGM sensor signals are analyzed and reconciled in SED&FR module before transmission to other modules of the controller. This module uses two techniques, an outlier-robust Kalman filter (ORKF) and a locally-weighted partial least squares (LW-PLS) regression model, which leverage the advantages of automatic measurement error elimination with ORKF and data-driven prediction with LW-PLS. The module includes a nominal angle analysis (NAA) method to distinguish between signal faults and large changes in sensor values caused by real dynamic changes in glucose-insulin metabolism and insulin kinetics. The SED&FR module also smooths CGM signal jumps caused by CGM calibration with BGC measurements collected from finger sticks.

Figure 2.

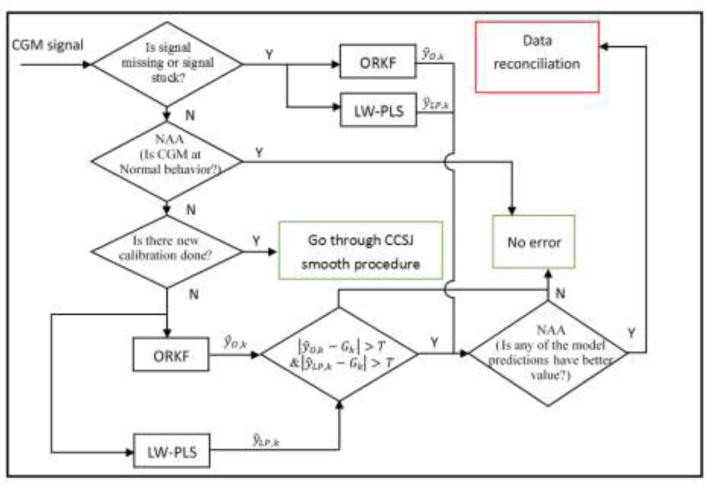
Flow diagram of SED&FR algorithm

At each CGM reading (5 min sampling time), the SLSM module (Figure 3) will first reconcile the CGM value in the SED&FR sub-module. The reconciled CGM value and the information from the controller will be sent to the CPA sub-module. CPA sub-module will generate 8 indexes to assess different aspects of controller performance and modify the controller parameters such as λ, insulin constraints, weight in controller objective function, and the aggressiveness parameter μ. GC prediction and insulin infusion rate suggestions will also be corrected based on the faults indicated by these indexes.

Figure 3.

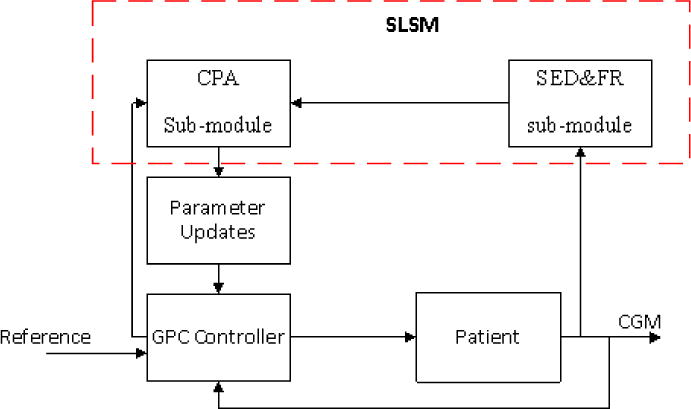
Flow diagram of SLSM procedure

2.2 Period-Level Supervision Module

The PLSM is developed based on LQG tradeoff curve to assess the performance of GC regulation during a specific period of time that may include various disturbances to GC such as meals and exercise.

For GPC objective function (Eq. 2) if N₁ = 1, N_u = N₂, N → ∞, the objective function converges to the LQG objective function(CLARKF et al., 1987):

$$\frac{J}{N_2}\to J_{\mathit{\text{GPC}}}=E{[GC-r]}^2+\mathit{w}E{[\mathrm{\Delta }I]}^2$$ (22)

The GPC control decisions optimized its objective function irrespective of the fact that only the first control move is actually implemented.(Huang, 1998) Hence, the LQG problem can be solved by the infinite GPC solution. The infinite value of N₂ may cause a large calculation burden to solve the linear least squares problem. The model in GPC may not accurate enough to give a GC prediction over a long horizon. In practice, a finite value of N₂ is usually enough to achieve the approximate infinite horizon LQG solution via the GPC approach(Huang, 1998). In this case, N₁, N₂, and N_u in LQG objective function are set to the same values used in the GPC objective function (Eq. 2).

Once the problem is formulated as an LQG problem, the tradeoff curve (Figure 4) can be calculated by varying the weight w. The weights used to generate the tradeoff curve are denoted as w_t. w is varying at each time step (Eq. 1 to 8). In order to generate the tradeoff curve, w_t is assigned values in the range 0.1 *w (k) to 2 * w (k) with increment of 0.1 * w (k). By using different w_t, a set of E [GC − r f]² and E [ΔI]² are plotted as tradeoff curve at each time period (period length=N_u). The operation point is calculated based on previous data by using

$$E_y(k)={\displaystyle {\sum }_{j=N_1}^{N_2}{[GC(k+j-N_2)-r(k+j-N_2)]}^2/N_u}$$ (23)

$$E_I(k)={\displaystyle {\sum }_{j=1}^{N_u}\mathrm{\Delta }I{(k+j-1-N_2)}^2/N_{\mathrm{u}}}$$ (24)

Figure 4.

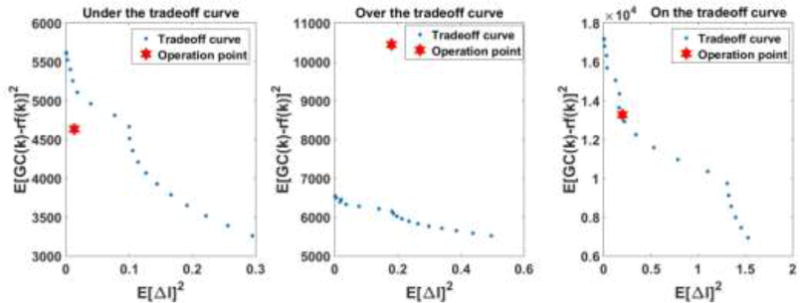
Example of tradeoff curve analysis

Comparing the tradeoff curve and the operation point positions, the performance of controller is as expected or better than expected if the operation point is at or below the tradeoff curve, respectively. If the operation point is above the tradeoff curve, the controller is not at its optimal condition. And if current GC(k) is close or at hypoglycemia or hyperglycemia thresholds (indicated by dangerous change index (I_DC) in Eq A.4) the controller will be retuned through the following procedure:

$$\mathit{\text{hypo}}(k)=\{\begin{array}{cc}1& if{I}_{DC}=-1\\ 0& \mathit{\text{otherwise}}\end{array}$$ (25)

$$\mathit{\text{hyper}}(k)=\{\begin{array}{cc}1& if{I}_{DC}=1\\ 0& \mathit{\text{otherwise}}\end{array}$$ (26)

When k mod N_u = 0, if operating point (E_I (k), E_y (k)) is above the tradeoff curve:

$$\mu (k)=\{\begin{array}{cc}\max (\mu (k-1)-{\mu }_{SL}^d,{\mu }_{\mathit{min}})& if\left[{\displaystyle \sum _{j=k-N_u}^k\mathit{\text{hypo}}(j)}\right]>0\\ \max ({\mu }_{SL}^i+\mu (k-1),{\mu }_{\mathit{max}})& if\left[{\displaystyle \sum _{j=k-N_u}^k\mathit{\text{hypo}}(j)}\right]=0\&\left[{\displaystyle \sum _{j=k-N_u}^k\mathit{\text{hyper}}(j)}\right]>0\\ \mu (k-1)& \mathit{\text{otherwise}}\end{array}$$

$$s.t.{\mu }_{SL}^d=\mu (k-N_u)-\min (\mu (k-N_u+1),\mu (k-N_u+2),\dots ,\mu (k-1))$$

$${\mu }_{SL}^i=\max (\mu (k-N_u),\mu (k-N_u+1),\dots ,\mu (k-1))-\mu (k-N_u)$$ (27)

hypo (k) and hyper(k) are denoting the hypoglycemia and hyperglycemia danger indicated by I_DC, respectively. Once the operation point (E_I (k), E_y (k)) is above the tradeoff curve if hypo =1 during every N_u samples, μ will be decreased by ${\mu }_{SL}^d$, and if no such hypo exists and hyper =1, μ will be increased by ${\mu }_{SL}^i$. The factor μ is still limited by upper and lower bounds, μ_mxa and μ_min. ${\mu }_{SL}^d$ and ${\mu }_{SL}^i$ are the largest reduction or increase increments of μ in the past N_u steps, respectively. This way, PLSM has a more aggressive parameter retuning strategy than SLSM since more information is available to PLSM.

2.3 Day Level Supervision Module

BGC dynamic changes can be affected by many factors such as a meal, physical activity and sleep throughout the day. The performance assessment of AP based on just one time period is not informative about various changes that may occur at different times and cannot tune the controller for optimal performance over a day. For example, a large value is assigned to μ for post-meal hyperglycemia, will yield an aggressive controller during sleep and may drive the BGC into hypoglycemia. The day Level Supervision Module (DLSM) analyzes the performance of AP during past 24 hours and guides future controller retuning accordingly.

In the DLSM, first the CGM values are separated into 3 different categories and their frequency of occurrence is captured by parameters C₁, C₂, and C₃ based on the values of GC. The classification procedure is:

When k mod 288 = 0, set C₁, C₂, and C₃ equal to 0.

For j from k − 287 to k:

$$\begin{array}{cc}\text{if}\text{GC}(\mathrm{j})\le 70& {\mathrm{C}}_1={\mathrm{C}}_1+1\\ \text{elseif}180\le \text{GC}(\mathrm{j})\le 70& {\mathrm{C}}_2={\mathrm{C}}_2+1\\ \text{else}& {\mathrm{C}}_3={\mathrm{C}}_3+1\end{array}$$ (28)

where, C₁, C₂, and C₃ indicate the number of GC samples in hypoglycemia, euglycemia, and hyperglycemia range in the last 24 hours, respectively. For a sampling time of 5 minutes, there are 288 samples in 24 hours. If C₁ > 0, hypoglycemia has occurred during the last 24-hours period and the adjustable range of the controller parameters and constraints for insulin need to be changed to be more conservative to reduce hypoglycemia potential in the future. The maximum and minimum GC within the previous 24 hours are denoted as GC_max and GC_min. The adjustable range of controller parameters and the constraints for insulin calculations are modified as

$${\text{ISF}}_{\mathrm{m}}={\displaystyle {\sum }_{\mathrm{j}=\mathrm{k}-287}^{\mathrm{k}}\text{ISF}(\mathrm{j},1,1)}$$ (29)

$$\begin{array}{l}\begin{array}{c}{I}_{\mathit{\text{cor}}}^{\mathit{max}}=\max (0.1,I_{\mathit{\text{cor}}}^{\mathit{max}}-\frac{r_0-G{C}_{\mathit{min}}}{{\text{ISF}}_{\mathrm{m}}})\\ {\mu }_{\mathit{max}}=\max (0.1,{\mu }_{\mathit{max}}-\min (0.05,\frac{r_0-G{C}_{\mathit{min}}}{r_0}))\\ {\mu }_{\mathit{min}}=\max (0.05,{\mu }_{\mathit{min}}-\min (0.05,\frac{r_0-G{C}_{\mathit{min}}}{r_0}))\end{array}\}if{C}_1>0\\ \begin{array}{c}{I}_{\mathit{\text{cor}}}^{\mathit{max}}=\max (3,I_{\mathit{\text{cor}}}^{\mathit{max}}+\frac{180-G{C}_{\mathit{max}}}{{\text{ISF}}_{\mathrm{m}}})\\ {\mu }_{\mathit{max}}=\min (1,{\mu }_{\mathit{max}}+\min (0.05,\frac{180-G{C}_{\mathit{max}}}{r_0}))\\ {\mu }_{\mathit{min}}=\min (0.05,{\mu }_{\mathit{min}}-\min (0.05,\frac{180-G{C}_{\mathit{max}}}{r_0}))\end{array}\}if{C}_3>0\&[{\displaystyle {\sum }_{j=k-287}^k\mathit{\text{hypo}}(k)=0}\end{array}$$ (30)

Hypoglycemia may cause more immediate treats than the hyperglycemia. Consequently, the constraints for aggressive control system modification are stricter when BGC is near the hypoglycemia limit. If there has been a hypoglycemia episode in the past 24 hours, the constraints for correction insulin and the upper bound of μ are reduced based on the distance between the minimum GC value and the reference value. And if GC values larger than 180mg/dl occurred in the past 24 hours and there were no hypoglycemia threat during that period, the constraints for correction insulin and the upper bound of μ are reduced based on the distance between the maximum GC value and the hyperglycemia threshold (180mg/dl). To prevent extreme cases causing large variation in $I_{\mathit{\text{cor}}}^{\mathit{max}}$ and μ_min, the absolute deviation of μ_max and μ_min is limited as 0.1 for each 24-hour period supervision and the constraints for the $I_{\mathit{\text{cor}}}^{\mathit{max}}$, μ_max,, and μ_min are set as [0.1, 3], [0.1 1], and [0.05 1], respectively. The initial values for $I_{\mathit{\text{cor}}}^{\mathit{max}}$, μ_max, and μ_min are 1, 0.65, and 0.4.

2.4 Multi-level Supervision Module

The ML-SCM (Figure 5) is developed to supervise the performance of AP system in different time scales by using and coordinating SLSM, PLSM, and DLSM. The ML-SCM is capable of detecting the errors in CGM readings reported to the AP, assessing the performance of the AP control system, and retuning it to improve its performance. The CGM signal is reconciled by SED&FR sub-module at each sampling time. The reconciled CGM signal is used by all other modules of the AP. SLSM and PLSM will modify the AP controller settings to suggest more accurate insulin infusion rate and these modifications are guided by DLSM.

Figure 5.

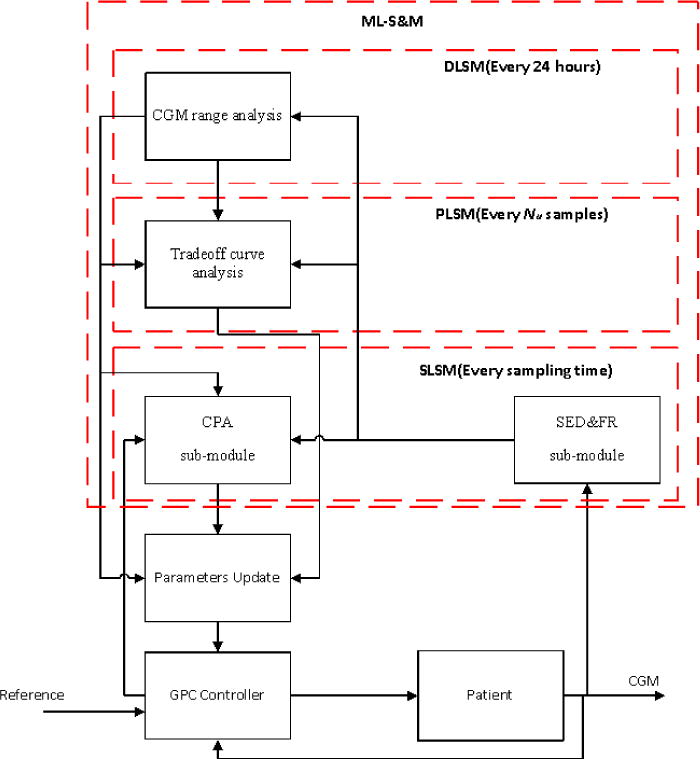
Flow chart of AP system with multi-level supervision module

The summary of parameters, index, and indicators used in the ML-SCM is described in Table 3.

Table 3.

Summary of parameters, index and indicators

Indexes and indicators	Definition	Equation number for definition
μ	Aggressiveness factor	4
Ii	idle index	9
Ipw	performance watchdog	12
Islug	sluggish control indicator	15
Ioff set	large offset indicator	16
Icor	correction insulin bolus	19
hypo	Hypoglycemia indicator	25
hyper	Hyperglycemia indicator	26
${\mu }_{SL}^d$	Aggressiveness factor decrement	27
${\mu }_{SL}^i$	Aggressiveness factor increment	27
$I_{\mathit{\text{cor}}}^{\mathit{max}}$	Maximum of correction insulin bolus	29
μmax	Maximum of aggressiveness factor	30
μmin	Minimum of aggressiveness factor	30

3. RESULTS

3.1 Simulations

Thirty in silico subjects (10 adults (Adu), 10 adolescents (Ado), and 10 children (Chi)) in the UVa/Padova simulator were tested by using AP control systems with four different supervision conditions: without any supervision and modification (S&M), with SLSM, with SLSM and PLSM, and with ML-(including SLSM, PLSM and DLSM). Each patient was simulated 10 times with a 3-day scenario. For CGM seeds provided by the simulator. Different meal plans are given for different age groups (Table 4). The detailed result of AP system when different sub-modules of ML-SCM are operational is displayed in the part II of appendix. The comparison of average percent time in various ranges of BGC for AP systems for each age group is reported in Table A.5 (Detailed data of each subject is displayed in Table A.4). The number of severe hyperglycemia and hypoglycemia periods, maximum and minimum BGC, and insulin usage are listed in Table A.6 and Table A.7. The BGC percent time in each BGC concentration range on different days for AP systems with different ML-SCM modules is given in Table A.6.

Table 4.

Three-day meal scenarios for different age groups (Carbohydrate (g))

Time		Adolescent	Adult	Children
Day 1	09:45	48	60	36
	13:30	47	59	35
	17:45	75	94	56
	21:30	31	39	23
Day 2	09:10	55	69	41
	13:45	70	88	53
	18:00	65	81	49
	22:00	20	25	15
Day 3	09:00	40	50	30
	14:00	68	85	51
	18:20	75	94	56
	22:30	25	31	19
Daily average		206	258	155

The performance of the AP system is consistently improving by using additional supervision modules (Tables A.5 to A.7). Overall, more BGC values are shown to be in the euglycemia range with ML-SCM, average the BGC values in range (70-180 mg/dl) have increased by 14% compared to the AP system without S&M. The AP system with the ML-SCM successfully modified its parameters to reduce serious hypo- and hyperglycemia (BGC>250 or BGC<50) (Table A.6). AP system with ML-SCM had better insulin efficiency for keeping BGC in target range. For the 3-day simulation, the total insulin use is reduced by about 2.3% on average compared to the AP system without S&M.

3.2 Clinical Assessment of the AP with ML-SCM

A clinical experiment was conducted to illustrate the performance of the AP with and without ML-SCM. A multivariable AP was used(Turksoy et al., 2014a). The same subject participated in two experiments using the AP with and without ML-SCM. Both experiments lasted for 56 hours (From first day 8:00 to third day 16:00). The AP suggested insulin boluses, and the subject had the same meal scenarios (Table 5) and basal insulin plan.

Table 5.

Meal scenarios for the clinical experiments

Day	Day1				Day2				Day3
Time	8:00	12:00	6:00	10:00	8:00	12:00	6:00	10:00	8:00	12:00
Carb(g)	67	82	89	24	67	82	89	24	67	82

Besides the meal, the subject may also eat additional carbohydrates, the so-called rescue carbohydrate (RC), when the BGC level is considered to be dangerous in order to prevent the occurrence of hypoglycemia. After the warning for RC is issued, consuming the RC is decided by the subject and the endocrinologist based on the CGM measurements and their experience. Since it is potentially dangerous to keep the subject in the low BGC range, the amount of RC is considered to evaluate the number of hypoglycemia episodes the subject may have during the experiment. The CGM measurements in the three days and insulin infusion rate of the two experiments are compared in Figure 6 along with the carbohydrate information.

Figure 6.

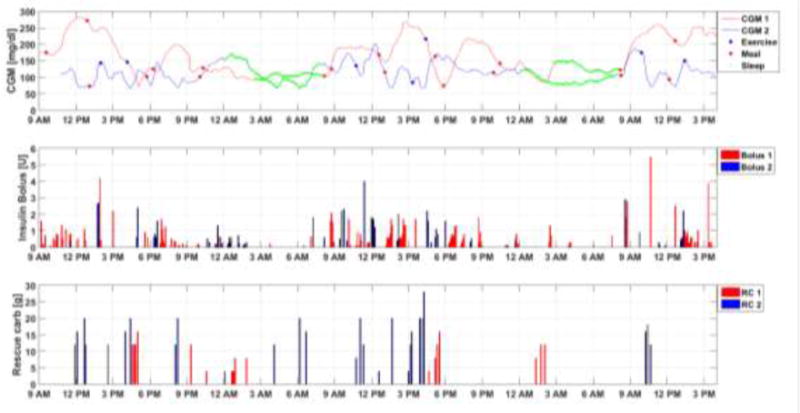
Performance comparison of AP system with and without ML-SCM (1: AP system with ML-SCM, 2: AP system without ML-SCM)

The CGM values are higher for the AP with ML-SCM for two reasons. First, the subject had much higher GC in the morning every day and then had breakfast and lunch but did not perform any exercise, challenging the AP controller. Second, the controller was modified to be less aggressive in order to reduce the reliance on RC for preventing hypoglycemia. The intent was to move away from the GC remaining close to hypoglycemia threshold because hypoglycemia is more dangerous in the short term to cause immediate harm to the subject (Cryer et al., 2003). For AP system without ML-SCM, the CGM values remain above the hypoglycemia limit but low even after taking RC based on predictive hypoglycemia alarms. Without taking RC, there would have been a large number of hypoglycemic events. During the three-day experiment, the subject consumed 184 g when the AP with ML-SCM was used compared to 402 g RC using the AP without ML-SCM. The AP without ML-SCM was too aggressive for this subject and the subject had to rely on taking additional carbohydrates as RC to maintain the CGM in range.

On the first day, since the initial CGM value is higher in CGM 1 (AP with ML-SCM) compared with CGM 2 (AP without ML-SCM), more small doses of insulin bolus were given to bring the CGM back to safe range (Figure 6). Around 5 PM on the first day a low CGM value appeared and the controller was modified to be less aggressive to prevent future hypoglycemia. For the CGM 2 trace (AP without ML-SCM), since the controller is not modified by the ML-SCM module, low CGM values appeared at 1 PM, 4:40 PM, 6:00 PM and 8:00 PM on the first day.

On the second day, CGM 2 still has multiple low CGM values including one after lunch (1:30PM). For CGM 1, only one CGM value is close to the hypoglycemia threshold because of exercise. On the third day, there was no exercise when the AP system with ML-SCM was used and the CGM 1 value is higher compared with CGM 2, and the controller is modified to be more aggressive. Hence, the insulin bolus amount is much larger on the third day compared to the case using the AP without ML-SCM.

4. DISCUSSION

The percentage of time in severe hyperglycemia (BGC>250 mg/dl) has increased for some subjects such as Adu3 and Adu10, when SLSM was used with respect to the AP without an ML-SCM (Table A.5). This is because the factors that influence the BGC dynamics, such as meals, often last much longer than one sampling time (5 minutes). The AP system modification based on one sample need to be more conservative to avoid a controller tuning that would be too aggressive. For example, as the BGC increases after a meal, the insulin infusion rate should be large enough to prevent hyperglycemia but not too large to cause hypoglycemia later. Since hypoglycemia may have more immediate threat to patient, the system is modified conservatively to reduce the potential for hypoglycemia.

By adding SLSM and PLSM, the improvement of BGC percentage between 180-70 mg/dl is almost the same in different days comparing with AP system without S&M (Table A.8). Improvement with ML-SCM is more significant in the second and third day than the first day, because DLSM has modified the adjustable range of the parameters in the AP system and constraints for correction insulin 24 hours after the beginning of the experiment. With data of a whole day, more information is available about the performance of the AP system, and the AP system is modified to reduce both hyperglycemia and hypoglycemia (Tables A.5, A.7, A.8).

In the PLSM, the horizon in LQG tradeoff curve is set the same as the GPC in the AP system, because there is no explicit information about the exact disturbance(s) (such as meal and sleep) to the glucose metabolism of the subject. If the information about the conditions were available, the range of the time period can be set to cover that condition from the beginning to end of the disturbance.

Besides meals, other factors such as exercise, stress and sleep may influence the dynamics of BGC. Because of the limitations of the simulator, the effects of exercise are not tested in this paper. In future work, different condition such as meal, exercise, and sleep need to be identified and the AP system should be modified to have a specified strategy to calculate insulin infusion rates for these various conditions.

5. CONCLUSION

A novel module for AP system performance assessment and modification based on multiple time scales is developed and tested. The ML-SCM integrates the CGM sensor error detection and signal reconciliation with controller performance assessment and modification. Three different levels of supervision modules are developed based on their time windows. The results indicate that the AP system with ML-SCM can improve its performance.

Table 1.

Acronyms List

Acronyms	Description
AP	Artificial Pancreas
BGC	Blood Glucose Monitoring
T1D	Type 1 Diabetes
CGM	Continuous Glucose Monitoring
PID	Proportional-Integral-Derivative
MLSM	Multi-level Supervision and Modification
SLSM	Sample-level Supervision Module
PLSM	Period-level Supervision Module
DLSM	Day-level Supervision Module
SED&FR	Sensor Error Detection and Functional Reconciliation
ORKF	Outlier-Robust Kalman Filter
LW-PLS	Locally-Weighted Partial Least Squares
LQG	Linear Quadratic Gaussian
GPC	Generalized Predictive Control
ARMAX	Autoregressive Moving Average Model with Exogenous Inputs
CPA	Controller Performance Assessment
NAA	Nominal Angle Analysis

Highlights.

• A multi-level supervision module is developed for model-based control systems.

• Sensor error detection and controller performance assessment are integrated.

• The performance of artificial pancreas is evaluated in different time scales.

• The controller is retuned by adjusting controller parameters and constraints.

APPENDIX

Part I: Index based controller failure detection and controller modification

Table A.1.

Summary of all indexes and indicators in CPA

Indexes and indicators	Definition	Equation number for definition
IMPE	Model prediction error index	A.1
IMEES	Error elimination speed index	A.2
IDCP	Dangerous change potential index	A.3
IDC	Dangerous change index	A.4
IICL	Insulin constraints limitation index	A.5
IWR	Weight ratio index	A.6
IPE	Prediction error indicator	A.7
IICE	Insulin constraints error indicator	A.8
IWRE	Weight ratio error indicator	A.9

Index generation:

$${\mathrm{I}}_{\text{MPE}}(\mathrm{k})=\left|{\text{GC}}^{\text{pred}}(\mathrm{k}|\mathrm{k}-1)-\text{GC}(\mathrm{k})\right|$$ (A.1)

$${\mathrm{I}}_{\text{MEES}}(\mathrm{k})=\{\begin{array}{cc}{\mathrm{I}}_{\text{MEES}}(\mathrm{k}-1)+\text{st}& \text{if}{\mathrm{I}}_{\text{MPE}}(\mathrm{k})\ge {\text{ME}}^{\max }\\ 0& \text{if}{\mathrm{I}}_{\text{MPE}}(\mathrm{k})<{\text{ME}}^{\max }\end{array}$$ (A.2)

$${\mathrm{I}}_{\text{DCP}}(\mathrm{k})=\{\begin{array}{cc}\frac{180-\text{GC}(\mathrm{k})}{\text{GC}(\mathrm{k})-\text{GC}(\mathrm{k}-1)}& \text{if}\text{GC}(\mathrm{k})-\text{GC}(\mathrm{k}-1)>0\&70<\text{GC}(\mathrm{k})<180\\ \frac{\text{GC}(\mathrm{k})-70}{\text{GC}(\mathrm{k}-1)-\text{GC}(\mathrm{k})}& \text{if}\text{GC}(\mathrm{k}-1)-\text{GC}(\mathrm{k})>0\&70<\text{GC}(\mathrm{k})<180\end{array}$$ (A.3)

$${\mathrm{I}}_{\text{DC}}(\mathrm{k})=\{\begin{array}{cc}1& \text{if}({\mathrm{I}}_{\text{DCP}}(\mathrm{k})<{\mathrm{I}}_{\text{DCP}}^{\max }\&\text{GC}(\mathrm{k})-\text{GC}(\mathrm{k}-1)>0)\text{or}(\text{GC}(\mathrm{k})>180)\\ -1& \text{if}({\mathrm{I}}_{\text{DCP}}(\mathrm{k})<{\mathrm{I}}_{\text{DCP}}^{\max }\&\text{GC}(\mathrm{k})-\text{GC}(\mathrm{k}-1)<0)\text{or}(\text{GC}(\mathrm{k})>70)\\ 0& \text{otherwise}\end{array}$$ (A.4)

$${\mathrm{I}}_{\text{ICL}}(\mathrm{k})=\{\begin{array}{cc}{\mathrm{I}}_{\text{ICL}}(\mathrm{k}-1)+1& \text{if}\mathrm{I}(\mathrm{k})={\mathrm{I}}_{Max}\\ 0& \text{if}\mathrm{I}(\mathrm{k})<{\mathrm{I}}_{Max}\end{array}$$ (A.5)

$${\mathrm{I}}_{\text{WR}}=\frac{{\displaystyle {\sum }_{\mathrm{j}=\mathrm{N}1}^{\mathrm{N}2}{[{\text{GC}}^{\text{pred}}(\mathrm{k}+\mathrm{j}|\mathrm{k})-\mathrm{r}(\mathrm{k}+\mathrm{j})]}^2}}{{\displaystyle {\sum }_{\mathrm{j}=1}^{\text{Nu}}\mathrm{w}\ast \mathrm{\Delta }\mathrm{I}{(\mathrm{k}+\mathrm{j}-1)}^2}}$$ (A.6)

Controller failure detection (Binary numbers 1 and 0 are used to indicate the presence or absence of such errors):

$${\mathrm{I}}_{\text{PE}}=\{\begin{array}{cc}1& \text{if}{\mathrm{I}}_{\text{MPE}}>{\mathrm{I}}_{\text{MPE}}^{\max }\text{or}{\mathrm{I}}_{\text{MEES}}\ge {\mathrm{I}}_{\text{MEES}}^{\max }\\ 0& \text{otherwise}\end{array}$$ (A.7)

$${\mathrm{I}}_{\text{ICE}}=\{\begin{array}{cc}1& \text{if}{\mathrm{I}}_{\text{DC}}=1\&{\mathrm{I}}_{\text{ICL}}\ge {\mathrm{I}}_{\text{ICL}}^{\max }\\ 0& \text{otherwise}\end{array}$$ (A.8)

$${\mathrm{I}}_{\text{WRE}}=\{\begin{array}{cc}1& \text{if}{\mathrm{I}}_{\text{WR}}>1\&{\mathrm{I}}_{\text{DC}}=1\text{or}{\mathrm{I}}_{\text{DC}}=-1\\ 0& \text{otherwise}\end{array}$$ (A.9)

Controller retuning based on indexes:

$${\lambda }^{\prime }(\mathrm{k}|\mathrm{k}-1)=\{\begin{array}{cc}1-\left(1-\frac{{\mathrm{I}}_{\text{MPE}}}{\text{den}}\right)\ast \lambda (\mathrm{k}|\mathrm{k}-1)& \text{if}{\mathrm{I}}_{\text{PE}}=1\&{\mathrm{I}}_{\text{MPE}}{\text{<I}}_{\text{MPE}}^{\text{SE}}\&{\lambda }^{\prime }(\mathrm{k}|\mathrm{k}-1)>0.5\\ 0.05& \text{if}{\mathrm{I}}_{\text{PE}}=1\&\left({\mathrm{I}}_{\text{MPE}}{\text{<I}}_{\text{MPE}}^{\text{SE}}\text{or}{\lambda }^{\prime }(\mathrm{k}|\mathrm{k}-1)<0.5\right)\end{array}$$ (A.10)

$${\mathrm{I}}^{\prime }(\mathrm{k})=\{\begin{array}{cc}\mathrm{I}(\mathrm{k})\ast \left(1+\frac{{\text{log}}_{10}\left(\text{GC}(\mathrm{k})-{\text{GC}}^{\text{pred}}(\mathrm{k}|\mathrm{k}-1)\right)\ast \text{BW}}{\alpha }\right)\ast \text{ISF}& \text{if}\text{GC}(\mathrm{k})-{\text{GC}}_{\mathrm{k}-1}^{\text{pred}}(\mathrm{k}|\mathrm{k}-1)>0\&({\mathrm{I}}_{\text{DC}}=1\text{or}{\mathrm{I}}_{\text{DC}}=0)\&{\mathrm{I}}_{\text{PE}}=1\\ \text{min(I}(\mathrm{k})\ast \left(1-\frac{{\text{log}}_{10}\left({\text{GC}}^{\text{pred}}(\mathrm{k}|\mathrm{k}-1)-\text{GC}(\mathrm{k})\right)\ast \text{BW}}{\alpha }\right)\ast \text{ISF}& \text{if}\text{GC}(\mathrm{k})-{\text{GC}}_{\mathrm{k}-1}^{\text{pred}}(\mathrm{k}|\mathrm{k}-1)<0\&{\mathrm{I}}_{\text{DC}}=0\&{\mathrm{I}}_{\text{PE}}=1\end{array}\mathrm{s}.\mathrm{t}.0<{\mathrm{I}}^{\prime }(k)<\mathrm{I}(\mathrm{k})+I_{\text{cor}}^{\max }$$ (A.11)

$${\text{GC}}^{{\text{pred}}^{\prime }}(\mathrm{k}+1|\mathrm{k})={\text{GC}}^{\text{pred}}(\mathrm{k}+1|\mathrm{k})-\left({\text{GC}}^{\text{pred}}(\mathrm{k}|\mathrm{k}-1)-\text{GC}(\text{k)}\right)\ast \beta \text{if}{\mathrm{I}}_{\text{PE}}=1$$ (A.12)

$${\mathrm{I}}_{Max}^{\prime }=\{\begin{array}{cc}{\mathrm{I}}_{Max}\ast \gamma & \text{if}{\mathrm{I}}_{Max}^{\prime }<35(\mathrm{U}/\text{hour})\&{\mathrm{I}}_{\text{ICE}}=1\\ 35(\mathrm{U}/\text{hour})& \text{if}{\mathrm{I}}_{Max}^{\prime }\ge 35(\mathrm{U}/\text{hour})\&{\mathrm{I}}_{\text{ICE}}=1\end{array}$$ (A.13)

$$\mathrm{J}(\mathrm{N}1,\mathrm{N}2)={\min }_{\mathrm{I}(\mathrm{k})}{\displaystyle {\sum }_{\mathrm{j}=\mathrm{N}1}^{\mathrm{N}2}{[{\text{GC}}^{\text{pred}}(\mathrm{k}+\mathrm{j}|\mathrm{k})-\mathrm{r}(\mathrm{k}+\mathrm{j})]}^2\text{if}{\mathrm{I}}_{\text{WRE}}=1}$$ (A.14)

Table A.2.

Value for parameter ISF

	Adult	Adolescent	Child
Sensitive	0.8	0.8	0.4
Normal	1	1	0.5
Resistant	1.2	1.2	0.6

Table A.3.

Summary of parameters and their values in CPA

Parameters	Definition	Equation number	Value
MEmax	Threshold of IMPE to determine IMEES	A.2	10
$I_{\mathit{\text{DCP}}}^{\mathit{max}}$	Threshold of IDCP to determine IDC	A.4	4
$I_{\mathit{\text{MPE}}}^{\mathit{max}}$	Threshold of IMPE to determine IPE	A.7	20
$I_{\mathit{\text{MEES}}}^{\mathit{max}}$	Threshold IMEES of to determine IPE	A.7	30
$I_{\mathit{\text{ICL}}}^{\mathit{max}}$	Threshold IICL of to determine IICE	A.8	40
$I_{\mathit{\text{MPE}}}^{SE}$	Threshold of IMPE to tuning λ	A.10	30
α	Parameter for tuning I′	A.11	270
β	Proportional feedback constant for ${\mathit{GC}}^{{\mathit{\text{pred}}}^{\prime }}$	A.12	0.35
γ	Filter constant determines how fast the insulin constraint is increasing	A.13	1.1
den	Parameter for tuning I′	A.10	60 (adults, adolescents) 90 (children)

Part II: Comparison of AP performance under different conditions

Table A.4.

Comparison of performance between AP system without S&M, with SLSM, SLSM and PLSM, and with ML-SCM (percent time in each concentration range. The insulin sensitivity level (ISL): S sensitive, N normal, and R resistant. A: <250 mg/dl, B: 250-180 mg/dl, C: 180-70 mg/dl, D: 70-50 mg/dl, E: >50 mg/dl)

Subject Type	ISL	BW (kg)	BGC without S&M					BGC with SLSM					BGC with SL&PLSM					BGC with ML-SCM
			A	B	C	D	E	A	B	C	D	E	A	B	C	D	E	A	B	C	D	E
Ado 1	S	68.7	0	3	83	8	5	0	4	84	8	4	0	2	88	6	4	0	0	91	5	4
Ado 2	R	51	22	30	48	0	0	20	27	53	0	0	16	22	62	0	0	12	15	73	0	0
Ado 3	N	44.8	28	33	38	1	0	26	33	40	1	0	25	28	47	0	0	24	23	53	0	0
Ado 4	N	49.6	14	20	64	1	1	13	20	66	0	1	13	19	67	1	0	10	11	78	1	0
Ado 5	S	47.1	17	26	57	0	0	16	23	61	0	0	13	20	67	0	0	10	14	76	0	0
Ado 6	N	45.4	4	8	85	1	2	4	7	86	1	2	4	6	89	1	0	4	5	90	1	0
Ado 7	N	37.9	37	40	23	0	0	35	37	28	0	0	31	33	36	0	0	26	24	50	0	0
Ado 8	R	41.2	36	39	25	0	0	35	36	29	0	0	32	33	35	0	0	29	26	45	0	0
Ado 9	R	43.9	42	41	17	0	0	41	40	19	0	0	40	38	22	0	0	38	28	34	0	0
Ado 10	N	47.4	10	17	73	0	0	10	16	74	0	0	9	15	76	0	0	5	7	88	0	0
Mean		47.7	21	26	51	1	1	20	24	54	1	1	18	22	59	1	0	16	15	68	1	0
Adu 1	S	102.3	0	3	86	5	7	0	5	84	5	6	2	4	86	5	3	2	4	89	3	2
Adu 2	S	111.1	0	1	84	8	7	0	3	84	7	6	2	3	88	3	4	1	4	92	2	1
Adu 3	S	81.6	2	6	74	18	0	4	9	74	13	0	4	7	77	12	0	0	3	88	9	0
Adu 4	S	63	1	3	78	10	7	2	4	79	9	6	3	2	80	9	6	3	3	82	9	3
Adu 5	R	94.1	6	10	74	8	2	6	10	76	6	2	6	9	77	6	2	6	7	79	8	0
Adu 6	N	66.1	5	3	24	1	67	2	3	41	1	53	3	4	49	5	39	2	3	80	6	9
Adu 7	S	91.2	2	7	86	2	2	2	5	89	2	2	2	4	90	2	2	2	5	92	1	0
Adu 8	N	102.8	0	3	84	7	7	1	3	84	6	6	1	4	84	6	5	0	1	88	5	5
Adu 9	R	74.6	1	4	91	3	1	1	4	92	2	1	1	2	94	2	1	0	1	99	0	0
Adu 10	S	73.9	0	3	76	16	5	2	4	78	12	4	2	3	81	10	4	2	4	82	9	4
Mean		86.1	2	4	76	8	11	2	5	78	6	9	3	4	81	6	7	2	4	87	5	2
Chi 1	S	34.6	40	43	17	0	0	39	39	22	0	0	38	37	25	0	0	37	28	35	0	0
Chi 2	N	28.5	21	30	47	2	1	20	29	49	2	0	13	20	65	2	0	11	14	74	1	0
Chi 3	S	41.2	11	19	69	1	0	10	18	71	1	0	9	13	77	1	0	7	11	82	0	0
Chi 4	S	35.5	0	5	82	7	6	0	4	84	7	5	3	4	87	4	2	3	6	88	3	0
Chi 5	N	37.8	14	24	62	0	0	13	21	66	0	0	13	19	68	0	0	10	13	77	0	0
Chi 6	N	41	4	8	74	9	5	4	7	77	8	4	4	8	77	7	4	4	6	80	8	2
Chi 7	R	45.5	6	14	76	2	2	5	10	82	2	1	4	8	85	2	1	4	8	85	2	1
Chi 8	R	23.7	3	8	89	0	0	2	8	90	0	0	2	5	93	0	0	2	3	95	0	0
Chi 9	R	35.5	9	15	75	0	1	9	13	78	0	0	8	13	79	0	0	8	10	82	0	0
Chi 10	N	35.2	42	44	14	0	0	40	38	22	0	0	33	33	34	0	0	28	24	48	0	0
Mean		35.9	15	21	61	2	2	14	19	64	2	1	13	16	69	2	1	11	12	75	1	0
Overall		56.6	13	17	62	4	4	12	16	65	3	3	11	14	70	3	3	10	10	76	2	1

Table A.5.

Comparison of performance between AP system without S&M, with SLSM, SLSM and PLSM, and with ML-SCM. Average percent time for each population group in each concentration range (A: <250 mg/dl, B: 250-180 mg/dl, C: 180-70 mg/dl, D: 70-50 mg/dl, E: >50 mg/dl)

Subject Type	BW (kg)	BGC without S&M					BGC with SLSM					BGC with SL&PLSM					BGC with ML-SCM
		A	B	C	D	E	A	B	C	D	E	A	B	C	D	E	A	B	C	D	E
Ado	47.7	21	26	51	1	1	20	24	54	1	1	18	22	59	1	0	16	15	68	1	0
Adu	86.1	2	4	76	8	11	2	5	78	6	9	3	4	81	6	7	2	4	87	5	2
Chi	35.9	15	21	61	2	2	14	19	64	2	1	13	16	69	2	1	11	12	75	1	0
Overall	56.6	13	17	62	4	4	12	16	65	3	3	11	14	70	3	3	10	10	76	2	1

Table A.6.

Comparison of performance between AP systems with SLSM and without S&M

Subject Type	BGC without S&M					BGC with SLSM
	Average daily hyper- glycemia episodes (GC>250 mg/dl)	Average daily hypo- glycemia episodes (GC<50 mg/dl)	Max GC (mg/dl)	Min GC (mg/dl)	Average total insulin use (U/3 days)	Average daily hyper- glycemia episodes (GC>250 mg/dl)	Average daily hypo- glycemia episodes (GC<50 mg/dl)	Max GC (mg/dl)	Min GC (mg/dl)	Average total insulin use (U/3 days)
Ado 1	0.00	0.13	246	12	93	0.00	0.11	248	13	88
Ado 2	2.38	0.00	326	98	148	2.14	0.00	307	98	151
Ado 3	3.01	0.00	297	69	128	2.94	0.00	293	77	129
Ado 4	1.63	0.17	349	25	151	1.31	0.17	348	32	150
Ado 5	1.84	0.00	291	95	131	1.70	0.00	287	95	132
Ado 6	0.45	0.43	271	17	91	0.45	0.43	271	30	91
Ado 7	4.28	0.00	308	99	134	4.18	0.00	296	99	134
Ado 8	4.10	0.00	424	100	218	3.86	0.00	423	100	219
Ado 9	4.73	0.00	479	100	270	4.55	0.00	474	95	270
Ado 10	1.17	0.00	271	95	143	1.15	0.00	269	95	147
Mean	2.36	0.07	326	71	151	2.23	0.07	322	73	151
Adu 1	0.00	0.83	217	37	133	0.00	0.81	218	39	131
Adu 2	0.00	0.80	239	29	140	0.00	0.77	245	30	140
Adu 3	0.21	0.00	222	50	87	0.45	0.00	223	51	85
Adu 4	0.11	0.67	262	32	110	0.22	0.64	263	33	110
Adu 5	0.63	0.50	306	31	205	0.68	0.49	307	49	205
Adu 6	0.52	1.07	291	7	76	0.20	0.99	289	8	94
Adu 7	0.21	0.30	274	43	147	0.22	0.29	279	45	141
Adu 8	0.00	0.47	238	31	146	0.11	0.47	239	29	146
Adu 9	0.10	0.97	253	27	157	0.11	0.34	253	33	149
Adu 10	0.00	0.70	242	41	106	0.22	0.70	251	43	105
Mean	0.18	0.63	254	33	131	0.22	0.55	257	36	131
Chi 1	4.54	0.00	338	83	158	4.51	0.00	318	81	158
Chi 2	2.32	0.50	373	23	115	2.30	0.43	353	30	112
Chi 3	1.26	0.00	290	40	110	1.16	0.00	288	44	103
Chi 4	0.00	0.50	249	28	86	0.00	0.39	250	37	85
Chi 5	1.43	0.00	320	83	128	1.39	0.00	320	82	128
Chi 6	0.43	0.93	318	19	128	0.43	0.92	330	26	128
Chi 7	0.69	0.57	295	26	115	0.58	0.56	302	26	117
Chi 8	0.31	0.00	283	80	59	0.24	0.00	279	80	60
Chi 9	1.06	0.37	309	21	111	0.97	0.15	309	22	109
Chi 10	4.22	0.00	341	96	157	4.58	0.00	337	96	162
Mean	1.63	0.30	312	50	117	1.62	0.25	309	52	116
Overall	1.39	0.33	297	51	133	1.35	0.29	296	54	133

Table A.7.

Comparison of performance between AP systems with SLSM and PLSM, and with ML-SCM

Subject Type	BGC with SLSM and PLSM					BGC with ML-SCM
	Average daily hyper- glycemia episodes (GC>250 mg/dl)	Average daily hypo- glycemia episodes (GC<50 mg/dl)	Max BGC (mg/dl)	Min BGC (mg/dl)	Average total insulin use (U/3 days)	Average daily hyper- glycemia episodes (GC>250 mg/dl)	Average daily hypo- glycemia episodes (GC<50 mg/dl)	Max BGC (mg/dl)	Min BGC (mg/dl)	Average total insulin use (U/3 days)
Ado 1	0.00	0.11	248	14	82	0.00	0.07	249	22	75
Ado 2	1.83	0.00	293	98	152	1.27	0.00	290	98	153
Ado 3	2.60	0.00	283	90	129	2.51	0.00	283	96	129
Ado 4	1.46	0.17	345	53	150	1.05	0.00	343	59	150
Ado 5	1.44	0.00	279	94	133	1.02	0.00	273	94	134
Ado 6	0.47	0.42	271	38	90	0.41	0.40	271	39	90
Ado 7	3.62	0.00	293	99	135	2.63	0.00	292	99	140
Ado 8	3.24	0.00	423	100	220	3.21	0.00	413	100	230
Ado 9	4.47	0.00	459	91	273	4.25	0.00	403	68	275
Ado 10	1.01	0.00	264	95	147	0.59	0.00	264	94	148
Mean	2.01	0.07	316	77	151	1.69	0.03	308	77	152
Adu 1	0.21	0.63	255	41	130	0.23	0.50	263	41	125
Adu 2	0.21	0.48	247	33	136	0.11	0.43	261	38	130
Adu 3	0.43	0.00	232	51	82	0.00	0.00	237	51	80
Adu 4	0.31	0.63	263	33	109	0.33	0.53	266	36	91
Adu 5	0.68	0.17	308	52	204	0.63	0.00	309	56	204
Adu 6	0.35	0.95	288	9	105	0.23	0.83	286	26	113
Adu 7	0.24	0.27	282	46	133	0.22	0.10	290	49	122
Adu 8	0.11	0.45	247	29	146	0.00	0.37	251	24	144
Adu 9	0.11	0.23	252	33	148	0.00	0.00	249	78	145
Adu 10	0.23	0.53	255	43	94	0.21	0.27	263	46	94
Mean	0.29	0.43	263	37	129	0.20	0.30	267	45	125
Chi 1	3.87	0.00	313	80	156	4.02	0.00	302	76	155
Chi 2	1.46	0.05	346	40	111	1.11	0.00	325	52	99
Chi 3	1.06	0.00	286	47	101	0.78	0.00	279	63	100
Chi 4	0.34	0.07	252	45	82	0.32	0.00	257	53	71
Chi 5	1.35	0.00	321	77	129	1.18	0.00	325	70	130
Chi 6	0.41	0.73	336	26	128	0.41	0.60	347	34	120
Chi 7	0.48	0.56	335	26	124	0.44	0.37	349	42	136
Chi 8	0.23	0.00	278	80	60	0.23	0.00	270	80	60
Chi 9	0.89	0.05	310	37	107	0.93	0.00	310	87	101
Chi 10	3.38	0.00	333	96	162	2.96	0.00	315	96	162
Mean	1.35	0.15	311	55	116	1.24	0.10	308	65	113
Overall	1.22	0.22	297	57	132	1.04	0.13	295	62	130

Table A.8.

Comparison BGC percent time in each concentration range for AP systems without S&M, with SLSM, SLSM and PLSM, and with ML-SCM on different days (percent time in each concentration range. A: >250 mg/dl, B: 250-180 mg/dl, C: 180-70 mg/dl, D: 70-50 mg/dl, E: <50 mg/dl)

Time		BGC without S&M					BGC with SLSM					BGC with SL&PLSM					BGC with ML-SCM
		A	B	C	D	E	A	B	C	D	E	A	B	C	D	E	A	B	C	D	E
Day1	Ado	20	29	50	1	0	19	28	52	1	0	17	26	56	1	0	17	26	56	1	0
	Adu	2	4	83	8	3	2	5	83	8	2	4	4	86	6	0	4	4	86	6	0
	Chi	16	25	57	2	0	15	22	61	2	0	12	18	68	2	0	12	18	68	2	0
	Mean	12	19	64	4	1	12	18	66	3	1	11	16	70	3	0	11	16	70	3	0
Day2	Ado	22	24	52	1	1	21	23	55	1	0	19	20	61	0	0	17	10	73	0	0
	Adu	2	5	72	7	14	3	6	75	5	11	3	5	77	5	10	3	4	87	4	2
	Chi	19	18	61	1	1	18	16	64	1	1	17	15	67	1	0	16	10	73	1	0
	Mean	14	16	62	3	5	13	15	65	3	5	13	13	69	2	3	12	8	78	2	1
Day3	Ado	22	24	51	2	1	20	22	55	2	1	19	20	59	1	1	16	8	74	1	1
	Adu	1	3	75	6	15	1	4	76	6	13	1	3	79	7	10	1	3	89	4	3
	Chi	11	21	62	3	3	10	19	66	3	2	9	16	71	3	1	9	6	83	1	1
	Mean	11	16	63	4	6	10	15	66	4	5	10	13	70	4	4	9	6	81	2	1