Abstract
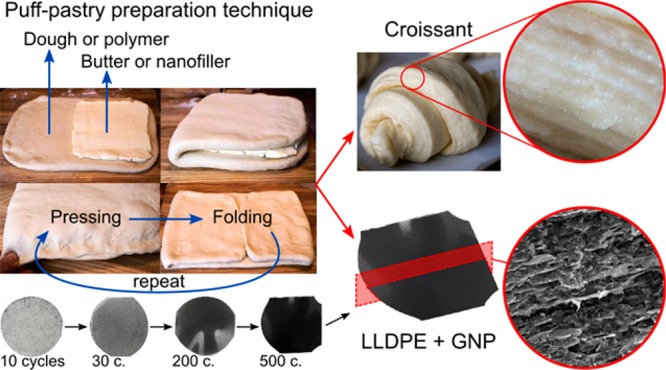
The intrinsic properties of nanomaterials offer promise for technological revolutions in many fields, including transportation, soft robotics, and energy. Unfortunately, the exploitation of such properties in polymer nanocomposites is extremely challenging due to the lack of viable dispersion routes when the filler content is high. We usually face a dichotomy between the degree of nanofiller loading and the degree of dispersion (and, thus, performance) because dispersion quality decreases with loading. Here, we demonstrate a potentially scalable pressing-and-folding method (P & F), inspired by the art of croissant-making, to efficiently disperse ultrahigh loadings of nanofillers in polymer matrices. A desired nanofiller dispersion can be achieved simply by selecting a sufficient number of P & F cycles. Because of the fine microstructural control enabled by P & F, mechanical reinforcements close to the theoretical maximum and independent of nanofiller loading (up to 74 vol %) were obtained. We propose a universal model for the P & F dispersion process that is parametrized on an experimentally quantifiable “D factor”. The model represents a general guideline for the optimization of nanocomposites with enhanced functionalities including sensing, heat management, and energy storage.
Keywords: polymer nanocomposites, nanoparticle dispersion, graphene, nanoclay, predictive model, multifunctional materials
Facing technological challenges in fields such as transportation, soft robotics, biomedical, and wearable electronics will require the availability of materials able to simultaneously bear loads and integrate multiple functionalities such as sensing, adaptation, responsiveness, energy harvesting, and communication.1 Polymer nanocomposites are promising candidates for meeting these requests because they employ nanoparticles having exceptional intrinsic properties. Graphene,2 for instance, has been proven to possess exceptional mechanical properties,3 excellent gas-barrier properties,4 high charge-carrier mobility and high thermal conductivity,5,6 and visual transparency.7 However, it has proven to be difficult to exploit the intrinsic properties of the embedded nanoparticles: the performance of nanocomposites are often disappointing and well below theoretical predictions. For example, according to classical composite theories,8 we would expect graphene nanocomposites to exhibit extraordinary mechanical performance. However, only a very limited number of papers have reported nanocomposites standing up to these expectations.9−12 Good performance and agreement with the theory is usually observed for very low nanofiller contents only (below 1 vol %).8 However, this is the range in which the absolute performance is low, questioning the use of nanoparticles in place of more-conventional alternatives. The issue lies in the following dilemma: the smaller the material’s size, the more appealing its intrinsic properties but also the more difficult the control over the nanoparticle dispersion quality during processing.13,14
However, nanocomposites are readily found in nature, and their intrinsic performance can surpass that of the best man-made composites. For instance, nacre, often taken as the golden standard in structured composites, combines CaCO3 “bricks” and protein “mortar” in a layered microstructured composite ∼3000 times tougher than each of nacre’s components.15 The hierarchical structure of nacre is believed to be the key to its properties. Hence, researchers have attempted to exploit nanoparticle properties by developing methods to obtain better microstructural control. The best resulting nanocomposites have demonstrated high mechanical performances,9−12 unusual interaction with light,16,17 resistance to flammability,18−22 self-regulating heating,23,24 energy management,25−27 high electrical and thermal conductivity,28 and sensing and structural health monitoring.29−32
However, the control over nanoparticle dispersion is usually compromised for high filler loading,11,12,33−37 making it impossible to exploit the desired large nanofiller–polymer interfacial area.38 As a consequence, nanocomposites often contain nanoparticle agglomerates that dramatically reduce performance11,12,33,39 unless they were prepared by bottom-up, but hardly scalable, approaches.40−42
To overcome the dichotomy between nanofiller loading and dispersion (and, hence, properties), herein we present an iterative materials processing technique (P & F) that draws inspiration from the process of preparation of puff pastry to make croissants (Figure 1a). This technique can create nanocomposites with well-defined nanofiller dispersion levels without the loss of dispersion efficiency, even at ultra-high nanofiller loadings. This is not achievable by traditional solution-mixing or melt-blending techniques. Moreover, we propose an analytical model that quantitatively correlates nanocomposite properties with nanofiller dispersion level. To prove the potential of the P & F technique, we produce nanocomposites with exceptional combination of functionalities, including energy management, self-heating, and strain sensing.
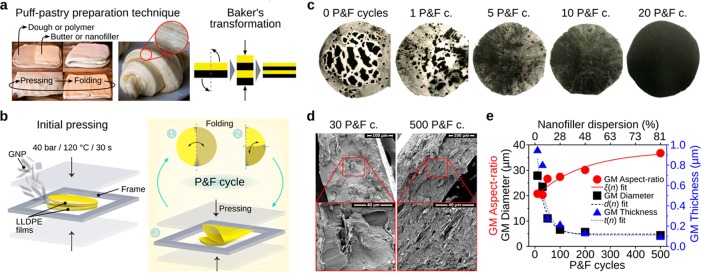
Figure 1.
Nanofiller dispersion process. (a) The P & F technique draws inspiration from the puff-pastry preparation technique (left), and its stretching and folding effect can be idealized as a Baker’s transformation (right). (b) Schematic of the P & F technique. (c) Top-view images of samples of LLDPE containing 4.8 vol % of graphite nanoplatelets (GNP) after different P & F cycles (sample diameter of ∼8 cm and sample thickness of ∼300 μm). (d) Cross-sectional SEM images of LLDPE containing 4.8 vol % GNP samples for very different filler dispersion levels: the left image shows thick and well-separated GNP agglomerates, and the right image shows well-dispersed GNPs. (e) Geometric mean (GM) values of diameter, thickness, and aspect ratio (ratio between diameter and thickness) of GNP agglomerates. The GM values were obtained from the analysis of cross-sections of LLDPE containing 4.8 vol % GNP samples for different P & F cycles. The lines are best fits using eq 4.
Results and Discussion
Micromechanical Considerations and Modeling of the P & F Dispersion Process
The P & F technique is based on the addition of nanoparticles (i.e., graphite nanoplatelets, GNP) in between two polymer films (i.e., linear-low density polyethylene, LLDPE; Figure 1b, left), followed by the application of P & F cycles (Figure 1b, right) an arbitrary number of times. Each P & F cycle is composed of a folding step in which an approximately circular GNP-containing layer is folded twice to produce a quadrant slice and a pressing step executed at a temperature slightly above the polymer melting point (≅120◦C for LLDPE). The pressing step produces a strong flow that simultaneously breaks down the agglomerates, aligns the dispersed particles, and substantially increases the GNP–LLDPE contact area, yielding a well-mixed dispersion after a number of cycles. The P & F process implements Baker’s transformation43 (Figure 1a, right) at very high applied viscous stresses.
As shown in Figure 1c, after a few P & F cycles the color of the nanocomposites becomes homogeneous to the naked eye (see also Figure S5). At small cycle numbers, the nanocomposites present large GNP agglomerates (Figure 1d, left). The size of the agglomerates decreases with increasing cycles (Figure 1e), and many well-dispersed individual particles appear throughout the samples, forming a layered structure (see further microstructural observations in section S.7.1 of the Supporting Information). After 500 P & F cycles, the initial agglomerates have mostly disappeared (Figure 1d, right), and the thickness of the dispersed particles approaches that of individual GNP (∼30 nm, see section S.3 of the Supporting Information for GNP characterizations).
The combined effect of dispersion and
orientation obtained by P
& F cannot be reached by conventional melt processing like twin-screw
melt-compounding or multilayer co-extrusion44 (which is also based on the Baker’s transformation). The
flow has a dominant extensional component that orients the particles
with their flat faces perpendicular to the pressing direction. The
squeeze flow in the thin gap between the plates produces large shear
rates. Such high shear rates may not be achievable by conventional
multilayer co-extrusion because the materials are processed at temperatures
much higher than the polymer melting point, otherwise they will hardly
flow through the extrusion line. By solving the velocity profile for
a power-law fluid using the lubrication approximation, we estimate
the volume-averaged shear rate magnitude during each P & F cycle
to be between γ̇ = 12 s–1 and
γ̇ = 1150 s–1 in the final
stages of compression, depending on whether the polymer is assumed
to slip freely from the wall or to adhere perfectly to it. Given the
high viscosity of the polymer (we are working just above the melting
temperature), the corresponding viscous stresses are large, between
3 kPa and 90 kPa (assuming 4.8 vol %; see section S.11.1 of the Supporting Information), and sufficient to break
down the initial aggregates (from the surface energy of graphene Γ≅70 mN/m
and the diameter of the platelets Dp, we
estimate the yield strength 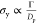 of the initial aggregates to be
smaller
than 0.74 kPa; see section S.11.1 of the Supporting Information). The controlled flow in P & F has a further
crucial benefit. With conventional processing methods, characterized
by complex flow streamlines, the flow can promote re-agglomeration
rather than dispersion if converging streamlines are present that
force the particles to come into contact with each other. In contrast,
in the P & F approach, the dominant extensional flow increases
the particle separation at each cycle by “stretching”
the fluid containing the suspended platelets.
of the initial aggregates to be
smaller
than 0.74 kPa; see section S.11.1 of the Supporting Information). The controlled flow in P & F has a further
crucial benefit. With conventional processing methods, characterized
by complex flow streamlines, the flow can promote re-agglomeration
rather than dispersion if converging streamlines are present that
force the particles to come into contact with each other. In contrast,
in the P & F approach, the dominant extensional flow increases
the particle separation at each cycle by “stretching”
the fluid containing the suspended platelets.
A key aspect of the method is that after the pressing step has ended, the shear rate goes practically to zero. As a consequence, the sample viscosity increases dramatically, “freezing” the microstructure (for samples at 120 °C containing 4.8 vol % GNP, the viscosity increases from η ≅ 10 Pa·s for γ̇ ≅ 10 s–1 to η ≅ 105 Pa·s for γ̇ ≅ 10–3 s–1). Moreover, the sample is cooled and folded at room temperature. Hence, once dispersed, the platelets remain dispersed until the next pressing step. To quantify the dispersion during the P & F process, we can define a dispersion factor D as:
| 1 |
where A(n) and Ap are the nanofiller–matrix contact area at cycle n and the total nanofiller surface area, respectively. The D factor ranges from 0 for completely agglomerated GNPs to 1 for perfectly dispersed GNPs. This parameter can either be measured indirectly [e.g., by analyzing scanning electron microscopy and transmission electron microscopy (SEM and TEM, respectively) images]39 or analytically derived a priori from the preparation technique used (see section S.11.3 of the Supporting information for melt-blending and section S.11.4 of the Supporting Information for solution mixing and casting).
By assuming that the variation of D within a Δn interval depends on a distribution rate I (a constant that describes how fast the polymer melt erodes the agglomerates and distributes the nanoparticles) and on a saturation term Ap – A(n) (once all of the GNPs are in contact with LLDPE, D becomes 1 and cannot further increase; see section S.11.2 of the Supporting Information), we can estimate that D changes with n according to:
| 2 |
where A0 is the initial contact area. We calculate a pre-exponential factor (Ap – A0)/Ap of 0.999 by analyzing the optical pictures of the samples at the first few cycles and a distribution rate I ≈ 3.3 × 10–3 using two different methods (sections S.11.5 and S.11.6 of the Supporting Information): one based on the analysis of the optical pictures of films prepared at low P & F cycles and the other one determined by fitting the mechanical and electrical properties of the nanocomposites presented later. We used eq 2 to convert the number of P & F cycles into a nanofiller dispersion level on the top axis of Figures 1e and 2b,c. The knowledge of the dispersion state allows the prediction of nanocomposite physical properties.
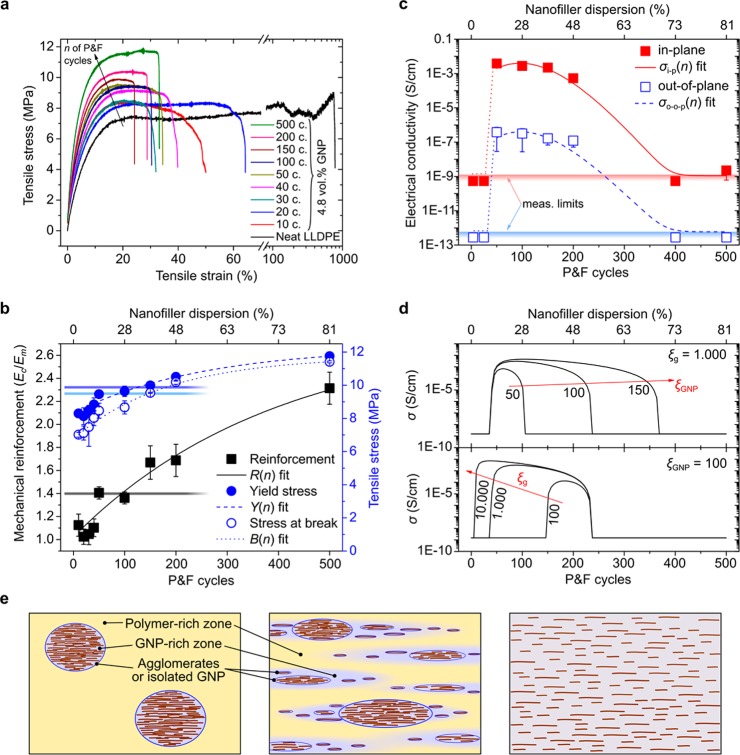
Figure 2.
Effect of nanofiller dispersion on mechanical and electrical properties of LLDPE containing 4.8 vol % GNP nanocomposites. (a) Representative stress–strain curves. (b) Measured mechanical reinforcement R, stress at yield Y, and stress at break B with best fits using eq 4.The three horizontal lines represent the yield stress (top line), stress at break, and reinforcement (bottom line) of the reference sample prepared by traditional melt blending. (c) Electrical conductivity as a function of P & F cycles n (horizontal shades areas indicates the lower measurement limits for in-plane and out-of-plane electrical conductivities; dotted lines are guides for the eye) fitted with eq 5. The measurement limits are due to the apparatus employed that could measure a minimum conductance of 2 × 10–11 S, multiplied by the geometries of the samples used: 1.5/(0.8 × 0.03) cm–1 for in-plane measurements and 0.03/(1 × 1) cm–1 for out-of-plane. (d) Theoretical predictions of nanocomposite electrical conductivities based on the model of Wang et al.(51) for different GNP aspect-ratios (top graph, assuming that ξg reaches the value of 1000 after 500 cycles) and for GNP-rich zones that reach different aspect ratios after 500 P & F cycles (bottom graph). (e) Representation of the nanocomposite microstructures with the polymer-rich and GNP-rich zones.
Prediction of Nanocomposite Properties for Different Dispersion Levels
Nanocomposite physical properties can be parametrized on D assuming that the effective nanofiller loading Vpeff scales with the nominal nanofiller loading Vp in the same way as the area does:
| 3 |
The effective volume fraction can be used to replace Vp inside theoretical models for composites (such as the Halpin–Tsai model45,46 for the elastic modulus or the Pukanszky model47 for the yield stress), provided that the nanofiller dispersion level is known, or to back-calculate an unknown D factor. Any physical properties P that follows the rule-of-mixture,48,49 such as the Young’s modulus or the thermal conductivity, can be expressed (see section S.11.2 of the Supporting Information) as:
| 4 |
where P0 is the value of P for D = 0, and Pth is the value of P when the nanofiller is perfectly dispersed. In contrast, properties that are very sensitive to percolation, such as the electrical conductivity σ, are expected to follow an exponential relation (section S.11.2 of the Supporting Information):
| 5 |
where σth is the theoretical conductivity at high dispersion levels, σM is the maximum conductivity reached at a critical nanofiller dispersion level Dc, and a is a parameter that describes how fast the conductivity changes with interparticle distance (and thus with the dispersion level). In the next section, we will explain this correlation between nanofiller dispersion and electrical conductivity in more detail. Despite their simplicity, eqs 4–6 are very useful for both interpreting nanocomposites physical properties and predictions and materials design.
Effect of GNP Dispersion Level on Nanocomposite Properties
Figure 2a shows representative stress–strain curves corresponding to different P & F cycles for samples containing 4.8 vol % GNP. The mechanical reinforcement Ec/Em (ratio between elastic modulus Ec of the composite and elastic modulus of the matrix, with Em = 140 ± 5 MPa), the stress at yield Y, and the stress at break B are improved by nanofiller dispersion (Figure 2b), as expected from previous studies.39,50 Because the yield stress depends also on the nanofiller specific surface area,38 its increase compared to neat LLDPE (7.85 ± 0.27 MPa) is likely explained by an increasing nanofiller–matrix interfacial area with P & F cycles. However, nanofiller dispersion may change also the crystallinity and the spherulitic and lamellar features of the polymer, which, in turn, can further affect the nanocomposite mechanical properties. In sections S.4 and S.5 of the Supporting Information, we show that these changes are negligible for our samples, so any mechanical improvement must be mainly caused by an increased nanofiller–polymer interface. The stress at break overtakes the value of neat LLDPE (9.5 ± 0.7 MPa) only after 150 P & F cycles; for this number of cycles, the failure of initiation due to stress concentrations generated by GNP agglomerates is overcome (see fracture surfaces in section S.7.2 of the Supporting Information). For comparison, a reference sample containing 4.8 vol % GNP prepared by melt-blending followed by compression-molding presents mechanical properties as low as those of samples prepared between 100 and 150 P & F cycles (Figure 2b and section S.8 of the Supporting Information). This is believed to be mainly due to the reduced in-plane alignment of the GNP nanoparticles.
The anisotropic microstructure observed by SEM is reflected in the electrical properties (Figure 2c): the in-plane conductivity is approximately 4 orders of magnitude higher than the out-of-plane conductivity. The in-plane and out-of-plane conductivities of samples prepared with less than 50 P & F cycles are not measurable, suggesting well-isolated GNP agglomerates inside the matrix. Between 50 and 150 P & F cycles, the dispersion of the particles leads to an optimally conductive network, and the conductivities reach a maximum (this rise in conductivity with the nanofiller dispersion agrees with several literature observations).39,52,53 The conductivities then decrease at higher P & F cycles, suggesting a breakup of the percolating network. This other behavior agrees with the results of Tkalya et al., who reported increased percolation thresholds in nanocomposites with improved graphene dispersions.54 The reduction in electrical conductivity can also be explained by a partial fragmentation of GNP. This effect, however, should be less dominant than the nanofiller dispersion/distribution effect because there is no evidence of a reduction of mechanical properties with P & F cycles. Notably, a reference sample prepared by melt-blending and compression molding (also containing 4.8 vol % GNP) is not electrically conductive.
To better understand the reasons behind the trend of the electrical conductivities with the P & F cycles, we refer to the study of Wang et al., who developed a conductivity model based on the continuum theory that takes into account the effects of nanofiller agglomeration, imperfect nanofiller–matrix interface, and electron tunnelling.51 Because of the GNP agglomerates, the volume of nanocomposites must be divided into two different zones: a GNP-rich zone and a polymer-rich zone (Figure 2e). The size of the GNP-rich zones may not be the same of those reported in Figure 1e for the GNP agglomerates: the GNP-rich zones (represented by violet areas in Figure 2e as opposed to the blue contours used to denote the agglomerates and individual GNP that can be measured by SEM) can consists also of well-dispersed GNP that are just well close to each other so that their local concentration is higher than Vp. Assuming that the polymer-rich zone does not contain any GNP, the GNP concentration inside the GNP-rich zones is VGNP = Vp/Vg,51 where Vg is the volume fraction of the GNP-rich zones inside the nanocomposites. The value of Vg must increase from Vp at the first few P & F cycles to one at very high cycles, where there is no more distinction between GNP-rich and polymer-rich zones (Figure 2e). Unfortunately, there is no direct way to measure the size of the GNP-rich zones. However, considering that the P & F dispersion mechanism involves repetitive extensional flows, it is reasonable to expect that the GNP-rich zones increase their aspect-ratio ξg with the number of P & F cycles. Based on the model of Wang et al.,51 when ξg is higher than the aspect ratio ξGNP of the individual GNP, the overall electrical percolation decreases and the conductivity of the nanocomposites increases. Indeed, approximating their model, the nanocomposite conductivity σ is controlled by the electrical percolation between the GNP-rich zones:
| 6 |
where Vgc is the critical volume fraction of the GNP-rich zones, and σg is their conductivity, which is based in turn on the percolation of the GNP within the GNP-rich zones:
| 7 |
where VGNPc is the critical volume fraction of the GNP inside the GNP-rich zones. Some literature studies55,56 suggest that the critical volume fractions are inversely correlated to the filler aspect ratio: Vg ∝ 1/ξg and VGNPc ∝ 1/ξGNP and, hence, the reason why ξg must be higher than ξGNP to enhance the conductivity of nanocomposites. Using eq 7 inside eq 6, we can simulate the trend of nanocomposite conductivity with P & F cycles (Figure 2d, where we assumed a linear increment of Vg and ξg with P & F cycles). This trend is quite similar to that of data in Figure 2c and to the model of eq 5. Therefore, the parameter Dc of eq 5 represents the situation in which there is the best compromise between ξg and VGNP during the P & F process that gives the maximum possible conductivity, σM: Dc ∝ VGNP/ξg and σM ∝ ξGNP/Dc.
In summary, our nanocomposites can be divided in three categories according to the nanofiller dispersion state: (1) nanocomposites with D < 15% containing inhomogeneous GNP distribution and isolated GNP agglomerates that do not form an electrically conductive network and for which the mechanical properties are comparable with or worse than those of the neat LLDPE; (2) nanocomposites with 15% < D < 50% containing well-dispersed and aligned GNPs, showing high and anisotropic conductivities and good mechanical reinforcement; and (3) nanocomposites with D > 50% presenting highly dispersed and aligned GNP, having enhanced mechanical properties but poor electrical conductivity. The combination of electrical and mechanical properties is thus a strong function of the parameter D.
Toward Ultrahigh Nanofiller Loadings
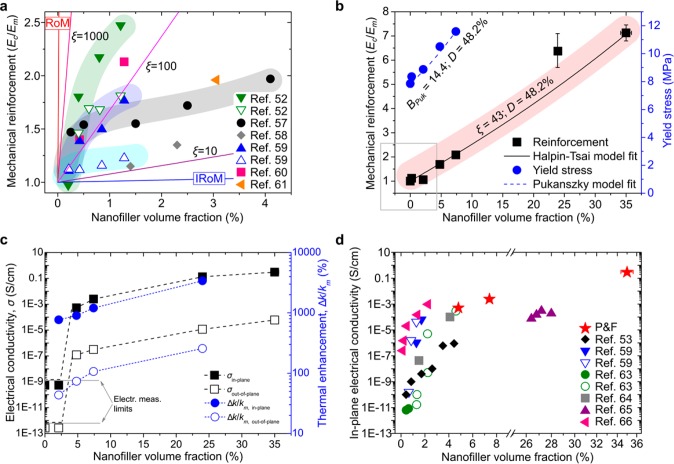
Figure 3a compares values found in literature52,57−61 for the reinforcement of layered nanocomposites of LLDPE and GNP/graphene with theoretical predictions using the Halpin–Tsai model, which assumes “optimally dispersed” systems. None of the literature data sets follow the linear trend expected from the theory: the data sets show the typical reduction in reinforcing efficiency with nanofiller loading, commonly attributed to decreasing nanofiller dispersion quality as the concentration of nanoparticle increases. Here, we examine the properties of nanocomposites prepared at 200 P & F cycles (LLDPE and GNP are not affected by such high cycles, as demonstrated in section S.9 in the Supporting Information) as a function of GNP loading.
Figure 3.
Properties of LLDPE nanocomposites for different GNP loadings but similar dispersion level (48.2%). (a) Mechanical reinforcement of GNP–LLDPE nanocomposites from literature, together with prediction lines of the Halpin–Tsai model at different aspect ratios ξ of monolayer graphene. The shadowed areas are a guide for the eye to highlight the decrease of reinforcing efficiency with nanofiller loading. For some cases, there are two data sets per reference corresponding to nanocomposites prepared by different techniques or with different matrix and nanofiller functionalization. (b) Mechanical reinforcement and yield stress of GNP–LLDPE nanocomposites for n = 200 P & F cycles. The frame corresponding to low-volume fractions indicates the region where literature data typically fall (see Figure 3a). Because of the high GNP loading that increases nanocomposite brittleness, the sample containing 35 vol % GNP does not show any yield before fracture. The modified Halpin–Tsai and Pukanszky models modified by eq 3 fit the reinforcement and yield data. In both fits, the D factor was kept constant at 48.2% (value found for previous nanocomposites containing 4.8 vol % GNP prepared at n = 200). (c) Electrical conductivity of GNP–LLDPE nanocomposites prepared with n = 200 (lines are guides for the eye) and thermal conductivity enhancement with respect to the value obtained for LLDPE, km. (d) In-plane electrical conductivity of LLDPE–GNP nanocomposites. Note the high in-plane conductivity of 0.3 S/cm for the sample at 35 vol % obtained via P & F.
We find that the mechanical reinforcement vs volume fraction data for P & F (representative stress–strain curves can be found in Figure S10) can be well-fitted by the Halpin–Tsai and Pukanszky models using Vpeff with a fixed value of D = 48.2% (Figure 3). The model parameters correspond to a nanofiller aspect-ratio of 43 (in agreement with the theoretical one, ξth = 38, from the fit in Figure 1e) and nanofiller–matrix interaction parameter BPuk of 14.4, similar to values reported for clay nanocomposites.62 Considering that no compatibiliser was used, the high value of the parameter BPuk suggests a fairly good GNP–LLDPE interaction. These results demonstrate that the dispersion efficiency of the P & F technique (and, hence, the resulting reinforcement) does not decrease at high nanofiller loadings (i.e., D factor remains constant), contrary to what is usually reported (Figure 3a).
The in-plane conductivity of our samples is 4 orders of magnitude higher than the out-of-plane conductivity (Figure 3c). This reflects the anisotropic layered microstructure of the nanocomposite. Considering the aspect ratio of our GNP (∼40), we should expect a percolation threshold around 15 vol % if GNP were perfectly dispersed.55 The measured percolation threshold lies between 2.1 and 4.8 vol % (Figure 3c). This range is theoretically expected for perfectly dispersed nanoplatelets with aspect ratios of 150–250. Therefore, the nonhomogeneous, imperfect GNP dispersion (D ≈ 50%) in our nanocomposites increases the electrical conductivity (as depicted in Figure 2c), hence lowering the percolation threshold to values theoretically expected for higher aspect-ratio fillers. This result corroborates our conductivity model of eq 5.
The high electrical conductivities come with massive in-plane thermal conductivity enhancements: >10 W/m·K, more than 3000% higher than LLDPE thermal conductivity. The out-of-plane conductivity increases up to ∼1 W/m·K. To the best of our knowledge, this is the highest combination of thermal conductivity enhancement and thermal anisotropy ever reported. A comparison of the in-plane electrical conductivity data with the values found in the literature53,59,63−66 for layered nanocomposites of LLDPE with GNP/graphene (Figure 3d) shows how our samples are the most-conductive nanocomposites reported. It is noted that the conductivity is predicted to be even higher for a D-factor close to Dc ≈ 25%.
Material Multifunctional Design and General Applicability of the Approach
The P & F approach addresses the optimization of nanocomposite microstructures to fulfill particular technological applications. For example, a layered microstructure with perfectly dispersed nanoparticles is needed for materials with enhanced mechanical, gas-barrier, or thermal properties, e.g., films for food packaging and flexible electronics67,68 and heat-dissipating devices.28 We measured the thermal conductivity of polymer nanocomposites with 4.8 vol % GNP after 400 P & F cycles. Unexpectedly, thermal conductivities were ∼3 W/m·K in-plane (∼900% higher than neat LLDPE thermal conductivity) and ∼0.3 W/m·K out-of-plane while being electrically insulating in all directions (average interparticle distance longer than electron mean free path).69 The combination of high thermal conductivity and low electrical conductivity makes these nanocomposites promising for anisotropic thermal interface management of modern electronic, optoelectronic and photonic devices.69
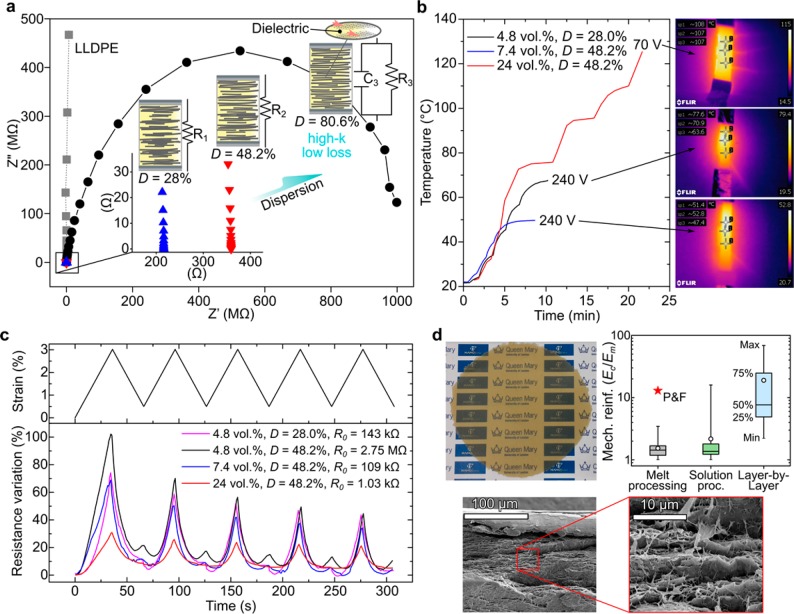
High dispersion levels can be useful for energy-storage devices25,26 (Figure 4a), provided that the electrical conductivity (σth) is small enough to allow huge polarization effects inside the layered microstructure without dielectric loss. A much-lower nanofiller dispersion (corresponding to the critical level Dc) is sufficient if high electrical conductivity is required, for example, in Joule-heating materials (Figure 4b) for de-icing70 or safety self-limiting power devices.23,24 An intermediate level of electrical conductivity, close to that corresponding to the percolation threshold, is normally required for resistive sensors (Figure 4c, for instance, shows the strain sensitivity of the nanocomposite) that could find applications in smart textile and structural health-monitoring applications.29,30
Figure 4.
Examples of nanocomposites with optimized microstructures (nanofiller dispersion) for a variety of applications. (a) Imaginary (Z′′) vs real impedance (Z′) obtained from electrochemical impedance spectroscopy of LLDPE containing 4.8 vol % GNP for different dispersion levels. In accordance with value of σth expected from eq 5 the sample with D = 80.6% is the only one showing a capacitive effect, demonstrated by the Nyquist semicircle. (b) Self-heating originating from the Joule effect of LLDPE composites at different GNP loadings and dispersion levels. The sample with 4.8 vol % GNP shows a better self-heating effect than the sample containing 7.4 vol % GNP because its nanofiller dispersion level (D = 28) is closer to the critical value Dc= 25% predicted by eq 5. (c) Strain sensing of LLDPE composites with different GNP loadings and dispersion levels. High values of D give high resistance variations (gauge factor of ∼30) because the nanocomposite conductivity approaches the theoretical value σth more quickly with the strain (see sample containing 4.8 vol % GNP with D = 48.2%). Dispersions closer to Dc provide better electrical signals. The resistance variation becomes less evident for increasing amounts of GNP because the difference between σM and σth is smaller (for details, see section S.12.2 in the Supporting Information). (d) Optical picture (top left) of LLDPE containing 70 wt % MMT (∼10 cm wide and ∼400 μm thick), SEM cross-sections (bottom), and comparison (top right) of mechanical reinforcement with literature values for MMT nanocomposites grouped by the processing method. We achieved the highest mechanical reinforcement ever reported for melt processing. The QMUL logo is used with permission.
If a combination of properties is simultaneously desired, a compromise in nanofiller dispersion needs to be found. We found a good balance between mechanical and electrical properties when our GNP is ∼50% dispersed. At high nanofiller loadings, the theoretical conductivity at high dispersion states (σth) should not be very different from that at the critical dispersion level (σM). Therefore, one should find good electrical properties even if the nanofiller dispersion is greater than Dc. This is the case for our nanocomposites prepared with more than 20 vol % GNP, which appear to be simultaneously promising for self-heating devices triggered by low voltages (Figure 4b), health monitoring (Figure 4c), and mechanical applications.
To prove the general applicability of our technique to different filler–matrix combinations, a number of different nanocomposites were prepared by dispersing using P & F four types of nanoparticles of different shapes and sizes (GNP with low specific surface area, GNP with high specific surface area, montmorillonite MMT, and magnetite nanoparticles) into five different polymeric matrices. Independent from the specific filler–matrix system selected, nanofillers could always be efficiently dispersed into a given polymer matrix after a sufficient number of P & F cycles (section S.11.6 of the Supporting Information). The performance of the resulting material is extremely promising. Let us take a LLDPE containing MMT nanocomposite for example. Because we found a distribution rate of ∼7 × 10–2 for MMT in LLDPE (much higher than ∼3 × 10–3 for GNP), we expected to reach a dispersion of ∼99% after only ∼50 P & F cycles. Therefore, we prepared a sample containing an ultrahigh MMT loading of ∼74 wt %, and it appeared to be transparent indeed (Figure 4d) because of the good MMT dispersion and alignment. The nanocomposite had a Young’s modulus of ∼1.8 GPa, approximately 13 times higher than that of the pure polymer. This is a surprisingly high value for a nanocomposite based on a commodity or engineering plastic prepared by a top-down technique (Figure 4d and section S.12.4 of the Supporting Information).
Conclusions
The lack of control over nanofiller dispersion, exacerbated at high nanofiller loadings, has often prevented nanocomposites from fulfilling multifunctional requirements. In this study, we have demonstrated a top-down scalable polymer processing method, the P & F method, that can enable the dispersion of ultrahigh concentrations of nanofiller (at least up to 74 vol %) by selecting a sufficient number of P & F cycles. With this method, we have been able to achieve mechanical reinforcements close to the maximum theoretical prediction levels, independent of nanofiller loading. Key aspects of the method are the controlled mixing, the use of a strong flow with a dominant elongational component, and the processing at temperatures just above the melting temperature. As an example of the potential of the method to optimize microstructures to achieve multifunctional properties, we have produced nanocomposites by P & F simultaneously presenting enhanced mechanical reinforcement, strain sensing, self-heating, and energy-management properties.
Methods
Linear low-density polyethylene (density of 0.921 g/cm3 and melting point of 116 °C), Flexirene MS20A (Versalis S.p.A., Italy), and the GNP (an expanded graphite of bulk density of 0.04 g/cm3 and BET specific surface area of 25 m2/g) Timrex C-Therm 002 (Timcal Ltd., Switzerland), were used as polymer matrix and nanofiller, respectively.
The P & F technique used to prepare the nanocomposites can be divided in three steps. First, two LLDPE films (∼100 μm thick) were prepared by hot-pressing polymer pellets inside a hot press (Collin P 300 E). Subsequently, GNP powder was deposited with a spatula in the middle of the surface of one LLDPE film so that the other film could be placed on top preventing the powder from spilling out. This “sandwich” was then hot-pressed inside of an aluminum frame (∼300 μm thick) at 40 bar and 120 °C for 30 s to join the two materials. In the final processing step, LLDPE and GNP were gradually dispersed by repetitive folding and hot-pressing these films. In particular, at each P & F cycle, the sample was manually folded twice in a symmetric manner and pressed at 40 bar and 120 °C for 30 s inside the aluminum frame to maintain the resulting thickness at ∼300 μm after the pressing. The weight concentration of GNP inside each sample was calculated by measuring the weight of the initial LLDPE films before and after adding GNP (after the second step).
To study the properties of the nanocomposites as a function of P & F cycles (corresponding to GNP dispersion and distribution throughout the matrix), samples of LLDPE containing 10.7 wt % (4.8 vol %) of GNP were prepared at different P & F cycles. To study the effect of possible degradation of the polymer matrix with the P & F cycles, samples of neat LLDPE at 1, 50, 100, and 150 P & F cycles were also prepared.
A reference sample of LLDPE containing 10.7 wt % of GNP was prepared by traditional melt-blending followed by a compression molding technique. Here, LLDPE pellets and GNP were used without drying. The composite was prepared by melt-blending at 120 °C under nitrogen atmosphere using a DSM X’plore 15 cm3 micro compounder. Compounding was performed for 9 min at a screw speed of 180 rpm. The resulting compound was hot-pressed at 40 bar and 120 °C for 30 s inside an aluminum frame ∼300 μm thick.
Finally, samples of 0.5, 5, 10.7, 16, 43.6, and 56 wt % (corresponding to 0.21, 2.1, 4.8, 7.4, 24, and 35 vol %) of GNP were prepared at 200 P & F cycles to validate the effectiveness of this technique in dispersing different concentrations of nanofiller. It was chosen to prepare all samples at 200 P & F cycles because we found that this number of cycles gave optimal mechanical properties, which were even higher than those of the reference sample prepared by melt-blending, whereas electrical conductivity values were among the highest reported in literature.
The methods used to characterize the nanofiller, matrix, and nanocomposites are described in the Supporting Information. Methods used to test the self-heating effect, strain-sensing, and impedance and energy storage are also reported in the Supporting Information.
Acknowledgments
This project has received funding from Innovate UK (KTP no. KTP009619) and the European Union’s Seventh Framework Programme for research, technological development, and demonstration under grant agreement no. 604143. This project has also received funding from the EPSRC Grant Graphene 3D Networks (EP/K01658X/1). N. M. Pugno is supported by the European Commission under the Graphene Flagship Core 2 grant no. 785219 (WP14 “Composites”) and FET Proactive “Neurofibers” grant no. 732344 as well as by the Italian Ministry of Education, University and Research (MIUR) under the ’’Departments of Excellence’’ grant no. L.232/2016. Activities by A. Fina and S. Colonna in this work were financially supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 639495-INTHERM-ERC-2014-STG. E. Barbieri is supported by JSPS KAKENHI grant no. JP18K18065. The authors acknowledge S. Vidotto for helping with the preliminary characterization of the nanofiller, P. Rajamani for helping with the preparation of some samples, and R. Wilson for collecting the XRD patterns. LMK Thermosafe Ltd. is gratefully acknowledged as well as Nanoforce Technology Ltd. for use of facilities.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.8b02877.
Additional details on characterization techniques, XRD observations, nanofiller characterization, influence of P & F cycles, filler agglomerates inside nanocomposites, tensile failure, nanocomposites of LLDPE containing 4.8 vol % GNP prepared by melt blending, influence of GNP loading, rheology study, model derivation, potential applications, and an overview of classical composite theories (PDF)
Author Contributions
E. Bilotti designed the experiments. G. Santagiuliana, L. Rubini, and Y. Li developed the P & F technique. G. Santagiuliana and L. Rubini prepared the P & F samples. O. T. Picot prepared the melt-blended reference sample. G. Santagiuliana and H. Zhang tested the strain-sensing behavior of samples. H. Porwal performed the self-heating tests and analyzed the related data. M. Crespo performed the EIS tests and analyzed the related data. S. Colonna and A. Fina performed thermal conductivity tests. A. B. Spoelstra, G. Mirabello, and J. P. Patterson performed the transmission electron microscopy. G. Santagiuliana, O. T. Picot, and L. Rubini carried out all other samples characterizations. G. Santagiuliana, O. T. Picot, N. M. Pugno, T. Peijs, E. Barbieri, L. Botto, and E. Bilotti interpreted and discussed the results. G. Santagiuliana analyzed the data, derived the dispersion model and wrote the paper under the supervision of N. M. Pugno, T. Peijs, and E. Bilotti. L. Botto derived the micromechanical model of the P & F technique.
The authors declare no competing financial interest.
Supplementary Material
References
- McEvoy M. A.; Correll N. Materials That Couple Sensing, Actuation, Computation, and Communication. Science 2015, 347, 1261689. 10.1126/science.1261689. [DOI] [PubMed] [Google Scholar]
- Geim A. K.; Novoselov K. S. The Rise of Graphene. Nat. Mater. 2007, 6, 183–191. 10.1038/nmat1849. [DOI] [PubMed] [Google Scholar]
- Lee C.; Wei X.; Kysar J. W.; Hone J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. 10.1126/science.1157996. [DOI] [PubMed] [Google Scholar]
- Bunch J. S.; Verbridge S. S.; Alden J. S.; van der Zande A. M.; Parpia J. M.; Craighead H. G.; McEuen P. L. Impermeable Atomic Membranes from Graphene Sheets. Nano Lett. 2008, 8, 2458–2462. 10.1021/nl801457b. [DOI] [PubMed] [Google Scholar]
- Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [DOI] [PubMed] [Google Scholar]
- Balandin A. A.; Ghosh S.; Bao W.; Calizo I.; Teweldebrhan D.; Miao F.; Lau C. N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. 10.1021/nl0731872. [DOI] [PubMed] [Google Scholar]
- Nair R. R.; Blake P.; Grigorenko A. N.; Novoselov K. S.; Booth T. J.; Stauber T.; Peres N. M. R.; Geim A. K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308–1308. 10.1126/science.1156965. [DOI] [PubMed] [Google Scholar]
- Young R. J.; Kinloch I. A.; Gong L.; Novoselov K. S. The Mechanics of Graphene Nanocomposites: A Review. Compos. Sci. Technol. 2012, 72, 1459–1476. 10.1016/j.compscitech.2012.05.005. [DOI] [Google Scholar]
- Vlassiouk I.; Polizos G.; Cooper R.; Ivanov I.; Keum J. K.; Paulauskas F.; Datskos P.; Smirnov S. Strong and Electrically Conductive Graphene-Based Composite Fibers and Laminates. ACS Appl. Mater. Interfaces 2015, 7, 10702–10709. 10.1021/acsami.5b01367. [DOI] [PubMed] [Google Scholar]
- Liu P.; Jin Z.; Katsukis G.; Drahushuk L. W.; Shimizu S.; Shih C.-J.; Wetzel E. D.; Taggart-Scarff J. K.; Qing B.; Van Vliet K. J.; et al. Layered and Scrolled Nanocomposites with Aligned Semi-Infinite Graphene Inclusions at the Platelet Limit. Science 2016, 353, 364–367. 10.1126/science.aaf4362. [DOI] [PubMed] [Google Scholar]
- May P.; Khan U.; O’Neill A.; Coleman J. N. Approaching the Theoretical Limit for Reinforcing Polymers with Graphene. J. Mater. Chem. 2012, 22, 1278–1282. 10.1039/C1JM15467B. [DOI] [Google Scholar]
- Khan U.; May P.; O’Neill A.; Bell A. P.; Boussac E.; Martin A.; Semple J.; Coleman J. N. Polymer Reinforcement Using Liquid-Exfoliated Boron Nitride Nanosheets. Nanoscale 2013, 5, 581–587. 10.1039/C2NR33049K. [DOI] [PubMed] [Google Scholar]
- Vaia R. A.; Maguire J. F. Polymer Nanocomposites with Prescribed Morphology: Going beyond Nanoparticle-Filled Polymers. Chem. Mater. 2007, 19, 2736–2751. 10.1021/cm062693+. [DOI] [Google Scholar]
- Schaefer D. W.; Justice R. S. How Nano Are Nanocomposites?. Macromolecules 2007, 40, 8501–8517. 10.1021/ma070356w. [DOI] [Google Scholar]
- Sun J.; Bhushan B. Hierarchical Structure and Mechanical Properties of Nacre: A Review. RSC Adv. 2012, 2, 7617. 10.1039/c2ra20218b. [DOI] [Google Scholar]
- Zhang J.; Feng W.; Zhang H.; Wang Z.; Calcaterra H. A.; Yeom B.; Hu P. A.; Kotov N. A. Multiscale Deformations Lead to High Toughness and Circularly Polarized Emission in Helical Nacre-like Fibres. Nat. Commun. 2016, 7, 10701. 10.1038/ncomms10701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.; Yeom B.; Arteaga O.; Jo Yoo S.; Lee S.-G.; Kim J.-G.; Kotov N. A. Reconfigurable Chiroptical Nanocomposites with Chirality Transfer from the Macro- to the Nanoscale. Nat. Mater. 2016, 15, 461–468. 10.1038/nmat4525. [DOI] [PubMed] [Google Scholar]
- Morgan A. B. Flame Retarded Polymer Layered Silicate Nanocomposites: A Review of Commercial and Open Literature Systems. Polym. Adv. Technol. 2006, 17, 206–217. 10.1002/pat.685. [DOI] [Google Scholar]
- Kashiwagi T.; Du F.; Douglas J. F.; Winey K. I.; Harris R. H.; Shields J. R. Nanoparticle Networks Reduce the Flammability of Polymer Nanocomposites. Nat. Mater. 2005, 4, 928–933. 10.1038/nmat1502. [DOI] [PubMed] [Google Scholar]
- Bourbigot S.; Duquesne S. Fire Retardant Polymers : Recent Developments and Opportunities. J. Mater. Chem. 2007, 17, 2283–2300. 10.1039/b702511d. [DOI] [Google Scholar]
- Holder K. M.; Smith R. J.; Grunlan J. C. A Review of Flame Retardant Nanocoatings Prepared Using Layer-by-Layer Assembly of Polyelectrolytes. J. Mater. Sci. 2017, 52, 12923–12959. 10.1007/s10853-017-1390-1. [DOI] [Google Scholar]
- Costes L.; Laoutid F.; Brohez S.; Dubois P. Bio-Based Flame Retardants: When Nature Meets Fire Protection. Mater. Sci. Eng., R 2017, 117, 1–25. 10.1016/j.mser.2017.04.001. [DOI] [Google Scholar]
- Rybak A.; Boiteux G.; Melis F.; Seytre G. Conductive Polymer Composites Based on Metallic Nanofiller as Smart Materials for Current Limiting Devices. Compos. Sci. Technol. 2010, 70, 410–416. 10.1016/j.compscitech.2009.11.019. [DOI] [Google Scholar]
- Yi X.-S.; Wu G.; Pan Y. Properties and Applications of Filled Conductive Polymer Composites. Polym. Int. 1997, 44, 117–124. . [DOI] [Google Scholar]
- Yuan J.; Luna A.; Neri W.; Zakri C.; Schilling T.; Colin A.; Poulin P. Graphene Liquid Crystal Retarded Percolation for New High-k Materials. Nat. Commun. 2015, 6, 8700. 10.1038/ncomms9700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raccichini R.; Varzi A.; Passerini S.; Scrosati B. The Role of Graphene for Electrochemical Energy Storage. Nat. Mater. 2015, 14, 271–279. 10.1038/nmat4170. [DOI] [PubMed] [Google Scholar]
- Blackburn J. L.; Ferguson A. J.; Cho C.; Grunlan J. C. Carbon-Nanotube-Based Thermoelectric Materials and Devices. Adv. Mater. 2018, 30, 1704386. 10.1002/adma.201704386. [DOI] [PubMed] [Google Scholar]
- Jones W. E.; Chiguma J.; Johnson E.; Pachamuthu A.; Santos D. Electrically and Thermally Conducting Nanocomposites for Electronic Applications. Materials 2010, 3, 1478–1496. 10.3390/ma3021478. [DOI] [Google Scholar]
- Thostenson E. T.; Chou T.-W. Real-Time in Situ Sensing of Damage Evolution in Advanced Fiber Composites Using Carbon Nanotube Networks. Nanotechnology 2008, 19, 215713. 10.1088/0957-4484/19/21/215713. [DOI] [PubMed] [Google Scholar]
- Luo S.; Liu T. Graphite Nanoplatelet Enabled Embeddable Fiber Sensor for in Situ Curing Monitoring and Structural Health Monitoring of Polymeric Composites. ACS Appl. Mater. Interfaces 2014, 6, 9314–9320. 10.1021/am5017039. [DOI] [PubMed] [Google Scholar]
- Li X.; Yang T.; Yang Y.; Zhu J.; Li L.; Alam F. E.; Li X.; Wang K.; Cheng H.; Lin C.-T.; Fang Y.; Zhu H. Large-Area Ultrathin Graphene Films by Single-Step Marangoni Self-Assembly for Highly Sensitive Strain Sensing Application. Adv. Funct. Mater. 2016, 26, 1322–1329. 10.1002/adfm.201504717. [DOI] [Google Scholar]
- Picot O. T.; Rocha V. G.; Ferraro C.; Ni N.; D’Elia E.; Meille S.; Chevalier J.; Saunders T.; Peijs T.; Reece M. J.; Saiz E. Using Graphene Networks to Build Bioinspired Self-Monitoring Ceramics. Nat. Commun. 2017, 8, 14425. 10.1038/ncomms14425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kashiwagi T.; Fagan J.; Douglas J. F.; Yamamoto K.; Heckert A. N.; Leigh S. D.; Obrzut J.; Du F.; Lin-Gibson S.; Mu M.; Winey K. I.; Haggenmueller R. Relationship between Dispersion Metric and Properties of PMMA/SWNT Nanocomposites. Polymer 2007, 48, 4855–4866. 10.1016/j.polymer.2007.06.015. [DOI] [Google Scholar]
- Mackay M. E.; Tuteja A.; Duxbury P. M.; Hawker C. J.; Van Horn B.; Guan Z.; Chen G.; Krishnan R. S. General Strategies for Nanoparticle Dispersion. Science 2006, 311, 1740–1743. 10.1126/science.1122225. [DOI] [PubMed] [Google Scholar]
- Hooper J. B.; Schweizer K. S. Contact Aggregation, Bridging, and Steric Stabilization in Dense Polymer–Particle Mixtures. Macromolecules 2005, 38, 8858–8869. 10.1021/ma051318k. [DOI] [Google Scholar]
- Hooper J. B.; Schweizer K. S. Theory of Phase Separation in Polymer Nanocomposites. Macromolecules 2006, 39, 5133–5142. 10.1021/ma060577m. [DOI] [Google Scholar]
- Hall L. M.; Jayaraman A.; Schweizer K. S. Molecular Theories of Polymer Nanocomposites. Curr. Opin. Solid State Mater. Sci. 2010, 14, 38–48. 10.1016/j.cossms.2009.08.004. [DOI] [Google Scholar]
- Keledi G.; Hári J.; Pukánszky B. Polymer Nanocomposites: Structure, Interaction, and Functionality. Nanoscale 2012, 4, 1919. 10.1039/c2nr11442a. [DOI] [PubMed] [Google Scholar]
- Šupová M.; Martynková G. S.; Barabaszová K. Effect of Nanofillers Dispersion in Polymer Matrices: A Review. Sci. Adv. Mater. 2011, 3, 1–25. 10.1166/sam.2011.1136. [DOI] [Google Scholar]
- Mamedov A. A.; Kotov N. A.; Prato M.; Guldi D. M.; Wicksted J. P.; Hirsch A. Molecular Design of Strong Single-Wall Carbon Nanotube/Polyelectrolyte Multilayer Composites. Nat. Mater. 2002, 1, 190–194. 10.1038/nmat747. [DOI] [PubMed] [Google Scholar]
- Sui L.; Huang L.; Podsiadlo P.; Kotov N. A.; Kieffer J. Brillouin Light Scattering Investigation of the Mechanical Properties of Layer-by-Layer Assembled Cellulose Nanocrystal Films. Macromolecules 2010, 43, 9541–9548. 10.1021/ma1016488. [DOI] [Google Scholar]
- Sellam C.; Zhai Z.; Zahabi H.; Picot O. T.; Deng H.; Fu Q.; Bilotti E.; Peijs T. High Mechanical Reinforcing Efficiency of Layered Poly(Vinyl Alcohol) – Graphene Oxide Nanocomposites. Nanocomposites 2015, 1, 89–95. 10.1179/2055033215Y.0000000001. [DOI] [Google Scholar]
- Luan C. Baker’s Transformation and Its Irreversibility. Phys. Lett. A 1991, 152, 6–10. 10.1016/0375-9601(91)90618-I. [DOI] [Google Scholar]
- Li X.; McKenna G. B.; Miquelard-Garnier G.; Guinault A.; Sollogoub C.; Regnier G.; Rozanski A. Forced Assembly by Multilayer Coextrusion to Create Oriented Graphene Reinforced Polymer Nanocomposites. Polymer 2014, 55, 248–257. 10.1016/j.polymer.2013.11.025. [DOI] [Google Scholar]
- Affdl J. C. H.; Kardos J. L. The Halpin-Tsai Equations: A Review. Polym. Eng. Sci. 1976, 16, 344–352. 10.1002/pen.760160512. [DOI] [Google Scholar]
- Halpin J. C.; Thomas R. L. Ribbon Reinforcement of Composites. J. Compos. Mater. 1968, 2, 488–497. 10.1177/002199836800200409. [DOI] [Google Scholar]
- Turcsányi B.; Pukánszky B.; Tüdõs F. Composition Dependence of Tensile Yield Stress in Filled Polymers. J. Mater. Sci. Lett. 1988, 7, 160–162. 10.1007/BF01730605. [DOI] [Google Scholar]
- Voigt W. Ueber Die Beziehung Zwischen Den Beiden Elasticitätsconstanten Isotroper Körper. Ann. Phys. 1889, 274, 573–587. 10.1002/andp.18892741206. [DOI] [Google Scholar]
- Reuss A. Berechnung Der Fließgrenze von Mischkristallen Auf Grund Der Plastizitätsbedingung Für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. 10.1002/zamm.19290090104. [DOI] [Google Scholar]
- Wu T.-L.; Lo T.-S.; Kuo W.-S. Effect of Dispersion on Graphite Nanosheet Composites. Polym. Compos. 2009, 31, 292–298. 10.1002/pc.20802. [DOI] [Google Scholar]
- Wang Y.; Shan J. W.; Weng G. J. Percolation Threshold and Electrical Conductivity of Graphene-Based Nanocomposites with Filler Agglomeration and Interfacial Tunneling. J. Appl. Phys. 2015, 118, 065101. 10.1063/1.4928293. [DOI] [Google Scholar]
- Kim H.; Kobayashi S.; AbdurRahim M. A.; Zhang M. J.; Khusainova A.; Hillmyer M. A.; Abdala A. A.; Macosko C. W. Graphene/Polyethylene Nanocomposites: Effect of Polyethylene Functionalization and Blending Methods. Polymer 2011, 52, 1837–1846. 10.1016/j.polymer.2011.02.017. [DOI] [Google Scholar]
- Noorunnisa Khanam P.; AlMaadeed M. A.; Ouederni M.; Harkin-Jones E.; Mayoral B.; Hamilton A.; Sun D. Melt Processing and Properties of Linear Low Density Polyethylene-Graphene Nanoplatelet Composites. Vacuum 2016, 130, 63–71. 10.1016/j.vacuum.2016.04.022. [DOI] [Google Scholar]
- Tkalya E.; Ghislandi M.; Otten R.; Lotya M.; Alekseev A.; van der Schoot P.; Coleman J.; de With G.; Koning C. Experimental and Theoretical Study of the Influence of the State of Dispersion of Graphene on the Percolation Threshold of Conductive Graphene/Polystyrene Nanocomposites. ACS Appl. Mater. Interfaces 2014, 6, 15113–15121. 10.1021/am503238z. [DOI] [PubMed] [Google Scholar]
- Li J.; Kim J.-K. Percolation Threshold of Conducting Polymer Composites Containing 3D Randomly Distributed Graphite Nanoplatelets. Compos. Sci. Technol. 2007, 67, 2114–2120. 10.1016/j.compscitech.2006.11.010. [DOI] [Google Scholar]
- Barwich S.; Coleman J. N.; Möbius M. E. Yielding and Flow of Highly Concentrated, Few-Layer Graphene Suspensions. Soft Matter 2015, 11, 3159–3164. 10.1039/C4SM02855D. [DOI] [PubMed] [Google Scholar]
- Kuila T.; Bose S.; Mishra A. K.; Khanra P.; Kim N. H.; Lee J. H. Effect of Functionalized Graphene on the Physical Properties of Linear Low Density Polyethylene Nanocomposites. Polym. Test. 2012, 31, 31–38. 10.1016/j.polymertesting.2011.09.007. [DOI] [Google Scholar]
- Carotenuto G.; De Nicola S.; Palomba M.; Pullini D.; Horsewell A.; Hansen T. W.; Nicolais L. Mechanical Properties of Low-Density Polyethylene Filled by Graphite Nanoplatelets. Nanotechnology 2012, 23, 485705. 10.1088/0957-4484/23/48/485705. [DOI] [PubMed] [Google Scholar]
- Vasileiou A. A.; Kontopoulou M.; Docoslis A. A Noncovalent Compatibilization Approach to Improve the Filler Dispersion and Properties of Polyethylene/Graphene Composites. ACS Appl. Mater. Interfaces 2014, 6, 1916–1925. 10.1021/am404979g. [DOI] [PubMed] [Google Scholar]
- Gong J.; Niu R.; Liu J.; Chen X.; Wen X.; Mijowska E.; Sun Z.; Tang T. Simultaneously Improving the Thermal Stability, Flame Retardancy and Mechanical Properties of Polyethylene by the Combination of Graphene with Carbon Black. RSC Adv. 2014, 4, 33776–33784. 10.1039/C4RA04623D. [DOI] [Google Scholar]
- Mittal V.; Chaudhry A. U. Polymer - Graphene Nanocomposites: Effect of Polymer Matrix and Filler Amount on Properties: Polymer - Graphene Nanocomposites: Effect of Polymer Matrix and Filler Amount on Properties. Macromol. Mater. Eng. 2015, 300, 510–521. 10.1002/mame.201400392. [DOI] [Google Scholar]
- Bilotti E.; Zhang R.; Deng H.; Quero F.; Fischer H. R.; Peijs T. Sepiolite Needle-like Clay for PA6 Nanocomposites: An Alternative to Layered Silicates?. Compos. Sci. Technol. 2009, 69, 2587–2595. 10.1016/j.compscitech.2009.07.016. [DOI] [Google Scholar]
- Kim S.; Seo J.; Drzal L. T. Improvement of Electric Conductivity of LLDPE Based Nanocomposite by Paraffin Coating on Exfoliated Graphite Nanoplatelets. Composites, Part A 2010, 41, 581–587. 10.1016/j.compositesa.2009.05.002. [DOI] [Google Scholar]
- Kuila T.; Bose S.; Hong C. E.; Uddin M. E.; Khanra P.; Kim N. H.; Lee J. H. Preparation of Functionalized Graphene/Linear Low Density Polyethylene Composites by a Solution Mixing Method. Carbon 2011, 49, 1033–1037. 10.1016/j.carbon.2010.10.031. [DOI] [Google Scholar]
- Zhang P.; Cao D.; Cui S. Resistivity-Temperature Behavior and Morphology of Low Density Polyethylene/Graphite Powder/Graphene Composites. Polym. Compos. 2014, 35, 1453–1459. 10.1002/pc.22798. [DOI] [Google Scholar]
- Iqbal M. Z.; Abdala A. A.; Mittal V.; Seifert S.; Herring A. M.; Liberatore M. W. Processable Conductive Graphene/Polyethylene Nanocomposites: Effects of Graphene Dispersion and Polyethylene Blending with Oxidized Polyethylene on Rheology and Microstructure. Polymer 2016, 98, 143–155. 10.1016/j.polymer.2016.06.021. [DOI] [Google Scholar]
- Arora A.; Padua G. w. Review: Nanocomposites in Food Packaging. J. Food Sci. 2010, 75, R43–R49. 10.1111/j.1750-3841.2009.01456.x. [DOI] [PubMed] [Google Scholar]
- Priolo M. A.; Holder K. M.; Greenlee S. M.; Grunlan J. C. Transparency, Gas Barrier, and Moisture Resistance of Large-Aspect-Ratio Vermiculite Nanobrick Wall Thin Films. ACS Appl. Mater. Interfaces 2012, 4, 5529–5533. 10.1021/am3014289. [DOI] [PubMed] [Google Scholar]
- Shahil K. M. F.; Balandin A. A. Graphene–Multilayer Graphene Nanocomposites as Highly Efficient Thermal Interface Materials. Nano Lett. 2012, 12, 861–867. 10.1021/nl203906r. [DOI] [PubMed] [Google Scholar]
- Enríquez E.; Fernández J. F.; De Frutos J.; De la Rubia M. A. Tailoring of the Electrical Properties of Carbon Black–Silica Coatings for de-Icing Applications. Ceram. Int. 2015, 41, 2735–2743. 10.1016/j.ceramint.2014.10.088. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.